Dynamic and asymmetric fluctuations in the microtubule wall captured by high-resolution cryoelectron microscopy

Significance

The dynamic behavior of microtubules, a tubular polymer, is essential for numerous processes throughout the cell. Cryoelectron microscopy (cryo-EM) has provided high-resolution snapshots of the microtubule during its GTP hydrolysis cycle, which regulates assembly and depolymerization. However, the dynamic structural properties of microtubules remain less well understood, due to limitations in cryo-EM analysis methods. Here we present a method to subdivide the microtubule wall into elemental components during cryo-EM refinement. This method substantially enhances the quality of 3D cryo-EM reconstructions, and reveals stochastic fluctuations in the geometry of the microtubule wall. Distinct microtubule subpopulations were identified that exhibit large and systematic deviations from helical symmetry, with potential implications for microtubule assembly/disassembly and other dynamic behaviors that remains incompletely understood.

Abstract

Microtubules are tubular polymers with essential roles in numerous cellular activities. Structures of microtubules have been captured at increasing resolution by cryo-EM. However, dynamic properties of the microtubule are key to its function, and this behavior has proved difficult to characterize at a structural level due to limitations in existing structure determination methods. We developed a high-resolution cryo-EM refinement method that divides an imaged microtubule into its constituent protofilaments, enabling deviations from helicity and other sources of heterogeneity to be quantified and corrected for at the single-subunit level. We demonstrate that this method improves the resolution of microtubule 3D reconstructions and substantially reduces anisotropic blurring artifacts, compared with methods that utilize helical symmetry averaging. Moreover, we identified an unexpected, discrete behavior of the m-loop, which mediates lateral interactions between neighboring protofilaments and acts as a flexible hinge between them. The hinge angle adopts preferred values corresponding to distinct conformations of the m-loop that are incompatible with helical symmetry. These hinge angles fluctuate in a stochastic manner, and perfectly cylindrical microtubule conformations are thus energetically and entropically penalized. The hinge angle can diverge further from helical symmetry at the microtubule seam, generating a subpopulation of highly distorted microtubules. However, the seam-distorted subpopulation disappears in the presence of Taxol, a microtubule stabilizing agent. These observations provide clues into the structural origins of microtubule flexibility and dynamics and highlight the role of structural polymorphism in defining microtubule behavior.

Microtubules are a critical component of many different cellular processes, including cell motility (1), division (2), and transport (3). These polymers consist of α/β-tubulin heterodimers that polymerize longitudinally in the presence of GTP to form protofilaments, and interact laterally to form microtubules (4). In general, lateral protofilament interactions are mediated by “B-lattice” type interactions, wherein neighboring protofilaments are in register (α-tubulin contacts α-tubulin, and β-tubulin contacts β-tubulin). However, microtubules also have one or more “seams” wherein “A-lattice” type interactions occur (α-tubulin interacts laterally with β-tubulin and vice versa), disrupting helical symmetry (5, 6). Microtubules can rapidly switch between phases of elongation and depolymerization, a property known as dynamic instability (7). Modulating microtubule stability is crucial for proper function of various cellular roles (8). Polymerization is favored upon GTP binding to tubulin, whereas hydrolysis of GTP within the microtubule destabilizes the lattice, encouraging depolymerization (9). Microtubule interactions with various binding proteins provide an additional layer of regulation for dynamic instability (10). The microtubule seam has been speculated to be a weak point in the microtubule structure, potentially serving as the origin of depolymerization (6, 11).

Structural studies have provided important insights into these processes. GTP-bound tubulin converts from a “bent” to a “straight” conformation when it incorporates into the microtubule lattice (12). Structural analysis of microtubules reveals that the helical lattice then twists and shortens upon GTP hydrolysis and/or phosphate release (11, 13, 14), although this behavior is not observed in yeast microtubules (15), nor is it consistently observed in mammalian microtubules (15, 16). These observations have been incorporated into a “lattice compaction” model, which proposes a key role for longitudinal interactions (i.e., between neighboring dimers within a protofilament) in controlling microtubule stability. Structural studies of microtubule binding agents have identified numerous allosteric binding sites associated with differing effects on microtubule stability and structure (11, 17–20). In particular, the binding of Taxol, a widely used chemotherapeutic agent (21), has been shown to straighten protofilaments (22), providing a potential mechanism for inhibiting depolymerization.

In addition to protofilament bending and compaction, lateral interactions between protofilaments are also implicated in microtubule stability and dynamics. Lateral protofilament interactions are mediated by the m-loop of one tubulin subunit and the H1′-S2 and H2-S3 loops of the adjacent subunit in a “lock and key” configuration (11, 23, 24). Formation of the lateral m-loop interaction is thought to facilitate the straightening of protofilaments during microtubule elongation (25, 26). The m-loop also acts as a flexible hinge, allowing microtubules to form structures with variable numbers of protofilaments, corresponding to different hinge angles (27). As a consequence of this flexibility, the m-loop could accommodate deformations that occur at microtubule ends during polymerization.

The observed m-loop flexibility suggests that microtubules may deviate from helical symmetry. Consistent with this prediction, recent structural studies indicate that neighboring protofilaments at the seam of a microtubule can rotate with respect to one another by ∼3° (11, 14, 20). These data led to the suggestion that the microtubule seam could be a structural weak point and could help initiate depolymerization. Other studies have presented three-dimensional (3D) reconstructions of microtubules that exhibited elliptical cross-sections, suggesting that microtubules may “squash” under certain conditions (20, 28). However, conclusions about the nature and origin of the observed lateral distortions in these studies were limited due to the extensive use of averaging during cryo-EM structure refinement.

Here we introduce a method that follows trajectories of individual protofilaments within a microtubule during cryo-EM structure refinement. By accounting for distortions in the microtubule lattice, this “protofilament refinement” method substantially improves the resolution of all analyzed samples. Moreover, quantification of microtubule distortions and further structural analysis reveals that microtubule shape is controlled by a characteristic behavior of the m-loop. Rather than acting as a free hinge, the m-loop switches between several discrete conformations that are inconsistent with helical symmetry, such that the microtubule forms irregular and highly variable cross-sections that are not detectable by conventional cryo-EM image processing techniques. These and other results presented in the current work emphasize the importance of dynamic microtubule behaviors that cannot be captured by a single static structure.

Results

Protofilament Refinement Increases the Resolution of Microtubule Reconstructions by Correcting for Lattice Distortions.

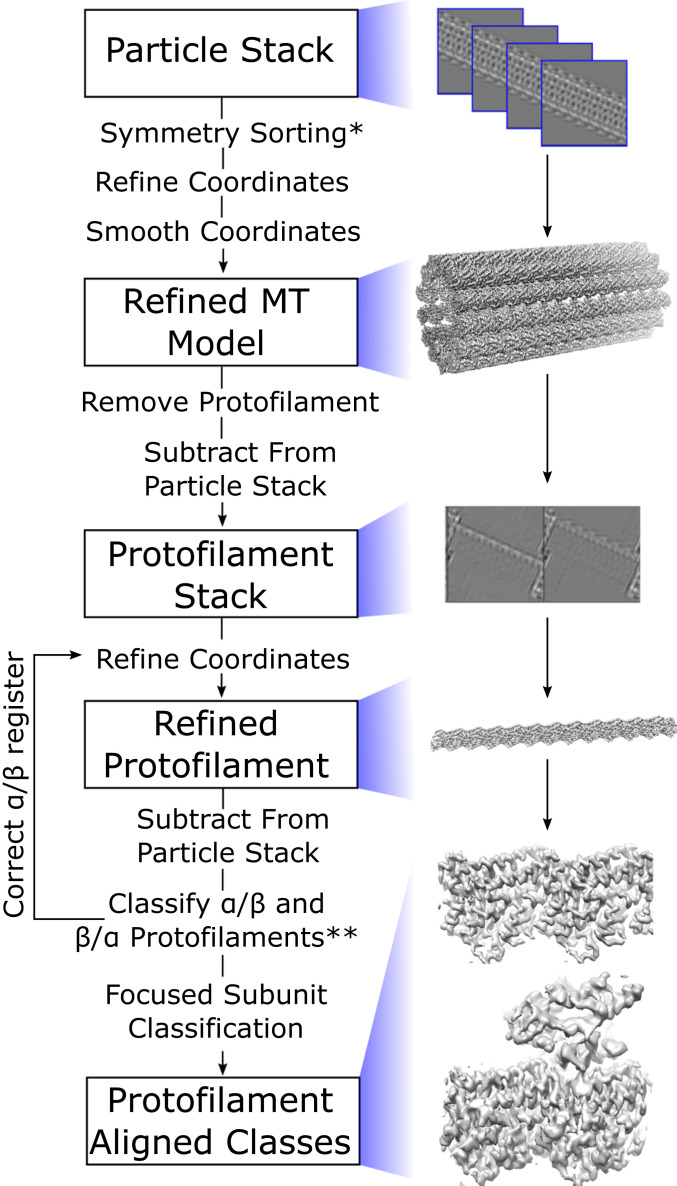
To overcome challenges associated with refining 3D structures from cryo-EM images of distorted microtubules, we developed a strategy to align individual protofilaments within the imaged microtubules (Fig. 1). First, previously established methods for microtubule symmetry sorting and helical processing are applied to microtubule image segments to obtain an initial 3D reconstruction of the intact microtubule. Using the initial microtubule volume, masked signal subtraction is then performed to erase all but a single protofilament in each microtubule segment. This process is repeated for each protofilament in a given microtubule segment, resulting in N times more segment images, where N corresponds to the number of protofilaments for a given microtubule symmetry type. The resulting “protofilament particles” are then further refined as single particles. This protofilament refinement method increases N-fold the number of degrees of freedom explored compared with the original microtubule refinement, thus enabling deviations from helical symmetry to be explicitly accounted for and corrected. Furthermore, this method can correctly account for multiseamed microtubules during the analysis, because α- and β-tubulin subunits are distinguished within individual protofilaments rather than entire microtubule segments (described below).

Fig. 1.

Protofilament refinement reconstruction workflow that allows for correction of lattice distortions and single subunit classification. Microtubule particles are first sorted based on their symmetry type and the coordinates are refined and smoothed to fit the expected helical geometry. A protofilament is removed from this model and used to subtract from the initial particle stack in order to generate a stack of protofilament particles. These protofilament particles are then refined. The protofilament coordinates are used for a second round of improved subtraction in order to generate a second stack of protofilament particles. These are then classified in order to determine the register of the ⍺- and β-tubulin. The protofilament coordinates are corrected in order to put all protofilaments in the correct register and the protofilament particles are refined again. Following the second refinement, potential protein binding sites are classified in order to reconstruct their density as well. *If microtubule is fully decorated with kinesin, the seam is determined at this step. **Once the seam(s) has been found, proceed to focused subunit classification.

The ability of the protofilament refinement method to account for distortions in the microtubule lattice was first tested using synthetic micrographs (SI Appendix, Fig. S1). The cross-section of synthetic microtubule models was randomly perturbed to vary the aspect ratio and produce squashed microtubules. These models were then projected using randomized Euler angles to produce a series of synthetic micrographs (SI Appendix, Extended Methods). Protofilament refinement of the resulting synthetic, distorted-microtubule images yielded a 3D map where all features, including side chains, were resolved to the Nyquist frequency (∼2.5-Å resolution). This volume is essentially indistinguishable from the 3D map obtained by refining a corresponding set of synthetic, undistorted-microtubule images. In contrast, conventional helical processing of the synthetic, distorted-microtubule images yielded 3D maps without visible side-chain densities and poorly resolved secondary structural elements. Additionally, the protofilament-refined Euler angles more closely resemble the behavior of the true projected Euler angles when compared with the helically refined coordinates. This result suggests that the protofilament refinement method is capable of accounting for the distortion in the microtubule lattice.

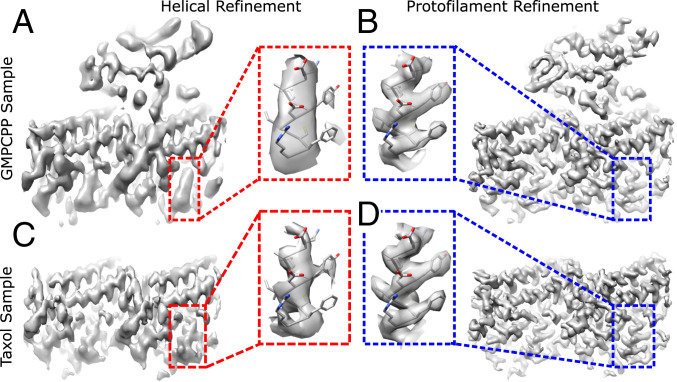
Application of protofilament refinement to experimentally imaged microtubules further demonstrated the ability of the method to better resolve high-resolution features. Two sample types with distinct compositions were analyzed: GMPCPP (guanylyl-(a,(3)-methylene-diphosphonate)-stabilized microtubules, fully decorated with monomeric kinesin motor domains, and a more heterogenous sample containing Taxol-stabilized microtubules sparsely decorated with dimeric kinesin motor domains. For the GMPCPP sample, helical refinement of 14-protofilament microtubules (the predominant symmetry type with this nucleotide analog) (18) yielded a map with an estimated resolution of 4.1 Å using ∼400,000 tubulin dimers (Fig. 2A). This resolution is substantially worse than was reported for several previous cryo-EM analyses of GMPCPP-microtubule structures that used similar numbers of particles (11, 14, 29), which may reflect intrinsic heterogeneity associated with the kinesin nucleotide state found in our sample (30). Moreover, anisotropic blurring is evident in many regions of the volume, particularly within the kinesin region where β-sheet strands are not resolved. Following protofilament refinement, map resolution is substantially improved (3.6 Å overall), anisotropic blurring is no longer evident, side chains are well resolved throughout most of the map, and the kinesin backbone is nearly entirely traceable (Fig. 2B and SI Appendix, Fig. S2 A and C).

Fig. 2.

Improved resolution of microtubule reconstructions following protofilament refinement. (A) Reconstruction of a representative tubulin dimer from a 14-protofilament, GMPCPP-stabilized microtubule, fully decorated with kinesin following helical refinement. (B) Corresponding reconstruction using protofilament refinement. (C) Reconstruction of a representative tubulin dimer from a 13-protofilament Taxol-stabilized microtubule following helical refinement. (D) Corresponding reconstruction using protofilament refinement. (Insets) The difference of map quality between the four reconstructions by comparing the density of a representative α-helix.

Applying protofilament refinement to the Taxol sample similarly resulted in pronounced gains in map quality. For 13-protofilament, Taxol microtubules (the more populated symmetry type with this stabilizing drug) (31), helical refinement yielded a map with an estimated resolution of 3.3 Å using ∼550,000 particles (Fig. 2C). Similar to the GMPCPP sample, the helically refined Taxol structure shows pronounced anisotropic blurring. Despite the improvement in estimated resolution relative to the helically refined GMPCPP map, the Taxol map is not significantly more detailed. Following protofilament refinement, the Taxol map resolution improved to 2.9 Å (Fig. 2D and SI Appendix, Fig. S2 B and D), anisotropic blurring is no longer evident, and side chains are clearly resolved throughout the map. While we attribute most of these gains to improved particle alignments, the protofilament refined map also benefitted from an increased number of particles compared with the helical refinement (∼850,000 vs. ∼550,000). This increase is due to the inclusion of multiseamed microtubules during protofilament refinement, made possible by the additional classification step described below. Because conventional helical processing cannot correctly align multiseamed microtubules, they were excluded from the helical refinement.

Focused 3D Classification Can Be Used to Identify and Reconstruct Different Subunit Types within the Microtubule Lattice.

Two important challenges for microtubule cryo-EM analysis are discriminating between α- and β-tubulin and reconstruction of cofactors with incomplete or mixed occupancies within the microtubule lattice. In principle, classification can handle these issues by discriminating between different structural states of an image segment. However, when there are many independent filament subunits per image segment (∼100 tubulin dimers per microtubule image segment) the corresponding number of classes becomes prohibitive (i.e., n¹⁰⁰ classes for n distinct states per tubulin dimer). We therefore adopted a focused classification strategy (32), wherein individual subregions of a filament are classified at a time (33). To apply this strategy to microtubule samples, we selected a region of interest within the microtubule structure, and signal outside this region was subtracted from the original particle images. The resulting particles were then subjected to 3D classification without alignment. To address the problems of 1) distinguishing α- vs. β-tubulin and 2) determining cofactor occupancy, two different regions of interest were defined: an envelope enclosing a single protofilament, and an envelope enclosing the kinesin binding locus, respectively.

We distinguished α- vs. β-tubulin in the Taxol dataset by using focused classification with the protofilament envelope. Prior to classification, inability to discriminate α- vs. β-tubulin leads to the possibility that a given protofilament will be offset from its correct position (referred to as “α/β-register”) by ∼40 Å (referred to as “β/α-register”). Classification was seeded with synthetic maps generated from α/β-register and β/α-register protofilament atomic models. The resulting class assignments clearly established the register of each protofilament in ∼60% of the microtubules. The remaining microtubules, for which the register of one or more protofilaments could not be unambiguously assigned due to “noise” in the class assignments, were excluded from further analysis. Coordinates of protofilaments that were classified to be in the β/α-register were shifted by ∼40 Å along the microtubule axis, thereby aligning all protofilaments to a common register.

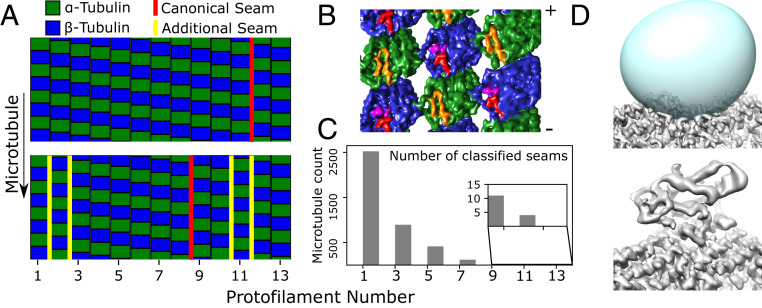
This α/β-tubulin classification procedure not only determined the seam orientations in imaged microtubules, but also identified a substantial population of multiseamed microtubules in the Taxol-stabilized sample (Fig. 3 A–C). Our method identified multiple seams in ∼36% of the processed 13-protofilament microtubules and ∼10% of the processed 12-protofilament microtubules. To validate this finding, microtubule particles containing two adjacent seams were used to generate a 3D reconstruction, which exhibited the expected protofilament register pattern (Fig. 3B). This multiseamed property of our Taxol-stabilized sample is evidently distinct from the GMPCPP sample, where only one additional seam was identified in a total of 270 analyzed microtubules (13-protofilament microtubules were selected in this case for a more direct comparison with the Taxol analysis). However, it is not currently possible to quantify the relative abundance of multiseamed microtubules in the two samples due to our inability to completely analyze the Taxol dataset. This difficulty reflects the challenges associated with differentiating α- from β- tubulin in cryo-EM micrographs, but lattice discontinuities—which appear to be common in taxane-stabilized microtubules (34)—could also contribute. Multiseamed microtubules have been previously observed in Taxol-stabilized microtubules (6, 35, 36), and may be a common feature of yeast microtubules, which are not stabilized by Taxol (15).

Fig. 3.

Classification of individual protofilaments/subunits identifies multiseam microtubules (A–C) as well as bound proteins (C). (A) Classification results for a single-seam microtubule (Top, marked in red), and a five-seam microtubule (Bottom). Two protofilaments in the five-seam microtubule are displaced by half the dimer repeat distance, generating four seams (yellow) in addition to the canonical seam (red). (B) Three-dimensional reconstruction of out-of-register protofilaments as in A; the map (viewed from the microtubule lumen) illustrates the two additional seams created. ⍺-Tubulin is colored green with the S9-S10 loop colored orange, while β-tubulin is blue with the S9-S10 loop in red and Taxol in purple. Note that this reconstruction was generated using helically refined coordinates to reduce the possibility of a spurious artifact resulting from, i.e., overfitting during protofilament refinement (SI Appendix, Fig. S3). (C) Quantification of the number of multiseam microtubules. Note that 1.5-start microtubules as seen here (corresponding to a 1.5-start helix of tubulin dimers with 8 nm axial repeat spacing, equivalent to a three-start helix of generic tubulin monomers with 4 nm axial repeat spacing) have an odd number of seams, due to geometric constraints (6, 36). (D) Classification of the kinesin binding site. The averaged microtubule structure (Top) shows a vacant kinesin binding site, due to low occupancy of the motor protein. The predicted kinesin binding location is defined by a mask (Top, in cyan), which is used to subtract away the remaining tubulin density from boxed microtubule segments. Classification of the resulting image stack identifies a bound state (Bottom), in addition to the unbound state that closely resembles the average structure.

Following protofilament register assignment, a second round of focused classification was used to identify bound kinesin sites within the Taxol sample. The kinesin envelope region of interest was then used to perform reference-free focused classification with n = 2 classes. Classification was initially restricted to a small random subset of our data (∼25,000 subunits), which consistently converged to two classes: 1) a bare tubulin class, and 2) a class exhibiting a bound kinesin motor domain (Fig. 3D). These two classes were then used to seed a classification of the entire dataset, resulting in a bare tubulin class with ∼730,000 particles and a kinesin class with ∼120,000 particles.

The Microtubule Wall Is Flexible and Exhibits Preferred Geometries.

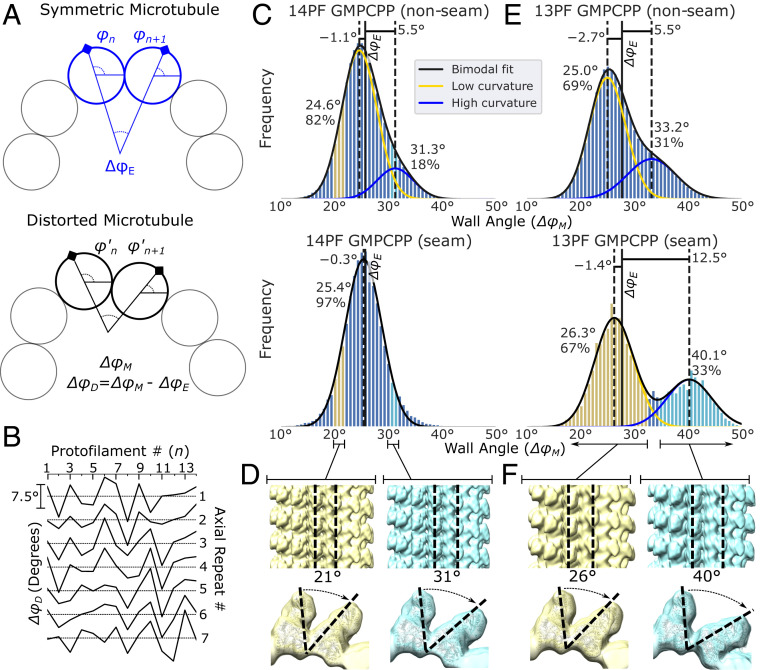
Analysis of the alignment parameters derived from protofilament refinement reveals that the microtubule wall distorts irregularly. Distortions were quantified by using the refined rotation angles of adjacent protofilaments (φ_n and φ_n+1) to calculate the angle between these protofilaments (Δφ_M). Comparing this value to a symmetric protofilament geometry (Δφ_E = 360/N, where N is the number of protofilaments) reveals the deviation from helical symmetry (Fig. 4A). Δφ_M, or “the wall angle,” was calculated for each adjacent protofilament pair in a microtubule cross-section, for every segment of an individual microtubule, and for every microtubule in the dataset. Analysis of the wall angle at laterally adjacent sites reveals a “crinkling” behavior, characterized by sharp and frequent transitions of Δφ_M above and below the symmetric Δφ_E value (Fig. 4B). This behavior contrasts with previous results indicating that microtubules can squash to form cross-sections similar to an ellipse (28). Whether this discrepancy is due to different sample conditions (i.e., different microtubule binding proteins) or the increased sensitivity of our method is not yet known.

Fig. 4.

Quantification of GMPCPP-microtubule geometries reveals that distortions are irregular, common, and can be bimodally distributed. (A) Illustration of the expected rotation difference between neighboring filaments in a symmetric microtubule (Top, Δφ_E) and in a distorted microtubule (Bottom, Δφ_M). The difference between the symmetric and measured rotational difference is the distortion (Δφ_D). (B) The estimated wall angle distortion (Δφ_D) as a function of the protofilament number n for a representative microtubule, plotted separately for each of seven consecutive axial repeats. Scale bar for the y axis (Δφ_D), identical for each graph, is shown on the Left. (C) Histogram of nonseam (Top) and seam (Bottom) wall angles for 14-protofilament GMPCPP-stabilized microtubules. (D) Particles corresponding to the highlighted wall angles in C were selectively reconstructed, yielding angles of 21° and 31° between the target protofilaments. See also SI Appendix, Fig. S3. (E) Histogram of nonseam (Top) and seam (Bottom) wall angles for 13-protofilament GMPCPP-stabilized microtubules. A double Gaussian curve was fit to all displayed distributions, except the 14-protofilament seam distribution, which was fit by a single Gaussian function. The mean and relative population of each Gaussian distribution is noted by the respective peak. The distance of each mean from the symmetric wall angle (Δφ_E, denoted by the solid black line) is also indicated above each peak. (F) The 13-protofilament seam particles corresponding to the low and high angular components of the distribution (highlighted in E in yellow and cyan) were separated and selectively reconstructed.

The above analysis also reveals that the microtubule wall is highly flexible. The wall angle for a given microtubule symmetry type spans beyond the range of curvatures required to form 11- to 16-protofilament microtubules that are typically observed in in vitro polymerization reactions. For the 14-protofilament GMPCPP dataset, the observed wall angles approximately follow a normal distribution (with a minor rightward shoulder, see Discussion) with significant populations seen from 18° to 33°, which correspond to Δφ_E values for 20- and 11-protofilament microtubules, respectively (Fig. 4C). The magnitude of these distortions far exceeds values previously reported in other microtubule structural studies, which do not exceed ∼4° (11, 14, 20, 28). To directly visualize the distorted wall structure, particles corresponding to wall angles of 20.7° ± 1° and 30.7° ± 1° (5° above and below the symmetric value) were selectively reconstructed. The measured angles between the reconstructed protofilaments (21.3° and 30.8°) are consistent with the selected wall angles. Moreover, comparison of the two maps reveals a hinge-like motion between protofilaments, with the axis of rotation centered at the lateral contact site (primarily the m-loop) (Fig. 4D and SI Appendix, Fig. S3).

Analysis of the 13-protofilament sample reveals that the majority of protofilament pairs maintain a similar wall geometry as observed in the 14-protofilament microtubule, as reflected by conserved peak positions in the respective wall angle distributions. However, because the average wall curvature of a 13-protofilament microtubule must increase to account for the loss of a protofilament, at least part of the microtubule wall must adopt higher curvature. This is accomplished in one of two ways. In the majority of microtubule segments, the seam adopts a 14-protofilament-like wall geometry (left peak in Fig. 4 E, Bottom and SI Appendix, Fig. S4). In this scenario, a minority population of more highly curved wall segments is observed in the nonseam protofilament pairs (right shoulder of Fig. 4 E, Top). Alternatively, in a minority of segments the seam distorts by ∼12.5° above the ideal helical symmetry to a wall angle of ∼40° (right peak, Fig. 4 E, Bottom). In this latter scenario, only a few additional protofilament pairs adopt the more highly curved wall geometry (SI Appendix, Fig. S5). These data suggest that tubulin in a GMPCPP microtubule prefers to adopt a less curved, 14-protofilament wall geometry, even in 13-protofilament microtubules.

Large Excursions from Helical Symmetry Can Occur at the Seam.

The above results describe a microtubule wall geometry that frequently deviates from helical symmetry (by 5° or more), with especially large deviations (>10°) occurring at the seam. In contrast, previous analyses of similarly prepared (kinesin-decorated) GMPCPP microtubules report a structure with symmetric wall angles for nonseam protofilaments (Δφ_M ∼ Δφ_E) and slightly increased wall curvature (∼3°) at the seam (11, 14, 20). While our microtubule refined model produces the same average structure, our analysis indicates this structure represents a conformation that is rarely sampled due to the preference to adopt nonsymmetric wall angles. Our results indicate that at the seam, the microtubule wall is most frequently less curved than the symmetric geometry, which is opposite the behavior of the average structure. Nevertheless, the average curvature at the seam is ∼3° greater than the symmetric value (as previously observed) due to the presence of a minority population with a greatly increased wall curvature. These results emphasize that the behavior of the microtubule wall may not be well represented by an average, and that the wall curvature is not necessarily a simple function of protofilament number.

A Shift toward the More Curved Wall Population in Taxol-Stabilized Microtubules.

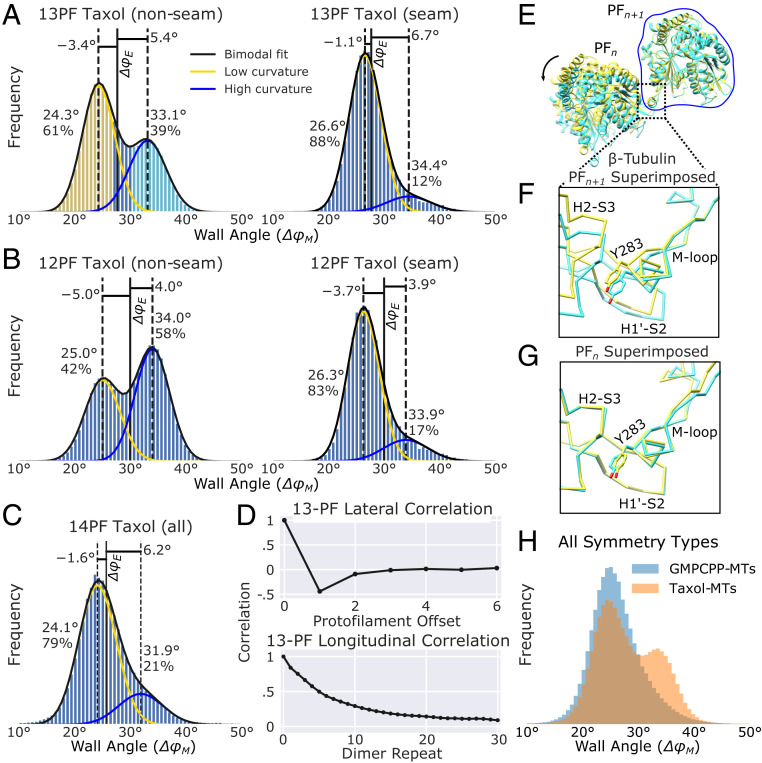
Similar to the GMPCPP sample, nonseam protofilament pairs in the Taxol sample exhibit two populations with distinct wall angles (Fig. 5 A–C); however, microtubules tend to adopt symmetry types with higher wall curvature (i.e., a higher percentage of 12- and 13-protofilament microtubules). In the GMPCPP sample 14-protofilament microtubules were favored over 13 by ∼3.6-fold, while this preference was reversed for the Taxol sample; which preferred 13-protofilament microtubules over 14-protofilament ones by ∼5.6-fold. Moreover, a substantial population of 12-protofilament microtubules was observed in the Taxol sample, while these were rare in the GMPCPP sample. Despite these differences, nonseam wall angle distributions were quite similar for a given symmetry type between the two sample types. For the Taxol sample, a large majority of protofilament pairs in 14-protofilament microtubules adopt the low curvature state (Fig. 5C), similar to what was observed with the GMPCPP sample (Fig. 4C). Also similar to the GMPCPP sample (Fig. 4E), the proportion of protofilament pairs in the high curvature state is larger in the 13-protofilament Taxol sample (Fig. 5A). Altogether, these data show that the highly curved wall conformation in the Taxol sample is more favored relative to the GMPCPP sample (Fig. 5H), which could explain why the average protofilament number is reduced in Taxol microtubules (31).

Fig. 5.

Distortion analysis of Taxol-stabilized microtubules reveals two conformations of the tubulin m-loop. (A–C) Distribution of wall angles for 13-, 12-, and 14-protofilament (PF) microtubules, respectively. All bimodal fits are labeled as in Fig. 4. (D, Top) Autocorrelation between Δφ_M values for lateral neighbors. The plots have been truncated at the point of symmetry, 6 protofilaments away from the initial protofilament. (D, Bottom) Longitudinal Δφ_M autocorrelation plot for 13-protofilament microtubules that are at least 31 subunits long. (E) Overlay of atomic models representing the high (cyan: 6WVM) and low (yellow: 6WVL) curvature states as defined by the colored bins in A. (F) Zoomed-in view of the lateral interaction site of β-tubulin subunits when the atomic models are aligned to protofilament n + 1. (G) Zoomed-in view of the lateral interaction site when the atomic models are aligned to protofilament n. Note the majority of the structural changes at the interaction site occur in the m-loop, whereas the H1′-S2 and H2-S3 loops remain nearly constant. The same behavior is observed for α-tubulin. (H) Distribution of wall angles for GMPCPP- and Taxol-stabilized microtubules across all symmetry types.

While the wall angle behaviors are largely consistent between the Taxol and GMPCPP samples, two differences are evident. First, for the nonseam case, bimodal peaks are more widely separated in Taxol microtubules compared with GMPCPP ones (8.8° vs. 8.2° respectively; compare Figs. 4E and 5A). Second, 13-protofilament Taxol microtubules lack the minority, high curvature population observed at the seam in the GMPCPP sample. These differences may be the result of interactions between Taxol and the β-tubulin m-loop (see Discussion). Furthermore, we note that while there are small differences in peak values between different symmetry and sample types, these differences are likely explained by changes in the local environment (e.g., additional forces due to supertwist).

Distinct, Nonseam Wall Geometries Are Associated with Different Tubulin M-Loop Conformations.

High-resolution 3D reconstructions of the microtubule wall at low and high curvatures reveals a hinge-like rotation centered at the α- and β-tubulin m-loops. The bimodal wall angle distribution observed in the nonseam 13-protofilament, Taxol sample, with clearly separated peaks, provided sufficient numbers of particles to reconstruct protofilament pairs in both low and high curvature states. Curve fitting the nonseam Δφ_M distribution to a double-Gaussian function, provided wall angle estimates for the low and high curvature states (24.3° and 33.1°, respectively: Fig. 5 A, Left). Reconstructions of particles centered around these values yielded ∼3.3-Å structures of both states. These maps were of sufficient resolution to generate atomic models representing both the low and high curvature states (Fig. 5E and SI Appendix, Fig. S6). Comparison of these two models reveals structural changes associated with the change in curvature are localized to the α- and β-tubulin m-loops of adjoining protofilament pairs (Fig. 5F). Correspondingly, there are minimal structural changes occurring in the H1′-S2 and H2-S3 loops of the neighboring protofilaments (Fig. 5G). These observations indicate that the m-loop functions as a flexible hinge (27), whose local rearrangements translate to large wall geometry shifts corresponding to the low and high curvature states.

Distortion analysis of microtubules of additional symmetry types indicate that the above features are general. Protofilament refinement resolved structures from 12- and 14-protofilament Taxol microtubules to high resolution (3.2 Å and 3.6 Å, respectively). For the 12-protofilament case, the wall angle distribution is bimodal, but with an increased population of the high curvature state (Fig. 5B), relative to 13-protofilament case. Gaussian curve fits also reveal that the low and high curvature wall geometries for the 12-protofilament microtubules (25.0° and 34.0°, respectively) are consistent with the 13-protofilament case. Moreover, 3D reconstructions of the low and high curvature states from the 12-protofilament Taxol sample exhibit hinge-like behavior of the m-loops that is consistent with the 13-protofilament results. For the 14-protofilament case, most protofilament pairs shift to the low curvature geometry, with a minority population in the high curvature state (Fig. 5C). Thus, the behavior of the 14-protofilament Taxol microtubules parallels that of the 14-protofilament GMPCPP microtubules. Overall, these data indicate that the m-loop has two favored conformations for nonseam protofilaments and changing the relative population of these conformations enables microtubules to accommodate varying number of protofilaments.

Distortions in the Microtubule Lattice Are Local.

We quantified the crinkling behavior observed in the microtubule wall (Fig. 4B) by autocorrelation analysis of neighboring wall angles. This analysis revealed that neighboring wall angles are highly anticorrelated, while correlation is weak for more distant protofilament pairs (Fig. 5 D, Top). These properties define a simple behavior in which two protofilaments counterrotate against each other, while the remainder of the microtubule structure remains mostly unchanged (Fig. 6 A–C). In this way, variation of the central wall angle is accompanied by smaller changes, of opposite sign, in the two neighboring wall angles. This behavior was observed in all symmetry types, across both sample conditions. These data illustrate an irregular microtubule wall geometry that is defined by highly local lateral deformations resulting from preferred m-loop conformations that deviate from perfect symmetry.

Fig. 6.

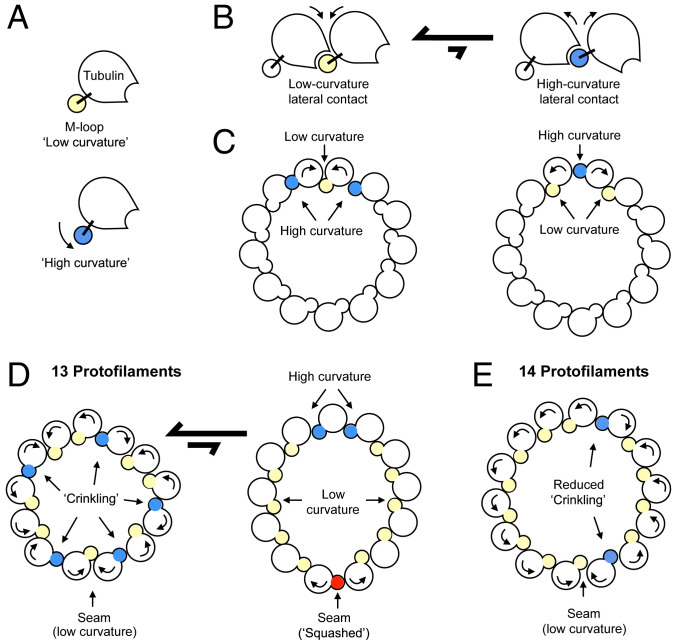
Model of microtubule wall dynamics. (A) Schematic of tubulin, depicting the two m-loop conformations (low curvature and high curvature) identified at nonseam lateral protofilament contacts, which differ by a rotation of ∼8 to 9°. (B) Schematic depicting the two types of lateral contacts formed by the tubulin conformations in A. Our data indicate that the low curvature lateral contact is energetically preferred for the GMPCPP-microtubule sample. (C) Model for anticorrelation of neighboring protofilament hinge angles. Rolling the top two protofilaments toward each other decreases the hinge angle between them (yellow), while increasing the hinge angles (blue) with the next nearest neighbors. This motion can occur with minimal disturbance to the position and orientation of the remaining protofilaments (uncolored). (C) Conversely, rolling the same 2 protofilaments away from each other increases the central hinge angle (blue) and decreases the angles with the next nearest neighbors (yellow). Thus, changes in the central hinge angle are anticorrelated with those of the two adjacent hinge angles, and other hinge angles are minimally affected. (D) Model of microtubule wall dynamics for a 13-protofilament microtubule. Microtubules are in equilibrium between two states. In the first, majority-populated state, the seam adopts a low curvature wall angle, and superposition of many elemental distortions as depicted in C at the remaining lateral contact sites gives rise to a stochastic distribution of hinge geometries (crinkling). In the second, squashed state (∼33% of the 13-protofilament GMPCPP-microtubule population), buckling occurs at the seam. The hinge angle for the buckled seam conformation is ∼7° greater than observed at the “high curvature” contact. To accommodate this larger deformation at the seam, the microtubule deforms to an elliptical profile with an increased tendency to form the high angle hinge conformation at the opposite side of the microtubule wall, and mainly low angle hinge conformations at other lateral contact sites. (E) For 14-protofilament microtubules, crinkling is reduced due to the need for fewer high curvature hinge angles, resulting in a somewhat more homogeneous wall geometry. An increased percentage of more-favorable low curvature contacts found in 14-protofilament microtubules, compared with 13-protofilament microtubules, likely penalizes the formation of a “buckled” seam—explaining why it is not observed in 14-protofilament microtubules from the GMPCPP sample.

In contrast to the highly local lateral behavior, microtubule wall deformations tend to persist longitudinally along protofilaments for many subunits (Fig. 5 D, Bottom). Correlation analysis of wall angles along single protofilaments reveal consistently positive correlation that decays monotonically, but remains positive to a separation of at least 30 subunits. This result suggests that the mechanical coupling between neighboring subunits along a protofilament is strong, consistent with the extensive interface between longitudinally neighboring tubulin subunits.

Discussion

Previous studies have described bending, flexing, and distortions in microtubules, but this behavior has remained incompletely characterized. Moreover, it has remained unclear how these types of distortions are related to the underlying ultrastructural properties of tubulin and its cofactors. Here, by introducing a cryo-EM image processing methodology, we have demonstrated that microtubules make significant, stochastic excursions from helical symmetry. We have further linked this behavior to specific structural properties of the m-loop that mediate lateral protofilament interactions, as summarized in Fig. 6.

Microtubule wall deformations observed here appear to be governed by a bistable hinge movement that defines two possible lateral contact geometries between protofilaments (Fig. 6 A and B). In our GMPCPP-microtubule sample, representative of GTP microtubules (37), the low curvature lateral contact type predominates over the high curvature type (Fig. 5H). The low curvature geometry, however, is not well matched to a symmetric 13-protofilament wall geometry, and thus lateral contacts in 13-protofilament microtubules are a mixture of low and high curvature types. Moreover, because the two lateral contact types frequently alternate with each other at consecutive, adjacent sites (Figs. 6C and 5D), the microtubule wall crinkles (Fig. 6 D, Left).

The strong preference for the low curvature lateral geometry in the GMPCPP sample may also contribute to the presence of a secondary population of 13-protofilament microtubules where the seam buckles by an additional 7° compared with the high curvature state (Fig. 6 D, Right). This squashed microtubule shape allows the majority of lateral contacts to adopt the low curvature state (SI Appendix, Fig. S5), albeit at the expense of more severe, but localized, high curvature deformations. Notably, all of these deviations from helical symmetry in our GMPCPP sample are significantly attenuated in the 14-protofilament subpopulation (Fig. 6E), where the squashed conformation was not even detectable (Fig. 4C). The above behavior is readily explained by the propensity of the m-loop to remain in a low curvature conformation—which nearly (although not precisely) matches the symmetric geometry for a 14-protofilament microtubule.

Our results provide a structural rationale for how the inherent behavior of tubulin leads to preferences for certain microtubule symmetry types. Similar to results shown here for our GMPCPP sample, cryo-EM microtubule studies utilizing several nucleotide states, with or without decorating kinesin molecules (as were present in our samples), indicate a strong and universal preference for the 14-protofilament symmetry type over 13-protofilament or other types (at least in the absence of other cofactors; see below). However, microtubule symmetry can be influenced by a variety of factors, including stabilizing drugs and protein cofactors (18, 29, 31, 35, 38). Here we have shown that within microtubules, the wall adopts preferred geometries corresponding to distinct conformations of the m-loop that laterally connect adjacent protofilaments. While none of these geometries perfectly matches any given microtubule symmetry type, they serve as building blocks that can be mixed and matched to generate microtubules with a variety of different symmetry types. Therefore, stabilizing (or destabilizing) one of these wall geometries provides a mechanism for changing the symmetry type.

Our data indicate that Taxol microtubules adopt this mechanism because, while preferred wall geometries are consistent between Taxol and GMPCPP microtubule samples, the higher curvature state is more populated in the Taxol sample (Fig. 5H). This result explains why Taxol reduces the number of protofilaments compared with drug-free microtubules (31). A probable explanation for this behavior is that direct or indirect interactions between Taxol and the β-tubulin m-loop selectively stabilize its high curvature conformation (SI Appendix, Fig. S8). Interestingly, however, Taxol does not have this effect at the seam, where the strong preference for the low curvature state observed in the GMPCPP sample (Fig. 4 C and E) is maintained (Fig. 5 A and B). Moreover, Taxol appears to inhibit the larger wall deformations that can occur at the seam of 13-protofilament, GMPCPP microtubules (Figs. 4 E and F and 6F), perhaps by conformationally restricting the β-tubulin m-loop (39) (SI Appendix, Fig. S8C). Regardless of the mechanism, our data indicate that the microtubule seam can make large excursions from helical symmetry, but these are blocked by Taxol. If depolymerization originates at the seam as previously hypothesized (6, 11), then Taxol could stabilize microtubules by constraining the β-tubulin m-loop from buckling at the seam.

Because Taxol microtubules favor the 12- and 13-protofilament forms (38), whose wall shapes are more irregular, these microtubules deviate more from helical symmetry than GMPCPP microtubules, where the 14-protofilament type is more favored. Wall irregularity in the Taxol sample is further amplified due to a larger difference between wall angles of the low and high curvature states compared with the GMPCPP sample (Figs. 4E and 5A). It is noteworthy that averaging these two discrete states together in a 3D reconstruction is not expected to accurately depict either state. The above observations provide an explanation for why 3D reconstructions of Taxol microtubules exhibit higher anisotropy and lower resolution compared with other sample types (20).

Our 3D maps have captured structural states corresponding to the high- and low-angle wall conformations at high resolution. However, the precise structural origin of the discrete behavior remains unclear, including whether it is dictated by stereospecific interactions within the m-loops of either α-tubulin and/or β-tubulin, or perhaps elsewhere in the structure. Comparison of structural models built into the two maps suggests that a change in hydrogen-bonding patterns within one or both loops may accompany the hinge rotation, but the resolution of the maps (∼3.3 Å) remains too low to confirm this idea. The structural basis of the distinct wall behavior observed at the seam, where the lateral interaction environments of α-tubulin and β-tubulin are swapped, likewise remains unclear. It also needs to be noted that additional wall geometries clearly must exist to account for tubulin architectures observed at microtubule ends and in flattened tubulin sheets (40–42). Further studies will be required to elaborate these aspects of microtubule dynamical behavior.

The microtubule wall behavior observed here is likely to extend beyond the sample conditions examined in the current work. In the absence of drugs or stabilizing protein cofactors, microtubules preferentially adopt the 14-protofilament symmetry type (43) consistent with the wall behavior observed in our GMPCPP sample. In contrast, microtubules in vivo tend to adopt the 13-protofilament form (44, 45), assisted by cofactors that, for example, bind between protofilaments to modify the wall geometry [e.g., EB3 (14) and doublecortin (18)]. Our results indicate that such cofactors could operate by increasing the relative stability of the high curvature state. Alternatively, they could operate by shifting the most probable wall geometry to match 13-protofilament symmetry. The methods described in this paper provide a route to better defining this behavior.

While it has long been known that microtubules diverge from symmetry at the seam, our results clearly demonstrate that the microtubule wall systematically deviates from helical symmetry, not just at the seam, but throughout its cross-section. As we have shown, averaging of such behavior is not necessarily representative of the underlying structures (Fig. 4 E and F). Microtubule reconstruction strategies that rely on averaging full microtubule segments are thus unable to capture the inherently irregular behavior of the microtubule wall. Moreover, asymmetric fluctuations of the type described here remain too subtle to readily visualize by cryoelectron tomography (SI Appendix, Fig. S9), likely due to limitations of the latter method, including reduced signal-to-noise and missing wedge artifacts; although with improved methodologies (46) and updated instrumentation, it may be possible. By characterizing and accounting for this behavior, methods like those described here are poised to improve our understanding of microtubules and their associated proteins.

Materials and Methods

Sample preparation and microtubule refinement were performed as previously described (30, 47). However, high-resolution microtubule refinement was performed in RELION (48) rather than FREALIGN (49), and Taxol microtubules were sorted into symmetry types using RELION 3D Classification, similar to recently described methods (50). Protofilament refinement was performed by subtracting a microtubule model missing a protofilament from experimental images and aligned using RELION. Analysis of microtubule distortions was performed in Python using custom scripts to read and manipulate the alignment data from RELION. For a more detailed description of the refinement and analytical methods as well as sample preparation and imaging conditions, see SI Appendix, Extended Methods.