Individual differences determine the strength of ecological interactions

Significance

Demonstrating asymmetric competition in natural systems is difficult, as the effect of large individuals on small ones has to be measured, and vice versa. Numerous experiments have quantified one side of the interaction, typically the effect of large individuals on small ones. Here, we demonstrate, using a long-term study of guppies, that an individual’s performance depends on its relative size, with large individuals being competitively dominant. Accurate prediction of both the mean and variance in body size was possible by using models incorporating asymmetric competition, whereas in models where individuals are competitively equivalent, the predictions were poor.

Abstract

Biotic interactions are central to both ecological and evolutionary dynamics. In the vast majority of empirical studies, the strength of intraspecific interactions is estimated by using simple measures of population size. Biologists have long known that these are crude metrics, with experiments and theory suggesting that interactions between individuals should depend on traits, such as body size. Despite this, it has been difficult to estimate the impact of traits on competitive ability from ecological field data, and this explains why the strength of biotic interactions has empirically been treated in a simplistic manner. Using long-term observational data from four different populations, we show that large Trinidadian guppies impose a significantly larger competitive pressure on conspecifics than individuals that are smaller; in other words, competition is asymmetric. When we incorporate this asymmetry into integral projection models, the predicted size structure is much closer to what we see in the field compared with models where competition is independent of body size. This difference in size structure translates into a twofold difference in reproductive output. This demonstrates how the nature of ecological interactions drives the size structure, which, in turn, will have important implications for both the ecological and evolutionary dynamics.

Interactions between the individuals in a population, such as competition, cooperation, and cannibalism, have been shown to play a central role in governing both ecological and evolutionary dynamics. Over the past 150 years, the strength and impacts of these biotic interactions have often been assessed by determining how an individual’s performance relates to the density of competitors (1–3). This density dependence is a fundamental principle in ecology and determines the struggle for existence that drives evolution (4). However, simple metrics, such as population density, entirely ignore differences between individuals in traits such as body size, weight, and condition, although numerous experimental studies and theory clearly indicate that the strength of interaction between individuals should depend on their traits (5–8).

Individual traits often influence physiology and behavior. Body size, in particular, frequently influences feeding rates and the ability to preempt access to territories, mates, or resources (9, 10). This size-dependent ability to acquire resources leads to the expectation that competition will be size-asymmetric (11), with interference competition leading to a competitive advantage for larger individuals. In contrast, for resource competition, competitive ability depends on the scaling of energy and maintenance costs, which, in fish, can lead to smaller individuals being dominant (5). This means that competitive ability should depend not only on an individual’s absolute size, but also on the relative size of its competitors. In contrast, the simplistic metrics underpinning our classical understanding of intraspecific biotic interactions assume that all individuals acquire resources at an equal rate. This implies that competition is symmetric, and so differently sized individuals are competitively equivalent.

Demonstrating asymmetric competition in natural systems is difficult, as the effect of large individuals on small ones has to be measured, and vice versa. Very few studies do this, and in those that do, the results are often difficult to interpret. For example, ref. 12 found that removal of large or small individuals had no effect on growth of intermediate-sized fish. In contrast, adding large fish resulted in slower growth of intermediate-sized ones, whereas adding small fish had no effect, suggesting that asymmetric competition only occurs at artificially high densities. Experimental manipulations usually treat body size as discrete rather than continuous, where interactions occur over the complete size range. These difficulties argue for the development of a new approach that can estimate size-specific competitive effects across the complete size spectrum at natural population densities.

As a consequence of these difficulties, little is known about where, in nature, the asymmetry of competition lies on the continuum between the extreme competitive dominance of either large or small individuals and competitive equivalence (13). This is problematic, as a large body of theory has demonstrated the importance of asymmetric competition for life-history evolution (14–16) and population and community dynamics (13, 17–19). We provide a quantification of the degree of size-asymmetric competition in wild animal populations. Using detailed individual-based life history data from four long-term field-study populations of the Trinidadian guppy (Poecilia reticulata), we quantify how the strength of competition influencing growth and survival rates depends on the size structure of competitors relative to the size of the focal individual. We then examine how quantifying trait-dependent competitive interactions alters our ability to project the size-structured dynamics in these populations.

Methods

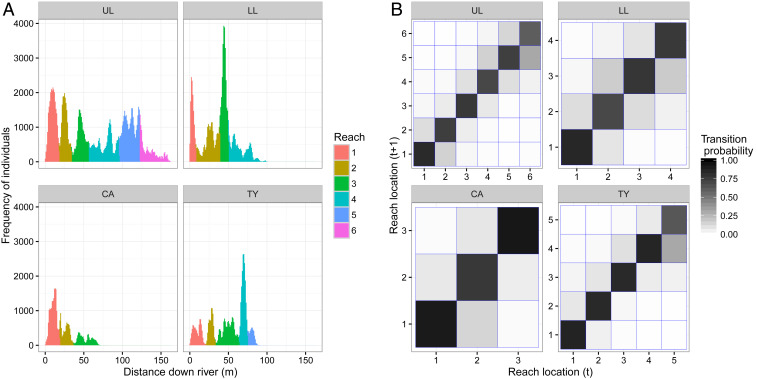
The study populations are located in four independent predator-free tributaries of montane streams in the Northern Range of Trinidad (SI Appendix, section S1a) (20). Monitoring of individual body weight and location was conducted under a University of California, Riverside Institutional Animal Care and Use Committee approved Animal Use Protocol (A20170006). Habitat quality varies along and among the four streams (21). Two streams (Upper Lalaja [UL] and Taylor [TY]) have received experimentally enhanced primary productivity, attained via canopy thinning. The remaining two streams (Lower Lalaja [LL] and Caigual [CA]) are neighboring control streams with intact canopies. Although flooding events sometimes restructure the detailed stream topologies, certain sections of the streams consistently harbored much higher numbers of individuals (Fig. 1A). Each stream’s population was partitioned into between three and six discrete spatial subpopulations (reaches), by using a clustering algorithm (Fig. 1A, colored regions) (SI Appendix, section S1c). Individual observations were classified as occurring within a specific reach of the stream with a high degree of certainty (average classification certainty $>$ 95%). Individuals rarely moved to a different reach between sampling occasions (Fig. 1B), indicating that the reaches represent spatially distinct habitat patches within which individuals compete.

Fig. 1.

Identification of discrete reaches of the four Trinidadian streams (panels of each subplot). (A) The frequency of individual observations at different distances along the streams (bar height). Reaches are spatial subpopulations, identified by applying a clustering algorithm to the locations of observations. Individual observations were categorized into a specific reach (bar color). (B) The frequency at which individuals transition between reaches in the time between sampling occasions. The diagonal elements of this transition matrix represent individuals remaining in the same reach. Dark coloration indicates a high transition probability.

We determined the degree of size-asymmetric competition influencing monthly growth and survival by fitting hierarchical, nonlinear additive models to the life-history datasets for each stream (SI Appendix, section S1d). Demographic rates are known to depend on an individual’s weight and sex, independent of the impacts of biotic interactions (22). Individuals inhabit a variable environment, and stochastic perturbations, especially flooding events, drive density-independent variation in survival and growth over time and space (23). Similarly, the seasonal Trinidadian climate drives variability in resource availability (24), altering the intensity of competition. Month-specific deviations in mean demographic rates and the intensity of competition were included to account for these processes. Individual-specific effects were also added to describe interindividual differences in quality. The resulting growth and survival models shared the same structure:

$$\begin{array}{c}\hfill g\left(E\left[Y\right]\right)={\beta }_{sex\left[i\right]}^{\left(0\right)}+{\beta }_{sex\left[i\right]}^{\left(1\right)}{Z}_{irt}+{\beta }_{sex\left[i\right]}^{\left(2\right)}{Z}_{irt}^2+u_i^{\left(1\right)}+u_{rt}^{\left(2\right)}+\frac{\left({\gamma }_r+u_{rt}^{\left(3\right)}\right)}{L_r}N\left(X_{irt},{\overrightarrow{X}}_{rt}\right),\end{array}$$ [1]

where $E\left[Y\right]$ is either the expected size at the next sampling occasion or the probability of survival over the transition, and $g$ is the identity or logit link function, respectively. $X$ and $Z$ refer to body weight on the original and log-transformed scales, respectively. Terms could vary by individual ($i$), reach ($r$), or sampling occasion ($t$), as defined in Eq. 1. We drop the $r$ and $t$ subscripts in the following summary of the model to simplify its presentation (a more complete description is given in SI Appendix, section S1d). Differences in growth and survival between the sexes were incorporated by including sex-specific intercepts and linear-size and quadratic-size slopes (the $\beta$ terms). The intercepts were allowed to vary among individuals and between sampling occasions by including normally distributed random-effect terms, $u^{\left(1\right)}$ and $u^{\left(2\right)}$, respectively.

To model asymmetric competition, the density of competing individuals of different sizes ($\overrightarrow{X}$) must be translated into an “equivalent density” of individuals with body weight equal to that of the focal individual ($X_i$), denoted by $N\left(X_i,\overrightarrow{X}\right)$. The impact of this equivalent density was then scaled by a fixed effect ($\gamma$), a time-varying random-effect term ($u^{\left(3\right)}$), and the length of a reach ($L$). The equivalent density of competitors was calculated as:

$$N\left(X_i,\overrightarrow{X}\right)=\sum _{j=1}^n\alpha \left(X_i,X_j\right),$$ [2]

where the strength of interaction between two individuals, $\alpha \left(X_i,X_j\right)$, depended on the body weight (natural scale) of the focal individual ($X_i$) relative to the competitor’s weight ($X_j$). This trait dependence was captured by using the functional form $\alpha \left(X_i,X_j\right)={\left(X_j/X_i\right)}^{\varphi }$. The degree of competitive asymmetry between differently sized individuals is determined by the value of the parameter $\varphi$. When $\varphi =0$, competition is symmetric, and the model reverts to classical density dependence based on total population size. Nonzero values of $\varphi$ indicate size-asymmetric competition. Positive values signify the competitive dominance of large individuals, while negative values indicate that smaller individuals are competitively superior. The total impact of competition on an individual’s growth or survival was calculated by summing the interaction strengths, $\alpha \left(X_i,X_j\right)$, of all individuals in the reach. Consequently, under size-asymmetric competition ($\varphi \ne 0$), the total interaction strength will vary depending on the focal individual’s size and the size distribution of its competitors. In the growth analysis, we analyzed body weight (log-transformed) rather than length, as individuals at their asymptotic length can lose or gain weight in response to competition and the environment. Individual-recapture and size-measurement rates are very high in this study system (over 90%). On occasions when individuals were not recaptured, body size was imputed based on weight at prior and subsequent times (SI Appendix, section S1b).

Results and Discussion

Observed patterns of growth and survival rates in both males and females were accurately described by the fitted demographic models, including size-asymmetric competition (Fig. 2). The sex and size dependence of both demographic rates were highly consistent between stream populations. The growth rate of both sexes decreased nonlinearly with body weight. Males and females had similar growth rates at small sizes, but the growth rate of males decreased more rapidly. This caused males to reach a maximum weight of around half the maximum for females. Survival probability also varied with both sex and body weight. Female survival increased with weight initially; however, survival probability declined again in the largest individuals. Small males had a comparable survival to females; however, survival rates decreased with weight. As a result, males had a lower survival probability than females.

Fig. 2.

Observed and predicted growth (A) and survival (B) rates for females and males in the four stream populations. Demographic rates are plotted as a function of individual body weight (log-transformed). Observations are shown as points, and model expectations are indicated by lines. A growth rate of zero is indicated by a horizontal dashed line to identify the weight on the x axis at which no further increases are expected.

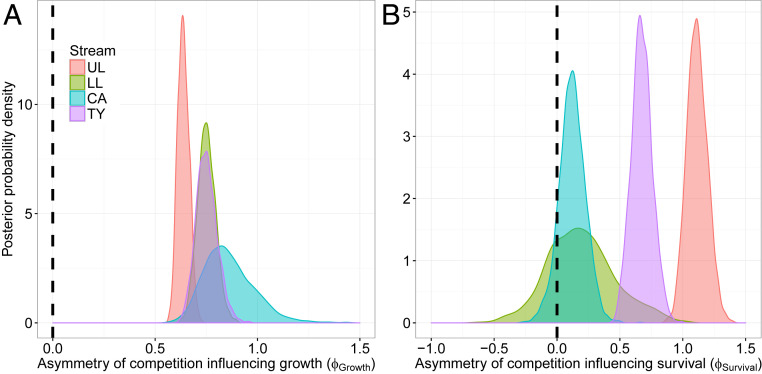
Growth rates were influenced by size-asymmetric competitive interactions, with larger individuals being competitively dominant and disproportionately suppressing the growth of smaller individuals (${\varphi }_{Growth}>0$; Fig. 3A). The degree of size-asymmetric competition influencing growth (${\varphi }_{Growth}$) was between 0.55 and 1. This is a substantial asymmetry, implying that, despite considerable fluctuations in the environment, the largest individuals frequently experienced almost no effect of competition from their smallest competitors (Fig. 4). Conversely, the small guppies experienced a disproportionately large competitive effect from the large ones, and the intensity of competition was more variable over time. This competitive asymmetry is not a consequence of the response of large individuals being constrained because they are close to their asymptotic size, as Fig. 2A clearly shows that large individuals have highly variable growth rates and can often lose up to 40% of their body weight in a month. This degree of asymmetric competition is consistent with dynamic energy budget theories, where resource consumption scales with an individual’s surface area–volume ratio, leading to the assumption that resource preemption should follow a $2/3$ power scaling with weight (10).

Fig. 3.

The estimated degree of size asymmetric competition influencing growth (A) and survival (B). The posterior densities for the asymmetry of competition parameters (${\varphi }_{Growth}$ and ${\varphi }_{Survival}$) are shown for each of the four streams. Distributions not overlapping zero indicate that there is significant size asymmetry between competitors. Positive values indicate a competitive dominance of large individuals, and negative values imply a superiority of smaller individuals.

Fig. 4.

The estimated equivalent density of competitors experienced by female (Left) and male (Right) individuals in the four stream populations. Equivalent density measures the effective density an individual experiences ($\sum \alpha \left(X_i,X_j\right)$). On average, across years, the expected relationship between an individual’s body weight and the equivalent density of competitors it experiences is shown by the solid line. The variation in this relationship over time is shown by the shaded regions in each panel. These signify the 25th to 75th quantiles (dark shaded area) and the 5th to 95th percentiles (light shaded region) of the competition experienced by individuals. Horizontal lines show the overall mean (black dotted) and sex-specific average (colored dashed) equivalent density of competitors experienced in each stream.

Survival probability was also influenced by size-asymmetric competition in the streams with experimentally increased productivity (UL and TY; Fig. 3). Larger competitively dominant individuals disproportionately reduced the survival probability of smaller individuals (${\varphi }_{Survival}>0$; Fig. 3B). In the two lower-productivity streams, the effects of competitive interactions on survival were approximately symmetric (${\varphi }_{Survival}\simeq 0$). That is, the size composition of competitors did not greatly influence individual survival. The frequent environmental perturbations, especially flooding events (23, 24), may overwhelm or mask the impacts of asymmetric interactions in these streams, as population densities are lower. In contrast, in high-productivity streams, competitor densities reached considerably higher peak levels (21), and so survival rates remained coupled with population size structure. The occurrence of size-asymmetric impacts of competition on growth, but not survival, suggests that growth rates are more sensitive to competition. This heightened sensitivity is expected if resources are redirected away from growth toward buffering survival (25).

Finally, we explored how asymmetric competitive interactions alter our ability to project population-size distributions through time. Integral projection models (IPMs) (26) were used to link the processes of individual growth and survival and project body-weight distributions from one sampling occasion to the next (SI Appendix, section S1e). First, a set of simplified demographic models were fitted, in which competition was constrained to be symmetric ($\varphi =0$). By constructing IPMs using demographic models containing either symmetric or size-asymmetric competition, we obtained two distributions of predicted body weights, which were compared with observed body-weight distributions.

The IPM incorporating size-asymmetric competition greatly outperformed the model with simple symmetric competition. Accurate prediction of body-weight distributions could be made for both males and females across the streams (Fig. 5A). This was despite the spatial variation in habitat quality along streams and the frequent and largely random impacts of environmental perturbations, such as flooding events. In contrast, when competition was assumed to be symmetric, predicted body-weight distributions were highly inaccurate, with the projected mean and variance of body weights often being much smaller than observed. Examination of the separate survival and growth components revealed that the growth process was poorly captured when competition was assumed to be symmetric. When population density was high, simple density-dependent models predicted that all but the smallest individuals would lose a biologically unrealistic proportion of body weight. The asymmetry of competition means that large individuals do not lose much weight under these conditions, which increases their survival and shifts the body-weight distributions toward higher values. We cannot quantify reproduction in the natural populations, but in mesocosms, larger females have a higher probability of reproducing, and reproductive output does not scale isometrically with body weight, so shifts in size structure change the total reproductive output of the population. Using the mesocosm data, we found that the predicted reproductive output was over two times larger when we compared asymmetric with symmetric competition (SI Appendix, section S1e).

Fig. 5.

Relationships between the observed and predicted mean and variance in body-weight distributions after each sampling transition. Predictions are made by using an IPM with either size-asymmetric competition or symmetric competition. Predictions for females and males are made separately by using sex-specific IPMs. Points are colored according to the stream. The dashed diagonal line indicates the 1:1 correspondence between observations and predictions.

Guppies also exhibit size-dependent microhabitat use (27) and a degree of ontogenetic niche differentiation (28). These behaviors will reduce the degree of competition between individuals of different sizes (29). Despite this, we have demonstrated that guppy demography is strongly influenced by size-asymmetric competition. Competition is likely to be even more asymmetric in species exhibiting size-based competitive hierarchies, such as rutting ungulates, marine mammals, territorial birds, and a wide array of fish species. Size-asymmetric competition is also expected to influence reproductive demography, affecting both the number and quality of offspring produced. In terms of selection when the genetic influences on an individual’s phenotype arise from both its genotype and the genotypes of its competitors, there are indirect genetic effects (30), which have important implications for trait evolution (31, 32). As an individual’s body weight determines competitive ability and this, in turn, is influenced by many other traits, this suggests that indirect genetic effects may be widespread. From an evolutionary perspective, these results imply that fitness will be frequency-dependent, resulting in potentially complex evolutionary dynamics (14–16).

The size-structured models of competition developed here can be used to assess the role of asymmetric competition on all components of a life history. This will allow an understanding of how phenotypic variability drives both population dynamics and evolution. Biotic interactions undoubtedly play a central role in ecological and evolutionary dynamics. Our findings underline the importance of determining the trait dependence of these interactions and the need to move away from crude metrics of density dependence. The classical approach, involving simple metrics of density, is insufficient to capture the strength of interactions between individuals, and, hence, a reevaluation of the role of biotic interactions in both ecological and evolutionary processes may now be required.

Data Availability.

Demographic data have been deposited in the publicly accessible Dryad Digital Repository (20).