Modeling the competitive diffusions of rumor and knowledge and the impacts on epidemic spreading

Highlights

• •The impacts of knowledge diffusion on rumor and epidemic are studied in a two-layer network.
• •The competitive diffusions of rumor and knowledge are modeled on the communication layer.
• •The outbreak threshold of rumor increases linearly with the penetration intensity of knowledge.
• •The outbreak threshold of epidemic increases concavely with the penetration intensity of knowledge.
• •Rumor and epidemic can be stopped more efficiently by knowledge when people have more connections in the communication layer.

Abstract

The interaction between epidemic spreading and information diffusion is an interdisciplinary research problem. During an epidemic, people tend to take self-protective measures to reduce the infection risk. However, with the diffusion of rumor, people may be difficult to make an appropriate choice. How to reduce the negative impact of rumor and to control epidemic has become a critical issue in the social network. Elaborate mathematical model is instructive to understand such complex dynamics. In this paper, we develop a two-layer network to model the interaction between the spread of epidemic and the competitive diffusions of information. The results show that knowledge diffusion can eradicate both rumor and epidemic, where the penetration intensity of knowledge into rumor plays a vital role. Specifically, the penetration intensity of knowledge significantly increases the thresholds for rumor and epidemic to break out, even when the self-protective measure is not perfectly effective. But eradicating rumor shouldn’t be equated with eradicating epidemic. The epidemic can be eradicated with rumor still diffusing, and the epidemic may keep spreading with rumor being eradicated. Moreover, the communication-layer network structure greatly affects the spread of epidemic in the contact-layer network. When people have more connections in the communication-layer network, the knowledge is more likely to diffuse widely, and the rumor and epidemic can be eradicated more efficiently. When the communication-layer network is sparse, a larger penetration intensity of knowledge into rumor is required to promote the diffusion of knowledge.

1. Introduction

Epidemics continue to trigger world alarms in recent decades [1], [2], and have become a serious threat to human health [3], [4], [5]. Currently, a new type of coronavirus (COVID-19) is circulating worldwide [6], and its plateaus hasn’t been reached up to the time of writing this manuscript [7]. However, the world is still not fully prepared for the outbreak of an epidemic [8]. There are many reasons behind this, including the widespread presence of viral vectors (such as mosquitoes) [9], virus mutation [10], low effect of treatment [11], [12], seasonal outbreak (such as influenza) [13], [14], etc. As a consequence, the global protection is not enough, and people are usually encouraged to strengthen personal protection to reduce the risk of being infected, and they are also willing to do that [15], [16]. Previous researches have discovered the important role of individual-level self-protection in eliminating epidemics and saving human lives [17]. Wang et al. reviewed the researches on the coupled dynamics of behavior and epidemic, and summarized that people’s precautions obviously affect the prevalence of an epidemic [18], [19].

More importantly, the self-protective awareness will spread across the population [20], yielding an interdisciplinary research area: interaction between information diffusion and epidemic spreading [21]. Previous complex network models have found that information diffusion plays an important role in promoting the spread of self-protective measures during an epidemic [22], [23]. However, in the era of information explosion, the accuracy of information is difficult to guarantee. The spread of incorrect information may mislead people to choose the measures of low effect or no effect. Tai et al. reviewed in detail the rumors on protective measures during the outbreak of SARS, such as fumigating vinegar [24]. In addition, even if the correct information is spreading in social networks, rumors against it may discourage people from adopting it [25]. One of the reasons for the inaccurate information to prevail in social networks is that, most people only have common sense and lack relevant professional knowledge to make accurate judgments. The professional knowledge is usually mastered by a few people. For example, Prelec et al. conducted a survey on the knowledge of US state capitals [26]. One question is “Philadelphia is the capital of Pennsylvania, yes or no?” The answer given by most respondents is “yes”, which is incorrect. Although the respondents are from world-class universities, they failed to give the right answer. To explore the reason behind, Prelec et al. found that almost all respondents have the common sense that Philadelphia is the largest city in Pennsylvania, while the knowledge that “Harrisburg is the capital of Pennsylvania” is mastered by a few people. Similarly, during SARS, people may have the common sense that acetic acid has a certain bactericidal effect, but the knowledge is that the concentration of acetic acid in vinegar is not enough to kill the virus. In this research, we define inaccurate information as rumor and accurate information as knowledge. As what we learn from the study of Prelec et al., rumor may spread more widely than knowledge, which is very harmful to controlling an epidemic.

Therefore, it is important to know how the diffusion of rumor affects the spread of an epidemic, and whether rumor and epidemic can be contained by the diffusion of knowledge. We adopt a two-layer network to model the processes of information diffusion (including rumor diffusion and knowledge diffusion) and epidemic spreading. In the communication-layer network, we adopt a UA₁A₂ model to describe the competitive diffusions of rumor and knowledge. Specifically, we propose a unidirectional transition probability from the rumor-believed state to the knowledge-believed state, which represents the penetration of knowledge into rumor. In the contact-layer network, we adopt an SEIS model to describe the spread of epidemic. The infected state is divided into two stages: infected but undetected (E), infected and detected (I). When infected nodes are detected, they will be quarantined immediately. Previous epidemic models often assumed that the diffusion of information is driven by local risk information (e.g., whether the linked neighbors are infected [27]). However, in our epidemic model, the direct risk sources (i.e., unobserved infected nodes) are not detected, which makes the local risk information less “protective” [28]. Moreover, people prefer to making pre-protection, regardless of whether there is any infected neighbor [29]. For instance, in the previously mentioned vinegar case, people’s pre-protection is mainly induced by global risk information. As another example, since the COVID-19 virus was proved to be infectious, the knowledge of wearing appropriate masks is widely spread on social networks of 1.4 billion Chinese users. Therefore, unlike previous models, we will focus on pre-protection and assume that once the infected node is detected globally, information diffusion will begin. When a node receives a piece of rumor or knowledge, s/he is likely to take corresponding protective measures.

We use three methods to analyze the model: numerical prediction, agent-based simulation and mean-field analysis. The results of the three methods are very close. Based on the results, we summarize three main findings. First, the diffusion of knowledge can not only eradicate rumor, but also help to eradicate the epidemic, and the penetration of knowledge into rumor plays a key role. We analyzed the relationship of the outbreak thresholds (of rumor and of epidemic) with the penetration intensity of knowledge into rumor. In the communication-layer network, when the penetration intensity of knowledge is increased, the rumor outbreak threshold is increased linearly, so that the rumor becomes easier to control. In the contact-layer network, no matter whether the self-protective measure is perfectly effective or not, the threshold of epidemic outbreak increases nonlinearly with the penetration intensity of knowledge, but only if the penetration intensity of knowledge is large enough to make the knowledge widely spread. Second, it is not necessary to eradicate rumor in order to eradicate epidemic. Eradicating rumor is undoubtedly helpful to contain the epidemic, but it may cost too much. When there are enough knowledge-believed nodes, the epidemic outbreak threshold will be increased greatly. Our results show that when rumor and knowledge are diffusing simultaneously in the communication-layer network, the epidemic can also be eradicated by the diffusion of knowledge. However, it should be noted that when rumor is eradicated, if the effectiveness of self-protective measures is very low, the epidemic may not be eradicated. Third, the topology structure of the communication-layer network is very important for eradicating epidemic in the contact-layer network. When more links are added to the communication-layer network, which allows people to receive information from more sources, knowledge is more likely to break out, and rumor and epidemic are more likely to be eradicated. In addition, in a sparse communication-layer network, a higher penetration intensity of knowledge into rumor is required to diffuse the knowledge.

2. Models

The coupled dynamics of information diffusion and epidemic spreading have been extensively studied [18], [21], [30], [31]. A typical method is to build a two-layer network, with one layer to model the diffusion of information, and the other layer to model the spread of epidemic [32], [33], [34], [35], [36]. For this research, such method is more necessary because there are two competitive dynamics for information diffusion.

2.1. Two-layer network

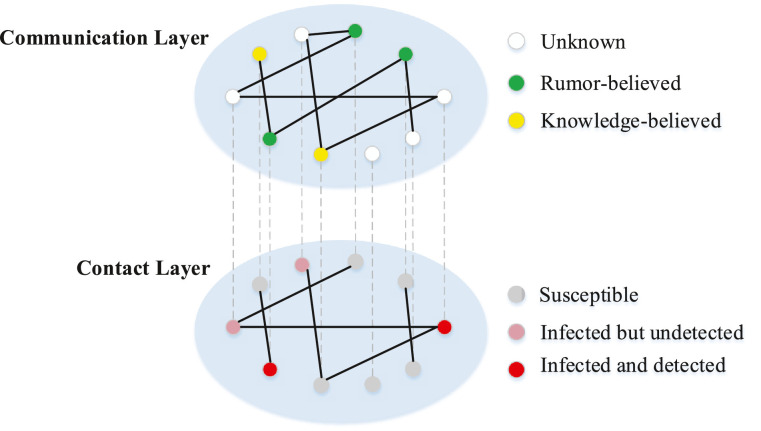
The structure of the two-layer network is presented in Fig. 1 . The nodes in the two layers are the same, while the links are not exactly the same. Wang et al. considered a case that the links in the two layers are uncorrelated [27]. Some other researches proposed a coefficient to denote the overlap (or correlation) of links in the two layers [30], [37]. In this research, we propose a different overlapping method1 . We assume that the communication-layer network is the extension of the contact-layer network. It is because that the spread of epidemic is based on offline contact, while the diffusion of information can be induced by both online and offline communication. People may never have any face-to-face contact with some online friends.

Fig. 1.

Illustration of the communication-contact two-layer network.

To build the two-layer network, we first create a random network of node count N and average node degree k′ using the classical Watts-Strogatz (WS) network model [38]. The first created random network is the contact-layer network. Next, the nodes and links in the contact network are mapped to the communication-layer network. Moreover, the network is extended by letting each node randomly link with k″ other nodes, generating the second random network with the average node degree $k=k^{\prime }+k^{″}$. The second created random network is the communication-layer network.

2.2. Communication layer

Previous studies have successfully modeled the diffusion of rumor [39], and found that the denying of rumor affects the outbreak size and threshold of rumor [40], [41]. But the denying of rumor in their studies is usually described by a constant probability, not driven by the diffusion of knowledge. During an epidemic, it is easy to discover the diffusion of knowledge against rumor. For instance, during the COVID-19 epidemic, knowledge about the functions of different medical masks was widely spread on social media, which helps people to choose the appropriate masks [42]. Moreover, Cyberspace Administration of China (CAC) builds a specialized zone for sharing knowledge and refuting rumor during the COVID-19 epidemic [43].

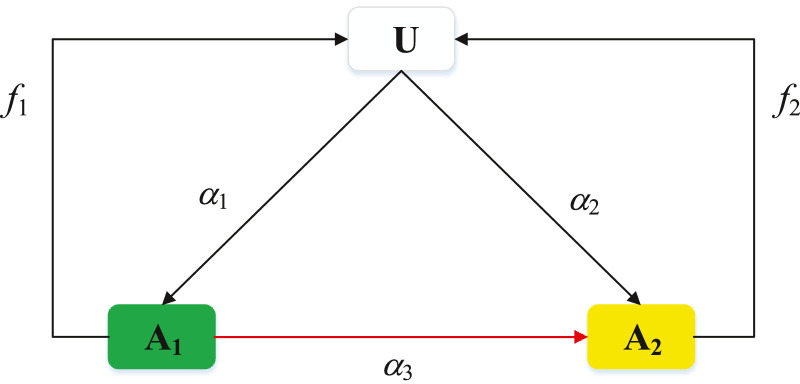
Inspired by previous rumor models and combined with the findings of Prelec et al., we propose a UA₁A₂ model to describe the competitive diffusions between rumor and knowledge, extended from the SIS model [44], [45]. Each node has three possible states: unknown (U), rumor-believed (A₁), and knowledge-believed (A₂). The transition of the three states are well presented in Fig. 2 . When an unknown node receives information from a rumor-believed (or knowledge-believed) neighbor, s/he may become rumor-believed (or knowledge-believed), as well. The “infectivity” of rumor (or knowledge) is α ₁ (or α ₂). After a considerable period of time, the rumor-believed (or knowledge-believed) node may forget the information and return to the unknown state [46], [47], [48]. The expected period length is 1/f ₁ (or 1/f ₂). Namely, the probability for the rumor-believed (or knowledge-believed) node to return to the unknown state is f ₁ (or f ₂). Moreover, there is an important unidirectional transition between the rumor-believed (A₁) state and the knowledge-believed (A₂) state. When the rumor-believed node receives information from a knowledge-believed neighbor, s/he is likely to become knowledge-believed. The “infectivity” of knowledge on the rumor-believed node is defined as α ₃. Apparently α ₃ denotes the penetration intensity of knowledge into rumor. It should be noted that a node can transit from the rumor-believed state to the knowledge-believed state because the knowledge-believed nodes have the extra accurate information (namely knowledge). Thus, the “infectivity” of knowledge may be lower than that of rumor because people have to take more time/efforts to learn such extra knowledge. Besides, previous studies also suggested that rumor might be more contagious. For example, in the New York Times, awe-inspiring tales are likely to be more contagious than the regular news [49]. Therefore, we set α ₂ < α ₁.

Fig. 2.

State transition diagram for the competitive diffusions of information. Here “U” denotes the state that people are unknown about rumor and knowledge. “A₁” denotes the state that people believe rumor, and “A₂” denotes the state that people believe knowledge. α₁ and α₂ denote the infectivities of rumor and knowledge. α₃ denotes the penetration intensity of knowledge into rumor. f₁ and f₂ denote the forgetting probabilities of rumor and knowledge.

We propose φ₁(t) and φ₂(t) to denote the probabilities of a randomly selected link pointing to a rumor-believed node and a knowledge-believed node [50]. They are obtained as

$$\{\begin{array}{c}{\phi }_1\left(t\right)=\frac{{\sum }_{k}kP\left(k\right)·A_{1k}\left(t\right)}{{\sum }_{k}kP\left(k\right)}=\frac{{\sum }_{k}kP\left(k\right)·A_{1k}\left(t\right)}{〈k〉}\hfill \\ {\phi }_2\left(t\right)=\frac{{\sum }_{k}kP\left(k\right)·A_{2k}\left(t\right)}{{\sum }_{k}kP\left(k\right)}=\frac{{\sum }_{k}kP\left(k\right)·A_{2k}\left(t\right)}{〈k〉}\hfill \end{array}$$ (1)

where A _1k(t) and A _2k(t) denote the densities of rumor-believed and knowledge-believed nodes among the nodes with degree k at time t. P(k) denotes the distribution function of the node degree. For ease of analysis, we assume that the communication-layer network is homogeneous and the nodes have similar degrees. Thus, it can be approximately derived that ${\phi }_1\left(t\right)=A_1\left(t\right),$ and ${\phi }_2\left(t\right)=A_2\left(t\right)$. Here A ₁(t) and A ₂(t) denote the densities of rumor-believed and knowledge-believed nodes, respectively. Correspondingly, the probability that a node has n ₁ rumor-believed neighbors and n ₂ knowledge-believed neighbors can be given by a trinomial distribution

$$T(k,n_1,n_2)=\frac{k!}{n_1!n_2!(k-n_1-n_2)!}·A_1{\left(t\right)}^{n_1}{A}_2{\left(t\right)}^{n_2}{(1-A_1\left(t\right)-A_2\left(t\right))}^{k-n_1-n_2}$$ (2)

where k is the degree of node.

The discrete-time information diffusion process can be described as follows

$$\{\begin{array}{c}U(t+1)=U\left(t\right)+A_1\left(t\right)P_{A_1\to U}+A_2\left(t\right)P_{A_2\to U}-U\left(t\right)P_{U\to A_1}-U\left(t\right)P_{U\to A_2}\hfill \\ A_1(t+1)=A_1\left(t\right)-A_1\left(t\right)P_{A_1\to U}-A_1\left(t\right)P_{A_1\to A_2}+U\left(t\right)P_{U\to A_1}\hfill \\ A_2(t+1)=A_2\left(t\right)-A_2\left(t\right)P_{A_2\to U}+A_1\left(t\right)P_{A_1\to A_2}+U\left(t\right)P_{U\to A_2}\hfill \end{array}$$ (3)

where the discrete-time probabilities of state transitions are derived following the research of Liu et al [41] as blow

$$\{\begin{array}{c}{P}_{U\to A_1}=\sum _{n_1,n_2}[1-{(1-{\alpha }_1)}^{n_1}]{(1-{\alpha }_2)}^{n_2}T(k,n_1,n_2)\hfill \\ P_{U\to A_2}=\sum _{n_1,n_2}[1-{(1-{\alpha }_2)}^{n_2}]T(k,n_1,n_2)\hfill \\ P_{A_1\to A_2}=\sum _{n_1,n_2}[1-{(1-{\alpha }_3)}^{n_2}]T(k,n_1,n_2)\hfill \\ P_{A_1\to U}=f_1\sum _{n_1,n_2}{(1-{\alpha }_3)}^{n_2}T(k,n_1,n_2)\hfill \\ P_{A_2\to U}=f_2\hfill \end{array}$$ (4)

When an unknown node receives information from a rumor-believed neighbor and a knowledge-believed neighbor at the same time, s/he is first affected by the knowledge-believed neighbor and then affected by the rumor-believed neighbor, as shown in Eq. (4). Namely, we set the priority of knowledge higher than that of rumor.

Based on the discrete-time probabilities of state transitions, we derive the continuous-time probabilities following Wu et al. [51], as detailed in the Appendix A-1. The mean-field dynamic equations of information diffusion are then derived as below,

$$\{\begin{array}{c}d\frac{U\left(t\right)}{dt}=f_1{A}_1\left(t\right)+f_2{A}_2\left(t\right)-k{\alpha }_1{A}_1\left(t\right)U\left(t\right)-k{\alpha }_2{A}_2\left(t\right)U\left(t\right)\hfill \\ d\frac{A_1\left(t\right)}{dt}=-f_1{A}_1\left(t\right)+k{\alpha }_1{A}_1\left(t\right)U\left(t\right)-k{\alpha }_3{A}_2\left(t\right)A_1\left(t\right)\hfill \\ d\frac{A_2\left(t\right)}{dt}=-f_2{A}_2\left(t\right)+k{\alpha }_2{A}_2\left(t\right)U\left(t\right)+k{\alpha }_3{A}_2\left(t\right)A_1\left(t\right)\hfill \end{array}$$ (5)

Let $d\frac{U\left(t\right)}{dt}=d\frac{A_1\left(t\right)}{dt}=d\frac{A_2\left(t\right)}{dt}=0,$ we calculate the equilibrium of information diffusion, based on which we are able to derive the thresholds for rumor and knowledge to break out, as detailed in the Appendix A-2. The outbreak of rumor requires the following inequality to be satisfied

$$\frac{{\alpha }_1{f}_2+{\alpha }_3{f}_2}{k{\alpha }_2{\alpha }_3+{\alpha }_2{f}_1}\ge 1$$ (6)

while the outbreak of knowledge requires the following inequality to be satisfied

$$\frac{k{\alpha }_1{\alpha }_3+{\alpha }_2{f}_1}{{\alpha }_1{f}_2+{\alpha }_3{f}_1}\ge 1$$ (7)

2.3. Contact layer

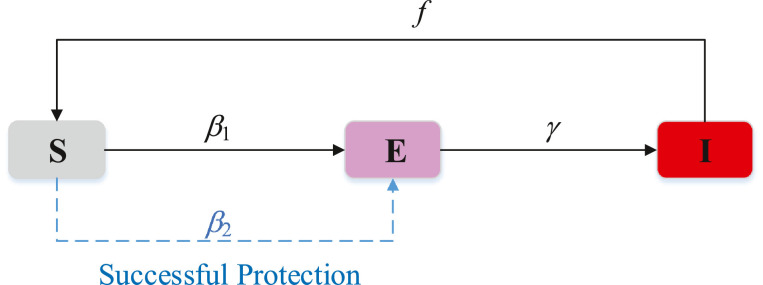
Previous studies have extensively modeled the spread of epidemic in the contact-layer network [52], [53], [54], [55]. As shown in Fig. 3 , we adopt a transformed SEIS model (or SIIS model [28]), which is slightly different from the typical SEIS models [56], [57], to describe the spread of epidemic. When a susceptible node contacts with an undetected infected peer, s/he may become infected but is not detected (e.g., with mild symptoms). The infectivity of the epidemic is β ₁. The undetected infected nodes are detected at rate γ. Once detected (e.g., with severe symptoms), the infected nodes will be quarantined immediately and cannot infect other susceptible nodes. After a period of treatment, the detected infected nodes recover to the susceptible state at rate f.

Fig. 3.

State transition diagram for the spread of epidemic. Here “S” denotes the state that people are susceptible to the epidemic, “E” denotes the state that people are infected but are not detected, and “I” denotes the state that people are infected and detected. β₁ denotes the infectivity of epidemic. β₂ denotes the infectivity of epidemic on the knowledge-believed nodes. γ denotes the detecting probability of the infected nodes. f denotes the recovery probability of the infected nodes.

In addition, the diffusion of information has an important impact on the spread of epidemic. When the knowledge-believed nodes take an effective protective measure, s/he will reduce her/his susceptibility to the epidemic. Without loss of generality, we propose that the infectivity of epidemic on the knowledge-believed nodes changes to β ₂. Apparently, β ₂ < β ₁. However, the rumor-believed nodes adopt an ineffective measure and the epidemic infectivity on them remains β ₁. Previous studies assumed that the spread of epidemic would continuously promote the diffusion of information, because the infected nodes were identified as risk sources for their neighbors [27]. In this research, the detected infected nodes are quarantined and “of no risk”, while the direct risk sources are undetected. As a result, the effect of local risk information on containing the epidemic is greatly reduced [28]. Moreover, we focus on pre-protection instead of local-risk protection (e.g., high-risk immunization [58]). Therefore, we don’t consider such local risk information in this research.

We use φ_E(t) to denote the probability of a randomly selected link pointing to an undetected infected node. It can be calculated as [50]

$${\phi }_E\left(t\right)=\frac{{\sum }_{k}kP\left(k\right)·E_k\left(t\right)}{{\sum }_{k}kP\left(k\right)}=\frac{{\sum }_{k}kP\left(k\right)·E_k\left(t\right)}{〈k〉}$$ (8)

where E_k(t) denotes the density of undetected infected nodes among the nodes with degree k at time t. The contact-layer network is a sub-network of the communication-layer network. We assume that it is also homogeneous. The node degree is set as k′. It can be approximately obtained that ${\phi }_E\left(t\right)=E\left(t\right)$. The probability that a node has m undetected infected neighbors can be given by a binomial distribution

$$B(k^{\prime },m)=\frac{k^{\prime }!}{m!(k^{\prime }-m)!}·E{\left(t\right)}^m{(1-E\left(t\right))}^{k^{\prime }-m}$$ (9)

Correspondingly, the discrete-time epidemic process can be described as follows

$$\{\begin{array}{c}S(t+1)=S\left(t\right)-S\left(t\right)[1-A_2\left(t\right)]P_{S\to E_1}-S\left(t\right)A_2\left(t\right)P_{S\to E_2}+fI\left(t\right)\hfill \\ E(t+1)=E\left(t\right)+S\left(t\right)[1-A_2\left(t\right)]P_{S\to E_1}+S\left(t\right)A_2\left(t\right)P_{S\to E_2}-\gamma E\left(t\right)\hfill \\ I(t+1)=I\left(t\right)+\gamma E\left(t\right)-fI\left(t\right)\hfill \end{array}$$ (10)

where the discrete-time probabilities of state transitions are derived as

$$\{\begin{array}{c}{P}_{S\to E_1}=\sum _m[1-{(1-{\beta }_1)}^m]B(k^{\prime },m)\hfill \\ P_{S\to E_2}=\sum _m[1-{(1-{\beta }_2)}^m]B(k^{\prime },m)\hfill \\ P_{E\to I}=\gamma \hfill \\ P_{I\to S}=f\hfill \end{array}$$ (11)

Similar to the analysis in the information diffusion model, we derive the continuous-time probabilities of state transitions based on the discrete-time probabilities, as detailed in the Appendix A-1. The mean-field dynamic equations of epidemic spreading are derived as below,

$$\{\begin{array}{c}d\frac{S\left(t\right)}{dt}=-k^{\prime }{\beta }_{1}S\left(t\right)[1-A_2\left(t\right)]E\left(t\right)-k^{\prime }{\beta }_{2}S\left(t\right)A_2\left(t\right)E\left(t\right)+fI\left(t\right)\hfill \\ d\frac{E\left(t\right)}{dt}=k^{\prime }{\beta }_{1}S\left(t\right)[1-A_2\left(t\right)]E\left(t\right)+k^{\prime }{\beta }_{2}S\left(t\right)A_2\left(t\right)E\left(t\right)-\gamma E\left(t\right)\hfill \\ d\frac{I\left(t\right)}{dt}=\gamma E\left(t\right)-fI\left(t\right)\hfill \end{array}$$ (12)

Let $d\frac{S\left(t\right)}{dt}=d\frac{S\left(t\right)}{dt}=d\frac{I\left(t\right)}{dt}=0,$ we calculate the equilibrium of epidemic spreading, based on which we are able to derive the outbreak threshold of epidemic, as detailed in the Appendix A-3. Specifically, the outbreak of epidemic requires the following inequality to be satisfied

$$\frac{k^{\prime }}{\gamma }[{\beta }_1(1-A_2\left(\infty \right))+{\beta }_2{A}_2\left(\infty \right))]\ge 1$$ (13)

where the equilibrium density of the knowledge-believed nodes A ₂(∞) is expressed in the Appendix A-1. When $A_2\left(\infty \right)=0,$ the epidemic threshold degenerates to ${\beta }_1=\gamma /k^{\prime }$.

3. Results

To evaluate the model, we adopt three different methods including two numerical methods and one theoretical method. The two numerical methods are: prediction based on the discrete-time state transition equations (abbreviated as predicted results), and agent-based simulation (abbreviated as simulated results). The theoretical method is the mean-field analysis based on the continuous-time state transition equations (abbreviated as mean-field results). The predicted results are first compared with the simulated results for verification. And the mean-field outbreak thresholds are then presented with the predicted results to reveal more interesting findings.

3.1. Predicted results vs. simulated results

To get the predicted results, we adopt MATLAB to iterate the discrete-time state transition equations of information diffusion and epidemic spreading. For the simulated results, we adopt REPAST to perform a series of agent-based simulations. Initially, rumor and knowledge are believed by only the minority. But rumor has a much larger “infectivity” than knowledge and diffuses much faster. The topology of the communication layer and the contact layer are set to be random network, with the average degree defaulted as $k=8$ and $k^{\prime }=6,$ respectively. Some other parameters are defaulted as: $f_1=0.2,$ $f_2=0.2,$ $f=0.2,$ $\gamma =0.2$.

3.1.1. Communication layer

Compared with a neutral unknown node, a rumor-believed node is often less susceptible to knowledge. The concept of a popular decision model, that is belief decision model [59], can support this conjecture. According to the belief decision model, each node beliefs on three options: rumor-believed, knowledge-believed, and neutral (or hesitating). When a neutral node receives knowledge, her/his belief on knowledge will be quickly increased. While a rumor-believed node receives knowledge, her/his belief is first transferred from the rumor-believed option to the neutral option, and then transferred from the neutral option to the knowledge-believed option. Apparently, the knowledge-believed belief of the rumor-believed node is less increased due to information fading during belief transfer. Thus, the value of α ₃ is lower than the value of α ₂. When ${\alpha }_3=0,$ for example, the two information diffusion dynamics are completely separated. While ${\alpha }_3={\alpha }_2,$ the rumor-believed nodes have no reluctance against knowledge, and rumor is unable to affect the diffusion of knowledge. Therefore, the value of α ₃ is vital for the competition between rumor and knowledge, and we select it as a key parameter for analysis.

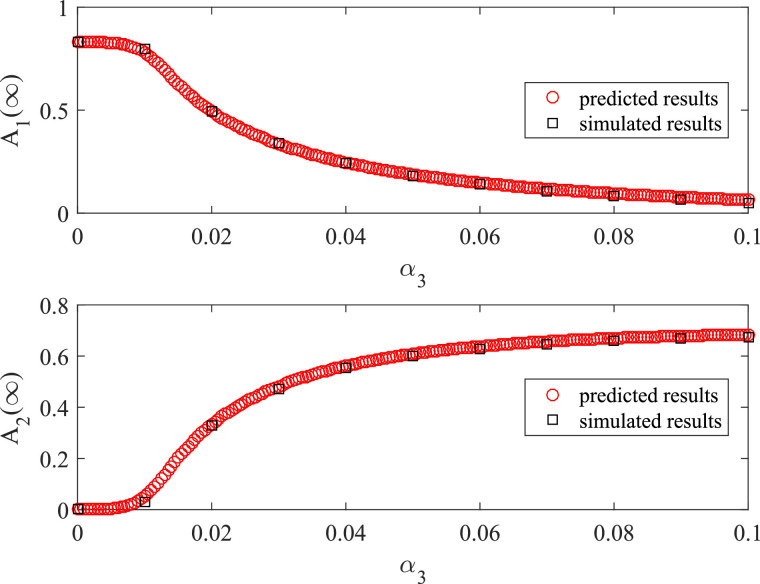
As shown in Fig. 4 , the equilibrium densities of the rumor-believed nodes A ₁(∞) and the knowledge-believed nodes A ₂(∞) over α ₃ are well presented. Increasing α ₃ decreases the density of the rumor-believed nodes and increases the density of the knowledge-believed nodes. More importantly, the simulated results and the predicted results are consistent with each other. Besides, from the results, we infer that both rumor and knowledge may have outbreak thresholds. Specifically, the outbreak of rumor may require α ₃ to be smaller than 0.1, while the outbreak of knowledge may require α ₃ to be larger than 0.01. That is to say, when α ₃ is larger than 0.01 and smaller than 0.1, rumor and knowledge will diffuse simultaneously.

Fig. 4.

Predicted and simulated densities of rumor-believed and knowledge-believed nodes (A₁(∞) and A₂(∞)) against α₃ at the equilibrium of information diffusion. The simulated results are draw by black square, and the predicted results are draw by red circle. Other parameters are set as ${\alpha }_1=0.5,$${\alpha }_2=0.1$. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.1.2. Contact layer

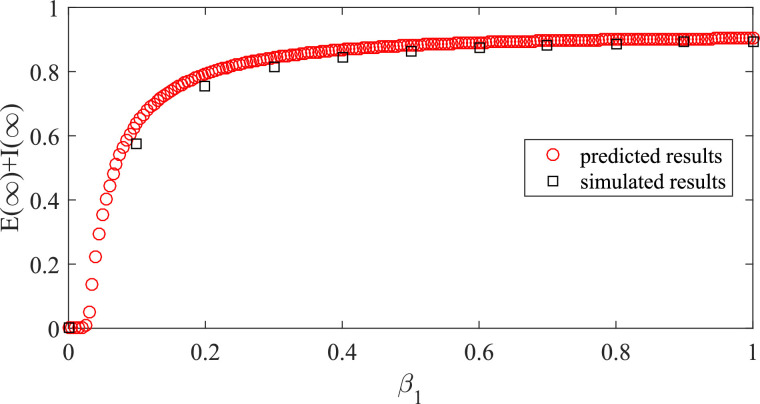
we select the infectivity of epidemic (β ₁) to compare the predicted results and the simulated results of epidemic prevalence. As shown in Fig. 5 , the equilibrium density of the (undetected and detected) infected nodes over β ₁ is well presented. Increasing β ₁ will undoubtedly increase the density of the infected nodes. Moreover, the simulated results and the predicted results are very close to each other. Besides, from the results, we can detect the epidemic outbreak threshold. It is important to study whether the diffusion of information (especially the diffusion of knowledge) could affect the epidemic outbreak threshold.

Fig. 5.

Predicted and simulated infected densities ($E\left(\infty \right)+I\left(\infty \right)$) against β₁ at the equilibrium of epidemic spreading. The simulated results are draw by black square, and the predicted results are draw by red circle. Other parameters are set as ${\alpha }_1=0.5,$${\alpha }_2=0.1$ and ${\beta }_2=0.1$. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.2. Outbreak thresholds of information

To analyze the outbreak thresholds in the communication-layer network, especially to study whether and how rumor can be eradicated by the penetration of knowledge into rumor, we focus on the parameter space ${\alpha }_3-{\alpha }_1$ to draw the heat maps of rumor-believed densities and knowledge-believed densities. The value of α ₂ is set as 0.1, α ₃ is confined in the interval [0, 0.1], and α ₁ is confined in the interval [0.1, 1].

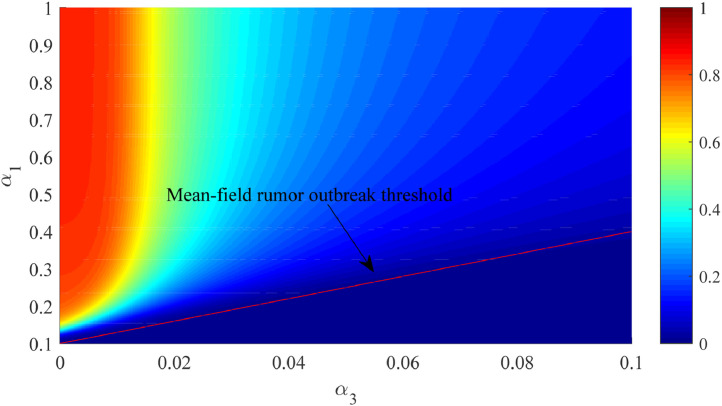
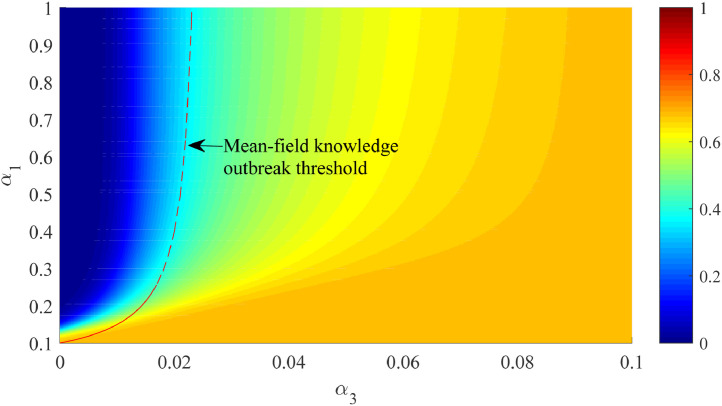
As shown in Figs. 6 and 7 , the equilibrium densities of rumor-believed nodes and knowledge-believed nodes over ${\alpha }_3-{\alpha }_1$ are almost complementary, reflecting the competition between them. Increasing rumor infectivity (α ₁) will increase the density of the rumor-believed nodes and reduce that of the knowledge-believed nodes, while increasing the intensity of knowledge penetrating into rumor (α ₃) will reduce the density of the rumor-believed nodes and increases that of the knowledge-believed nodes. These two parameters could determine which wins in the competition, especially whether the rumor can be eradicated by knowledge.

Fig. 6.

Equilibrium densities of the rumor-believed nodes in the parameter space ${\alpha }_3-{\alpha }_1$. The red dashed line denotes the mean-field thresholds for rumor to break out. The value of α₂ is set as 0.1. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 7.

Equilibrium densities of the knowledge-believed nodes in the parameter space ${\alpha }_3-{\alpha }_1$. The red dashed line denotes the mean-field thresholds for knowledge to break out. The value of α₂ is set as 0.1. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Moreover, from the two figures, we observe the effects of α ₁ and α ₃ on the outbreak thresholds of rumor and of knowledge, and we compare the numerical predictions with the mean-field thresholds in Eqs. (6) and (7). It can be found that the numerical threshold of rumor is highly matched with the mean-field rumor threshold. As α ₁ (i.e., infectivity of rumor) increases, a larger α ₃ (i.e., penetration intensity of knowledge into rumor) is required to eradicate rumor. And the rumor outbreak threshold indicates that α ₃ should increase linearly with α ₁, as shown below2

$${\alpha }_3=\frac{{\alpha }_1{f}_2-{\alpha }_2{f}_1}{k{\alpha }_2-f_2}$$ (14)

The numerical threshold of knowledge is also close to the mean-field knowledge threshold3 With the increase of α ₁ (i.e., infectivity of rumor), a larger α ₃ (i.e., penetration intensity of knowledge into rumor) is required for knowledge to diffuse. But it should be noted that the equilibrium density of the knowledge-believed nodes increases sharply with α ₃. Even if the infectivity of rumor is extremely high, a small α ₃ (e.g. ${\alpha }_3=0.2$) will make knowledge ineradicable. The knowledge outbreak threshold indicates that α ₃ increases nonlinearly with the increase of α ₁, as shown below

$${\alpha }_3=\frac{f_2}{k}-\frac{k{\alpha }_2{f}_1-f_1{f}_2}{k^2{\alpha }_1-k{f}_1}$$ (15)

Therefore, from the above results, we observe a three-phase phenomenon of information diffusion over α ₃. When ${\alpha }_3<f_2∕k-(k{\alpha }_2{f}_1-f_1{f}_2)∕(k^2{\alpha }_1-k{f}_1),$ knowledge dies out and rumor is dominant. When $f_2∕k-(k{\alpha }_2{f}_1-f_1{f}_2)∕(k^2{\alpha }_1-k{f}_1)<{\alpha }_3<({\alpha }_1{f}_2-{\alpha }_2{f}_1)∕(k{\alpha }_2-f_2),$ knowledge starts to diffuse. As a result, rumor is gradually confined. When ${\alpha }_3>({\alpha }_1{f}_2-{\alpha }_2{f}_1)∕(k{\alpha }_2-f_2),$ knowledge takes the dominant position and rumor is eradicated. Thus, the value of α ₃ (i.e., penetration intensity of knowledge into rumor) is crucial to information diffusion. It largely determines whether rumor can be eradicated by knowledge.

3.3. Outbreak threshold of epidemic

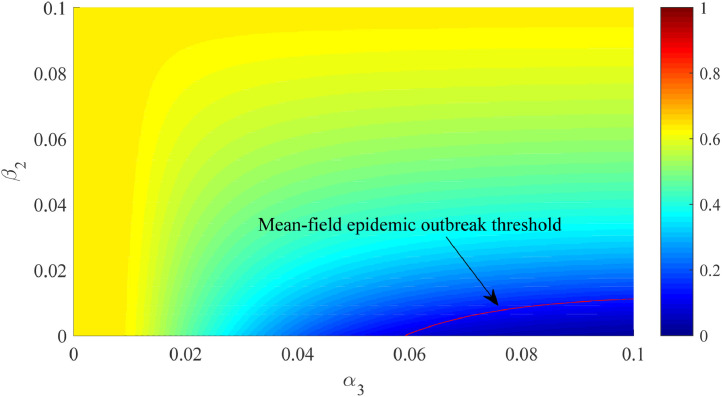
To analyze the outbreak threshold of epidemic in the contact-layer network, especially to study whether the diffusion of knowledge helps to eradicate the epidemic, we consider two situations: perfect self-protection and imperfect self-protection. Firstly, we focus on the parameter space ${\alpha }_3-{\beta }_1$ with the value of β ₂ set to 0 (i.e., perfect self protection). α ₃ is confined in the interval [0, 0.1], and β ₁ is confined in the interval [0, 1]. Secondly, we fix the infectivity of epidemic (${\beta }_1=0.1),$ and focus on the parameter space ${\alpha }_3-{\beta }_2,$ in order to explore how imperfect self-protection (β ₂ ∈ [0, 0.1]) affects the spread of epidemic by knowledge diffusion.

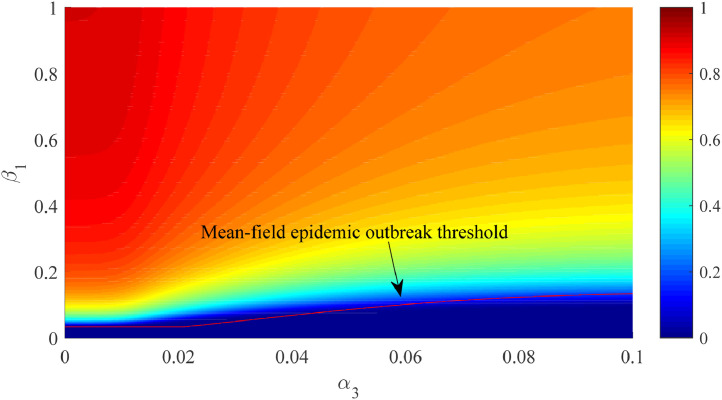
As shown in Fig. 8 , in the case of perfect self-protection, increasing the value of epidemic infectivity (β ₁) will increase the density of the (undetected and detected) infected nodes, while increasing the penetration of knowledge into rumor (α ₃) will decrease the density of the infected nodes. The finding verifies that the diffusion of knowledge helps to contain the epidemic. Moreover, the numerical epidemic threshold is very close to the mean-field epidemic threshold in Eq. (13). As epidemic infectivity (β ₁) increases, a larger penetration intensity of knowledge into rumor (α ₃) is required to eradicate the epidemic. The epidemic outbreak threshold indicates that the epidemic infectivity (β ₁) can increase nonlinearly with the increase of α ₃, as shown below

$${\beta }_1=\{\begin{array}{cc}{\displaystyle \frac{\gamma }{k^{\prime }}}\hfill & {\displaystyle \mathit{if}{\alpha }_3\le \frac{f_2}{k}-\frac{k{\alpha }_2{f}_1-f_1{f}_2}{k^2{\alpha }_1-k{f}_1}}\hfill \\ {\displaystyle \frac{\frac{\gamma }{k^{\prime }}-{\beta }_2}{1-A_2\left(\infty \right)}+{\beta }_2}\hfill & {\displaystyle \mathit{if}{\alpha }_3>\frac{f_2}{k}-\frac{k{\alpha }_2{f}_1-f_1{f}_2}{k^2{\alpha }_1-k{f}_1}}\hfill \end{array}$$ (16)

where $A_2\left(\infty \right)=(k{\alpha }_1{\alpha }_3-{\alpha }_1{f}_2+{\alpha }_2{f}_1-{\alpha }_3{f}_1)∕k({\alpha }_1-{\alpha }_2+{\alpha }_3){\alpha }_3,$ Namely,

$${\beta }_1=\{\begin{array}{cc}{\displaystyle \frac{\gamma }{k^{\prime }}}\hfill & {\displaystyle \mathit{if}{\alpha }_3\le \frac{f_2}{k}-\frac{k{\alpha }_2{f}_1-f_1{f}_2}{k^2{\alpha }_1-k{f}_1}}\hfill \\ {\displaystyle \frac{(\frac{\gamma }{k^{\prime }}-{\beta }_2)k({\alpha }_1-{\alpha }_2+{\alpha }_3){\alpha }_3}{(k{\alpha }_3+f_1)({\alpha }_3-{\alpha }_2)+{\alpha }_1{f}_2}+{\beta }_2}\hfill & {\displaystyle \mathit{if}{\alpha }_3>\frac{f_2}{k}-\frac{k{\alpha }_2{f}_1-f_1{f}_2}{k^2{\alpha }_1-k{f}_1}}\hfill \end{array}$$ (17)

Fig. 8.

Equilibrium densities of the infected nodes ($E\left(\infty \right)+I\left(\infty \right)$)in the parameter space ${\alpha }_3-{\beta }_1$. The red dashed line denotes the mean-field thresholds for epidemic to break out. The value of α₁, α₂ and β₂ are set as 0.5, 0.1 and 0, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

As shown in Fig. 9 , in the case of imperfect self-protection, improving the effectiveness of self-protection (i.e., reducing β ₂) can significantly decreases the density of the infected nodes, but highly depending on the penetration intensity of knowledge into rumor (α ₃). When the intensity of knowledge is insufficient to penetrate the rumor-believed nodes (e.g., α ₃ < 0.02), reducing β ₂ will not have much impact on the density of infected nodes. While α ₃ is large enough (e.g., α ₃=0.08), reducing β ₂ can eradicate the epidemic. Moreover, the numerical epidemic threshold is compared with the mean-field epidemic threshold in Eq. (13). With the increase of the penetration intensity of knowledge into rumor (α ₃), a less effective self-protection, namely a larger β ₂, can be enough to eradicate the epidemic. The epidemic outbreak threshold indicates that β ₂ can increase nonlinearly with the increase of α ₃, as shown below

$${\beta }_2={\beta }_1-({\beta }_1-\frac{\gamma }{k^{\prime }})\frac{k({\alpha }_1-{\alpha }_2+{\alpha }_3){\alpha }_3}{(k{\alpha }_1-f_1){\alpha }_3-{\alpha }_1{f}_2+{\alpha }_2{f}_1}$$ (18)

where $k({\alpha }_1-{\alpha }_2+{\alpha }_3){\alpha }_3∕[(k{\alpha }_1-f_1){\alpha }_3-{\alpha }_1{f}_2+{\alpha }_2{f}_1]>1-\gamma ∕k^{\prime }{\beta }_1$.

Fig. 9.

Equilibrium densities of the infected nodes ($E\left(\infty \right)+I\left(\infty \right)$) in the parameter space ${\alpha }_3-{\beta }_2$. The red dashed line denotes the mean-field threshold for epidemic to break out. The value of α₁, α₂ and β₁ are set as 0.5, 0.1 and 0.1, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.4. Phase diagram

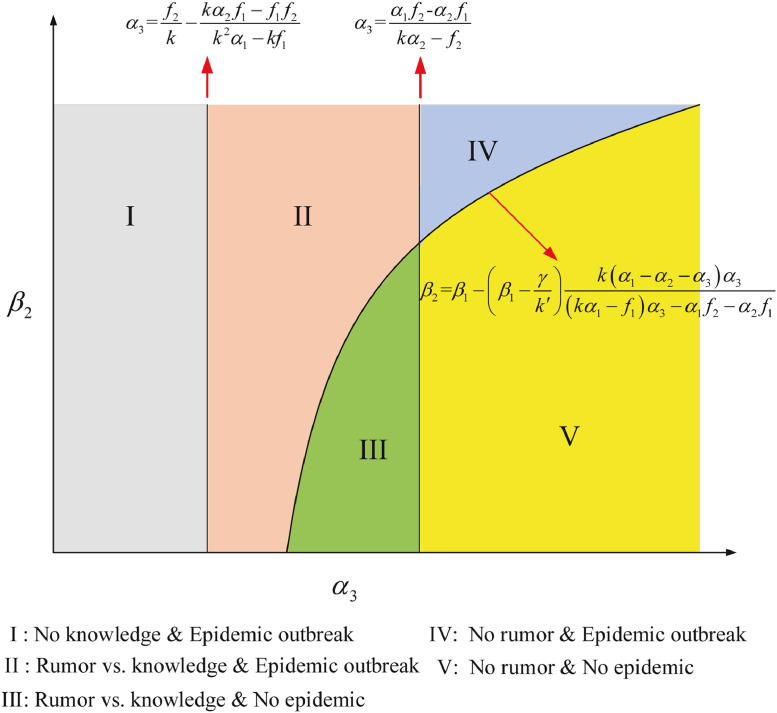
It can be seen from the above results that information diffusion has significant influence on the epidemic spreading. As knowledge becomes more “penetrating” into rumor, rumor and epidemic are more likely to be eradicated. Moreover, based on the outbreak thresholds in the communication-layer network, information diffusion can be divided into three phases. In this section, we try to explore the phase diagram of the whole two-layer system based on the outbreak thresholds in both layers.

As shown in Fig. 10 , the two-layer system can be divided into five phases by ${\alpha }_3-{\beta }_2$. First, information diffusion can be divided into three phases: “No knowledge”, “Rumor vs. knowledge”, and “No rumor”. Second, epidemic spreading can be divided into two phases: “Epidemic outbreak” and “No epidemic”. Specifically, the epidemic spreading phases and the information diffusion phases are overlapped, generating five phases: “No knowledge $\&$ Epidemic outbreak”, “Rumor vs. knowledge $\&$ Epidemic outbreak”, “Rumor vs. knowledge $\&$ No epidemic”, “No rumor $\&$ Epidemic outbreak”, “No rumor $\&$ No epidemic”4 Therefore, it is not necessary to equate rumor eradication with epidemic eradication. When rumor cannot be eradicated, the epidemic can also be eradicated by the spread of knowledge. When rumor can be eradicated, the epidemic may be uneradicated when the effectiveness of self-protection is very low. Moreover, the adjacent phases are interconvertible. For example, the “Rumor vs. knowledge $\&$ No epidemic” phase can convert to the “No rumor $\&$ No epidemic” phase with the increase of α ₃, and can convert to the “Rumor vs. knowledge $\&$ Epidemic outbreak” phase with the increase of β ₂. Based on the phase diagram, it is possible to find an optimal strategy to contain rumor or epidemic. For example, if the two-layer system is in the “Rumor vs. knowledge $\&$ Epidemic outbreak” phase (Phase II), the optimal strategy of containing the epidemic is to develop an effective self-protective measure to reduce β ₂.

Fig. 10.

Phase diagram of the two-layer system.

3.5. Network structure

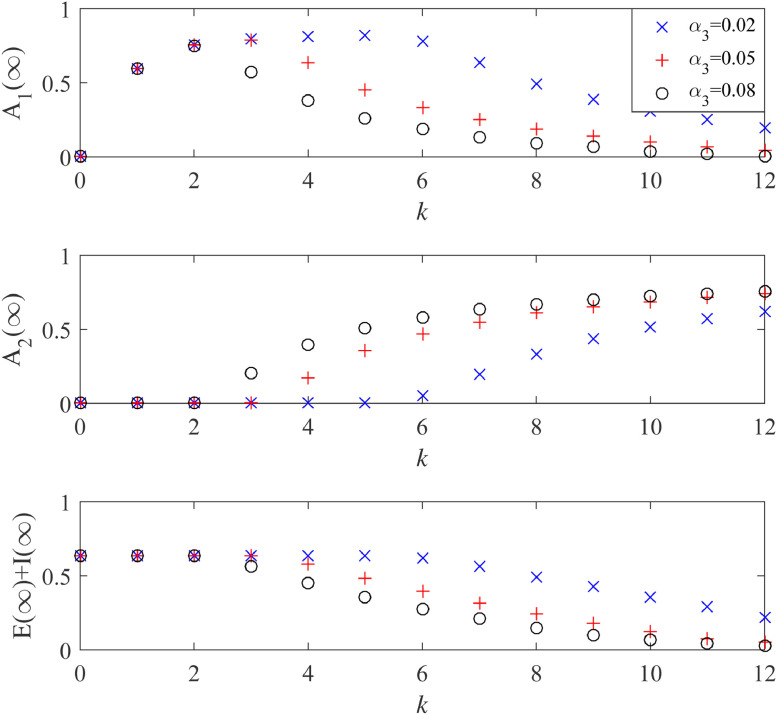
The network structure highly affects the outbreak size and threshold of the spreading dynamics [60], [61]. In a two-layer network, the overlap of the two layers is also important for the spreading dynamics [37]. This research assumes that the communication-layer network is an extension of the contact-layer network. In the information age, the cost of communication is greatly reduced, and it becomes easier to extend the communication-layer network. It is interesting to know whether the extension of the communication-layer network helps to contain rumor and epidemic. Therefore, in this section, we try to explore the evolution of the rumor-believed density and the infected density with the change of average node degree k in the communication-layer network.

As shown in Fig. 11 , when k increases from 0 to 12, the rumor-believed density will increase first and then decrease, while the knowledge-believed density will increase monotonically. Obviously, rumor is more likely to break out in a sparse network than knowledge because rumor infectivity (α ₁) is much larger than knowledge infectivity (α ₂). However, when knowledge starts to break out (e.g., $k=3$), rumor will be confined immediately and the rumor-believed density will begin to decrease. It should be noted that a higher penetration of knowledge into rumor helps knowledge to break out in a very sparse network. Moreover, when the knowledge-believed density starts to increase, the infected density begins to decrease. More importantly, with the increase of k, the infected density gradually decreases to 0, which indicates that extending the communication-layer network helps to eradicate the epidemic in the contact-layer network, consistent with Eq. (13). Besides, a larger α ₃ in the communication-layer network is also helpful to eradicate the epidemic.

Fig. 11.

Equilibrium densities of the rumor-believed nodes, of the knowledge-believed nodes, and of the infected nodes over average node degree k in the communication-layer network. Other parameters are set as ${\alpha }_1=0.5,$${\alpha }_2=0.1,$${\beta }_1=0.1,$ and ${\beta }_2=0.01$.

In summary, extending the communication-layer network is helpful to eradicate the epidemic, but it largely depends on the condition that knowledge is able to penetrate the rumor. When people can get information from diverse sources, s/he is more likely to get access to the accurate information (i.e., knowledge) and get rid of rumor. This will make her/him be better protected from the epidemic. Besides, compared with reducing rumor infectivity or epidemic infectivity, the cost of widening information sources is usually lower.

4. Conclusion and discussion

During an epidemic, individuals are usually willing to take protective measures to avoid being infected. However, the diffusion of rumor sometimes prevents them from choosing the effective measures. To make things worse, such rumor is often contagious and hard to be eradicated, making the epidemic difficult to contain. Therefore, how to contain rumor and epidemic has become a critical issue to the human society.

In this research, inferred from the study of Prelec et al. and the practice of Chinese authorities during COVID-19, we propose that the diffusion of knowledge is the key to controlling both rumor and epidemic. To model interaction between information diffusion and epidemic spreading, we adopt a two-layer network structure. The UA₁A₂ model is adopted to describe the competitive diffusions of information and the SEIS model is adopted to describe the spread of epidemic. Specifically, in the UA₁A₂ model, we explicitly propose a unidirectional transition probability from A₁ (rumor-believed state) to A₂ (knowledge-believed state), which denotes the penetration of knowledge into rumor. Three frequently used methods are used to evaluate the impact of knowledge diffusion on the spread of rumor and epidemic.

The diffusion of knowledge is able to eradicate both rumor and epidemic, where the penetration intensity of knowledge into the rumor-believed nodes (α ₃) plays a vital role. The rumor outbreak threshold increases linearly with α ₃, while the epidemic outbreak threshold increases nonlinearly with α ₃. In particular, even if the self-protective measure is not perfectly effective, increasing α ₃ is helpful to contain and even eradicate the epidemic.

It is inappropriate to equate eradicating rumor with eradicating epidemic, although eradicating rumor is helpful to eradicate the epidemic. On one hand, when the density of knowledge-believed nodes increases, the outbreak threshold of epidemic will significantly increase, no matter whether rumor dies out or not. On the other hand, when rumor is eradicated, the epidemic may still prevail if the self-protective measure is not effective enough.

The overlapping of the contact layer and the communication layer is a research focus in the two-layer network structure. We assume that the communication-layer network is an extension of the contact-layer network. When adding links to the communication-layer network, namely when people get information from more sources, knowledge is more likely to break out, while rumor and epidemic are more likely to be eradicated. Moreover, a larger penetration intensity (α ₃) makes knowledge more likely to break out in a sparse network.

From the above conclusions, it can be obtained that information diffusion has significant influence on the epidemic spreading. Increasing penetration intensity of knowledge or improving effectiveness of self-protection is helpful to eradicate an epidemic. Therefore, for policy-makers, it is necessary to know which is more suitable for a specific case. The phase diagram provides lots of implications. First, it should be evaluated at which phase the present two-layer system is located. Second, an effective strategy is the one that can convert the system from a bad phase (e.g., “Rumor vs. knowledge” & “Epidemic breakout”) to a nearby better phase (e.g., “Rumor vs. knowledge & “No epidemic”).

Our research has several limitations, which can be extended in future studies. First, the dynamic impact of epidemic spreading on information diffusion is not fully considered. In particular, the spread of rumor may be dynamically affected by the severity of epidemic. For example, people’s susceptibility to rumor may not be constant, but inversely related to the outbreak size of epidemic. In other words, when the epidemic outbreak size increases, the infectivity of rumor may increase, as well. We set the rumor infectivity to a very large value (${\alpha }_1=0.5$), but we didn’t consider its dynamic feature. In a dynamic case, rumor and epidemic may be more easily contained at the early stage. Second, the transition from the knowledge-believed state to the rumor-believed state is not considered, which is consistent with most of previous rumor models [41]. In extreme cases, such transition may occur. For example, a wicked rumor may make people to abandon the effective practice [25]. Introducing such transition into our model may make the competition between rumor and knowledge more salient. Third, the topology structures of the contact-layer network and the communication-layer network may be different, which may affect the spreading process. Fortunately, although we only study the random network, this research can be easily extended to different network structures.

Appendix A. Supplementary materials

Supplementary Data S1

Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/