Watching helical membrane proteins fold reveals a common N- to C-terminal folding pathway

Abstract

To understand membrane protein biogenesis, we need to explore folding within a bilayer context. Here we describe a single-molecule force microscopy technique that monitors the folding of helical membrane proteins in vesicle and bicelle environments. After completely unfolding the protein at high force, we lower the force to initiate folding while transmembrane helices are aligned in zigzag manners within the bilayer, thereby imposing minimal constraints on folding. We used the approach to characterize the folding pathways of the Escherichia coli rhomboid protease GlpG and the human β₂-adrenergic receptor. Despite their evolutionary distance, both proteins fold in a strict N-to-C-terminal fashion, accruing structures in units of helical hairpins. These common features suggest that integral helical membrane proteins have evolved to maximize their fitness with co-translational folding.

One Sentence Summary

Single molecule experiments reveal that translation, insertion and folding can be coupled during membrane protein biogenesis.

Tens of thousands of mutations associated with diseases are thought to affect membrane protein folding and trafficking (1). The biogenesis of most helix bundle membrane proteins has been divided conceptually into two stages (2, 3). First, co-translational insertion of the hydrophobic protein into the membrane occurs through the Sec translocon pathway (4, 5), thereby establishing much of the transmembrane helical structure and initial topology. Second, the protein completes folding to its final tertiary structure. The two stages, however, are not necessarily cleanly separable (6–9). Studying folding mechanisms of membrane proteins by single-molecule force spectroscopy has been challenging and limited mostly to observing unfolding (10–13), because folding intermediates are usually invisible at the lower forces where folding occurs on a practical time scale. Here, we employ physicochemical conditions that strongly favor folding, thereby enabling the observation of folding at forces high enough to achieve 1 nm resolution.

To develop an experimental method that can be generally applied to the observation of the folding pathways of polytopic membrane proteins, we build on a single-molecule approach we have developed using magnetic tweezers (MT) (Fig. 1A) (14, 15). We link DNA handles to the N- and C-termini of the protein using a SpyTag/SpyCatcher attachment system (16). The handles are in turn attached to a magnetic bead and a polymer-coated glass surface, respectively. The target membrane protein is embedded in bicelles that provide a lipid bilayer-like environment (Fig. 1A). While applying pN- to tens of pN-scale force to the magnetic bead, we record the vertical position of the bead relative to a reference bead stuck on the surface (referred to as the extension value) (fig. S1).

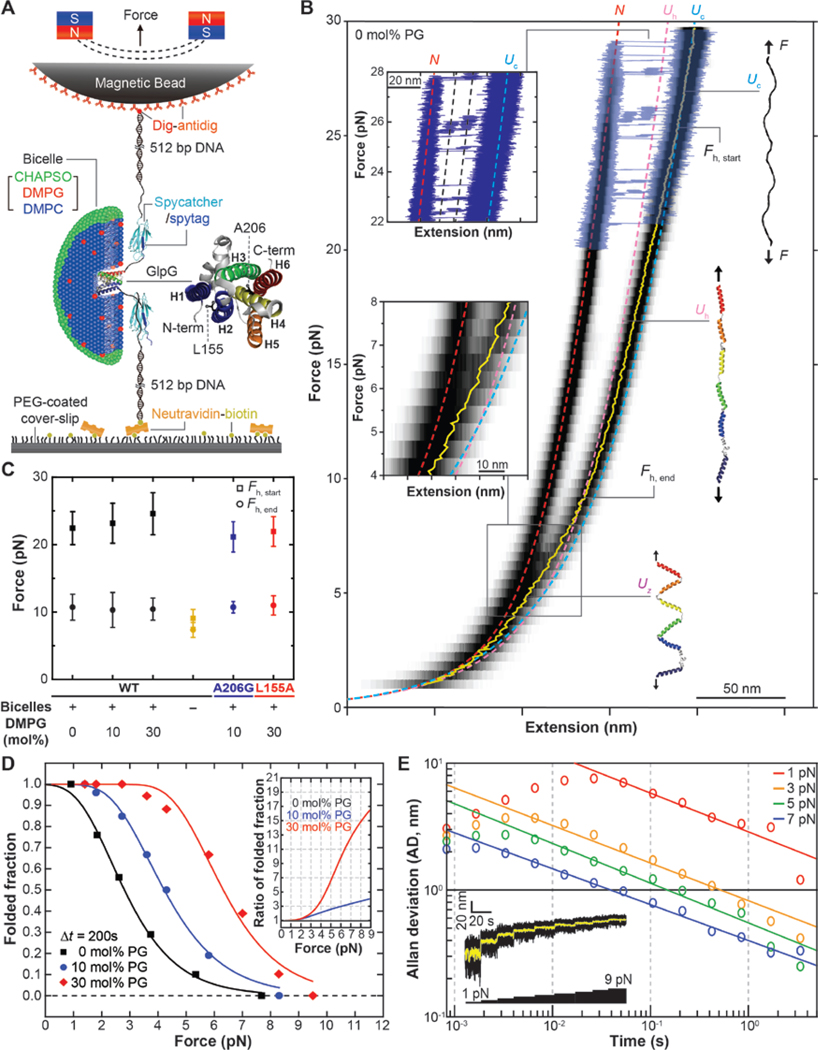
Fig. 1. Physicochemical search for refolding conditions of polytopic helical membrane proteins.

(A) Schematic of single-molecule MT folding experiment for a single GlpG protein reconstituted in a bicelle. (B) FEC of single GlpG proteins averaged over 28 cycles of mechanical stretching and relaxation (black heat map). To show individual unfolding events, representative raw traces are overlaid above 20 pN tension (blue traces). Yellow trace shows the mean extension value in the relaxation phase. F_h,start and F_h,end indicates the force levels at which the coil-to-helix transition starts and ends. Theoretical FECs for the N, U_c and U_h states are shown as red, light blue and pink dashed lines, respectively. Upper inset: a close-up view of the unfolding events. Lower inset: a magnified view of the FEC between 8 and 4 pN force. (C) Average F_h,start and F_h,end values determined under different refolding conditions. n = 34, 42, 58 for the 0, 10 and 30 mol% DMPG cases. n = 16 for the no bicelle case. n = 6, 10 for the A206G and L155A single-point GlpG mutant cases. All error bars represent mean ± s.d. (D) Refolding probability determined using a simple force jump experiment (see fig. S3) at different applied force levels (n = 125, 147, 111 for the 0, 10 and 30 mol% PG cases, respectively). Inset shows the refolding probability normalized to the 0 mol% PG case. (E) Allan deviation of the magnetic bead fluctuation at different force levels. Inset: Representative trace showing the Brownian fluctuation of a magnetic bead at different force levels (black trace: raw data at 1.2 kHz sampling, yellow trace: a median-filtered data with a 5 Hz window).

We applied this method to study the folding of Escherichia coli rhomboid protease GlpG. Figure 1B shows force-extension curves (FECs) averaged over multiple cycles of mechanical stretching and relaxation for single GlpG proteins. At high force levels above 20 pN, the single GlpGs show cooperative unfolding of six transmembrane (TM) helices to an unstructured polypeptide (referred to as the Unfolded Coil or U_c state) while exhibiting two unfolding intermediates as we described previously (Fig. 1B, upper inset) (14, 15). When relaxing the mechanical tension, we detect a gradual transition in FEC from the theoretical curve for U_c to a more compact state that is dependent on the presence of bicelles (Fig. 1, B and C and fig. S2). We designate the new state as Unfolded Helical (U_h) because it fits the FEC expected for a state in which all α-helical structures are restored for the TM helices and linkers. But the protein remains fully stretched along the pulling direction (Fig. 1B). Below the U_c to U_h transition, the FEC shifts to a yet more compact state (Fig. 1B, bottom inset), which we call the U_z state (unfolded zig-zag state). As discussed below, the U_z state appears to consist of bilayer inserted, but weakly interacting TM helices, arranged in a zigzag-like fashion. Finally, at low forces, GlpG finds its folded, native conformation (referred to as the N state) (Fig. 1B). Because formation of the native state could only be achieved at low tension below 2 pN, Brownian motions of the magnetic bead precludes observation of any detailed intermediates during the refolding process under these conditions.

In hopes of seeing folding at higher forces where extension measurements can be more precise, we screened for more favorable folding conditions using a simple force jump experiment (fig. S3) (10, 17, 18). We find that addition of 1,2-dimyristoyl-sn-glycero-3-phosphorylglycerol (DMPG) is effective in enhancing GlpG refolding. When we add 30 mol% DMPG lipids in the bicelle phase, the refolding probability after a waiting time of 200 s at 5 pN tension increases by a factor of 7 (Fig. 1D). The FECs obtained with and without 30 mol% DMPG lipids almost exactly overlap with one another, preserving the coil-to-helix transition as well as the formation of the U_z state (fig. S2 and S4). These observations suggest that the addition of negatively charged lipids does not fundamentally alter the folding pathway, but selectively enhances refolding commencing from the U_z state.

With the ability to observe folding at higher forces, we tested the potential for achieving high resolution by examining the Brownian motion of magnetic beads in the bicelle phase. With high-speed tracking at 1.2 kHz and the force above 5 pN, we obtain an Allan deviation (i.e., uncertainty in our tracking) of less than 1 nm when median filtered at 5 Hz (200 ms), corresponding to a resolution of a few amino acids (Fig. 1E). Also, we observe folding with a reasonable probability up to 8 pN tension, the force where the U_z state starts to form (Fig. 1D).

On the basis of these observations, we developed a force-application protocol to monitor the folding process of single GlpG proteins (Fig. 2). We first induce full unraveling of GlpG to the U_c state by applying a high mechanical tension above 20 pN, and then make a force jump to a low force level between 5 and 8 pN (Fig. 2A). The force jump takes a finite time of ~300 ms, during which single GlpGs relax to the U_z state (Fig. 2B, right). We experimentally confirmed that the force jump indeed reaches the same extension state as that reached through slow gradual force relaxation at –1 pN/s (Fig. 2B, left). When maintained at the low force level, the magnetic bead begins to show complex up-and-down movements, finally culminating in a compact N state (Fig. 2A, 5 pN phases). Achievement of the N state is verified by observing the extension expected for the N state after jumping the tension back to ~20 pN. By repeating our designed mechanical cycle, we can observe folding of single GlpG molecules multiple times.

Fig. 2. Direct observation of single GlpG folding.

(A) Designed mechanical cycle for inducing refolding of single GlpG proteins. The gray and black traces are 1.2-kHz raw data and 5 Hz median-filtered data, respectively. (B) Representative time-resolved traces comparing the extensions following slow force relaxation and force jump. Lower inset shows the extension difference (ΔzUz) at indicated force levels. Right inset shows a closed-up trace of the force jump that takes ~300 ms. (C) Representative folding traces for WT, A206G and L155A GlpG under 6 pN tension. Right insets show close-up traces exhibiting reversible transitions among the U_z, I₁, and I₂ states. (D) BIC values for indicated number of states. n = 20, 21 and 11 for the WT, A206G and L155A cases, respectively. (E) Positions of the intermediate states in the normalized extension space (at 6 pN, n is same as (D); at 5 pN, n = 21, 24 and 14 for WT, A206G and L155A, respectively). Error bars represent s.e.m. (F) Transition kinetics between the neighboring states at indicated force levels. In N-to-I₂ transition, both slow (inset, black) and fast (red) rates are displayed. Error bars represent s.e.m.

With the reduced Brownian motion of the magnetic bead in the 5–8 pN force window, we are able to see distinct conformational changes during refolding when the extension traces are median filtered down to 5 Hz (Fig. 2C, black traces). Application of hidden Markov modeling (HMM) and Bayesian information criteria (BIC) to the time-resolved extension traces indicates that the data are best fit by a total of four states: two intermediate states (referred to as I₁ and I₂) in addition to the U_z and N states (Fig. 2, C to E and fig. S5) (19).

The magnetic beads show many upward (i.e., local unfolding) and downward movements (local folding) before reaching the native N state extension. Thus, the resultant time-resolved traces report reversible intermediate folding/unfolding events—equilibrium processes from which we can directly reconstruct the folding energy landscape. The local folding and unfolding processes pass through the same I₁ and I₂ intermediate states, justifying a one-dimensional representation of the energy landscape (20, 21). Our HMM analysis indicates that while rates connecting non-neighboring states are negligible, the transitions connecting the neighboring states are well described by single rates falling in a narrow region between 0.1 to 10 s⁻¹ (Fig. 2F and fig. S6). An exception is the N-to-I₂ transition that shows two different rates. One N-to-I₂ transition is relatively fast with an average dwell time in N of only ~5 s, indicating incomplete refolding (fig. S6 and Fig. 2F, red symbols). The other subset of the N states has higher stability, requiring higher forces (~ 8 pN) to show unfolding within our observation time, and presumably corresponds to a correctly folded state (fig. S7 and Fig. 2F, inset).

We next examined whether we could extend our MT folding experiment to true bilayers, by reconstituting GlpG in vesicles produced through slow detergent removal (Fig. 3A and fig. S8). For the vesicle-reconstituted GlpGs, we observe cooperative unraveling of six TM helices to the U_c state, similar to what is observed for the bicelle-reconstituted GlpGs (Fig. 3B, 1st stretching cycle). We also observe the expected coil-to-helix transition during the relaxation phase (Fig. 3C) as well as complete refolding, albeit with low probability (Fig. 3B, 6th stretching). Since there are no free vesicles, these observations suggest that single GlpGs remain bound to the vesicle membranes after their unraveling to unstructured polypeptides. Nevertheless, many of the vesicle-reconstituted GlpGs fail to refold (e.g., Fig. 3B, 2nd and 5th stretching). The refolding probability at 1 pN is only ~15 % with a 200 s wait time, in contrast with a refolding probability approaching 100 % seen for the bicelle-reconstituted GlpGs. We also find that the FECs of vesicle-reconstituted GlpGs persistently follow the U_h curve and fail to form the loosely stretched U_z state (Fig. 3C, lower inset).

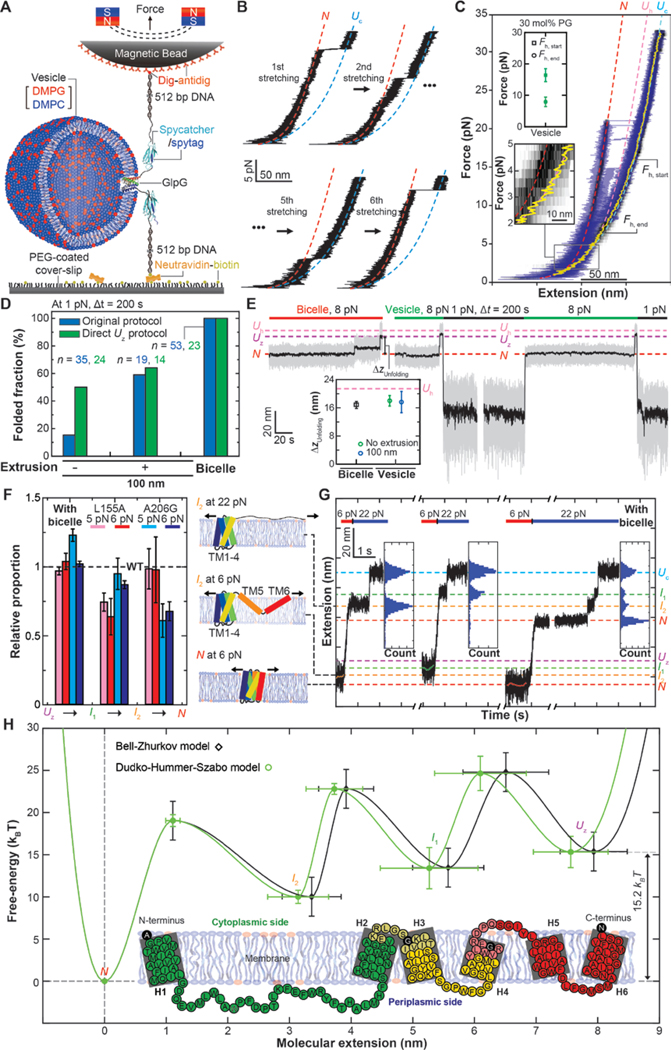
Fig. 3. Characterization of folding properties for vesicle- and bicelle-reconstituted single GlpGs.

(A) Schematic of single-molecule MT folding experiments for GlpGs reconstituted in vesicle membranes. (B) Representative FECs showing successive stretching cycles applied to a single GlpG protein in a vesicle membrane. (C) FEC of vesicle-reconstituted single GlpG proteins averaged over 5 cycles of mechanical stretching and relaxation (black heat map). To show individual unfolding events, representative raw traces during stretching are overlaid (blue traces). Other definitions are the same as in Fig. 1B. Upper inset shows the average F_h,start and F_h,end values. Lower inset: a magnified view of the FEC between 5 and 2 pN force. (D) Refolding probability determined under different membrane conditions. n is the number of trials. (E) Representative traces of the folding protocol that directly induces the U_z state. Inset shows the extension changes (Δz_Unfolding) during unfolding at 8 pN under indicated membrane conditions. Pink dotted line is the expected extension change when reaching the U_h state. (F) Normalized transition rates determined for the A206G and L155A single-point mutants relative to the WT case (dashed line). Right illustrations show an anticipated conformational status of GlpG in each indicated state. Error bars represent s.e.m (G) Representative force-jump experiments applied for the intermediate states. Each inset shows the distribution of extension values recorded during high-force unfolding. Estimated extensions for individual states are shown as the dashed lines. (H) Folding energy landscapes of a single GlpG protein along the molecular extension reconstructed based on the Bell-Zhrukov (black trace) and the Dudko-Hummer-Szabo models (green trace). Inset: detailed structural segments in the folding pathways of GlpG. Each structurally segment is denoted in distinct colors. Black-colored amino acids correspond to the boundaries of the intermediate states. Faint colors around the boundaries represent the measurement errors (s.d.).

We hypothesized that polypeptide insertion into bilayers may be more difficult in vesicles compared to bicelles, which would explain the barrier to folding and the block to formation of the U_z state if the U_z state was indeed membrane inserted. To explore this possibility, we tested whether decreasing vesicle size would enhance folding because increased bilayer curvature may allow more facile insertion of the TM helices into the membrane (22). Indeed, when we decrease the diameter of reconstitution vesicles to 100 nm by extrusion, the refolding probability at 1 pN increases to ~60 % (Fig. 3D and fig. S8).

We next attempted to avoid membrane extraction and directly access the U_z state by applying a moderate force of 8 pN, a tension at which the U_z state was seen to form in FEC (referred to as the direct-U_z protocol). We tested the feasibility of this protocol first with the bicelle-reconstituted GlpGs, and found that application of 8 pN indeed directly induces the U_z state (Fig. 3E, left). Subsequent lowering of the force leads to complete refolding in bicelles (fig. S9). When we apply 8 pN to the vesicle-reconstituted GlpGs, the resultant unfolding step is almost identical to that expected for the U_z state (Fig. 3E, right and inset). When we subsequently induce refolding by lowering the force to 1 pN, the refolding probability in vesicles increases relative to refolding from the U_c state (~50 % versus ~15%) (Fig. 3, D and E), consistent with the possibility that this 8 pN unfolding selectively disrupts the tertiary structure while decreasing exposure of the TM helices to outside of the lipid bilayer, thereby reducing the need to reinsert TM helices during refolding.

Our analysis of the end-to-end distance of the U_z state further suggests that the penetration depths of TM helices in the U_z state might not be enough to completely reach the other side of the lipid bilayer (fig. S10 and Fig. 3F, right). If so, tertiary structure formation would be intimately coupled with the membrane insertion (Fig. 3F, right; compare I₂ and N at 6 pN). To determine whether membrane insertion or tertiary structure formation dominate the energy barriers, we examined the local folding/unfolding kinetics of the two single-point GlpG mutants in the bicelle phase (23). The N-terminal (L155A on TM helix 2) and C-terminal (A206G on TM helix 4) mutants selectively slow down the I₁-to-I₂ and the I₂-to-N transitions, respectively (Fig. 3F, left and fig. S11). These observations suggest that the tertiary structure formation makes a major contribution to the observed energy barriers. Moreover, these mutant data are consistent with GlpG folding occurring in a unidirectional manner from the N- to C-terminus.

To map the partially folded structures in I₁ and I₂, we made force jumps to ~20 pN while the protein sampled either I₁ or I₂ in the course of refolding (Fig. 3G). Surprisingly, the extensions after the force jump exactly coincide with the two intermediates of the high-force unfolding (Fig. 3G and Fig. 1B, upper inset), which indicates that the low-force folding/unfolding and the high-force unfolding intermediates share the same partially folded structures, albeit with different levels of stretching in the unfolded regions (Fig. 3F, right; compare I₂ at 6 pN with I₂ at 22 pN). We therefore used the extension difference between I₂ and N at 22 pN to estimate that I₂ is positioned at the C-terminus of TM helix 4 (Fig. 3H, inset). Likewise, we used the extension difference between U_c and I₁ at 22 pN to estimate that I₁ is positioned after the TM helix 2. Combined with the mutant data above, we conclude that GlpG folds in an N-to-C direction, largely in units of helical hairpins.

Based on the structural assignments made above, we examined one more GlpG mutant in which two hydrophobic residues in the long linker region between TM helix 1 and 2 are mutated to negatively charged residues (L121E/F133E) (Fig. 3H, inset and fig. S12B). Although such mutations reportedly increase the energy barrier for membrane insertion and flip-flop (24, 25), we did not detect any sign of slowing down in the transition between U_z and I₁ (fig. S12). This data supports again our conclusion that the TM helices have made their initial membrane integration as the U_z state forms. In particular, because of the many polar and charged residues in the long linker, we suspect that TM helices 1 and 2 of GlpG are inserted more deeply than other TM helices in the zigzag-aligned U_z state.

Finally, we constructed one-dimensional energy landscapes for the reversible folding/unfolding process of single GlpG proteins using the Bell (26) and the Dudko-Hummer-Szabo models (27). Both models indicate a free energy difference (ΔG₀) of 15.2 k_BT between the native state (N) and the zigzag Uz state albeit with slightly different intermediate positions (Fig. 3H). As expected, this ΔG₀ value is slightly larger than the estimates from previous ensemble measurements under less favorable folding conditions (7.1 to 13.9 k_BT) (23, 28, 29). When we apply the Crooks fluctuation theorem to the FECs as shown in Fig. 1B, we obtain an estimate of ~115 k_BT for a free energy difference between the N and the U_c states (fig. S13 and Table. S1), almost 8-fold larger than 15.2 k_BT estimated between the N and U_z states. We attribute this larger free energy difference to additional processes imposed on the high-force unfolding, such as pulling TM helices out of the membrane and disruption of secondary structures. These observations attest to the fundamental difference between the energy barriers seen during high-force unfolding and the low-force folding/unfolding processes. At lower forces, we can explore rearrangements of intact TM helices that occur largely within the lipid bilayer, more closely reflecting the process expected for second stage folding (2).

Using the experimental methods established with GlpG, we next sought to observe the folding process of a single human β₂-adrenergic receptor (β₂AR), which belongs to the G protein coupled receptor (GPCR) family (Fig. 4A). We first examined the FEC and again observed a large mechanical hysteresis in the unfolding and refolding of β₂AR (Fig. 4B). Because β₂AR has an odd number of TM helices, the DNA handles are pulling on opposite sides of the bilayer and we note the possibility that after the cooperative unraveling, some part of β₂AR may reside within the lipid bilayer (most likely the first TM helix; see fig. S14). During the relaxation phase, we observed the coil-to-helix transition in nearly the same force range as that observed for GlpG. Moreover, below 8 pN, the FEC of β₂AR became shorter than the U_h extension consistent with the formation of a zigzag-aligned U_z state (Fig. 4B and fig. S15).

Fig. 4. Direct observation of the complete folding pathway of human β₂AR.

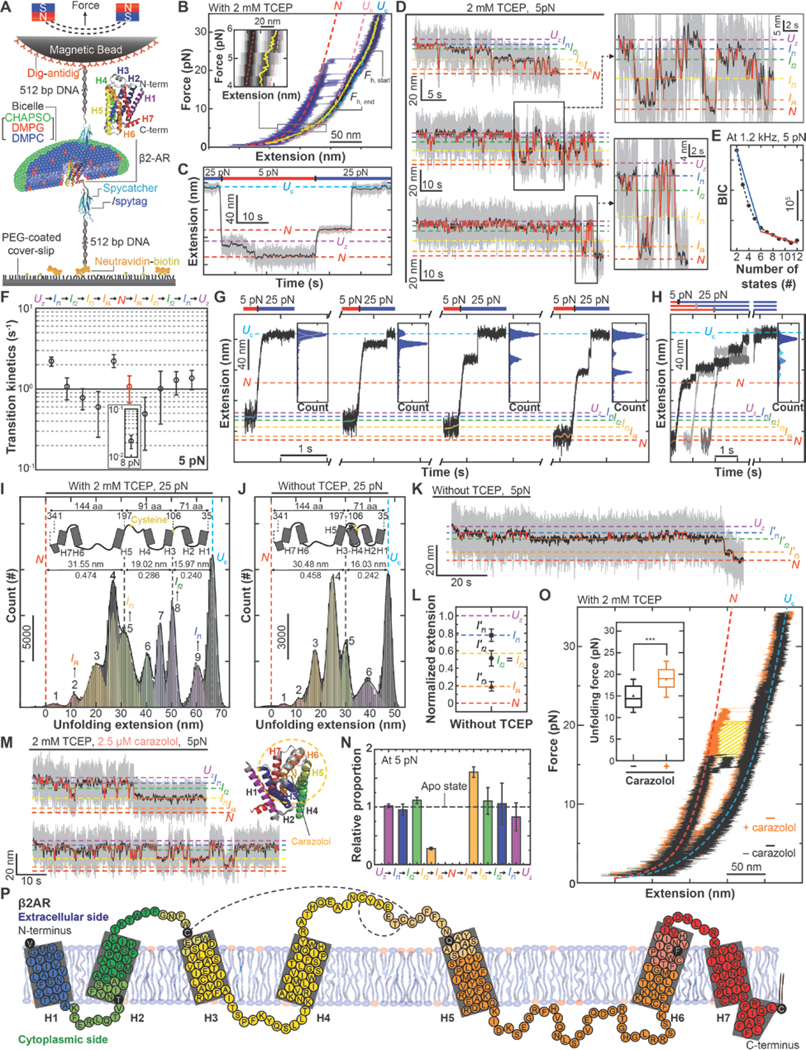
(A) Schematic diagram of single-molecule MT folding experiment for β₂AR. (B) FEC of single β₂AR proteins averaged over 6 cycles of mechanical stretching and relaxation (black heat map). To show individual unfolding events, representative raw traces during stretching are overlaid (blue traces). Other definitions are the same as in Fig. 1B. Inset: an enlarged view of the FEC between 6 and 4 pN force. (C) Designed mechanical cycle for inducing refolding of human β₂AR at low force levels. (D) Representative time-resolved traces for β₂AR folding under 5 pN tension (with 2 mM TCEP). Right insets show close-up trajectories. Red traces show the transitions between four intermediates identified the HMM. (E) BIC values for indicated numbers of states (n = 18). (F) Transition kinetics between the neighboring states at 5 pN. In N-to-I_f4 transition, both slow (inset, black) and fast (red) rates are displayed. Error bars represent s.e.m. (G, H) Representative traces for the force jump experiments applied to individual folding intermediates (G) and the native state (H). Each inset shows an extension distribution during high-force unfolding. (I, J) Extension distribution during high-force unfolding initiated from the native N state. (n = 29, 13 for the cases with 2 mM TCEP and without TCEP, respectively). The peaks indicate the fit centers of multiple Gaussian functions (colored for each function). Upper insets show structural diagrams of β₂AR to guide mapping onto the structure. (K) Representative β₂AR folding trace at 5 pN with no TCEP (n = 10). HMM analysis finds three intermediate states (I_f1^´, I_f2^´, I_f3^´). (L) Normalized extensions for β₂AR folding intermediates under no TCEP condition. Dashed lines are anticipated extensions for the intermediates under 2 mM TCEP condition. Error bars are s.d. (M) Representative folding traces for β₂AR at 5 pN in the presence of 2.5 μM carazolol (with 2 mM TCEP). Right inset shows the structure of carazolol-bound human β₂AR. Yellow circle indicates interaction regions between carazolol and β₂AR. (N) Normalized rates determined for carazolol-bound β₂AR relative to the apo β₂AR case (dashed line). (O) Representative FECs of β₂AR showing high-force cooperative unfolding in the presence (orange) and absence (black) of 2.5 μM carazolol (with 2 mM TCEP). N and U_c are defined the same as in (B). Inset: distributions of unfolding forces with (orange, n = 26) and without (black, n = 35) carazolol. Error bars are s.d. (P) Detailed structural segments in the folding pathways of β₂AR. Each structurally segment is denoted in distinct colors. Other notations are same as inset in Fig. 3H.

To observe the folding process of human β₂AR, we used the original folding protocol starting from the U_c state (Fig 4C). We first induced mechanical unraveling of a single β₂AR U_c state by applying 25 pN tension, and then induced the U_z state through force quenching to 5 pN. We re-confirmed that the force quenching within 300 ms yielded the same U_z state as that obtained through slow force relaxation (fig. S16). With the mechanical tension kept at 5 pN, the magnetic bead shows complex up-and-down movements, ending in a compact N state (confirmed to be the native state through re-application of high force) (Fig. 4C).

By applying the HMM and BIC analyses to the time-resolved extension traces of the magnetic beads, we identify six major states (thus four intermediates) in the folding process of human β₂AR (Fig. 4, D and E). Both local folding and unfolding processes share these four intermediate states (referred to as I_f1, I_f2, I_f3 and I_f4), indicative of the one-dimensionality of the folding energy landscape. The transition rates connecting the neighboring states fall between 10⁻¹ and 10 s⁻¹ while all other rates are negligibly small (Fig. 4F and fig. S17). As was the case for GlpG, we observed two groups of the N states: one with a lower stability (Fig. 4F, red symbol) and the other reflecting a correctly folded structure (Fig. 4F, inset).

To measure the number of amino acids unfolded in the structures of the four intermediates, we applied the force-jump technique to each intermediate observed during the low-force folding/unfolding processes. We find that all the four intermediates correspond to distinct extension states at 25 pN, reflecting a direct connection between the low-force folding/unfolding and the high-force unfolding intermediates (Fig. 4G). We thus sought to use the extension states of the high-force unfolding intermediates to infer the partially folded structures in individual low-force intermediates. The distribution of intermediate extension states during high force unfolding clearly revealed a total of nine peaks (Fig. 4, H and I).

To map the unfolded structures on the high-force unfolding intermediates, we took advantage of the fact that in the native structure of human β₂AR, there is one conserved disulfide bond formed between C106 and C191, which locks TM helices 3 and 4 and the extracellular linker 2 (ECL2) into one structural unit (Fig. 4, I and J, upper insets). We reasoned that with removal of the reducing agent tris(2-carboxyethyl)phosphine (TCEP), the high-force unfolding intermediates related to the region linked by the disulfide bond might disappear from the extension distribution. Indeed, in the absence of TCEP, the first five peaks (peaks 1 to 5) and the last two peaks (peaks 9 and U_c) are essentially preserved, but the three peaks in the middle (peaks 6 to 8) selectively disappear (Fig. 4, I and J). We further note that in the absence of TCEP, the extension change spanning the first five peaks is distinctly larger than that spanning the last two peaks by a factor of 1.98. This value closely matches the 2.02 ratio of the number of amino acids placed C–terminal to the disulfide bond (144 a.a.) to that N-terminal to the disulfide bond (71 a.a.) (Fig. 4I). Thus, our observations point to a hypothesis that the first five peaks correspond to unfolding from C-terminus to TM helix 5. In the absence of TCEP, unfolding from ECL2 to TM helix 3 is prevented by the disulfide, so that the last two peaks correspond to unfolding of the two N-terminal helices and ECL1. By aligning the unfolding traces in Figure 4G and 4H with one another, we find that folding intermediates I_f1, I_f2, I_f3 and I_f4 correspond to the high force unfolding intermediate peaks 9, 8, 5 and 2, respectively (Fig. 4I and fig. S18). Together, our data suggested the human β₂AR shows unidirectional folding from the N- to the C-terminus.

To test the validity of our structural assignment, we monitored the folding process at 5 pN in the absence of TCEP. The HMM and BIC analyses indicate a reduction in the number of folding intermediates to three (Fig. 4K and fig. S19). The positions of these three folding intermediates (I_f1^′, I_f2^′ and I_f3^′) matched well with those expected when I_f2 and I_f3 are merged (Fig. 4L), reaffirming that the transition from I_f2 to I_f3 corresponds to folding of TM helices 3 and 4 and ECL2.

We also examined the effect of carazolol, a partial inverse agonist of human β2ARs, on the 5-pN folding process. While the presence of 2.5 μM carazolol did not change the positions of the four intermediates in the extension space, it markedly inhibited any transition beyond I_f3 (Fig. 4M and fig. S19). This inhibition was highly selective because the transition U_z to If3 remained minimally affected (Fig. 4N), suggesting that single human β₂ARs folds normally up to ECL2, but fails to fold TM helices 5 and 6 onto the growing structure in the presence of carazolol. When we examined unfolding by force ramping, carazolol increases the forces at which unfolding occurs by 4.5 pN on average (Fig. 4O, inset), indicating that additional work of more than 50 k_BT is required to induce the unraveling of single β₂ARs in the presence of carazolol (Fig. 4O, shaded area). Thus, our observations suggest distinct effects of carazolol on human β₂AR folding and unfolding. Carazolol inhibits the addition of TM helices 5 and 6 during folding, perhaps being loosely located in the incomplete ligand binding pocket formed by TM helices 1–4 and sterically interfering with incoming TM helices 5 and 6. In the presence of excess carazolol, it is also possible that carazolol is already bound to TM helices 5 and 6 as carazolol makes an extended aromatic network with the residues on TM helices 5 and 6. However, once folded, carazolol binding dramatically stabilizes the tertiary structure as expected (30, 31).

The identified folding pathway of the human β₂AR reveals several interesting features (Fig. 4P). The first intermediate I_f1 corresponds to association between the first TM helix and the following linker helix, completing insertion of this nascent structure with respect to the residing membrane structure. The second TM helix folds on to this structure to form the first helical hairpin, completing intermediate I_f2. The next folding step involves the addition of TM helices 3 and 4 as well as ECL2 (forming I_f3). We note that the positions of I_f2 and I_f3 closely map to the cysteine residues of C106 and C191, thereby potentially consolidating the formed tertiary structure via disulfide bonding. The transition from I_f3 to I_f4 involves formation of the helical hairpin consisting of the TM helices 5 and 6. This folding step is found to be markedly inhibited in the presence of carazolol. The last step from I_f4 to N involves addition of the TM helix 7 and the C-terminal membrane-associated helix onto the structure, completing the known structure of human β₂AR (30, 31). Although our experimental data consistently support the folding pathway delineated above, we cannot rule out the possibility that an alternative folding pathway exists in physiological milieu. We also note that the folding pathway presented here is a coarse-grained one down to a 5 Hz sampling rate. Enhancing the bandwidth of our methods would reveal a more complex and dynamic nature of the polytopic membrane protein folding (12). Finally, we note the possibility that the strategy of using disulfide bonds to map the four folding intermediates of β₂AR can be extended to other membrane proteins.

Although E. coli GlpG and human β₂AR are at an enormous evolutionary distance, both integral membrane proteins accrue structure largely in units of helical hairpins, with a unidirectional N-to-C folding as a single, predominant pathway out of a countless number of permutations in the possible folding pathways. Unidirectional N-to-C folding is consistent with several prior studies (28, 32–36), and would permit the nascent N-terminal chain to commence folding without needing to wait for the more C-terminal TM helices to be translated, thereby reducing the risk of generating misfolded structures. Thus, the folding processes of integral membrane proteins may be evolutionarily selected and tailored to fit with co-translational folding.