On the Practical Consequences of Misfit in Mokken Scaling

Abstract

Mokken scale analysis is a popular method to evaluate the psychometric quality of clinical and personality questionnaires and their individual items. Although many empirical papers report on the extent to which sets of items form Mokken scales, there is less attention for the effect of violations of commonly used rules of thumb. In this study, the authors investigated the practical consequences of retaining or removing items with psychometric properties that do not comply with these rules of thumb. Using simulated data, they concluded that items with low scalability had some influence on the reliability of test scores, person ordering and selection, and criterion-related validity estimates. Removing the misfitting items from the scale had, in general, a small effect on the outcomes. Although important outcome variables were fairly robust against scale violations in some conditions, authors conclude that researchers should not rely exclusively on algorithms allowing automatic selection of items. In particular, content validity must be taken into account to build sensible psychometric instruments.

Item response theory (IRT) models are used to evaluate and construct tests and questionnaires, such as clinical and personality scales (e.g., Thomas, 2011). A popular IRT approach is Mokken scale analysis (MSA; e.g., Mokken, 1971; Sijtsma & Molenaar, 2002). MSA has been applied in various fields where multi-item scales are used to assess the standing of subjects on a particular characteristic or the latent trait of interest. In recent years, the popularity of MSA has increased. A simple search on Google scholar with the keywords “Mokken Scale Analysis AND scalability” from 2000 through 2019 yielded about 1,200 results, including a large set of empirical studies. These studies were conducted in various domains, such as in personality (e.g., Watson et al., 2007), clinical psychology and health (e.g., Emons et al., 2012), education (e.g., Wind, 2016), and in human resources and marketing (e.g., De Vries et al., 2003). Both the useful psychometric properties of MSA and the availability of easy-to-use software (e.g., the R “mokken” package; van der Ark, 2012) explain the popularity of MSA.

As discussed in the following, within the framework of MSA, there are several procedures that can be used to evaluate the quality of an existing scale or set of items that may form a scale. In practice, however, a set of items may not comply strictly with the assumptions of a Mokken scale and a researcher is then faced with a difficult decision: Include or exclude the offending items (Molenaar, 1997a)? The answer to this question is not straightforward. On one hand, the exclusion of items must be carefully considered because it may compromise construct validity (see American Educational Research Association et al., 2014, for a discussion of the types of validity evidence). On the other hand, it is not well known to what extent the retention of items that violate the premises of a Mokken scale affect important quality criteria.

The present study is aimed at investigating the effects of retaining or removing items that violate common premises in MSA on several important outcome variables. This study therefore offers novel insights into scale construction for practitioners applying MSA, going over and beyond what MSA typically offers. This study is organized as follows. First, some background on MSA is provided. Second, the results of a simulation study are presented, in which the effect of model violations on several important outcome variables was investigated. Finally, in the discussion section, an evaluative and integrated overview of the findings is provided and main conclusions and limitations are discussed.

MSA

For analyzing test and questionnaire data, MSA provides many more analytical tools than classical test theory (CTT; Lord & Novick, 1968), while avoiding the statistical complexities of parametric IRT models. One of the most important MSA models is the monotone homogeneity model (MHM). The MHM is based on three assumptions: (a) Unidimensionality: All items predominantly measure a single common latent trait, denoted as θ; (b) Monotonicity: The relationship between θ and the probability of scoring in a certain response category or higher is monotonically nondecreasing; and (c) Local independence: An individual’s response to an item is not influenced by his or her responses to other items in the same scale. Assumptions (a) through (c) allow the stochastic ordering of persons on the latent trait continuum by means of the sum score, when scales consist of dichotomous items (e.g., Sijtsma & Molenaar, 2002, p. 22). For a discussion on how this property applies to polytomous items, see Hemker et al. (1997) and van der Ark (2005).

In MSA, Loevinger’s H coefficient (or the scalability coefficient; Mokken, 1971, pp. 148–153; Sijtsma & Molenaar, 2002, chapter 4) is a popular measure to evaluate the quality of each item i and of sets of items, in relation to the test score distribution. The H coefficient can be obtained for pairs of items (H_ij), for individual items (H_i), and for the entire scale (H). The H_i is defined as following for dichotomous items (Sijtsma & Molenaar, 2002, pp. 55–58):

$$H_i=\frac{\mathrm{Cov}(X_i,R_{-i})/({{\sigma }_X}_i\times {{\sigma }_R}_{-i})}{\mathrm{Co}{v}_{\max }(X_i,R_{-i})/({{\sigma }_X}_i\times {{\sigma }_R}_{-i})}=\frac{\mathrm{Cov}(X_i,R_{-i})}{\mathrm{Co}{v}_{\max }(X_i,R_{-i})}=1-\frac{\sum _{j\ne i}(P_i-P_{\mathrm{ij}})}{\sum _{j>i}{P}_i\times (1-P_j)+\sum _{j>i}{P}_j\times (1-P_i)}$$

In this formula, X_i denotes individuals’ responses to item i. P_i and P_j denote the probability of a correct response to—or endorsing—items i and j, P_ij denotes the probability of correct response to or endorsing both items i and j, R_−i denotes the vector of restscores (that is, the individuals’ sum scores excluding item i), and σ_Xi and σ_R−i denote the standard deviation of the item scores and of the restscores, respectively. The item-pair and scale coefficients can be easily derived from H_i, by removing the summation symbols (for H_ij) or adding an additional one (for H) from/to all the terms in the equation above. For polytomous items, the scalability coefficients are based on the same principles as for dichotomous items, but their formulas are more complex, as probabilities are defined at the levels of item steps (Molenaar, 1991; Sijtsma & Molenaar, 2002, p. 123; see also Crişan et al., 2016 for a comprehensive explanation of how these can be obtained).

Loevinger’s H coefficient reflects the accuracy of ordering persons on the θ scale using the sum score as a proxy. If the MHM holds, then the population H values for all item pairs, items, and the entire scale are between 0 and 1 (Sijtsma & Molenaar, 2002, Theorem 4.3). Larger H coefficients are indicative of better quality of the scale (“stronger scales”), whereas values closer to 0 are associated with “weaker scales.” A so-called Mokken scale is a unidimensional scale comprised of a set of items with “large-enough” scalability coefficients, which indicate that the scale is useful for discriminating persons using the sum scores as proxies for their latent θ values. There are some often-used rules of thumb that provide the basis for MSA (Mokken, 1971, p. 185). A Mokken scale is considered a weak scale when .3 ≤H < .4, a medium scale when .4 ≤H < .5, and a strong scale when H≥ .5 (Mokken, 1971; Sijtsma & Molenaar, 2002). A set of items for which H < .3 is considered unscalable. The default lower bound for H_i and H is .3 in various software packages, including the R “mokken” package (van der Ark, 2012) and MSP5 (Molenaar & Sijtsma, 2000).

A popular feature of MSA is its item selection tool, known as the automated item selection procedure (AISP; Sijtsma & Molenaar, 2002, chapters 4 and 5). The AISP assigns items into one or more Mokken (sub-)scales according to some well-defined criteria (see e.g., Meijer et al., 1990) and identifies items that cannot be assigned to any of the selected Mokken scales (i.e., unscalable items). The unscalable items may not discriminate well between persons and, depending on the researcher’s choice, may be removed from the final scale.

Both the AISP selection tool and the item quality check tool are based on the scalability coefficients. However, it is important to note that a suitable lower bound for the scalability coefficients should ultimately be determined by the user (Mokken, 1971), taking the specific characteristics of the data and the context into account. Although several authors emphasized the importance of not blindly using rules of thumb (e.g., Rosnow & Rosenthal, 1989, p. 1277, for a general discussion outside MSA), many researchers use the default lower bound offered by existing software when evaluating or constructing scales.

How is MSA Used in Practice?

Broadly speaking, there are two types of MSA research approaches: In one approach, MSA is used to evaluate the item and scale quality when constructing a questionnaire or test (e.g., De Boer et al., 2012; Ettema et al., 2007). In the other approach, MSA is used to evaluate an existing instrument (e.g., Bech et al., 2016; Bielderman et al., 2013; Bouman et al., 2011). Not surprisingly, researchers using MSA in the construction phase tend to remove items more often based on low scalability coefficients and/or the AISP results (e.g., Brenner et al., 2007; De Boer et al., 2012; De Vries et al., 2003) than researchers who evaluate existing instruments. However, researchers seldom use sound theoretical, content, or other psychometric arguments to remove items from a scale.

Researchers evaluating existing scales often simply report that items have low coefficients, but they are typically not in a position to remove items (e.g., Bech et al., 2016; Bielderman et al., 2013; Bouman et al., 2011; Cacciola et al., 2011, p. 12; Emons et al., 2012, p. 349; Ettema et al., 2007). Thus, practical constraints often predetermine researchers’ actions, but it is unclear to what extent other variables, such as predictive or criterion validity (American Educational Research Association et al., 2014), are affected by the inclusion of items with low scalability. What is, for example, the effect on the predictive validity of the sum scores obtained from a more homogeneous scale as compared to a scale that includes lower scalability items? For some general remarks about the relation between homogeneity and predictive validity, and about one of the drawbacks of relying on the H coefficient, see the online supplementary materials.

Practical Significance

In this study, the existing literature on the practical use of MSA (see Sijtsma & van der Ark, 2017 and Wind, 2017 for excellent tutorials for practitioners in the fields of psychology and education) is extended by systematically investigating how practical outcomes, such as scale reliability and person rank ordering, were affected by scores obtained from scales containing items with low scalability coefficients. This study also extends previous literature on the practical significance (Sinharay & Haberman, 2014) of the misfit of IRT models (e.g., Crişan et al., 2017) by focusing on nonparametric IRT models.

In the remainder of this article, the methodology used to answer the research questions is described, the findings of this study are presented, and some insights for practitioners and researchers regarding scale construction and/or revision are provided.

Method

A simulation study using the following independent and dependent variables was conducted.

Independent Variables

The following four factors were manipulated:

Scale length

Scales consisting of I = 10 and 20 items were simulated. These numbers of items are representative for scales often found in practice (e.g., Rupp, 2013, pp. 22–24).

Proportion of items with low H_i values

In the existing literature using simulation studies, the number of misfitting items can vary between 8% and 75% or even 100% (see Rupp, 2013, for a discussion). In the present study, three levels for the proportion of items with H_i < .30 were considered: I_LowH = .10, .25, and .50. These levels of I_LowH operationalized varying proportions of misfitting items in the scale, which are labeled here as “small,”‘medium,’ and “large” proportions, respectively.

Number of response categories

Responses to both dichotomously and polytomously scored items with the number of categories equal to C = 2, 3, and 5 were simulated. Each dataset in a condition was based on one C value only.

Range of H_i values

For the I_LowH items, two ranges of item scalability coefficients H_i were considered: R_H = [.1, .2) and [.2, .3). Hemker et al. (1995) and Sijtsma and van der Ark (2017) suggested using multiple lower bounds for the H coefficients within the same analysis. They suggested using 12 different lower bounds, ranging from .05 through .55 in steps of .05. However, to facilitate the interpretation and to avoid a very large design, the authors chose the two ranges of item scalability coefficients mentioned above. For all fitting items, .3 ≤H_i≤ .7. The authors set the upper bound to .7 instead of 1 because few operational scales have H_i values larger than .7.

Design

The simulation was based on a fully crossed design consisting of 2(I) × 3(I_LowH) × 3(C) × 2(R_H) = 36 conditions, with 100 replications per condition.

Data Generation

Population item response functions according to two parametric IRT models were generated: The two-parameter logistic model (2PLM; e.g., Embretson & Reise, 2000) in the case of dichotomous items and the graded response model (GRM; Samejima, 1969) in the case of polytomous items. The 2PLM is defined as follows:

$$P(X_i=1|\theta )=\frac{e^{{\alpha }_i(\theta -{\beta }_i)}}{1+e^{{\alpha }_i(\theta -{\beta }_i)}},$$

where X_i denotes the response to item i (coded 0 and 1), a_i denotes the discrimination of item i, β_i denotes the difficulty of item i, and θ denotes the person’s level on the latent characteristic (or trait) continuum. Thus, the 2PLM defines the conditional probability of scoring a 1 (typically representing the “correct” answer) on item $i$ as a function of item and person characteristics. The GRM is a generalization of the 2PLM in case of polytomous items and is defined as follows:

$$P_{\mathrm{ix}}^{*}=\frac{e^{{\alpha }_i(\theta -{\beta }_{\mathrm{ix}})}}{1+e^{{\alpha }_i(\theta -{\beta }_{\mathrm{ix}})}},$$

where $P_{\mathrm{ix}}^{*}=P(X_i\ge x|\theta ),x=1,\dots ,C$, denotes the probability of endorsing at least category x on item i and β_ix denotes the category threshold parameters. By definition, the probability of endorsing the lowest category (x = 0) or higher is 1 and the probability of endorsing category C+ 1 or higher is 0. Thus, the GRM defines the probability of scoring at response category $x$ or higher on item $i$ as a function of item and person characteristics. The probability of endorsing response option x is computed as $P(X_i=x|\theta )=P_{\mathrm{ix}}^{*}-P_{i(x+1)}^{*}$.

The 2PLM or the GRM was used to generate item scores, using discrimination parameters¹ that were constrained to optimize the chances of generating items with H_i in the suitable ranges as required by $R_H$; see Table 1 for the values used for the true discrimination parameters during the data generation. These values were found after preliminary trial-and-error calibration analyses.

Table 1.

Ranges of Discrimination Parameters Used for Data Generation.

	${\alpha }_i$
$R_H$	Fitting items	Misfitting items
$.10\le H_i>.20$	U(2.30, 2.70)	U(0.35, 0.75)
$.20\le H_i>.30$	U(2.30, 2.70)	U(0.50, 0.90)

Note. The discrimination parameters were randomly generated from a uniform distribution U bounded by the values in parentheses.

In Table 1, the column labeled “Misfitting items” denotes the (100 ×I_LowH)% of items with scalability coefficients within the ranges R_H = [.2, .3) and [.1, .2). The column labeled “Fitting items” concerned the remaining items with scalability coefficients in the range [.3, .7]. In all cases, the difficulty/threshold parameters were randomly drawn from a category-specific uniform distribution U[0.3, 1.0], ensuring that consecutive threshold parameters differed by at least 0.3 units on the latent scale (the GRM requires that the threshold parameters are ordered) and that the items were randomly centered around 0 (thus allowing to generate “easy” and “difficult” items equally likely). This procedure resulted in threshold parameters ranging between approximately −3 and 3. The true θs were randomly drawn from the standard normal distribution. The item parameters together with the $\theta$ values defined the item response functions according to the 2PLM/GRM, which represent probabilities of responding in a particular response category. These probabilities were then used to determine the expected scalability coefficients H_i (Molenaar, 1991, 1997b; see also Crişan et al., 2016). The procedure was repeated for each replication within each simulation condition, until a set of items with (100 ×I_LowH)% of items having scalability coefficients within the range given by R_H was generated. Hence, the expected H_i coefficients were used to reject sets of item parameters that did not yield appropriate H_i values, and then, the acceptable sets of item parameters were used for item response generation.

Finally, item scores for N = 2,000² simulees were drawn from multinomial distributions with probabilities given by the 2PLM or the GRM. The resulting datasets constituted the Misfitting datasets. Subsequently, from each misfitting dataset, the (100 ×I_LowH)% of items with H_i < .3 were removed, resulting in the Reduced datasets. Dependent variables (listed below) on both the Misfitting and the Reduced datasets were computed, and the effect of DataSet = “Misfitting” and “Reduced” on each outcome was investigated.

Dependent Variables

The authors used the following outcome variables:

1. Scale reliability. Scale reliability was determined as the ratio of true scale score variance to observed scale score variance: $r_{\mathrm{XX}}={\sigma }_{\mathrm{True}}^2/{\sigma }_{\mathrm{Observed}}^2$. The observed scale scores were the sum scores across all items, for the entire sample. The true scale scores were computed as the sum of the expected item scores:

$$\mathrm{True}\mathrm{scale}\mathrm{score}=\sum _{i=1}^I\sum _{k=0}^{C-1}k\times P(X_i=k|\theta ).$$

• 2. Rank ordering. Spearman rank correlations between the true and the observed scale scores were computed. The goal was to investigate the differences in the rank ordering of simulees across the simulated conditions. Spearman rank correlations were always computed on the entire sample of simulees.

• 3. The Jaccard Index. The Jaccard Index (Jaccard, 1912) to compare subsamples of top selected simulees was used, according to their ordering based on either true scores or observed scores. The authors focused on subsamples of the highest scoring simulees to mimic decisions based on real selection contexts (e.g., for a job, educational program, or clinical treatment). Four selection ratios were considered: SR = 1.0, .80, .50, and .30, thus ranging from high through low selection ratios. The Jaccard Index is a measure of overlap between two sets and is defined as follows:

$$J(A,B)=\frac{|A\cap B|}{|A\cup B|}$$

The index ranges from 0% (no top selected simulees in common) through 100% (perfect congruence). For each dataset, the authors therefore computed four values of the Jaccard Index, one for each selection ratio.

• 4. Bias in criterion-related validity estimates. For each dataset, four criterion variables were randomly generated such that they correlated with the true θs at predefined levels (r = .15, .25, .35, and .45; e.g., Dalal & Carter, 2015). The bias in criterion-related validity for each criterion variable was computed as follows:

$$\mathrm{Bias}=r(\mathrm{observed}\mathrm{scale}\mathrm{score},\mathrm{criterion})-r(\mathrm{True}\mathrm{scale}\mathrm{score},\mathrm{criterion}).$$

The method was applied to the entire sample (SR = 1.0) as well as to the top selected simulees (SR = .80, .50, and .30). The goal was to assess the effect of low scalability items on the criterion validity, both for the entire sample and in the subsamples of the top selected candidates. Zero bias indicated that observed scores are as valid as true scores, whereas positive/negative bias indicated that observed scores overpredict/underpredict later outcome variables (in terms of predictive validity, for example).

Implementation

The simulation in R (R Development Core Team, 2019) was implemented. All code is freely available at the Open Science Framework (https://osf.io/vs6f9/).

Results

To investigate the effects of the manipulated variables on the outcomes, mixed-effects analysis of variance (ANOVA) models to the data were fitted, with DataSet as a within-subjects factor and the remaining variables as between-subjects factors. To ease the interpretation of the results, the authors plotted most results and they used measures of effect size (η² and Cohen’s d) to determine the strength and practical importance of the effects. Test statistics and their associated p values were not reported in this article for two reasons. First, the focus of this study is not on statistical significance of misfit. Second, due to the very large sample sizes, even small size effects can be statistically significant, which is of little interest. In addition, the authors did not report or interpret negligible effects in terms of effect size for parsimony (i.e., η² < .01; Cohen, 1992).

Scale Reliability and Rank Ordering

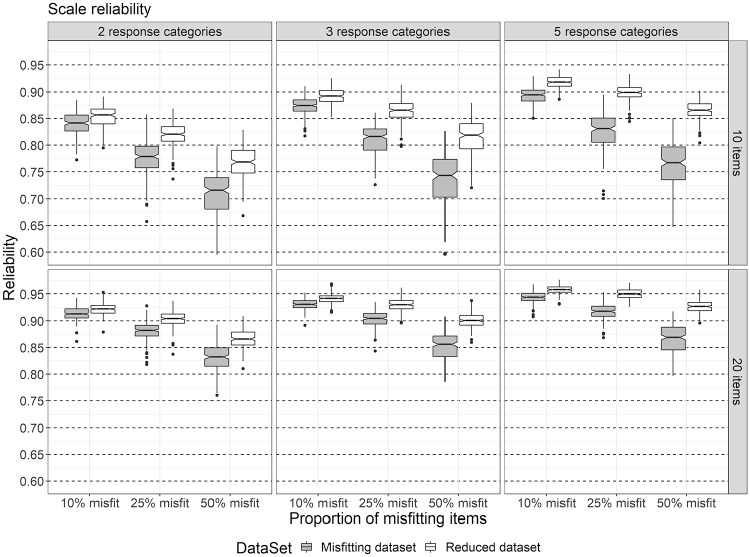
For score reliability, an average of 0.87 (SD = 0.07) was obtained; 95% of the estimates of reliability were distributed between 0.71 and 0.96. The ANOVA model with all main effects and two-way interactions explained 91% of the variation in reliability scores. Variation was partly explained by the two-way interactions between I_LowH× DataSet (η² = .02), and I × I_LowH (η² = .02), and largely explained by the main effects of I (η² = .36), I_LowH (η² = .26), C (η² = .11), and DataSet (η² = .10). As such, score reliability decreased as I_LowH increased, and this effect was stronger for shorter scales of I = 10. Removing the misfitting items from the scale led to an increase in score reliability, and this difference in reliability between the datasets increased slightly with I_LowH (see Figure 1 for an illustration of these effects).

Figure 1.

The distribution of reliability scores across the levels of I, C, and I_LowH, over all levels of R_H.

Elaborating on the effects of I_LowH and of removing the misfitting items on score reliability, the following was found: Averaged over I and C, score reliability decreased with .10 (from .91 to .81) in the DataSet = “Misfitting” as I_LowH increased from 10% to 50%. Removing the misfitting items improved reliability with .02 for I_LowH = 10%, .04 for I_LowH = 25%, and .06 for I_LowH = 50%. For these differences, Cohen’s d values of 1.70, 1.73, and 1.78 (for I_LowH =10%, 25%, and 50%, respectively) were obtained.

Similar conclusions can be drawn for the rank ordering of persons. The average rank correlation over all conditions was 0.93 (SD = 0.04); 95% of the estimated rank correlation coefficients ranged between 0.83 and 0.98. The ANOVA model with all main effects and two-way interaction effects explained 89% of the variability in the Spearman rank correlation values. The findings for person rank ordering were very similar to what the authors have found for scale reliability. In terms of the values of the Spearman correlation coefficient, as I_LowH increased in the DataSet = “Misfitting” conditions from 10% to 50%, they decreased, on average, from .95 to .93 and .90, respectively, averaged over I and C. Removing the misfitting items led to an improvement in the rank correlation of 0.02, on average. The rank ordering of individuals as determined by their true score was preserved by the observed score, even when 25% to 50% of items in a scale had scalability coefficients below .3. Removing those items led to a small increase in Spearman’s rank correlation.

Regarding score reliability and person rank ordering, our findings show that scale length together with the proportion of MSA-violating items and number of response categories were the main factors affecting these outcomes: Score reliability and rank ordering were negatively affected by the proportion of items violating the Mokken scale quality criteria, especially when shorter scales were used. These outcomes were more robust against violations when longer scales were used. Removing the misfitting items improved scale reliability and person rank ordering to some extent.

Person Classification

Because large rank correlations do not necessarily imply high agreement regarding sets of selected simulees (Bland & Altman, 1986), the Jaccard Index across conditions was computed. For SR = 1, the Jaccard Index is always 1 (100% overlap), as all simulees in the sample are selected. The top panel of Figure 2 shows the effect of the manipulated variables on the agreement between sets of selected simulees, for C = 2. The effects for the remaining values of C were similar and are therefore not shown here.

Figure 2.

The distributions of the Jaccard Index (top panel) and of bias in criterion-related validity estimates (bottom panel) as a function of I_LowH, DataSet, SR, and I, when C = 2.

The degree of overlap between sets of selected simulees was 80.9% averaged over all conditions, with a standard deviation of 0.09; 95% of the values of the Jaccard Index were distributed between 0.61 (about 61% overlap) and 0.94 (about 94% overlap). The ANOVA model with all main effects and two-way interactions accounted for 92.7% of the variation in the Jaccard Index. The variation was, to a large extent, accounted for by SR (η² = .66), I (η² = .10) and I_LowH (η² = .07) and to some extent by C (η² = .04), DataSet (η² = .02), and the interaction between I and SR (η² = .01). All other effects were negligible (η² < .01). As such, the overlap between sets of selected simulees increased as scale length and number of response options increased, it decreased as selection rate decreased, and it decreased as the proportion of items with H_i < 0.3 increased. Removing the misfitting items from the scale had a positive effect on the overlap between sets.

Elaborating on the previous findings and focusing on the effects of selection ratio, scale length, proportion of items with H_i < 0.3, and removing the misfitting items, the authors conclude that the Jaccard Index decreased from 0.91, on average, in the conditions with SR = .80, to 0.73 in the conditions with SR = .30 (Cohen’s d for this difference was 3.33). Moreover, the Jaccard Index value increased from 0.78, on average, when I = 10 to 0.84 when I = 20 (Cohen’s d for this difference was 0.68). The Jaccard Index decreased, on average, from 0.83 in the conditions where 10% of items had H_i < .3, to 0.76 in the conditions where 50% of items had H_i < .3 (Cohen’s d = 0.78). Removing the misfitting items resulted in an increase of the Jaccard Index to 0.85 (I_LowH = 10%; Cohen’s d = 0.97) and 0.80 (I_LowH = 50%; Cohen’s d = 1.13). Thus, it has been concluded that person selection is only marginally affected by the proportion of unscalable items or the extent to which the scalability coefficients are deviating from the 0.3 threshold.

Bias in Criterion-Related Validity Estimates

The authors results indicated that the bias in criterion validity estimates varied, on average, between −0.05 (SD = 0.03; true criterion validity of 0.45) and −0.02 (SD = 0.02; true validity of 0.15). The ANOVA model with all main effects and two-way interactions explained between 12.1% and 57.1% of the variance in bias, as true criterion validity increased. Thus, all effects became stronger as true validity increased. The largest effects corresponded to SR (η² between .04 and .20 across true validity scores), I (η² between .03 and .15), I_LowH (η² between .02 and .09), and C (η² between .01 and .06). There was also an effect of DataSet (η² between .01 and .03). More specifically, the absolute bias in criterion-related validity estimates increased as SR and I decreased, as I_LowH increased from 10% to 50%, and as C decreased. Removing the misfitting items from the scale led to a very slight reduction in bias. The bottom panel of Figure 2 depicts these effects, shown for a validity coefficient of 0.45 and scales consisting of dichotomous items. The effects of SR, C, I_LowH, and DataSet for the scale characteristics depicted in the bottom panel of Figure 2 were discussed.

Bias in validity estimates was larger in the top 30% subsample (median of −0.09) compared to the full sample (median of −0.05). Cohen’s d for this difference was 1.5. In terms of the correlation between predictor and criterion, the absolute difference between the full sample and SR = .30 was 0.05, on average. In other words, in the full sample, the average estimated validity coefficient was 0.41, while in the SR = .30 condition, it was 0.36. For scales with 10 dichotomous items, the average absolute bias in validity estimates was 0.07, and for scales with 20 items, it was 0.04.

Furthermore, the results showed that criterion-related validity was also affected by the proportion of misfitting items. For example, when the authors wanted to predict the scores on a criterion variable of the top 30% of the simulees using a short scale, the difference in bias between I_LowH = 10% and I_LowH = 50% was 0.03, with Cohen’s d = 0.67. Thus, a short scale of 10 dichotomous items of which five items violated the MSA quality criteria yielded an average criterion validity coefficient of .34. Removing the 50% misfitting items from the scale yielded on average a criterion validity coefficient of .35.

Discussion

In this study, the effects of keeping or removing items that are often considered “unscalable” in many empirical MSA studies were evaluated. Many empirical studies using Mokken scaling either remove items with H_i values smaller than .3 or try to explain why these items should be kept in the scale in spite of them violating this condition. By means of a simulation study, the authors systematically investigated whether scale reliability, person rank ordering, criterion-related validity estimates, and person classifications were affected by varying levels of incidence of misfitting items (in the MSA sense). Authors main results showed that all the outcomes considered were affected, to varying degrees, by some of the manipulated factors (scale length, number of response categories, and proportion of items with low scalability). Removing the misfitting items from the scales had a positive effect on the outcome measures.

Scale score reliability, person rank ordering, and bias of criterion-related validity estimates were most affected by the proportion of items with low scalability. The authors found a decrease of about .10 in reliability and of about .05 in the Spearman correlation as the proportion of misfitting items increased from 10% to 50%. Removing the misfitting items from the scales led to a slight improvement in reliability and rank correlation (with .04 and .02, respectively). Furthermore, short scales with many misfitting items resulted in an underestimation of the true validity of .11, when predicting the scores on a criterion variable of the top 30% simulees. Removing the misfitting items reduced the bias by .01. Finally, the overlap between sets of selected simulees also decreased with .07, on average, as the proportion of misfitting items increased, and removing the misfitting items improved the overlap with .03. Interestingly, the effect of the range of item scalability coefficients had a negligible effect on the outcomes the authors studied.

In line with previous findings, scale length, number of response categories, and selection rates also had an effect on the outcome variables (e.g., Crişan et al., 2017; Zijlmans et al., 2018). The item scalability coefficient is equivalent to a normed item-rest correlation, which, in turn, is used as an index of item-score reliability (e.g., Zijlmans et al., 2018). Therefore, it is not surprising that overall scale reliability decreased as the item scalability coefficients decreased. Moreover, it is well-known that there is a positive relationship between scale length and reliability. This also partly explains our findings regarding the exclusion of misfitting items: Removing the misfitting items from the scales resulted in shorter scales, which had a negative impact on reliability.

Take-Home Message

The take-home message from this study is that depending on the characteristics of a scale (in terms of length and number of response categories), on the specific use of the scale (e.g., to select a proportion of individuals from the total sample), and on the strength of the relationship between the scale scores and some criterion, the consequences of keeping items that violate the rules-of-thumb often used in MSA item selection can vary in their magnitude. The authors tentatively conclude the following:

1. The number of items with H_i < .3 in a scale has a negative effect on scale reliability, person rank ordering and classification, and on predictive accuracy. The magnitude of this effect varies in terms of variance accounted for, depending on the characteristics and specific uses of the test/scale. In general, (relatively) long scales with several response categories are fairly robust against these violations, especially when they have modest criterion-related validity and they are used with selection ratios above .50.

2. Removing misfitting items from the scale improves practical outcome measures, but the effect is moderate at best. Based on these and previous findings, the authors do not recommend removing the misfitting items from the scales when there are no other (content) arguments to do so. The relatively small gains in reliability, person selection results, and predictive validity might not outweigh the loss in construct coverage and criterion validity.

3. The distance between the H values of the violating items and the .3 threshold had a negligible effect on practical outcomes. So, the results of this study indicate that researchers should not overinterpret H_i differences between .1 and .3.

On one hand, these findings are reassuring because, as discussed above, researchers are often not in a position to simply remove items from a scale (see also Molenaar, 1997a). It also discharges the researcher from trying to find opportunistic arguments for keeping an item in the scale with, say, a relatively low H value. On the other hand, this is certainly not a plea for lazy test construction. Ideally, when conducting MSA either on existing operational measures or in the scale construction phase, the decision whether to keep or remove items from a scale should be based primarily on theoretical considerations and applied researchers should be careful not to use psychometric rules-of-thumb to blindly remove items. In particular, one should not feel obliged to strictly adhere to the discrete qualitative labels of H (“weak,”“medium,” and “strong” scale); paraphrasing Rosnow and Rosenthal (1989, p. 1277): “surely, God loves the .29 nearly as much as the .31.” In line with these observations, Sijtsma and van der Ark (2017) recommended that several MSAs should be run on the data using varying lower bounds for the item scalability coefficients, and the final scale should be chosen such that it satisfies both psychometric and theoretical considerations.

On a more general note, one should keep in mind that items can exhibit other kinds of misfit apart from low scalability, such as violations of invariant item ordering or of local independence. Thus, adequate scalability does not mean that items are free from other potential model violations.

Limitations and Future Research

This study has the following limitations: (a) The data generation algorithm of the simulation study was based on a trial-and-error process to sample items with scalability coefficients within the desired range. A more refined method to generate the data could have improved the efficiency of the algorithm used here. (b) In this study, the authors only considered either dichotomous or polytomous items with a fixed number of response categories (i.e., either three or five) per replication. It is of interest to consider mixed-format test data in future studies. (c) The practical outcomes the authors considered here are by no means exhaustive or equally relevant in all situations. Depending on the type of data and the application purpose, other outcomes might also be relevant. Therefore, this type of research can be extended to other outcomes of interest. Moreover, other types of scalability (e.g., person scalability) could have important practical consequences. These aspects should be addressed in future research.