Finite element analysis of bone strength in osteogenesis imperfecta

Abstract

As a dedicated experimentalist, John Currey praised the high potential of finite element (FE) analysis but also recognized its critical limitations. The application of the FE methodology to bone tissue is reviewed in the light of his enthusiastic and colorful statements. In the past decades, FE analysis contributed substantially to the understanding of structure-function properties in the hierarchical organization of bone and to the simulation of bone adaptation. The systematic experimental validation of FE analysis of bone strength in anatomical locations at risk of fracture led to its application in clinical studies to evaluate efficacy of antiresorptive or anabolic treatment of bone fragility. Beyond the successful analyses of healthy or osteoporotic bone, FE analysis becomes increasingly involved in the investigation of other fragility-related bone diseases. The case of osteogenesis imperfecta (OI) is exposed, the multiscale alterations of the bone tissue and the effect of treatment summarized. A few FE analyses attempting to answer open questions in OI are then reported. An original study is finally presented that explored the structural properties of the Brtl/+ murine model of OI type IV subjected to sclerostin neutralizing antibody treatment using microFE analysis. The use of identical material properties in the four-point bending FE simulations of the femora reproduced not only the experimental values but also the statistical comparisons examining the effect of disease and treatment. Further efforts are needed to build upon the extraordinary legacy of John Currey and clarify the impact of different bone diseases on the hierarchical mechanical properties of bone.

1. Introduction

“Despite finite element analysis being a good exemplar of the old saying ‘garbage in–garbage out’ there is no doubt that already many great insights have come from its use, and with the increasing power and sophistication of computers, much more will come in the next decade or so.” [1]. Not an entire decade, but already seven years have passed since John wrote this sentence, and unfortunately, almost one year without him. John, a dedicated experimental researcher, believed that finite element (FE) modeling is “an enormously valuable technique” [2] that “fortunately … is becoming more and more precise (and often more accurate!)” [1] and thus can complement experimental methods to gain even deeper insight into the fascinating properties of bones. We can ask ourselves: did that “much more” come from FE modeling, as he anticipated? Does FE analysis belong to the key technologies that contributed to the “New Golden Age” of bone research John anticipated in the 1970’s? We may not be able answer these questions, but rather hope to show how FE analysis, a tool that has been applied to investigate the mechanical behavior of healthy and osteoporotic bone, also has the potential to be utilized in the exploration of other bone diseases such as osteogenesis imperfecta.

As John wrote, “Predicting accurately the behavior of a whole bone involves knowing the kinds of loads that are put on the bone, their directions and relative magnitudes, knowing the 3-D structure of the bone in some detail, and finally knowing the mechanical properties of the material throughout the bone.” [2]. By incorporating geometry and structure, material properties and boundary conditions, FE models simulate the mechanical behavior of bones via virtual loading scenarios. John acknowledged the potential and challenges of these models when he stated, “The range and complexity of bones, quite unanalyzable except by the use of CT with FEA, and even then only with enormous difficulty.” [2]. Indeed, even with FE simulations, it is not straightforward to predict the mechanical behavior of bones. “The structure of whole bones is fiendishly complex” [2] as John said and bone material is “remarkably hierarchical” [2]. Therefore, one needs to consider the finer-scale properties when modeling the coarser-scale behavior. Fie mentioned: “Whole bone properties (which in the end is what we should be interested in, presumably) will develop quickly when FEA becomes increasingly rapid as computers intensify in power, particularly when paired with an improved understanding of the mechanical properties of little subvolumes of the bones themselves” [2]. The basic constituents of the extracellular matrix (ECM) of bone must be considered when determining the tissue-scale material property input for micro finite element (microFE) models, which also incorporate a high level of bony microstructure detail. Volume elements of compact and cancellous bone can be used to determine the apparent properties on the meso-scale via homogenization [3, 4]. Bone volume fraction and architectural anisotropy (fabric) were found to be the most important determinants of apparent stiffness and strength of bone [5, 6]. The meso-scale properties serve as input for homogenized finite element (hFE) models that utilize coarser spatial discretization compared to microFE and thus do not directly describe the geometrical details of bone microstructure. hFE models are well suited for modeling whole bones as the related computational efforts are moderate compared to microFE models because “at the moment, FEA of complex micro-CT images is very, very computer intensive” [2]. Indeed, nonlinear microFE simulations require extreme computational resources for particular bones such as the vertebral body [7] or the proximal femur [8].

The application of FE analysis in bone research is manifold and includes the reproduction of the elastic behavior of bones, investigation of the deformation fields at several length scales, simulation of bone adaptation for improved understanding of structure-function relationships, replication of the post-yield behavior and prediction of bone stiffness and strength for clinical applications. John believed that “one can do more or less what one wants with a finite element model, given time and money” [1]; however, he warned against increasing the complexity too far since “the best is the enemy of the good” [9]. Indeed, one challenge in FE analysis is, shared with all models used, finding the optimal level of complexity that was formulated by John as the following: “It must be remembered that unless you know everything you are using a model. A model is an abstraction, and in real science the trick is to get the right balance between the need to get near absolute ‘truth’, by using a model as complicated as you can make it, and the need to come up with an answer at all, without the use of a ridiculous amount of experimental and computational time and effort” [9]. Appropriate FE models are just as (but not less) complicated as required by the investigated problem. The correctness of the FE models and results must be controlled via experimental validation. As John warned, “… there are dangers in leaping with cries of joy on new techniques. … Validation of results, if at all possible, by other techniques, is most important if good science is to be done.” [1 ] and “… often not enough attention is paid to validation in many studies using finite element analysis, and people writing (and reading) papers using it need to be wary” [1]. Biomechanical testing has been used as the basis for the validation of FE models. Validation studies confirmed that FE simulations achieve better predictions of ex vivo bone fracture load compared to conventional density-based measures [10] at the proximal femur [11], vertebral bodies [12] and distal radius [13]. When high quality input data is available for bone geometry and material properties, and for well-defined loading cases, microFE and hFE simulations deliver highly accurate, equivalent predictions. This was previously demonstrated for high resolution computed tomography (CT) based modelling of human distal radius and vertebral sections under uniaxial compression as well as the proximal femur in the fall configuration [14–18]. Nevertheless, even if validated for a given case, one must be aware of the limits of a model’s applicability. Good FE models are generally applicable and can predict failure load in various loading modes, e.g. stance and fall for femora [19]. Versatility of the model is highly relevant since the fracture resistance of bone is good against loads acting along physiological loading directions, but can be weak along abnormal orientations [20].

One of the most important, clinically relevant objectives of FE simulations is to predict the risk of fracture. Strength refers to the load bearing capacity of bones and it is often used as a surrogate measure of fracture risk. FE-derived bone strength predictions can help identify patients at risk of fracture and select the ideal treatment option that alleviates this risk by increasing the factor of safety in the bone. Thus, the goal is to find out whom to treat and how to (or how not to) treat. Ideally, FE models should be able to provide accurate prediction of bone strength based on clinically available data. As John wrote, “The advance in technique allowing FEA to progress so much in bone studies was computer-aided tomography (CT) … these data can be turned, almost directly, into an FEA model” [2]. CT images are indeed the most important data sources for FE analysis of bones, providing quantitative information on the magnitude and the spatial distribution of mineral density [21]. Imaging of frequently fractured skeletal sites such as the hip and spine is, to date, only possible with conventional CT instruments, providing moderate resolution images, but quantitative information on bone density. Accordingly, hFE models are well suited for predicting strength of these bones [22–24].

High-resolution peripheral quantitative CT (HR-pQCT) provides insight into the bony microstructure of the human distal radius and tibia and opened a new era for FE models [25]. MicroFE modeling became the standard approach for HR-pQCT-based strength prediction at distal peripheral sites and has been utilized in several studies [26]. Second generation HR-pQCT devices now allow routine imaging of diaphyseal sites as well as more proximal sites (e.g. knee and elbow) with custom-made casts, which will open more possibilities [27]. HR-pQCT-based FE analysis was shown to predict experimental failure load better than bone density [13, 26, 28]. The recent BoMIC study confirmed these findings, reporting superior fracture risk prediction by failure load (hazard ratio [HR] = 1.82–1.98) compared with all other HR-pQCT density and microstructural parameters (HR = 1.09–1.44), even after adjusting for DXA femoral neck aBMD [29]. CT-based FE analysis has been used to predict bone strength primarily in osteoporosis, but also in other conditions including bone metastases [30] and spinal cord injury [31]. Moreover, FE has been utilized to monitor treatment efficacy in primary and secondary osteoporosis [32]. Most of these simulations used tissue properties of healthy bone, which may be an appropriate assumption for certain conditions like osteoporosis. However, given the altered mechanical behavior of bone tissue in other bone diseases, such as osteogenesis imperfecta (OI), the parameters of the constitutive laws developed for the healthy condition may need to be adjusted to appropriately predict bone strength.

OI is an example of a disease with an altered bone matrix at the ECM level, which likely influences the higher scales through regulatory mechanisms. As John wrote in his book, “A difficulty in determining how strength is affected by the mineral and organic components is that, almost inevitably, if they are altered, by disease or experiment, they are both altered, and one cannot distinguish which, if either, is the important effect. For instance, Landis (1995) shows how the crystal form in cases of osteogenesis imperfecta is different from normal. This difference is almost certainly caused by the deranged packing of the collagen fibrils in this disease. However, since both the collagen and the mineral are deranged, it is not possible to say what causes the undoubted degraded mechanical properties of osteogenesis imperfecta bone.” [33]. The use of healthy bone properties in FE models of OI bone may therefore be incorrect. Moreover, OI often involves treatment with bisphosphonates throughout growth that may necessitate further adjustments of the material properties in FE simulations. Nevertheless, referring to the above-mentioned thoughts of John on model complexity, one should attempt to avoid overcomplicated FE simulations. The question arises if and how FE models, which were developed for healthy and osteoporotic conditions, should be applied to bone diseases such as OI, without making them overly complex and falling into the above-mentioned “garbage in–garbage out” trap.

In the next sections, we review the effects of OI and its drug treatments on bone properties and report an original study utilizing FE analysis and illustrating our incomplete understanding of the biomechanical alterations of OI bone.

2. Osteogenesis imperfecta – effect of the disease and its treatment

Osteogenesis imperfecta (OI) or “brittle bone disease” refers to a group of heritable bone dysplasia disorders that are heterogenous both phenotypically and genetically [34, 35]. However, in the majority of cases (85%), OI is caused by mutations in the genes encoding type I collagen (COL1A1 and COL1A2), leading to increased bone fragility attributed to reduced bone mass and quality. Historically OI has been classified based on clinical severity using the Sillence types [36, 37]; type I (mild), type II (perinatally lethal), type III (severe) and type IV (moderate). The discovery of multiple forms of OI due to mutations in non-collagen genes has led to additional Sillence types V-XVI (moderate to severe), as well as an alternate classification system based on mutated genes. OI has a prevalence of 1/10,000 to 1/20,000 and despite widely diverging genetic heterogeneity results in many common skeletal manifestations that include deformities, growth deficiencies, scoliosis and/or kyphosis [38]. Fracture incidence associated with low bone mass and altered bone material properties is highest in growing children and young adults, with fewer fractures occurring in adulthood, but again increasing in old age [38]. This pattern of increased fracture risk in OI subjects compared to a non-OI reference subjects over their lifespan is elegantly captured in a Danish nation-wide register-based cohort study [39]. Since there is no cure, management of OI is aimed at reducing fracture incidence, correcting deformity, alleviating pain, and improving mobility through rehabilitation, surgical interventions and pharmacological treatment [40].

Since the 1990s, bisphosphonates (e.g. zoledronate, pamidronate), which inhibit bone resorption, continue to be widely administered in children with OI until growth has ended, and are used to a lesser extent in adults [41, 42]. More recently, clinical trials have been investigating the effect and long-term safety of various antiresorptive and anabolic drugs in OI including denosumab (Prolia, Amgen) [43, 44], teriparatide (recombinant human PTH 1-34, Forteo, Eli Lilly and Co.) [45, 46], sclerostin neutralizing antibody (Scl-Ab, Setrusumab/BSP804, Mereo BioPharma) [47], and TGF-beta neutralizing antibody (Fresolimumab/GC1008, Genzyme). Surgical interventions most often are used to correct limb deformity by corrective surgeries with osteotomies in long bones combined with intramedullary rod fixation [48]. These corrections are meant to improve function and alleviate fracture risk. However, identifying subjects at high risk of fracture remains challenging due to limitations associated with two-dimensional density-based diagnostic approaches, where specificity is weak in OI subjects due to confounding factors such as bone size and shape [49, 50]. FE analysis may provide a more objective measure to predict fracture risk in this group of patients if the required inputs are available (e.g. shape, mass, density and potentially also microstructure and material properties of OI bone). Assessment of these properties remains challenging, and the question arises: what are the essential input parameters that must be correctly quantified and incorporated into these computational models? To answer this question, one must understand how OI and associated drugs used to treat the disease affect bone composition, structure and mechanical properties.

2.1. Alterations in OI bone at multiple hierarchical levels

The pathophysiological effects of the various mutations of OI on the skeleton that cause increased brittleness and high bone fragility are not fully understood. Numerous factors at several hierarchical scales may contribute to the inferior bone strength and the associated increased fracture risk in OI [51]. These are discussed here with no claim to completeness. While OI type I usually results from COL1A1 haploinsufficency that leads to a reduction in amount of healthy collagen produced [52]. Other OI types result in both qualitative and qualitative defects in the collagen. The main consequences commonly arising from most OI mutations include disturbed osteoblast and osteoclast function, abnormalities in collagen production and altered inorganic and organic bone matrix components, including abnormal collagen synthesis, processing (post-translational collagen modifications, chaperoning, and assembly), and/or altered mineralization associated with abnormal collagen. In many common forms of OI, the structure of collagen I is altered, and its properties are inferior compared to the healthy state. Depending on the underlying mutation, there can be fewer fibrils of smaller diameter in a disorganized structure and of decreased quality with ruptured crosslinks [53, 54]. The ultimate stress and strain of OI-affected bone collagen is only 50% of that of healthy collagen [55]. Interestingly, despite widely varying genetic pathophysiology, OI bone tissue exhibits similar abnormal mineralization profiles across most types, with increased bone mineral density distribution (BMDD), smaller and thinner platelets that are densely packed with lower heterogeneity in mild OI compared to normal bone [53, 56–59]. However, the heterogeneity is increased in more severe OI types [60]. Nanoindentation-based modulus and hardness were found to be inversely correlated with OI severity [61], but still higher than normal bone independently of bisphosphonate treatment [62]. However, lower Young’s modulus in OI versus controls, positively correlated with tissue mineral density, was also observed [53]. The broad age range, the low number of samples and the different surface preparation/orientation and indentation protocols may explain this lack of consistency. Unfortunately, indentation modulus is a purely elastic property and the dissipated indentation energy associated with post-yield behavior and toughness was not reported. Multi-directional analyses found that elasticity of OI bone tissue was closely isotropic [63–65]. The disturbed arrangement and cross-linking of collagen fibrils and the disorganized lamellar structure may impair plasticity and toughening mechanisms [66]. The high mineralization density is speculated to be a reason for brittleness [51]. Nevertheless, when examining these findings, one must take into account that material properties may be affected based on the anatomical origin and condition of the tissue examined, since some studies included bone biopsies taken from the iliac crest, while others often examined otherwise discarded, deformed limb bone removed during surgery. Moreover, most studies investigated pharmacologically treated bone since non-treated OI bone samples are difficult to obtain.

OI impairs the meso-scale structure and properties of bone. Trabecular bone architecture was reported to be more heterogeneous, with smaller average thickness and larger spacing, resulting in lower bone volume fraction and BMD in the distal radius and tibia [67, 68] (Figure 1), despite a higher tissue level BMDD. In cortical bone, vascular porosity was reported to be larger in OI [54, 69, 70] while lacunar porosity was reported to be unaffected [70] or increased [71]. Mouse models of OI exhibited unaltered intracortical porosity, but a larger number of canals with smaller diameter and more branches, which increase the amount of bone tissue at risk of failure [72] and less efficient against stopping cracks [66]. Compressive and bending experiments of human cortical beams found significantly lower meso-scale stiffness and yield stress, but not yield strain, compared to healthy bone [69, 70]. On this scale, cortical bone was found to be clearly anisotropic [69], but to a smaller extent compared to healthy samples [70]. Several studies reported significant correlation between vascular porosity and the elastic and ultimate properties [54, 69–71]. They propose that, since OI bone tissue is closely isotropic and stiffer than healthy bone, the higher intracortical porosity is predominantly responsible for the anisotropy and the impaired mechanical properties on the coarser scales. On lower resolution CT images, increased cortical porosity appears as decreased BMD, which was also demonstrated to be correlated with the meso-scale mechanical properties [70].

Figure 1:

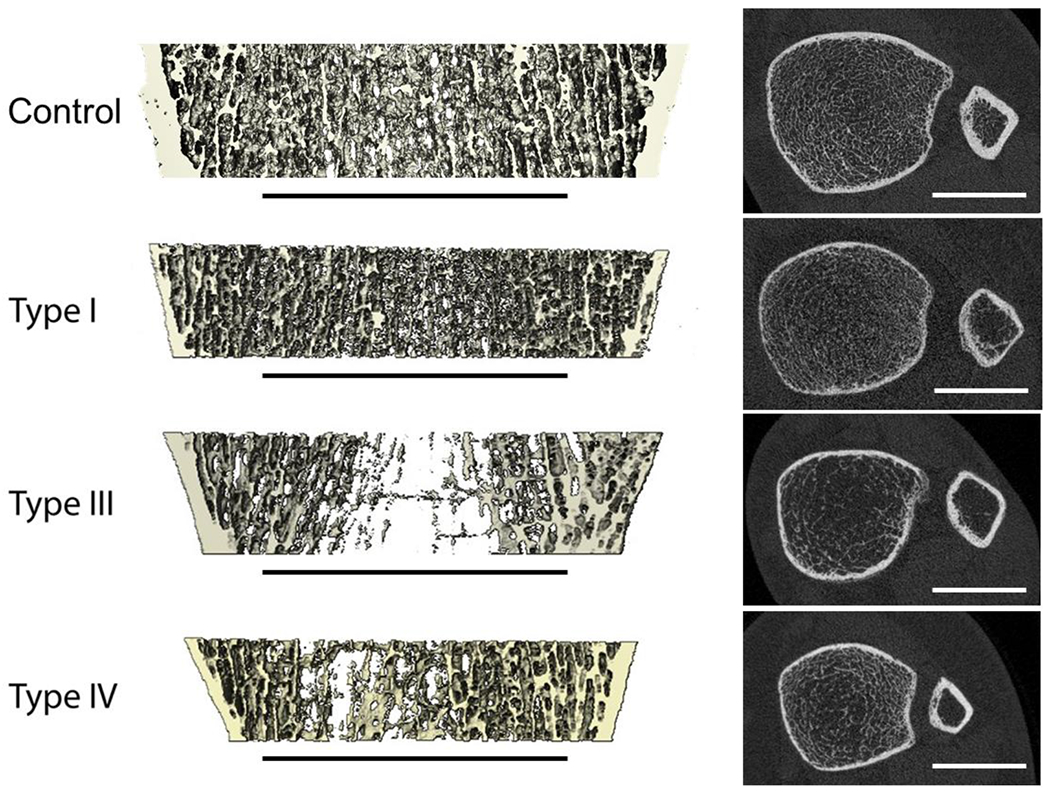
HR-pQCT images of the distal tibiae of healthy and OI subjects with different clinical severity of the disease. Left: 3D renderings of sagittal sections; right: axial HR-pQCT slices. Scale bars indicate 20 mm.

Regarding the macro-scale properties, the cortex of long bones was found to be thinner, with a smaller diameter and area [35, 67, 68], resulting in lower bone mass and density. Since the organ-scale bone dimension are smaller, the density may appear higher, but strength is still lower [50]. Additionally, long bone curvature can be exaggerated in disease-associated bowing, implying larger moment arms for the acting forces and causing higher stresses on the limb. The loading conditions in OI also differ from the healthy state and depend on the level of activity and mobility, ranging from slightly or severely altered gait patterns [73, 74] and lower muscle strength, to the use of crutches or wheelchairs.

2.2. Effect of drug treatment on the properties and strength of OI bone

Investigating the effect of drug treatment in humans is challenging due to the rarity of the disorder, phenotypic variation, and lack of samples from untreated controls [75]. OI subjects often have a background of previous bisphosphonate use, which is typically initiated at an early age and continued until cessation of growth. Additionally, depending on disease severity, there are ethical concerns with the use of placebo treatment and obtaining bone biopsies from subjects to examine cellular dynamics in response to therapy is challenging. Thus mouse models recapitulating various features of OI have been developed and utilized [76].

Although there have been numerous clinical observational studies, a limited number of randomized control trials have investigated bisphosphonates in OI [77]. Clinical studies have provided ample evidence that bisphosphonates increase bone mass, cortical thickness and BMD [35, 78–82]. Although associations between bisphosphonate treatment and decreased fracture rates have been reported [83–85], meta-analyses have revealed mixed findings [77, 78, 86]. In the oim/oim mouse model of OI, bisphosphonates increased cortical area and trabecular bone volume, but had no effect on mechanical properties assessed via 3 point bending, nor on bone mineralization density distributions [87, 88]. In Brtl/+ mice, alendronate treatment improved volumetric BMD, cortical thickness, and trabecular number, but not the mechanical properties [89].

Clinical and preclinical studies suggest that the RANKL inhibitor, denosumab leads to enhanced OI bone density and strength. Two years of denosumab (Prolia, Amgen) treatment in four patients with Type VI OI resulted in increased areal BMD, normalization of vertebral shape, and a reduced fracture rate [44]. Another study in ten children with Type I, III, and IV OI also showed enhanced aBMD after 48 weeks of denosumab treatment [43]. A study examining RANK-Fc treatment, a surrogate for denosumab, reported increased brittleness in oim/+ mice compared to either their saline and alendronate treated counterparts [90]. They observed decreased fracture incidence and increased trabecular bone volume via an increased number of thinner trabeculae after either RANK-Fc or alendronate treatment. RANKL inhibition improved density and some geometric and biomechanical properties of oim/oim bone, but it did not decrease fracture incidence[91]. Boskey et al. [92] reported that neither RANKL inhibition nor bisphosphonate treatment corrected any FTIR-determined material property parameters in oim/oim of either sex to WT values.

Two clinical trials have investigated teriparatide (recombinant human PTH 1-34, Forteo, Eli Lilly and Co.) in adults with OI [45, 46]. Gatti [46] reported increased lumbar spine BMD after 18 months of treatment in thirteen women with Type I OI. Orwoll et al. [45] also reported increased BMD and FE estimated vertebral strength in subjects with Type I, but the differences did not reach significance in subjects with Type III or IV OI after 18 months of treatment. A promising anabolic approach for OI is using Scl-Ab. Pharmacological inhibition of sclerostin, the product of the Sost gene and a negative regulator of Wnt signaling was recently approved by the FDA for treatment of postmenopausal women with osteoporosis at high risk for fracture (Romosozumab, Evenity™, Amgen and UCB). Another antibody (Setrusumab, formerly called BPS804, Mereo BioPharma) is being investigated in adults with Type I, III or IV OI in a phase 2a [47] and a phase 2b, multicentre, double-blind, dose-finding study. The open label arm of the 2b study recently revealed enhanced areal bone mineral density (BMD) at the lumbar spine and trabecular volumetric BMD at the radius after 6 months of treatment compared to baseline [93]. Studies are ongoing to investigate tissue level changes in bone biopsies from the Phase 2b trial. Some studies on Scl-Ab treated murine OI models (Brtl/+, Crtap(−/−), oim/oim) reported significantly improved mechanical properties at the whole-bone scale and reduced fracture rate [94–99]. However, the tissue-scale properties of OI bone including tissue mineral density, nanoindentation modulus and hardness, as well as the Young’s modulus and ultimate stress estimated from bending using the beam theory were not affected by Scl-Ab [94–98]. Interestingly, the newly formed bone of Brtl/+ mice, treated with Scl-Ab showed a mineralization profile more closely resembling new bone from untreated WT mice than untreated Brtl/+ mice, but as the bone matured it reverted to a more Brtl-like profile [97]. Therefore, the improved bone strength was due rather to the increased trabecular thickness and volume fraction, cortical parameters, bone mass and size [94–96]. A study in the mild-to-moderate Amish OI mouse (Col1a2 G610C) reported only modest changes in the cortical bone, with significant effects observed in trabecular bone, including increased vertebral compression strength [100]. Interestingly, a mouse model replicating severe dominant OI (Col1a1^jrt) [98] was found not to benefit biomechanically from Scl-Ab treatment, despite significant gains in femoral cortical thickness [98].

3. Original contribution: microFE modeling of bone strength in a murine OI model treated with Scl-Ab

3.1. Background

Only a few studies have utilized FE analysis to investigate the effect of OI on bone strength [45, 101–107]. These studies were performed on human bones, with the ultimate translational goal to predict patient-specific fracture risk and evaluate the necessity of surgical intervention. They investigated the effect of various lower limb long bone deformities on the stresses induced by ambulation, muscle force, or impact [101, 103, 105, 106]. Each of these studies analyzed a small number of patients (one to three) with bone geometry derived from unaffected individuals and deformed artificially to the OI-specific shape based on a single radiograph [106] or a combination of biplanar EOS scans and peripheral quantitative CT slices, being the standard clinically available image data [101–104]. The effect of bowing was analyzed also parametrically [101, 103, 104]. Cortical bone was modelled as isotropic and linearly elastic with properties based on previously reported nanoindentation results [101, 103–106]. Fracture risk was predicted using either a von Mises stress threshold [103] or an asymmetric strain-based yield criterion previously established for healthy bone [101, 102]. Some studies analyzed the forces during gait [106] and the effect of various muscles [107] while others considered various physiological and accidental loading cases [101, 104]. All studies predicted low fracture risk for the investigated patients.

A common limitation of these prior studies is the lack of rigorous biomechanical validation, which is difficult due to the limited availability of relevant cadaveric bones. Nevertheless, the lack of complete CT information derived directly from the subject may prevent accurate description of the patient-specific bone geometry and density distribution. The previously used approach of adjusting healthy geometries to OI-relevant shapes may not be sufficient and may be sensitive to the level of details of the patient-specific data [102]. A single study utilized FE analysis to investigate the effect of drug treatment on vertebral strength in OI patients [45]. Nonlinear FE models were generated based on CT images using a previously developed methodology that was validated from healthy and osteoporotic bone. Nevertheless, the computer simulations may require more refined material properties including a failure criterion that can appropriately model the failure of bone tissue affected by OI [101]. Therefore, the results of all previous FE studies may be restricted to relative comparisons and indication of trends, rather than the evaluation of absolute failure load or fracture risk.

As summarized in the previous sections, murine models of OI are essential for developing well-controlled and well-powered studies to better understand the disease and efficacy of new treatment strategies. The application of CT-based FE simulations on these animal models may help to reduce the number of animals and may provide deeper insights into the causes of increased fragility and the effects of treatments that remain hidden experimentally. A single study investigated the mechanical effects of altered vascular pore morphology on failure in a murine OI model, using FE simulations based on synchrotron tomography images of the tibial and radial shaft [72]. Nevertheless, the models of that study were not validated experimentally. Further, the applicability of the FE method in drug treatment of murine OI has not been investigated before. It has remained unexplored if and how the parameters of FE simulations developed for healthy conditions should be modified when modeling OI bone.

Considering these, we aimed to investigate which input parameters are essential to incorporate into FE models to appropriately model bone strength in a murine model of OI and changes in strength resulting from Scl-Ab treatment. The specific goal was to indirectly evaluate the need for OI-specific and treatment-specific tissue material property definitions as inputs to future microFE models.

3.2. Materials and Methods

Rapidly growing 3-week-old wildtype (WT) and Brtl/+ male mice were treated with vehicle (saline) or Scl-Ab (100 mg/kg, Setrusumab, Mereo BioPharma), administered via intravenous injection once a week for 5 weeks. The Brtl/+ model of Type IV OI was selected as a suitable species as it is heterozygous for a typical Gly → Cys substitution on col1a1 (G349C) and recapitulates many features of the OI phenotype including reduced bone mass, reduced bone strength, and increased bone resorption relative to bone formation [89, 108, 109]. Sixty-seven mice were randomized into the following groups: WT vehicle (n = 19), WT Scl-Ab (n = 20), Brtl/+ vehicle (n = 14), Brtl/+ Scl-Ab (n = 14). Following euthanasia, the left femora were scanned using a lab microCT (Skyscan 1176; Bruker, Billerica, MA, USA) at 9 μm isotropic resolution utilizing a 0.3° rotation step, 0.5 mm aluminum filter, and 2 frame averaging. The hydrated bones were then tested in four-point bending to failure, with the posterior surface loaded under tension. The span widths for the upper and lower supports were 6.35 mm and 2.2 mm, respectively (Figure 2). According to a previously established setup, displacement-driven tests were carried out at rate of 0.05 mm/s using a servohydraulic testing machine (MTS 858; MiniBionix, Eden Prairie, MN, USA)[94]. Ultimate load was defined as the maximum of the resulting force-displacement curve.

Figure 2.

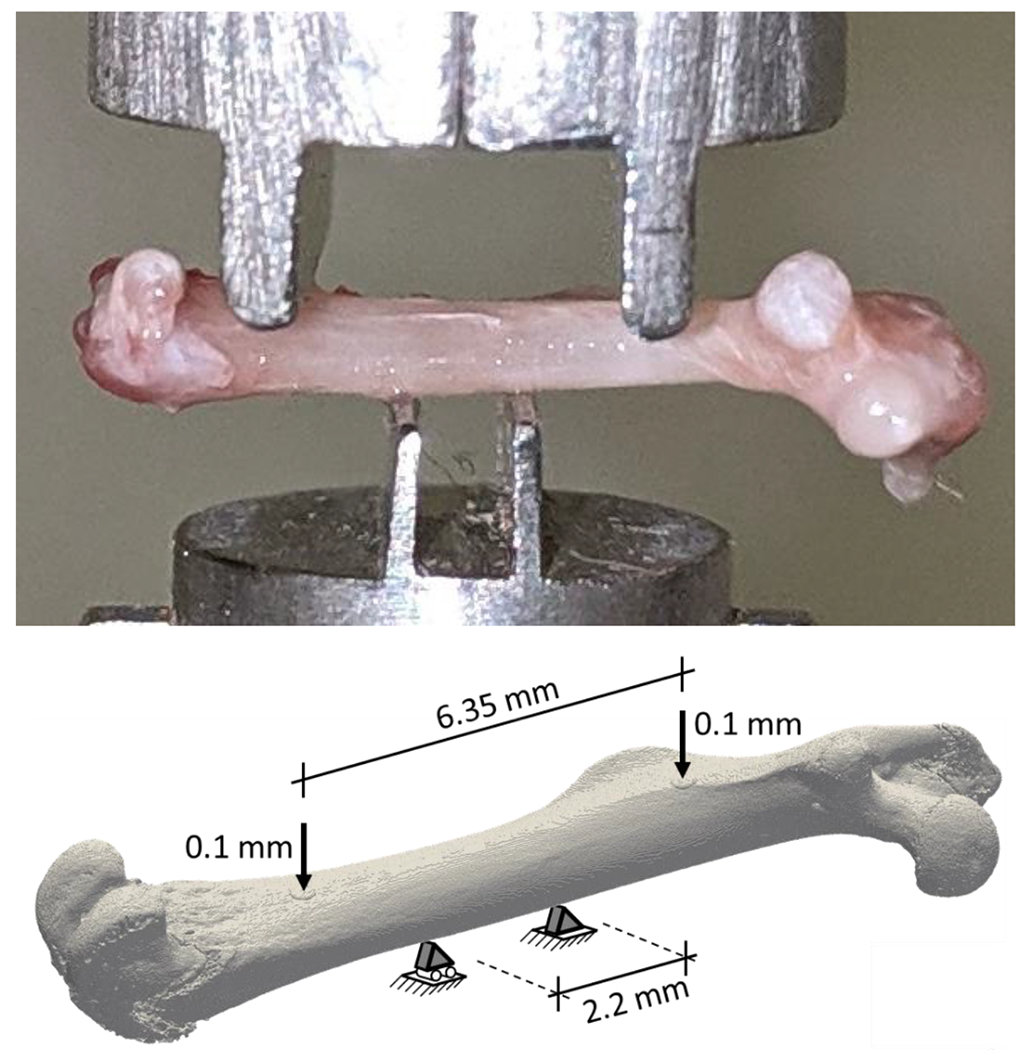
Experimental four-point bending setup of the murine femora (top) and the corresponding microFE analysis (bottom), replicating the experimental boundary conditions. Note that the specimens are not the same in the two sub-figures.

The microCT images were segmented using a global threshold value of 500 mgHA/cm³ identified with Otsu’s method [110] (Figure 3) and transformed, using anatomical landmarks, to match the experimental alignment. The moment of inertia around the bending axis was calculated for the cross section of the femoral midshaft, corresponding to the center of the four-point bending setup.

Figure 3:

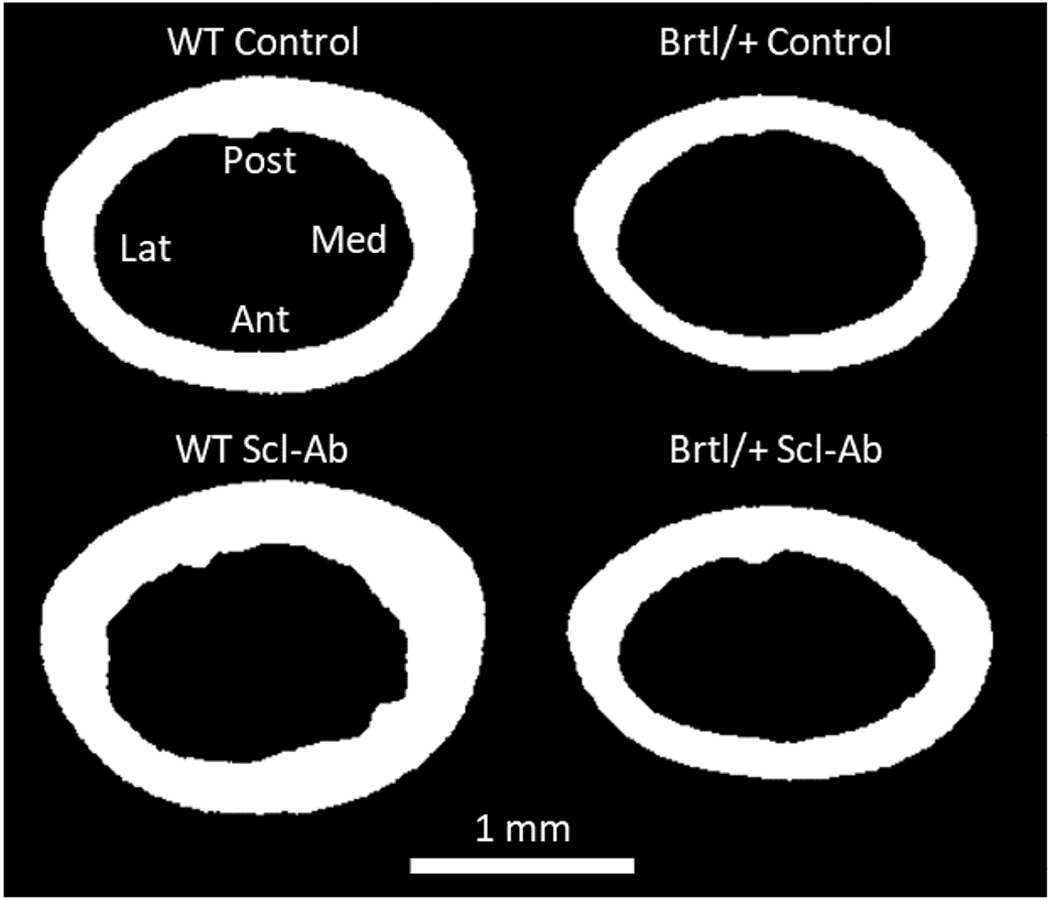
Segmented microCT cross-sections at the femoral mid-shaft for a representative sample per group. The alignment is according to the experimental testing, the anatomical orientations are indicated as Lat: lateral, Med: medial, Ant: anterior, Post: posterior.

MicroFE models of the femora were created from the segmented microCT images, each bone voxel was converted to an eight-node hexahedral element (Figure 2, bottom), resulting in 31.4 ± 7.9 million elements per sample. Material properties were assumed to be homogeneous and linear elastic, with Young’s modulus of bone tissue set to 15 GPa based on previous nanoindentation data measured in femora of the same mouse model [97]. Poisson’s ratio was set to 0.3. Spatial alignment, loading and boundary conditions were set to mimic the experimental four-point bending test (Figure 2, bottom). Due to the limitations of the voxel FE solver, there were only restricted options to set boundary conditions and no contact was available. Therefore, the areas of contact between the parts of the metal test supports contacting the bone were approximated as small horizontal disks of 20 voxels diameter and 3 voxels thickness that were attached to the corresponding bone surfaces. These disks were modelled as stainless steel with elastic modulus of 210 GPa and Poisson’s ratio of 0.3. The contact conditions were mimicked by emulating horizontal hinge joints around the center of each disk transverse to the bone axis (Figure 2, bottom). This was achieved by controlling the degrees of freedom of two control nodes per disk: the central node and the neighboring node in transverse direction. Horizontal translations perpendicular to the bone axis were blocked for all control nodes, and the vertical motion of the bottom disks located on the anterior bone surface was also fixed. One of the bottom disks was fixed also horizontally along the bone length to avoid rigid body motion. The other disks were free to move along the proximal-distal direction, simulation potential sliding of the bone on the supports. A vertical displacement of 0.1 mm was applied on the control nodes of the upper disks located on the posterior bone surface. The simulations were performed with the ParOSol solver [111] and the reaction forces were computed. Bending stiffness was evaluated as the summed vertical reaction forces of the bottom constraints divided by the 0.1 mm displacement applied on the control node on the top. Surrogate bone strength was evaluated from the linear elastic analysis results using the criterion introduced by Pistoia et al. [13]. This method assumes that failure occurs when a given portion of the bone’s volume is deformed beyond the yield strain level. This approach was originally developed and calibrated to predict the ultimate force of human distal radii, based on HR-pQCT scans of 4 cm long bone regions. Pistoia et al. assumed the tissue yield strain to be 0.7% and performed a parametric analysis to identify the optimal value for the relative failed volume within a range of 1% - 7% that provided the strongest correlation with the experimentally measured fracture force [13]. The Pistoia method was utilized in a previous study to predict the location and amount of bone tissue at high risk of failure in tibial and radial shaft sections of a murine OI model [72]. The yield strain was assumed to be 0.7%, but the models were not validated. In the present study, the approach of Pistoia et al. was used to back-calculate the force level that would cause yielding in a certain relative volume of the femoral midshaft region by scaling the results of the elastic simulation. Similarly to Pistoia et al., we performed a parametric analysis involving all samples from each of the four groups to evaluate the optimal relative yielded volume. Additionally, as our simulations included the entire femur, it was not clear which part of the midshaft should be considered as the total volume of the Pistoia-analysis and thus the width of the considered bone region was included into the optimization as a second parameter. The optimization was performed by maximizing the Pearson’s correlation coefficient of the linear regression between the experimentally measured ultimate forces and the microFE-based Pistoia forces. Finally, the magnitude of the Pistoia forces were scaled linearly to obtain quantitatively correct predictions of the experimental results. This was achieved by adjusting the level of yield strain; this procedure did not affect the correlation coefficient. The optimized parameters of the Pistoia criterion in this study were: 7.0 mm midshaft region width, 3.0% relative yielded volume and 1.0% yield strain. The same parameters were used for all groups.

The experimental ultimate forces of the four study groups were compared with an unpaired student’s t-test or the Wilcoxon signed-rank test, depending on whether the data was normally distributed. Normality was evaluated using the Shapiro-Wilk test. Statistical significance was defined at α = 0.05 and the Bonferroni correction was applied for multiple comparisons. The same comparison was done for the FE-based Pistoia force. Statistical tests were performed with ‘R’ software, v3.3.3 [112] (R Core Tearn, https://www.r-project.org/).

3.3. Results

Experimental ultimate force was significantly larger in the WT femora compared to the Brtl/+ femora, both in the control (p < 0.001) and the Scl-Ab-treated animals (p < 0.001). Scl-Ab treatment caused significant increases in ultimate force in both groups (WT: p < 0.001, Brtl/+: p < 0.05). Results of the Scl-Ab treated Brtl/+ femora were not significantly different from the control WT.

The experimental ultimate force was strongly correlated with the moment of inertia at midshaft (R² = 0.83, Figure 4, left) and even more strongly with the optimized microFE-based Pistoia force (R² = 0.93, Figure 4, right). When correcting for the slope and the intercept of the linear regression, the standard error of estimate (SEE) of microFE was 2.4 N, corresponding to 8% of the mean. When analyzing sub-groups based on genotype or treatment status, the prediction in the Scl-Ab treated groups (R² = 0.87 for WT and R² = 0.91 for Brtl/+) were stronger than for the vehicle treated groups (R² = 0.61 and R² = 0.60 for WT and Brtl/+, respectively). A similar trend was observed for the moment of inertia based correlations, but with lower correlation coefficients compared to the FE-based results (Scl-Ab WT: R² = 0.74, Scl-Ab Brtl/+: R² = 0.86, vehicle WT: R² = 0.40, vehicle Brtl/+: R² = 0.49). The stronger correlation coefficients in the treated groups was partially due to the wider range (difference between maximum and minimum values) of the experimental ultimate force in the Scl-Ab treated groups (approximately 20 N span) compared to the vehicle treated groups (approximately 10 N span). The SEE of the FE-based prediction was comparable between the groups, being 2.4 N and 2.6 N for WT Control and WT Scl-Ab, respectively, and 1.8 N and 1.9 N for Brtl/+ Control and Brtl/+ Scl-Ab, respectively. MicroFE stiffness showed a slightly weaker, but still strong correlation with the experimental ultimate force (R² = 0.89). The optimized microFE-based Pistoia force delivered the same statistical conclusions and significance levels between all four groups as the experimental results.

Figure 4.

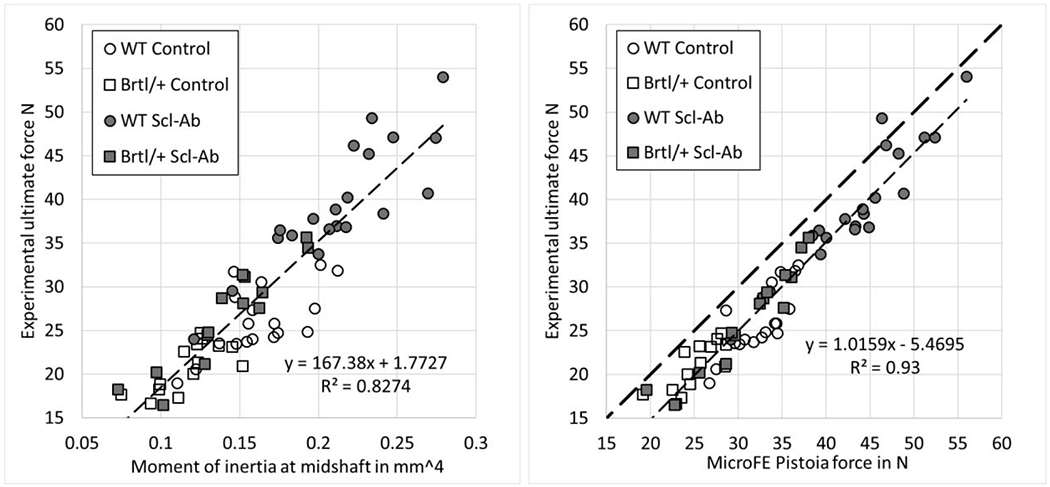
Linear regression analysis between the experimental ultimate force and the moment of inertia at midshaft (left) or the microFE-based Pistoia force (right) for all study groups.

3.4. Discussion

In light of the aim to evaluate the need for OI-specific or treatment-specific tissue material properties for microFE models, the main finding of this study was that the data of all four groups were aligned along the same regression line in the correlation analysis between experimental and predicted ultimate force. These results were achieved using homogeneous material properties that were identical for the four groups. This finding alone is not sufficient to determine if the tissue material properties of the four groups were similar. Indeed, there may be individual differences in the tissue properties, i.e. mineralization, porosity, etc., that can affect bone strength and produced the relatively high SEE and low correlation coefficients of the group-wise analyses. However, our results suggests that, when considering the pooled analysis of the four groups, the geometrical effect of OI and Scl-Ab treatment on the extrinsic bone properties (i.e. shaft diameter, cortical area and thickness), which were incorporated in the microFE models, dominated any potential differences between the groups in the material properties of bone tissue, which were assumed to be the same in the FE models of all groups. This indicates that the microFE models can predict ultimate force for all groups using the same material parameters and there may be no need to tune the setting for OI or treatment.

These findings have two potential implications. Firstly, the mechanical properties of bone tissue at the ECM level were assumed to be the same. The achieved predictions indicate that potential differences between the groups in terms of these properties remain secondary compared to differences in morphology in terms of determining the fracture load. These results cannot be compared directly with previous literature due to lack of tissue-scale bone strength (i.e. failure stress) data and can only be compared indirectly with other measures as indentation results (elastic modulus) and toughness (post-yield energy absorption capacity). In this regard, our results are in line with those of Sinder et al. [97] showing no significant differences in nanoindentation modulus between WT and Brtl/+ murine bone with or without Scl-Ab treatment. Others have also suggested that the reported small increase (1 – 2%) in mineral content [56, 58, 59, 113] could not account for the decreased toughness in OI. They suggest the reduced alignment of collagen and diminished lamellar structure, reduces the bone’s armamentarium of toughening mechanisms [114]. Moreover, as discussed above, neither bisphosphonates [51, 62], nor short-term sclerostin inhibition [97] appear to alter bone material properties at the tissue scale, although genetic depletion has been shown to alter bone composition [115].

Secondly, intracortical porosity was neglected in all models due to the microCT image resolution being close to the average vascular pore diameter (approximately 9 – 15 μm on average) and larger than the dimensions the osteocyte lacunae (approximately 3 – 10 μm) [72, 116]. Intracortical porosity was therefore not resolved (Figure 3) and not included as the geometrical input of the microFE models. The lack of porosity input may also have contributed to the relatively low prediction accuracies. However, since the pooled analysis data from the four groups was aligned along the same regression line despite ignoring the contributions from porosity, suggests that the potential difference in cortical porosity between the groups was less influential on ultimate load compared to the extrinsic bone morphology. These results are in line with the findings of a previous study showing that the extent of cortical porosity was not altered in the oim/oim murine model of OI compared to WT mice [72]. However, increased number and branching of vascular porosity and higher lacunar density were reported and shown to increase the local effective strain [72] and to contribute to the capacity of bone to resist microcracks [66]. It cannot be excluded that changes in ECM properties and porosities cancelled each other out; however, it is rather improbable considering the consistent prediction trends in terms of both phenotype and treatment.

Potential differences in mineral density may have been present in the unsegmented microCT images. Nevertheless, accurate assessment of the heterogeneity of tissue mineral density with desktop microCT instruments is limited due the polychromatic beam. Incorporation of this heterogeneity into microFE models were reported to deliver only negligible benefits in human bone [117]. Further, due to the limited resolution, the intracortical porosities were indirectly present in the microCT images, in the form of decreased attenuation coefficients, i.e. BMD values. The effects of mineral density and porosity may have been better represented by using inhomogeneous models, mapping the properties of the finite elements based on the local BMD value of the microCT images [118]. Our preliminary tests with inhomogeneous models (not reported here) did not indicate any improvement in the prediction of the experimental ultimate force, but rather a reduction in the prediction accuracy.

Thus, our FE results indirectly suggest that morphology is a much more dominant determinant of the whole bone strength than any potential differences in the material properties of the bone matrix, including the effect of the collagen pathology in the Brtl/+ mouse, or intracortical porosity. These findings indicate that the same material properties may be applicable in microFE simulations of the Brtl/+ murine model of OI and after short-term treatment with Scl-Ab. Indeed, using this technique, the simulations delivered the same statistical findings as the experiments regarding the characteristic differences in the maximum bending properties of the Brtl/+ vs. WT mice and in the Scl-Ab-treated vs. untreated animals.

The simulations achieved similar SEE values in all four groups as well as for the pooled data. The remaining scatter may be partially related also to an inability of the FE to reproduce the variability in bone alignment and loading conditions that exists between specimens during the experiment. The strength of prediction in the pooled analysis is comparable with a previous study using nonlinear microFE models to predict femoral yield load of WT and knock-out mice in three-point bending (R² = 0.94, n = 24) [119], corroborating the appropriateness of our approach. The Pistoia criterion was used here to derive the surrogate measure for ultimate force. The parameters of this criterion were optimized to maximize the correlation coefficient and the yield strain value was selected to achieve quantitatively correct prediction. Previous studies also utilized this strategy [118], or modified the elastic modulus of bone tissue to correctly predict the experimental bone strength [26]. Nevertheless, the microFE-based prediction of the femoral bending stiffness was not optimized in this study, but achieved similar prediction strength (R² = 0.89) as the optimized bone strength prediction (R² = 0.93).

This study reported partial results from an ongoing work and thus no final conclusions can be drawn regarding the differences between the groups. A mouse model was used to investigate OI; the results may not be applicable to the human disease given the differences between murine and human bone including micro-architecture and osteonal remodeling, which have been shown to be large contributors of bone fragility in OI patient biopsies [70]. In contrast to human bone, the cortex of mouse long bones include islands of rather poorly ordered bone material, surrounded by higher organized lamellar bone material [120, 121]. Further, unlike humans, mice do not normally undergo intracortical bone remodeling, although it has been observed [122]. Thus it remains unknown to what extent unorganized murine bone material is subsequently substituted with lamellar bone [120, 123] and whether increased and/or altered porosity contributes to brittleness similarly in OI human and mouse bone, since mouse bone mainly undergoes surface (re)modeling. Therefore, our findings in this mouse model of OI require confirmation in human OI bone. Moreover, these findings may reflect the moderate severity of the Brtl/+ model for OI. Unlike other mouse models, Brtl/+ typically does not suffer spontaneous fractures, and its 40-60% reduction in post-yield behavior [89, 109, 124] may mean that ultimate load values are less sensitive to post-yield alterations than other more severe OI models with more substantial reductions in bone brittleness (e.g. −77% post-yield displacement in PPIB−/− [125], −80% work-to-failure in Jrt/+ [126]; −80% post-yield displacement in CRTAP−/− [127]). Considering the Brtl/+ model, we cannot exclude that the abnormal collagen causes the development of the abnormal morphology. In fact, others have speculated that osteocytes in OI bone do not properly sense the mechanical strain stimulus, thereby contributing to the low bone mass phenotype and abnormal morphology [128–130]. Frost [128, 129] suggested that OI bone may have a higher set point, or threshold above which an anabolic response to loading occurs, while Rauch [130] suggested the increased tissue level stiffness of OI bone leads to a reduced strain stimulus, and thus bone mass adapts to the underestimated mechanical loads.

The findings may further be limited to four-point bending of the diaphyseal section and may not hold for meta/epiphyseal anatomical regions dominated by cancellous bone. Strength was tested in bending which is a typical loading mode of the femoral shaft. Bone adaptation attempts to optimize the structure with respect to average physiological loads, and these are probably unaffected in OI. Nevertheless, the curvature of long bones in OI can be smaller than in healthy conditions. In physiological loading conditions like walking, the altered curvature can increase the lever arm of the acting forces and thus the bending moments [101, 103, 105, 106]. This effect has not been considered in the used four-point bending setup, but does not compromise the interpretation of our results. Furthermore, it is not known how OI bone strength is affected in non-habitual loading modes, to which the femur is not well adapted even in healthy conditions [20, 131].

4. Summary and Conclusions

The application of FE to the human skeleton started with biomechanics in the 1970s and represents today a powerful methodology to investigate multiscale mechanics of healthy, but also diseased bone. Progress in CT imaging deliver better geometrical input, while novel mechanical testing techniques at the ECM level provide improved homogenized material properties. Additionally, musculoskeletal simulation tools are helping to determine refined boundary conditions for FE models that continuously gain in complexity and accuracy. However, these innovations also contain the limitations of FE analysis at the macroscopic, whole-bone level, that is of interest for clinical applications. The path of FE analysis to the patient is long and strewn with many difficulties that will require further efforts in experimental validation and statistical analysis of the input data. Clinical applications are associated with pathologies and the use of material properties of healthy bone may not be adequate in bone diseases such as OI.

The number of phenotypes and underlying genotypes of OI expanded substantially in the past decades, which complicates the management of this disease. OI represents a broad spectrum of supramolecular alterations at the ECM level that impact all upper hierarchical organization levels of bone. Bone mineral density distribution increases, intracortical porosity tends also to increase, while cortices become thinner and the long bone smaller. All these changes lead to reduced BMD that is difficult to interpret during growth. Intravenous bisphosphonate therapy has been beneficial during skeletal growth by adding trabecular bone density, reducing cortical porosity and increasing BMD, which result in a reduction of vertebral fracture incidence and recovery of vertebral shape [132–134]. Despite strong evidence showing deteriorated biomechanical properties at the whole-bone level that is responsible for bone fragility, the actual changes in the mechanical properties of OI bone ECM remain controversial. Nanoindentation depends on sample preparation, is sensitive to experimental conditions, solicits bone tissue mostly in compression and only partially reflects the tensile properties of the disturbed collagen fibrils. Moreover, there is little information about the effect of treatment on bone ECM material properties as the most severe OI cases can be treated as early as several days after birth until the end of growth.

Our investigation of the femora of 8 weeks old Brtl/+ versus WT mice with and without Scl-Ab treatment suggest that, in this murine model, the potential changes in bone ECM properties or intracortical porosities from OI and Scl-Ab treatment are not detectable with microFE analysis, as the structural changes seem to dominate the whole-bone properties in four-point bending of the femoral shaft. Although a number of limitations exist, material properties of this murine model may not need to be adjusted for OI or treatment in the current stage of knowledge and FE accuracy. Further studies are required to confirm if results in this mouse model of OI translate to other more severe mouse models of OI or human OI bone. Previous literature suggests that the recurrent argument that increased mineralization leads to increased brittleness may have to be tempered by the rather modest shift observed in the mean of the bone mineral density distribution [59]. Clearly, further combinations of experimental and computational research are needed to elucidate the origin of brittleness in OI bone and to answer the original question of whether FE needs to be refined to eventually help improve fracture risk prediction in OI.

We are probably not yet there to be able to “do more or less what one wants with a finite element mode1”, as John Currey formulated [1], but the field is still progressing. Indeed, John’s last published paper utilized the FE method [135]. Nevertheless, he once mentioned: “papers on Finite Element Analysis are often what Peter Medawar once called methodological chambers of horrors” [1], … we sincerely hope that the present paper will not be perceived as one of those.

Highlights.

• The application of the finite element (FE) method to bone is reviewed in the light of John Currey’s statements

• The use of FE to investigate osteogenesis imperfecta (OI) is targeted

• The multiscale alterations of the bone tissue in OI and the effect of treatment are reviewed

• An original microFE study is presented to predict bone strength in a murine model of OI subjected to sclerostin neutralizing antibody treatment

• microFE models with identical material properties well predict experimental strength and reproduce statistical comparisons of disease and treatment