Abstract
We study the effect of delaying treatment in the presence of (unobserved) heterogeneity. In a homogeneous population and assuming a proportional treatment effect, a treatment delay period will result in notably lower cumulative recovery percentages. We show in theoretical scenarios using frailty models that if the population is heterogeneous, the effect of a delay period is much smaller. This can be explained by the selection process that is induced by the frailty. Patient groups that start treatment later have already undergone more selection. The marginal hazard ratio for the treatment will act differently in such a more homogeneous patient group. We further discuss modeling approaches for estimating the effect of treatment delay in the presence of heterogeneity, and compare their performance in a simulation study. The conventional Cox model that fails to account for heterogeneity overestimates the effect of treatment delay. Including interaction terms between treatment and starting time of treatment or between treatment and follow up time gave no improvement. Estimating a frailty term can improve the estimation, but is sensitive to misspecification of the frailty distribution. Therefore, multiple frailty distributions should be used and the results should be compared using the Akaike Information Criterion. Non‐parametric estimation of the cumulative recovery percentages can be considered if the dataset contains sufficient long term follow up for each of the delay strategies. The methods are demonstrated on a motivating application evaluating the effect of delaying the start of treatment with assisted reproductive techniques on time‐to‐pregnancy in couples with unexplained subfertility.
Keywords: dynamic treatment regimens, frailty, observational data, treatment delay, unobserved heterogeneity
1. INTRODUCTION
For many diseases effective treatments exist that can speed up the time to recovery. However, treatments may be costly, bring burden to patients, and/or carry side effects. Therefore, when patients' chances of recovery without treatment are reasonable, a doctor may recommend a delay period in which the patient first gets the chance to recover naturally before embarking on treatment. Introducing a delay period before starting treatment is sometimes called a “wait‐and‐see” period or “expectant management.” While the general idea of such an approach is well understood, little is known about the optimal duration of delay periods. This is, for instance, currently an issue in the management of children presenting with acute otitis media. How long should doctors wait for spontaneous remission of symptoms and when should they start an antibiotic treatment, see for example Venekamp et al. (2015). Another example is from insurance medicine: when to start with a return‐to‐work intervention after the onset of sick leave, see, for example, Van Duijn et al. (2010). The application that motivated the current work is from Reproductive Medicine: when to start with assisted reproductive techniques such as IVF in couples who are subfertile with unexplained cause as set forward in, for example, Kamphuis, Bhattacharya, van der Veen, Mol, and Templeton (2014).
To evaluate different treatment delay periods, one would typically want to know the expected cumulative recovery percentages at some fixed time horizon for treatment strategies that differ with respect to the time point at which treatment is started. Knowledge of these cumulative recovery rates is needed to make an evidence‐based trade‐off between the effectiveness of the treatment strategy and its associated costs, burden, and risks. For instance, we may want to estimate the 3 year cumulative recovery percentage for a strategy where treatment is started immediately at diagnosis, and compare the recovery percentage to strategies where treatment is started only in patients who have not yet recovered after a delay period of half a year or one year.
The effect of treatment delay has been studied in the statistical literature by several authors (Huitfeldt, Kalager, Robins, Hoff, & Hernán, 2015; Johnson, Ribaudo, Gulick, & Eron, 2013; Li, Eron, Ribaudo, Gulick, & Johnson, 2012). The problem can be cast in terms of the more general situation of the evaluation of dynamic treatment regimens. A dynamic treatment regimen is a rule that dictates the level of treatment at time t as a function of information available on the patient up to time t (Murphy, van der Laan, & Robins, 2001). The regimens that we will study in this manuscript are of the following simple types: start treatment from a certain intended starting time on, unless the patient has already recovered before the target starting time, in that case never start treatment. If a study would randomly assign patients to different treatment regimens, estimation of the expected outcome of a certain regimen would be straightforward by stratifying the data according to the assigned regimen (Johnson & Tsiatis, 2004). However, implementing randomized designs for evaluating dynamic treatment regimens has proved extremely challenging in practice. The prospect of possibly being randomized to a trial arm where patients have to wait before getting a treatment complicates recruitment. An example is the ACTG A5115 randomized trial aiming to study immediate versus delayed switch to second line antiretroviral therapies in HIV patients. That study failed to meet target accrual and therefore remained inconclusive (Johnson et al., 2013; Riddler et al., 2007). Also, a trial comparing more than two delay strategies would need multiple treatment arms requiring large sample size.
Observational data are often the only available source for evaluating dynamic treatment regimens. Two main challenges have been described in this setting. First, in observational data the intended treatment starting time will not be observed for all patients. In particular, for patients experiencing the recovery event before starting treatment, the potential time at which treatment would have been started is unobserved. Unobserved intended starting or stopping times of treatment, possibly also due to other intermediate events such as adverse events, have been denoted as “treatment‐terminating events” (Johnson & Tsiatis, 2004) or “censored treatment times” (Johnson et al., 2013). The methods in this manuscript will account for such partly unobserved exposure. In the situation we study, we observe a time‐dependent treatment indicator. All patients start untreated and we only observe the treatment strategy for those who switch to treatment before they experience the event of interest.
Second, observational data harbour the risk of confounding as the received treatment was not chosen by design, but left to the discretion of the patient and their doctor. Therefore, patients receiving different delay periods may not be prognostically similar. Many solutions to correct for possibly time‐dependent confounding have been proposed in the literature, see, for example, Murphy et al. (2001), Johnson and Tsiatis (2004), Cain et al. (2010), Huitfeldt et al. (2015). Our main focus in this manuscript is however on a third important challenge that has not yet been studied in the setting of treatment delay: unobserved heterogeneity. By this we mean differences in the prognosis of patients that cannot be explained by observed characteristics. In particular we study the situation where the outcome is a time‐to‐event variable of which the distribution varies among patients according to an unknown frailty distribution. In order to isolate this third challenge from the issue of confounding, we will make the assumption that despite studying observational data, the treatment decisions were not influenced by prognostic factors. We come back to this in the discussion.
It is well known that unobserved heterogeneity leads to misspecification of hazard ratios in the Cox model as explained in for instance Gail (1984) and Bretagnolle (1988) and more recently in Hernán (2010). However, most of the work on this topic focusses on time fixed covariates. In case of studying treatment this means that patients are either treated or untreated, and this status does not change during follow up. Unobserved heterogeneity induces a selection process over time with high susceptible patients getting the event earlier, so also leaving the risk sets earlier. With a time fixed treatment covariate, the changes in frailty distribution over time caused by the selection process are well understood. Less well known is the behavior of time varying treatments in the presence of unobserved heterogeneity. When patients switch treatment condition (so either start or stop treatment), this additionally influences the frailty distributions in both treatment groups. This may lead to unexpected behavior of marginal survival quantities. Aalen and colleagues have pointed out some of these artifacts in the situation where patients switch from a treated to an untreated condition, that is, in the setting of treatment discontinuation (see, e.g., Aalen, Børgan & Gjessing, 2008; Aalen, Cook & Røysland, 2015; and Aalen, Valberg, Grotmol, & Tretli, 2015b). In this paper, we study the mirrored situation: patients switch from untreated to treated status, that is, the setting of treatment initiation. Within this setting, we compare strategies with different treatment delay periods. The duration of the selection process in the untreated condition differs between these strategies. Therefore, we hypothesize that unobserved heterogeneity and the associated selection process may also play an important role in the evaluation of treatment delay. First, we study the potential impact by opposing theoretical scenarios with and without heterogeneity. Second, we compare modeling approaches estimating the effect of treatment delay periods from data in a simulation study.
The main motivational application is from Reproductive Medicine and we will use this example throughout the paper. It is known that there is a huge variability between couples’ chances of conceiving naturally, varying in the general population from 0% to 60% per month as described in Te Velde, Eijkemans, and Habbema (2000). We can only explain a small part of this heterogeneity by measurable factors. Our focus is on the role of unobserved heterogeneity in the evaluation of different starting times of assisted reproductive techniques such as IVF. Our target parameter is the cumulative percentage of couples who have become pregnant (and are thus recovered from their subfertility) 3 years after the initial diagnosis. We want to estimate this quantity for different treatment strategies where treatment is started immediately upon diagnosis, after half a year or after one year.
2. THEORETICAL SCENARIO COMPARISON
In this section, we consider theoretical scenarios of time‐to‐pregnancy distributions with and without heterogeneity. We make the scenarios as comparable as possible on all other aspects. We calculate the cumulative recovery percentages for different delay strategies in both scenarios and compare results.
2.1. Scenarios with heterogeneity
We consider a population of couples who are trying to become pregnant and denote the time‐to‐pregnancy as T. When studying time‐to‐pregnancy, the event of interest is a desirable outcome. Therefore the term “hazard rate” is less appropriate and instead we will use the term fecundity rate for what is usually termed hazard rate, see, for example, Evers (2002). To formalize the heterogeneity among the couples, we study the multiplicative frailty model, that is, we assume that the conditional fecundity rate, that is, the conditional hazard rate, of a couple is given as the product of a couple specific frailty and a basic rate that is shared among all couples:
We will assume in all frailty models that the fecundity rate for an individual couple remains constant over the follow up time: . Though this assumption might not be realistic for older women who are followed for a longer time period (Eijkemans et al., 2014), previous studies have shown that such a simplification is feasible (Sozou & Hartshorne, 2012). For Z, which is a random variable that specifies the degree of heterogeneity in fecundity among couples, a distribution has to be chosen. Below we will describe in detail the model when assuming that Z follows a gamma distribution. We consider other frailty distributions in later sections.
2.1.1. Scenario with gamma frailty
For Z we assume the gamma distribution with mean 1 and variance δ, . The individual couple fecundity rate and the frailty variable are unobservable. What is observed in a population is the net result for a number of couples with different frailties, also called the population (or marginal) fecundity rate. As is shown in Aalen et al. (2008) through Laplace transformation, for the gamma distribution the population fecundity rate has the following simple form:
| (1) |
with the cumulative fecundity rate at time t, which due to our assumption of constant fecundity rate is . Our primary interest is in the cumulative recovery percentages at the population level, that is, one minus the population survival function which, again by use of Laplace transformation, can be written as:
We assume that there is an effective binary treatment X. Couples can switch from off treatment to on treatment over time, so X is a time varying covariate which we denote by , before t start and from t start onward. We assume that the treatment has an immediate effect: from the moment of treatment start on it increases the fecundity rate of an individual couple by a factor r. We will denote as the conditional fecundity ratio, generally known as the conditional hazard ratio. Proportionality of the treatment effect is thus assumed to hold at the individual couple level:
| (2) |
If the treatment is given to all couples who are not yet pregnant at t start, then for the population fecundity rate over time becomes:
with marginal cumulative recovery percentage for :
In Figure 1a we plot the cumulative event curves for , and for a regimen where the treatment is started immediately (), after half a year (), one year (), or where treatment is never started. Reading off the cumulative recovery percentages at 3 years from the curves, it may be seen that an immediate treatment start results in the highest recovery rate of 63%, as can be expected. Waiting one year before starting treatment leads to a cumulative recovery percentage of 61%. In this scenario 39% of patients would be spared the treatment and the remaining 61% would have a much shorter treatment period, at the cost of only a 2% lower cumulative recovery rate. If we would express the expected extra number of patients that need to receive treatment relative to the expected extra number of couples who will conceive, compared to the scenario where treatment is started after 1 year (similar to the common “number needed to treat” effect measure), we would get .
Figure 1.
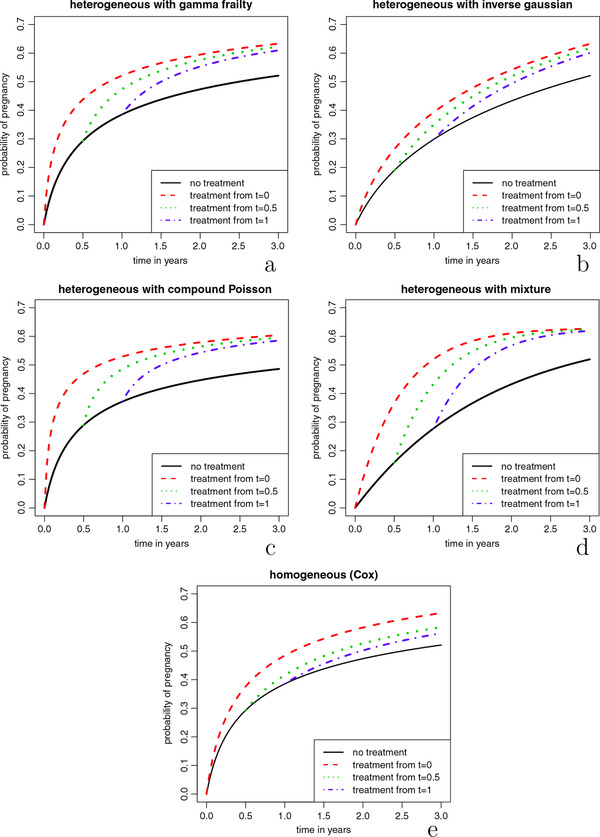
Theoretical scenario comparison. Marginal cumulative recovery percentages () for different treatment starting times. For the formulas and parameters used, see Table 1. For background on the parametrization, see the appendix of Balan and Putter (2019)
Over time, the two curves belonging to delayed treatment start in Figure 1a get closer to the curve of the immediate treatment regimen. One way to understand this “converging” behaviour of the cumulative recovery percentages, is to look at the fecundity ratios at the population level over time. A known property of frailty models is that the marginal hazard ratio decreases over time, and attenuates toward one if when t increases as shown by Aalen et al. (2008). This is due to a selection effect. The treated group starts out with a clear advantage in recovery chances compared to the untreated group. However, over time in both groups patients with relatively high chances are removed from the risk set as they recover (become pregnant). In this way, over time, the chances of the patients still present in the treated group become highly similar to those in the untreated group. Figure 2 illustrates this process.
Figure 2.
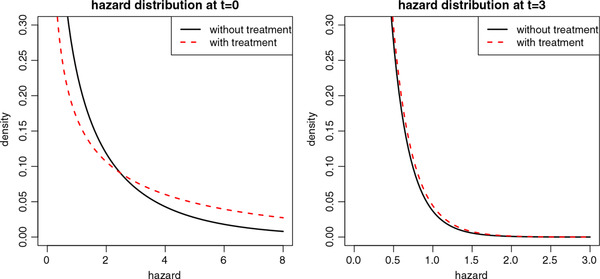
Illustration of the selection effect. The hazard distributions are plotted for an untreated (solid black lines) and a treated group (dashed red lines), at time = 0 (left panel) and for those who have survived (have not yet recovered) at t = 3 (right panel). We assumed a constant baseline hazard of 1.5, a proportional conditional hazard ratio of 3, and a gamma frailty with mean 1 and variance 2. At the hazard of the untreated group has mean 1.5 and variance 1.52*2 = 4.5, the treated group has mean 4.5 and variance 4.52*2 = 40.5. For patients who have not yet recovered after 3 years (t = 3), the hazard of the untreated patients has a mean of = 0.15 and variance = 0.045, while the hazard of the treated patients has mean 0.16 and variance 0.052. The treated group will have become smaller than the untreated group, but the hazard distributions of both groups are very similar
The decreasing hazard ratios over time from the theoretical scenario with gamma frailty are pictured in Figure 3. We observe that when the treatment is started at a later time point, the attenuation is slower, as by that time the frailty distribution among couples still at risk has lower variance than at earlier time points. Couples with the highest frailties are already pregnant. Loosely speaking, the marginal treatment effect is higher when starting the treatment later as then the patients are treated who really need it.
Figure 3.

Fecundity ratios at the population level for different treatment starting times in the theoretical scenario with heterogeneity according to gamma frailty
2.1.2. Scenarios with inverse Gaussian, compound Poisson, and Bernoulli frailties
Figure 1 shows three other heterogeneous scenarios where we used different distributions for Z: inverse Gaussian, compound Poisson, and the Bernoulli distribution. The latter leads to a “two peak” mixture distribution in which part of the population is sterile, that is, has fecundity rate zero and the other part has constant fecundity rate. Also with the compound Poisson distribution there is mass at zero. In all three scenarios we used the same assumptions as in the gamma scenario: multiplicative frailty, constant individual fecundity rate, and a proportional treatment effect at the individual level, so that relation (2) holds. The formulas used for making these cumulative recovery curves are based on Laplace transformations and are depicted in Table 1. We chose the parameter values in all three scenarios in such a way that the end values (at ) of the marginal cumulative recovery percentages in the “no treatment” and “immediate treatment” strategies were the same as in the model with gamma distribution. For the inverse Gaussian and the compound Poisson frailty we kept the frailty variance δ at 4 as in the gamma scenario. The shape of the curves of all three heterogeneous scenarios is very different than when using the gamma distribution. However, the “converging” behaviour of the lines for the active treatment regimens is visible in all.
Table 1.
Formulas for the cumulative recovery curves in Figure 1
| Scenario |
|
Parameter values | ||
|---|---|---|---|---|
| Gamma |
|
|
||
| Inverse Gaussian |
|
|
||
| Compound Poisson |
|
|
||
| Bernoulli |
|
, | ||
| No frailty |
|
|
2.2. Scenario without heterogeneity
To provide a reference case for the above heterogeneous scenarios, we constructed a comparison scenario without heterogeneity. If all couples have the same fecundity rate, then the individual fecundity rates are equal to the population rates. We set the individual fecundity rate in this second scenario equal to the marginal fecundity rate without treatment from the heterogeneous gamma scenario. Indicating the parameters of this homogeneous scenario with an *, we thus define , with as in formula (1). The marginal fecundity ratio was again chosen in such a way that the marginal cumulative recovery percentage at with “immediate treatment” start was the same as in the heterogeneous scenarios. In the homogeneous scenario a proportional marginal treatment effect implies a proportional individual treatment effect, so the homogeneous scenario follows the model:
| (3) |
Figure 1e shows the marginal cumulative recovery percentages under this homogeneous scenario. In contrast to the four heterogeneous scenarios, here the lines of the two delayed treatment strategies do not converge to the line of the strategy with immediate treatment start. An immediate treatment start leads to a notably higher cumulative recovery percentage compared to waiting 1 year (63% vs. 56% at 3 years, respectively). The number of patients needed to treat immediately instead of waiting 1 year to achieve on average one additional pregnancy is now much lower at only 6.
3. MODELING APPROACHES
The previous section pointed out that heterogeneity plays a role in how marginal cumulative recovery percentages depend on treatment delay. In this section we describe several modeling options that aim to retrieve the correct marginal cumulative recovery percentages from observed data.
Evaluations of treatment delay usually have to rely on observational data. In such data one can typically discern when patients recovered and when they were treated, but not what treatment strategy was used. If a patient recovers before starting treatment, the intended time of treatment start will be unknown for this patient. For this reason data cannot be simply split up according to observed treatment strategies. We will evaluate the five modeling approaches listed below. In the next section we evaluate if these can accurately estimate the cumulative recovery percentages from simulated datasets.
Cox The most commonly used modeling approach is fitting a Cox proportional hazard model where the treatment exposure is entered as a time varying covariate: 0 if not yet treated and 1 from treatment start on. This model makes the assumption of proportional marginal and individual hazards, so it is assumed that relation (3) holds.
Cox + frailty In the second method we account for heterogeneity by extending the Cox model with a frailty term, so we assume that relation (2) holds. Since in real‐life problems the shape of the frailty distribution will be unknown, we will look at different frailty distributions and in particular we consider a scenario where the assumed frailty distribution is based on the best fit of the model to the data according to Akaike Information Criterion (AIC). The frailty models were estimated using the R package frailtyEM developed by Balan and Putter (2019). The same package was used to transform the individual level parameters from the models to marginal cumulative event curves. For the compound Poisson frailty we fixed m at 0.5 in the following analyses, see Table 1 for the parametrization. More details on the parametrization can be found in the Appendix of Balan and Putter (2019).
Cox + Tx* t start In the third approach we circumvent the direct estimation of the heterogeneity and instead accommodate its impact by allowing for non‐proportionality of the marginal treatment effect. In particular we assume the marginal effect of treatment increases according to the starting time, but remains constant for the treated duration thereafter. We assume , with a vector of regression coefficients and a vector of three time‐dependent indicator variables denoting the treatment status according to starting treatment after 0, 0.5 year, or 1 year, with the reference category being no treatment. So for instance is zero for all couples from to and one afterward for the couples who start treatment at .
Cox + Tx*t Non‐proportionality in the marginal Cox model can also be accommodated by including an interaction between treatment and follow‐up time. This is a common way to deal with non‐proportional hazards as advised in, for instance, Kleinbaum and Klein (2005). Here we assume , with a function of time, in this case we choose .
Non‐parametric approach In this approach we do not assume any parametric shape of the treatment effect. To overcome the problem of unobserved treatment starting times, we use methods proposed by Cain et al. (2010) and by Huitfeldt et al. (2015). In particular we split the follow‐up information of the patients into (possibly replicated) periods where they were consistent with one or more of the treatment strategies. This method has also been referred to as the three step procedure of cloning, censoring, and weighting by Hernán (2018). Since we assume no confounding is present in the current manuscript, we only need the first two steps of the procedure. We thus clone observation periods that are consistent with multiple treatment delay strategies and administratively censor these periods when the patient deviates from the strategy. For example, a patient who starts treatment after half a year, is represented by four rows in the dataset. The untreated time period from 0 to 6 months is replicated in three rows labeled with the strategies “never treat,” “treat after 1 year,” and “treat after 6 months,” respectively. The fourth row covers the treated time period from 6 months up to end of follow up and is labeled as belonging to the strategy “treat after 6 months.” Lumping together all periods labeled under one strategy, we use the non‐parametric Kaplan–Meier estimator to estimate the cumulative recovery percentages on the restructured data for that strategy.
4. SIMULATIONS
4.1. Simulation settings
We compared the different modeling approaches in a simulation study. In our first simulation setting, we simulated data from the heterogeneous scenario with gamma frailty described in Section 2.1. The parameters used in the simulation were loosely based on the data application presented in Section 5. Couples were first randomly assigned to one of the treatment strategies: . Then we drew a random frailty from a distribution, calculated individual hazards before and after treatment start according to formula (2) () and drew a random time‐to‐pregnancy from the individual hazards. We simulated 1000 datasets in this way.
As the frailty modeling approaches could be sensitive to misspecification, we simulated data from a second heterogeneous setting for which all frailty models were misspecified. We assumed here that Z followed a Bernoulli distribution, that is, the time‐to‐pregnancy followed a mixture distribution. We used a similar simulation scheme as in the first scenario: couples were first randomly assigned to one of the treatment strategies: . Then we drew a random “sterility indicator” from a Bernoulli distribution with success probability 0.37. When not sterile, we assumed an individual hazard of 0.58 before treatment and 3 × 0.58 after treatment start. We used these hazards to randomly draw a time‐to‐pregnancy (which is infinite in case of sterility). Again 1000 datasets were simulated in this way.
In these two main simulation settings, we assumed no censoring occurred before the follow up of 3 years. In the Supporting Information the same two settings are evaluated with censoring added. The aim of the simulation study was to compare the accuracy of the modeling approaches by comparing the bias and variance of their estimates of the 3 year cumulative recovery percentages.
4.2. Simulation results
Results of simulations using a gamma frailty distribution are shown in Figure 4 and using a mixture distribution in Figure 5. The estimated 3 year marginal cumulative pregnancy percentages are compared to the true values.
Figure 4.

Simulation results from the heterogeneous scenario with gamma frailty. Red horizontal lines indicate the true cumulative recovery rates at . Plots are based on N = 1000 simulated datasets with n = 4000 couples per dataset
Figure 5.
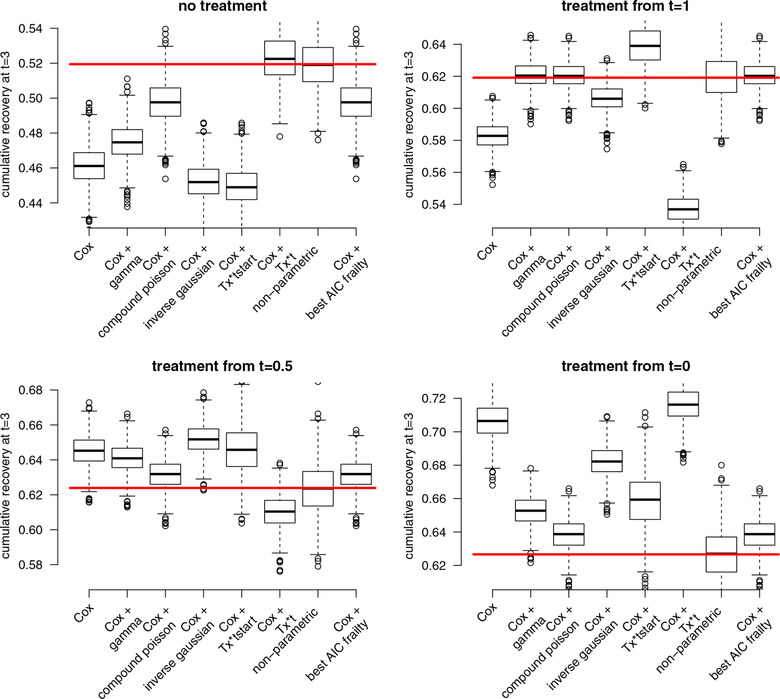
Simulation results from the heterogeneous scenario with mixture distribution (all frailty distributions are misspecified). Red horizontal lines indicate the true cumulative recovery rates at t = 3. Plots are based on N = 1000 simulated datasets with n = 4000 couples per dataset
Especially the commonly used methods, Cox and Cox + Tx*t, highly overestimated the benefit of an early treatment strategy. The pregnancy percentages for the immediate treatment strategy were estimated too high and the percentages for the strategy where treatment is delayed were estimated too low. The Cox + frailty models were sensitive to misspecification of the frailty shape. Choosing the optimal frailty distribution in each simulated dataset based on the AIC gave good results in the first simulation setting. However, in the second setting where all frailty distributions were misspecified, this “best AIC” approach was biased for three of the four treatment strategies. The non‐parametric approach through “cloning and censoring” was unbiased in both simulation settings. The variance of the estimates in this approach was somewhat larger compared to the other approaches, indicating that the method requires large enough sample size to give precise estimates.
In particular, when part of the event times are censored, the number of observations for the strategies with delayed treatment start may become too low for the non‐parametric method to give reliable results. In the Supporting Information we show a simulation scenario where about three quarters of the event times before 3 years were censored by an independent exponential censoring mechanism. In that scenario, the frailty model with distribution chosen based on best AIC clearly outperformed the non‐parametric method in terms of root mean squared error, both in the gamma and in the mixture scenario for which all frailty distributions were misspecified.
Source code to reproduce the simulation results is available as Supporting Information on the journal's web page. The simulation parameters (sample size, degree of heterogeneity, survival distribution, degree of censoring, etc.) can be adjusted in the code to compare the methods in a particular data situation.
5. DATA APPLICATION: WHEN TO START WITH INTRA‐UTERINE INSEMINATION?
To study the potential impact of (not) accounting for heterogeneity in the analysis of treatment delays, we analyzed a recent dataset from Reproductive Medicine. We present the results from the conventional Cox model, from the frailty models where the optimal distribution was determined based on AIC and from the non‐parametric cloning and censoring approach.
We analyzed data from a prospective cohort following 1896 couples diagnosed with unexplained subfertility included in seven centres in the Netherlands between January 2002 and February 2004. Details on data collection were described by Van der Steeg et al. (2007) and Steures et al. (2004). This cohort has recently been analyzed in Van Eekelen et al. (2019). Patients were included in the cohort (time zero) at the end of a fertility workup that showed no abnormalities, rendering the diagnosis of unexplained subfertility. All couples started on expectant management (no treatment) and could start with the first line treatment IUI at any time point during follow up. The primary endpoint was time to conception leading to an ongoing pregnancy, with ongoing pregnancy defined as a foetus reaching a gestational age of at least 12 weeks visualized by ultrasound. Ongoing pregnancy is generally considered an appropriate proxy for live birth in clinical research: approximately 95% of ongoing pregnancies lead to a live birth (Clarke et al., 2010; Braakhekke et al., 2014). The date of conception was defined as the first day of the last menstruation period prior to the pregnancy.
863 couples started IUI at a median time of 7.2 months after diagnosis (range 0–4 years). The research question we want to answer is what pregnancy percentages can be expected 3 years after diagnosis if treatment would be started in all couples immediately after diagnosis versus after a delay of 6 months or 1 year. Follow up time was censored at the last date of contact, after the last IUI cycle, or if patients moved on to a second line treatment (IVF). We assumed no confounding by indication was present. In this observational study this might not be a realistic assumption, but we make this simplification so that we can focus on the unobserved heterogeneity aspect of the data.
Results from the modeling approaches are presented in Figure 6. The analyses show that there may be a very relevant influence of heterogeneity in this data. The frailty model with gamma distribution had best AIC, the other frailty distributions with compound poisson and inverse gaussian distributions each had 11 points worse AIC. The frailty variance in the gamma model was 22, reflecting huge differences between the individual hazards. According to this model, delaying treatment by one year compared to starting treatment immediately would not lower the 3 year pregnancy rate at all, whereas of couples would be spared the treatment (NNT 1000). The conventional Cox model suggest a 10% benefit of an immediate treatment start versus a 1 year delay strategy (NNT 3).
Figure 6.
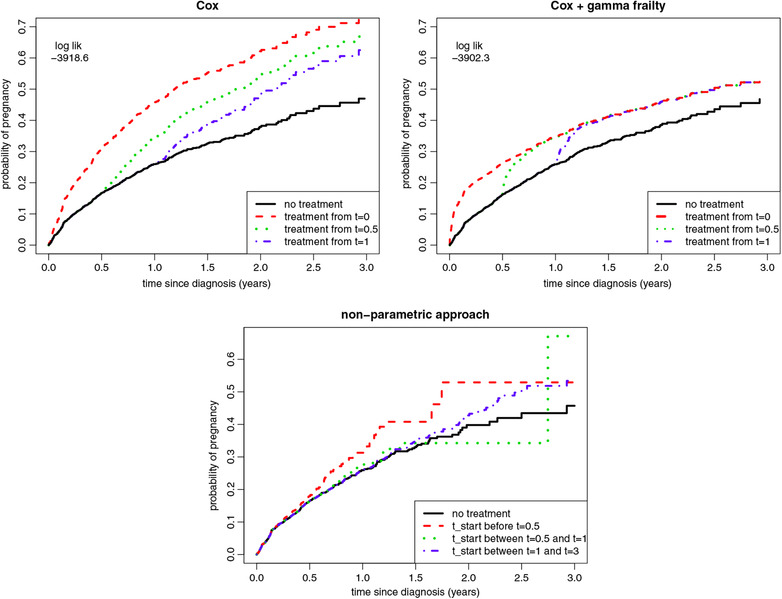
Data application results. Marginal cumulative recovery percentages for different treatment starting times estimated from the IUI data
Unlike the conventional Cox and frailty approaches, the non‐parametric approach is not able to assess treatment strategies with a single fixed starting point, when patients in the data started treatment at many different time points. Therefore we categorized starting time, before we could apply the non‐parametric cloning and censoring approach, see Van Geloven, Dekkers, and le Cessie (2019). The categories were defined as: start treatment within 6 months, start treatment between 6 and 12 months, start treatment between 12 and 36 months, or do not start treatment during the full 3 year follow up. For the treat‐within‐6‐months and treat‐between‐6‐and‐12‐months strategies, the number of patients in follow up after 2 years was too low (<10) for accurate estimation of the long term probabilities, showing that this dataset was too small for use of the non‐parametric approach.
6. DISCUSSION
Unobserved heterogeneity plays an important role in the evaluation of treatment delay strategies. In a theoretical illustration using multiplicative frailty models, we have shown that in the presence of heterogeneity cumulative recovery percentages of different timing strategies get closer to each other over time. In a real‐life dataset we illustrated that this might substantially influence the comparison of delay strategies.
Our simulations showed that the only unbiased estimation method was the non‐parametric approach. However, the wider simulation standard deviation and the real‐life data example showed that a sufficient long term follow up of each of the strategies is needed for this technique. Also, with this approach treatment strategies have to be defined using intervals (e.g., start treatment between months 6 and 12), the method does not provide a direct way to evaluate a single starting time. The simulation study further showed that estimating the cumulative recovery rates with a Cox model including a frailty term is sensitive to misspecification of the frailty distribution. The approach in which the distribution of the frailty term was selected based on the AIC criterium gave relatively best results, but should still be used with caution. We advise in this case to consider several frailty distributions, including some with mass at zero like the compound poisson. We advice against the commonly used Cox proportional hazards models for comparing timing strategies as they can severely overestimate the benefit of early treatment start in the presence of unobserved heterogeneity. Allowing for time varying treatment effects in the usual way (Cox + Tx*t) or stratifying the treatment effect according to starting time (Cox + Tx*t start) gave no improvement.
In case of a positive treatment effect, an earlier treatment start should always result in higher cumulative recovery chances. The question of interest is “how much higher?”. A potential direction of further research could be to consider estimation approaches under monotonicity constraints, that is, forcing later treatment to result in lower cumulative pregnancy percentages but letting the estimation method determine how much lower.
Analysis methods for evaluation of treatment delay strategies in observational data should be able to address all three challenges mentioned in the introduction: partially unobserved treatment starting times, unobserved heterogeneity, and confounding. In this paper we addressed the first two challenges, but ignored the third. All discussed methods could however be easily combined with well‐established correction techniques for confounding such as inverse probability of treatment weighting as proposed by Murphy et al. (2001), Johnson and Tsiatis (2004), Cain et al. (2010), and Huitfeldt et al. (2015).
We conclude that similar to the situation of treatment discontinuation studied in, for instance, Aalen et al. (2008), Aalen et al. (2015), and Aalen et al. (2015b), frailty also leads to unexpected behavior of marginal survival quantities in the situation of treatment initiation. In particular, we showed that the marginal survival percentages of delayed treatment strategies converge toward those of an immediate treatment strategy. Conventional modeling approaches such as the Cox model or the Cox model with time varying coefficient are prone to overestimate the benefit of early treatment regimens in the presence of unobserved heterogeneity. When unobserved heterogeneity is expected to play a role, using frailty models could be an alternative but a large range of frailties should be considered of which the best model based on the AIC should be selected. The non‐parametric approach is a sensible choice if there is sufficient long term follow up in the data.
CONFLICT OF INTEREST
The autors have declared no conflict of interest.
Open Research Badges
This article has earned an Open Data badge for making publicly available the digitally‐shareable data necessary to reproduce the reported results. The data is available in the Supporting Information section.
This article has earned an open data badge “Reproducible Research” for making publicly available the code necessary to reproduce the reported results. The results reported in this article could fully be reproduced.
Supporting information
Supporting Information
ACKNOWLEDGMENTS
We are grateful to the CECERM study group (Collaborative Effort for Clinical Evaluation in Reproductive Medicine) who collected the data presented here with grant support from ZonMw, The Netherlands Organization for Health Research and Development, The Hague, The Netherlands, grant 945/12/002.
van Geloven N, Balan TA, Putter H, le Cessie S. The effect of treatment delay on time‐to‐recovery in the presence of unobserved heterogeneity. Biometrical Journal. 2020;62:1012–1024. 10.1002/bimj.201900131
REFERENCES
- Aalen, O. O. , Børgan, O. , & Gjessing, H. K. (2008). Survival and event history analysis: a process point of view, (Chapter 6). New York: Springer. [Google Scholar]
- Aalen, O. O. , Cook, R. J. , & Røysland, K. (2015). Does Cox analysis of a randomized survival study yield a causal treatment effect? Lifetime Data Analysis, 21, 579–593. [DOI] [PubMed] [Google Scholar]
- Aalen, O. O. , Valberg, M. , Grotmol., T. , & Tretli, S. (2015b). Understanding variation in disease risk: The elusive concept of frailty. International Journal of Epidemiology, 44, 1408–1421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balan, T. A. , & Putter, H. (2019). frailtyEM: An R package for estimating semiparametric shared frailty models. Journal of Statistical Software, 90, 1–29. [Google Scholar]
- Braakhekke, M. , Kamphuis, E. I. , Dancet, E. A. , Mol, F. , van der Veen, F. & Mol, B. W. (2014). Ongoing pregnancy qualifies best as the primary outcome measure of choice in trials in reproductive medicine: An opinion paper. Fertility and Sterility, 101, 1203–1204. [DOI] [PubMed] [Google Scholar]
- Cain, L. E. , Robins, J. M. , Lanoy, E. , Logan, R. , Costagliola, D. , & Hernán, M. A. (2010). When to start treatment? A systematic approach to the comparison of dynamic regimens using observational data. International Journal of Biostatistics, 6, Article 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clarke, J. F. , van Rumste, M. M. , Farquhar, C. M. , Johnson, N. P. , Mol, B. W. , & Herbison, P. (2010). Measuring outcomes in fertility trials: Can we rely on clinical pregnancy rates? Fertility and Sterility, 94, 1647–1651. [DOI] [PubMed] [Google Scholar]
- Eijkemans, M. J. , van Poppel, F. , Habbema, D. F. , Smith, K. R. , Leridon, H. , te Velde, E. R. (2014). Too old to have children? Lessons from natural fertility populations. Hum Reprod, 29(6), 1304–12. 10.1093/humrep/deu056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evers, J. L. H. (2002). Female subfertility. The Lancet, 360, 151–159. [DOI] [PubMed] [Google Scholar]
- Hernán, M. A. (2010). The hazards of hazard ratios. Epidemiology, 21, 13–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernán, M. A. (2018). How to estimate the effect of treatment duration on survival outcomes using observational data. The BMJ, 360, k182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huitfeldt, A. , Kalager, M. , Robins, J. M. , Hoff, G. , & Hernán, M. A. (2015). Methods to estimate the comparative effectiveness of clinical strategies that administer the same intervention at different times. Current Epidemiology Reports, 2, 149–161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson, B. A. , Ribaudo, H. , Gulick, R. M. , & Eron, J. J., Jr. (2013). Modeling clinical endpoints as a function of time of switch to second‐line ART with incomplete data on switching times. Biometrics, 69, 732–740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson, B. A. , & Tsiatis, A. A. (2004). Estimating mean response as a function of treatment duration in an observational study, where duration may be informatively censored. Biometrics, 60, 315–323. [DOI] [PubMed] [Google Scholar]
- Kamphuis, E. I. , Bhattacharya, S. , van der Veen, F. , Mol, B. W. , & Templeton, A. (2014). Are we overusing IVF? The BMJ, 348, g252. [DOI] [PubMed] [Google Scholar]
- Kleinbaum, D. G. , & Klein, M. (2005). Survival analysis: A self‐learning text, (2nd ed.). New York: Springer. [Google Scholar]
- Li, L. , Eron, J . J., Ribaudo, H. , Gulick, R. M. , & Johnson, B. A. (2012). Evaluating the effect of early versus late ARV regimen change if failure on an initial regimen: Results from the AIDS clinical trials group study A5095. Journal of the American Statistical Association, 107, 542–554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy, S. A. , van der Laan, M. J. , & Robins, J. M. (2001). Marginal mean models for dynamic regimens. Journal of the American Statistical Association, 96, 1410–1423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riddler, S. , Jiang, H. , Tenorio, A. , Huang, H. , Kuritzkes, D. R. , Acosta, E. , Bartlett, J. A. (2007). A randomized study of antiviral medication switch at lower‐versus higher‐switch thresholds: AIDS Clinical Trials Group Study A5115. Antiviral Therapy, 12, 531–541. [DOI] [PubMed] [Google Scholar]
- Sozou, P. D. , & Hartshorne, G. M. (2012). Time to pregnancy: A computational method for using the duration of non‐conception for predicting conception. PLoS ONE, 7, e46544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steures, P. , van der Steeg, J. W. , Mol, B. W. , Eijkemans, M. J. , van der Veen, F. , Habbema, J. D. , & van Dop, P. A. (2004). Prediction of an ongoing pregnancy after intrauterine insemination. Fertility and Sterility, 82, 45–51. [DOI] [PubMed] [Google Scholar]
- Te Velde, E. R. , Eijkemans, R. , & Habbema, H. D. (2000). Variation in couple fecundity and time to pregnancy; an essential concept in human reproduction. The Lancet, 355, 1928–1929. [DOI] [PubMed] [Google Scholar]
- Van der Steeg, J. W. , Steures, P. , Eijkemans, M. J. , Habbema, J. D. , Hompes, P. G. , Broekmans, F. J. , & Mol, B. W. (2007). Pregnancy is predictable: A large‐scale prospective external validation of the prediction of spontaneous pregnancy in subfertile couples. Human Reproduction, 22, 536–542. [DOI] [PubMed] [Google Scholar]
- Van Duijn, M. , Eijkemans, M. J. , Koes, B. W. , Koopmanschap, M. A. , Burton, K. A. , & Burdorf, A. (2010). The effects of timing on the cost‐effectiveness of interventions for workers on sick leave due to low back pain. Occupational and Environmental Medicine, 67, 744–750. [DOI] [PubMed] [Google Scholar]
- van Eekelen, R. , van Geloven, N. , van Wely, M. , McLernon, D. J. , Mol, F. , Custers, I. M. , & Eijkemans, M. J. (2019). Is IUI with ovarian stimulation effective in couples with unexplained subfertility? Human Reproduction, 34, 84–91. [DOI] [PubMed] [Google Scholar]
- Van Geloven, N. , Dekkers, O. M. , & le Cessie, S. (2019). Estimating the effect of treatment duration using observational data in practice. Epidemiology, 30, e7–e8. [DOI] [PubMed] [Google Scholar]
- Venekamp, R. P. , Sanders, S. L. , Glasziou, P. P. , Del Mar, C. B. , & Rovers, M. M. (2015). Antibiotics for acute otitis media in children. Cochrane Database Systematic Reviews, (6), CD000219. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information


