Non-Arrhenius Reaction-Diffusion Kinetics for Protein Inactivation over a Large Temperature Range

Abstract

Understanding protein folding and unfolding has been a long-standing fundamental question and has important applications in manipulating protein activity in biological systems. Experimental investigations of protein unfolding have been predominately conducted by small temperature perturbations (e.g. temperature jump), while molecular simulations are limited to small timescales (microseconds) and high temperatures to observe unfolding. Thus, it remains unclear how fast a protein unfolds irreversibly and loses function (i.e. inactivation) across a large temperature range. In this work, using nanosecond pulsed heating of individual plasmonic nanoparticles to create precise localized heating, we examine the protein inactivation kinetics at extremely high temperatures. Connecting this with protein inactivation measurements at low temperatures, we observe that the kinetics of protein unfolding is less sensitive to temperature change at the higher temperatures, which significantly departs from the Arrhenius behavior extrapolated from low temperatures. To account for this effect, we propose a reaction-diffusion model that modifies the temperature-dependence of protein inactivation by introducing a diffusion limit. Analysis of the reaction-diffusion model provides general guidelines in the behavior of protein inactivation (reaction-limited, transition, diffusion-limited) across a large temperature range from physiological temperature to extremely high temperatures. We further demonstrate that the reaction-diffusion model is particularly useful for designing optimal operating conditions for protein photo-inactivation. The experimentally validated reaction-diffusion kinetics of protein unfolding is an important step towards understanding protein-inactivation kinetics over a large temperature range. It has important applications including molecular hyperthermia and calls for future studies to examine this model for other protein molecules.

Graphical Abstract

Understanding protein unfolding kinetics is important for both fundamental studies of protein folding and unfolding as well as for applications including hyperthermia therapy, a well-known mechanism to destroy malignant cells and tissues.^{1, 2} Hyperthermia has been attempted by plasmonic nanoparticle heating,³ magnetic nanoparticle heating,⁴ radiofrequency and microwave ablation,⁵ and high intensity focused ultrasound⁶. The temperature rise in current hyperthermia based therapies are subject to heating a significant volume of tissue.^{7, 8} Further extension of the precision and control of thermal therapy leads to thermal heating of sub-cellular organelles by ultrashort laser pulses.^9–11 There has been a lack of understanding on how fast protein molecules unfold and lose function (i.e. inactivation) over a large temperature range. At temperatures below water boiling temperature (< 373 K), experimental measurements suggest that protein inactivation can be described by Arrhenius kinetics, which shows a large temperature dependence and high activation energy^{9, 12–14} (E_a ≈ 20 – 50 kcal/mol). The long timescale associated with these events (seconds) makes it challenging for molecular simulation studies. On the other hand, at high temperatures (> 373 K) and short times (microseconds to nanoseconds, 10⁻⁶ ~ 10⁻⁹ s), molecular simulations suggest a weak temperature dependence as characterized by a relatively small activation energy^15–19 (E_a ≈ 2–10 kcal/mol). For small peptides and nucleic acids, it has been demonstrated using molecular simulations that the kinetics at different temperatures exhibit a non-Arrhenius behavior.^{18, 20, 21}

It is challenging to perform experimental studies to probe protein inactivation kinetics at extremely high temperatures and short times (Figure 1). Advanced spectroscopic methods have been developed to record ultrafast events.^22–26 For instance, laser T-jump experiments use a pump-probe laser system and can probe protein unfolding between milli to nanoseconds.^{9, 27, 28} However, the experiments are limited to a short temperature range (300 – 370 K) and thus the results exhibit good agreement with Arrhenius kinetics. Steel et al., used a nanosecond laser apparatus (5 ns) to transiently heat a 135 nm gold film adhered to a glass substrate with a 15nm chromium under layer. The results suggest that the kinetics of protein inactivation closely fits the Arrhenius model to the limit of 0.1 ns. However, only a single data point in the nanosecond timescale was reported. Recently, we have extended the concept of molecular hyperthermia, where protein molecules can be targeted and manipulated using an ultrashort nanosecond laser pulse.^9–11 Plasmonic nanoparticles can superheat the neighboring water without vaporization,²⁹ which can lead to selective inactivation of protein molecules that are targeted by the plasmonic nanoparticle.

Figure 1:

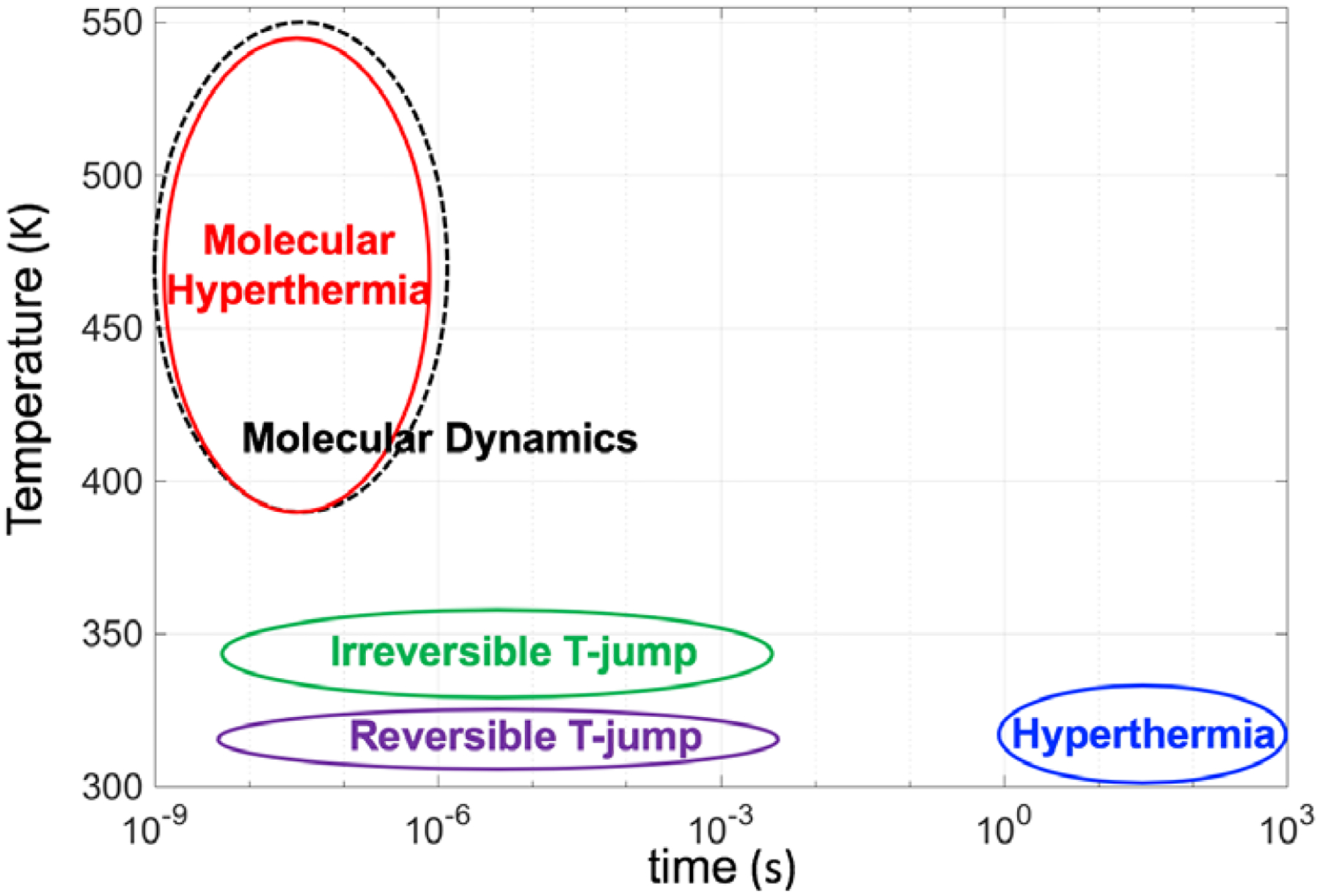
Comparison of techniques to probe protein inactivation across a large temperature range (300 −600 K) and corresponding time durations (10³ s – 10⁻⁹ s).

In this study, we attempt to address the protein inactivation kinetics across a large temperature range by incorporating experimental findings at high temperature and ultrashort time scale (nanoseconds). By comparing protein unfolding rates over a large temperature range, and taking inspiration from the “convex” Arrhenius behavior in enzyme kinetics and diffusion in metastable liquids,^{30, 31} we propose a reaction-diffusion model to describe the inactivation kinetics over a large temperature range. The results illustrate that, at elevated temperatures, the overall kinetics of protein inactivation caused by nanoscale localized heating of plasmonic nanoparticles display a non-Arrhenius behavior. At low temperatures and long times (microseconds to seconds), the protein unfolding is highly temperature dependent and adopts reaction-limited kinetics. At high temperatures and short times (nanoseconds), however, the rate of unfolding is less sensitive to further temperature increases and exhibits diffusion-limited kinetics. We further demonstrate that the reaction-diffusion model is particularly useful for optimizing operating conditions for molecular hyperthermia experiments. The experimentally validated reaction-diffusion kinetics is an important step towards understanding protein-inactivation kinetics over a large temperature range.

Results and Discussion

Analysis of protein inactivation rates over a large temperature range:

First, experiments were performed to determine the protein inactivation kinetics at extremely high temperatures and nanoseconds (Figure 2). Protein molecules (α-chymotrypsin (Cht)) are conjugated to plasmonic gold nanoparticles (GNP with radius r_NP) using a molecular linker (e.g. polyethylene glycol, Figure 2A). Subsequently after laser treatment, the protein activity was measured by an enzymatic reaction (Figure 2B). The enzyme α-Cht was used in our experiments because the enzymatic activity can be readily measured as compared with other proteins. This allows us to determine the loss in protein activity (thus inactivation) due to plasmonic heating of the gold nanoparticle. The derived inactivation rate constants of our high temperature experiments from the enzyme activity can be compared against the low temperature T-jump experiments on the same enzyme⁹.

Figure 2:

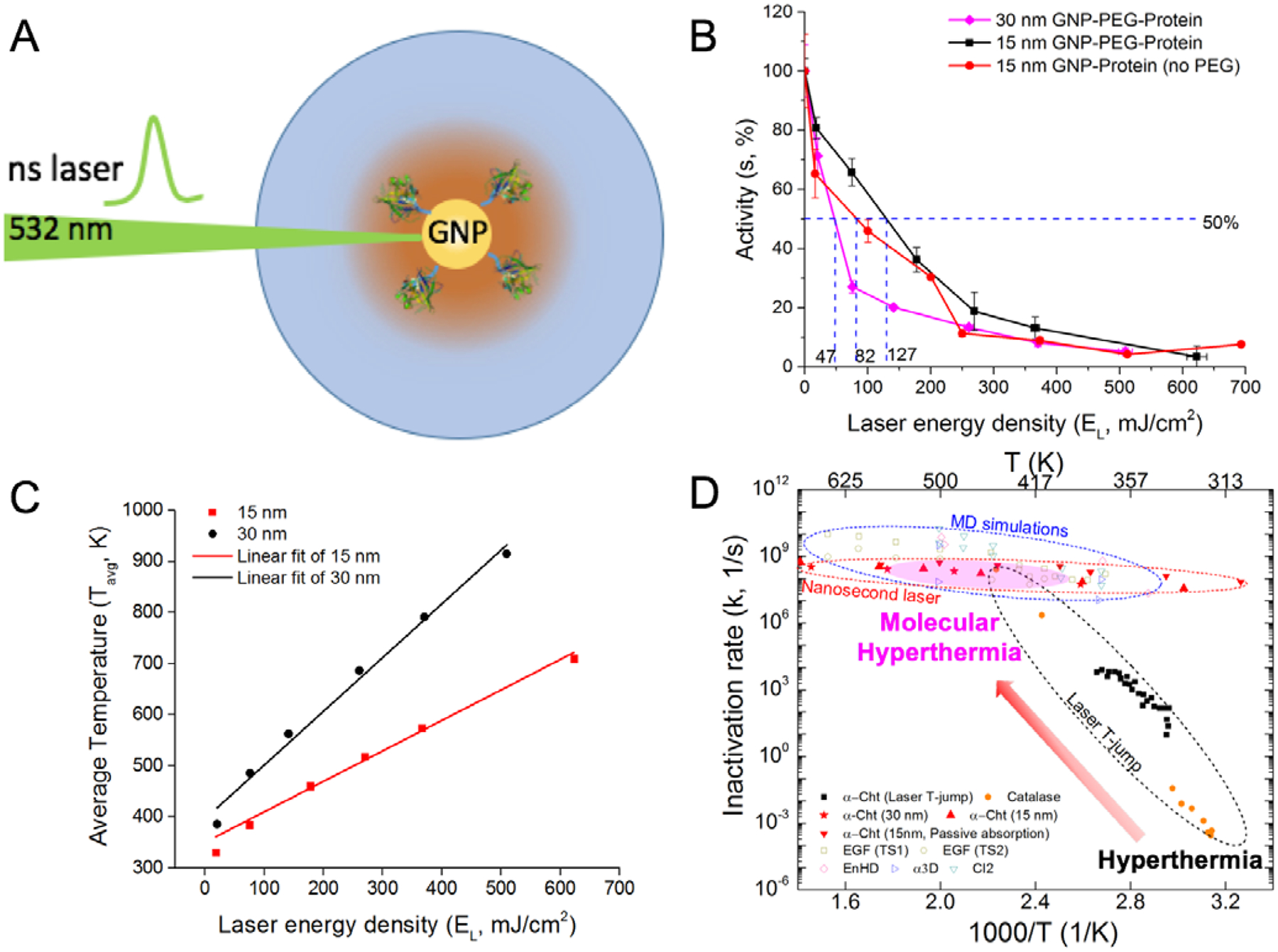
Molecular hyperthermia enables measurement of protein inactivation rate constant at temperature and time regions. (A) Schematic of molecular hyperthermia setup. Length L_total is defined as the center to center distance between the gold nanoparticle (GNP) and protein. (B) Protein activity as function of laser energy density and nanoparticle size (15 and 30 nm) measured in molecular hyperthermia experiments.¹¹ The label GNP-PEG-Protein refers to the case where the protein is covalently conjugated to the GNP using a PEG linker and GNP-PEG (no PEG) label refers to the passive absorption case. (C) Average temperature experienced by the protein (at distance L_total) during molecular hyperthermia. (D) Arrhenius plot over a large temperature range (300 – 625 K). Additional data used in this figure is from experimental and molecular simulations of different proteins (α-chymotrypsin (Cht),^{9, 11} Catalase,¹³ EGF,¹⁷ EnHD,¹⁵ α3D,¹⁶ CI2¹⁶).

Temperature-dependent protein inactivation kinetics can be described by the Lumry - Eyring kinetic model^32–35 which can be further reduced to a simplified two-state model,^{32, 35, 36} represented by the following equation.

$$N\stackrel{k}{\to }I$$ (1)

where, N is the native state and I is the inactivated state. The inactivation rate constant ‘k’ is then obtained using the measured enzyme activity ‘s’ (Figures 1B and S1),

$$\text{ln}\left(s\right)=-\underset{t=0}{\overset{{\tau }_{\mathit{\text{laser}}}}{\int }}kdt$$ (2)

$$k=-\frac{\text{ln}\left(s\right)}{{\tau }_{\mathit{\text{laser}}}}$$ (3)

where τ_laser is the laser pulse duration (FWHM = 6 ns). Here we provide a rationale for using a nanosecond laser pulse towards protein inactivation. For a pulse duration of less than 100 fs the photothermal effects include a rapid increase of the electron temperature due to electron-electron scattering in gold. In the ps regime (10 −100 ps), the lattice temperature increases due to electron-phonon coupling in the gold.³⁷ The choice of a longer duration laser pulse, such as nanosecond serves well for irreversible protein inactivation as it allows heat dissipation into the surrounding medium unlike femtosecond and picosecond laser pulse durations. Also, it has been earlier demonstrated that ps laser pulses (~1000) don’t denature the surrounding protein.³⁸ Other’s¹⁰ and our own attempts using ps laser also didn’t lead to obvious and efficient protein inactivation. As a result, the ns laser pulse seems to be optimal to induce protein inactivation.

To obtain the corresponding temperature during laser irradiation, a Gaussian laser pulse (equations 5–6) are considered as a source term in the heat conduction model (equation 3) using the Finite Element Method (see SI Figure S3). From this numerical solution, we obtain the temperature history at the protein center and then average above the melting temperature (333 K) to obtain T_avg for different laser energy densities (Figure 2C). Combining the inactivation rate constant ‘k’ and ‘T_avg’ for different nanosecond laser energy densities, the points (red solid) in the Arrhenius plot are generated (Figure 2D).

The use of continuum heat equation to describe GNP heating has been reported and validated in the literature. For example, Plech and co-workers have measured the gold temperature directly during pulsed laser excitation by time-resolved x-ray scattering. The measured temperature change was in good agreement with the analytical solution of the heat equation.^{39, 40} Published work from Carlson et al.,²⁹ Baffou et al.⁴¹ and others⁴² using various thermometry techniques have confirmed that continuum heat equation (solved analytically or by finite element method) adequately describes the GNP heating under CW laser heating. These studies suggest that the water adjacent to the gold nanoparticle can be superheated beyond the boiling point up to the spinodal decomposition temperature (SDT at 594 ± 17 K) without bubble formation.²⁹

We further compared the rate constants from our experimental measurements of protein activity with previous experimental and molecular dynamics simulation (MD) studies for different proteins. As evident in Figure 2D, the protein unfolding kinetics in high temperatures and nanoseconds (inactivation rate constant k, 10⁹ s⁻¹), was only previously available from MD simulations.^{13, 15–17} Our molecular hyperthermia measurements provide the first comprehensive experimental results to probe the protein inactivation rate in this region (400 – 600 K). Here we analyzed 15 nm and 30 nm gold nanoparticles. Note that for 5 nm gold nanoparticle, there was not sufficient temperature rise due to the small size and absorbed laser energy and does not lead to complete protein inactivation.¹¹ As illustrated in Figure 2D, there is a significant change in the temperature dependence of protein unfolding kinetics between the low temperature and high temperature regions. Specifically, the unfolding kinetics at high temperature departs from the low temperature Arrhenius kinetics and shows a plateau or “speed-limit” in the protein inactivation kinetics. This is similar to the “speed-limit” observed during protein folding.⁴³

It is important to note that the protein inactivation is irreversible in molecular hyperthermia experiments. Previous studies by T-jump spectroscopy uses relaxation dynamics to probe the kinetics of protein folding by increasing the temperature. This is achieved by generating a small temperature jump (around 10 °C in 5 ns)⁴⁴ and studying the folding pathway from an unfolded state. In our experiment using nanosecond laser pulse, the local temperature rise within a few nanometers around the nanoparticle surface is in range of 100 – 400 K and confined to the time window of a single laser pulse (Fig S3-C). Hence the protein unfolds and loses function due to rapid heating, and the process is irreversible. To compare with protein inactivation at lower temperatures, we obtained measurements from Huttmann et al., which was based on laser T-jump and measures the protein inactivation rate.⁹ In the T-jump experiments, the reverse reaction from unfolded to folded was neglected,⁹ thereby accounting only for the irreversibility (equation 1). We next use this experimental data to develop and validate a model for determining the protein unfolding and inactivation kinetics over a wide temperature range.

Model development:

The Arrhenius model is used to describe protein unfolding rates at low temperatures (300 – 370 K, Model 1, Figure 3A) and high temperatures (Model 2, 370 – 600 K), respectively. Here we focus on α-Cht, for which the low temperature measurements were obtained by a laser temperature jump (T-jump) experiment,⁹ and the data for high temperature is from our experimental measurements.¹¹ When the results from our experiments and previously reported T-jump experiments are analyzed by the Arrhenius model and compared, the activation energy (E_a) for the high temperature range (2.12 kcal/mol, Figure 3A) is one order of magnitude lower than the low temperature range (37.71 kcal/mol). Similar trends are observed in E_a values (2.89 kcal/mol in the high temperature range and 42.28 kcal/mol⁴⁵ for the low temperature range) for trypsin and (2.32 kcal/mol in the high temperature range and 38.19 kcal/mol⁴⁶ for the low temperature range) for HRP (Figure S1). Furthermore, the pre-factor (A, s⁻¹) in the Arrhenius model, which is the fastest unfolding rate constant (at infinite temperature), differs by 17 orders of magnitude for the two models (10²⁶ s⁻¹ vs 2 × 10⁹ s⁻¹). To put the pre-factors in context, the lifetime of a hydrogen bond was determined experimentally to be 0.0077 ps or 1.3 × 10¹⁴ s^{−1 47} Since protein unfolding requires that at least one hydrogen bond be broken, a pre-factor greater than 1 × 10¹⁴ s⁻¹ is thus unphysical and extrapolating the low-temperature Arrhenius model to high temperatures with pre-factor A = 10²⁶ s⁻¹ is clearly not possible.

Figure 3:

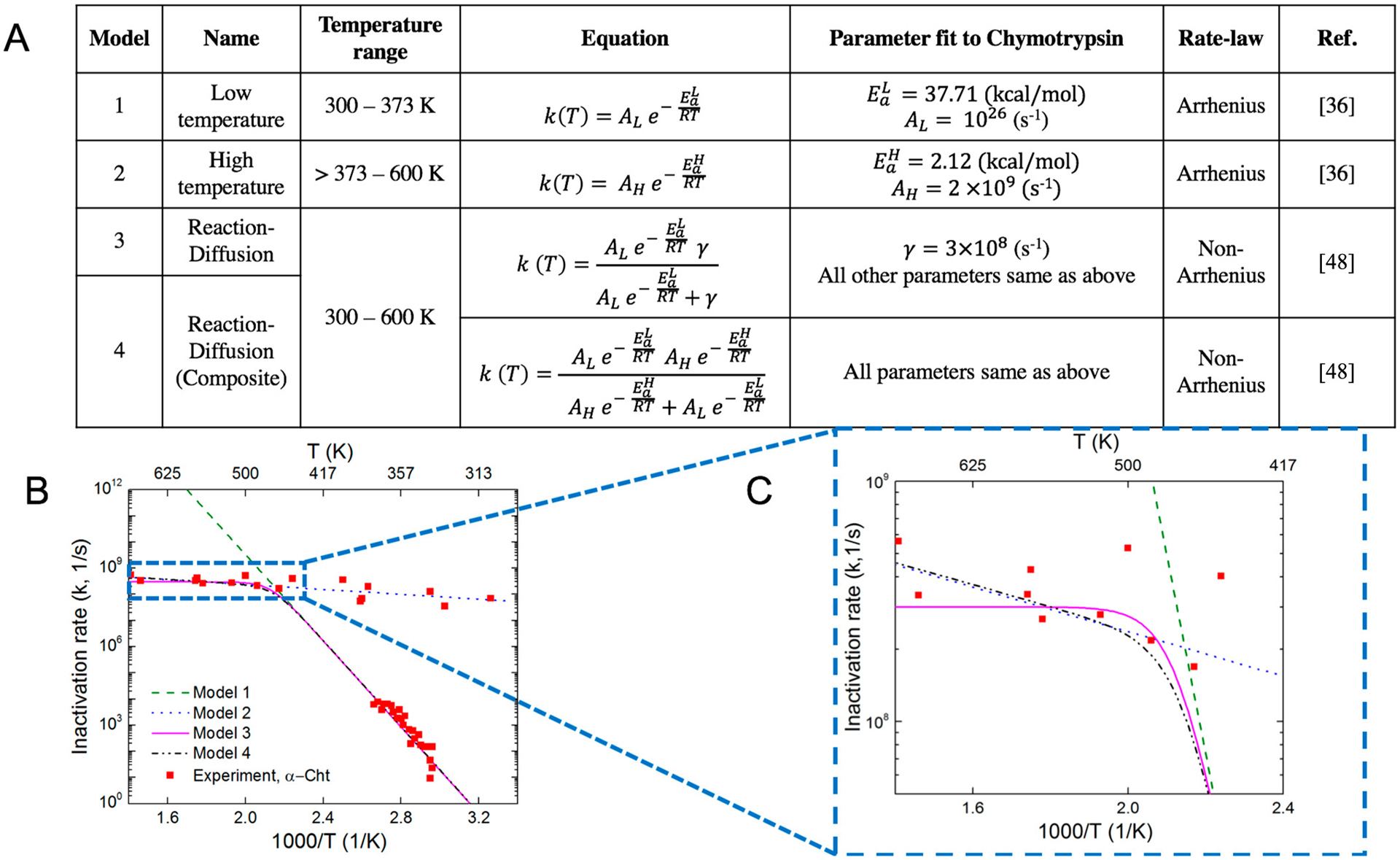
Comparison of different temperature-dependent kinetic models with experimental results. (A) Different kinetic models categorized based on low and high absolute temperatures (Arrhenius kinetics) and Arrhenius/non-Arrhenius kinetics. (B) Kinetic models for the inactivation rate of enzyme α−Cht, including both low and high temperature range 300 – 600 K (C) magnified of temperature range (417 – 600 K) to illustrate model 3 best represents the experiments for the temperature range, 310 – 600 K, (R² = 0.84). The R² values is calculated using the parametric values listed in (A) for the protein enzyme α−Cht.

To develop a model that can describe the temperature-dependent inactivation kinetics across both the high and low temperature regions (300 – 600 K), we propose a reaction-diffusion model (Model 3, Figure 3A), which was previously used in first order catalytic reactions.⁴⁸ In this model, a diffusion parameter (γ) is defined to account for the upper “speed limit” for protein inactivation. The Arrhenius parameters (pre-factor and activation energy) in the reaction-diffusion model (Model 3) are based on the fit from the low temperature T-jump experiments. A second reaction-diffusion model is a hybrid between the low and high temperature models and assumes that the diffusion parameter γ(T) takes the form of Arrhenius kinetics given by the high temperature range (model 2, $\gamma \left(T\right)=A_H\text{ exp}\left[\frac{-E_a^H}{RT}\right]$) while the other terms remain similar to Model 3. The reaction-diffusion models give a much-improved representation of protein inactivation kinetics in both the low and high temperature ranges (Figure 3B). Comparison of models 3 and 4 (Figure 3C) shows that the reaction-diffusion model 3 presents the best fit (R² = 0.84) over the full temperature range. We have also demonstrated the method on other two proteins including trypsin and horseradish peroxidase (HRP) and obtained similar results (see Figure S1). To compare our choice of average temperature, we use other cases such as a simple average of the temperature history (T_avg), maximum temperature (T_max) and half-maximum temperature (T_half-max). Results from the corresponding fit are included in (SI, Figure S2A). The resulting model parameters (E_a, A and γ) do not vary significantly (SI, Figure S2B).

Characteristics of the reaction-diffusion model:

The reaction-diffusion model is then optimized to obtain the value of the diffusion parameter γ, which provides the best fit to experimental data. From Figure 4A, the values of γ = 3 × 10⁸ s⁻¹, A_L = 10²⁶ s⁻¹, $E_a^L=37.71\text{kcal}/\text{mol}$, best represent the experimental data (R² = 0.84) for α-Cht over the full temperature range. Further analysis of the reaction-diffusion model leads to several distinct zones across a large temperature range (Figures 3B and C):

1. Reaction-limited zone (Z₁): At low temperatures, $A_L{e}^{-E_a^L/RT}\ll \gamma$, so that $k\left(T\right)\cong A_L{e}^{-E_a^L/RT}$. In this zone, the protein unfolding rate constant is highly temperature dependent and is thus reaction-limited. The reaction depends strongly on the temperature and follows an Arrhenius kinetics. The reaction-limited zone spans a temperature range of 300 – 437 K or 27 – 164 °C, and a timescale of 0.1 μs or longer.

2. Transition zone (Z₂): Between the high and low temperature regions, the protein unfolding kinetics transitions from reaction-limited to diffusion-limited behavior. Here, we define a transition point (T_TR = 470 K or 197 °C) by using the condition, $\gamma =A_L\text{ exp}\left[\frac{-E_a^L}{R{T}_{TR}}\right]$ from model 3, where the diffusion-limited and reaction-limited rate constant have the same values. Correspondingly, the transition zone as illustrated in Figure 4B can be determined based on the criteria that the inactivation rate is within 95% of the individual reaction and diffusion rates, 0.95 $A_L{e}^{-E_a^L/RT}$ and 0.95 γ respectively, giving a temperature range from 438 K to 507 K (represented by magenta dashed lines in Figure 4B). This corresponds to a temperature range of 165 – 234°C and a time duration of 4 ns to 0.1 μs.

3. Diffusion-limited zone (Z₃): At high temperatures, $A_L{e}^{-E_a^L/RT}\gg \gamma$ and the inactivation kinetics has a low temperature dependence and eventually becomes independent of temperature to yield k(T) ≅ γ. For high temperatures, the protein inactivation rate constant saturates beyond a certain temperature value (> 545 K or 272 °C) and suggests a “speed-limit” in protein denaturation. The diffusion-limited zone spans a temperature range of 510 – 600 K or 237 – 327 °C, below the critical temperature of water (647 K or 374 °C), and a time duration of 3 ns or shorter.

Figure 4:

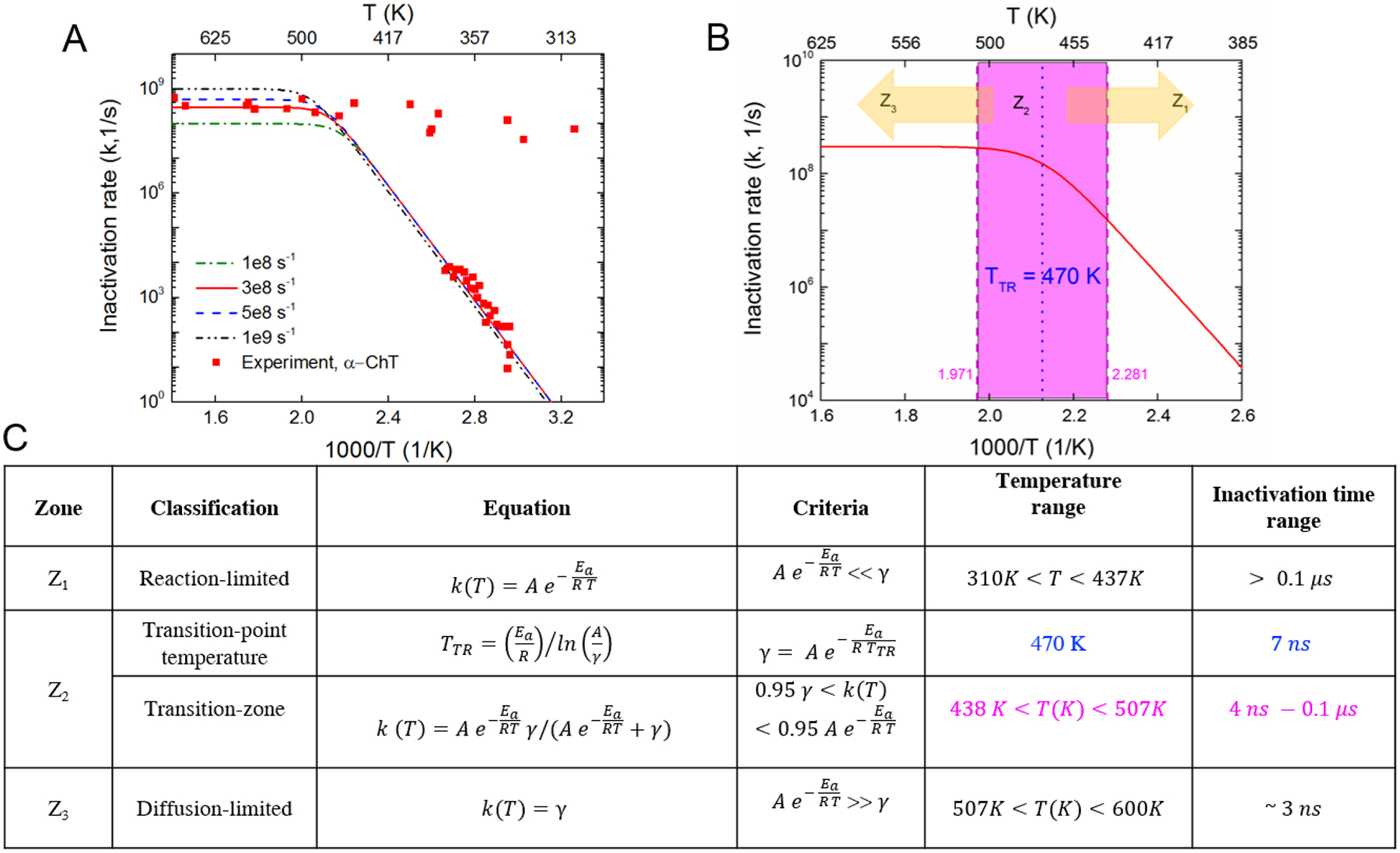
Characterization of the reaction–diffusion kinetic model: (A) Parametric optimization to find γ to best fit low temperature and high temperature experimental data, (γ=3×10⁸ s⁻¹), R² = 0.84) (B) Zonal characterization of the reaction diffusional model - reaction-limited zone (Z₁), transition zone (Z₂) within the absolute temperature range of 437–507K (pink dashed lines), transition point temperature (T_TR = 470 K, marked in blue dotted lines) and diffusion limited zone (Z₃) (C) Tabulated criteria for zonal characterization, temperature range and inactivation time.

While the physical significance of reaction-diffusion models have been discussed in chemical engineering applications,⁴⁸ their interpretation for protein inactivation kinetics is less clear. The reaction component is presumably the protein unfolding process, while the diffusion component refers to the diffusion of the protein backbone due to large thermal fluctuations, causing significant secondary structure change thereby making the process irreversible. Although very little work has been done on the kinetics of protein inactivation across a large temperature range (310 – 600 K) as given by the present reaction-diffusion model, there do exist models of temperature dependent non-Arrhenius behavior⁴⁹ diffusion-collision models,⁵⁰ and first passage analysis of the Smoluchowski equation⁵¹ for protein folding/unfolding. Moreover, recently the temperature dependent kinetics of F1-ATPase kinetics was studied and shown to have a reaction-diffusion formalism.^{52, 53} Other instances using proton NMR spectroscopy has been used to study the reversibility and irreversibility of protein unfolding across different heating cycles. Results indicate, that the activation energy remains constant within a small temperature range but varies over a large temperature range.⁵⁴ Also, recent computational efforts using molecular dynamics showed that there is a decrease in the exponential behavior of the kinetics (Arrhenius) up to 450K and after which the kinetics shows a weaker temperature dependence for higher temperatures, indicating the kinetics is diffusion limited rather than barrier crossing in high temperature ranges.⁵⁵ Methods to homogeneously heat liquid samples are restricted to temperatures below boiling temperature of the solvent. Our method using molecular hyperthermia overcomes that challenge and offers a unique opportunity to experimentally probe protein changes where it was only possible by temperature accelerated MD simulations.

Also, it is worth noting that the ‘reaction-diffusion’ model for the chemical kinetics should not be confused with the ‘diffusive heat transfer’ model for heat conduction from the nanoparticle to the aqueous solvent. Hence, in creating the Arrhenius plot using the above methodology, no prior assumption has been made related to ‘reaction-diffusion’ kinetics. The heat diffusion or conduction is well known and is the dominant mechanism for heat to dissipate from the nanoparticle to the surrounding molecules.^{3, 39, 40, 56, 57} Furthermore, the presence of proteins on the nanoparticle surface does not significantly affect the heat transfer from the GNP to the surrounding medium. Here we estimate on an average 15 α-Cht or 35 trypsin molecules conjugated to the 15 nm GNP surface. For HRP the conjugation efficiency is not as high as the other two proteins and we estimate on average 0.05 HRP per gold nanoparticle. This means for the case of HRP there are many gold nanoparticles without any protein conjugated to it. Based on this stoichiometry and assuming that the proteins are localized within 6 nm shell of the GNP, we estimate the local protein concentration (see SI section 2) to be 77 mg/mL for α-Cht (MW = 25 kDa) and 182 mg/mL for trypsin (MW = 23.3 kDa). Similarly, the local protein concentration is estimated to be 8.55 mg/mL for HRP (MW = 44 kDa) assuming one HRP molecule on GNP. Previous studies have measured the thermal conductivity of protein solution and found only 5% change even for protein concentration at 100 mg/mL from the solvent (water).⁵⁸ Thus, we estimate that the protein conjugation only causes a small change (< 10%) in the thermal conductivity and thus doesn’t significantly affect the heat dissipation from GNP to water. Finally, the changes in protein conformation and the resulting inactivation are not expected to have a significant impact on the heat dissipation since there is no major changes in the composition.

Validation and application of the reaction-diffusion model:

To demonstrate the use of the models developed in this work, we attempted to predict the extent of protein inactivation during molecular hyperthermia. With a finite element model (Figure S3), the local temperature variation of the protein is obtained (Figure 5A) for different laser fluence values (18 – 180 mJ/cm²). The local temperature increases as the laser fluence increases.

Figure 5:

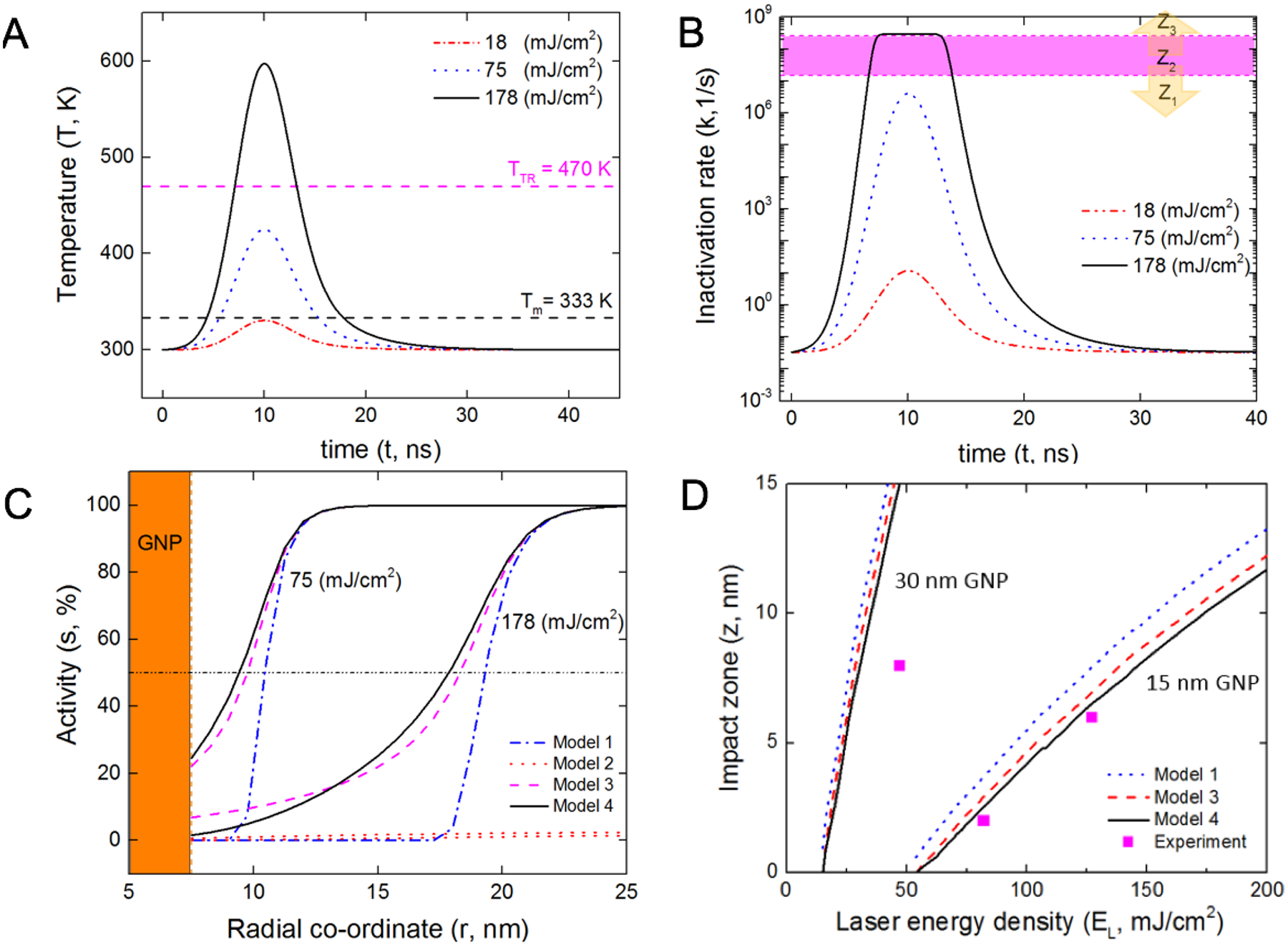
Validation and application of the reaction-diffusion model to analyze protein inactivation distribution during molecular hyperthermia. (A) Local protein temperature and (B) Inactivation rate at different laser energy densities (Gaussian pulse, FWHM ~ 6ns). (C) Estimation of impact zone from different kinetic models shows the change in protein activity distribution. (D) Comparison of the impact zone calculated using different kinetic models for 15 and 30 nm gold nanoparticles and comparison with experimental measurements.¹¹

The temperature histories are used to calculate the inactivation rate using the reaction-diffusion model (Figure 5B). For moderate laser fluence (74.75 mJ/cm²), the local temperature history is below the transition temperature (Figure 5B) and hence the inactivation rate constant of the protein is in the reaction-limited zone (Z₁). However, for higher laser fluence values, the inactivation rate constants enter the diffusion-limited zone (Z₃) and further temperature increase does not lead to faster inactivation (Figure 5B). This important feature sets upper limit of protein inactivation rate and also provides a rationale for further analysis and optimal design of molecular hyperthermia.

We further calculated the spatial distribution of protein inactivation from the temperature history and the different kinetic models (Figure 5C). As expected, higher laser fluence leads to a larger region in which the protein is inactivated. Here we define this region as an “impact zone”, the spatial location in the aqueous medium where the protein activity is reduced to 50% due to the heat penetration from the GNP surface, given by z = r_50%activity − r_NP. We note that model 2, which is the Arrhenius model based only on the high temperature region (373 – 600 K), does not provide a reasonable estimate of the protein inactivation as it significantly overestimates the protein unfolding rate constants at low temperatures. Following the definition of the impact zone, we analyzed the two GNP sizes (15 and 30 nm) that were used in the experimental measurements.¹¹ The reaction-diffusion model provides the best agreement with experimental data (Figure 5D). This is expected since the model is built upon insights from experimental observations. The Arrhenius model based on low temperature data (Model 1) over-predicts the protein inactivation due to the overestimated inactivation rate at higher temperatures (Figure 3B). To further quantify the percentage difference between the Arrhenius and non-Arrhenius models, given by expression, $\left|\frac{z_{\mathit{\text{Arrhenius}}}-z_{non-\mathit{\text{Arrhenius}}}}{z_{\mathit{\text{Arrhenius}}}}\right|\times 100$, for the laser fluence 127 mJ/cm² is 15% between models 1 and 3 and 18% between model 1 and 4.

Optimizing the ultrashort time scales for molecular hyperthermia:

Faster laser irradiation timescales such as femtosecond pulse have been used to photorelease biomolecules such as DNA^59–61 by breaking Au-thiol bond and reshaping nanoparticles^{62, 63} while picosecond laser pulses have been used primarily towards the generation of plasmonic nanobubbles to release of anticancer drugs^64–66 and merging of nanoparticles.⁶⁷ Using longer laser pulse duration such as nanosecond, it has been demonstrated by us and others that molecular hyperthermia can selectively inactivate the targeted proteins.^{10, 11} This may find interesting applications such as optical control of cell membrane receptors such as G-protein coupled receptors (GPCRs). For example, we have recently shown that molecular hyperthermia can photo-inactivate a specific GPCR (protease-activated receptor 2, or PAR2)^{68, 69} while keeping other GPCRs intact on the membrane (for example somatostatin receptor, SSTR2).⁷⁰ This indicates that the highly localized effect of molecular hyperthermia.⁷¹ The model developed here can be used towards optimal design of molecular hyperthermia and other nano-bio applications.

There are two rationales for optimal design of molecular hyperthermia. Firstly, while an ultrashort laser pulse (6 ns) heats up a very localized region around the plasmonic nanoparticle,⁷² the nanoparticle can in fact overheat to above the gold melting temperature⁷³ (1050 K) and fragment as reported earlier.^{11, 74, 75} Secondly, increasing the protein temperature in the diffusion-limited zone (Figure 4) does not further increase the protein unfolding rate. Therefore, an optimal experimental condition is to stay well below the nanoparticle melting temperature while increasing the protein temperature such that the inactivation kinetics remains in the transition zone - Z₂ (Figure 4B) for prolonged time.

We applied the reaction-diffusion model to explore this concept. Here we considered three different pulse widths (5, 50 and 500 ns, Figure 6A) and obtained the temperature history for the GNP surface and protein (Figure 6B) as well as the protein inactivation rate constants (Figure 6C). Under these conditions, all cases yield the same impact zone (10 nm, Figure S4). Note that the temperature distribution due to an ultrashort laser pulse (5 ns) reaches a high temperature value of 772 K at the GNP surface which is close to the gold nanoparticle melting temperature, 1050 K.⁷³ By increasing the laser pulse duration from 5 ns to 500 ns, we demonstrate that the absorbed laser power within the nanoparticle reduces from 32 to 19 μW (Figure 6D and Table S2). As a result, the maximum gold temperature reduced from 772 K to 607 K, a significant reduction to prevent melting or fragmentation. Figure 6D further shows that the maximum (or fastest) protein temperature drops from 530 K to 456 K, and the protein inactivation rate decreases from 3 × 10⁸ (s⁻¹) to 9 × 10⁷ (s⁻¹). The 5 ns laser pulse heats up the protein to the diffusion-limited zone while laser pulses of widths 50 ns and 500 ns only heats the protein up to the transition zone. Further increasing pulse duration (micro- to milli-seconds) may lead to global heating and hence can’t localize the protein inactivation around the nanoparticle. Hence, we have demonstrated that by optimizing the laser energy and pulse width, the probability of nanoparticle fragmentation can be reduced during molecular hyperthermia while creating similar protein unfolding impact zones. Further analysis of the impact zone shows that the different laser pulse widths (5 ns, 50 ns and 500 ns) give similar range of impact zones to inactivate proteins when the laser fluence is varied over two orders of magnitude (Figure S5).

Figure 6:

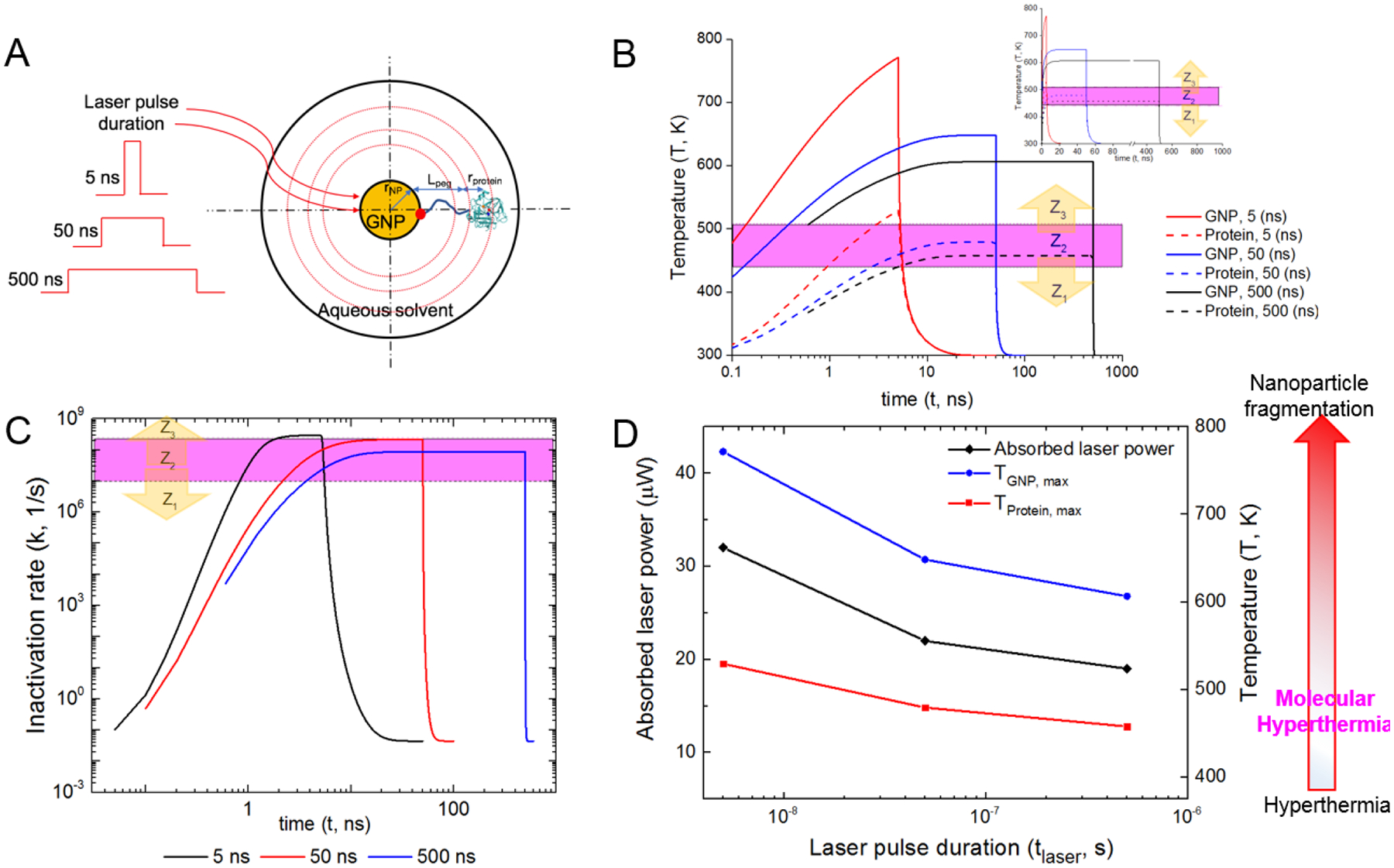
Optimizing the ultrashort timescale for molecular hyperthermia. (A) Schematic represents molecular hyperthermia at different laser pulse durations (5 ns, 50 ns and 500 ns). (B) Local temperature histories at the protein center and GNP surface (15 nm). All cases give the same impact zone of 10 nm. Inset shows the temperature profile with linear x-axis. (C) Protein inactivation rate calculated using the reaction-diffusion model and temperature history in (B). (D) Absorbed laser power in GNP and maximum temperatures of protein and GNP at different pulse durations.

Limitations of the kinetic model for protein inactivation

First, there are limitations of using a simplified one-step irreversible kinetic process (equation 1) to model protein unfolding across a large temperature range (300 – 600 K). The complex pathways of protein folding and unfolding^{76, 77} are active areas of research and has revealed the complex nature of the protein structural changes. Second, for low temperature region (< 400 K in Fig. 1D), our calculation gives rate constants in the order of 10⁷ s⁻¹ for the different cases and overestimates the inactivation rate constant. Instead, the irreversible T-jump data is used to cover this temperature range. Since the nanosecond laser pulse is used to probe the kinetics, the analysis is naturally limited within the nanosecond time regimes and high temperatures, an area where there were no experimental studies before. Thus, we take caution in the analysis and compare with other data in the literature to cover the full temperature range of interest.

Conclusion

The inactivation of proteins has been analyzed over a large temperature range. It has been shown that selected proteins can be inactivated using ultrashort nanosecond laser pulses. It is challenging to determine the kinetics of protein inactivation over a large temperature range and time scale (nanoseconds to seconds). Enabled by nanoparticle heating to create ultrahigh temperatures, the present study proposes and validates a reaction-diffusion model to describe the protein unfolding kinetics across large ranges of temperature and timescales. The rate at which proteins undergo structural and conformational changes across a large temperature range plays a crucial role in our fundamental understanding of protein folding/unfolding, as well as to design novel nanoparticle assisted thermal therapeutics for selective manipulation of protein function. In this work, we demonstrate that a reaction-diffusion based kinetic model is suitable to represent protein inactivation across a large temperature range. The temperature range includes both traditional hyperthermia (< 373 K, seconds) and molecular hyperthermia (>373 K, nanoseconds). We also explored a range of ultrashort time scales (5 to 500 ns) to optimize the laser heating in molecular hyperthermia and found that extending the pulse duration decreases the GNP surface temperature, thus significantly reducing the chance of nanoparticle fragmentation. Hence, the reaction-diffusion model also helps in our understanding of designing molecular hyperthermia. Our work also calls for future studies to examine this model for a large range of protein molecules.

Methods:

Molecular hyperthermia:

15 nm GNP was synthesized by the Fren’s method.⁷⁸ 30 nm GNP was synthesized by seed growth method using freshly made 15 nm GNP solution.⁷⁹ To covalently conjugate protein onto GNP, GNP were first modified with carboxyl group by coating with heterofunctional polyethylene glycol (PEG) molecules (1kDa, Nanocs, Boston, MA, SH-PEG-COOH). Then GNP-PEG conjugate was activated by 1-Ethyl-3-(3-dimethylaminopropyl) carbodiimide (EDC, ThermoFisher, Waltham, MA) and sulfo-22 N-hydroxysuccinimide (sulfo-NHS, ThermoFisher, Waltham, MA). Finally, GNP was mixed with α-Cht (from bovine pancreas, type II, Sigma-Aldrich, St. Louis, MO) solution, and incubate for 2 hours. The protein-conjugated GNP was stored at 4 °C and used within 2 days.

The laser experiment was executed with a Nd:YAG laser (Quantel Q-smart, 532 nm). The full width half maximum (FWHM) of the laser pulse is 6 ns. The 40 μL sample was diluted to OD = 0.1 and held in a micro UV cuvette. The laser beam was guided to pass into the cuvette. A beam splitter was used to separate laser beam in order to check the laser pulse energy simultaneously.

To measure the Cht enzymatic activity, a substrate cleavage colorimetric assay was used.⁸⁰ Briefly, 12 μL sample was mixed with 60 μL substrate solution (Suc-Ala-Ala-Pro-Phe-NA, Sigma-Aldrich, St. Louis, MO). The absorbance was recorded at 410nm for 2 minutes using a BioTek Synergy 2 Multi-mode plate reader. The slope of the absorbance change was used to calculate the enzyme activity.

Heat transfer analysis

The principle of heat transfer from the nanoparticle to the solvent is governed by heat conduction, especially when the laser pulse duration is in nanoseconds and longer.^{3, 39, 40, 56, 57} Radiative heat transfer is considered negligible for the timescales of nanoseconds.³⁹ Thus, the temperature distribution in an aqueous medium due to heating of a single GNP during pulsed laser irradiation is given by the transient heat conduction equation,

$$\frac{{\partial }^2{T}_j}{\partial r^2}+\frac{2}{r}\frac{\partial T_j}{\partial r}+g_j\left(t\right)=\frac{1}{{\alpha }_j}\frac{\partial T_j}{\partial t}$$ (4)

for j = 1, 2 and r, t are the space and time variables. T_j is the temperature in the GNP (j =1) and water (j = 2), g_j (t) is the time-dependent heat generation with g₁ (t) is the volumetric heat generation in the GNP due to a Gaussian laser pulse and can be defined as,

$$g_1\left(t\right)=\frac{A_g}{\sigma \sqrt{2\pi }}\text{exp}\left[\frac{-{\left(t-t_o\right)}^2}{2{\sigma }^2}\right]$$ (5)

where A_g is the amplitude of the Gaussian pulse, σ is the standard deviation (≈FWHM/2.355). There is no volumetric heating term in the aqueous domain, g₂ (t) = 0. The relation between the amplitude of the Gaussian pulse and laser energy density can be calculated by integrating equation (5) over a 99% confidence interval and equating to the source term,

$$A_g=\frac{E_L}{\text{erf}\left(\frac{3}{\sqrt{2}}\right)}\left(\frac{C_{abs}}{V_{GNP}}\right)$$ (6)

where, E_L is the laser energy density, C_abs is the absorption cross-section area of GNP and V_GNP is the volume of the GNP with diameter, D. C_abs is defined as Q_abs πD²/4 where Q_abs is the absorption efficiency as calculated from Mie theory for different GNP sizes. The system defined by equations (4 – 6) is initially maintained at room temperature (300 K) and the aqueous medium (water) is made relatively large, approximately 10 times the radius of a GNP to minimize any boundary effects. The effect of laser induced heat generation in the specified volume is modeled using a Gaussian to represent a pulsed laser and a rectangular pulse. The assumption here is that the laser absorption is linear function of laser intensity. However, when the nanoparticle temperature increases, this may change the C_abs due to nanoparticle melting or even fragmentation. This occurs when the nanoparticle temperature exceeds the gold nanoparticle melting temperature at 1050 K.⁷³ In all cases of data used from experiments to construct the reaction-diffusion model, the GNP temperature is below the gold nanoparticle melting temperature. Thus, using a linear function for laser energy absorption is considered to be a valid assumption here. The interface between GNP and water is assumed to have perfect thermal contact. The thermophysical properties of gold and water were used in our simulations with consideration given to temperature-dependent properties for the aqueous solvent. The temperature solution is obtained using finite element method implemented in COMSOL Multiphysics v5.3. All COMSOL simulations were performed using axisymmetric geometry consisting 2089 triangular elements, 139 edge elements, 5 vertex elements. Mesh element statistics provides a minimum element quality of 0.645 (usually > 0.1 is considered to be a good mesh quality).

Revised kinetic model

A two-state, first order kinetic model is considered with the native (N) and inactivated state (I) as the two thermodynamic macro-states, occurred during the course of molecular hyperthermia experiments as experienced by the protein,

$$N\stackrel{k\left(T\right)}{\to }I$$ (7)

Then, the survival fraction of protein activity for a first–order reaction between two macro states can be defined as,

$$s\left(r\right)=e^{-\int k\left(T\left(r,t\right)\right)dt}$$ (8)

where, s(r) represents the survival fraction of the protein activity due to a given kinetic model and corresponding temperature history. In equation (8), the integrand k (T(r, t)) represents the local temperature-dependent protein inactivation kinetics as represented by the models described in Figure 3A. Note, the difference between equation (1) from equation (7) is the inactivation rate in the latter equation, which in the latter equation is dependent on temperature, contrary to the other.