Pharmacokinetic/pharmacodynamics modeling of drug-loaded PLGA nanoparticles targeting heterogeneously vascularized tumor tissue

Abstract

PURPOSE:

Nanoparticle-mediated drug delivery and efficacy for cancer applications depends on systemic as well as local microenvironment characteristics. Here, a novel coupling of a nanoparticle (NP) kinetic model with a drug pharmacokinetic/pharmacodynamics model evaluates efficacy of cisplatin-loaded poly lactic-co-glycolic acid (PLGA) NPs in heterogeneously vascularized tumor tissue.

METHODS:

Tumor lesions are modeled with various levels of vascular heterogeneity, as would be encountered with different types of tumors. The magnitude of the extracellular to cytosolic NP transport is varied to assess tumor-dependent cellular uptake. NP aggregation is simulated to evaluate its effects on drug distribution and tumor response.

RESULTS:

Cisplatin-loaded PLGA NPs are most effective in decreasing tumor size in the case of high vascular-induced heterogeneity, a high NP cytosolic transfer coefficient, and no NP aggregation. Depending on the level of tissue heterogeneity, NP cytosolic transfer and drug half-life, NP aggregation yielding only extracellular drug release could be more effective than unaggregated NPs uptaken by cells and releasing drug both extra- and intra-cellularly.

CONCLUSION:

Model-based customization of PLGA NP and drug design parameters, including cellular uptake and aggregation, tailored to patient tumor tissue characteristics such as proportion of viable tissue and vascular heterogeneity, could help optimize the NP-mediated tumor drug response.

1. Introduction

Despite improvements in the understanding of cancer biology, cancer remains an elusive disease difficult to treat, especially in advanced stages. Drug targeting systems such as nanoparticle (NP) mediated drug delivery platforms offer potential for more effective treatment. Unfortunately, the efficacy of many nanotherapeutic formulations has been limited due to an incomplete understanding of the complex interactions between NPs, drugs, immune system components, and heterogeneous tumor tissue conditions (1). In particular, a heterogeneously vascularized tumor microenvironment may act as a barrier that prevents the penetration of NPs and their drug payload to reach all of the cancerous cells (2–4). Tumors produce uncoordinated angiogenic stimuli, resulting in an irregular and inefficient vascular supply (5, 6) through which the NPs are delivered. Inadequate vascularization impedes adequate delivery of therapeutic agents, and also results in tumors with regions of transient or chronic hypoxic tissue which may be insensitive to chemotherapeutic drugs targeting cycling cells (6). Consequently, lower than expected efficacy and off-target toxicity remain major concerns with cancer nanotherapy.

Two major factors influencing NP efficacy in heterogeneously vascularized tumor tissue include NP aggregation and cellular uptake. Aggregation is a well-known physical phenomenon that has been observed with drug nanocarriers (7). This phenomenon can be evaluated at various length scales; up to the scale of one meter by turbulent reacting flow, down to the sub-nanometer scale by quantum chemistry (8–12). Much effort has been spent studying the nature of aggregation within this wide range of length scales, but there is currently no established methodology to determine how specific NP formulations will behave in vivo. It has been observed that NPs can form large aggregates around tumor tissue due to entrapment by capillaries (13), which can have a direct impact on the efficacy of cancer nanotherapy. Whether or not NP aggregation would be beneficial or detrimental in terms of tumor response remains poorly understood.

A major challenge with the development and implementation of effective NP drug delivery platforms has been the sheer number of combinations of NP and drug parameters along with variable tumor tissue conditions. Due to cost and time constraints, finding and fine-tuning effective platforms based purely on experimental effort is practically not feasible. Detailed kinetic models that describe NP and drug behavior at the cellular and tissue level are scarce yet are critically important for understanding these interactions, as they enable abstracting complex biological behavior into mathematical formulations to explore parameter variations and system constraints. Simulation of cancer nanotherapy provides a platform that could allow faster and more focused clinical translation of new NP formulations. In conjunction with experimental efforts such as in vitro laboratory studies, the flexibility provided by modeling and simulation offers the potential to evaluate patient tumor-specific responses prior to a particular treatment regimen (14–25). Recently, mathematical modeling has been applied to evaluate the extravasation, uptake, and distribution of NPs subject to heterogeneously vascularized tumor tissue (26–29), while NP aggregation has been modeled in various materials (30, 31).

To further advance the ability to predictively simulate nanotherapy performance in vivo, this study seeks to establish the capability to evaluate both the NP and drug pharmacokinetics in a spatial model of heterogeneous tumor tissue. Previously, the pharmacokinetics and pharmacodynamics of combination chemotherapy on heterogeneously vascularized tumor tissue were evaluated (32) via multicompartmental drug kinetic models for cisplatin (33) and gemcitabine (34). This study implements a NP multicompartmental kinetic model and couples it with the cisplatin multicompartmental model in (33) to evaluate the efficacy of drug-loaded PLGA NPs. The magnitude of NP extracellular to cytosolic transport is varied to evaluate tumor-dependent cellular uptake. The effect of NP aggregation is assessed in terms of drug distribution and tumor response. Tumor lesions with various levels of vascular heterogeneity, inducing differential viable and necrotic tissue fractions, are simulated for evaluation of response. It has been shown that tumor tissue vascular heterogeneity can have a dramatic effect on the efficacy of cisplatin nanotherapy (29). Accordingly, the range of tumor vascular heterogeneity was chosen to represent the characteristics of a variety of cancer types. This study offers a further step towards understanding the response to NP-mediated drug delivery in the heterogeneously vascularized tumor microenvironment.

2. Materials and Methods

2.1. Tumor Growth

Tumor tissue is spatially represented by viable and necrotic regions. Viable tissue with sufficient access to oxygen and nutrients σ above a certain threshold (σ > σ_H) can proliferate, while tissue with sufficient oxygen and nutrients above a certain threshold σ_N to survive but not proliferate is hypoxic (σ_N < σ < σ_H). Necrotic tissue lacks sufficient oxygen and nutrients for viability (σ < σ_N). These three regions are updated every output interval of the simulations in response to the change in the surrounding availability of oxygen and nutrients, supplied by the vasculature. The tumor growth component of the model is based on (35, 36), for which non-dimensionalized tumor growth velocity is represented as a function of the tumor oncotic pressure P and extracellular matrix (ECM) density E:

$${\mathbf{\text{v}}}_c=-\mu \nabla P+{\chi }_E\nabla E$$ [Equation 1]

where μ is cell-mobility and χ_E is haptotaxis. A more detailed description of μ and χ_E is in (35).

The ECM density E modulates the tumor growth (36), as follows:

$$\frac{\partial E}{\partial t}={\overline{\lambda }}_{\mathit{\text{sprout.production}}}^E\frac{1}{1+k_{p}E}{\mathbf{1}}_{\mathit{\text{sprout.tips}}}+{\overline{\lambda }}_{\mathit{\text{production}}}^E\frac{1}{1+k_{p}E}{\mathbf{1}}_{{\Omega }_V}-{\overline{\lambda }}_{\mathit{\text{degradation}}}^E\frac{EM}{1+k_{d}E},$$ [Equation 2]

where ${\overline{\lambda }}_{\mathit{\text{sprout.production}}}^E$ and ${\overline{\lambda }}_{\mathit{\text{production}}}^E$ are the rates of ECM production by angiogenic vessels and proliferating tumor tissue, respectively, k_p and k_d are production and degradation scaling constants, 1_sprout.tips and ${\mathbf{1}}_{{\Omega }_V}$ are the locations of angiogenic vessel tips and viable tumor tissue, and ${\overline{\lambda }}_{\mathit{\text{degradation}}}^E$ is degradation rate. The ECM degradation is affected by the density M of matrix degrading enzymes (MDEs), which allows remodeling of the ECM by angiogenic vessel tips and proliferating tumor cells (35, 36).

The overall tumor growth is associated with the rate of volume change by assuming that the cell density within the proliferating region remains constant (35):

$$\nabla \cdot {\mathbf{\text{v}}}_c={\lambda }_p$$ [Equation 3]

where λ_p is the (non-dimensionalized) net rate of proliferation (described below). Combining these equations enables solving for the position of the tumor boundary as it changes in time (35).

2.2. Angiogenesis

The angiogenesis component is based on (37) to represent blood flow, vascular leakage and vascular network remodeling resulting from wall shear stress and mechanical stress imposed by the tumor tissue as it grows or shrinks in time. As the tumor volume changes within this vascularized environment, the tissue has differential access to oxygen and nutrients diffusing from the vasculature. The interstitial flow of oxygen and nutrients is influenced by distance from the nearest vessel and the tumor tissue pressure. For a detailed description of the angiogenesis component of the model, please refer to (35, 36).

2.3. Transport of Oxygen and Nutrients

Oxygen and nutrients σ are delivered by the vasculature and extravasate into the tumor tissue. Neo- and pre-existing vessels have particular extravasation rates, while σ is diffused with a coefficient D_σ and is taken up by host, proliferating, and hypoxic tissue, and decays in necrotic tissue. The mass balance of oxygen and nutrients is modeled under steady-state conditions (35):

$$0=\nabla \cdot \left(D_{\sigma }\nabla \sigma \right)+{\lambda }_{ev}^{\sigma }\left(x,t,1_{\text{vessel}},p_i,\sigma ,h\right)-{\lambda }^{\sigma }\left(\sigma \right)\sigma$$ [Equation 4]

where x is position, t is time, 1_vessel is the characteristic function for the vasculature (equals 1 at vessel locations and 0 otherwise), p_i is interstitial pressure, h is the hematocrit in the vascular network, and λ^σ is the rate of decay of σ (35). Extravasation is modulated by the extravascular interstitial pressure p_i, scaled by the effective pressure p_e. The weight of the convective transport component of small molecules is $k_{p_i}$ (24). Extravasation from the vascular network is represented as (36):

$${\lambda }_{ev}^{\sigma }={\lambda }_{ev}^{-\sigma }{\mathbf{1}}_{\mathit{\text{vessel}}}\left(\mathit{x},t\right)\left(\frac{h}{{\overline{H}}_D}-{\overline{h}}_{\mathit{\text{min}}}\right)+\left(1-k_{p_i}\frac{p_i}{p_e}\right)\left(1-\sigma \right)$$ [Equation 5]

where ${\overline{H}}_D$ and ${\overline{h}}_{\text{min}}$ are the normal and minimum hematocrit necessary for extravasation, and ${\overline{\lambda }}_{ev}^{\sigma }$ is the constant transfer rate from tumor-induced and pre-existing vessels. The main parameters associated with the tumor component are in Table I.

Table I.

Tumor component main parameters and associated values. All other model parameters are as in (36).

Parameter	Value	Reference
Tumor proliferation rate	1 day−1	Measured in (26)
Oxygen diffusivity	1 (*)	(36)
Oxygen transfer rate from vasculature	5 (*)	(36)
Oxygen uptake rate by proliferating tumor cells	1.5 (*)	(36)
Oxygen uptake rate by hypoxic tumor cells	1.3 (*)	(36)
Oxygen uptake rate by tumor microenvironment	0.12 (*)	(36)
Oxygen decay rate	0.35 (*)	(36)
NP extravasation from angiogenic vs. normal vessels	10	Estimated
NP decay	6hr half-life	(38)
CDDP decay rate	0.5hr half-life	(39)
CDDP in vitro IC50 (48 h) for A549 cells (spheroid)	15.9 ± 1.2 μM	Measured in (26)
CDDP release profile from NP		Estimated from (40)

^(*)Value is rescaled by the square of the simulation system characteristic length (1 cm) and divided by the system characteristic time (1 sec) multiplied by the oxygen diffusivity (41) (1 × 10⁻⁵ cm² s⁻¹). CDDP: cisplatin;

2.4. Tumor Tissue Heterogeneity

The proportion of hypoxic and necrotic tissue and the extent of tissue vascularization are varied in the simulations by changing the response to the tumor angiogenic factors, as in (29). Accordingly, angiogenesis-induced tumor vascularization was varied to simulate four distinct levels of tissue heterogeneity, respectively labeled “VERY LOW”, “LOW”, “MEDIUM”, AND “HIGH.” The values for the levels and the associated tumor characteristics are summarized in Table II.

Table II.

Levels of tumor tissue heterogeneity based on the thresholds for inducing hypoxia and necrosis. Values for HIGH are based on the previously calibrated tumors simulated in (24, 26). Tumor tissue characteristics resulting from these values include viable (proliferating + hypoxic) tumor tissue fraction, necrotic (dead) tissue fraction, and vessel fraction (vascular surface area divided by tumor area).

Level of Tissue Heterogeneity	Hypoxic Threshold	Necrotic Threshold	Viable Fraction	Necrotic Fraction	Vessel Fraction
VERY LOW	0.305	0.300	0.98	0.01	0.017
LOW	0.405	0.400	0.87	0.12	0.020
MEDIUM	0.485	0.480	0.78	0.22	0.024
HIGH	0.575	0.570	0.75	0.25	0.032

2.5. Transport of Nanoparticles

NPs s diffuse into the extracellular compartment from the location of extravasation from the vasculature, modulated by the interstitial pressure (22, 24). The extravasation is modeled as:

$${\lambda }_{ev}^s={\lambda }_{ev}^{-s}{\mathbf{1}}_{\mathit{\text{vessel}}}\left(\mathit{x},t\right)\left(1-k_{p_i}\frac{p_i}{p_e}\right)\left(\frac{C_t^s}{{\overline{C}}^s}-s\right)$$ [Equation 6]

NP concentration in the vasculature is initially ${\overline{C}}^s$, with extravasation assumed to be of the form $C_t^s={\overline{C}}^s{e}^{-\alpha t}$. The decay α was calibrated to match an estimated half-life of 6 hours,, based on experimental data measuring PLGA NP tissue concentration in vivo (38).

A set of rate equations was implemented to describe the multicompartmental NP kinetic model. This model, inspired by the kinetic model in (33), includes the extracellular and cytosolic compartments:

$$\frac{\partial C_E}{\partial t}=D_E{\nabla }^2{C}_E-\frac{k_{EC}{C}_E}{F}+\frac{k_{CE}{C}_C}{F}\left(\frac{{10}^6}{V_c}\right)+D\left(t\right)$$ [Equation 7]

$$\frac{\partial C_C}{\partial t}=k_{EC}{C}_E\left(\frac{V_c}{{10}^6}\right)-k_{CE}{C}_C-k_D{C}_C$$ [Equation 8]

where C_E is NP concentration in the extracellular compartment, which equals s in Equation 6, C_C is NP concentration in the cytosolic compartment, D_E is the diffusivity of NPs coming out of the vasculature k_EC is the rate constant for the transport of NPs from the extracellular to the cytosolic compartment, F is the extracellular fraction, k_CE is the rate constant for the transport of NPs from the cytosolic to the extracellular compartment, k_D is lysosomal loss, V_c is cell volume, and D(t) is a forcing function that represents the source of NPs via a bolus injection into the vasculature. Drug is initially released with a burst release, as has been experimentally observed for cisplatin-loaded PLGA NPs (42), and is diffused from NPs in both the extracellular and cytosolic compartments, and also transfers from the extracellular compartment into the cytosolic and DNA-bound compartments (see below) (32). The NP kinetic parameters are defined in Table III.

Table III.

Nanoparticle kinetic parameters (based on (33, 43) and associated references).

Parameter	Description	Value
Vc	Cell Volume (fL/cell)	520
F	Interstitial Fraction	0.48
DE	NP Diffusivity (μm2/min)	3E-3
kEC	Cytosolic transfer coefficient	Varied: 0,5,10 and 50
kCE	Cytosolic efflux coefficient	1.5E-3 (estimated)
kD	Lysosomal loss	2E-3 (estimated)

To simulate a variety of NP and cell interactions, the NP cytosolic transfer coefficient (k_EC) was varied between (non-dimensionalized) values of 0, 5, 10, and 50. This range provided adequate values for the transfer, enabling investigation of different cases of NP cellular uptake. Since the transfer saturated when using coefficients higher than 50, this value was chosen as an upper bound.

2.6. Transport of Drug

The following rate equations, coupled with the NP kinetic model described above, define the multi-compartmental pharmacokinetic model for cisplatin, based on (33) and as implemented in (32).

$$\frac{\partial C_E}{\partial t}=D_s{\nabla }^2{s}_1-k_1{s}_1-\frac{k_{12}}{F}{s}_1+\frac{k_{21}}{F}{s}_2\left(\frac{{10}^6}{V_c}\right)+D\left(t\right)$$ [Equation 9]

$$\frac{\partial C_C}{\partial t}=k_{12}\frac{V_c}{{10}^6}{s}_1-k_2{s}_2-k_{21}{s}_2+k_{32}{s}_3-k_{23}{s}_2\left(1-\frac{s_3}{s_m}\right)+D\left(t\right)$$ [Equation 10]

$$\frac{\partial C_{DNA}}{\partial t}=k_{23}{s}_2\left(1-\frac{s_3}{s_m}\right)-k_{32}{s}_3-k_3{s}_3$$ [Equation 11]

Drug concentration in each compartment is represented by s, where s₁ is the extracellular compartment, s₂ is the cytosolic (intracellular) compartment, s₃ is the DNA-bound compartment, s₄ is the organelle compartment, and s_m is the drug-DNA binding capacity. k_i,j represents the transfer rate constants between the compartments, F is the extracellular fraction of the tissue (0.48), and V_c is cell volume (estimated to be 520fL/cell). Drug diffused from NPs in either the extracellular or cytosolic compartment can transfer into the DNA-bound compartment, where it then can exert its cytotoxic effect. The drug pharmacokinetic parameters are defined in Table IV.

Table IV.

Cisplatin pharmacokinetic parameters (from (33) and associated references).

Parameter	Description	Value
Vc	Cell Volume (fL/cell)	520
F	Interstitial Fraction	0.48
Ds	Drug Diffusivity (μm2/min)	0.6
k1	Plasma elimination rate (min−1)	2.77E-2 (25 min half-life)
k12	Cytosolic transfer coefficient (min−1)	5.4E-2
k21	Cytosolic efflux coefficient (min−1)	1.56E-3
k23	DNA-Bound efflux coefficient (min−1)	3.82E-4
k32	Efflux from DNA (min−1)	0
k3	Drug-DNA repair (min−1)	1.5E-2
sm	Drug-DNA capacity (fmole)	∞

2.7. NP Aggregation

NP concentration was calculated at every node in the system once every output interval. For simplicity, three levels of drug-loaded NP aggregation were simulated by changing the size of aggregation “blocks,” with each block size containing a different number of nodes (5×5, 10×10, 15×15). With larger block sizes, a greater number of NPs were contained within each aggregate, and the spatial separation between aggregates was correspondingly larger. Block sizes larger than 15×15 did not appreciably change the drug release, indicating saturation. A threshold value (300) was used to determine if aggregation occurs in a particular block based on the total number of NPs within that block. Aggregation was simulated by effectively “stacking” the extracellular drug-loaded NPs within each block. Drug was then diffused away from the central aggregate in all compartments immediately following the simulation output interval where the initial aggregation occurred.

2.8. Cisplatin Cytotoxic Effect

Drug induced tissue death was included into the pharmacodynamic model that describes the rate of net tumor proliferation (λ_p) (as in (32)):

$${\lambda }_p=\{\begin{array}{cc}\begin{array}{c}0\\ {\lambda }_M\sigma \left(1-\left[{\overline{\lambda }}_{\mathit{\text{CDDP}}}{\sum }_{t-t_d}^t{s}_{3\mathit{\text{CDDP}}}\right]-{\lambda }_A\right)\\ 0\\ -{\lambda }_N\end{array}& \begin{array}{c}\text{outside\hspace{0.17em}tumor}\\ \text{in\hspace{0.17em}proliferating\hspace{0.17em}tissue}\\ \text{in\hspace{0.17em}hypoxic\hspace{0.17em}tissue}\\ \text{in\hspace{0.17em}necrotic\hspace{0.17em}tissue}\end{array}\end{array}$$ [Equation 12]

where λ_M is the mitosis rate, λ_A is the apoptosis rate, and λ_N is the rate of tissue loss in the necrotic region. ${\overline{\lambda }}_{\mathit{\text{CDDP}}}$ is the rate of cisplatin induced tissue death. Currently, apoptosis is simplified, as cell death is assumed to be instantaneous (35). ${\overline{\lambda }}_{\mathit{\text{CDDP}}}$ represents the overall drug effect which is a function of drug concentration within the proliferating region. The DNA-bound drug concentration is multiplied by a scaling factor to achieve the desired drug effect.

2.9. Coupling of the Models

The NP kinetic model was applied before the aggregation model during each simulation output interval, which allowed for a burst release of drug from the vessels into the extracellular compartment before NP aggregation could occur. The drug kinetic model was then applied after NP aggregation. In this case, it was assumed that no NPs were transferred into the cytosolic compartment due to size constraints of the aggregates. In all treatment cases, simulations were run for 30-hours in simulated real-time, as the cisplatin effect becomes null after this time.

2.10. Calibration of Drug-Induced Cell Death

Cytotoxicity data obtained with experiments with Non-Small Cell lung cancer (NSCLC) tumor spheroids were used to calculate a 48hr IC50 for simulated avascular spheroids, as in (26). Interpolation was used to determine a scaling factor to achieve the desired IC50, for which the simulated avascular spheroid size was reduced by 50%. This factor was assigned the units of drug concentration that had achieved the IC50 with the spheroids in vitro (26). The trapezoid method was used to calculate the areas-under the-curve (AUC’s) to quantify the NP and drug concentrations.

2.11. Numerical Methods

Briefly, the equations in the model are solved iteratively at each time step (36). In all equations which involve a diffusion term, a fully nonlinear diffusion solver was used to solve the equation u(t) = Δ(D(u, x, y) · Δ(u) + source(u, x, y). This equation is solved in space using centered finite difference approximations and the backward Euler time-stepping algorithm (35, 36). The discrete equations are then solved using a nonlinear adaptive Gauss-Seidel iterative method (44, 45). Further details of the numerical solution are in (35) and references therein.

3. Results

The transport of cisplatin-loaded PLGA nanoparticles (NPs) into heterogeneously vascularized tumor tissue was evaluated as a function of the NP cytosolic transfer coefficient, thus assessing the capability of the NPs to remain in the extracellular interstitium or penetrate into the cellular compartment. The effect of the drug release from NPs both in the interstitium and in the intracellular space was first qualitatively evaluated on the tumor tissue. Figure 1 and Figure 2 show representative images of NP localization for the HIGH and VERY LOW cases of vascular heterogeneity immediately after bolus injection, with the NP transfer coefficient ranging from 0 (no transfer) to 5 (medium transfer) to 50 (high transfer). Supplementary Figure 1 and Supplementary Figure 2 show the results for the intermediate MEDIUM and LOW vascular heterogeneity cases. The corresponding drug concentrations are shown for the extracellular, cytosolic, and DNA-bound compartments.

Figure 1 -. Variation of NP cytosolic transfer for tumor lesion of HIGH vascular heterogeneity,

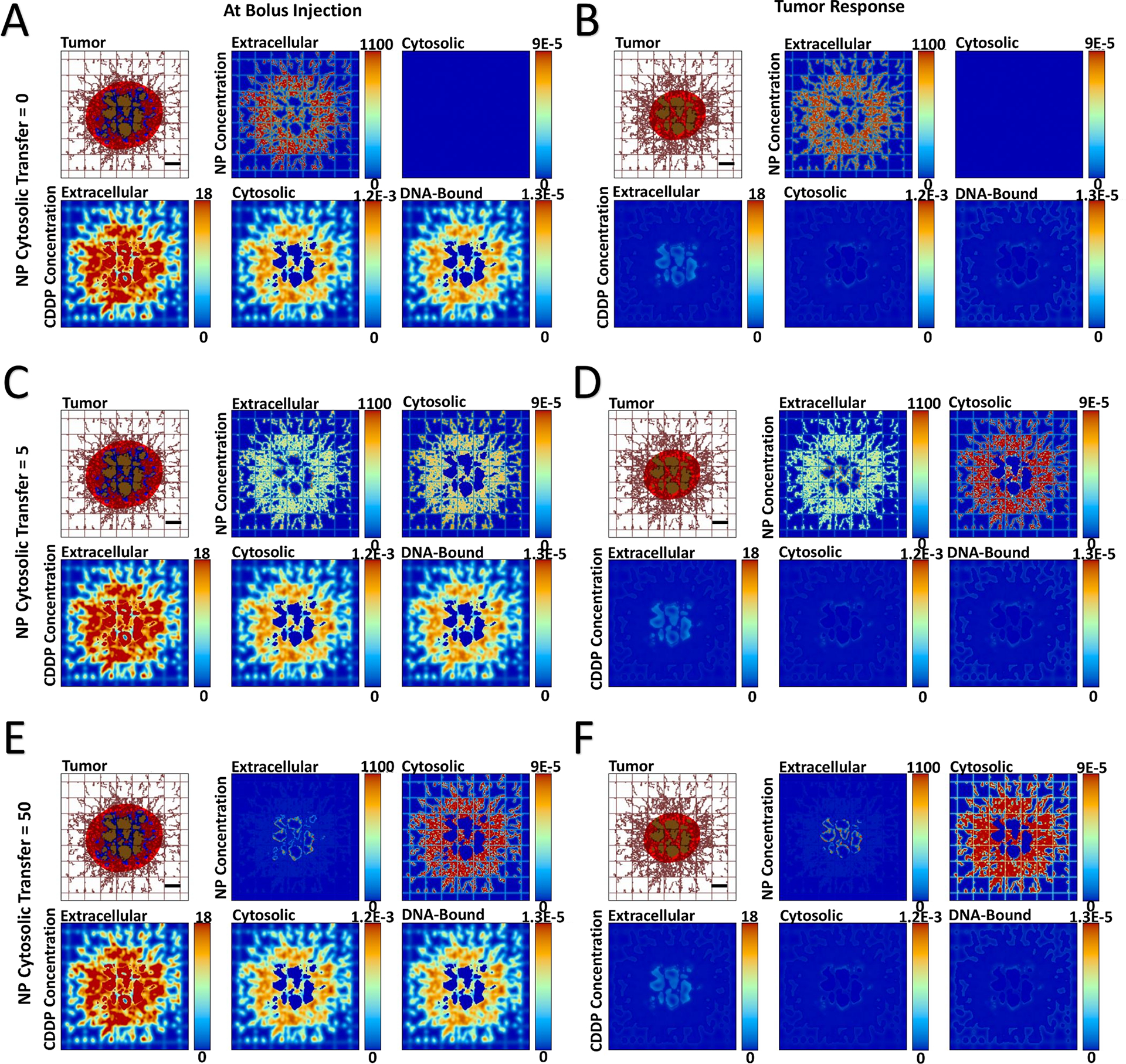
showing spatial distribution of PLGA NPs and cisplatin (CDDP) in the three compartments of the model. The NP cytosolic transfer coefficient was varied from low (=0), medium (=5), and high (=50) values. Images are from the first output interval immediately after bolus injection of CDDP-loaded NPs (Panels A, C, E) and the second output interval after the drug has taken effect (Panels B, D, F). The top left figure in each panel depicts the tumor (red: proliferating tissue; blue: hypoxic tissue; brown: necrotic tissue) along with surrounding capillary network (brown lines). Pre-existent (normal) vasculature is shown as a regular rectangular grid and neo-vasculature induced by angiogenesis is shown as irregular lines. Drug concentration is shown for extracellular (μM), cytosolic (Fmol × hr), and DNA-bound (Fmol × hr) compartments. Bar = 200 μm.

Figure 2 -. Variation of NP cytosolic transfer for tumor lesion of VERY LOW vascular heterogeneity,

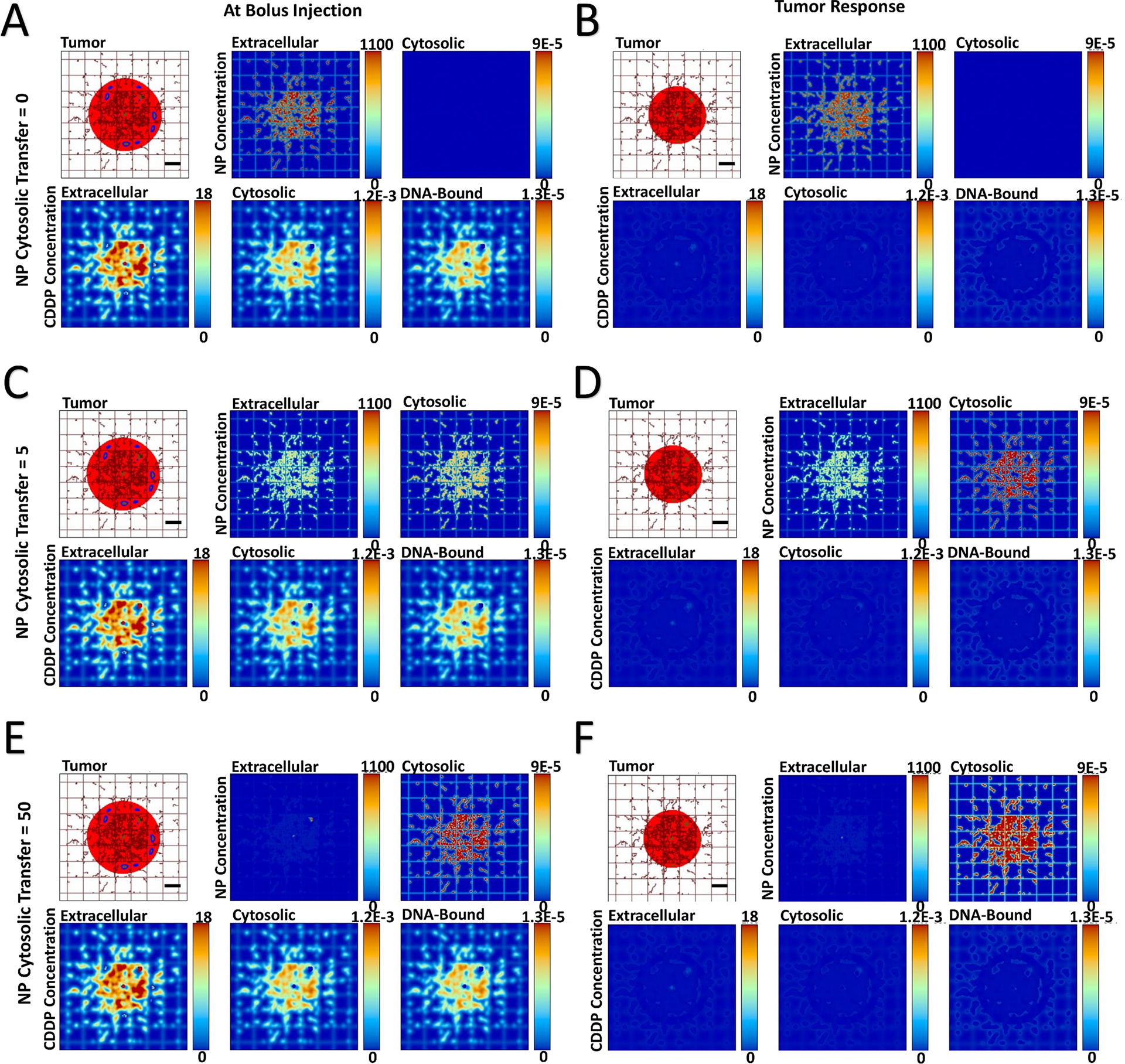
showing spatial distribution of PLGA NPs and cisplatin (CDDP) in the three compartments of the model. The NP cytosolic transfer coefficient was varied from low (=0), medium (=5), and high (=50) values. Images are from the first output interval immediately after bolus injection of CDDP-loaded NPs (Panels A, C, E) and the second output interval after the drug has taken effect (Panels B, D, F). Drug concentration is shown for extracellular (μM), cytosolic (Fmol × hr), and DNA-bound (Fmol × hr) compartments. Colors are as in Figure 1. Bar = 200 μm.

In the case of no cytosolic transfer (NP transfer coefficient = 0), the NPs remain confined to the extracellular space, with the NPs essentially acting as sources of drug external to the tumor cells. Once the drug diffuses through the cytosolic compartment in order to reach the DNA (Panels A), its cytotoxic effect shrinks the tumor (Panels B). When the cytosolic transfer coefficient is of medium (= 5) value, a substantial number of NPs are able to locate to the cytosolic compartment post injection (Panels C). The NP distribution varies depending on the tissue heterogeneity, with a higher concentration in the tumor tissue periphery in case of HIGH heterogeneity and more internalized, lower concentrations within tumor tissue as this heterogeneity decreases. This phenomenon is consistent with previous modeling work showing that tumor tissue heterogeneity has a nonlinear effect on NP distribution (46) and effect (47), and with recent optimization analyses of NP parameters (48).

As in the case of no NP cytosolic transfer, a medium value of transfer coefficient leads to drug diffusion into the cytosol from the interstitium after release from the extracellular NPs. Additionally, the drug is now transported by NPs into the cytosol and released intracellularly. The drug concentration in the DNA-bound compartment can be qualitatively observed to increase slower compared to the case with no cytosolic transfer. The drug effect shrinks the tumor (Panels D), with the more heterogeneous tumors showing a higher response. When the NP cytosolic transfer coefficient is high (= 50), the majority of NPs enters the cytosol (Panels E). Nevertheless, the NPs in the extracellular compartment still release a substantial amount of drug, which has to diffuse into the cytosol in order to reach the DNA. Compared to the previous two cytosolic transfer values, this case qualitatively seems to increase the DNA-bound drug the slowest, while yielding the highest tumor regression (Panels F).

Next, the effect of varying levels of NP aggregation was qualitatively evaluated, assuming no NP cytosolic transfer. Figures 3 and 4 show the spatial release of drug for tumors with HIGH and VERY LOW vascular-induced heterogeneity. Supplementary Figure 3 and Supplementary Figure 4 show the results for the intermediate MEDIUM and LOW heterogeneity cases. As expected, as the level of NP aggregation increases (Panels A, C, E), the drug released from the NPs becomes correspondingly more localized (clustered) (Panels B, D, F). As the drug only affects proliferating tissue due to its cell cycle-specific cytotoxicity, localized regions of eliminated tumor tissue become evident as tumor tissue heterogeneity increases. These regions become larger for higher aggregation, with correspondingly higher localized pockets of drug.

Figure 3 -. Variation of NP aggregation for tumor lesion of HIGH vascular heterogeneity,

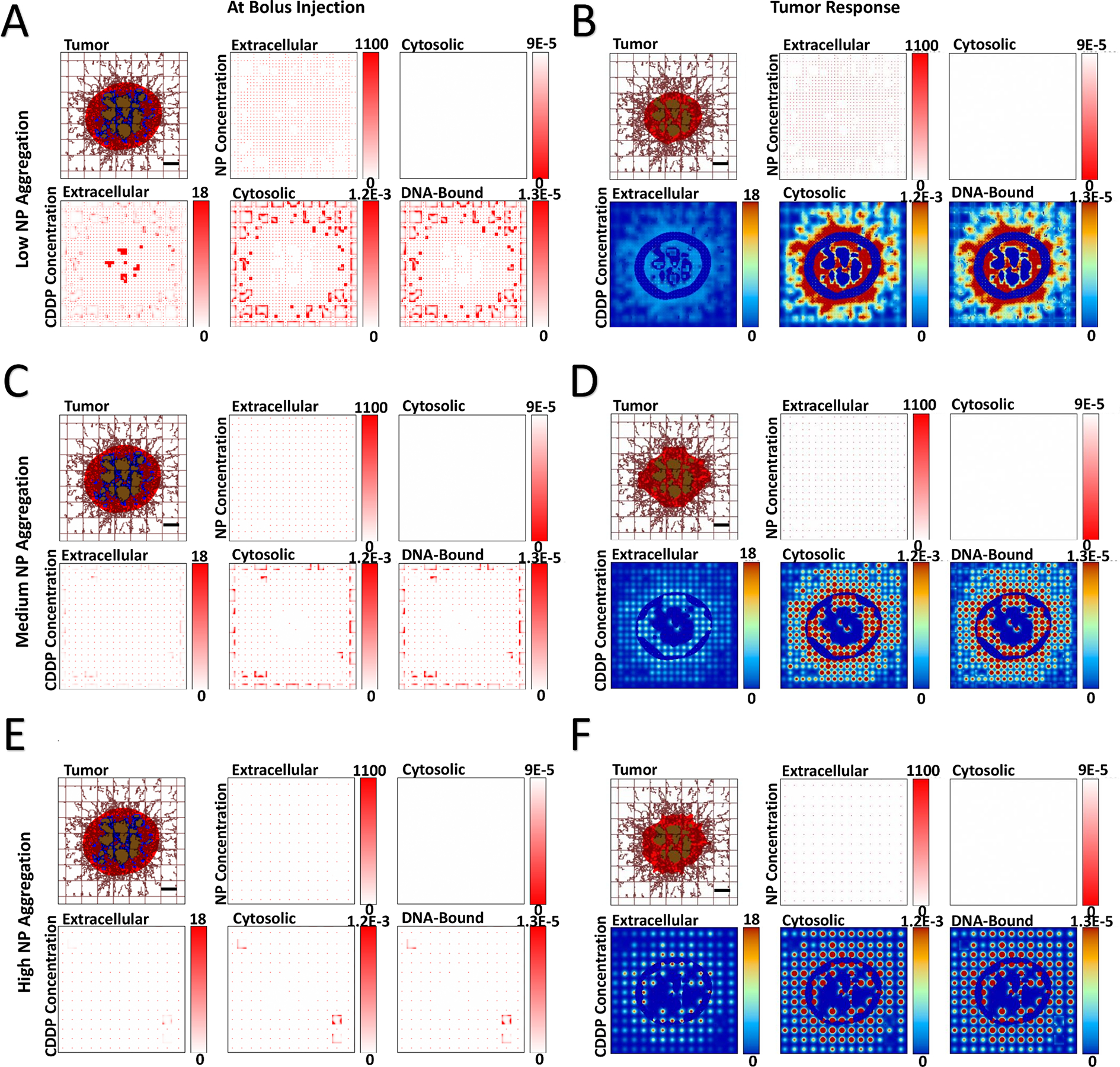
showing spatial distribution of PLGA NPs and cisplatin (CDDP) in the three compartments of the model. NP aggregation was varied from low (5×5 blocks), medium (10×10 blocks), and high (15×15 blocks). Images are from the first output interval (immediately after bolus injection of CDDP-loaded NPs (Panels A, C, E) and the second output interval (after the drug has taken effect (Panels B, D, F). Drug concentration is shown for extracellular (μM), cytosolic (Fmol × hr), and DNA-bound (Fmol × hr) compartments. Colors are as in Figure 1. Bar = 200 μm.

Figure 4 -. Variation of NP aggregation for tumor lesion of VERY LOW vascular heterogeneity,

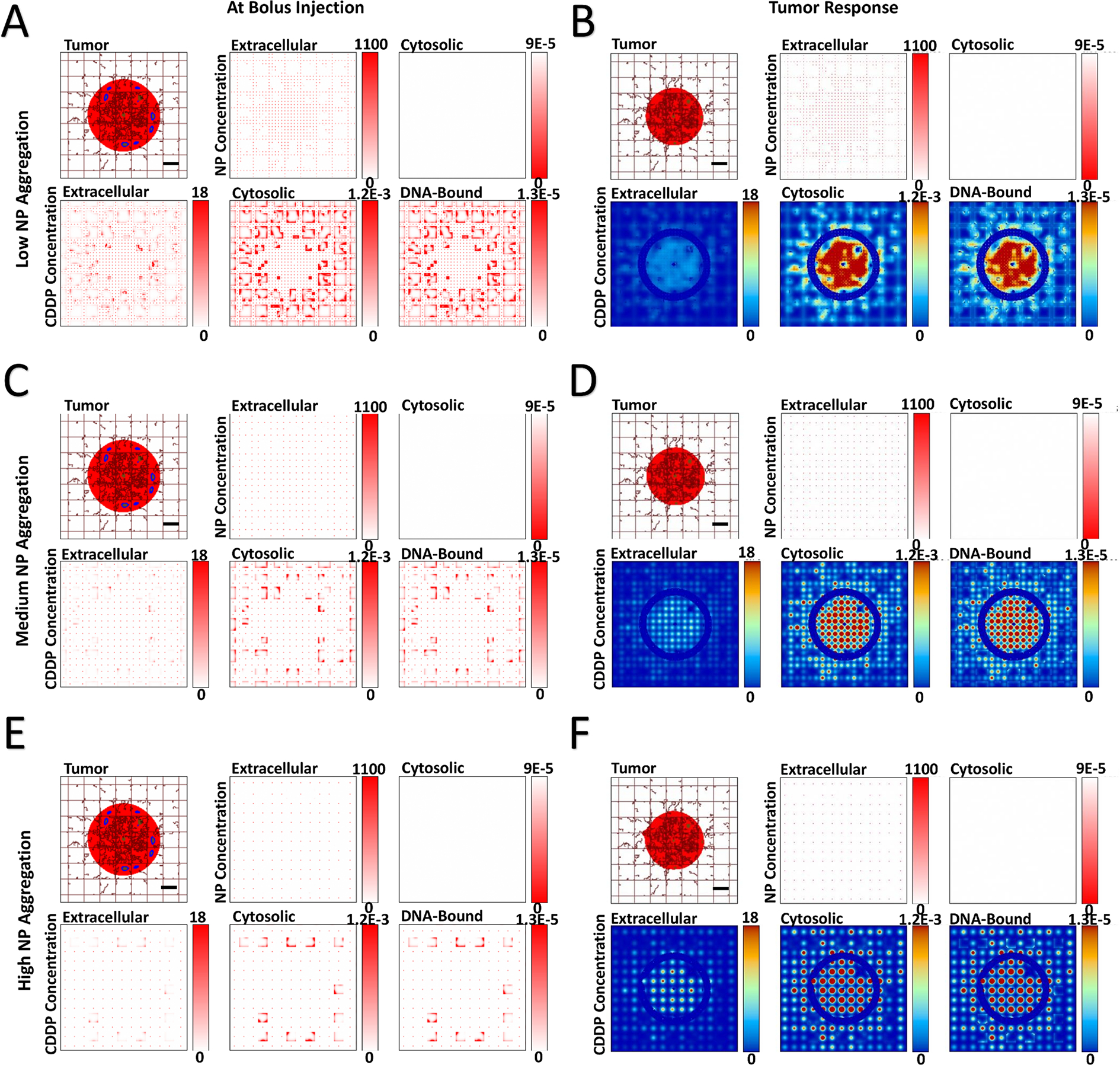
showing spatial distribution of PLGA NPs and cisplatin (CDDP) in the three compartments of the model. NP aggregation was varied from low (5×5 blocks), medium (10×10 blocks), and high (15×15 blocks). Images are from the first output interval (immediately after bolus injection of CDDP-loaded NPs (Panels A, C, E) and the second output interval (after the drug has taken effect (Panels B, D, F). Drug concentration is shown for extracellular (μM), cytosolic (Fmol × hr), and DNA-bound (Fmol × hr) compartments. Colors are as in Figure 1. Bar = 200 μm.

Figure 5 quantifies the NP area-under-the-curve (AUC) achieved in the extracellular, and cytosolic compartments, as a function of tumor vascular heterogeneity. When considering no NP aggregation, the NP cytosolic transfer rate was varied from none to high. Increasing this rate dramatically reduced the NP concentration in the extracellular compartment while increasing it in the cytosol, as expected (Figure 5A). However, the AUC variation between the levels of tissue vascular heterogeneity was nonlinear. As this heterogeneity increased from VERY LOW to MEDIUM, the corresponding decrease in AUC became less pronounced as the transfer coefficient increased, with, the highest transfer rate evincing a steady AUC increase from VERY LOW to HIGH. The cytosolic NP AUCs corresponding to these cases (Figure 5B) show that as the tumor vascular heterogeneity increases, the AUCs decrease accordingly. The highest AUC values are established for the highest value of transfer rate, as expected.

Figure 5 -. Extracellular and cytosolic nanoparticle area-under-the-curve (AUC) as a function of vasculature-induced tumor tissue heterogeneity.

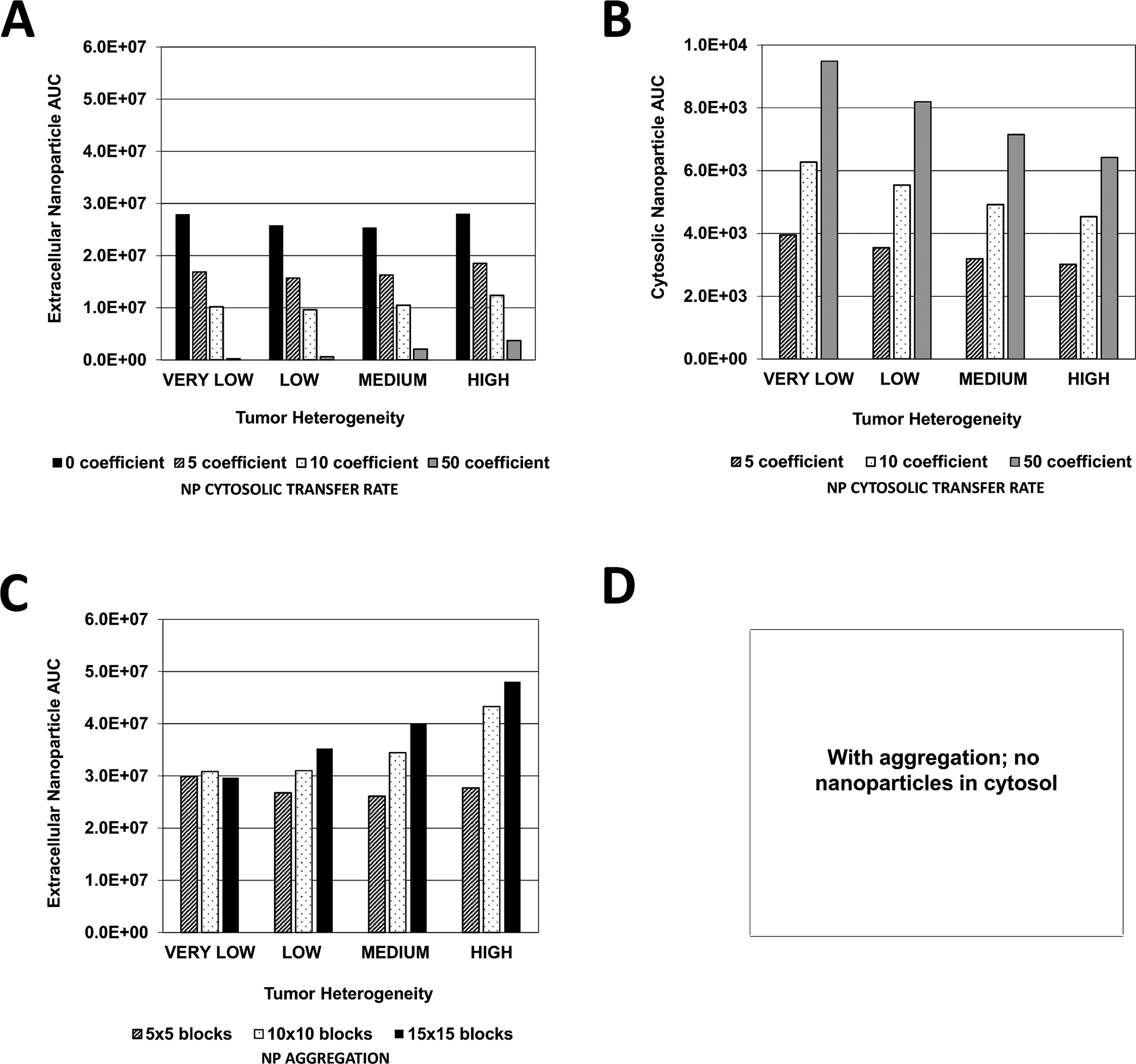
Graphs represent the magnitude of the AUC calculated within the tumor boundary at every output interval during treatment with cisplatin-loaded NPs. (A) Extracellular and (B) Cytosolic NP AUC due to variation in NP cytosolic transfer rate (non-dimensional units); (C) Extracellular and (D) NP AUC due to variation in NP aggregation (non-dimensional units).

In the case of NP aggregation, the extracellular NP AUC behaved nonlinearly with respect to the tumor vascular heterogeneity as a function of the extent of this aggregation (Figure 5C). The AUC was similar for all values of aggregation in the case of VERY LOW heterogeneity, whereas it was the most different based on aggregation for HIGH heterogeneity. Overall, it seems that the AUC initially declines as heterogeneity increases, and then starts to increase with even higher heterogeneity. The minimum AUC along this trend as a function of heterogeneity shifts depending on the extent of aggregation, with the low aggregation declining the most before increasing as heterogeneity increases.

With no NP aggregation, the magnitude of the NP cytosolic transfer rate did not seem to make much difference in regards to the extracellular drug AUC (Figure 6A). This AUC increased with higher tissue vascular heterogeneity. The corresponding cytosolic drug AUC also increased accordingly; however, a larger transfer rate led to increased AUC values (Figure 6B). The same pattern was observed with the DNA-bound AUC (Figure 6C). In contrast, NP aggregation evinced different dynamics. The extracellular drug AUC increased not only as a function of tissue heterogeneity but also with higher NP aggregation (Figure 6D). The cytosolic AUC also increased with higher tissue heterogeneity, but was lower for high aggregation for each level of heterogeneity (Figure 6E), with the highest AUC attained for lowest aggregation and highest tissue heterogeneity (2×10⁻⁷ Fmol/cell × hr). The DNA-bound AUC (Figure 6F) followed a similar pattern, albeit at overall lower values of drug concentration than in the cytosol.

Figure 6 -. Extracellular, cytosolic, and DNA-bound cisplatin area-under-the-curve (AUC) as a function of vasculature-induced tumor tissue heterogeneity.

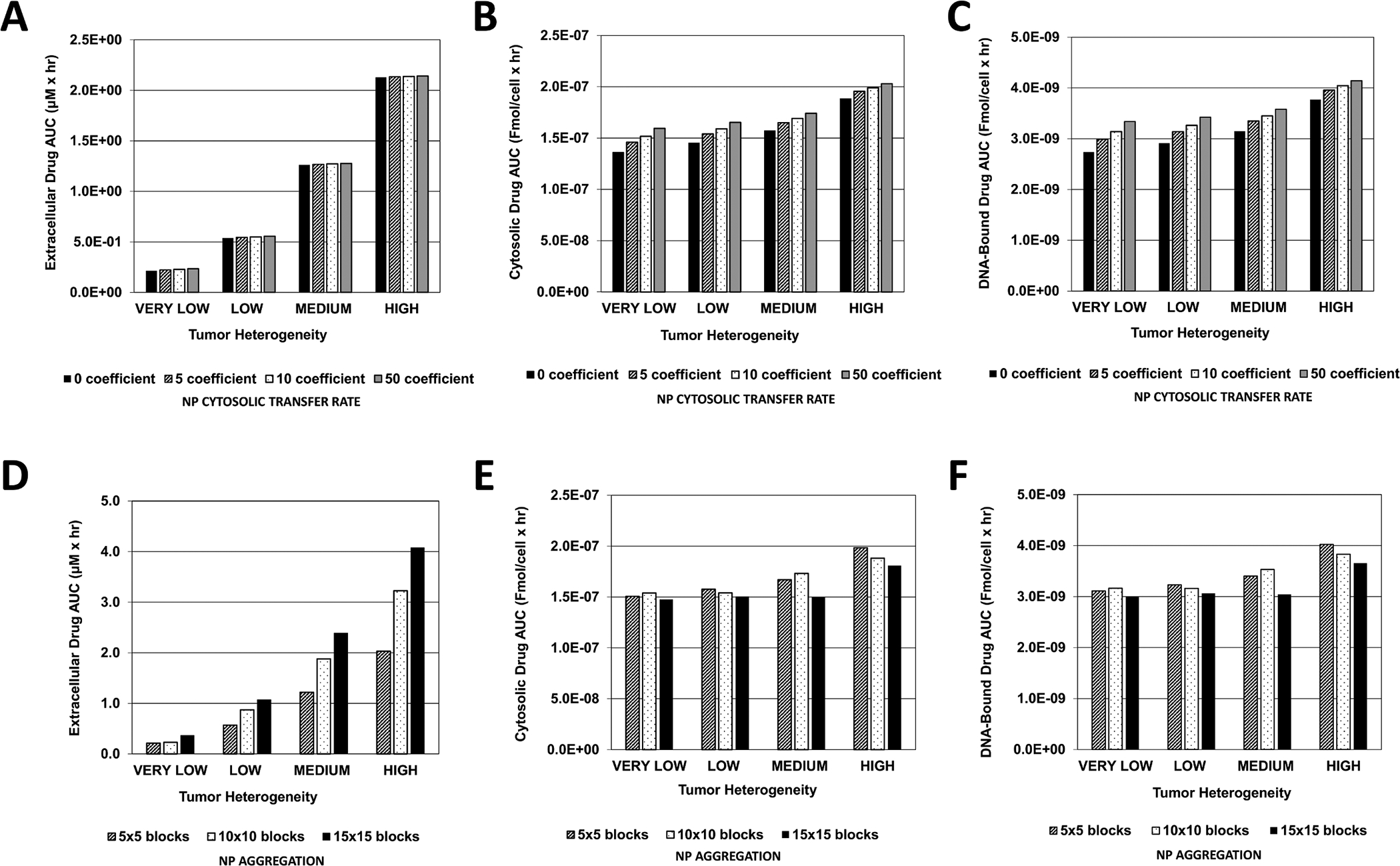
Graphs represent the magnitude of the AUC calculated within the tumor boundary at every output interval during treatment with cisplatin-loaded NPs. (A) Extracellular (μM × hr), (B) Cytosolic, and (C) DNA-Bound drug AUC due to variation in NP cytosolic transfer rate (Fmol/cell × hr); (D) Extracellular (μM × hr), (E) Cytosolic, and (F) DNA-Bound drug AUC due to variation in NP aggregation (Fmol/cell × hr).

The minimum tumor radius calculated as a fraction of Initial value is shown in Figure 7. In general, the highest NP cytosolic transfer coefficient (=50) yielded the highest response for each case of tumor vascular heterogeneity (Figure 7A). While in the case of HIGH vascular heterogeneity the worst response resulted with the lowest transfer coefficient (=0), as the tumor heterogeneity decreased, the worst response was evinced by the low coefficient (=5). When NP aggregation occurs (Figure 7B), for each case of tissue heterogeneity the response was proportional to the level of aggregation, with the most effective response resulting with the lowest aggregation.

Figure 7 -. Tumor response as a function of vasculature-induced tumor tissue heterogeneity.

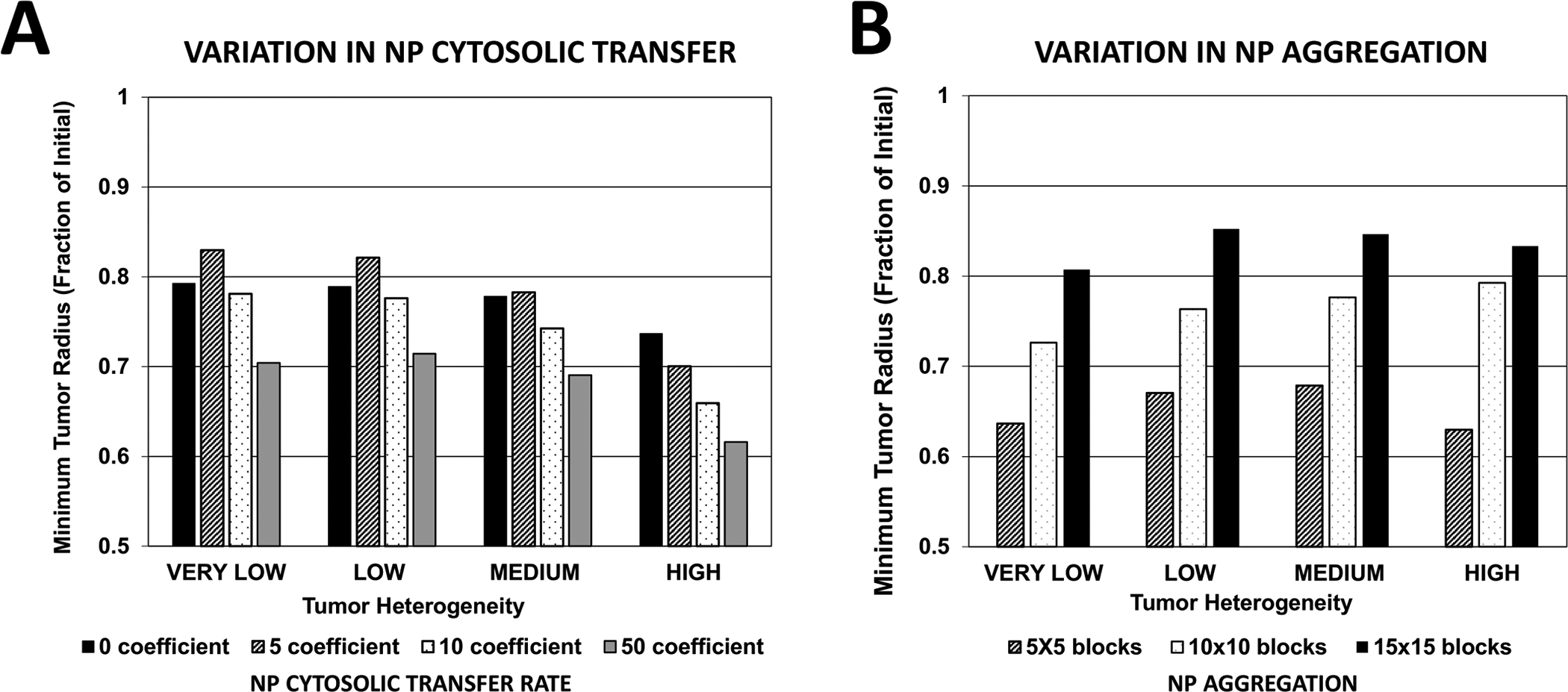
(A) Minimum tumor radius resulting from variation in NP cytosolic transfer rate (non-dimensional units); (B) Minimum tumor radius resulting from variation in NP aggregation (non-dimensional units).

Interestingly, the case of medium (10×10) aggregation resulted in decreased effectiveness as tissue heterogeneity increased. However, with low (5×5) or high (15×15) aggregation, cases of VERY LOW and HIGH tissue heterogeneity responded more strongly to the nanotherapy than the LOW and MEDIUM heterogeneity cases. For high levels of NP aggregation, these two cases yielded the least tumor regression. Overall, nanotherapy was most effective in the case of HIGH tissue heterogeneity, no NP aggregation, and a high cytosolic transfer coefficient. However, depending on the level of tissue heterogeneity and cytosolic transfer, NP aggregation, yielding only extracellular drug release, could be more effective than NPs that avoid aggregation and are uptaken by cells, releasing drug extra- and intra-cellularly.

4. Discussion

This study couples a multi-compartmental kinetics model of NP transport through heterogeneously vascularized tumor tissue with a PKPD drug model to further enable in silico evaluation of NP-mediated drug delivery and efficacy. The NP cytosolic transfer rate is varied to evaluate the effect on tumor response of differential drug release in extracellular and cytosolic compartments. The effect on tumor response of varying degrees of NP aggregation are also assessed, simulating a commonly occurring phenomenon known to affect NPs in solution as well as in vivo.

Although extracellular NP AUC increased for higher levels of tissue heterogeneity as the cytosolic transfer coefficient became larger (Figure 5), cytosolic NP AUC correspondingly decreased. This phenomenon reflects the difference in the proliferative fraction for each case of tissue heterogeneity. Although tumors with higher vascular heterogeneity are associated with a larger vascular network, which allows for increased NP transport into tumor tissue, a smaller overall proliferative tissue region implies that fewer NPs are able to transfer into the cytosolic compartment compared to tissue with lower heterogeneity but larger proliferative region. Further, as cytosolic NP AUC increased with higher cytosolic transfer coefficients and lower tissue vascular heterogeneity (Figure 5), the associated drug AUC increased in the extracellular, cytosolic and DNA-bound compartments, and also rose with higher tissue heterogeneity (Figure 6). This observation implies that with the given NP and drug parameters, release of drug in the extracellular compartment was a primary source of drug for the cytosolic and DNA-bound compartments, especially for heterogeneous tissue, implying that NP extracellular drug release was critical for achieving higher drug intracellularly.

Although the extracellular NP AUC assumed a nonlinear pattern based on amount of aggregation and degree of tissue vascular heterogeneity (Figure 5), initially decreasing or remaining constant for low and medium aggregation, respectively, as tissue heterogeneity increased, the corresponding extracellular drug AUC increased exponentially with higher aggregation and higher heterogeneity (Figure 6). The associated cytosolic and DNA-bound drug AUC, however, did not increase as much with increasing aggregation or tumor heterogeneity. Interestingly, both cytosolic and DNA-bound drug AUC values were highest for the low aggregation when the tissue heterogeneity was LOW or HIGH, while these AUC values were highest for medium aggregation when the heterogeneity was VERY LOW or MEDIUM. This result suggests that high NP aggregation coupled with highly heterogeneous tissue can lead to sub-optimal DNA drug uptake, as the drug becomes concentrated at specific locations and unable to adequately diffuse to all of the tumor tissue. In contrast, some aggregation could be beneficial if the tissue is less heterogeneous, as it helps to create local “depots” of concentrated drug, from which it can diffuse into the surrounding tissue. A similar effect has been observed when modeling the uptake and transport of drug-loaded NPs by macrophages into tumor tissue (49, 50).

The tumor response based on variation of the NP cytosolic transfer coefficient correlates with the value of this coefficient as well as with the degree of tissue vascular heterogeneity (Figure 7A). As expected, lower cytosolic transfer decreases the response, and so does lower tissue heterogeneity. However, a low transfer coefficient yields the least response as tissue heterogeneity decreases, worse than no transfer at all, which suggests that tailoring the cytosolic transfer to this heterogeneity would be critical in case the drug release from the NPs can only occur intracellularly.

The overall response based on variation in the degree of NP aggregation (Figure 7B) indicates that when aggregation is low, tumors with VERY LOW or HIGH tissue heterogeneity respond best. Regardless of heterogeneity, higher aggregation leads to worse response, although the magnitude of this response is not linearly dependent on the level of tissue heterogeneity. These results indicate that NP aggregation can sometimes be beneficial for increasing the efficacy of cancer nanotherapy, depending on the drug used and the characteristics of the tumor tissue and associated vasculature.

Main NP parameters considered in this study include diffusivity (which depends on NP size and affinity), cellular uptake, and aggregation potential. These parameters depend on specific NP formulations, including surface modifications. For any particular formulation, the goal would be to experimentally measure values for these parameters (e.g., via in vitro experiments), and then to evaluate via the computational model how adjusting these values affects the expected NP performance under conditions of varying tissue vascularization and heterogeneity. These tissue conditions can be clinically assessed and used as input to the model with the goal to tailor the NP formulations to patient tumor-specific conditions. Given that tumor heterogeneity is typically not uniform, a combination of NP formulations may be appropriate, which could also be explored via the in silico model. Expansion of the model to include acidity in tumor tissue due to lactic acid production as well as NP interactions with ECM may enhance the predictive value of the performance to be expected from particular formulations.

The physico-chemical properties of a drug, and in particular its hydrophilic or hydrophobic nature, are expected to affect the model primarily in terms of transport and cellular uptake/retention. These properties relate directly to the drug diffusivity, decay, and kinetic parameters. In particular, for small hydrophilic drugs such as cisplatin, passive transmembrane diffusion across the lipid bilayer would be facilitated, as previously confirmed (51). In comparison, hydrophobic drugs are expected to face impaired transport as well as aggregation within cell membranes (52). To improve hydrophilicity, drugs such as Paclitaxel are commonly combined with a solvent (e.g., Cremophor EL) or delivered via encapsulation (e.g., albumin-stabilized Paclitaxel or nab-PTX).

In future work, the aggregation model could be enhanced via a dynamic drug release rate. This rate should be lower for aggregated NPs and dependent on the physical interactions between drug and NPs. Further, a dynamic aggregation model could be implemented, which does not rely on predetermined aggregation block sizes and spatial positions, as the size and position of each aggregate could be based on the concentration of NPs within a particular tissue region. The scope of this study focused on the development of a theoretical framework, which will require validation in the future by comparing model predictions to experimentally-observed in vivo data. With additional refinement and capability, and coupled with experimental data informing the model parameter values, this modeling platform could move towards clinical application. This would offer the capability to design nanotherapy based on patient tumor-specific characteristics, such as vascularization density and associated tissue heterogeneity.

5. Conclusion

A novel coupling of a kinetic model of NP transport in heterogeneously vascularized tumor tissue with a multicompartmental drug model was implemented to evaluate the efficacy of cisplatin-loaded poly lactic-co-glycolic acid (PLGA) NPs in heterogeneously vascularized tumor tissue. The magnitude of the extracellular to cytosolic NP transport was varied to assess tumor-dependent cellular uptake. NP aggregation was simulated to evaluate its effects on drug distribution and tumor response. The overall results highlight the nonlinear dynamics of NP and drug transport into tumor tissue. The model system provides a means to evaluate customization of NP-mediated drug treatment based on NP and drug design parameters, including cellular uptake and aggregation, and taking into account patient-specific tumor tissue characteristics such as proportion of viable tissue and vascular heterogeneity.

Abbreviations

AUC

area-under the-curve

ECM

extracellular matrix

NSCLC

Non-small cell lung cancer

NP

nanoparticle

PLGA

poly lactic-co-glycolic acid

PD

pharmacodynamic

PK

pharmacokinetic