Parameter Estimation and Uncertainty Quantification for Systems Biology Models

Abstract

Mathematical models can provide quantitative insights into immunoreceptor signaling, and other biological processes, but require parameterization and uncertainty quantification before reliable predictions become possible. We review currently available methods and software tools to address these problems. We consider gradient-based and gradient-free methods for point estimation of parameter values, and methods of profile likelihood, bootstrapping, and Bayesian inference for uncertainty quantification. We consider recent and potential future applications of these methods to systems-level modeling of immune-related phenomena.

Introduction

Immunoreceptors such as the T cell receptor (TCR) [1], B cell antigen receptor (BCR) [2], and high-affinity IgE receptor (FcϵRI) [3] serve as initiation points for information processing by extensive cell signaling networks, which have been characterized over decades of experimental work. These networks have also attracted significant attention from modelers [4].

Mathematical models can enable new quantitative insights into immune cell signaling dynamics, but present challenges: each interaction in the signaling network is characterized by one or more rate constants, which are often unknown. A model encompassing even a small subset of the known protein-protein interactions could have tens to hundreds of unknown parameters. Such models raise problems of estimating parameter values, and quantifying uncertainty in parameter estimates and in model predictions. These challenges are compounded by the fact that the state space (i.e., the number of different chemical species present) can grow large, making simulations computationally demanding. Thus, parameterization tools for biological modeling must deal with a high-dimensional search space while minimizing the number of expensive model simulations. Parameterization and uncertainty quantification, which are our focus in this review, are important aspects of analysis of quantitative models. Another aspect, not covered here, is model selection [5].

Various software tools such as COPASI [6], Data2Dynamics [7], AMICI [8, 9, 10] used in combination with PESTO [11], and PyBioNetFit [12] make parameterization of detailed models possible without the need for problem-specific code. PyBioNetFit and AMICI/PESTO are the newest of these tools; they provide features that are complementary to those available in older tools.

Here, we review recent advances in methods and tools that address the parameterization problem for compartmental models (i.e., models that account for one or more compartments, each taken to be well-mixed/spatially homogeneous). We focus on modeling cell signaling in immunity, but note that the same methodology has applications across systems biology. This review serves as a guide for a systems biology modeler: given a particular model and experimental dataset for a cellular process of interest, we discuss our recommended approaches for parameter estimation and uncertainty quantification and the available software implementations. Our discussion touches on several applications to modeling immunoreceptor signaling that have been enabled by recent methodological developments in parameterization.

Model formulation

We assume that a compartmental model of interest has been constructed based on known molecular mechanisms of signaling. Traditionally, model structure (i.e., the set of protein-protein interactions and biochemical reactions included in a model) is defined through a hand-crafted approach, but recent tools have been developed to make this process computer-aided [13, 14]. Ideally the model should be specified in a standardized format to enable compatibility with the general-purpose tools discussed in this review. For immunoreceptor signaling models, BioNetGen language (BNGL) [15] is often a useful format because it supports rule-based modeling. Rule-based modeling is a preferred approach to describe biomolecular site dynamics, which are often important in receptor signaling systems [16]. Another available format is the Systems Biology Markup Language (SBML) [17], which has a wider range of software support. The current SBML standard (Level 3) [18] includes a core language, which can be supplemented with extension packages, such as SBML Multi [19], which supports rule-based modeling. However, software support for extensions is more limited. Software is available to convert from BNGL to SBML [20], so BNGL models can benefit from SBML-compatible tools. An advantage of using these standardized formats is the availability of databases of published models - BioModels Database [21] archives many SBML models and RuleHub (https://github.com/RuleWorld/Rulehub) archives many BNGL models. Models in these databases can be used for benchmarking or as starting points for new modeling studies.

A model of interest is assumed to describe the concentrations or populations of chemical species over time, but could take several formats. It could be a system of nonlinear ODEs that are numerically integrated to generate deterministic time courses for each chemical species. It could also be a stochastic model simulated using Gillespie’s direct method [22], for example, or a network-free method [23], such as that implemented in NFsim [24]. In network-free methods, the system state is tracked in terms of features of the set of molecules currently present in the system, without enumerating all possible chemical species and reactions (which could be too many to practically enumerate).

We also assume that experimental data are available, which are related to quantities that are represented in the model (possibly via a measurement model). In the conventional case, the data are quantitative time courses or dose-response curves. An objective function is specified to measure model misfit to experimental data. One common choice is a (weighted) residual sum of squares function, ${\sum }_i{\omega }_i{\left(y_i-{\widehat{y}}_i\right)}^2$ where y_i are experimental data, ${\widehat{y}}_i$ are model predictions, and w_i are constants. One choice for w_i is $1/{\sigma }_i^2$, where ${\sigma }_i^2$ is the sample variance associated with y_i; this formulation is sometimes called the chi-squared objective function. We consider a less conventional objective function below.

The parameterization problem becomes a problem of minimizing the chosen objective function.

Parameter estimation through optimization

Several classes of methods, which have strengths for different types of problems, are available to perform minimization of the objective function.

Gradient-based optimization

Gradient-based optimization consists of a family of methods that involve computing the gradient of the objective function with respect to the parameters. Such methods can be classified as first-order (using only first derivatives of the objective function with respect to parameters) or second-order (using both first and second derivatives). First-order methods include gradient descent and stochastic gradient descent, with the latter commonly used in machine learning applications. Modelers often prefer second-order methods, which avoid becoming mired down at saddle points by leveraging the curvature information in the second derivatives. A common second-order choice is the Levenberg-Marquardt algorithm [25], but this algorithm is specialized to objective functions expressed as a sum of squares (i.e., least squares problems). For the more general case, quasi-Newton methods (e.g., L-BFGS-B [26]) can be used. These methods entail approximation of second derivatives, for efficiency. The above algorithms are standard, but for systems biology models, computation of the gradient is not always straightforward. Below we discuss four possible approaches.

The finite difference approximation is a naive method in which the gradient is estimated by systematically perturbing each parameter by a small amount. This method is simple and can be applied to any model, but is inefficient for models with high-dimensional parameter spaces. Moreover, performance can be negatively affected by inexact gradient information.

The forward sensitivity method is a more sophisticated method for exact gradient computation (reviewed by Sengupta et al. [27]). For the models of interest here, the method is limited to ODE models. The method consists of augmenting the original ODE system with additional variables and equations for the derivative of each species concentration with respect to each parameter. These derivatives can be used to calculate the gradient.

Benchmarking has shown forward sensitivity analysis to outperform finite differencing and non-gradient-based methods for ODE systems [28]. The method has also been used to obtain reasonable fits for a library of benchmark problems [29], including models relevant to immune cell signaling [30, 31]. Most problems in this library featured systems of 5–30 ODEs.

The forward sensitivity method requires solving an ODE system of sensitivity equations for each parameter [32]. Each system of sensitivity equations has the same size as the original ODE model. Therefore, the gradient calculation grows expensive when a problem has both many parameters (resulting in many sensitivity equations) and many ODEs (which makes each integration expensive). This cost can become limiting, for example, for systems derived from rule-based models, which often consist of hundreds of ODEs, augmented to thousands of sensitivity equations.

Adjoint sensitivity analysis uses a more complex mathematical framework to reduce the problem to the original integration combined with the (backward) integration of a newly derived adjoint system [27, 33]. The adjoint system, with size equal to the original system, can be used to compute just the gradient vector, making for considerably less integration work than with standard forward sensitivity analysis in certain cases [27, 33]. The specific adjoint problem to be solved depends on the formulation of the optimization problem. One common case is minimization of a weighted sum of squares objective function derived from time-series data and a known initial condition. Fröhlich et al. [34] demonstrated that adjoint sensitivity analysis can be used to parameterize large biological models. Adjoint sensitivity analysis is also promising for ODE systems derived from rule-based models, but currently lacks software support for typical problems, such as problems where the initial condition is non-trivial [35].

Automatic differentiation (AD) [36] is an intriguing option given its applications to neural networks [37]. In principle, any algorithm can be represented as a computational graph consisting of elementary computer operations. Derivatives of the algorithm outputs can then be calculated by propagating the derivatives of each operation in the graph via the chain rule. Although no tools dedicated to biological modeling support AD, it is supported in the statistical modeling package Stan [38, 39], for example, where it can be applied to ODE models. Benchmarking of AD compared to other ODE sensitivity analysis methods suggests AD is efficient for small models, but scales poorly compared to adjoint sensitivity analysis [40]. It remains to be seen whether AD is computationally feasible for algorithms relevant for detailed biological models (i.e., algorithms for numerical integration of stiff and large initial value problems associated with ODE models).

A drawback of all forms of gradient-based algorithms is that each optimization run may only reach a local minimum or saddle point of the objective function. This limitation can be addressed by performing multiple, independent replicates of optimization starting from different initial points, which is referred to as multistart optimization. Each additional replicate provides an additional opportunity to converge to the global minimum.

Metaheuristic optimization

Metaheuristic optimization algorithms [41] are a family of methods that operate by repeated objective function evaluations, typically without the use of gradient information. (The method of Kuo and Zulvia [42] is an example of a metaheuristic that uses gradient information.) Metaheuristic algorithms aim to find a global (rather than local) optimum, and although they have no guarantee of good performance, they been found to perform acceptably in many use cases [43, 44, 45]. Examples of such algorithms include evolutionary algorithms (e.g., differential evolution [46] and scatter search [47]), particle swarm optimization [48], and simulated annealing [49]. A feature of many but not all of these algorithms is the maintenance of a population of good parameter sets, which are used to generate new trial parameter sets. Many modern population-based metaheuristic algorithms (e.g., [50, 51, 52]) allow for parallelized function evaluations within a single run of the algorithm, which enables these algorithms to take advantage of parallel computing resources (computer clusters).

Note that the parallelization of these algorithms is not simply from performing multiple independent fitting replicates (which can be trivially done for any algorithm); evaluations are parallelized within each iteration of the algorithm. Some metaheuristic algorithms (e.g., [51]) are asynchronous. Such algorithms improve load balancing by running simulations on all available cores at all times (cores are never left idle). However, selection of new trial parameter sets is made with only limited new data. In contrast, synchronous algorithms require all simulations of one iteration to complete before any core can move on to the next iteration. Both asynchronous and synchronous parallelized algorithms can use multiple cores to lower the total wall time required for fitting. In contrast, multistart optimization, which is commonly used with gradient-based algorithms, requires a minimum expected wall time (the average run time of an optimization job) regardless of the number of cores used. Running multiple jobs in parallel only increases the chance that some replicate finds a global optimum, as noted earlier.

Metaheuristic optimization algorithms are useful for a range of problems for which gradient-based methods are problematic (e.g., estimating parameters of a stochastic model). Such algorithms are implemented in PyBioNetFit and have been demonstrated on a library of problems [12] including rule-based models and stochastic models. A notable example problem features a rule-based model of TCR signal initiation analyzed by network-free simulation [53].

Hybrid methods are available that incorporate both metaheuristic and gradient-based optimization. For example, many descriptions of scatter search (e.g., [54]) include gradient-based local refinement of solutions found by the metaheuristic method. Such an algorithm outperformed both pure gradient-based and pure metaheuristic algorithms on a benchmark library [45] featuring models with tens to hundreds of ODEs and parameters. Memetic algorithms [55] represent a larger class of algorithms that alternate between local and global search. In cases where gradient-based methods are not applicable, local refinement of solutions can be performed using gradient-free methods, such as the simplex method [56], which can be parallelized [57] to boost efficiency.

Parameter estimation using qualitative data

In the above discussion, it was assumed that an objective function was derived from quantitative data. Recent methodological developments allow non-numerical, qualitative data to be leveraged in parameterization. These advances are notable because they allow new types of data, which may be easier to generate or already available in the literature, to be used in parameterization.

An early example of using qualitative data is the work of Tyson and co-workers on the cell cycle [58, 59]. Successive versions of a model for cell cycle control were parameterized by hand-tuning, and in one case refined by an automated method [60]. Automated parameterization using qualitative data was also performed by Umulis and co-workers [61, 62]

In related, more recent work [63], qualitative data were formalized as soft inequality constraints imposed on the outputs of a model. We note that these inequality constraints on model outputs differ from box constraints on parameter values, which are used in many parameterization problems. The inequalities were incorporated into the objective function (which can also include quantitative data) as static penalty functions [64]. A static penalty function takes a value of zero when an inequality constraint is satisfied and a value proportional to the extent of constraint violation when a constraint is violated (and thus is shaped like the ReLU activation function f (x) = max(0, x) used in machine learning). This method is available for general use in PyBioNetFit [12]. For general overviews of constrained optimization methods, see Nocedal and Wright [65] and Mezura-Montes and Coello Coello [66].

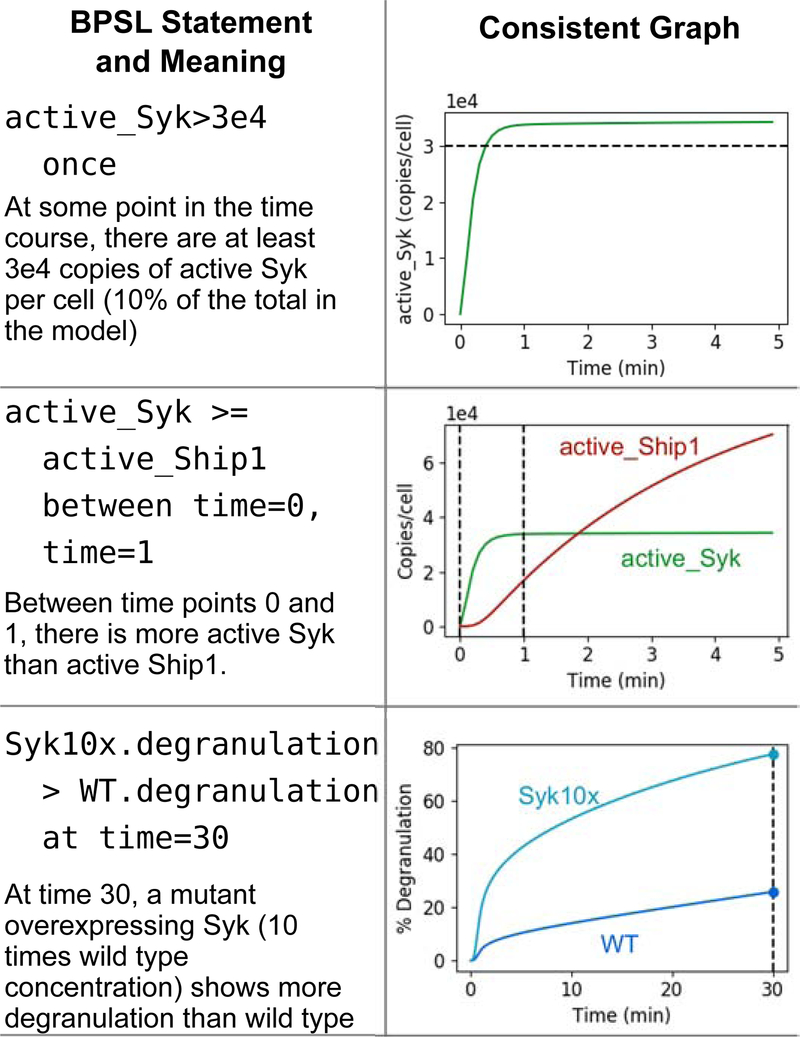
PyBioNetFit introduces the Biological Property Specification Language (BPSL) as a means to define inequality constraints to be imposed on outputs of a model. BPSL is designed for the definition of qualitative properties of time courses or dose-response curves that might be observed experimentally. In particular, BPSL has enforcement keywords, always, once, at, and between, which are used to declare where in a time course or dose-response curve an inequality should be enforced. For example, always indicates an inequality should be enforced at all points, and at indicates an inequality should be enforced at one specific value of the independent variable. BPSL also supports case-control comparisons, such as differences between mutant and wild type. Figure 1 illustrates example BPSL statements applicable to a model of FcϵRI signaling.

Figure 1:

Illustration of three statements in BPSL about a model of IgE receptor signaling. This model is adapted from ref. [67] using the published parameterization. The published model is consistent with all three of these BPSL statements

To our best knowledge, BPSL is the first language designed specifically for the definition of qualitative biological data. At present, the main use case is to configure parameterization in PyBioNetFit. More generally, BPSL can be seen as a knowledge engineering tool for formalizing qualitative information about the behavior of a biological system. This type of formalization has other applications, such as verifying that a given model agrees with known system properties (i.e., model checking) and for choosing perturbations of a system to achieve a desired set of properties (i.e., design). We hope that the BPSL standard will be adopted by other software tools beyond PyBioNetFit.

Methods for Uncertainty Quantification

Although the above methods are useful for obtaining a parameterized model consistent with data, one should also ask how well identified are the model parameters and how uncertainty in parameter estimates propagates to uncertainty in model predictions. Such analysis is especially important when considering high-dimensional parameter spaces with limited experimental data. In such a case, we cannot reasonably expect to identify every parameter. Remarkably, one may sometimes be able to identify only some of the parameters and still be able to make reliable predictions, as in the study of Harmon et al. [67].

Profile likelihood

Profile likelihood [68] is a relatively inexpensive method to assess the identifiability of model parameters. In the most commonly used version of this method, one parameter of interest is scanned over a series of fixed values. At each fixed parameter value considered, optimization of the objective function is repeated, allowing the values of all other free parameters to vary. Then the minimum objective function value achieved in optimization is plotted against the fixed parameter value. A smaller objective function value indicates a more likely value for the parameter. Prediction uncertainty can be calculated by an analogous approach [69]. For ODE models, methods are available to calculate profiles by numerical integration instead of repeated optimization [70, 71].

Profile likelihood requires that the objective function is related to a statistical likelihood function, that is, the probability of generating the experimental data given the chosen model and a parameterization. We note that the chi-squared objective function corresponds to the negative log likelihood under the assumption that the measurement errors are drawn from independent Gaussian distributions.

Profile likelihood is useful for efficiently quantifying the identifiability of individual parameters and model predictions. It can be applied to models with high-dimensional parameter spaces for which other methods are not feasible. However, standard profile likelihood analysis, with 1-dimensional parameter scans, does not provide information about relationships between parameters. For example, if a ratio of two parameters is identifiable but neither parameter is identifiable individually, this analysis will simply show both to be unidentifiable. A relationship between two parameter values can be discovered by calculating the value of the likelihood function over the corresponding two-dimensional parameter space [72]. Discovery of relationships in this manner has a cost that increases exponentially with the number of correlated parameter values.

Bootstrapping

Bootstrapping is a method that performs uncertainty quantification by resampling data. It is a useful technique when applicable but should be avoided when parameters are non-identifiable [73, 74].

In bootstrapping, the available dataset is first resampled. Multiple resampling methods are available [75], one example being to choose n points with replacement from an original data set of n points [76]. Then the optimization algorithm is repeated on the resampled data, and the best fit is saved as a bootstrapped parameter set. The procedure is repeated many times to generate a desired number of bootstrapped parameter sets, which are examined (sorted) to determine confidence intervals for each parameter.

The idea is that resampling the data is roughly equivalent to repeating the experiment. Resampling followed by refitting gives what can be thought of as a potential result if both the experiment and optimization were repeated. In the case of a perfect algorithm that always finds a unique global optimum, the result would depend only on the data. However, if optimization is biased (e.g., toward a local minimum near the starting point of optimization), this bias would appear in the bootstrap estimates of confidence intervals.

Bayesian methods

In Bayesian statistics, model parameters are taken to be random variables with unknown probability distributions. In this framework, uncertainty quantification is performed by finding the (multivariate) probability distribution of the parameters Θ given the experimental data y, P(Θ|y). This distribution, called the posterior, is proportional to P(y|Θ)P(Θ). P(y|Θ) can be calculated using a likelihood function—the chi-squared function is equal to — log P(y|Θ) plus a constant when measurement noise is Gaussian—and P(Θ) is a user-defined prior. The distribution P(Θ|y) is estimated using a sampling algorithm. A simple example is the Metropolis-Hastings (MH) Markov Chain Monte Carlo (MCMC) algorithm [77]. MH-MCMC performs well in simple cases, but its efficiency declines for multimodal distributions [78] and high-dimensional parameter spaces [79]. The Gelman-Rubin statistic [80], or a more recent improvement on it [81], can be used to determine when a sufficient number of MCMC samples have been collected.

More sophisticated sampling algorithms are available for cases where MH-MCMC is inefficient. Parallel tempering [78] is a MCMC algorithm designed to improve sampling of multimodal distributions. If gradient information is available for the problem at hand, Hamiltonian Monte Carlo (HMC) [79] is possible. By utilizing gradient information to make moves non-randomly, HMC can be more efficient than MH in high-dimensional parameter spaces [82]. The no U-turn sampler (NUTS) [83] is a particularly useful version of HMC because with this method, algorithmic parameters are selected automatically. HMC can also be improved by choosing a problem-specific distance metric to make sampling more efficient [84].

Bayesian uncertainty quantification tends to be the most computationally intensive of the methods discussed here, but also provides the most complete picture of parametric uncertainty. The algorithm to calculate the multidimensional posterior probability distribution is unbiased by design (aside from the initial choice of a likelihood function and prior). The resulting distribution can be used to determine a credible interval for each parameter (by examining the marginal distribution of the parameter) and to assess correlations between parameters. In addition, it is straightforward to quantify prediction uncertainty of the model by examining simulation outputs for sampled parameter sets. We recommend using Bayesian methods whenever computationally feasible. Such analysis was possible for a rule-derived ODE model of FcϵRI signaling [67] with 16 parameters and 23 equations, for example, but is expected to be more challenging for models with higher dimensional parameter spaces.

Software tools

Most methods we have described have been implemented in recently developed, general-purpose software tools. Although many optimization tools are available, we focus our discussion here on tools that provide direct support for models supplied in standard formats (BNGL or SBML) and built-in support for complete workflows. Such tools are valuable because they enable parameterization and uncertainty quantification without the need for problem-specific coding. These tools help promote reproducible modeling [85, 86], and allow modelers to focus on model analysis rather than debugging code.

Table 1 summarizes the key features of four major software tools that are applicable to problems of interest: PyBioNetFit [12], COPASI [6, 87], Data2Dynamics (D2D) [7], and AMICI/PESTO [8, 9, 10, 11]. All of these tools remain under active development. PyBioNetFit, COPASI, and D2D support complete model parameterization workflows. AMICI is notable for its support for adjoint sensitivity analysis, but must be interfaced via problem-specific code to another package providing optimization functionality, such as the MATLAB package PESTO [11]. Other low-level optimization and uncertainty quantification packages include the Python packages SciPy (https://www.scipy.org/), MEIGO [88], and BayesSB [89] and the R packages MEIGO [88] and dMod [71]. Another package of note is PySB [90], which has support for BNGL and SBML, but, like AMICI, does not contain optimization functionality, except through external dependencies

Table 1:

Summary of usage and features of four major software tools for parameterization and uncertainty quantification of models defined in BNGL or SBML.

	PyBioNetFit	COPASI	Data2Dynamics	AMICI
Installationa	Python package	Downloadable application	MATLAB source code	C++ source code
User Interfaceb	Command-line	GUI or command-line	MATLAB	MATLAB, Python, or C++
BNGL support	✓
SBML support	✓	✓	✓	✓
Gradient-based algorithms		c	✓	d
Adjoint sensitivity				✓
Metaheuristic algorithms	✓	✓	✓
Parallelized algorithms	✓	e	e	e
Optimization using qualitative data	✓
Numerical integration	✓	✓	✓	✓
Stochastic simulation	✓	✓f
Profile likelihood		✓	✓
Bootstrapping	✓
Bayesian methods	✓		✓

^a.PyBioNetFit is installed through the pip package manager. COPASI is a downloadable application that can be run without further configuration. Data2Dynamics is provided as MATLAB source code that can be run using commercial MATLAB software. AMICI is provided as C++ source code that must be compiled after performing machine-specific configuration of dependencies.

^b.PyBioNetFit is run on the command line using text files for configuration. COPASI has a GUI as well as a command line interface. Data2Dynamics provides functions that must be called through MATLAB code. AMICI provides functions that must be called through MATLAB, Python, or C++ code.

^c.COPASI’s gradient-based algorithms use the finite difference approximation, making them less effective than those of other tools.

^d.PESTO has been used in combination with AMICI to enable gradient-based optimization.

^e.These tools enable parallelization to a limited extent. For example, they support multiple independent fitting runs, i.e., multistart optimization. The available algorithms do not support evaluating multiple trial parameter sets in parallel within an individual fitting run.

^f.In addition to Gillespie’s stochastic simulation algorithm, COPASI supports stochastic differential equations.

The four tools considered in Table 1 have different strengths, suitable for different applications. PyBioNetFit is unique in its support for BioNetGen models and simulators, and for including parallelization within its algorithms, making its metaheuristics more efficient than those of other tools, provided that they are run on a cluster or multi-core workstation. COPASI is notable for its ease of installation and user interface while providing many comparable features to other tools. D2D provides forward sensitivity analysis and a MATLAB interface. AMICI is the only tool supporting adjoint sensitivity analysis, but has a more difficult workflow requiring some problem-specific coding.

Outlook

Mathematical models will be increasingly important tools for understanding immunoreceptor signaling. New developments in software, coupled with increasing availability of computing resources, offer new opportunities for robust model parameterization.

Model parameterization using qualitative data is an exciting direction that we hope to see explored more deeply in future work. Use of qualitative data in model parameterization has so far been limited [58, 59, 60, 61, 62, 63, 91, 92, 93]. With the development of general-purpose software designed specifically for the purpose of leveraging qualitative data in model parameterization, namely PyBioNetFit [12], use of qualitative data in modeling has become easier. It should be noted that the approach initially implemented in PyBioNetFit, optimization based on an objective function incorporating static penalty terms, is limited to point estimation of parameter values. A recent extension of PyBioNetFit allows for Bayesian parameter estimation and uncertainty quantification [94].

Another promising direction given increased computational power is the parameterization of spatial models. One such example is a spatial model for receptor tyrosine kinase signaling [95], which was parameterized using problem-specific code. At present, multiple spatial simulators designed for biological applications are well-developed [96, 97] and in the future could be integrated with general-purpose parameterization tools.

These opportunities will enable the development of more detailed models supported by data, providing new means of studying cellular signaling processes.

Highlights.

• Mathematical models include parameters that must be estimated from data.

• New tools including PyBioNetFit and AMICI/PESTO support automated parameter estimation.

• Optimization algorithms can be used to obtain point estimates of parameter values.

• Parameter estimation can incorporate both quantitative and qualitative data.

• Uncertainty quantification assesses confidence in parameter values and model predictions.