Abstract
Objective:
To enable non-invasive dynamic metabolic mapping in rodent model studies of mitochondrial function using 31P-MR spectroscopic imaging (MRSI).
Methods:
We developed a novel method for high-resolution dynamic 31P-MRSI. The method synergistically integrates physics-based models of spectral structures, biochemical modeling of molecular dynamics, and subspace learning to capture spatiospectral variations. Fast data acquisition was achieved using rapid spiral trajectories and sparse sampling of (k, t, T)-space; image reconstruction was accomplished using a low-rank tensor-based framework.
Results:
The proposed method provided high-resolution dynamic metabolic mapping in rat hindlimb at spatial and temporal resolutions of 4×4×2 mm3 and 1.28 s, respectively. This allowed for in vivo mapping of the time-constant of phosphocreatine resynthesis, a well established index of mitochondrial oxidative capacity. Multiple rounds of in vivo experiments were performed to demonstrate reproducibility, and in vitro experiments were used to validate the accuracy of the estimated metabolite maps.
Conclusions:
A new model-based method is proposed to achieve high-resolution dynamic 31P-MRSI. The proposed method’s ability to delineate metabolic heterogeneity was demonstrated in rat hindlimb.
Significance:
Abnormal mitochondrial metabolism is a key cellular dysfunction in many prevalent diseases such as diabetes and heart disease; however, current understanding of mitochondrial function is mostly gained from studies on isolated mitochondria under nonphysiological conditions. The proposed method has the potential to open new avenues of research by allowing in vivo and longitudinal studies of mitochondrial dysfunction in disease development and progression.
Index Terms: Magnetic resonance spectroscopic imaging, subspace models, low rank models, metabolic imaging, mitochondrial oxidative capacity, dynamic phosphorus-31 MRSI
I. Introduction
MITOCHONDRIA play a critical role in biological processes by supplying the energy needed for maintaining tissue viability and functional integrity. Abnormal or altered mitochondrial metabolism has been shown to be a key factor in a wide range of diseases, including diabetes and cardiovascular diseases [1]. To date, our understanding of mitochondrial function is mostly gained from in vitro studies on isolated mitochondria under nonphysiological conditions. Phosphorous-31 magnetic resonance spectroscopic imaging (31P-MRSI) serves as a powerful tool for enabling in vivo quantification of phosphate metabolites such as adenosine-triphosphate (ATP) and phosphocreatine (PCr), which are the chemical currency for almost all of the energy-consuming processes in living organisms. In particular, dynamic 31P-MRSI allows the monitoring of the depletion and resynthesis of PCr during metabolic perturbations such as ischemia/reperfusion or exercise/recovery. During ischemia or exercise, the creatine kinase system buffers intracellular ATP levels at the expense of PCr, leading to the depletion of the PCr pool. During reperfusion or recovery, the resynthesis of PCr is driven primarily by mitochondrial oxidative metabolism. Hence, the rate of PCr resynthesis is a functional biomarker for mitochondrial oxidative capacity [2]. This approach has been shown to be highly reproducible and well correlated with in vitro methods for assessing mitochondrial oxidative capacity [3].
The ability to perform dynamic 31P-MRSI on small animal models is of particular interest because of the prevalence of these models in preclinical research. However, the small subject size and the time scale of PCr resynthesis place stringent requirements on the spatial and temporal resolution needed for dynamic 31P-MRSI studies. Previous studies using rat models have reported an exponential recovery of PCr after its depletion by either ischemia or electrical stimulation, with a time-constant ranging from 30 to 150 s [4]–[6]. Hence, a temporal resolution of less than 15 s is needed to accurately observe the kinetics of PCr during a metabolic perturbation protocol. Furthermore, spatial resolutions on the order of 4 × 4 × 4 mm3 are needed if metabolic heterogeneity in different muscle groups is to be observed. However, due to the inherently low signal-to-noise ratio (SNR) of the 31P signal, dynamic 31P-MRSI methods are typically limited to spatial resolutions above 1 cm3, which is inadequate for small animal imaging. Hence, preclinical studies have been largely limited to nonlocalized or single voxel MRS studies [1].
With the advent of fast MR imaging techniques, several methods have been proposed for accelerated imaging of PCr, ATP, and Pi [7]–[11]. Recently, a subspace-based approach known as SPICE (SPectroscopic Imaging by exploiting spatiospectral CorrElation) has been shown to enable ultrafast proton MRSI with high spatial resolution [12], [13]. In a pilot study, we employed a low-rank tensor model-based extension of SPICE for dynamic 31P-MRSI studies, and demonstrated the feasibility of sub-centimeter spatial resolution with 30 s temporal resolution on rats [14]. Building on this progress, we have developed a new model-based method that incorporates a priori information, such as physics-based models of spectral structure and the kinetic profile of PCr recovery after its depletion, to enable dynamic metabolic mapping in rat hindlimb at spatial, spectral, and temporal resolutions of 4 × 4 × 2 mm3, 0.1 ppm, and 1.28 s, respectively. The accuracy and robustness of metabolic mapping using this method were evaluated in vitro using phantoms, and the reproducibility of metabolic mapping was demonstrated in vivo. Furthermore, the utility of this method for in vivo mapping of the time-constant of PCr resynthesis was demonstrated in stimulation-recovery experiments.
II. Background
A. Dynamic MR Spectroscopic Imaging
Mathematically, the data measured from a dynamic MRSI experiment can be modeled as
| (1) |
where ρ(x, f, T) denotes the dynamic spectroscopic image representing spatial (x), spectral (f) and temporal (T) variations; k represents spatial frequency and t is the conjugate variable of f (distinguished from T by its much shorter time-scale). Conventional MRSI methods sample d(k, t, T) uniformly and use a truncated Fourier series representation of ρ(x, f, T) to reconstruct from the data as
| (2) |
It is well known that if d(k, t, T) is sampled at the Nyquist rate along k and t over a large enough region of (k, t)-space and within a short enough time interval around Tm, then is a good approximation of ρ(x, f, Tm). However, due to various practical constraints on data acquisition (e.g., scan time, signal-to-noise ratio (SNR), and hardware limitations), obtained from Eq. (2) is often of low resolution which significantly limits its practical utility.
B. Subspace Models
Subspace-based models overcome some of the limitations of the Fourier series model by decoupling the spatial, spectral, and temporal sampling requirements. These models take advantage of a mathematical property of dynamic MRSI signals, known as partial separability (PS) [14]–[16], and represent the dynamic spectroscopic image as
| (3) |
where the θm(x), φℓ(f), and ψp(T) are the spatial, spectral, and temporal basis functions; M, L, and P are the respective model orders, and the σm,ℓ,p are the model coefficients.
The PS model, often referred to as a low-rank tensor model, can be justified based on the fact that the object being imaged has a small number of distinct MR-visible molecules. With proper selection of θm(x), φℓ(f), the spatial and spectral distributions of these molecules are in the spaces spanned by {φℓ(f)} and {θm(x)}, respectively. The temporal changes of the spatiospectral distributions are often due to tissue-level effects of metabolic processes, such as oxidative phosphorylation, and can also be captured by the temporal basis {ψp(T)} [14]–[16]. An important advantage of the model is the significant reduction in the degrees of freedom (DOF) as compared with the truncated Fourier series image representation. This provides greater flexibility in data acquisition and image reconstruction, which is described in the subsequent section.
III. Methods
A. Image Model
In this work, we propose to model the dynamic spectroscopic image as the sum of PS signals from the MRI-observable phosphate molecules, e.g., ATP, PCr and inorganic phosphate (Pi):
| (4) |
where M is the number of MRI-observable molecules, cm,ℓ,p(x) are spatially varying combination coefficients for each molecule, rm(x) is a reference image used to incorporate a priori knowledge of the spatial variations of the molecular signals; Lm and Pm are the spectral and temporal model orders of each molecule. Mathematically, this model is equivalent to (3) given proper selection of the model coefficients and spatial basis functions; however, by combining the model coefficients and spatial basis functions into cm,ℓ,p(x), it reduces the DOF in the image representation and enables the incorporation of molecule-specific reference images rm(x) for imposing high-resolution spatial support and distribution priors.
The explicit molecular decomposition also makes it easier to incorporate physics- and biochemistry-based a priori information into the model. For example, a priori information about the subspace structures of each molecule can be easily incorporated into the model in image reconstruction. Such information can be obtained from literature and quantum-mechanical simulations. In this work, we incorporated a priori information about the spectral structure of each molecule via the following constraint on the spectral basis functions
| (5) |
where Ωm is the set of relaxation time-constants and resonance frequencies for the mth molecule [17]–[19]. Further, to exploit the exponential behavior of PCr recovery [1], [3], [4], [20], [21], we also constrained the temporal basis functions as
| (6) |
where Γm is the set of recovery time-constants and start-times for the mth molecule, and u(T) is the unit step function. The incorporation of these biochemistry-based constraints leads to higher-SNR estimates of the spectral and temporal basis functions which, combined with the reduction in DOF provided by the model and the incorporation of rm(x), enabled additional acceleration.
Compared to the Fourier-based representation, (4) can reduce the DOF by one to two orders of magnitude. A typical dynamic 31P-MRSI experiment with a duration of 5 min, a temporal resolution of 10 s, and a spectral resolution of 0.1 ppm acquires 30 and 350 points along the temporal and spectral dimensions, respectively. For a spatial matrix size of 8×8×8, Fourier-based reconstruction entails 5.4×106 DOF, while the proposed molecule-based subspace model needs only 1.3 × 104 DOF. This 400-fold reduction in DOF is a result of the inherent low-dimensionality of 31P-MRSI signals. In 31P-MRSI of skeletal muscle, the spectra are dominated by signals from PCr, ATP and Pi, so an M of 3 is sufficient for describing features of the phosphate metabolites. Furthermore, the spectral and temporal model orders are typically much smaller than the number of samples acquired along the respective dimensions [12], [14], [19], [22]–[28]. Specifically, because of the simple structure of 31P spectra, 1 to 2 spectral basis function(s) can be sufficient to represent each molecule (i.e., Lm = 1 or 2 for each molecule). In addition, because cellular ATP levels are relatively constant and the temporal dynamics of PCr and Pi are only expected to vary between muscle groups, the temporal model order may also be very small; ATP will need one or two basis functions to capture its temporal dynamics, and PCr and Pi only 3 or 4 (i.e. Pm = 1 to 2 for ATP, and 3 to 4 for PCr and Pi).
B. Data Acquisition
The proposed model enables the use of special data acquisition schemes that sparsely sample (k, t, T)-space to achieve the high spatiotemporal resolution needed to image mitochondrial oxidative capacity in rat hindlimb during stimulation-recovery experiments. The acquisition scheme developed in this study is illustrated in Fig. 1. At the start of each experiment, electrical stimulation was used to induce muscle contractions and deplete PCr levels. Once PCr was depleted, spectral subspace training data were acquired using a 3D chemical shift imaging (CSI) sequence [9]. A proton reference image and field map were also acquired for determining rm(x) and B0 field inhomogeneities using a fast low angle shot (FLASH) sequence [29]. Following these acquisitions, stimulation was stopped and the dynamic imaging data acquisition was started immediately to capture the kinetics of PCr recovery using a repeated 3D stack-of-spirals-CSI acquisition. At the end of the recovery period additional spectral subspace training data and proton reference and field map scans were acquired. Lastly, these scans were followed by the acquisition of a higher resolution proton reference scan, used for manual segmentation of muscle groups.
Fig. 1.
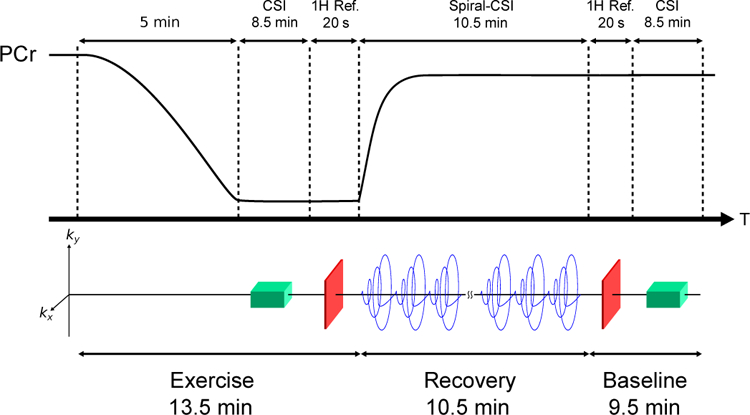
Schematic of the in vivo exercise-recovery protocol. Electrical stimulation was used to induce muscle contractions and deplete PCr levels. Following 5 min of stimulation, spectral subspace training data were acquired using a CSI sequence, which was followed by a proton reference scan, a spiral-CSI dynamic imaging scan, and another set of proton reference and CSI scans. The start of the spiral-CSI acquisition corresponded with the ending of electrical stimulation.
We acquired the spiral-CSI scan with the following parameters: field of view (FOV) = 24 × 24 × 16 mm3, matrix size = 6 × 6 × 8, repetition/echo time (TR/TE) = 160/0.69 ms, readout bandwidth = 27.8 kHz, flip angle = 17°, number of preparation pulses = 100. The spiral acquisition sampled the entire (kx, ky)-plane with a single readout in 3.78 ms. A total of 20 spiral readouts were acquired during each TR. Therefore, the total time for a single spiral-CSI acquisition, i.e., the frame-rate, was 1.28 s. To capture the kinetics of metabolite changes during recovery, 450 repetitions of spiral-CSI data were acquired. In addition, non-localized navigators were acquired every 50 repetitions to monitor gradient-heating induced frequency drift [30]. Each navigator was acquired with 40 signal averages. The total acquisition time for dynamic imaging data was 10.7 min.
The CSI sequence for acquiring spectral subspace training data used a matrix size of 8×8×6. For each readout, 8 averages were acquired with 512 readout points and a bandwidth of 6 kHz. The total acquisition time was 8.5 min. FOV, TR, TE, and flip angle were the same as that of the spiral-CSI acquisition.
The temporal subspace training dataset consisted of 23 non-localized dynamic spectra acquired with a 2 s frame-rate from 14 healthy rats in an existing depletion-recovery study that had similar molecular dynamics [4].
The parameters of the first two proton reference scans were: FOV = 48×48×16 mm3, matrix size = 64×64, 8 slices, 2 mm slice thickness, readout bandwidth = 50 kHz; TR/TE1/TE2 = 100/4.1/4.6 ms, flip angle = 20°, number of preparation pulses = 10, and number of averages = 2. The parameters of the third, higher-resolution proton reference scan were the same except that TR/TE = 200/5.4 ms, matrix size = 256 × 256, slice thickness = 1 mm, and the number of averages was 16.
C. Image Reconstruction
Image reconstruction was performed in two phases: subspace estimation and coefficient estimation. In the first phase, the spectral subspace training data acquired both before and after recovery were corrected for field inhomogeneity and then fitted to the model in (5) using a nonlinear method [31]. The spectral subspace of each molecule was then learned by arranging the molecular spectra from individual voxels into a Casorati matrix and performing a singular value decomposition (SVD). The spectral model orders were determined from an analysis of the singular value decay curves.
The temporal subspace was learned from the temporal subspace training data using a similar procedure. After correction for field-inhomogeneity, the molecular concentration time-curves were obtained from spectral quantification and fitted to the model in (6) using a non-linear least-squares algorithm [32]. The temporal subspace of each molecule was obtained by performing an SVD of the Casorati matrix formed from the fitted molecular time-curves.
With estimates of the spectral and temporal basis functions, the dynamic imaging data were then used to estimate the model’s combination coefficients, i.e. cm,ℓ,p(x) in (4), by solving the following regularized least-squares fit of the data to the model
| (7) |
where d is the vector of dynamic imaging data, is the Fourier encoding operator corresponding to (1) but with the effect of B0 field inhomogeneity included; rm and cm,ℓ,p are vectors corresponding to rm(x) and cm,ℓ,p(x) the spatial grid of the reconstruction; φm,ℓ and ψm,p are the learned spectral and temporal basis vectors (corresponding to φm,ℓ(f) and ψm,p(T)); R is a regularization functional, and λ is an empirically determined regularization parameter. The symbols ○ and ꕕ denote the element-wise and outer products, respectively. In the current work, the same proton reference image was used as the rm for each molecule.
The high-dimensionality of the dynamic spectroscopic image makes solving (7) computationally challenging. Therefore, an approximate solution to (7) was efficiently computed using a two-step procedure. First, frame-by-frame estimation of time-varying spatial coefficients, bm,ℓ(x, T), was performed by solving
| (8) |
for all k, where d(k) is the data from the kth time-frame. Then, denoting by , and the array of by , the {cm,ℓ,p} were computed by solving
| (9) |
for each combination of m and ℓ.
In this work, R1 and R2 were chosen to be of the form
| (10) |
where is a weighted spatial difference operator with weights w determined from a priori edge information obtained from the proton reference scans [12], [33]. λ1 and λ2 were chosen empirically to provide the best tradeoff between SNR enhancement and spatial blurring.
We note that when no temporal training data or pre-learned temporal subspaces are available, a set of low-SNR frame-by-frame reconstructions can be generated using the as
| (11) |
where is the reconstruction of the kth frame. These frame-by-frame reconstructions can then be used to estimate a temporal subspace, albeit with lower SNR.
D. Spectral Quantification
Following the approach described in [19], we quantified time-varying molecular concentrations from the spectral basis coefficients at different time points. By rewriting (4) as
| (12) |
with
| (13) |
it can be seen that am,ℓ(x, T) are the spectral basis coefficients for molecule m at time T. We used the am,ℓ(x, T) to obtain the square-root of molecular signal energy, a common molecular concentration index; with {φm,ℓ(f)} constrained to be orthogonal, the mth molecule’s dynamic concentration map was computed as .
E. In Vivo Experimental Protocol
To validate the proposed method under realistic in vivo conditions, we performed experiments on adult male Sprague-Dawley rats in accordance with approved institutional IACUC guidelines. At the start of each experiment the animals were anesthetized with isoflurane and placed laterally in a Bruker Avance II 9.4 T horizontal scanner (Bruker Biospin Inc., Billerica, MA). The hindlimb was secured in a custom-built 15-mm 31P saddle coil placed within a 1H volume coil and positioned at the isocenter of the scanner. Respiration rate and body temperature were monitored during the experiments. The respiratory rate was maintained between 45 and 60 breaths per minute by manually adjusting the anesthesia level. Body temperature was maintained at 35 to 37°C via a feedback control system (SA Instruments, Stony Brook, NY, USA). Three rats underwent electrical stimulation, in which two needle electrodes were placed subcutaneously over the third lumbar vertebrae and the greater trochanter, respectively. Muscle contraction was induced by applying square wave pulses with a 15-V amplitude and 2-ms pulse duration at a rate of 2 Hz [34]. A control experiment was performed on one rat without electrical stimulation.
To evaluate the reproducibility of our measurements, two identical rounds of experiments were performed on each animal following the protocol described above and with an approximately 20 min rest period between each round.
F. In Vitro Experimental Protocol
We performed an in vitro experiment to directly validate the reproducibility of our high-resolution metabolic mapping approach in a static phantom. Data were acquired from a two-compartment phantom containing phosphate metabolites at physiological concentrations (PCr, 10 and 30 mM; ATP, 10 mM; and Pi, 5 and 10 mM). All acquisition parameters were the same as those in in vivo experiments, except for the spiral-CSI acquisition which was acquired at a slightly higher resolution (matrix size = 8 × 8 × 8) and only 64 repetitions (82 s acquisition time).
IV. Results
A. In Vivo Dynamic Metabolic Mapping in Rat Hindlimb
Figure 2 shows the reconstructed dynamic MRSI data from one round of stimulation-recovery. The nominal resolutions in the spatial, spectral, and temporal dimensions were 4 × 4 × 2 mm3, 0.1 ppm, and 1.28 s, respectively. During the recovery period, the PCr concentration showed exponential recovery kinetics accompanied by a rapid decrease in Pi levels, while ATP levels remained relatively constant, as reported in the literature [4]–[6], [35].
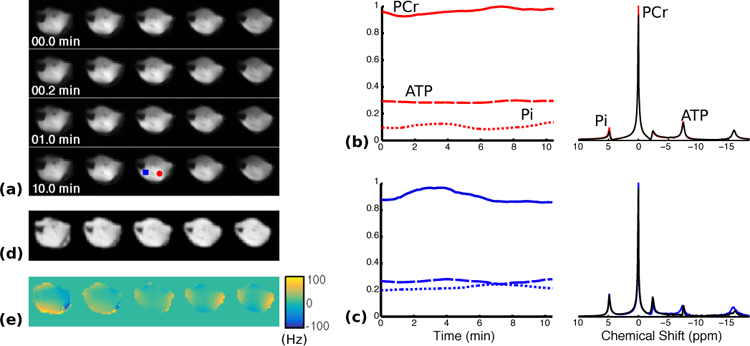
Fig. 2.
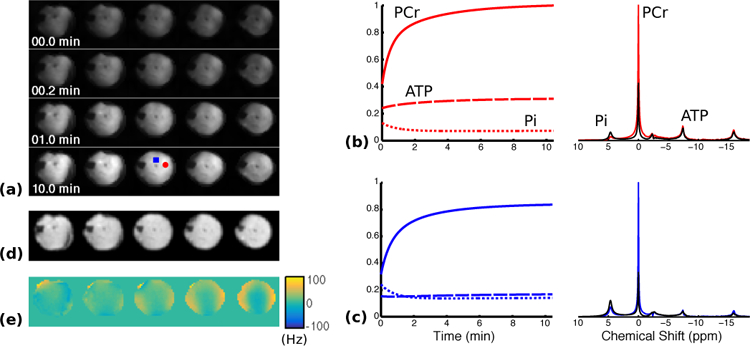
Reconstruction of dynamic MRSI data from rat hindlimb during stimulation-recovery. (a) Changes in baseline-normalized PCr concentration in the central five slices during the recovery period. (b-c) Normalized metabolite concentration curves (left) as well as selected spectra (right) from the first (black) and last (colored) time points in the reconstruction. The locations of the selected voxels are indicated by the color-coded markers (red circle and blue square, respectively) shown in the last row of (a). (d-e) Anatomical reference image and the B0 field inhomogeneity map, respectively, acquired immediately after the PCr recovery.
By fitting the PCr concentration dynamics to an exponential function, we generated time-constant maps of the PCr resynthesis from each round of stimulation-recovery. Figure 3(a) shows these time-constant maps overlaid on anatomical reference images of the hindlimb. Figure 3(b) shows the mean and the standard deviation of the time-constants in four manually-segmented regions of interest (ROIs), and Fig. 3(c) shows the voxel-wise comparison of the measured time-constants in the two rounds. The estimated time-constants were in agreement with values reported in the literature [4]–[6], [20]. Furthermore, the variations in the recovery time-constants among different ROIs were also in agreement with an existing study on humans [7]. In particular, the posterior tibialis and flexor digitorum longus muscles (ROI #1) and the gastrocnemius (ROI #2) showed relatively fast PCr recovery after electrical stimulation in both rounds, while the time-constants of the anterior tibialis, extensor digitorum longus (ROI #3), soleus, peroneus and plantaris (ROI #4) were longer and approximately the same. The time-constants were noticeably reduced in the second round, especially for regions 3 and 4 (Fig. 3(c)); however, the relative variations among the regions were preserved. A paired t-test with unequal variances suggested that the shortening of the time-constants in each region was statistically significant (p < 0.05).
Fig. 3.
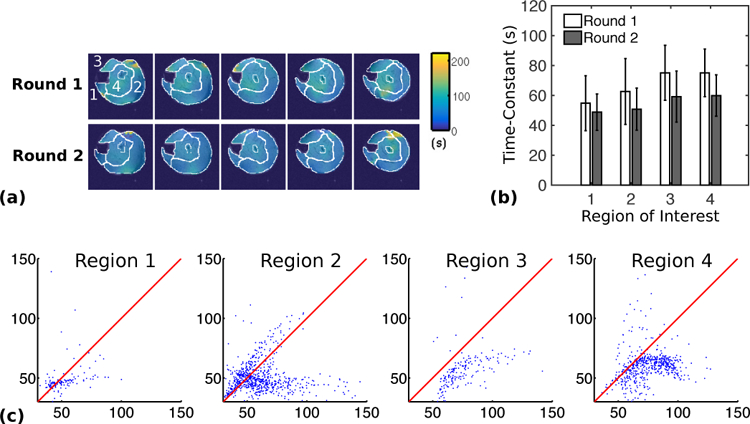
Estimated PCr resynthesis time-constant maps and regional averages from two rounds of stimulation-recovery experiments performed on the same animal with a 20 min interval between experiments. (a) Time-constant maps overlaid onto anatomical reference images from the two rounds of in vivo experiments. (b) The mean PCr resynthesis time-constants in the ROIs indicated in (a). The error bars indicate the standard deviation. All changes were statistically significant (p ≤ 0.05). The regions roughly consisted of: (1) the posterior tibialis and flexor digitorum longus, (2) the gastrocnemius, (3) the anterior tibialis and extensor digitorum longus, and (4) the soleus, peroneus, and plantaris. (c) Voxel-wise comparison of the time constants from the two rounds. Horizontal and vertical axes in the correlation plots show the time constants from the first and second rounds, respectively. The red line in each plot indicates the line of identity.
To evaluate the reproducibility of our approach, we compared the estimated metabolite distributions from each round. Figure 4 shows a comparison between snapshots of the dynamic PCr concentration maps over the recovery period. The maps from the two rounds are visually similar, suggesting that the dynamic PCr concentrations are consistent and reproducible. This is further demonstrated in correlation plots of the PCr concentration from voxels in the hindlimb region. The same plots for the background, noise-only region show minimum correlation, implying the proposed method did not introduce significant bias. A side-by side video comparison of the PCr, and Pi concentration distributions over time is also provided which further indicates a high degree of reproducibility (Fig. S1).
Fig. 4.
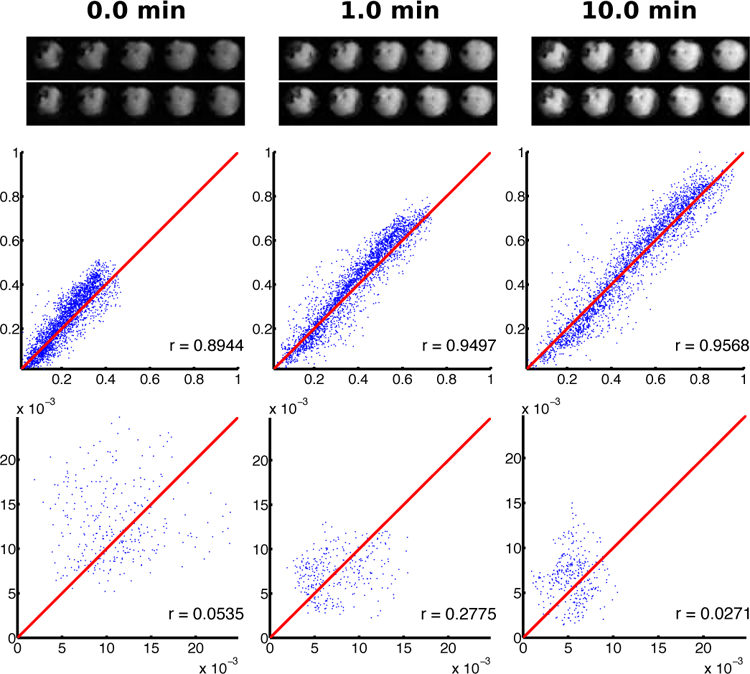
Reproducibility of dynamic metabolite maps from two rounds of stimulation-recovery experiments performed on the same animal. The two rows of images are the PCr distributions at different time-frames from the first (top) and second (bottom) rounds. The correlation plots of the PCr distributions from the leg (middle) and background (bottom) regions are provided below the respective images. The times of each frame are provided at the top of each column. Horizontal and vertical axes in the correlation plots show the normalized concentrations from the first and second rounds, respectively. The red line in each plot indicates the line of identity. Correlation coefficients are given in the lower right corner of each plot.
Figure 5 shows a comparison of metabolite concentrations produced by averaging frame-by-frame reconstructions (11) from data acquired during the end of each recovery period. The results again suggest that the distributions of PCr, ATP, and Pi concentrations at the end of each recovery period are highly correlated, supporting reproducibility. Furthermore, a comparison of the plots in the Figs. 4 and 5 indicates that the proposed dynamic reconstruction actually provides better reproducibility at a frame-rate of 1.28 s than the single time-frame reconstruction generated from data acquired over a longer period. This is because the molecule-based subspace model effectively exploits the spatiospectral-temporal correlations in the high-dimensional data to provide higher quality reconstructions.
Fig. 5.
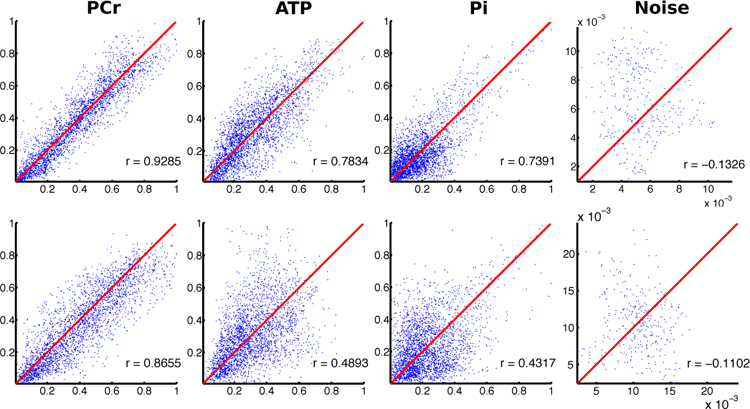
Reproducibility of metabolite maps obtained from static reconstructions of the data in Fig. 4. Correlation plots of metabolite maps were obtained by averaging frame-by-frame reconstructions (see Image Reconstruction) of the last 64 (top row) and 16 frames (bottom row), corresponding to the last 82 s and 20 s of data acquisition, respectively. The plot layouts are the same as in Fig. 4.
As a control, we evaluated the kinetic changes of phosphorous metabolites during two rounds of in vivo experiments performed without electrical stimulation but with data acquisition kept the same. Because the molecular dynamics in the control experiment were expected to be negligible, the exponential model constraint in (6) and the temporal subspace training data used for the stimulation-recovery experiment were inappropriate for the reconstruction of the control data. Instead we took advantage of the high frame-rate of our spiral-CSI data and estimated the temporal subspace from the initial frame-by-frame reconstructions of the molecular signals (11). To improve the SNR of the estimated basis functions a temporal smoothness prior was employed during subspace estimation instead of the exponential model constraint in (6). As expected, the reconstruction exhibited relatively constant levels of all three phosphate metabolites in the absence of electrical stimulation (Fig. 6). Further, the reconstructed metabolite maps from two rounds of data acquisition also showed a high degree of correlation, suggesting reproducibility (Fig. S2).
Fig. 6.
Reconstruction of dynamic MRSI data from rat hindlimb data acquired from control experiments. The experimental protocol and acquisition were the same as the stimulation-recovery experiment, except that no stimulation was used. The layout is the same as that of Fig. 2.
It may be noted that the reconstructed metabolic concentrations from the control data showed larger variability compared to those from stimulation/recovery data. This is due to the lack of appropriate temporal subspace constraints and training data. To compare these two different basis learning methods, we also reconstructed the dynamic data using the same temporal subspace estimation method that was used to reconstruct the control data (Fig. S3). A comparison of Fig. S3 to Fig. 2 shows that, while the trend of molecular time courses were similar, there is greater variability in the reconstruction generated without using the biochemical-based constraints of (6), especially in lower-SNR metabolites such as ATP and Pi.
Lastly, to demonstrate the effect of incorporating the reference image rm(x) into the model, we generated two additional reconstructions: one without using rm(x) (Fig. S4), and another without using either rm(x) or reference image-derived edge weights (Fig. S5). A comparison of these figures to Fig. 2 suggests that the incorporation of higher-resolution support and edge constraints through the reference image led to improved resolution and SNR.
B. In Vitro Evaluation
Our in vivo results indicate that high-resolution metabolic maps can be generated from data acquired in less than 90 s (Fig. 5, top row), and our in vitro results further validate this capability. Figure S6 shows the metabolite maps and representative localized spectra from an 82-s phantom acquisition with a nominal spatial resolution of 3 × 3 × 2 mm3. Calculated metabolite ratios were in strong agreement with ground truth values. The normalized mean concentrations (±standard deviation) of the two vials were: 1.0 ± 0.2:0.4 ± 0.1 (PCr), 1.0 ± 0.2:0.9±0.2 (ATP), 1.0±0.5:1.5±0.6 (Pi), and the respective ground truth values were: 1:0.33, 1:1, and 1:2.
We compared our reconstruction to a reconstruction of the CSI data acquired for spectral subspace estimation and interpolated to the same grid size. To improve SNR and better match the PCr line-width, a 15-Hz exponential filter was applied to the CSI reconstruction. Fig. S6(b) shows spectra from the reconstructed CSI data superimposed on the corresponding spectra from our reconstruction. Our reconstruction showed better quantitative agreement with the ground truth, especially for Pi quantification.
V. Discussion
Motivated by the success of PS-based methods for accelerating proton MRSI [12], [14], [19], [22] and dynamic MRI [23]–[28], we developed a PS-based dynamic 31P-MRSI method suitable for evaluating the heterogeneity of mitochondrial oxidative capacity in popular rodent models of disease. The key feature of our method is its use of a novel molecule-based subspace image model. By representing the dynamic spectroscopic image as a linear combination of signals from MR-observable molecules, the model allowed us to take advantage of readily available physical and biochemical information and provided a greater reduction of the DOF in the image representation than existing PS-based methods. This DOF reduction enabled the use of a specialized data acquisition strategy that sparsely sampled (k, t, T)-space and provided the high spatiotemporal resolutions needed for delineating metabolic heterogeneity in rat hindlimb.
An important component of our dynamic MRSI reconstruction method was the use of pre-learned spectral and temporal subspaces. There are many ways in which these subspaces can be obtained. In this study the spectral subspace was learned from CSI training data acquired directly from each individual animal during the experiments, while the temporal subspace was learned from MRS data acquired from a previous study [4] (since acquiring temporal subspace training data entails repeated stimulation-recovery and may alter the kinetics of PCr recovery, as suggested by our current data). In general, the subspace training data does not need to be acquired together with the imaging data. Subspaces can be obtained directly from learned distributions of basis function parameters [19] which can be learned from different subject populations (i.e. diseased and healthy) using a variety of acquisition schemes and imaging modalities. Hence, there is great flexibility in the design of experimental protocols. For large cohort studies, it is also possible to learn the molecular subspaces from only a subset of the subjects in each population, allowing for considerable reduction in the total acquisition time.
One limitation of the current method is that it leads to a bias in the estimation of the chemical shift of Pi, an indicator of intracellular pH [1], [4]. To capture the changes in both the amplitude and the resonance frequency of Pi during stimulation and recovery, the subspace of Pi needs to be learned from training data acquired both during electrical stimulation and recovery. Hence, we designed our data acquisition protocol to acquire two spectral training datasets, one at the end of electrical stimulation and one at the end of the recovery period. However, since the Pi signal was significantly higher at the end of stimulation, the derived basis functions were dominated by a Pi peak with a chemical shift representative of the end-stimulation stage. As a result, the rapid decrease in Pi at the initial phase of recovery was not accompanied by the expected increase in the chemical shift of the Pi (Fig. 2(b–c)). Obtaining molecular spectral subspaces from learned distributions of basis function parameters for robust estimation of changes in chemical shift will be a direction of future work.
Another area for future development is the selection of the reference image. While the incorporation of rm(x) into the model significantly reduced background noise and provided improved resolution, our in vivo results indicated that the dynamics of low-SNR metabolites, such as Pi, appeared to be in better agreement with literature results when rm(x) was excluded from the model. The cause of this result is unclear; however, it may be related to the sensitivity of our reconstruction with respect to correct registration of the proton reference image and the spiral-CSI data. If this is the case, other methods for incorporating high-resolution support information, such as weighted Tikhonov regularization, may be more robust to this type of mis-registration.
An interesting observation, enabled by the high resolution of our current method, was a significant decrease in the PCr resynthesis time-constant after the second round of electrical stimulation. Since the time-constant was quantified from the kinetics of PCr recovery, this decrease was unlikely caused by frequency drift. The voxelwise comparison of Fig. 3(c) suggests that the increase is more pronounced in regions 3 and 4. Previously, we used magnetization-transfer 31P-MRS (MT-MRS) and 31P magnetic resonance fingerprinting (31P-MRF) to quantify the effect of ischemia-reperfusion on the creatine kinase rate constant [36]. Both MT-MRS and 31P-MRF reported an increase in the creatine kinase rate constant after two rounds of transient ischemia-reperfusion protocol. Our current finding of shortened PCr recovery seems to be consistent with our previous observation in ischemia-reperfusion. Together, these results suggest a “preconditioning” effect induced by metabolic perturbations resulting in a transient imbalance in energy production and utilization. The mechanisms and the relationship between the duration of metabolic perturbation on subsequent changes in creatine kinase kinetics need further investigation.
While this study was focused on metabolite and mitochondrial oxidative capacity mapping in rat hindlimb using 31P-MRSI, the imaging framework can be readily extended to MRSI of other organs and even other nuclei. Although in skeletal muscle, low SNR metabolites such as PME and PDE [37], [38] can be excluded from the model without compromising the accuracy of measuring PCr dynamics, their inclusion will make the method well suited for metabolic mapping in the brain or liver. The methodology developed in the current study is also highly translatable to hyperpolarized 13C studies, since 13C spectra acquired from tissue metabolizing 13C-enriched substrate also have simple spectral structures, wide chemical shift dispersion, and immunity to water and lipid contamination. Preliminary studies of performing static 13C-MRSI using similar subspace-based models have already demonstrated the impressive capabilities of these types of models [39].
Like all MRSI methods, the current method is susceptible to intrascan motion and variations in B0 field inhomogeneity. These non-ideal experimental conditions result in spatial leakage artefacts and spectral peak broadening thereby leading to reduced SNR. Because the combination of high spatial, and temporal resolutions needed for imaging mitochondrial oxidative capacity necessitates relatively high gradient duty cycles compared to conventional MRSI methods, such as chemical shift imaging (CSI), field drift caused by excessive gradient heating [30] can be problematic on MR scanners with less efficient gradient cooling systems. Gradient heating is therefore an important factor to be considered during sequence design. The choice of readout gradient is a trade-off between maintaining scanner stability and achieving adequate spatial resolution. In a preliminary investigation of this trade-off, we monitored intrascan variations in temperature and field inhomogeneity using a temperature sensor attached to the center of the scanner bore wall and frequency drift navigators [30] interleaved into our dynamic acquisition. We found that improving the in-plane resolution of our dynamic acquisition to 1.5×1.5 mm2 resulted in significant intrascan temperature increases (15–20° C) and frequency drift (10–15 Hz) during a 10 minute acquisition on our scanner. This led us to use the current spiral trajectory which had a lower gradient duty cycle. We expect that implementing this method on the new generation of MRI scanners with more efficient gradient cooling will lead to further improved spatial resolution.
In addition to using interleaved navigators for tracking frequency drift, it is also possible to use dynamic imaging to track changes in subject motion and spatially-dependent B0 field variations. Reference images and field maps obtained for each time-frame could easily be incorporated into the first step of our reconstruction algorithm and therefore improve the method’s robustness to both intrascan motion and B0 field variation. This increased robustness would allow us to provide reproducible dynamic reconstructions at even higher spatial resolutions. The use of a dual-tuned 31P/1H coil could potentially allow 1H reference scans to be interleaved into the dynamic acquisition. These scans could then be used for dynamic mapping of both rm(x) and B0 field maps. Improved gradient systems of state-of-the-art preclinical scanners may also significantly reduce gradient heating, and improvements in coil design as well as multichannel acquisition may provide additional SNR.
VI. Conclusions
We have developed a novel 31P-MRSI method that enables dynamic mapping of phosphorous metabolites in preclinical rodent models, providing spatial, spectral, and temporal resolutions of 4 × 4 × 2 mm3, 0.1 ppm, and 1.28 s, respectively. This new capability has been evaluated using both phantom and in vivo experiments and may offer new opportunities for gaining mechanistic understandings of metabolic function, disease progression, and treatment efficacy. The ability to observe heterogeneity in metabolic function may also pave the way towards early disease detection since metabolic changes frequently occur long before the manifestation of microscopic and macroscopic structural changes.
Supplementary Material
Acknowledgments
This work was supported in part by the National Institutes of Health (R01EB023704 and R21EB021013) and the UIUC Yang Award.
Contributor Information
Bryan Clifford, Department of Electrical and Computer Engineering and the Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign.
Yuning Gu, Department of Biomedical Engineering and the Case Center for Imaging Research, Case Western Reserve University.
Yuchi Liu, Department of Biomedical Engineering and the Case Center for Imaging Research, Case Western Reserve University.
Kihwan Kim, Department of Biomedical Engineering and the Case Center for Imaging Research, Case Western Reserve University.
Sherry Huang, Department of Biomedical Engineering and the Case Center for Imaging Research, Case Western Reserve University.
Yudu Li, Department of Electrical and Computer Engineering and the Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign.
Fan Lam, Department of Bioengineering and the Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign.
Zhi-Pei Liang, Department of Electrical and Computer Engineering and the Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL 61801 USA.
Xin Yu, Departments of Biomedical Engineering, Radiology, and Physiology and Biophysics, as well as the Case Center for Imaging Research, Case Western Reserve University, Cleveland, OH 44106-7207 USA.
References
- [1].Liu Y, Gu Y, and Yu X, “Assessing tissue metabolism by phosphorous-31 magnetic resonance spectroscopy and imaging: A methodology review,” Quant Imag Med Surg, vol. 7, pp. 707–716, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Paganini AT, Foley JM, and Meyer RA, “Linear dependence of muscle phosphocreatine kinetics on oxidative capacity,” Am J Phys, vol. 272, pp. C501–C510, 1997. [DOI] [PubMed] [Google Scholar]
- [3].Lanza I et al. , “In vivo ATP production during free-flow and ischaemic muscle contractions in humans,” J Physiol, vol. 577, pp. 353–367, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Liu Y et al. , “Mitochondrial function assessed by 31P MRS and BOLD MRI in non-obese type 2 diabetic rats,” Phys Rep, vol. 4, p. e12890, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Macia M et al. , “Insulin resistance is not associated with an impaired mitochondrial function in contracting gastrocnemius muscle of gotokakizaki diabetic rats in vivo,” PLoS One, vol. 10, p. e0129579, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Forbes SC et al. , “Phosphocreatine recovery kinetics following low- and high-intensity exercise in human triceps surae and rat posterior hindlimb muscles,” AJP: Reg Int Comp Phys, vol. 296, pp. R161–R170, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Forbes SC et al. , “Comparison of oxidative capacity among leg muscles in humans using gated 31P 2-D chemical shift imaging,” NMR Biomed, vol. 22, pp. 1063–1071, 2009. [DOI] [PubMed] [Google Scholar]
- [8].Greenman RL, Wang X, and Smithline HA, “Simultaneous acquisition of phosphocreatine and inorganic phosphate images for Pi:PCr ratio mapping using a RARE sequence with chemically selective interleaving,” Magn Reson Imag, vol. 29, pp. 1138–1144, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Brown R, Khegai O, and Parasoglou P, “Magnetic resonance imaging of phosphocreatine and determination of BOLD kinetics in lower extremity muscles using a dual-frequency coil array,” Sci Rep, vol. 6, pp. 1–8, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Schmid AI et al. , “Dynamic PCr and pH imaging of human calf muscles during exercise and recovery using 31P gradient-echo MRI at 7 tesla,” Magn Reson Med, vol. 75, pp. 2324–2331, 2016. [DOI] [PubMed] [Google Scholar]
- [11].Valkovic L et al. , “Dynamic 31PMRSI using spiral spectroscopic imaging can map mitochondrial capacity in muscles of the human calf during plantar flexion exercise at 7T,” NMR Biomed, vol. 29, pp. 1825–1834, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Lam F et al. , “High-resolution 1H-MRSI of the brain using SPICE: Data acquisition and image reconstruction,” Magn Reson Med, vol. 76, pp. 1059–1070, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Ma C et al. , “High-resolution 1H-MRSI of the brain using short-TE SPICE,” Magn Reson Med, vol. 77, pp. 467–479, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Ma C et al. , “High-resolution dynamic 31P-MRSI using a low-rank tensor model,” Magn Reson Med, vol. 78, pp. 419–428, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Liang Z-P, “Spatiotemporal imaging with partially separable functions,” in Proc IEEE Int Symp on Biomed Imag, Arlington, VA, USA, 2007, pp. 988–991. [Google Scholar]
- [16].Lam F, Ma C, and Liang Z-P, “Performance analysis of denoising with low-rank and sparsity constraints,” in 2013 IEEE 10th Intl Symp Biomed Imag, 2013, pp. 1211–1214. [Google Scholar]
- [17].Soher BJ et al. , “GAVA: Spectral simulation for in vivo MRS applications,” J Magn Reson, vol. 185, pp. 291–299, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Ning Q et al. , “Removal of nuisance signal from sparsely sampled 1H-MRSI data using physics-based spectral bases,” in Proc Int Symp Magn Reson Med, Singapore, 2016, p. 2361. [Google Scholar]
- [19].Li Y et al. , “A subspace approach to spectral quantification for MR spectroscopic imaging,” IEEE Trans Biomed Eng, vol. 64, pp. 2486–2489, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Morikawa S, Kido C, and Inubushi T, “Observation of rat hind limb skeletal muscle during arterial occlusion and reperfusion by 31P MRS and 1H MRI,” Magn Reson Imag, vol. 9, pp. 269–274, 1991. [DOI] [PubMed] [Google Scholar]
- [21].Prompers JJ et al. , “Dynamic MRS and MRI of skeletal muscle function and biomechanics,” NMR Biomed, vol. 19, pp. 927–953, 2006. [DOI] [PubMed] [Google Scholar]
- [22].Peng X et al. , “Simultaneous QSM and metabolic imaging of the brain using SPICE,” Magn Res Med, vol. 79, pp. 13–21, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Christodoulou AG, Kellman P, and Liang Z-P, “Accelerating cardiovascular magnetic resonance imaging: Signal processing meets nuclear spins [life sciences],” IEEE Signal Process Mag, vol. 31, pp. 138–143, 2014. [Google Scholar]
- [24].Zhao B et al. , “Accelerated MR parameter mapping with low-rank and sparsity constraints,” Magn Reson Med, vol. 74, pp. 489–498, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Fu M et al. , “High-frame-rate full-vocal-tract 3D dynamic speech imaging,” Magn Reson Med, vol. 77, pp. 1619–1629, 2017. [DOI] [PubMed] [Google Scholar]
- [26].He J et al. , “Accelerated high-dimensional MR imaging with sparse sampling using low-rank tensors,” IEEE Trans Med Imag, vol. 35, pp. 2119–2129, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Christodoulou AG et al. , “Fast dynamic electron paramagnetic resonance (EPR) oxygen imaging using low-rank tensors,” J Magn Reson, vol. 270, pp. 176–182, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Christodoulou AG et al. , “Magnetic resonance multitasking for motion-resolved quantitative cardiovascular imaging,” Nat Biomed Eng, vol. 2, pp. 215–226, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Haase A et al. , “FLASH imaging. rapid NMR imaging using low flip-angle pulses,” J Magn Reson, vol. 67, pp. 258–266, 1986. [DOI] [PubMed] [Google Scholar]
- [30].Ebel A and Maudsley AA, “Detection and correction of frequency instabilities for volumetric 1H echo-planar spectroscopic imaging,” Magn Reson Med, vol. 53, pp. 465–469, 2005. [DOI] [PubMed] [Google Scholar]
- [31].Barkhuysen H, de Beer R, and van Ormondt D, “Improved algorithm for noniterative time-domain model fitting to exponentially damped magnetic resonance signals,” J Magn Reson, vol. 73, pp. 553–557, 1987. [Google Scholar]
- [32].O’Leary DP and Rust BW, “Variable projection for nonlinear least squares problems,” Comput Optim Appl, vol. 54, pp. 579–593, 2013. [Google Scholar]
- [33].Haldar JP and Liang Z-P, “Spatiotemporal imaging with partially separable functions: A matrix recovery approach,” in Proc IEEE Int Symp on Biomed Imag, Rotterdam, Netherlands, 2010, pp. 716–719. [Google Scholar]
- [34].Shah P et al. , “In-vivo 31P NMR spectroscopy assessment of skeletal muscle bioenergetics after spinal cord contusion in rats,” Eur J Appl Physiol, vol. 114, pp. 847–858, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Parasoglou P et al. , “Rapid 3D-imaging of phosphocreatine recovery kinetics in the human lower leg muscles with compressed sensing,” Magn Reson Med, vol. 68, pp. 1738–1746, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Wang C et al. , “31P magnetic resonance fingerprinting for rapid quantification of creatine kinase reaction rate in vivo,” NMR Biomed, vol. 30, p. e3786, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Valkovic L et al. , “Depth-resolved surface coil MRS (DRESS)-localized dynamic (31) P-MRS of the exercising human gastrocnemius muscle at 7T,” NMR Biomed, vol. 27, pp. 1346–1352, 2014. [DOI] [PubMed] [Google Scholar]
- [38].de Graaf RA, In Vivo NMR Spectroscopy. John Wiley & Sons, Ltd, 2007. [Google Scholar]
- [39].Lee H et al. , “High resolution hyperpolarized 13C MRSI using SPICE at 9.4T,” Magn Res Med, vol. 80, pp. 703–710, 2018. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


