Broadband Resonator-Waveguide Coupling for Efficient Extraction of Octave Spanning Microcombs

Abstract

Frequency combs spanning over an octave have been successfully demonstrated in Kerr nonlinear microresonators on-chip. These micro-combs rely on both engineered dispersion, to enable generation of frequency components across the octave, and on engineered coupling, to efficiently extract the generated light into an access waveguide while maintaining a close to critically-coupled pump. The latter is challenging as the spatial overlap between the access waveguide and the ring modes decays with frequency. This leads to strong coupling variation across the octave, with poor extraction at short wavelengths. Here, we investigate how a waveguide wrapped around a portion of the resonator, in a pulley scheme, can improve extraction of octave-spanning microcombs, in particular at short wavelengths. We use coupled mode theory to predict the performance of the pulley couplers, and demonstrate good agreement with experimental measurements. Using an optimal pulley coupling design, we demonstrate a 20 dB improvement in extraction at short wavelengths compared to straight waveguide coupling.

Kerr solitons generated in nonlinear microresonators [1] are promising for many applications in telecommunications [2], range measurement [3], and optical frequency metrology [4]. However, for frequency metrology in particular, many applications require octave-spanning bandwidth for full stabilization through f-2f technique [5]. Suitable engineering of the resonator dispersion profile for octave bandwidth [6, 7], or even super-octave bandwidth [8], has been widely reported and octave-spanning soliton frequency combs have been demonstrated [9, 10], along with f-2f stabilization [4, 11]. Such stabilization requires sufficient power at the frequencies of interest. This ultimately depends not only on the generated intracavity field and ability to take advantage of effects like targeted dispersive wave (DW) emission [7, 12, 13], but also on the extraction of the intracavity field, usually through evanescent coupling to an in-plane waveguide (or waveguides) for microring resonators. Efficient extraction over an octave of bandwidth is particularly non-trivial due to the wavelength dependence of both the phase matching and the spatial mode overlap between the resonator and waveguide modes.

In this letter, we characterize an approach to overcome this challenge, particularly at short wavelengths, based on a pulley configuration in which a portion of the access waveguide is wrapped around the microring [14]. Though utilized in our recent octave-spanning microcomb works [4, 9, 11], this approach was not studied in detail. Here, we present a basic coupled mode theory (CMT) formalism to design the pulley to improve resonator-waveguide coupling, thus comb extraction at short wavelengths, while maintaining desirable coupling in the pump and long wavelength bands. One consequence of pulley coupling is the introduction of narrow spectral windows in which essentially no coupling occurs, due to complete phase-mismatch between the ring and waveguide modes. Consequently, it is important to control the spectral position of these windows in which no coupling occurs, which we refer to as anti-phase-matched frequencies, so that they are separated from the regions of interest, namely the pump and DW frequencies. Experimentally, we validate both the control of the pulley anti-phase-matched frequencies and the enhancement of short wavelength extraction, by ≈ 20 dB relative to conventional point coupling using straight waveguides.

A number of computational approaches have been used to model coupling between ring resonators and waveguides [14–16]. Here, we model resonator-waveguide coupling in an integrated planar geometry by considering only the region over which their fields interact (Fig. 1(a)), with microring outer radius R and ring width RW separated by a gap G from the coupling waveguide of width W. Using the spatial CMT formalism common to waveguide directional couplers [17, 18], we determine the per-pass coupling coefficient from resonator to waveguide κ_r→wg, based on the overlap of the ring and waveguide fields, integrated over the coupling portion. From there, the coupling quality factor Q_c is obtained, and compared to a typical resonator intrinsic quality factor (Q_i) to gauge whether the coupling is at an appropriate level, namely close to critical coupling at the pump Q_c ≈ Q_i.

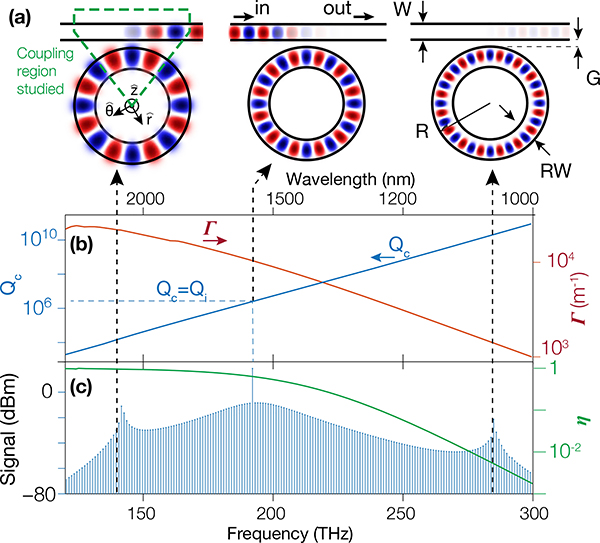
Fig. 1.

(a) Schematic of the optical modes of the ring resonator coupled to a straight waveguide at the DW and pump frequencies. (b) Coupling quality factor Q_c (blue, left y-axis) and ring/waveguide mode overlap Γ at the coupling point (red, right y-axis), for R = 23.3 μm, RW = 1600 nm, W = 550 nm, and G = 700 nm. (c) Simulated intracavity comb spectrum. The variation in Q_c in (b) indicates that high frequency comb components will not be well extracted, as shown through the extraction efficiency η assuming Q_i = 3 × 10⁶ (green).

The coupling coefficient between the ring and the waveguide is:

$${\kappa }_{\text{r}\to \text{wg}}={\int }_L\mathrm{\Gamma }(\omega ,l){\text{e}}^{i\varphi }\text{d}l$$ (1)

with L being the optical path and Γ the overlap of the ring mode projected onto the waveguide mode as:

$$\mathrm{\Gamma }(\omega ,l)=\frac{i\omega }{4}{\int }_S\left({\epsilon }_{\mathrm{w}g}-{\epsilon }_{\mathrm{R}}\right)E_{\mathbf{R}}^{*}\cdot E_{\mathbf{wg}}\text{d}r\text{d}z$$ (2)

with ω the angular frequency, E_R,wg the electric field of ring and waveguide mode respectively, normalized such that $P=\frac{1}{2}\iint \left(\mathit{E}\times {\mathit{H}}^{*}\right)\cdot \widehat{\theta }\text{d}r\text{d}z=1$ [18], with r, θ, and z being the radial, azimuthal, and vertical directions as taken from the center of the ring (Fig. 1(a)). ε_R,wg is the dielectric permittivity considering only the ring and waveguide, respectively. The accumulated phase term in Eq. (1) corresponds to $\varphi =l\sqrt{{(\mathrm{\Delta }\beta /2)}^2+{\mathrm{\Gamma }}^2}$, where $\mathrm{\Delta }\beta =\frac{m}{R_{\mathrm{wg}}}-n_{\text{eff}}^{\mathrm{wg}}\frac{\omega }{c_0}=\frac{\omega }{c_0}\mathrm{\Delta }{n}_{\text{eff}}^{\mathrm{wg}}$ is the difference of propagation constant between the ring and the waveguide mode, within the waveguide, with m the azimuthal mode number of the ring for a given resonance frequency, R_wg = R + G + W/2, and c₀ the speed of light in vacuum.

The effects of the coupling coefficient, κ_r→wg, the phase-mismatch Δβ and the mode overlap Γ can be combined into a single quantity describing the coupling strength known as the coupling quality factor Q_c, defined as:

$$Q_{\text{c}}=\omega \frac{n_{\text{g}}^{\text{R}}}{c_0}\frac{2\pi R}{{\left|{\kappa }_{\text{r}\to wg}\right|}^2}$$ (3)

where $n_{\text{g}}^{\text{R}}$ is the group index of the ring resonator. It is convenient to compare Q_c with the intrisic quality factor Q_i, and to define the extraction efficiency as $\eta ={\left(1+Q_{\mathrm{c}}/Q_{\mathrm{i}}\right)}^{-1}$.

The basic challenge that we address is conceptually illustrated in Fig. 1, and is easy to explain using this CMT framework. Straight waveguide coupling to a ring resonator involves a limited interaction length over which the waveguide and resonator modes spatially overlap, leading to close to a point-like coupling region, particularly for small diameter rings. At long wavelengths (low frequencies) and for a carefully chosen gap size G, the overlap Γ can be appreciable enough that a short interaction length is adequate, yielding Q_c comparable to Q_i (i.e., critical coupling). However, as seen in Fig. 1(a,b), as the wavelength decreases (frequency increases), each mode is more confined, leading to a reduction in Γ, and Q_c increases exponentially with frequency. This results in poor coupling at short wavelengths, with Q_c orders of magnitude higher than Q_i (Fig. 1(b)). This is problematic for octave-spanning combs, as illustrated in Fig. 1(c). Here, the spectrum of the intracavity field is simulated by solving the Lugiato-Lefever equation with the open-source pyLLE package [20], for a geometry appropriate for supporting octave-span operation. Though the dispersion has been engineered to support nearly harmonic dispersive waves at 280 THz and 155 THz, the >100 × difference in Q_c will lead to very different out-coupled powers (given a Q_i ≈ 3 × 10⁶ that is not expected to significantly vary with wavelength), as seen in the plot of η in Fig. 1(c). This will be a major impediment to direct self-referencing.

To overcome this issue, it is possible to increase the interaction length between the waveguide and the ring by wrapping the former around the latter, resulting in a pulley coupling design [14] shown schematically in Fig. 2(c). We note that the overlap coefficient Γ in Eq. (2) is independent of position along the optical path L, and the accumulated phase has to be accounted for across the pulley length L_c, length for which the gap is constant between the ring and the waveguide. Thus Eq. (1) becomes:

$${\kappa }_{\text{r}\to wg}=\mathrm{\Gamma }(\omega ){\int }_{L_{\text{c}}}{\text{e}}^{i\varphi }\text{d}L=\mathrm{\Gamma }{L}_{\text{c}}\mathrm{sinc}\left(L_{\text{c}}\sqrt{{(\mathrm{\Delta }\beta /2)}^2+{\mathrm{\Gamma }}^2}\right)$$ (4)

with $\mathrm{sinc}(x)=\sin (x)/x$. Hence Eq. (3) can be rewritten as:

$$Q_{\text{c}}=\omega \frac{n_{\text{g}}^{\text{R}}}{c_0}2\pi R{\left[\mathrm{\Gamma }{L}_{\text{c}}\mathrm{sinc}\left(L_{\text{c}}\sqrt{{(\mathrm{\Delta }\beta /2)}^2+{\mathrm{\Gamma }}^2}\right)\right]}^{-2}$$ (5)

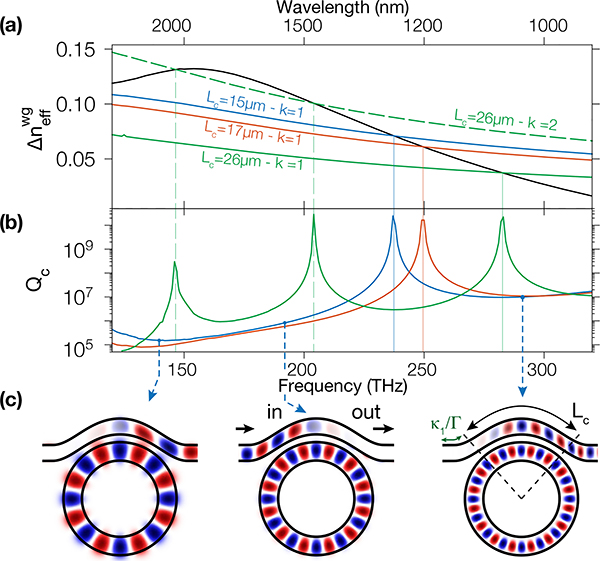
Fig. 2.

(a) Difference in effective index between the ring and waveguide mode $\mathrm{\Delta }{n}_{\text{eff}}^{\text{wg}}$ (black) and the anti-phase matching condition (right hand side of Eq. (6)) for L_c={15, 17, 26} μm (blue, red, green). L_c=26 μm supports an anti-phase condition for both the first and second order (solid and dashed green lines). (b) Q_c for the corresponding pulley lengths. (c) Cartoon depicting the behavior of the electric field for the three frequencies shown as dashed lines in (b), corresponding to the DW and pump frequencies, for L_c =15μm

The above only accounts for the region where the resonator-waveguide gap is constant, and not where the waveguide bends towards and away from the ring, as seen in Fig. 2(c). To account for this, we evaluate Eq. (1) in these regions, resulting in a coupling coefficient κ₁. The ratio ${\kappa }_1(\omega )/{\mathrm{\Gamma }}_{\text{pulley}}(\omega )$ gives the effective length of the curved portion (Fig. 2(c)). Hence, one can then introduce an effective pulley length ${\tilde{L}}_{\text{c}}(\omega )=L_{\text{c}}+2^{{\kappa }_1}(\omega )/{\mathrm{\Gamma }}_{\text{pulley}}(\omega )$ that replaces the pulley length in Eq. (4).

Interestingly, Eqs. (4) and (5) suggest that resonances in the coupling will happen according to:

$$\mathrm{\Delta }{n}_{\text{eff}}^{\text{wg}}=2\frac{c_0}{\omega }\sqrt{{\left(k\pi /{\tilde{L}}_{\text{c}}\right)}^2-{\mathrm{\Gamma }}^2};k\in \mathbb{N}.$$ (6)

Physically, these resonances correspond to locations where the access waveguide and the ring waveguide are anti-phase-matched, and are not observed for a straight waveguide due to the limited interaction length (over which the gap is continuously varying). To investigate further, we calculate Q_c using parameters that correspond to the experimental system studied, that is, 780 nm thick silicon nitride (Si₃N₄) microrings that are symmetrically clad in silica (SiO₂), with R =23.3 μm. We pick RW = 1600 nm (resulting in the simulated frequency comb shown in Fig. 1(b)), along with W = 550 nm and G = 700 nm. As shown in Fig. 2, the anti-phase-matching condition results in sharp peaks in Q_c for frequencies that vary with L_c. At these frequencies, regardless of the overlap between the ring and the waveguide modes, no transfer of energy occurs. The behavior of Q_c on either side of the resonances is important for octave-spanning comb applications. On the blue side (short wavelengths), the overall increase in interaction length results in smaller Q_c (improved coupling) than in the straight waveguide case. On the red side (longer wavelengths), the difference in $\mathrm{\Delta }{n}_{\text{eff}}^{\text{wg}}$, accumulated over L_c, keeps Q_c larger than in the straight waveguide case, where the rings are generally overcoupled. The net result is a reduced wavelength-dependence in Q_c (outside of the anti-phase-matched window) than for a straight waveguide. We also note that when the pulley is sufficiently long, higher orders of anti-phase-matching can be satisfied (i.e., k > 1), leading to multiple resonances in Q_c.

To validate the CMT modeling, we first verify the pulley resonance behavior through linear transmission measurements of devices designed to show a Q_c resonance within the 182 THz to 207 THz tuning range of our laser source. We keep the pulley parameters fixed, namely gap G = 800 nm, waveguide width W = 750 nm, and pulley coupling length L_c = 40 μm, while the ring width RW is varied. This results in variation of the effective index of the microring $n_{\text{eff}}^{\text{ring}}$, leading to a modification of the anti-phase-matching condition and hence the spectral position of the corresponding frequencies. By fitting approximately 25 resonances of the first order transverse electric (TE) mode family that appear within the laser scan range, we extract the spectral dependence of Q_c (Fig. 3(a)) for each RW, taking into account internal losses, coupling, and backscattering [19].

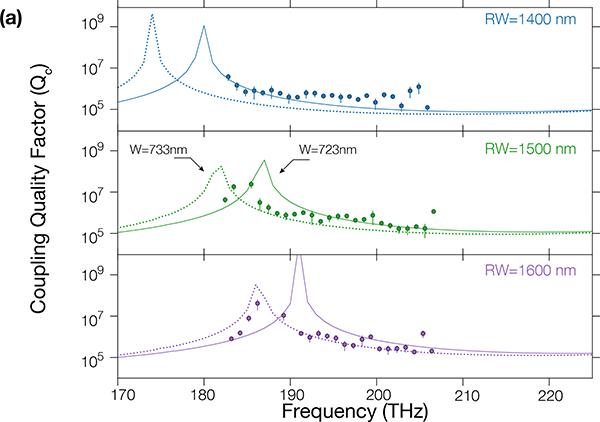
Fig. 3.

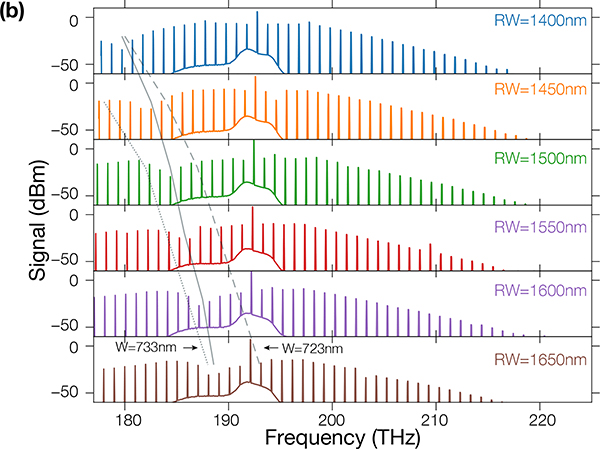
(a) Linear transmission measurement of Q_c (circles) for a L_c = 40 μm pulley waveguide, for a ring width of 1400 nm (blue), 1500 nm (green) and 1600 nm (puple). The solid and dashed lines represent the simulated Q_c for a waveguide width of 723 nm and 733 nm respectively. The error bars we report are one standard deviation values based on nonlinear least squares fits to the model from Ref [19]. (b) MI combs obtains for different ring widths. The dips in the comb profiles correspond to the pulley anti-phase-matched frequencies and are highlighted through the solid lines. The dotted and dashed lines represent the theoretical position of the pulley anti-phase-matched frequencies, and hence the expected dip in the MI comb spectra, for a waveguide width of 723 nm and 733 nm respectively

Simulations of Q_c through CMT match both the values and the trend of the experimental Q_c, including the divergence at resonance. Moreover, one can reproduce the variation in Q_c antiphase-matching spectral position with RW due to the change of effective index. The simulations also show the difference of sensitivity in dimension between the ring and the waveguide. As the waveguide is narrower with a mode less confined than the ring, a small variation of its width results in a significant change in its effective index. Hence, by only changing the waveguide width by 10 nm, the anti-phase matching frequency shifts by about 5 THz. To achieve the same shift, one needs to modify the RW by 50 nm. This gives the ability to tune the position of the pulley anti-phase-matched frequency while keeping the microring resonator at a fixed geometrical dimension that is likely already dispersion-optimized.

Outside of the tunable laser range, it is possible to extract the position of the pulley anti-phase-matched frequency by measuring the spectra of modulation instability (MI) combs generated through strong pumping (P_pmp = 200 mW) of the resonators at ≈ 1550 nm, on the blue-detuned side of a cavity resonance. The spectral components in these MI combs are not phase-locked, and the overall comb acts as a quasi-continuous-wave, spectrally broadband source. Thus, the pulley coupling can be studied using these states over a spectral range as broad as the comb bandwidth. To confirm this, we measure the MI comb spectra of the devices characterized linearly (Fig. 3(b)). We observe that the position of the anti-phase-matched frequency obtained through linear characterization of the device (by extracting Q_c) and through measuring the position of the dip in the MI comb are consistent. The latter method also agrees with the CMT simulations, and the position of the anti-phase-matched frequency is within the uncertainty in the fabricated geometry.

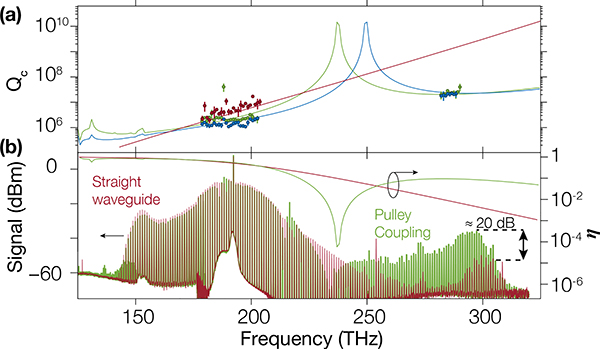
We now compare a pulley coupling design optimized for extraction of an octave-spanning microcomb, namely, with a coupling anti-phase-matched frequency in-between the pump and the short wavelength DW, against straight waveguide coupling for the same ring parameters. We first characterized Q_c (through linear transmission measurements) in both the pump band and near the short wavelength DW, around 193 THz and 280 THz, respectively (Fig. 4(a)) using two continuous tunable laser centered around 1550 nm and 1050nm. We were unable to measure any resonance of the first order TE mode in the 280 THz range for the straight waveguide, as expected from simulations where Q_c is orders of magnitude higher than the expected Q_i ≈ 3 × 10⁶ (as measured in other bands). In contrast, the pulley devices, for both L_c=15 μm and L_c=17 μm, exhibit a difference in Q_c of only one order of magnitude between the two bands, and show good agreement with the values predicted by the CMT. Finally, from MI comb spectra (Fig. 4(b)), the advantage of using the pulley coupling approach for extraction is apparent. Pumping both the straight waveguide and the L_c=15 μm pulley devices such that the long DW and overall comb shape are the same, the pulley coupling shows a clear advantage in extracting the short DW with > 20 dB increase in power obtained. This enhancement of short DW extraction has recently been applied in studies of octave-spanning soliton microcombs [4, 9, 11, 21].

Fig. 4.

(a) Linear transmission measurement of Q_c (circles) for a straight waveguide (red), and pulley coupling with L_c=15 μm (green) and L_c=17 μm (blue). Error bars are one standard deviation values extracted from nonlinear least squares fits. (b) MI comb spectra for straight waveguide (red) and pulley coupling with L_c=15 μm (green) with estimated extraction efficiency η assuming Q_i = 3 × 10⁶ (right axis).

In conclusion, we have presented a CMT formalism to design pulley couplers to help with the extraction of octave-spanning spectra from chip-integrated, microring-based frequency combs. We use the CMT to elucidate the roles of phase-mismatch and spatial overlap in the wavelength-dependent coupling spectrum. Finally, we show that using such pulley coupling increases by ≈20 dB the extraction of the short wavelength part of an octave-spanning frequency comb compared to the same resonator with a straight waveguide coupling.