Push-Ups are Able to Predict the Bench Press 1-RM and Constitute an Alternative for Measuring Maximum Upper Body Strength Based on Load-Velocity Relationships

Abstract

The aims of this study were firstly to compare the similarity in upper-body muscle activation between the bench press and push-up at similar loads, and secondly to establish a 1-RM prediction equation between the two exercises based upon the load-velocity relationship. Twenty resistance-trained male athletes (age 22.5 ± 5.24 years, body mass 83.7 ± 10.7 kg, body height 1.80 ± 0.06 m) performed push-ups and bench presses with four different loads. Push-ups were performed without a weight vest and with a 10-20-30 kg weight vest. Bench presses were performed at 50-80% of athletes’ assumed 1 repetition max (1-RM) in 10 kg steps, while a linear encoder measured performance during the exercises. A load-velocity relationship was established as a product of the load and velocity for the push-up and bench press per participant and the equation was used to establish a predicted 1-RM. Mean muscle activation of eight upper body muscles was recorded for each exercise and each load. The main findings of this study demonstrate an extremely large association between the predicted 1-RM loads performed with the push-up and bench press (r = 0.93) in experienced resistance trained men. Furthermore, most muscles showed similar activations between the two exercises with the different loads except the deltoid and biceps brachii muscles. It may be concluded that it is possible to predict a cross-over 1-RM between the two exercises based upon the load-velocity relationship in each exercise, and that training push-ups largely targets the same muscles as the bench press except the deltoid and biceps muscles. For coaches and athletes, the use of this method is a low cost and time-effective alternative for standard 1-RM bench press testing to predict maximal upper body strength.

Introduction

The bench press and push-up are two exercises used to both monitor upper body strength and enhance strength in upper body movement (Calatayud et al., 2015; Mayhew et al., 1991). The selection of which exercise to use is largely dependent on the athletes’ goal, movement capabilities and relative strength levels. As a monitoring tool, the bench press and push-up are typically used to assess different components (maximal load and velocity) on the load-velocity curve (Bartolomei et al., 2018; Gonzalez-Badillo and Sanchez-Medina, 2010). Within the bench press, the maximum load lifted for prescribed reps or the velocity of the lift measured with a linear encoder at a certain % of 1 repetition-maximum (1-RM), is frequently used to assess strength capabilities (Sanchez-Medina and Gonzalez-Badillo, 2010). In contrast, for push-ups the total number of repetitions is often used as an indication of upper body strength or strength endurance (Invergo et al., 1991; Mayhew et al., 1991). In addition to assessment of different expressions of strength, administering tests related to the two exercises is also different. Bench press 1-RM testing can take considerable time, requires spotters and necessitates mental focus and physical readiness in the lifter to produce a maximum that may be compromised in novice lifters (Bartolomei et al., 2018; Mayhew et al., 1993; van den Tillaar and Ettema, 2009). In contrast the push-up can be performed anywhere in many variations, like small-wide hand placement, one-two handed push-ups, on knees or feet (Cogley et al., 2005; Garcia-Masso et al., 2011; Gouvali and Boudolos, 2005; Marcolin et al., 2015; Wurm et al., 2010), making it particularly beneficial for novice lifters and in a team training environment as multiple tests can be run simultaneously. However unlike the bench press, quantifying the load lifted during a push-up is difficult as typically there is no external equipment to use for calculation. In push-ups, load modification is based on positional changes, with variations including a more vertical position (Giancotti et al., 2018; Wurm et al., 2010), anterior posterior shifting during the push-up (Marcolin et al., 2015), single arm (Freeman et al., 2006) or adding some load by wearing weight vests (Hinshaw et al., 2018; Vaseghi et al., 2013). A disadvantage is the difficulty in monitoring exactly how much load is added to the effort as a result of the changing position as other muscles could be targeted (Cogley et al., 2005; Freeman et al., 2006; Garcia-Masso et al., 2011; Marcolin et al., 2015; Suprak et al., 2011).

Very little research exists on establishing if there are neuromuscular differences between the bench press and the push-up (Blackard et al., 1999; Calatayud et al., 2015; Gottschall et al., 2018). While Calatayud et al. (2015) and Blackard et al. (1999) found no differences in muscle activation between the two exercises in the long head of the triceps, pectoralis major and anterior deltoid, Gottschall et al. (2018) found that the anterior deltoid and biceps brachii were more activated during the bench press than push-ups. This contrast in findings may be due to the variation in the push-up exercise used. Calatayud et al. (2015) only investigated the pectoralis major and anterior deltoid muscles during a 6-RM bench press compared with elastic band loaded 6-RM push-ups, while Gottschall et al. (2018) compared muscle activity during unloaded push-ups and equalised bench press weight to the same total load between the two exercises. Thus, the equivalency of the load lifted is a limiting factor in establishing neuromuscular differences between the exercises. Establishing neuromuscular differences based on exercises performed at similar loads is thus warranted to establish the true similarity between the movements.

Prior studies have investigated the relationship between push-up strength and bench press strength for the purposes of predicting performance (Bartolomei et al., 2018; Blackard et al., 1999; Invergo et al., 1991; Mayhew et al., 1991). Invergo et al. (1991) and Mayhew et al. (1991) found that the number of push-ups completed in 60 s was unable to predict the 1-RM bench press load. However, as Invergo et al. (1991) and Mayhew et al. (1991) suggested, the two different tests rely predominantly on different types of strength; maximal strength and strength endurance, thus prediction cannot be expected (Mayhew et al., 1991). Supporting the argument for testing similar types of strength used in a strength test, a ballistic push-up was able to predict the 1-RM bench press load based on large correlation (r = 0.87) of mean power as measured by a force plate (Bartolomei et al., 2018). However, the use of a force plate to assess relationships can limit its applicability to practitioners based on cost and accessibility. A more cost-effective method may be the use of a linear encoder, which has been used to predict the 1-RM bench press based on the load velocity relationship (Bosquet et al., 2010; Gonzalez-Badillo et al., 2011; Gonzalez-Badillo and Sanchez-Medina, 2010). The method of assessing the load-velocity relationship involves measuring concentric velocity at 3-4 different weight loads, and then through linear regression equations, predicting the load (% 1-RM) from velocity data. The similarities in joint actions in the upper body between the push-up and bench press suggest that performance in one exercise (Calatayud et al., 2015) may be able to predict performance in the other based on establishing a load-velocity relationship. No research has used push-up performance with varying external loads to predict the bench press 1-RM based on the load-velocity relationship. The use of push-ups to predict bench press performance would have benefits with regard to upper-body test administration in large scale teams and afford the progression from the push-up to bench press in novice athletes to be safer and more accurate.

Therefore, the aim of this study was twofold: 1) to assess the similarity in muscle activation between a bench press and a push-up at matched loads based on the load velocity relationship, and 2) to establish if a push-up and a bench press can predict a similar 1-RM based on the load-velocity relationship and thereby be an alternative for upper body strength testing. Based upon Calatayud et al. (2015) and Blackard et al. (1999) it was hypothesized that similar loads between the two exercises would result in similar muscle activation and load-velocity relationships.

Methods

A within-subjects, repeated-measures design was used to compare upper-body muscle activation between the bench press and push-ups and generate a predicted 1-RM based on load velocity relationships. Load-velocity relationships were established by assessing velocity at four different sub-maximal loads in randomized order. The independent variables were the different loads, while mean concentric velocity at each load for each exercise, and the upper-body muscle activation during the descending and ascending phase of the exercises were the dependent variables. The predicted 1-RM based on the load-velocity relationship established for the push-ups and bench press was compared for similarity to establish a prediction equation.

Participants

Twenty resistance-trained male athletes (age: 22.5 ± 5.24 years, body height: 1.80 ± 0.06 m, body mass: 83.7 ± 10.7 kg,) with previous resistance training experience (6.1 ± 2.3 years) agreed to participate in the study. Participants were instructed to avoid any additional resistance training targeting the upper body for 72 hours prior to testing. Written consent was obtained from each participant prior to the study. The study complied with the current ethical regulations for research, was approved by the regional ethical committee, and conformed to the latest revision of the Declaration of Helsinki.

Procedures

Participants visited the laboratory on two occasions. The first occasion was a familiarisation session which involved practice with the protocol and performing the actions with the linear encoder attached. No less than 48 hours following the familiarisation session, the testing session commenced by initially taking participants body height and mass. Each participant then completed a standardised warm up of a five-minute treadmill run at a submaximal level (8-10 km/h). Both conditions were performed within a single testing session and participants were randomly selected to complete either the bench press or push-up condition as the first test followed by the other condition. Participants performed each condition with four different weighted loads; push-up: without a weight vest, with a 10, 20, 30 kg weight vest (Titan Fitness, Memphis, TN, USA) and bench press: ~50-80% of their self-reported 1-RM in steps of 10 kg. Three repetitions per load were performed and the different loads were given in either increasing or decreasing order to each participant. Three to five minute rest intervals were given between each different load and exercise to avoid fatigue. Participants performed the bench press according to the rules and regulations set by the International Powerlifting Federation, except the requirement for a full stop on the chest; they were also allowed to touch and press the bar to the chest, although no bounce was allowed. Each participant used their preferred grip width in the bench press and this was measured and standardized for each load and maintained during each exercise. For the push-up condition, push-up handles were used that were positioned in such a way that it had the same grip width and orientation as in the bench press. To simulate the same depth as in the bench press barbell, participants had to lower their chest to the height of the push-up handles. Push-up depth was qualitatively validated by the lead author for each repetition. To avoid the risk of injury and the absence of enough weight in the weight vest for the push-up condition to conduct a 1-RM in push-ups, no actual 1-RM testing was performed in this study.

The push-up handles were placed on a strain gauge force plate, dimensions: 0.8 x 0.6 x 0.06 m (Ergotest Technology AS, Langesund, Norway), that sampled at 1000 Hz. Feet of the participant were placed behind the plate at the same height as the force plate. The initial ground reaction force was measured when the participant was in the start position and bearing full weight on the push-up handles. The ground reaction force at the starting position was then used to calculate how much absolute load and percentage of body weight (+ weight vest) had to be lifted during the different push-up conditions.

A linear encoder (ET-Enc-02, Ergotest Technology AS, Porsgrunn, Norway) was attached to the barbell when performing the bench press and attached at the sternacostal notch via a collar when performing a push-up, directly vertical to the ground, without disturbing the push-up depth. The linear encoder measured with a resolution of 0.019 mm and counted the pulses with 5 ms interval vertical displacement in relation to the lowest point of the barbell or person (zero distance). Both exercises were divided into two phases: the downward and the upward phase. These phases were identified based on the linear encoder mean concentric velocity output. Mean concentric velocity was calculated from the lowest barbell position over the chest full extension for the bench press; and from the lowest position to the highest position in the push-up by using a five point differential filter with Musclelab v10.5.67 software (Ergotest Technology AS, Porsgrunn, Norway) and used for further analysis. The maximal measurement error of velocity due to the system was less than 0.9% and a coefficient of variation of 2.3% (Bosco et al., 1995).

Wireless electromyography (EMG) was recorded using a Musclelab 6000 system and analyzed by Musclelab v10.5.67 software (Ergotest Technology AS, Porsgrunn, Norway). Following skin preparation, including shaving, abrading and alcohol swabbed, gel-coated self-adhesive electrodes (Dri-Stick Silver circular sEMG Electrodes AE-131, NeuroDyne Medical, USA) were applied to the skin. The electrodes (11 mm contact diameter and a 2 cm center-to-center distance) were placed along the presumed direction of the underlying muscle fiber according to the recommendations by SENIAM (Hermens et al., 2000; Saeterbakken and Fimland, 2013). The electrodes were placed on the right upper limb and positioned on the belly of the sternal and clavicular part of the pectoralis major, the anterior and medial deltoid, the lateral, medial and long head of the triceps brachii and the biceps brachii, and measured with a sampling rate of 1000 Hz. To minimize noise from the surroundings, the raw EMG signal was amplified and filtered using a preamplifier located close to the sampling point. The EMG signals were converted to root mean square (RMS) EMG signals using a hardware circuit network (frequency response 20–500 kHz, averaging constant 100 ms, total error ± 0.5%). The mean RMS EMG signals of each muscle during the downward and the upward phase of the lift with each load were used for further analysis to identify similarities in muscle activation between the two exercises. No normalization of the EMG signals was necessary since all measurements per participant were performed in one session and only a within subject design was used (Gomo and van Den Tillaar, 2016; van den Tillaar et al., 2017). Phase duration for mean RMS EMG analysis was defined using the linear encoder. Force plate, linear encoder and EMG signals were synchronized through the Musclelab 6000 system.

A load-velocity relationship was established for both exercises for each participant. The relationship was established as a product of the load, and average velocity of the three repetitions measured with the linear encoder at each of the four different loads. In the push-up, with the participant in the start position, the ground reaction force prior to the push-up commencement was used as the load for each of the four load conditions. Based on the athlete’s performance at the various loads, a linear regression was used to calculate the theoretical 1-RM for each participant. The x-variable was set as 0.18 m/s, which indicated the minimal velocity where 1-RM theoretically was attainable (Gonzalez-Badillo and Sanchez-Medina, 2010). Thus, to calculate 1-RM the following formula was used:

$$y=a\ast 0.18m/s+b$$ (Eq. 1)

Both the coefficient of x (a) and y-intercept (b) were individualized for each participant. To establish a and b in the linear equation for each participant, scatter plots were produced and a linear regression line was added using Microsoft Excel (Version 1812). For each participant, x was replaced with 0.18 to establish the load-velocity relationship for a 1-RM. To predict the 1-RM based upon the mean velocity in the normal push-up without any extra load also a linear regression was established between the percentage of the predicted 1-RM in the push-up and mean velocity at each load for each participant.

Statistical Analyses

To compare muscle activation between the two exercises with different loads a 2 (phase: ascending and descending) x 2 (exercise: push-up vs. bench press) x 4 (load: four different loads in each exercises) analysis of variance (ANOVA) with repeated measures was used for each of the muscles. When a significant effect was found a two-way ANOVA for each phase was performed. Where the sphericity assumption was violated we reported Greenhouse-Geisser-corrected p-values in the results. Post hoc tests using the Holm-Bonferroni probability adjustment were used to identify differences. In addition, a one-way ANOVA was performed on the relative load that had to be lifted with the four different loads during the push-ups. The effect size used and reported in this study was partial eta squared (η²), where 0.01 ≤ η² < 0.06 constituted a small effect, 0.06 ≤ η² < 0.14 constituted a medium effect, and η² > 0.14 constituted a large effect (Cohen, 1988).

Linear regression analysis was used to predict 1-RM bench press and push-up performance. Pearson product-moment correlation between the predicted 1-RM bench press and the 1-RM push-up was conducted together with the intraclass correlation coefficient (ICC) (2, 1) and the standard error of estimate (SEE) to inform about the typical error in the measurements. Bland–Altman plots were used to identify potential systematic bias, which were reported through mean-bias and standard deviations. Correlation coefficients of 0.1, 0.3, 0.5, 0.7 and 0.9 were interpreted as a small, moderate, large, very large, and extreme large relationship, respectively (Hopkins et al., 2009). The level of significance was set at p ≤ 0.05 for all tests and all analysis was carried out using SPSS Statistics v25 (SPSS, Inc., Chicago, IL).

Results

The actual load lifted during the four push-up conditions was from 52.3 kg at the 0 kg condition to 73.9 kg in the + 30 kg condition. This made the relative load from 62.6 to 65.1% of body mass (+ weight vest) that had to be lifted during the different push-ups (Table 1).

Table 1.

Mean absolute load, average velocity (± SD) with the four push-up and bench press loads and the percentage of body mass (+weight vest) that had to be lifted in the four push-up conditions.

Load	1	2	3	4
Push-up with(out) weight vest	0 kg	+10 kg	+20 kg	+30 kg
Body Mass plus weight vest (kg)	83.7 ± 10.6	93.7 ± 10.6	103.7 ± 10.6	113.7 ± 10.6
Actual Load lifted (kg)	52.3 ± 6.8	59.5 ± 6.4	66.7 ± 6.2	73.9 ± 6.8
% of body mass (+weight vest)	62.6 ± 4.3*	63.7 ± 3.6*	64.4 ± 3.4	65.1 ± 3.4#
Mean velocity (m/s)	0.86 ± 0.19	0.71 ± 0.15	0.57 ± 0.15	0.43 ± 0.15
Bench press
Actual load lifted (kg)	50 ± 14.9	60 ± 14.9	70 ± 14.9	80 ± 14.9
Mean velocity (m/s)	0.84 ± 0.15	0.69 ± 0.13	0.55 ± 0.14	0.43 ± 0.16

^*indicates a significant difference compared to all other conditions (p < 0.05)

^#indicates a significant difference compared to all other conditions except the +20 kg condition (p < 0.05)

The predicted 1-RM in the bench press was 93.5 ± 15.7 kg, while the predicted 1-RM in the push-up was 93.1 ± 14 kg (Figure 1) with similar mean velocities during the lifts with different loads in both exercises (Table 1). The predicted 1-RM levels showed a very large significant positive correlation between the two exercises (ICC = 0.96, r = 0.93, SEE = 5.1 kg, Figure 1), while the bias was only 0.31 ± 5.7 kg (p > 0.05). A large significant correlation between mean velocity at each load for each participant and the percentage of 1-RM in the push-up was observed (r = -0.90, SEE = 0.1%, Figure 2).

Figure 1.

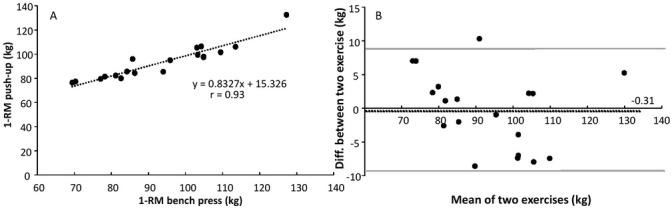
A) Correlation between the predicted 1-RM of the push-up and bench press for each participant.

B) Bland-Altman plots between the push-up and bench press. A dash line indicates a systematic bias between the two exercises (positive values mean a higher 1-RM obtained with the push-up than the bench press). The grey lines represent 95% Confidence intervals.

Figure 2.

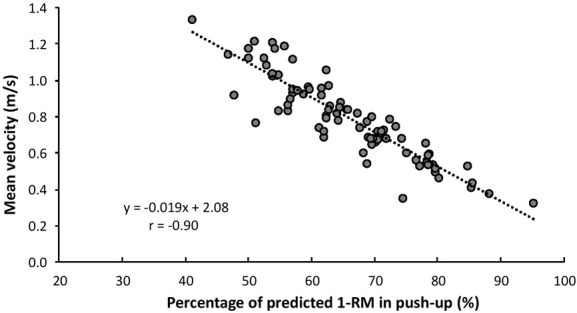
Correlation between mean velocity at the four different loads and the percentage of the predicted 1-RM in the push-up based upon all participants with the correlation coefficient and regression equation.

A significant difference for all muscles was observed between the descending and ascending phase for both exercises, with higher muscle activation during the ascending phase of all muscles across all loads, except the biceps brachii that had the highest activation during the descending phase in both exercises (Figures 3 and 4). When dividing the exercises into two phases (descending and ascending), a two-way ANOVA revealed a significant effect during the descending phase in the triceps medial head (F = 6.8, p = 0.019, η²=0.30), the acromial part of the deltoid muscle (F = 6.0, p = 0.027, η² = 0.27) and biceps brachii (F = 4.8, p = 0.046, η² = 0.26) in activation between the exercises. During the ascending phase only the anterior deltoid had significantly different activation between the two exercises (F = 5.4, p = 0.035, η² = 0.28). Post hoc comparison showed that the medial head of triceps brachii was more active during the bench press exercise than the push-up during the descending phase, while biceps brachii and medial part of the deltoid were more active in push-ups than the bench press (Figures 3 and 4). The anterior deltoid showed higher activation in the bench press than in the push-up during the ascending phase (Figure 4). An interaction effect (load x exercise) was found for the biceps brachii for both phases (F ≥ 3.3, p ≤ 0.031, η² ≥ 0.19) and in the descending phase for the medial and long head of the triceps (F ≥ 3.0, p ≤ 0.042, η² ≥ 0.16, Figure 3).

Figure 3.

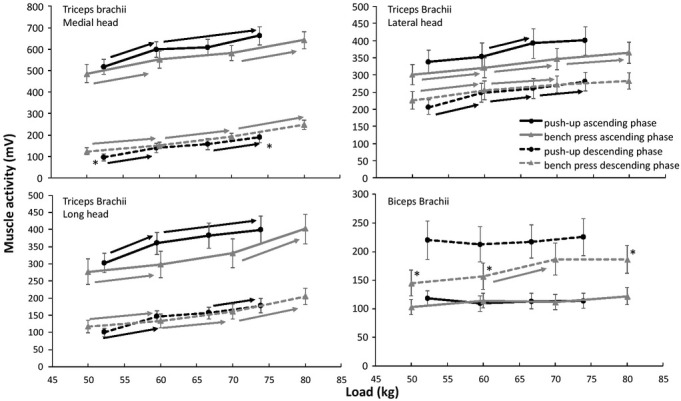
Mean (± Standard error of the mean) activation of Triceps and Biceps brachii muscles during the descending and ascending phase at each load and exercise averaged over all participants.

* indicates a significant difference in muscle activation between the two exercises with this load at a p ≤ 0.05 level.

→ indicates a significant increase in muscle activation from this load to all right of the arrow for this exercise at a p < 0.05 level.

Figure 4.

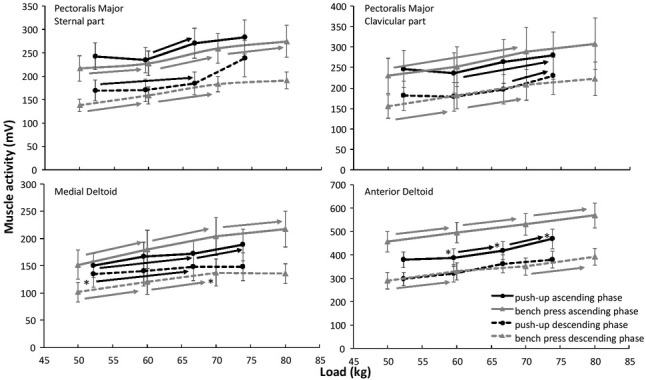
Mean (± Standard error of the mean) activation of Deltoid and Pectoralis Major muscles during the descending and ascending phase at each load and exercise averaged over all participants.

* indicates a significant difference in muscle activation between the two exercises with this load at a p ≤ 0.05 level.

→ indicates a significant increase in muscle activation from this load to all right of the arrow for this exercise at a p < 0.05 level.

Discussion

The aims of this study were to investigate if muscle activation was similar between the bench press and push-ups for similar loads and secondly, if it was possible to predict a similar 1-RM for the two exercises based upon the load-velocity relationship in each exercise. The main findings of this study demonstrate an extremely large association between the predicted 1-RM loads in the push-up and the bench press (r = 0.93) in experienced resistance trained men using the load-velocity relationship. Furthermore, nearly all muscles showed similar activation between the two exercises at different loads except for the anterior deltoid and the biceps brachii.

While prior studies have assessed the ability of push-up performance to predict the bench press 1-RM (Bartolomei et al., 2018; Blackard et al., 1999; Invergo et al., 1991; Mayhew et al., 1991), this study is the first to predict a 1-RM bench press load from a load-velocity relationship established from a push-up. The current study showed an extremely large association between the 1-RM predicted for both exercises (r = 0.93). This is a stronger relationship than reported by Bartolomei et al. (2018), who predicted a 1-RM bench press from push-ups based upon mean ground reaction force during the ascending phase of the push-up (r = 0.87). Bartolomei et al. (2018) also showed that the push-up performance overestimated the bench press 1-RM load by 10.5 ± 8.5 kg compared to the current study where no significant bias was found (0.31 ± 5.7 kg). Furthermore, in the present study the ICC was high (0.96) and SEE (5.1%) was low indicating that the relationship was reliable and valid. While the current study did not establish the actual 1-RM, Bosquet et al. (2010) has shown previously using the same commercial linear encoder that a correlation of 0.93 exists between the actual and predicted 1-RM load in the bench press. On this basis it is to be expected that the use of a loaded push-up protocol has the ability to predict a bench press 1-RM based on a load-velocity relationship (Figure 2). The equation (Eq. 1) generated from the load-velocity relationship in this study can thus be used to predict the 1-RM in the bench press using an unloaded push-up and calculating the velocity. As an example, when measuring a mean velocity of 1.19 m/s in a normal push-up using Eq. 1, this would equate to (1.19-2.08) / (0.019) = 46.8% of 1-RM. Based on a participant’s body mass of 81 kg, only 62.6% of the mass is lifted during the push-up, which results in a mean load lifted of 50.7 kg. Thus, the 1-RM in this set of parameters would be 50.7 / 0.468 = 108.3 kg, and the participant should be able to lift it in a loaded push-up. Thus an extra load of 57.6 kg could be added to this participant to perform a 1-RM in the push-up. Since the relationship between the two exercises is so high (Figure 1), the 1-RM load in the bench press, based on the relationship, would equate also to a 108.3 kg load.

Within Eq. 1, at 0 kg the percentage of body mass lifted is considered to be 62.6 ± 4.3% (Table1), which while similar to previous studies (64.0 and 63.2%) (Gouvali and Boudolos, 2005; Wurm et al., 2010) was lower than in the study (69%) of Suprak et al. (2011). The differences may be explained by the type of athletes used. In the study of Suprak et al. (2011) members of Special Forces and SWAT units who were reported to have many years of push-up experience were tested. This is in contrast to the current study and the work of Wurm et al. (2010) and Gouvali and Boudolos (2005), who used recreationally trained resistance-trained athletes. Based on the physical requirements of the military it is expected that this cohort had a different somatotype profile compared to recreationally trained athletes.

The majority of the upper body muscles assessed during both exercises behaved the same with an increasing load, which is in accordance with the studies of Gottschall et al. (2018) and Blackard et al. (1999). This indicates that the two exercises have similar neuromuscular demands, and align with the use of a bodyweight push-up as a pre-cursor to bench press exercise. Differences in the biceps brachii, anterior deltoid and medial head of the triceps were observed between the two exercises, which may be due to such factors as positioning and fundamental differences between the two exercises with regard to the kinetic chain. Similar to the current study, Gottschall et al. (2018) showed lower anterior deltoid activation during push-ups compared with the bench press. The causes of the anterior deltoid differences are supported by the proposed trajectory of the barbell in the bench press compared to the push-up trajectory. In the starting position of the bench the athlete lies supine on the bench with both arms vertical, holding the barbell above the shoulder joint to avoid creating a flexion or extension rotating moment at the shoulder joint. In the push-up starting position, the shoulders are straight over the hands in a vertical line, however, since feet are at the same height as the push-up handles, the shoulder flexion is less than the 90 degrees angle in the bench press. The push-up exercise would be more akin to a decline bench press. When lowering the body / barbell a shoulder abduction occurs (Mier et al., 2014; van den Tillaar and Ettema, 2009; van den Tillaar et al., 2012). Since the shoulder flexion angle at the start of the push-up would be less than 90 degrees following the shoulder abduction movement in the descent phase, the medial deltoid had to be more eccentrically active during the descending phase than in the bench press to avoid a larger leverage between the shoulder and hands (more shoulder extension movement) (Figure 3). Therefore, similarly to the decline bench press, the anterior deltoid muscles do not need to be as active compared to a normal bench press as shown by Barnett et al. (1995).

The biceps brachii showed greatest activity in the descending phase (Figure 3) compared to the ascending phase which aligns with the findings of Gottschall et al. (2018). This is likely based on its role as an antagonist at the elbow in the descending phase as it controls the gravitational effect of the bar or the body and additional weight (Figure 3). With increasing loads in the bench press, the biceps brachii activation increased in the descending phase, while as loads increased in the push-up no significant change occurred. An explanation for this could be the nature of the movement, as in a bench press the load is at peripheral part of the body, while loads in the push-up are centrally located (Blackard et al., 1999; Gottschall et al., 2018). In general when a load is more peripherally located more strength is necessary to maintain balance, which requires more involvement of the stabilization muscles (Townsend et al., 1991). The biceps brachii within a push-up is considered a stabilizer around the elbow joint and therefore will be more active during the bench press than the push-up. Therefore, with increasing loads more strength is required from the biceps brachii to stabilize the load during the descending phase in the bench press than the push-up.

An interaction effect was found in the descending phase for the medial and long head of the triceps, indicating that these muscles behave differently in the two exercises as a load increases. At each load in the bench press, triceps brachii activation increased, while in the push-up the increase was less clear. The greater activity of the medial head of the triceps in the descending phase of the bench press compared to the push-up may be due to the requirements for increased stabilization and control of the barbell. This is important to be sure that the barbell is lowered to the correct place on the chest to avoid failure in the sticking region (van den Tillaar and Ettema, 2009; van den Tillaar et al., 2012).

The limitations of the current study include the factors related to the aim of the exercise, voluntary exertion at sub-maximum loads and the possibility of the exact same loads not being used. As stated earlier, the actual 1-RM was not established for either exercise, thus a comparison of the predicted versus the actual 1-RM was not possible to be undertaken. While a familiarization session was performed, a weighted push-up is not as frequently used in resistance training as the bench press. Furthermore, the absolute loads between the two exercises were not exactly the same based on the complexity of only a proportion of the body mass being lifted in a push-up exercise. In addition, the load-velocity relationship and correlation between the push-up and the bench press might not be valid when performing the push-up without handles. A further consideration is related to the load relationship based on individual performance at the four varying loads. These relationships are dependent upon the assumption that participants performed each attempt with maximal effort, and although this was not highlighted in the current study, it was assumed that maximal effort was exerted. Future studies could consider validating the regression equation from the current study (Figure 2) using an actual 1-RM, to ensure that the velocity zones were effective in predicting the actual 1-RM. Studies could look at more time effective measures of determining push-up velocity including accelerometers (Baker, 2017) or video based applications (Balsalobre-Fernández et al., 2018) that would allow quicker recording of push-up velocity. Furthermore, the inclusion of female participants should be considered to verify whether a regression equation differs between sexes.

Conclusion

Based upon the findings of the present study we can conclude that it is possible to predict a similar 1-RM between the two exercises based upon the load-velocity relationship in each exercise. The study has shown the push-ups target the same muscles and when an additional load is added these muscles activate at similar levels to a bench press. The finding that it is possible to predict a similar 1-RM for the two exercises based upon the load-velocity relationship in each exercise suggests that loaded push-ups can possibly be used interchangeably with a bench press exercise. It also suggests that it has potential benefits for large scale administering of upper body strength testing. For coaches and athletes, using a system that could measure velocity during normal push-ups with maximal effort could make it more time and cost effective to predict maximal strength performance of the upper body.