How do Elite Soccer Teams Perform to Ball Recovery? Effects of Tactical Modelling and Contextual Variables on the Defensive Patterns of Play

Abstract

Researchers in soccer match analysis have been using limited procedures to express the dynamics of the game and mainly focus on the attack. Therefore, the aims of this paper were to detect the successful teams’ ball recovery defensive patterns of play and study the influence of tactical modelling, halves, match status, opponent quality and stage competition on those patterns. The sample consisted of 1323 situations of defensive ball possession of the semi-finalist teams from the 2014 FIFA World Cup play-offs, which was collected by a valid and reliable observational instrument (Soccer-Defence). The Kruskal-Wallis H, Mann-Whitney U, Chi-square, Z-, multinomial logistic regression tests and sequential analysis (p < .05; z > 1.96) were used accordingly to test the differences and associations among and within teams of tactical modelling, tactical-technical behaviours and contextual variables to ball recovery. We found that among teams ball recovery differed in duration; H(3) = 14.958, p = .002. Germany were more likely to perform ball recovery by the goalkeeper than Argentina (p = .04; OR = 0.47) or the Netherlands (p < .05; OR = 0.50). Nevertheless, Brazil was the least likely to concede a shot off goal. Teams facing lower-ranked opponents were 0.63 times less likely to perform ball recovery by interception (p <.001). Additionally, sequential analysis illustrated that teams varied between central and lateral high-pressure zones before ball recovery in lower zones of the field. Finally, coaches could use such findings to design training exercises, create their own style of play, and set strategies.

Introduction

The variability of actions in the complex soccer system emerges from the dynamic interactions between teams to control space and time (Garganta, 2009). That author maintains that observation and measurement are needed to better understand the complex dynamics of soccer, not only to improve team strategies, but also training quality. Indeed, team sports ecological dynamics and representative-task learning are becoming prominent in research and practice, where information about the competitive environment is essential to efficiently replicate competition in training exercises (Davids et al., 2013).

Nevertheless, it appears that a substantial problem in soccer is the lack of a reliable theoretical model and operational definitions to understand the phenomena (Garganta, 2009; Mackenzie and Cushion, 2013). In line with this perspective, some authors have outlined an organisational model using defensive and attacking dynamics according to phases of the game (Barreira et al., 2014). According to Barreira et al. (2014), information interpretation of behaviours about the tactical organisation model is fundamental since the tactics and strategies of team sports attempt to anticipate the opponent’s attacking and defensive actions. Also, it appears that modern soccer strategies and tactics are more focused on defensive aspects (Bangsbo and Peitersen, 2002). These authors believe that defensive organisation is related to offence building, arguing that a good defence is the best base for the attack. However, defensive strategies more often receive negative critiques, such as the public expression ‘parking the bus in front of the goal’.

Controversially, the systematic review of Mackenzie and Cushion (2013) reveals that researchers have generally focused on the attacking process. Exceptionally, some studies centered on aspects of the defensive phase. Liu et al. (2015), for example, detected that in the group stage of the 2014 FIFA World Cup, performing more tackles increased the chances of winning, compared to yellow cards or red cards. Furthermore, Delgado-Bordonau et al. (2013) observed that successful teams in the 2010 FIFA World Cup had lower values of goals against, total shots against and shots on goal against. Despite these results, Casal et al. (2016) specifically analysed the defensive transition success in the 2010 FIFA World Cup teams and suggested further research on how teams’ play before recovering the ball.

Considering the stated limitation of traditional notational analysis about discarding contextual information (e.g., quality of opponent) (Mackenzie and Cushion, 2013), there has been an increase of interest by researchers to explore the influence of situational variables in statistics (Almeida et al., 2014; Sarmento et al., 2018). For instance, Almeida et al. (2014) found that a tackle compared to interception was more likely to be executed against similar-ranked teams than lower-ranked teams. Moreover, Vogelbein et al. (2014) verified that top-ranked teams recovered the ball quicker than bottom-ranked teams when winning and had slower reaction times than in-between or bottom-ranked teams when losing.

This type of analysis highly influences the identification of results, particularly in defining patterns of play (Garganta, 2009). In this domain, multinomial logistic models estimate the probabilities of a discrete outcome according to a set of explanatory variables (Almeida et al., 2014), and sequential analysis provides insights into the probabilities of a specific chain of game behaviours, both retrospectively and prospectively (Barreira et al., 2013). However, to date and to our knowledge, no studies have focused on the defensive phase using sequential analysis.

The aims of this study were to: 1) identify and discriminate between the defensive patterns of play among and within successful teams of the 2014 FIFA World Cup to the End of the Defensive Phase (EDP), and 2) explore the influences of tactical defensive modelling and contextual variables (i.e., opponent quality, stage competition, match status and halves) in the teams’ defensive patterns.

Methods

Participants

For this study, we collected tactical and technical data from the play-off matches of the four semi-finalist teams of the 2014 FIFA World Cup (Germany, Argentina, the Netherlands and Brazil), all known as successful teams (Delgado-Bordonau et al., 2013). For each team, four observations were analysed through the regular time of play (90 minutes plus injury time) of 12 matches and 16 observations were analysed equally distributed among teams, resulting in 1323 non-ball possession situations (Germany, n = 357; Argentina, n = 332; the Netherlands, n = 297; Brazil, n = 337). No sequences were excluded in regular time. However, we did not include extra-time as in previous works (Barreira et al., 2015).

Measures

For data collection, the Soccer-Defence (SOC-DEF) Theoretical Dynamic System Model was used (Figure 1). The selected criteria and categories are shown in Table 1, and their definitions are accessible in the supplementary material (Table S1). Validity and reliability are presented elsewhere (Fernandes et al., 2019). This instrument was implemented using Lince 1.4 recording software (Gabin et al., 2012). Two types of visual footage (tactical and broadcast cameras), provided by the FIFA database, were used simultaneously to prevent data exclusion and to clarify ambiguous actions.

Figure 1.

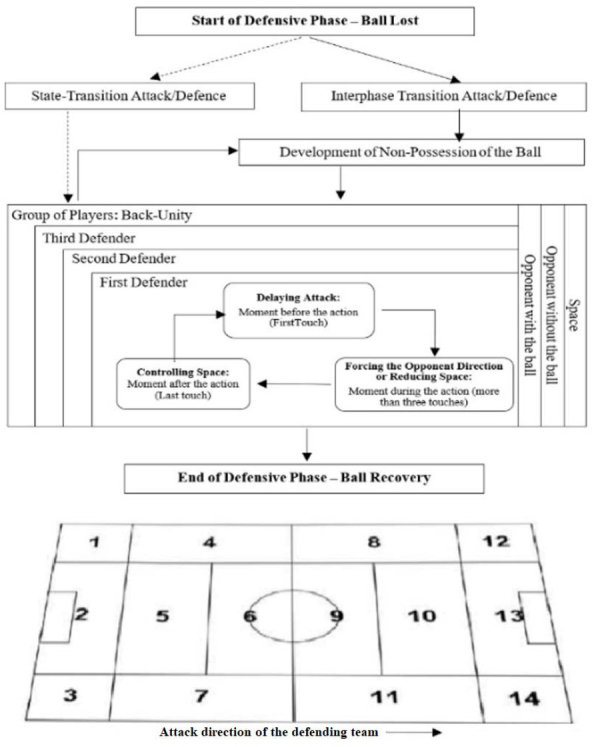
Soccer Defense Theoretical Dynamic System Model and Field Zones.

Table 1.

Soccer Defence (SOC-DEF) Observational System: Criteria and Categories.

Criteria		Categories	Code
Match Status		Winning > one goal difference	Rwm1
		Winning by one goal difference	Rw1
		Draw	Re
		Losing by one goal difference	Rl1
		Losing > one goal difference	Rlm1
Opponent Quality		Tier 1 (semi-finalists teams)	To
		Tier 2 (teams who lost in the eight-or quarterfinals)	Tt
Halvesa		First Halfa	FH
		Second Halfa	SH
Type and Stage of Competition		Play-offs excluding Third Place and Final	Csk
		Third Place gamea	Cdk
		Final	Cf
Type of Development		Transition-state Attack/Defence	DTSd
		Non-Possession of Ball after Transition-State Attack/Defence	DNpt
		Non-Possession of the Ball	DNpb
Type of Subphase		Delay	TSaa
		Forcing the opponent direction/Reducing space	TSfd
		Controlling space	TSce
Defenders Tactical-	First Defender	Pressure	cp
Technical Actions	(DD)	Temporisation	ct
	First(DD) /	Player Marking	mh
	Second (DS) /	Aerial Duel	da
	Third Defender	Unsuccessful Tackle	tr
	(DT)	Intervention without success	is
		Goalkeeper Tactical-Technical Action	ag
		Close Longitudinal Spaces	el
		Close Transversal Spaces	et
		Zonal Cover with player marking	cz
		Control or Balance Positioning	pe
		Displacements of Recovering	dr
		Goalkeeper Positioning	gp
	Second (DS) /	Contention	c
	Third (DT) Defender	Cover	cb
Centre of the game		Numerical Equality without Pressure	SPi
		Numerical Equality Pressure	Pi
		Relative Numerical Superiority	Pr
		Absolute Numerical Superiority	Pa
		Relative Numerical Inferiority	SPr
		Absolute Numerical Inferiority	SPa
Field Zones (see figure 1)		Field Zones of Ball	B1-B14
		Field Zones of 1st Defender	D1-D14
		Field Zones of 2nd Defender	S1-S14
		Field Zones of 3rd Defender	T1-T14
End of Defensive	Effective	Tackle	FEds
Phase		Interception	FEi
		Ball Carrier Error	FEep
		Heading	FEda
		Interruptions and Laws Infractions	FEil
		Offside	FEfj
		Goalkeeper Technique	FEtg
		Shot Blocked Conceded	FErb
	Ineffective	Shot on Goal Conceded	FIrb
		Shot off Goal Conceded	FIrf
		Goal Conceded	FIg

Note. Criteria/category added.

Design and Procedures

Following the procedures of systematic observation (Chacon-Moscoso et al., 2018), the study’s observational design was nomothetic (i.e., the unit is plural), followed-up (i.e., diachronic temporal character) and multidimensional (i.e., several levels of response), which was the fourth quadrant of observational methodology. The sample’s inter-session comprised the play-offs’ matches of semi-finalist teams, and intra-session, all sequences of non-possession of the ball, according to Barreira et al.’s (2014) definitions of the beginning and the end of the phase (Figure 1). Multi-codes of behaviours at three consecutive observation moments: the first touch, the moment after three touches and/or the last touch (Fernandes et al., 2019), were recorded.

A soccer performance analyst with eight years of soccer match analysis/coach/player experience and with the highest level of the Third National League coded the data of all matches. Although the operator was aware of the study, a commitment to procedures of the instrument protocol was followed so as not to interfere with the results and to ensure measurement blinding.

Statistical analysis

Descriptive statistics, Kolmogorov-Smirnov and Chi-square tests were performed as exploratory analysis. Kruskal-Wallis H and Chi-square tests were performed to check differences among teams. Mann-Whitney U and Z tests were used as post-hoc analysis. The contribution of independent variables (e.g., opponent quality), to the variance of the multiple response dependent variable (i.e., EDP), was verified by multinomial logistic regression analysis (Hosmer and Lemeshow, 2000).

To select the variables, we applied the thumb rule of five events per variable (47/5 = 8) to avoid overfitting (Vittinghoff and McCulloch, 2007). Multiple Chi-squares of dependent variables permitted inspection of zero cells and Spearman correlation verified the degree of the relationship between variables. For rho > .70, a variable was excluded (Dormann et al., 2013) before a purposefulness selection (Hosmer and Lemeshow, 2000).

The likelihood ratio, Wald, goodness-of-fit, pseudo-R-squared and classification rate accuracy statistics were computed to assess model assumptions (Hosmer and Lemeshow, 2000). Model diagnostics consisted in outliers’ detection using studentised residuals (>3) calculated from logistic regression (Osborne and Overbay, 2004), multicollinearity detection through the variance inflation factor (VIF > 10) (Dormann et al., 2013), and perturbation analysis (Hendrickx, 2015). The reference category was EDP by Tackle (FEds), since studies have shown statistical relationships in winning the match (e.g., Liu et al., 2015). Then, a retrospective five-lag choice (Barreira et al., 2013) sequential analysis of the criteria behaviour of EDP was applied to determine the probability of successive and concurrent occurrences (i.e., patterns of play).

Statistical significance was set as p < .05 and adjusted residual values, -1.96 < z > 1.96. The odds ratio (OR) and 95% confidence intervals (CI) were reported as the magnitude of significant effects for association tests. Moreover, for statistical difference tests, Chi-square and Z tests were used to compute effect size r (Rosenthal and DiMatteo, 2001), converted to Cohen’s d (Borenstein et al., 2009) and interpreted as follows: trivial (0–0.19), small (0.20–0.49), medium (0.50–0.79) and large (>0.80) (Cohen, 1992). Excel v.2013, SPSS v.24 and R v.3.5.1 were used simultaneously for descriptive, inferences, model fitting, and diagnostics analysis. SDIS-GSEQ v5.1 (Bakeman and Quera, 1995) was used for sequential analysis and ConceptDraw PRO 11 for graphics.

Results

Do successful teams differ in the number of sequences, multi-events, events and sequences’ duration?

Teams did not differ in the number of sequences among them, χ²(3) = 5.650, p = .130. However, they did differ in the number of sequences in different types of match status, χ²(12) = 613.880, p < .01; or stage competition, χ²(6) = 330.050, p < .01. On the other hand, they were similarly distributed in halves, χ²(3) = 9.96, p = .130; or by the type of opponent quality, χ²(3) = .917, p = .821. Teams were differentiated in mean ranks of time spent in defensive sequences, H(3) = 14.958, p = .002; and multi-events, H(3) = 7.257, p = .048. Despite these differences, the events’ median was similar among teams, H(3) = 7.896, p = .064. The Netherlands had multi-events and sequence duration medians greater than Germany (U = 46567.0, p = .007, d = .2; U = 44204.5, p <.001, d = .29) and Brazil (U = 44953.5, p = .027, d = .18; U = 43034.5, p < .01, d = .24). Additionally, the Netherlands had greater sequence duration than Argentina (U = 43355.5, p = .009, d = .21). Table 2 exhibits descriptive statistics and statistical differences between contextual variables.

Table 2.

Number of Sequences and Median (Interquartile Range) of Events, Multi-events and Duration by Team, Halves, Match Status, Opponent Quality and Stage of Competition.

	Argentina				Brazil				Germany				Netherlands			Total
	S	Mu	E	D	S	Mu	E	D	S	Mu	E	D	S	Mu	E	D	S	Mu	E	D
	n	Mdn	Mdn	Mdn	n	Mdn	Mdn	Mdn	n	Mdn	Mdn	Mdn	n	Mdn	Mdn	Mdn	n	Mdn	Mdn	Mdn
		(IQR)	(IQR)	(IQR)		(IQR)	(IQR)	(IQR)		(IQR)	(IQR)	(IQR)	(	IQR)	(IQR)	(IQR)		(IQR)	(IQR)	(IQR)
FH*	160	9.0	88.0	61.5	161	9.0	81.0	61.0	181	8.0	76.0	54.0	140	11.5	108.5	71.5	642	9.0	89.0	61.0
		(12.5)	(122.0)	(61.5)		(10.0)	(90.0)	(59.0)		(10.0)	(92.0)	(55.0)		(13.0)	(127.5)	(61.5)		(11.0)	(106.0)	(60.0)
SH	172	8.5	79.0	56.0	176	9.0	81.5	52.5	176	9.0	85.0	59.0	157	9.0	81.0	65.0	681	9.0	81.0	60.0
		(10.5)	(98.0)	(60.0)		(8.5)	(83.5)	(56.5)		(11.0)	(112.0)	(50.0)		(13.0)	(119.0)	(64.0)		(11.0)	(105.0)	(58.0)
Rlm1					117	10.0	91.0	64.0									117	10.0	91.0	64.0
						(11.0)	(109.0)	(64.0)										(11.0)	(109.0)	(64.0)
Rl1					26	8.5	84.5	60.5					29	7.0	63.0	61.0	55	8.0	72.0	61.0
						(8.0)	(82.0)	(52.0)						(8.0)	(76.0)	(42.0)		(9.0)	(80.0)	(54.0)
Re*	250	9.0	85.0	63.0	98	7.0	69.5	51.5	207	7.0	62.0	52.0	183	10.0	87.0	72.0	738	8.0	77.5	60.5
		(11.0)	(105.0)	(63.0)		(10.0)	(89.0)	(61.0)		(8.0)	(78.0)	(57.0)		(13.0)	(123.0)	(62.0)		(10.0)	(102.0)	(62.0)
Rw1*	82	9.0	79.5	52.5	83	9.0	81.0	57.0	90	11.0	100.0	57.5	18	9.5	89.0	45.5	273	10.0	88.0	54.0
		(13.0)	(129.0)	(51.0)		(8.0)	(72.0)	(54.0)		(10.0)	(101.0)	(50.0)		(7.0)	(69.0)	(64.0)		(10.0)	(93.0)	(51.0)
Rwm1*					13	11.0	102.0	37.0	60	13.5	127.5	66.5	67	13.0	123.0	71.0	140	13.0	120.5	65.5
						(5.0)	(48.0)	(38.0)		(15.5)	(156.0)	(47.0)		(15.0)	(140.0)	(62.0)		(14.0)	(143.0)	(53.0)
To*	152	12.0	108.0	70.0	153	9.0	90.0	65.0	164	10.0	92.5	65.5	145	13.0	121.0	71.0	614	11.0	100.0	68.0
		(18.0)	(168.0)	(70.5)		(11.0)	(106.0)	(63.0)		(14.0)	(134.0)	(57.0)		(14.0)	(147.0)	(61.0)		(14.0)	(140.0)	(64.0)
Tt*	180	7.0	68	54.0	184	8.0	77.5	50.5	193	8.0	72.0	52.0	152	8.0	77.5	69.5	709	8.0	73.0	55.0
		(8.0)	(72.5)	(48.0)		(8.0)	(77.5)	(55.0)		(8.0)	(76.0)	(52.0)		(10.0)	(99.0)	(64.0)		(8.0)	(79.0)	(55.0)
Csk*	246	9.0	80.0	61.0	262	8.5	81.0	53.5	274	9.0	86.5	55.0	216	9.0	85.0	70.5	998	9.0	83.0	60.0
		(11.0)	(103.0)	(59.0)		(9.0)	(87.0)	(59.0)		(10.0)	(96.0)	(51.0)		(11.5)	(113.5)	(61.0)		(10.0)	(101.0)	(57.0)
Cf	86	11.0	104.5	56.0					83	8.0	70.0	58.0					169	9.0	85.0	57.0
		(14.0)	(132.0)	(64.0)						(12.0)	(121.0)	(66.0)						(13.0)	(124.0)	(63.0)
Cdk*					75	9.0	90.0	62.0					81	12.0	113.0	71.0	156	10.0	98.5	65.0
						(10.0)	(106.0)	(67.0)						(13.0)	(122.0)	(64.0)		(14.0)	(128.5)	(65.0)
Total*	332	9.0	83.5	60.0	337	9.00	81.0	57.0	357	9.0	84.0	56.0	297	10.0	91.0	71.0	132	9.0	85.0	60.0
		(11.0)	(106.8)	(61.0)		(9.00)	(88.5)	(61.0)		(10.5)	(100.0)	(54.0)		(14.0)	(127.5)	(62.0)	3	(11.0)	(105.0)	(59.0)

Notes. Mdn = Median; IQR = Interquartile range; S = Sequences; Mu = Multi-events; E = Events; D = Duration of Sequences in seconds; A = Argentina; B = Brazil; G = Germany; Ne = Netherlands; * p < .05, z-test for proportions applied to sequences and Kruskal-Wallis H-test and Mann-Whitney U-test to Events, Multi-events and Duration of Sequences; FH = First Half; SH = Second Half; Rwm1 Winning more than one goal difference; Rw1 = Winning by one goal difference; Re = Draw; Rl1 = Losing by one goal difference; Rlm1 = Losing more than one goal difference; To = Tier 1 (semi-finalists teams); Tt = Tier 2 (teams who lost in the eight-or quarterfinals); Csk = Play-offs excluding Third Place and Final; Cdk = Third Place game; Cf = Final.

*Statistical differences at p<.05 in the following conditions: FH - Mu: Ne>B,G; E: Ne>B,G; D: Ne>B,G. Re- S: B<A,G,N; A>G,Ne; Mu: G<A,Ne; E: G<A,Ne; D: Ne>B,G; A>G. Rw1 - S: Ne<A,B,G. Rwm1 - S: G>B; D:B<G,Ne. To - Mu: Ne>B,G;E: Ne>B. Tt - D: Ne>A,B. Csk - D:Ne>A,B,G. Cdk - Mu: Ne>B; E: Ne>B. Total - Mu: Ne>B,G; D:Ne>A,B,G.

Bivariate analysis

EDP by Goal Conceded (FIg), EDP by Offside (FEfj) and EDP by Shot Blocked (FErb) were excluded because the minimum expected count by cell was violated (Table S2). Notwithstanding this, teams statistically differed in the types of EDP among them, χ²1258(21) = 33.819; p = .038. Differences were not found, however, when facing worse (i.e., Tier 2), χ²1258(21) = 28.794, p = .119; or similar opponents (i.e., Tier 1), χ²1258 (21) = 25.188, p = .239.

The German national team had the highest values for EDP by Heading (FEda, n = 64) and EDP by Goalkeeper Technique (FEtg, n = 37). However, only the values of FEtg were statistically greater than for Argentina (n = 16, z = 2.76, p = .006, d = .22) and the Netherlands (n = 18, z = 2.68, p = .007, d = .22). Argentina had the highest values for EDP by Shot on Goal Conceded (FIrb, n = 13) and EDP by Interruptions and Laws Infractions (FEil, n = 79), but only FEil was statistically greater than for Brazil (n = 54, z = 2.36, p = .018, d = .19). To the contrary, Brazil had the highest values for EDP by Interception, Ball Carrier Error and Tackle (FEi, n = 62; FEep, n = 43; and FEds, n = 60), showing significant differences from Argentina for FEds (n = 42, z = 2.02, p < .04, d = .16). Unexpectedly, the lowest frequencies for EDP by Shot off Goal Conceded (FIrf) were found in Brazil (n = 9), which was significantly different from Argentina (n = 20, z = 2.06, p < .04, d = .16) and the Netherlands (n = 20, z = 2.39, p < .02, d = .20).

Univariate and multivariate analysis

Due to the large number of comparisons and variable estimates, we focused on statistically significant results (Table 3). Nevertheless, all the results are available in the supplementary material (Table S3 and Table S4).

Table 3.

Significant Variable Estimates and Fitting Diagnostics of the Multinomial End of Defensive Phase Logit Models.

		Reference	B	SE	B 95%CI		Perturbation		Wald	Sig.	Exp(B)	Exp(B) 95%CI
					Lower	Upper	Min	Max				Lower	Upper
Univariatea
FEda	DNpt		-0.03	0.01	-0.05	-0.01	-0.03	-0.02	4.15	0.04	0.97	0.95	0.99
FEda	Tier 2		0.62	0.20	0.29	0.96	0.29	0.92	9.36	0.00	1.86	1.25	2.77
FEda	TSaa		-0.05	0.03	-0.09	-0.02	-0.06	-0.04	4.03	0.04	0.95	0.90	0.99
FEda	TSce		-0.06	0.03	-0.11	-0.02	-0.08	-0.03	3.90	<.05	0.94	0.88	0.99
FEda	TSfd		-0.55	0.08	-0.67	-0.42	-0.55	-0.28	50.58	0.00	0.58	0.50	0.67
FEep	Tier 2		0.49	0.22	0.13	0.85	0.11	0.74	5.10	0.02	1.64	1.07	2.51
FEep	TSce		-0.09	0.04	-0.15	-0.04	-0.11	-0.06	6.04	0.01	0.91	0.85	0.98
FEep	TSfd		-0.49	0.08	-0.62	-0.35	-0.49	-0.21	35.55	0.00	0.62	0.52	0.72
FEi	Tier 2		-0.47	0.20	-0.79	-0.14	-0.68	-0.10	5.64	0.02	0.63	0.43	0.92
FEi	TSfd		-0.33	0.06	-0.43	-0.23	-0.33	-0.16	27.57	0.00	0.72	0.64	0.81
FEil	Argentina	Brazil	0.74	0.27	0.30	1.77	0.42	0.97	7.58	0.01	2.09	1.24	3.53
FEil	TSfd		-0.34	0.06	-0.44	-0.24	-0.36	-0.18	31.18	0.00	0.71	0.63	0.80
FIrb	Argentina	Brazil	1.13	0.53	0.22	1.99	0.43	1.67	4.49	0.03	3.10	1.09	8.80
FIrf	TSaa		0.05	0.03	0.02	0.09	0.04	0.06	4.25	0.04	1.05	1.00	1.11
FIrf	TSce		0.07	0.03	0.03	0.12	0.05	0.09	5.07	0.02	1.07	1.01	1.14
FIrf	Argentina	Brazil	1.16	0.45	0.42	1.89	0.48	1.73	6.62	0.01	3.17	1.32	7.65
FIrf	Germany	Brazil	0.92	0.45	0.17	1.66	0.17	1.67¥	4.11	0.04	2.50	1.03	6.06
FIrf	Netherlands	Brazil	1.09	0.45	0.35	1.82	0.37	1.63	5.90	0.02	2.96	1.23	7.12
Multivariateb
FEda	DTSd		-0.09	0.04	-0.15	-0.03	-0.12	-0.04	6.23	0.01	0.91	0.85	0.98
FEda	Tier 2		0.55	0.21	0.21	0.89	0.18¥	0.76	7.09	0.01	1.74	1.16	2.61
FEep	TSaa		0.10	0.04	0.03	0.17	0.01	0.13	5.32	0.02	1.10	1.01	1.20
FEep	TSce		-0.17	0.06	-0.28	-0.06	-0.20	-0.02	6.94	0.01	0.84	0.74	0.96
FEi	Tier 2		-0.48	0.20	-0.81	-0.15	-0.71	-0.07¥	5.75	0.02	0.62	0.42	0.92
FEil	Argentina	Brazil	0.73	0.27	0.29	1.17	0.38	0.98	7.35	0.01	2.08	1.22	3.52
FEtg	Argentina	Germany	-0.76	0.37	-1.37	-0.15	-1.20	-0.29	4.25	0.04	0.47	0.23	0.96
FEtg	Netherlands	Germany	-0.70	0.36	-1.29	-0.12	-1.14	-0.30	3.87	<0.05	0.50	0.25	0.99
FIrb	Argentina	Brazil	1.10	0.54	0.22	1.99	0.25	1.99	4.19	0.04	3.01	1.05	8.65
FIrb	DTSd		0.10	0.05	0.02	0.17	0.04	0.13	4.53	0.03	1.10	1.01	1.20
FIrf	Argentina	Brazil	1.11	0.45	0.36	1.86	0.48	1.73	5.97	0.01	3.04	1.25	7.40
FIrf	Germany	Brazil	0.97	0.46	0.22	1.72	0.34	1.53	4.55	0.03	2.64	1.08	6.46
FIrf	Netherlands	Brazil	1.08	0.45	0.34	1.82	0.37	1.63	5.75	0.02	2.94	1.22	7.11

Notes. ¥ the value of perturbation analysis is out of 95% confidence interval range so careful interpretations should be done. The reference category is FEds (End of defensive phase by tackle); FEda = End of defensive by Heading; FEep = End of defensive phase by Ball carrier error; Fei = End of defensive phase by Interception; Feil = End of defensive phase by Interruptions and laws infractions; FEtg = End of defensive phase by Goalkeeper technique; FIrb = End of defensive phase by Shot on Goal; FIrf = End of defensive phase by Shot off Goal; DNpt = Non-possession of ball after transition-state attack/defence; DTSd = Transition-state attack/defence; Tier 2 = teams who lost in the eight-or quarterfinals; TSaa = Delay sub-phase; TSce = Controlling space sub-phase; TSfd = Forcing the opponent direction/Reducing space sub-phase; LL = Log-Likelihood; VIF = Variance inflation factor; df = degrees of freedom; Pseudo R Squared(Cox and Snell/ Nagelkerke); Classf = Classification accuracy; Χ² = Likelihood Ratio Tests. a. DNpb: -2LL = 705.7, Χ²(7) = 18.3, p = 0.01, Pseudo R² = .014/.015, Classf. = 20.3%; DNpt: -2LL = 673, χ²(7) = 14.6, p = 0.04, Pseudo R² = .012/.012, Classf. = 20.9%; DTSd: -2LL = 540.5, χ²(7) = 13.8, p = 0.06, Pseudo R² = 011/.011, Classf. = 21.0%; Halves: -2LL = 86.7, χ²(7) = 6.6, p = 0.47, Pseudo R² = .005/.005,

Classf. = 20.3%; Opponent Quality: -2LL = 123.1, χ²(7) = 43.2, p = .00, Pseudo R² = .034/.034, Classf. = 22.6%; Teams: -2LL = 174.8, χ²(21) = 34.6, p = .03, Pseudo R² = .027/.028, Classf. = 21.1%; TSaa: -2LL = 781.8, χ²(7) = 34.4, p = .00, Pseudo R² = .027/.028, Classf. = 20.0%; TSce: -2LL = 545.1, χ²(7) = 37.9, p = .00, Pseudo R² = .030/.030, Classf. = 0.8%; TSfd: -2LL = 389, χ²(7) = 108.3, p = .00, Pseudo R² = .082/.084, Classf. = 22.9%.

b. DNpb: -2LL = 4382, χ²(7) = 20, p = .011, VIF = 1.00; DTSd: -2LL = 4383.7, χ²(7) = 21.6, p = .00, VIF = 1.04; Teams: -2LL = 4396.8, χ²(21) = 34.8, p = 0.03, VIF = 2.09; Opponent Quality: -2LL = 4395.7, χ²(7) = 33.7, p = .00; VIF = 1.95; TSaa: -2LL = 4382.6, χ²(7) = 20.6, p = .00, VIF = 5.22; TSce: -2LL = 4384.2, χ²(7) = 22.1, p = .00, VIF = 5.31; Final Model: -2LL = 4362.7, χ²(56) = 157.1, p = .00, Hosmer and Lemeshow test = 50.4, p = 0.69, Pseudo R² = .117/.120, Classf. = 25.6%.

Model assessment

The final model provided satisfactory predictions of the dependent variable as the null hypothesis was rejected – H₀: there was no difference between the null model and the final model, χ²(56) = 157.161, p <.001. The Hosmer and Lemeshow test showed that the model adequately fitted the data, χ²(56) = 50.4, p = .69. The values of pseudo-R-squared indicated that the independent variables explained 11.7-12.0% of the variance of the dependent variable. In addition, the model proved useful because chance accuracy criteria of 23.1% (1.25 * (0.1552 + 0.1722 + 0.126 + 0.1822 + 0.2032 + 0.0772 + 0.0332 + 0.0532) * 100) were lower than the classification accuracy rate of 25.6%.

Accordingly, each independent variable revealed statistically significant relationships with the dependent variable (p < .05). Multicollinearity diagnostics and perturbation analysis revealed no flagged variables, as VIF were less than 10 and most of the minimum and maximum coefficients remained into the 95% CI range of coefficients, respectively (Table 3).

Defensive transition more associated with a shot on goal conceded

In Transition-State Attack/Defence (i.e., DTSd), successful teams were 1.10 times more likely to concede a shot on goal (FIrb, p = .03, 95% CI = 1.01-1.20) and 0.91 times less likely to perform FEda (p = .01, 95% CI = 0.85-0.98) compared to FEds. Also, univariate analysis revealed that in Non-Possession of the Ball after Transition-State Attack/Defence (i.e., DNpt), FEda was 0.97 times less likely to occur against FEds (p = .04, 95% CI = 0.93-0.99).

Forcing an opponent to play the first touch causes ball carrier error and controlling space induces tackles

The chances of successful teams were 1.10 times higher to FEep against FEds as a unit increase of Delay (i.e., TSaa) (p = .02, 95% CI = 1.01-1.20), and 0.84 times lower when defenders controlled the space (i.e., TSce) by a unit more (p = .01, 95% CI = 0.74-0.96). In univariate analysis, it seems that by comparing FEda and FIrf to FEds, the odds of FEda decreased 0.94 and 0.95 times, and the FIrf increased 1.07 and 1.05 times as a unit of Controlling Space and Delay subphases (i.e., TSce and TSaa) were enforced, respectively (p < .05). Likewise, the more Forcing the Opponent Direction/Reducing the Space (i.e., TSfd) was required, the more likely the teams were to recover the ball by FEds rather than another type of effective EDP, p < .05 (Table 3).

Influence of the opponent quality on the defensive patterns of play

Univariate analysis revealed that when facing worse opponents (i.e., Tier 2), successful teams were 1.86 and 1.64 times more likely to FEda (p < .001, 95% CI = 1.25-2.77) and FEep (p = .01, 95% CI = 1.07-2.51), respectively. On the other hand, successful teams were 0.63 times less likely to make FEi (p < .001, 95% CI = 0.43-0.92) compared to FEds. Similar results were found in multivariate analysis for FEda (p = .01, OR = 1.74, 95% CI = 1.16-2.61) and FEi (p = .02, OR = 0.62, 95% CI = 0.42-0.92).

The impact of goalkeeper technique in the 2014 FIFA World Cup Champion

Argentina and the Netherlands were 0.47 and 0.50 times less likely to FEtg than to FEds, compared to Germany (p < .05). However, significant results were not found between Germany and Brazil or any team in univariate analysis (p > .05).

Brazil was less likely to concede a shot off goal

Univariate and multivariate analysis showed that Argentina, Germany and the Netherlands were 3.17-3.04, 2.50-2.64, 2.96-2.94 times more likely to FIrf compared to FEds, respectively, than Brazil, p < .05 (Table 3). In addition, both statistics evidenced that Argentina was 3.04 and 3.01 times more likely to receive a shot on goal than Brazil (p < .05).

Sequential Analysis

All the z-values, significance levels and effect sizes of the relationships found (-1.96 < z > 1.96, p < .05) through the five lags are exhaustively listed in the supplementary material (Table S5 to Table S8). The values with more probable occurrence (i.e., z > 1.96) in a timescale (i.e., lag), opponent’s behaviour (i.e., ball field zones), and task (i.e., tactical-technical behaviours) are illustrated in Figures 2 and 3. Those reflect the sequential patterns with the multi-events that fulfilled the above requirements, which are numbered and identified by codes and z-values. The circles, meticulously, represent the ball field zone in a lag; the solid lines represent the direction of the ball trough time; the dashed line represents the defender coupled to the ball (i.e., discriminated by a triangle, diamond and square). In each shape, the codes and z-values of the tactical modelling and tactical-technical behaviours probable to occur are positioned nearest to their specific lag. Ball recovery is represented by an arrow and randomly numbered from top to bottom. The type of ball recovery with contextual variable codes linked by an asterisk is described in each numbered pattern. When a pattern is counted twice, it means that it started and ended equally, under the same conditions (i.e., contextual variables), but could have different paths. For example, the patterns 1, 2, 4 and 5 in Figure 3d represent the sequential pattern of FEep in the drawn matches of the playoffs (excluding the third-place match) that most likely begin two moments before ball recovery (i.e., lag is -2) in the field zone 8 (B5) through DTSd and TSaa. The ball is then likely to remain in field zone 8 or progress to field zone 6 (B6). In both situations, the first defender and the second defender are probably in field zone 8 and 6, respectively, with the latter most probably doing the tactical–technical action of contention (DSc). Lastly, FEep is likely to be performed in either field zone 4 or field zone 6.

Figure 2.

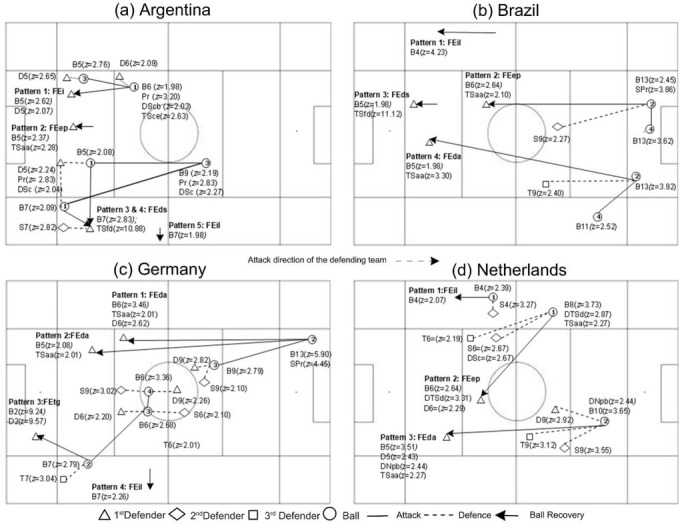
Successful Teams’ Defensive Patterns of Play in Field Zones. Notes. The greatest precision of positioning corresponds to field zones positive numbers in Figure 1; Negative numbers correspond to lags B = Ball Field Zones; D = First Defender Field Zones; S = Second Defender Field Zones; T = Third Defender Field Zones; FEda = End of defensive by Heading; FEds = End of defensive phase by tackle; FEep = End of defensive phase by Ball carrier error; FEi = End of defensive phase by Interception; FEil = End of defensive phase by Interruptions and laws infractions; FEtg = End of defensive phase by Goalkeeper technique; DNpb = Non-Possession of the Ball; DTSd = Transition-state attack/defence; DSc = Second defender contention; DScb = Second Defender Cover; Pr = Relative Numerical Superiority; SPr = Relative Numerical Inferiority; TSaa = Delay sub-phase; TSce = Controlling space sub-phase; TSfd = Forcing the opponent direction/Reducing space sub-phase.

Figure 3.

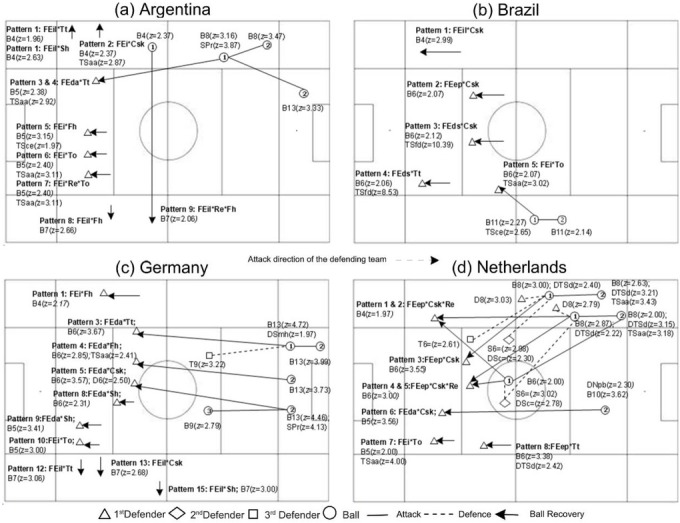
Successful Teams’ Defensive Patterns of Play in Field Zones According to Halves, Opponent Quality, Match Status and Stage of Competition.

Notes. The greatest precision of positioning corresponds to field zones positive numbers in Figure 1; Negative numbers corresponds to lags; B = Ball Field Zones; D = First Defender Field Zones; S = Second Defender Field Zones; T = Third Defender Field Zones; Tt = Tier 2; To = Tier 1; Fh = First Half; Sh = Second Half; Csk = Play-offs excluding Third Place and Final; Re = Drawing; FEda = End of defensive by Heading; FEds = End of defensive phase by tackle; FEep = End of defensive phase by Ball carrier error; FEi = End of defensive phase by Interception; FEil = End of defensive phase by Interruptions and laws infractions; DNpb = Non-Possession of the Ball; DTSd = Transition-state attack/defence; DSc = Second defender contention; DSmh = Second Defender Player Marking; SPr = Relative Numerical Inferiority; TSaa = Delay sub-phase; TSce = Controlling space sub-phase; TSfd = Forcing the opponent direction/Reducing space sub-phase;

How did successful teams generally perform to recover the ball?

As shown in Figure 2, we found sequential patterns for FEda in Brazil, the Netherlands and Germany. Furthermore, Brazil and Argentina showed a pattern of FEds and FEi, respectively. Germany did not show patterns of FEep, in contrast to the other three teams. However, Germany was the only one that presented a sequential pattern for FEtg. Lastly, FEil patterns were seen in all the teams.

Did successful teams play a defensive style according to the tactical modelling?

The Netherlands was the only team that evidenced sequential patterns related to a type of development of defensive play; specifically, Development by Non-Possession of the Ball (i.e., DNpb) in FEda and Development by Transition-state Attack/Defence (i.e., DTSd) coupled with the sub-phase of delay (i.e., TSaa).

Did the successful teams present self-similar patterns by halves?

Germany showed a self-similar pattern, i.e., part can be interpreted as a reduced scale of the whole (Mandelbrot, 1967), with a pattern of FEda and FEil in the first and the second half (i.e., FH and SH), respectively. Argentina also showed a self-similar pattern for the latter type of ball recovery in the first half. Similarly, both teams showed patterns of FEil in the second half, which ceased to appear in full matches.

Were the successful teams’ patterns related to the opponent’s quality?

Argentina and Germany performed more FEil and FEda when facing teams that lost in the eight- or quarterfinals (Tt), i.e., worse teams, but more FEi when facing the other semi-finalists’ teams (To), which were of similar quality. The Netherlands and Brazil also demonstrated this last association. The Netherlands and Brazil were associated to FEep and FEds, respectively, when they played against worse opponents.

Did the competition stage influence the sequential patterns?

The patterns of play to FEep, FEda, FEds, and FEil of Brazil, Germany and the Netherlands in the matches excluding the third-place (Csk) and final matches, were self-similar. However, the pattern of FEil of Argentina was not stable, as the final match disturbed the pattern.

Did the successful teams defend differently when losing, drawing or winning?

None of the teams showed patterns for any type of ball recovery in different match status, with the exception of the Netherlands and Argentina, which showed patterns of play to FEep and FEil when drawing and drawing in the first half (i.e., Re and Re*FH), respectively.

Discussion

The aims of this study were to identify the statistical differences and associations of EDP patterns among and within successful teams of the 2014 FIFA World Cup, according to tactical modelling and contextual variables such as halves, match status, opponent quality and stage competition.

Our findings of defensive sequence duration indicate differences between successful teams in time spent to EDP. Despite different methods, Vogelbein et al. (2014) showed similar results with respect to time to directly recover the ball. They found that defensive time reactions segregated top teams from in-between and bottom teams. However, defensive transition in this study resulted in fewer shots off goal in Brazil (i.e., fourth-placed). This partly contradicts the findings of Delgado-Bordonau et al. (2013), who found that shots received on target and off target were higher among losing teams. Thus, more complex approaches are required in addition to the analysis of specific tasks (Garganta, 2009).

Moreover, the Netherlands team had the most time on defence. A possible explanation could be the use of three/five defenders by this team. For instance, studies like Bradley et al. (2011) found that players in a 1-4-5-1 formation compared to 1-4-4-2 and 1-4-4-3 formations achieved more very-high intensity running when their teams were not in possession. Similar designs and the addition of formations with three/five defenders, should be encouraged when studying the defensive phase.

The main finding in this study is the prominence of goalkeeper’s technique in the World Cup 2014 Championship. Liu et al. (2015) found that high-level goalkeepers in the Spanish First Division performed fewer ball recoveries than intermediate and low-level teams. These differences could be explained by our study’s exclusive selection of high-level teams. Regardless of that, this emphasizes the importance of considering the goalkeeper in team play, and in research analysis, which sometimes is excluded (for a review see Sarmento et al., 2018).

Another finding of this study was that the defender’s timing to perform a tactical–technical behaviour against the ball carrier (i.e., delay) was associated with more effective ball recoveries. Related to this, sequential analysis showed that successful teams performed more interceptions when facing similar quality teams. Both findings demonstrate the importance of not only training players’ perception and decision-making (Roca et al., 2018), but also the coordination of their interactions (Davids et al., 2013; Ribeiro et al., 2017).

The sequential analysis results showed ball recovery patterns (i.e., FEda, FEds, FEi, FEil, FEep, FEtg). Additionally, as seen in Figure 2(a), a pattern for tackles (i.e., numbers 3 and 4) was found for Argentina, whose ball recovery occurred in the right strip and lower defensive midfield sector. Interestingly, this pattern started in lower zones and advanced into higher and lateral ones. If we then consider the different types of defending styles, such as low-high pressing and low-medium-high defensive blocks (Bangsbo and Peitersen, 2002; Fernandez-Navarro et al., 2016), it seems plausible to infer that, in this specific pattern, Argentina demonstrates a low defensive block style as it forces the opponent to retreat from an advantageous zone for goal scoring. Here, this zone is mentioned as number 10 for the attacking team, while in other studies it is Zone 14 (Taylor et al., 2002). These findings could help coaches recognize certain particularities of defensive play, to create their own team playing style, and design training exercises in Positioning or Game Training (O’Connor et al., 2017).

Nevertheless, it may be insufficient to consider only the exact moment that the ball is regained to infer defensive styles. For instance, it is apparent that teams performed a central high-pressure or lateral high-pressure (e.g., pattern number 2 in Figure 2d) before recovering the ball in their defensive midfield. This demonstrates the importance of using more holistic methods (Garganta, 2009; Ribeiro et al., 2017; Sarmento et al., 2018). Despite this, the results of ball recovery zones are consistent with previous works that considered the same competition with the same teams (Maleki et al., 2016), and the 2010 World Cup (Barreira et al., 2014).

In a study identical to ours, Almeida et al. (2014) used a multinomial model to analyse the different types of ball recovery in the UEFA Champions League teams. Both studies found that playing against lower-ranked teams increased the chances of recovering the ball by a tackle versus interception. Likewise, studies have found that tackling in the 2014 World Cup had a positive effect for winning teams (Liu et al., 2015). This implies that even if teams adopt a defensive style of play, they should be adaptive to the constraints of the environment (Davids et al., 2013) and consider having or switching the rule of exercise in training (Ishii et al., 2018).

On the other hand, because of lower frequencies in match status, stage competition and in ineffective EDP, the results of our study require careful interpretation. It is also challenging to generalize the teams’ performances from one competition alone. For a more comprehensive knowledge of teams’ defensive patterns of play, further research should emphasize the relationship across competitions (e.g., domestic competitions), and increase the number of EDP types.

The methods used in this study are believed to give pertinence and meaning to the practical context of soccer and coaches could use the findings either to generally prepare their defensive style of play or set strategies of the attack. In conclusion, successful defence in soccer seems to be associated with regularity and repeatability, and also flexibility, as different patterns in successful teams in the 2014 FIFA World Cup were found in halves, match status, and opponent quality, revealing the importance of not only consolidating the defensive play, but also including tasks and environment constraints in practice.