Abstract
Purpose
To investigate whether predictions of retinal nerve fiber layer (RNFL) thickness obtained from a deep learning model applied to fundus photographs can detect progressive glaucomatous changes over time.
Design
Retrospective cohort study.
Participants
Eighty-six thousand one hundred twenty-three pairs of color fundus photographs and spectral-domain (SD) OCT images collected during 21 232 visits from 8831 eyes of 5529 patients with glaucoma or glaucoma suspects.
Methods
A deep learning convolutional neural network was trained to assess fundus photographs and to predict SD OCT global RNFL thickness measurements. The model then was tested on an independent sample of eyes that had longitudinal follow-up with both fundus photography and SD OCT. The ability to detect eyes that had statistically significant slopes of SD OCT change was assessed by receiver operating characteristic (ROC) curves. The repeatability of RNFL thickness predictions was investigated by measurements obtained from multiple photographs that had been acquired during the same day.
Main Outcome Measures
The relationship between change in predicted RNFL thickness from photographs and change in SD OCT RNFL thickness over time.
Results
The test sample consisted of 33 466 pairs of fundus photographs and SD OCT images collected during 7125 visits from 1147 eyes of 717 patients. Eyes in the test sample were followed up for an average of 5.3 ± 3.3 years, with an average of 6.2 ± 3.8 visits. A significant correlation was found between change over time in predicted and observed RNFL thickness (r = 0.76; 95% confidence interval [CI], 0.70–0.80; P < 0.001). Retinal nerve fiber layer predictions showed an ROC curve area of 0.86 (95% CI, 0.83–0.88) to discriminate progressors from nonprogressors. For detecting fast progressors (slope faster than 2 μm/year), the ROC curve area was 0.96 (95% CI, 0.94–0.98), with a sensitivity of 97% for 80% specificity and 85% for 90% specificity. For photographs obtained at the same visit, the intraclass correlation coefficient was 0.946 (95% CI, 0.940–0.952), with a coefficient of variation of 3.2% (95% CI, 3.1%–3.3%).
Conclusions
A deep learning model was able to obtain objective and quantitative estimates of RNFL thickness that correlated well with SD OCT measurements and potentially could be used to monitor for glaucomatous changes over time.
Keywords: Artificial intelligence, Deep learning, Fundus photography, Glaucoma, OCT, Optic disc, Progression
Abbreviations and Acronyms: AUC, area under the receiver operating characteristic curve; CI, confidence intervals; CoV, coefficient of variation; ICC, intraclass correlation coefficient; MD, mean deviation; M2M, machine-to-machine; PSD, pattern standard deviation; ResNet, residual deep neural network; ROC, receiver operating characteristic; RNFL, retinal nerve fiber layer; SD, spectral-domain
Detection of glaucoma progression is a fundamental part of glaucoma management because it provides a means to identify patients who may require escalation in treatment.1 , 2 Although progression traditionally has been measured by assessing changes in visual field sensitivity,3, 4, 5 many patients show optic disc or retinal nerve fiber layer (RNFL) changes in the absence of detectable deterioration on perimetric tests, providing an opportunity to commence or increase treatment before significant decline in vision.6, 7, 8 In addition, detecting structural change can help to establish a diagnosis of glaucoma in those suspected of having the disease.9 Given the wide variability in the normal appearance of the optic nerve, confirmation of a diagnosis of glaucoma frequently requires demonstration of progressive damage over time.
Because of its ability to quantify neural loss objectively, spectral-domain (SD) OCT has established itself as a widely used tool for longitudinal assessment of structural changes in glaucoma, presenting high reproducibility at a micrometer-scale resolution.10 However, despite its increasing availability, SD OCT devices remain exceedingly rare in many clinical settings, notably in developing countries. In addition, the use of SD OCT for screening purposes or for monitoring glaucoma suspects outside of specialized centers is difficult because of the prohibitive costs and the requirement for well-trained technicians.
Recent advances in artificial intelligence algorithms, notably deep learning neural networks, have led to exciting prospects in automating the assessment of structural glaucomatous damage using fundus photography.11, 12, 13, 14 Fundus photography is an attractive method to document and identify optic nerve damage in glaucoma, given its low cost and widespread availability. However, subjective evaluation of photographs suffers from low reproducibility, even when performed by expert graders.15, 16, 17 Human graders frequently underestimate or overestimate the likelihood of glaucoma in cross-sectional evaluations and cannot identify longitudinal changes reliably when masked for the time sequence of photographs.18 Although deep learning models have been trained successfully to replicate human gradings of fundus photographs for glaucoma,11 these models are bounded to replicate these same errors, leading to low accuracy when applied to clinical settings or screening situations.
This realization prompted us to develop a novel deep learning algorithm that was trained to predict objective metrics of glaucomatous damage, rather than subjective gradings by humans. This was achieved by training the algorithm to analyze fundus photographs and to predict quantitative measurements of glaucomatous damage provided by SD OCT, such as RNFL thickness and neuroretinal rim measurements, an approach that we named machine-to-machine (M2M) algorithm.12 , 13 In previous publications, the M2M predictions showed high correlation with the original SD OCT observations.12 , 13 The M2M approach may offer advantages compared with previous deep learning approaches in glaucoma: training is objective and does not require human labeling, predictions generally are more accurate than human gradings,19 and the quantitative nature of the predictions allows for flexibility in determining cutoffs, rather than the yes-or-no binary outputs of previous approaches. Also, given its quantitative nature, potential exists for longitudinal monitoring of change over time, which would allow fundus photographs to be used as an objective method for structural assessment of glaucoma in settings where SD OCT may not be available.
In the present study, we investigated the ability of deep learning predictions of RNFL thickness from fundus photographs to detect glaucoma progression as measured by SD OCT in a cohort of patients followed over time. We also investigated the repeatability of the predictions, an essential step in validating a proposed tool for detection of change over time.
Methods
The dataset for this study was collected from the Duke Glaucoma Registry, a database of electronic medical and research records at the Vision, Imaging and Performance Laboratory of the Duke Eye Center.20 The institutional review board from Duke University approved this study with a waiver of informed consent because of the retrospective nature of this work. All methods adhered to the tenets of the Declaration of Helsinki for research involving human subjects, and the study was conducted in accordance with regulations of the Health Insurance Portability and Accountability Act.
The database contained longitudinal information on comprehensive ophthalmologic examinations during follow-up, diagnoses, medical history, visual acuity, slit-lamp biomicroscopy findings, intraocular pressure measurements, and results of gonioscopy and dilated slit-lamp funduscopic examinations. In addition, the repository contained fundus photographs obtained with the Nidek 3DX (Nidek) and Visupac FF-450 (Carl Zeiss Meditec, Inc), standard automated perimetry (Humphrey Field Analyzer II [Carl Zeiss Meditec, Inc.), and Spectralis SD OCT (software version 6.8; Heidelberg Engineering, GmbH) images and data. Standard automated perimetry was acquired with the 24-2 Swedish interactive threshold algorithm (Carl Zeiss Meditec, Inc.). Only patients with open angles on gonioscopy were included. Visual fields were excluded if they had more than 33% fixation losses or more than 15% false-positive errors. Patients also were excluded if they had other ocular or systemic diseases that could affect the optic nerve or the visual field. Therefore, tests performed after any diagnosis of retinal detachment, retinal or malignant choroidal tumors, nonglaucomatous disorders of the optical nerve and visual pathways, uveitis, and venous or arterial retinal occlusion according to International Classification of Diseases codes were excluded. In addition, tests performed after treatment with panretinal photocoagulation, according to Current Procedural Terminology codes, were also excluded.
Diagnosis of glaucoma was defined based on the presence of glaucomatous visual field loss on standard automated perimetry (pattern standard deviation of <5% or glaucoma hemifield test results outside normal limits) and signs of glaucomatous neuropathy as based on records of slit-lamp fundus examination. Glaucoma suspects were those with history of elevated intraocular pressure, with suspicious appearance of the optic disc on slit-lamp fundus examination, or with other risk factors for the disease.
Images were acquired with the Spectralis SD OCT to assess the RNFL. The device uses a dual-beam SD OCT and a confocal laser-scanning ophthalmoscope that uses a superluminescent diode light with a center wavelength of 870 nm and an infrared scan to provide simultaneous images of ocular microstructures. The Spectralis RNFL circle scan was used for this study. The global average circumpapillary RNFL thickness corresponds to the 360° measure automatically calculated by the SD OCT software from a total of 1536 A-scan points acquired from a 3.45-mm circle centered on the optic disc. Corneal curvature measurements were entered into the instrument software to ensure accurate scaling of all measurements, and the device’s eye-tracking capability was used during image acquisition to adjust for eye movements and to ensure that the same location of the retina was scanned over time. All scans that had a quality score lower than 15 were excluded from this analysis. Furthermore, scans that had average global RNFL thickness measurements with implausible values were excluded (i.e., less than 20 μm and more than 150 μm). Those cutoffs represent measurements above the higher range of reported RNFL thickness for normal control participants and less than the lower range for glaucoma patients21, 22, 23 and may indicate the presence of acquisition or segmentation errors in the presence of otherwise good-quality scores.24
For each eye of each patient, we considered all the available photographs that had been acquired at each visit over time and matched them to the closest Spectralis SD OCT RNFL scans acquired within a maximum of 6 months from the photograph date. Of note, multiple photographs and multiple Spectralis scans were obtained at each visit for some eyes, generating multiple pairs of photographs and SD OCT images at each visit for each eye. Having multiple pairs helped increase the variability of the sample for training the deep learning network. In addition, the repeated measurements at each visit also were used to assess the repeatability of the model predictions, as described below.
Development of the Machine-to-Machine Deep Learning Algorithm
A deep learning algorithm initially was trained to predict SD OCT global RNFL thickness from assessment of color fundus photographs. The trained M2M model then was used to predict RNFL thickness measurements from fundus photographs of eyes in an independent sample, and we investigated whether longitudinal change in RNFL thickness predictions was associated with change in the actual SD OCT measurements over time.
From a total of 86 123 pairs of SD OCT images and color fundus photographs collected at 21 232 visits from 8831 eyes of 5529 patients, we set aside a test sample consisting of 50% of all patients who had at least 2 longitudinal photograph visits during follow-up. The remaining patients were used for training and fine tuning (validation) of the model. This choice was justified by the fact that patients with only 1 visit would not contribute to assessing change over time, but rather would contribute to training and validating the model for predicting RNFL thickness measurements. Importantly, to prevent leakage and biased estimates of test performance, no data of any patient was present in both the training and validation sample and the test sample, that is, the randomization was carried out at the patient level. Furthermore, application of the model to the test sample was performed only after all steps of training and validation had been completed and the model was considered final.
For training the deep neural network, a pair of training targets consisted of a single optic disc photograph and the average RNFL thickness value from the corresponding SD OCT scan. Photographs initially were preprocessed to derive data for the deep learning algorithm. In the case of stereophotographs, the photograph was split, creating a pair of photographs from the stereoviews. An object detection deep learning network (single-shot detector) was used to extract the optic nerve and surrounding region from each photograph. The images then were downsampled to 256 × 256 pixels and pixel values were scaled to range from 0 to 1. Data augmentation was performed to increase heterogeneity of the photographs, reducing the possibility of overfitting and allowing the algorithm to learn the most relevant features. Data augmentation included the following: random lighting, consisting of subtle changes in image balance and contrast; random rotation, consisting of rotations of up to 10° in the image; and random flips, consisting of flipping the image vertically or horizontally.
We used the Residual deep neural Network (ResNet50) architecture.25 In brief, these networks use identity shortcut connections that skip 1 or more layers and greatly decrease the vanishing gradient problem when training deep networks. In the present work, a ResNet50 that had been trained previously on the ImageNet dataset was used.26 However, because the recognition task of the present work largely differed from that of ImageNet, further training was performed by initially unfreezing the last 2 layers. Subsequently, all layers were unfrozen, and training was performed using differential learning rates. The network was trained with minibatch gradient descent of size 64 and Adam optimizer.27 , 28 The best learning rate was found using the cyclical learning method with stochastic gradient descents with restarts.29
Statistical Analysis
Assessment of Longitudinal Change
The fully trained M2M model was used to obtain predictions of RNFL thickness in the test sample. A joint longitudinal mixed-effects model then was used to assess whether change over time in RNFL predictions from fundus photographs was correlated with change on actual SD OCT RNFL thickness measurements. These models have been described in detail elsewhere and are used routinely for investigating how 2 processes change over time, while considering the correlations among observations over time and among eyes of the same individual.30 , 31 The performance of the deep learning algorithm in predicting actual SD OCT RNFL thickness measurements in the test sample was quantified by measuring the correlation between predicted and observed measurements, as well as by calculating the median absolute deviation and mean absolute error of the predictions.
In addition to the overall association between longitudinal measurements, we were interested in whether the fundus photograph predictions would be able to detect substantial, likely clinically relevant, changes on SD OCT RNFL thickness over time. Although a cutoff for clinically significant change on SD OCT is not well established, information from previous studies on age-related RNFL loss may help in providing some suitable levels. For Spectralis SD OCT, it has been shown that 95% of healthy individuals show longitudinal change in global RNFL thickness at a rate slower than approximately 1 μm/year.32 , 33 Therefore, we considered eyes with statistically significant slopes of SD OCT RNFL thickness change over time at a rate faster than –1 μm/year as progressors. Nonprogressors were considered as those eyes that had nonstatistically significant slopes or with change slower than –1 μm/year. We also investigated the ability of M2M RNFL predictions to detect eyes with significant progression at rates faster than –1.5 μm/year (moderate) and –2.0 μm/year (fast progression).
Receiver operating characteristic (ROC) curves were used to assess the ability of change in M2M-predicted RNFL thickness from fundus photographs in discriminating nonprogressor eyes from eyes with progression as defined by SD OCT. The ROC curve provides the tradeoff between the sensitivity and 1 – specificity. The area under the ROC curve (AUC) was used to summarize the diagnostic accuracy of each parameter. An AUC of 1.0 represents perfect discrimination, whereas an AUC of 0.5 represents chance discrimination. Sensitivity at fixed specificities of 80% and 90% also were reported.
To account for using multiple images of both eyes of the same participant in the analyses, a bootstrap resampling procedure was used to derive confidence intervals (CIs) and P values, where the cluster of data for the participant was considered as the unit of resampling to adjust standard errors. This procedure has been used previously to adjust for the presence of multiple correlated measurements from the same unit.34
Assessment of Repeatability
Repeatability of M2M predictions of RNFL thickness was investigated by measurements obtained from multiple fundus photographs acquired during the same day in the test sample. The repeatability of measurements was assessed by the intraclass correlation coefficient (ICC), coefficient of variation (CoV), and intravisit standard deviation. The ICC was obtained from a mixed-effects model with 3 levels of nesting (i.e., visit, eye, and patient levels). The test–retest repeatability was defined as 2.77 times the intravisit standard deviation, which indicated the interval within which 95% of the differences between measurements are expected to lie.35
Results
The dataset included 86 123 pairs of optic disc photographs and SD OCT scans collected during 21 232 visits from 8831 eyes of 5529 patients. The median number of days between the photograph and corresponding SD OCT visit was 0 (interquartile range, 0–86 days). The test sample consisted of 33 466 pairs of fundus photographs and SD OCT images collected during 7125 visits from 1147 eyes of 717 patients. Eyes in the test sample were followed up for an average of 5.3 ± 3.3 years with an average of 6.2 ± 3.8 visits. Table 1 shows demographic and clinical characteristics of the eyes in the test sample.
Table 1.
Demographic and Clinical Characteristics of Eyes and Patients Included in the Test Sample
| Glaucoma Suspect | Glaucoma | |
|---|---|---|
| No. of pairs of SD OCT images and photographs | 16 534 | 16 932 |
| No. of eyes | 625 | 522 |
| Age (yrs), mean ± standard deviation | 56.8 ± 14.2 | 63.9 ± 12.5 |
| Female gender (%) | 65.6 | 58.2 |
| Race (%) | ||
| White | 59.5 | 56.5 |
| Black | 40.5 | 43.5 |
| SAP MD (dB), mean ± standard deviation | 0.01 ± 1.13 | –4.67 ± 5.49 |
| SAP PSD (dB), mean ± standard deviation | 1.57 ± 0.38 | 4.72 ± 3.62 |
| SD OCT global RNFL thickness (μm), mean ± standard deviation | 96.1 ± 11.2 | 77.7 ± 17.6 |
| M2M predicted global RNFL thickness (μm), mean ± standard deviation | 94.3 ± 8.9 | 79.5 ± 15.5 |
| Follow-up (yrs), mean ± standard deviation | 5.1 ± 3.1 | 5.5 ± 3.4 |
| Rate of change in SD OCT RNFL thickness (μm/yr), mean ± standard deviation | –0.93 ± 0.47 | –0.79 ± 0.57 |
| Rate of change in M2M predicted RNFL thickness (μm/yr), mean ± standard deviation | –0.80 ± 0.62 | –0.76 ± 0.71 |
| Follow-up change in SD OCT global RNFL thickness (μm), mean ± standard deviation | –4.8 ± 5.0 | –4.7 ± 5.6 |
| Follow-up change in predicted RNFL thickness (μm), mean ± standard deviation | –4.1 ± 5.4 | –4.5 ± 6.2 |
MD = mean deviation; M2M = machine-to-machine; PSD = pattern standard deviation; RNFL = retinal nerve fiber layer; SAP = standard automated perimetry; SD = spectral-domain.
The mean prediction of global RNFL thickness from all fundus photographs in the test sample was 84.6 ± 14.4 μm, whereas the mean average RNFL thickness from all the corresponding SD OCT scans was 84.5 ± 17.0 μm (P = 0.77). A strong correlation was found between the predicted and the observed RNFL thickness values (R 2 = 63.6%; P < 0.001), with a median absolute deviation of 6.85 μm and mean absolute error of 8.12 μm.
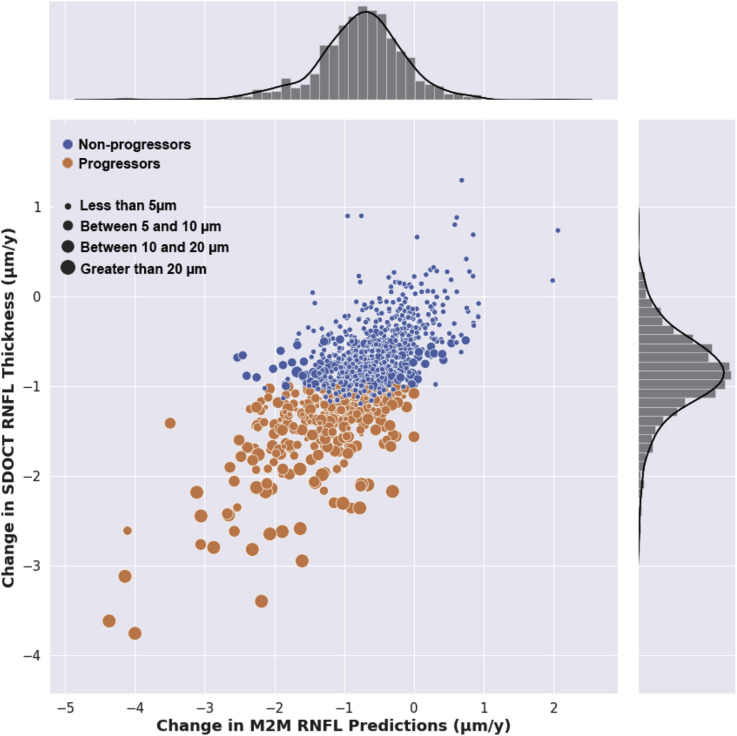
The average change in SD OCT global RNFL thickness for all eyes in the test sample was –4.8 ± 5.3 μm over the duration of follow-up, whereas the corresponding total change for M2M RNFL thickness predictions from fundus photographs was –4.3 ± 5.8 μm. The median absolute difference in total change over the duration of follow-up was 1.1 μm (interquartile range, 0.46–3.2 μm). A significant correlation was found between change over time in predicted and observed RNFL thickness (r = 0.76; 95% CI, 0.70–0.80; P < 0.001). Average rates of change for M2M predictions and SD OCT observations were –0.87 ± 0.52 μm/year and –0.77 ± 0.67 μm/year, respectively. Figure 1 illustrates a scatterplot of the relationship between rates of change over time in predicted versus observed RNFL thickness values, with the corresponding distributions in the sample. The correlations between predicted and observed RNFL thickness were not significantly different between glaucoma and glaucoma suspect eyes (r = 0.78 and r = 0.76, respectively; P = 0.31).
Figure 1.
Scatterplot illustrating the relationship between change in spectral-domain (SD) OCT retinal nerve fiber layer (RNFL) thickness over time and change in predicted RNFL thickness from fundus photographs (r = 0.76; P < 0.001). Different colors for scatter points indicate eyes of progressors and nonprogressors, as defined by SD OCT change. Size of points is proportional to the total amount of SD OCT RNFL thickness change during follow-up. M2M = machine-to-machine.
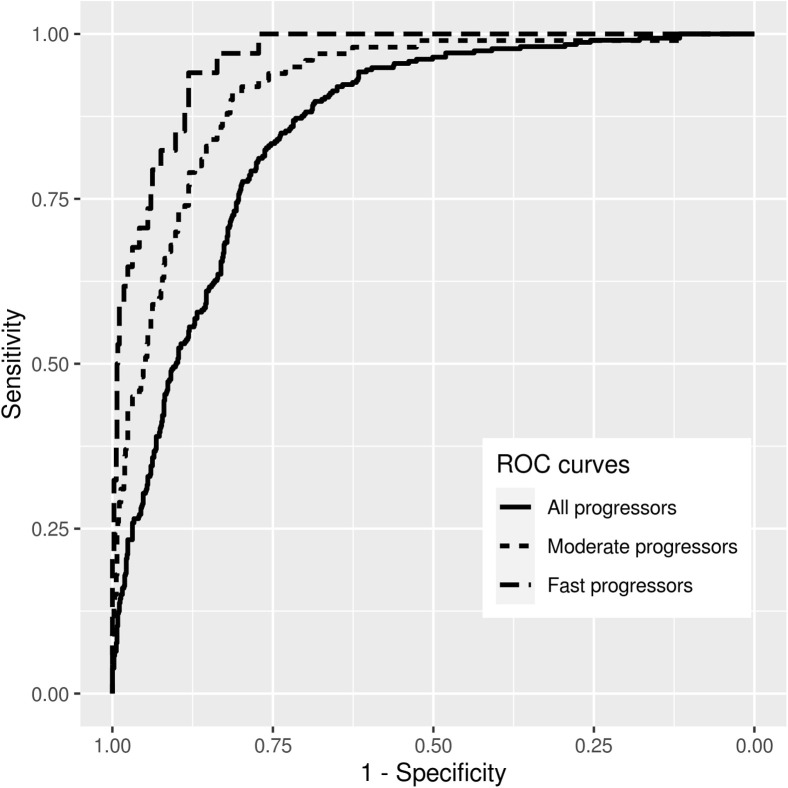
From the 1147 eyes in the test sample, 313 (27%) were considered progressors. These eyes had a mean slope of SD OCT RNFL change of –1.47 ± 0.45 μm/year and a mean total change of –10.5 ± 6.4 μm during the follow-up period. The remaining 834 eyes were considered nonprogressors and showed a mean slope of SD OCT change of –0.65 ± 0.34 μm/year and a mean total change of only –2.6 ± 2.5 μm during the follow-up period. Mean rates of change in M2M predictions of RNFL thickness were –1.30 ± 0.71 μm/year and –0.58 ± 0.53 μm/year for progressors and nonprogressors, respectively, with corresponding mean total changes during follow-up of –9.1 ± 7.0 μm versus –2.5 ± 4.0 μm, respectively. The M2M RNFL predictions showed an AUC of 0.86 (95% CI, 0.83–0.88) to discriminate progressors from nonprogressors. For specificity of 80%, the sensitivity was 76%; whereas, for specificity of 90%, the sensitivity was 50%. For detecting progressors that had rates of change faster than –1.5 μm/year, the M2M predictions showed an AUC of 0.92 (95% CI, 0.89–0.94). For specificity of 80%, the sensitivity was 91%; whereas, for specificity of 90%, the sensitivity was 70%. For detecting fast progressors with rates faster than –2 μm/year, the AUC was 0.96 (95% CI, 0.94–0.98). For specificity at 80%, the sensitivity for detecting fast progression was 97%. For specificity at 90%, the sensitivity was 85%. Figure 2 shows ROC curves for the ability of the M2M predictions to detect different rates of SD OCT change over time.
Figure 2.
Receiver operating characteristic (ROC) curves summarizing the ability of the fundus photograph deep learning model to discriminate progressors versus nonprogressors, as defined by spectral-domain OCT retinal nerve fiber layer (RNFL) thickness change during follow-up. Curves are shown for detecting overall progressors, as well as for detecting eyes progressing at rates faster than –1.5 μm/year (moderate progressors) and –2.0 μm/year (fast progressors).
During a total of 2112 visits in the test sample, repeated fundus photographs were obtained in the same visit and were used to estimate repeatability. The ICC was 0.946 (95% CI, 0.940–0.952), with CoV of 3.2% (95% CI, 3.1%–3.3%). The average intravisit standard deviation was 2.5 μm with calculated repeatability of 6.9 μm. No statistically significant relationship was found between intravisit standard deviation and mean of the predictions (Spearman ρ, –0.04; 95% CI, –0.08 to 0.001; P = 0.05). For SD OCT repeated tests, the ICC was 0.988 (95% CI, 0.987–0.990), with CoV of 1.6% (95% CI, 1.5%–1.7%). The average intravisit standard deviation was 1.3 μm with calculated repeatability of 3.6 μm.
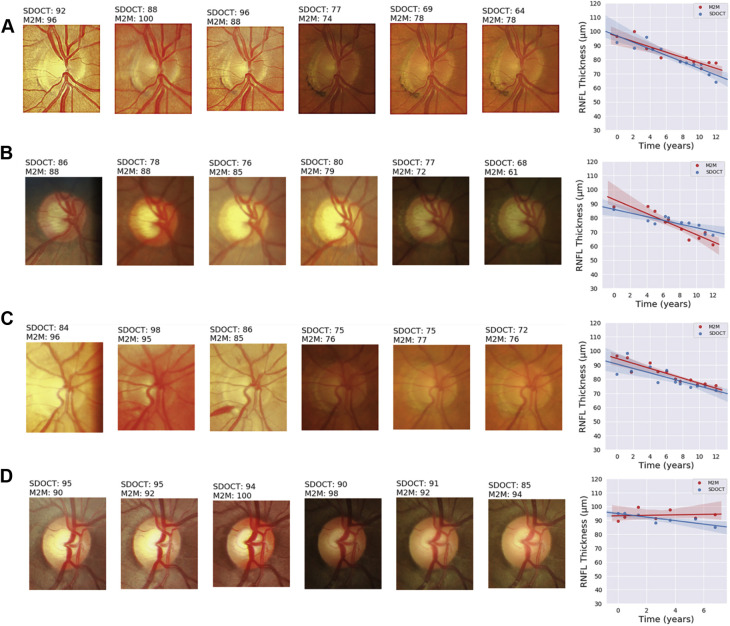
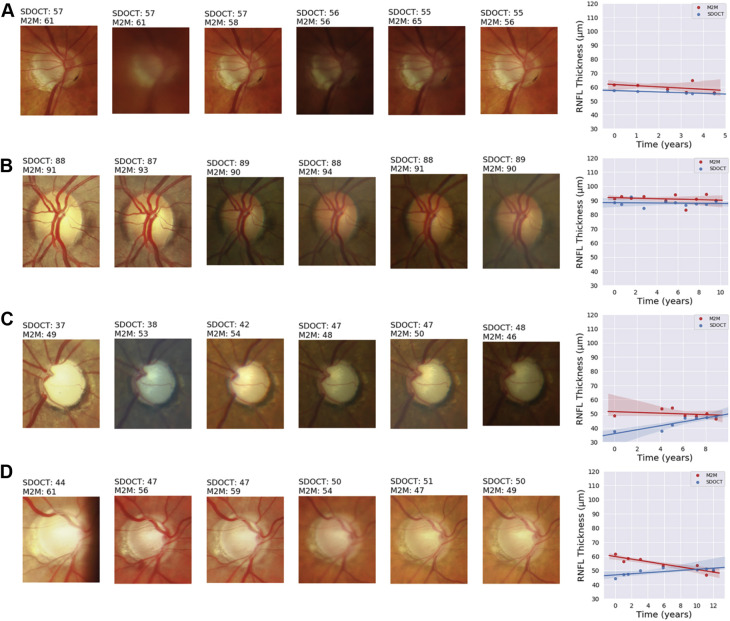
Figures 3 and 4 show several temporal sequences of fundus photographs from eyes included in the study classified as progressors and nonprogressors according to the rate of RNFL thinning during follow-up. Slopes of change, calculated for the actual RNFL thickness values measured by SD OCT and for the RNFL thickness predictions of the M2M, also are plotted for comparison.
Figure 3.
Illustrative examples of eyes included in the study that showed progression detected by spectral-domain (SD) OCT retinal nerve fiber layer (RNFL) thickness during follow-up. The sequence of fundus photographs shows 6 photographs, including the baseline (leftmost) and last (rightmost) available photographs during follow-up and randomly chosen intermediate ones. Slopes of change are shown adjacent to the sequence of photographs, colored in blue for the SD OCT slope and in red for the slope of predicted RNFL thickness from fundus photographs. A, B, C, Excellent agreement between SD OCT and predicted RNFL from photographs, with clear changes also seen by inspection of the fundus photographs. Of note, disc hemorrhages can be seen during follow-up in (A) and (C). D, Small, albeit statistically significant, changes on SD OCT, but the slope for predicted RNFL thickness from photographs remained relatively flat. M2M = machine-to-machine.
Figure 4.
Illustrative examples of eyes included in the study that were considered nonprogressors according to spectral-domain (SD) OCT retinal nerve fiber layer (RNFL) thickness during follow-up. The sequence of fundus photographs shows 6 photographs, including the baseline (leftmost) and last (rightmost) available photographs during follow-up and randomly chosen intermediate ones. Slopes of change are shown adjacent to the sequence of photographs, colored in blue for the SD OCT slope and in red for the slope of predicted RNFL thickness from fundus photographs. A, B, Good agreement in the slopes. C, Eye with advanced glaucoma that showed large variation on SD OCT RNFL thickness measurements, close to the floor. Predicted fundus photograph RNFL thickness remained stable over time. D, Mild decline of predicted RNFL thickness over time, whereas SD OCT remained essentially stable. Interestingly, this eye showed an inferior temporal disc hemorrhage over time, and also, changes in the inferior blood vessel seem to suggest an increase in the inferior cupping and rim loss. M2M = machine to machine.
Discussion
The present study showed that a deep learning algorithm trained to estimate objective RNFL thickness measurements using simple fundus photographs was able to detect significant glaucomatous changes over time that corresponded well to the changes seen on SD OCT. To the best of our knowledge, no previous study has investigated the potential of deep learning for detecting glaucoma progression using fundus photography.
Our current study confirms, now in a much larger sample of patients, the previous finding that accurate predictions of RNFL thickness can be obtained by applying deep learning to fundus photography.12 Overall, the correlation between predicted and observed RNFL thickness measurements was strong, with r = 0.80 and a median absolute deviation of only 6.85 μm. However, the main purpose of the present work was to investigate whether these predictions would be accurate enough to detect change over time. We found that changes in predicted RNFL thickness over time also were correlated strongly to changes in actual SD OCT measurements, with r = 0.76, and were able to discriminate progressors from nonprogressors, as defined by SD OCT change. It is important to qualify these findings according to the definition of progression used in our study and the context in which deep learning-assisted fundus photography eventually could be used. It would be unexpected for simple color fundus photographs to detect changes at the same level as a much more sophisticated and high-resolution imaging technique such as SD OCT. If enough tests are available, SD OCT theoretically can detect very small RNFL changes over time, even considerably less than 1 μm/year.22 , 36 However, such changes may be mostly the result of normal aging, as a previous study by Wu et al shows.32 We therefore wanted to investigate whether the M2M predictions would detect changes of magnitude large enough to be of clinical relevance. We considered statistically significant rates of change with magnitude faster than –1 μm/year as progression. Although the M2M predictions performed reasonably well to detect overall progressors, a more important result was the performance to detect fast progressors, because these likely would be of much greater risk for functional losses resulting from glaucoma developing.37 For detecting fast progressors, the predictions had an ROC curve area of 0.96, with a sensitivity of 97% for a specificity of 80%. For a high specificity of 90%, the predictions still detected 85% of fast progressors.
Our findings suggest that the M2M model applied to longitudinal optic disc photographs could be used to detect change and monitor structural glaucomatous progression reliably when SD OCT is not available, or perhaps as a complement to SD OCT assessment. As multiple studies have shown, many patients with glaucoma or suspected glaucoma may exhibit RNFL thickness change in the absence of detectable changes in perimetry.6, 7, 8 , 38 Progressive SD OCT RNFL loss has been shown to be significantly predictive of future visual field changes and also of decline in quality of life.39 By assessing photographs objective and quantitative, our algorithm creates opportunities for monitoring individuals suspected of disease at nonspecialized settings, with the potential of reducing the burden at highly specialized tertiary centers, which may be an especially important consideration given the aging population. This may be particularly important given recent concerns brought by the coronavirus 2019 pandemic and the requirements for social distancing.40 Of note, if used in the context of a screening tool for monitoring changes in patients with suspected glaucoma, a high specificity would be desirable while being able to detect significant changes with potential to trigger referral in most patients. If we consider eyes with fast progression, for example, the total loss over a 5-year average follow-up would amount to approximately 10 μm. Such loss would be highly predictive of glaucoma development, but it still would occur much earlier than any significant vision loss. For patients already diagnosed with glaucoma, the algorithm could still find applications in low-resource settings where SD OCT is not available and monitoring of nerve changes still relies on subjective funduscopy, cup-to-disc ratio measurements, and drawings.
Most previous studies on deep learning applied to fundus photography have attempted to replicate subjective gradings by humans in diagnosing glaucoma damage.11 , 14 However, subjective gradings are known to have low reproducibility and to misclassify eyes with physiologic large cups or small discs.15, 16, 17 Despite the reported high accuracy of such models, they essentially replicate some of the human biases and may have low performance when applied in clinical settings. In addition, they do not provide quantitative information, and therefore, would not be suitable for monitoring over time. In the assessment of glaucoma progression, a study by Jampel et al17 showed similarly that experts exhibit only slight to fair agreement when grading optic disc photographs for change. In contrast, the motivation behind the M2M model was to train a deep learning network to provide objective quantification of neural damage from fundus photographs that could be used not only to diagnose and stage glaucomatous damage on cross-sectional assessment, but also detect longitudinal changes.
A fundamental requirement of any test proposed to detect longitudinal change is to exhibit low test–retest variability. In our study, we were able to assess the repeatability of M2M predictions by analyzing fundus photographs that had been obtained on the same day. Both the ICC of 0.946 and the small CoV of 3.2% indicated high repeatability. The calculated repeatability of 6.9 μm indicated that 95% of the differences between measurements would be expected to lie within this value. This is compatible with the high accuracy of the algorithm in detecting changes in faster progressors. Importantly, no significant association was found between the intravisit standard deviation of predictions and the average value of the predictions, indicating that the predictions were repeatable throughout a large spectrum of disease severity. Coefficient of variation and repeatability interval were higher for the M2M predictions compared with original SD OCT measurements, as one would expect.
The assessment of repeatability as performed in our study had limitations. First, it was not planned prospectively, and we used an opportunistic sample of photographs that happened to have been obtained on the same visit day. It is possible that some photographs were retaken because of concerns about quality. However, this actually would decrease rather than increase the repeatability. In addition, we did not evaluate test–retest reproducibility of photographs obtained on different days and by different photographers. These other factors may also influence the variability of the predictions over time. Although photographs were obtained from 2 different cameras, it is unclear how the model would perform in photographs obtained from other cameras. Models evaluating quality of photographs potentially may be combined with the M2M approach potentially to improve the reliability of predictions. In fact, media opacities may affect the quality of photographs as individuals age, and this may affect the predictions of RNFL thickness. However, changes in media quality with aging also may affect SD OCT measurements to a large degree, as shown by Fortune et al.41 This underscores the need for progression definitions that account for expected age-related changes, as carried out in our study.
As another limitation of our study, the M2M algorithm was trained to estimate only the global average RNFL thickness measurements. Although algorithms in principle could be trained to predict sectoral measurements, the increase in variability may offset the gains in detecting change over time. Future studies should investigate and compare these different approaches. Finally, our model will benefit from external validation in populations from different geographic areas, with different prevalence of findings such as high myopia.
In conclusion, we demonstrated that a deep learning model was able to obtain objective and quantitative estimates of RNFL thickness that correlated well with SD OCT measurements and could be used to track RNFL changes over time. Given the widespread availability and simplicity of fundus photography, such a model could find application to screen for glaucomatous progression in settings where SD OCT may not be available or feasible.
Manuscript no. D-20-01026.
Footnotes
Disclosure(s): All authors have completed and submitted the ICMJE disclosures form. The author(s) have made the following disclosure(s): F.A.M.: Consultant – Aeri Pharmaceuticals; Allergan, Annexon, Biogen, Carl Zeiss Meditec, Galimedix, IDx, Stealth Biotherapeutics, Reichert; Financial support – Allergan, Carl Zeiss Meditec, Google, Inc., Heidelberg Engineering, Novartis, Reichert; Patent – nGoggle, Inc.
Supported in part by the National Eye Institute, National Institutes of Health, Bethesda, Maryland (grant nos.: EY029885 and EY031898 [F.A.M.]). The funding organization had no role in the design or conduct of this research.
HUMAN SUBJECTS: Human subjects were included in this study. The human ethics committees at Duke University approved the study with a waiver of informed consent because of the retrospective nature of this work. All research complied with the Health Insurance Portability and Accountability (HIPAA) Act of 1996 and adhered to the tenets of the Declaration of Helsinki.
No animal subjects were included in this study.
Author Contributions:
Conception and design: Medeiros
Analysis and interpretation: Medeiros, Jammal, Mariottoni
Data collection: Medeiros, Jammal, Mariottoni
Obtained funding: Medeiros
Overall responsibility: Medeiros, Jammal, Mariottoni
References
- 1.European Glaucoma Society Terminology and Guidelines for Glaucoma, 4th Edition—Chapter 3: Treatment principles and options supported by the EGS Foundation. Part 1: foreword; introduction; glossary; chapter 3 Treatment principles and options. Br J Ophthalmol. 2017;101(6):130–195. doi: 10.1136/bjophthalmol-2016-EGSguideline.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Prum B.E., Jr., Rosenberg L.F., Gedde S.J. Primary open-angle glaucoma Preferred Practice Pattern guidelines. Ophthalmology. 2016;123(1):P41–P111. doi: 10.1016/j.ophtha.2015.10.053. [DOI] [PubMed] [Google Scholar]
- 3.The AGIS Investigators The Advanced Glaucoma Intervention Study (AGIS): 7. The relationship between control of intraocular pressure and visual field deterioration. Am J Ophthalmol. 2000;130(4):429–440. doi: 10.1016/s0002-9394(00)00538-9. [DOI] [PubMed] [Google Scholar]
- 4.Leske M.C., Heijl A., Hussein M. Factors for glaucoma progression and the effect of treatment: the Early Manifest Glaucoma Trial. Arch Ophthalmol. 2003;121(1):48–56. doi: 10.1001/archopht.121.1.48. [DOI] [PubMed] [Google Scholar]
- 5.Heijl A., Leske M.C., Bengtsson B. Reduction of intraocular pressure and glaucoma progression: results from the Early Manifest Glaucoma Trial. Arch Ophthalmol. 2002;120(10):1268–1279. doi: 10.1001/archopht.120.10.1268. [DOI] [PubMed] [Google Scholar]
- 6.Abe R.Y., Diniz-Filho A., Zangwill L.M. The relative odds of progressing by structural and functional tests in glaucoma. Invest Ophthalmol Vis Sci. 2016;57(9):OCT421–OCT428. doi: 10.1167/iovs.15-18940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Garway-Heath D.F., Caprioli J., Fitzke F.W., Hitchings R.A. Scaling the hill of vision: the physiological relationship between light sensitivity and ganglion cell numbers. Invest Ophthalmol Vis Sci. 2000;41(7):1774–1782. [PubMed] [Google Scholar]
- 8.Medeiros F.A., Lisboa R., Weinreb R.N. A combined index of structure and function for staging glaucomatous damage. Arch Ophthalmol. 2012;130(9):1107–1116. doi: 10.1001/archophthalmol.2012.827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Silverman A.L., Hammel N., Khachatryan N. Diagnostic accuracy of the Spectralis and Cirrus reference databases in differentiating between healthy and early glaucoma eyes. Ophthalmology. 2016;123(2):408–414. doi: 10.1016/j.ophtha.2015.09.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tatham A.J., Medeiros F.A. Detecting structural progression in glaucoma with optical coherence tomography. Ophthalmology. 2017;124(12S):S57–S65. doi: 10.1016/j.ophtha.2017.07.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Li Z., He Y., Keel S. Efficacy of a deep learning system for detecting glaucomatous optic neuropathy based on color fundus photographs. Ophthalmology. 2018;125(8):1199–1206. doi: 10.1016/j.ophtha.2018.01.023. [DOI] [PubMed] [Google Scholar]
- 12.Medeiros F.A., Jammal A.A., Thompson A.C. From machine to machine: an OCT-trained deep learning algorithm for objective quantification of glaucomatous damage in fundus photographs. Ophthalmology. 2019;126(4):513–521. doi: 10.1016/j.ophtha.2018.12.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Thompson A.C., Jammal A.A., Medeiros F.A. A deep learning algorithm to quantify neuroretinal rim loss from optic disc photographs. Am J Ophthalmol. 2019;201:9–18. doi: 10.1016/j.ajo.2019.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Christopher M., Belghith A., Bowd C. Performance of deep learning architectures and transfer learning for detecting glaucomatous optic neuropathy in fundus photographs. Sci Rep. 2018;8(1):16685. doi: 10.1038/s41598-018-35044-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tielsch J.M., Katz J., Quigley H.A. Intraobserver and interobserver agreement in measurement of optic disc characteristics. Ophthalmology. 1988;95(3):350–356. doi: 10.1016/s0161-6420(88)33177-5. [DOI] [PubMed] [Google Scholar]
- 16.Varma R., Steinmann W.C., Scott I.U. Expert agreement in evaluating the optic disc for glaucoma. Ophthalmology. 1992;99(2):215–221. doi: 10.1016/s0161-6420(92)31990-6. [DOI] [PubMed] [Google Scholar]
- 17.Jampel H.D., Friedman D., Quigley H. Agreement among glaucoma specialists in assessing progressive disc changes from photographs in open-angle glaucoma patients. Am J Ophthalmol. 2009;147(1):39–44 e1. doi: 10.1016/j.ajo.2008.07.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chan H.H., Ong D.N., Kong Y.X. Glaucomatous Optic Neuropathy Evaluation (GONE) project: the effect of monoscopic versus stereoscopic viewing conditions on optic nerve evaluation. Am J Ophthalmol. 2014;157(5):936–944. doi: 10.1016/j.ajo.2014.01.024. [DOI] [PubMed] [Google Scholar]
- 19.Jammal A.A., Thompson A.C., Mariottoni E.B. Human versus machine: comparing a deep learning algorithm to human gradings for detecting glaucoma on fundus photographs. Am J Ophthalmol. 2020;211:123–131. doi: 10.1016/j.ajo.2019.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jammal A.A., Thompson A.C., Mariottoni E.B. Rates of glaucomatous structural and functional change from a large clinical population: the Duke Glaucoma Registry Study. Am J Ophthalmol. 2020 May 22;(20):S0002–9394. doi: 10.1016/j.ajo.2020.05.019. 30249-X. Online ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Varma R., Bazzaz S., Lai M. Optical tomography-measured retinal nerve fiber layer thickness in normal Latinos. Invest Ophthalmol Vis Sci. 2003;44(8):3369–3373. doi: 10.1167/iovs.02-0975. [DOI] [PubMed] [Google Scholar]
- 22.Patel N.B., Lim M., Gajjar A. Age-associated changes in the retinal nerve fiber layer and optic nerve head. Invest Ophthalmol Vis Sci. 2014;55(8):5134–5143. doi: 10.1167/iovs.14-14303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bowd C., Zangwill L.M., Weinreb R.N. Estimating optical coherence tomography structural measurement floors to improve detection of progression in advanced glaucoma. Am J Ophthalmol. 2017;175:37–44. doi: 10.1016/j.ajo.2016.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Asrani S., Essaid L., Alder B.D., Santiago-Turla C. Artifacts in spectral-domain optical coherence tomography measurements in glaucoma. JAMA Ophthalmol. 2014;132(4):396–402. doi: 10.1001/jamaophthalmol.2013.7974. [DOI] [PubMed] [Google Scholar]
- 25.He K., Zhang X., Ren S., Sun J. Deep residual learning for image recognition. ArXiv e-prints. 2016. https://arxiv.org/abs/1512 03385. Accessed 12.01.18.
- 26.Deng J., Dong W., Socher R. 2009 IEEE Conference on Computer Vision and Pattern Recognition. IEEE; Miami: 2009. ImageNet: a large-scale hierarchical image database; pp. 248–255. [Google Scholar]
- 27.Kingma D.P., Ba J. Adam: a method for stochastic optimization. ArXiv e-prints. 2014. https://arxiv.org/abs/1412.6980 Accessed 11.01.18.
- 28.Ruder S. An overview of gradient descent optimization algorithms. ArXiv e-prints. 2016. https://arxiv.org/abs/1609 04747. Accessed 11.01.18.
- 29.Smith L.N. Cyclical learning rates for training neural networks. ArXiv e-prints. 2017. https://arxiv.org/abs/1506 01186. Accessed 05.01.18.
- 30.Medeiros F.A., Leite M.T., Zangwill L.M., Weinreb R.N. Combining structural and functional measurements to improve detection of glaucoma progression using Bayesian hierarchical models. Invest Ophthalmol Vis Sci. 2011;52(8):5794–5803. doi: 10.1167/iovs.10-7111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Beckett L.A., Tancredi D.J., Wilson R.S. Multivariate longitudinal models for complex change processes. Stat Med. 2004;23(2):231–239. doi: 10.1002/sim.1712. [DOI] [PubMed] [Google Scholar]
- 32.Wu Z., Saunders L.J., Zangwill L.M. Impact of normal aging and progression definitions on the specificity of detecting retinal nerve fiber layer thinning. Am J Ophthalmol. 2017;181:106–113. doi: 10.1016/j.ajo.2017.06.017. [DOI] [PubMed] [Google Scholar]
- 33.Leung C.K.S., Ye C., Weinreb R.N. Impact of age-related change of retinal nerve fiber layer and macular thicknesses on evaluation of glaucoma progression. Ophthalmology. 2013;120(12):2485–2492. doi: 10.1016/j.ophtha.2013.07.021. [DOI] [PubMed] [Google Scholar]
- 34.Medeiros F.A., Sample P.A., Zangwill L.M. A statistical approach to the evaluation of covariate effects on the receiver operating characteristic curves of diagnostic tests in glaucoma. Invest Ophthalmol Vis Sci. 2006;47(6):2520–2527. doi: 10.1167/iovs.05-1441. [DOI] [PubMed] [Google Scholar]
- 35.Bland J.M., Altman D.G. Measurement error. BMJ. 1996;312(7047):1654. doi: 10.1136/bmj.312.7047.1654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Vianna J.R., Danthurebandara V.M., Sharpe G.P. Importance of normal aging in estimating the rate of glaucomatous neuroretinal rim and retinal nerve fiber layer loss. Ophthalmology. 2015;122(12):2392–2398. doi: 10.1016/j.ophtha.2015.08.020. [DOI] [PubMed] [Google Scholar]
- 37.Saunders L.J., Medeiros F.A., Weinreb R.N., Zangwill L.M. What rates of glaucoma progression are clinically significant? Expert Rev Ophthalmol. 2016;11(3):227–234. doi: 10.1080/17469899.2016.1180246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kuang T.M., Zhang C., Zangwill L.M. Estimating lead time gained by optical coherence tomography in detecting glaucoma before development of visual field defects. Ophthalmology. 2015;122(10):2002–2009. doi: 10.1016/j.ophtha.2015.06.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Medeiros F.A., Gracitelli C.P., Boer E.R. Longitudinal changes in quality of life and rates of progressive visual field loss in glaucoma patients. Ophthalmology. 2015;122(2):293–301. doi: 10.1016/j.ophtha.2014.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Centers for Disease Control and Prevention (CDC) Using telehealth to expand access to essential health services during the COVID-19 pandemic. 2020. https://www.cdc.gov/coronavirus/2019-ncov/hcp/telehealth.html Accessed 25.06.20.
- 41.Fortune B., Reynaud J., Cull G. The effect of age on optic nerve axon counts, SDOCT scan quality, and peripapillary retinal nerve fiber layer thickness measurements in Rhesus monkeys. Transl Vis Sci Technol. 2014;3(3):2. doi: 10.1167/tvst.3.3.2. [DOI] [PMC free article] [PubMed] [Google Scholar]