Mathematical model of Ebola and Covid-19 with fractional differential operators: Non-Markovian process and class for virus pathogen in the environment

Abstract

Differential operators based on convolution definitions have been recognized as powerful mathematics tools to help model real world problems due to the properties associated to their different kernels. In particular the power law kernel helps include into mathematical formulation the effect of long range, while the exponential decay helps with fading memory, also with Poisson distribution properties that lead to a transitive behavior from Gaussian to non-Gaussian phases respectively, however, with steady state in time and finally the generalized Mittag-Leffler helps with many features including the queen properties, transitive behaviors, random walk for earlier time and power law for later time. Very recently both Ebola and Covid-19 have been a great worry around the globe, thus scholars have focused their energies in modeling the behavior of such fatal diseases. In this paper, we used new trend of fractional differential and integral operators to model the spread of Ebola and Covid-19.

1. Introduction

Very recently, the world have been surprised with an outbreak of a fatal disease called COVID-19, Salath et al. [10], Zhu et al. [11], Tan et al. [14]. Severe Acute Respiratory Syndrome Coronavirus-2 (SARS-CoV-2) is a new type of virus family that has not been earlier identified in people. The virus seems to be transmitted mostly through the minute respiratory droplets via coughing, sneezing or when people interact with each other for some time in close proximity. These droplets can then be inhaled, or they can land on surfaces that others may come into touch with, who can then get contaminate when they contact their eyes, mouth, or nose.

The novel corona virus can live on different surface like few days (stainless steel and plastic) and few hours (cardboard, and copper). However, the amount of viable virus declines over time and may not always be present in sufficient numbers to cause infection. In humans, the symptoms of this virus can be experienced in between 1 to 14 days from the day of infection. From then it has been spreading at the speed of knots, giving no time to prepare against a newly identified infectious and notorious virus which have compelled the WHO to declare COVID-19 as a pandemic [1] due to its fast human to human transmission and people got infected in every continent and it had already taken so many lives. In applied mathematics, many new mathematical models have been suggested, some including fractional differential and fractal fractional operators [3], [4], [7], [12], [13].

EBOLA VIRUS DISEASE (EVD), caused by infection with the filo virus. The virus cause hemorrhagic fever to both monkeys and human. The disease was first observed in 1976 in the Ebola River valley in what is now the Democratic Republic of the Congo, Africa.1 Since then, Zaire ebola virus has caused a number of outbreaks over the past three decades and has culminated in the current largest outbreak, which has spanned a number of West African countries and spread throughout the world. The virus is transmitted via contact with mucous surfaces, non-intact skin, or through injury with contaminated needles. The disease course includes fever, aches, malaise, severe vomiting and diarrhea, as well as increased vascular permeability, which leads to profound intramuscular volume depletion. While the hemorrhagic manifestations can be as minor as petechiae and bruising, the disease can progress to include gastrointestinal hemorrhage, subsequent shock, and multi system organ dysfunction. Swelling of the brain and kidneys can occur as well as necrosis of internal organs including the liver, testis, and ovaries.The recent outbreaks in Liberia, Guinea, Sierra Leon, and Nigeria have been the largest to date. Furthermore, with cases appearing in the United States and Europe, concerns have been raised about the possibility of even further spread abroad. This article seeks to review the knowledge of the vascular, cardiac, and pulmonary effects of EVD collected across medical specialties. disease in tropical regions of the world.

Ebola virus that causes severe bleeding, organ failure and can lead to death. Humans may spread the virus to other humans through contact with bodily fluids such as blood. Initial symptoms include fever, headache, muscle pain and chills. Later, a person may experience internal bleeding resulting in vomiting or coughing blood. Treatment is supportive hospital care.

There are lots of Bio-mathematical models have been proposed to recognize the transferral dynamics of these type of infectious diseases. recently, modeling has become a valuable tool in the analysis of ebola disease transferral dynamics and to determine the factors that influence the spread of disease to support control measures. Many researchers have proposed epidemic model to study the transferral dynamics of ebola disease.

There is no specific medicine to cure ebola disease. Awareness programs can be helpful in reducing the prevalence of the disease. Different Bio-mathematical models have been proposed to study the impact of awareness in controlling ebola and these type diseases [5]. The study showed that, for small portion of infected individuals, the whole country could die out in a very short period of time in case there is not good prevention.

2. Preliminaries

In this section, we recall some basic definitions and properties of fractional calculus theory which are useful in the next sections.

Definition 2.1

Let $f:R+\to R$ and $\beta \in (n-1,n),n\in N$. The left Caputo fractional derivative of order f the function f is given by the following equality;

$${\displaystyle {}_0^C{D}_t^{\Theta }u\left(t\right)=\frac{1}{\Gamma (n-\Theta )}{\int }_0^t{(t-y)}^{n-\Theta -1}{u}^{\left(n\right)}\left(y\right)dy.}$$ (2.1)

Definition 2.2

Let $u\in H^1(a,b),b>a,\Theta \in [0,1]$ then the Caputo derivative of fractional order is given by (see in [9]):

$${\displaystyle D_t^{\Theta }\left(u\left(t\right)\right)=\frac{M\left(\Theta \right)}{(1-\Theta )}{\int }_a^t{u}^{{}^{\prime }}\left(x\right)\exp \left[{\displaystyle -\Theta \frac{t-x}{1-\Theta }}\right]dx.}$$ (2.2)

where $M\left(\Theta \right)$ is a normalization function such that $M\left(0\right)=M\left(1\right)=1$ [8]. But, if the function u ≠ H ₁(a, b) then, new derivative called the Caputo-Fabrizio fractional derivative can be defined as

$$D_t^{\Theta }\left(u\left(t\right)\right)=\frac{M\left(\Theta \right)}{(1-\Theta )}{\int }_a^t(u\left(t\right)-u\left(x\right))\exp [-\Theta \frac{t-x}{1-\Theta }]dx.$$ (2.3)

Definition 2.3

$u\in H^1(x,y),y>x,\Theta \in [0,1]$ with the function f differentiable then, the definition of the new fractional derivative (Atangana-Baleanu derivative in Caputo sense) is given as

$${}_a^{ABC}{D}_t^{\Theta }\left[u\left(t\right)\right]=\frac{B\left(\Theta \right)}{1-\Theta }{\int }_a^t\frac{d}{dt}u\left(x\right)E_{\Theta }[-\Theta \frac{{(t-x)}^{\Theta }}{1-\Theta }]dx.$$ (2.4)

where $B\left(\Theta \right)$ has the same properties as in the case of the Caputo-Fabrizio fractional derivative. Here $B\left(\Theta \right)=1-\Theta +\frac{\Theta }{\Gamma \left(\Theta \right)}.$

It should be noted that we do not recover the original function when $\Theta =0$ except when at the origin the function vanishes. To avoid this kind of problem, the following definition is proposed.

Definition 2.4

[2] Let $u\in H^1(x,y),y>x,\Theta \in [0,1]$ and not necessary differentiable then, the definition of the new fractional derivative (Atangana-Baleanu fractional derivative in Riemann-Liouville sense) is given as.

$${}_a^{ABR}{D}_t^{\Theta }\left[u\left(t\right)\right]=\frac{B\left(\Theta \right)}{1-\Theta }\frac{d}{dt}{\int }_a^{t}u\left(x\right)E_{\Theta }[-\Theta \frac{{(t-x)}^{\Theta }}{1-\Theta }]dx.$$ (2.5)

Definition 2.5

The fractional integral associate to the new fractional derivative with nonlocal kernel (Atangana-Baleanu fractional integral) is given as [2]:

$${}_a^{AB}{I}_t^{\Theta }\left[u\left(t\right)\right]=\frac{1-\Theta }{B\left(\Theta \right)}u\left(t\right)+\frac{\Theta }{B\left(\Theta \right)\Gamma \left(\Theta \right)}{\int }_a^{t}u\left(j\right){(t-j)}^{\Theta -1}dj.$$ (2.6)

When alpha is zero we recover the initial function and if also alpha is 1, we obtain the ordinary integral.

3. Model description

We begin to formulate the Ebola epidemic disease by considering the human population in three compartments, that is, the susceptible individuals, S(t), individuals infected with Ebola virus, I(t) and the individuals recovered from the Ebola virus, R(t). The individuals infected with Ebola and the deceased is D(t) and P(t) is the class for the Ebola virus pathogen in the environment. The model that describes the dynamics of Ebola disease modeled through differential equations is given by

$$\begin{array}{cc}& {\displaystyle \frac{dS}{dt}=\wedge -\lambda S-dS}\hfill \\ & {\displaystyle \frac{dI}{dt}=\lambda S-(d+\delta +{\varphi }_1)I}\hfill \\ & {\displaystyle \frac{dR}{dt}={\varphi }_{1}I-dR}\hfill \\ & {\displaystyle \frac{dD}{dt}=((d+\delta )I-ϵD),}\hfill \\ & {\displaystyle \frac{dP}{dt}=\varpi +\xi I+\theta D-\kappa P}\hfill \end{array}$$ (3.1)

where $\lambda ={\beta }_{1}I+{\beta }_{2}D+\psi P$ and the appropriate initial conditions are given by

$$S\left(0\right)=s_0,I\left(0\right)=I_0,R\left(0\right)=R_0,D\left(0\right)=D_0,P\left(0\right)=P_0.$$ (3.2)

The parameters of the model are given in the following Table.

Symbols	Description
$\wedge$	birth rate of the susceptible individuals
$d$	death rate
${\beta }_1\&{\beta }_2$	The susceptible individuals become infectious with the effective contact rate with the deceased human individuals
$\psi$	The susceptible are able to attract the disease from the contaminated environment rate
$\delta$	death rate of the infected individuals
${\varphi }_1$	recovery from infection
$ϵ$	people can be directly buried during funerals rate
$\varpi$	environment is contaminated by the Ebola virus rate
$\xi$	rate of infected shed the virus in the environment
$\xi$	rate of deceased shed the virus in the environment
$\kappa$	The virus decay of the Ebola virus from the population parameter

The sum of the first three equations of the Ebola disease model Eq. (3.1) is given by

$$\frac{dN}{dt}=\Lambda +dN-\delta I$$ (3.3)

where $N=S+I+R$ denotes the total alive human population. It should be noted that $ϵ\le (d+\delta )$ which is an appropriate condition for the compartment D for which the model becomes relevant, otherwise the deceased human individuals will disappear and the model would be irrelevant. Further, the model given by Eq. (3.1) is well posed and biologically feasible in the region given by

$$\Phi =\{M\in {\mathbb{R}}_{+}^5:N\left(t\right)\le \frac{\lambda }{d},D\left(t\right)\le \frac{(d+\delta )\lambda }{ϵd},P\left(t\right)=\frac{ϵ(d\varpi +\wedge \xi )}{d\kappa ϵ}\},$$ (3.4)

where $M=\left(S\right(t),I(t),R(t),D(t),P(t\left)\right).$

4. Existence and uniqueness

We present in this paper existence and uniqueness of system solution first we covert the model to volterra version

$$\begin{array}{cc}& S\left(t\right)=S\left(0\right)+{\int }_0^t(\wedge -(\lambda +d)S\left(\tau \right))d\tau \hfill \\ & I\left(t\right)=I\left(0\right)+{\int }_0^t(\lambda S\left(\tau \right)-(d+\delta +{\varphi }_1)I\left(\tau \right))d\tau \hfill \\ & R\left(t\right)=R\left(0\right)+{\int }_0^t({\varphi }_{1}I\left(\tau \right)-dR\left(\tau \right))d\tau \hfill \\ & D\left(t\right)=D\left(0\right)+{\int }_0^t\left(((d+\delta )I\left(\tau \right)-ϵD\left(\tau \right))\right)d\tau ,\hfill \\ & P\left(t\right)=P\left(0\right)+{\int }_0^t(\varpi +\xi I\left(\tau \right)+\theta D\left(\tau \right)-\kappa P\left(\tau \right))d\tau .\hfill \end{array}$$ (4.1)

we defined

$$\begin{array}{cc}& K_{1}S(t,S\left(t\right))=\wedge -\lambda S\left(t\right)-dS\left(t\right)\hfill \\ & K_{2}S(t,S,I))=\lambda S\left(t\right)-(d+\delta +{\varphi }_1)I\left(t\right)\hfill \\ & K_{3}S(t,S,R))`={\varphi }_{1}I\left(t\right)-dR\left(t\right)\hfill \\ & K_{4}S(t,I,D)=((d+\delta )I\left(t\right)-ϵD\left(t\right)),\hfill \\ & K_{5}S(t,P,I,D)=\varpi +\xi I\left(t\right)+\theta D\left(t\right)-\kappa P\left(t\right)\hfill \end{array}$$ (4.2)

The following norm will be used

$${\parallel \psi \parallel }_{\infty }=\underset{t\in D_{\psi }}{\sup }\left|\psi \right(t\left)\right|$$

To evaluate

$$|K_i(t,X)-K_i(t,X_1)|$$ (4.3)

and

$${|K_i(t,X)-K_i(t,X_1)|}^2$$ (4.4)

$$\begin{array}{cc}|K_1(t,S)-K_1(t,S_1)|\hfill & =\left|(x+d)(S-S_1)\right|\hfill \\ & =|\lambda +d||S-{\delta }_1|\hfill \\ & \le \underset{t\in [0,T]}{\sup }|\lambda +d||S-{\delta }_1|\hfill \\ & \le {\parallel \lambda +d\parallel }_{\infty }|S-{\delta }_1|\hfill \\ & \le r_1|S-{\delta }_1|\hfill \end{array}$$ (4.5)

$${|K_i(t,X)-K_i(t,X_1)|}^2$$ (4.6)

$$\begin{array}{cc}|K_2(t,I)-K_2(t,I_1)|\hfill & =\left|(d+\delta +{\varphi }_1)(I-I_1)\right|\hfill \\ & =\left|\right(d+\delta +{\varphi }_1\left)\right|\left|\right(I-I_1\left)\right|\hfill \\ & \le \left|\right(d+\delta +\varphi +ϵ\left)\right|\left|\right(I-I_1\left)\right|\hfill \\ & \le r_2\left|\right(I-I_1\left)\right|\hfill \end{array}$$ (4.7)

$$\begin{array}{cc}|K_3(t,D)-K_3(t,D)|\hfill & =ϵ|D-D_1(I-I_1)|\hfill \\ & \le (ϵ+\xi )\left|\right(D-D_1\left)\right|\hfill \end{array}$$ (4.8)

$$|K_4(t,R)-K_4(t,R_1)|\le (d+ϵ)\left|\right(R-R_1\left)\right|$$ (4.9)

$$|K_5(t,P)-K_5(t,P_1)|\le (K+d)\left|\right(P-P_1\left)\right|$$ (4.10)

In the same way

$$\begin{array}{ccc}& & {|K_1(t,S)-K_1(t,S_1)|}^2\hfill \\ & & ={\left|(\lambda +d)(S-S_1)\right|}^2\hfill \\ & & ={(\lambda +d)}^2{\left|\right(S-S_1\left)\right|}^2\hfill \\ & & =({\lambda }^2+2dX+d^2){\left|\right(S-S_1\left)\right|}^2\hfill \\ & & =({({\beta }_{1}I+{\beta }_{2}D+\psi P)}^2+2d({\beta }_{1}I+{\beta }_{2}D+\psi P)+d^2){\left|\right(S-S_1\left)\right|}^2\hfill \\ & & =({\beta }_1{I}^2+{\beta }_2{D}^2+{\psi }_2{P}^2+2{\beta }_{1}I{\beta }_{2}D+2{\beta }_{1}I\psi P\hfill \\ & & +2d\beta I+2d{\beta }_{2}D+2d\psi P+d^2){\left|\right(S-S_1\left)\right|}^2\hfill \\ & & \le ({\beta }_1^2\underset{t\in [0,T]}{\sup }\left|I^2\left(t\right)\right|+{\beta }_2^2\underset{t\in [0,T]}{\sup }|D^2\left(t\right)|+{\beta }_1^2\underset{t\in [0,T]}{\sup }\left|P^2\left(t\right)\right|\hfill \\ & & +2{\beta }_1{\beta }_2\underset{t\in [0,T]}{\sup }\left|I\right(t\left)\right|\underset{t\in [0,T]}{\sup }\left|D\right(t\left)\right|+2{\beta }_1\psi \underset{t\in [0,T]}{\sup }\left|I\right(t\left)\right|\underset{t\in [0,T]}{\sup }\left|P\right(t\left)\right|\hfill \\ & & +2d{\beta }_2\underset{t\in [0,T]}{\sup }\left|D^2\left(t\right)\right|+2{\beta }_1\psi \underset{t\in [0,T]}{\sup }\left|P\right(t\left)\right|+{\varphi }^2){\left|\right(S-S_1\left)\right|}^2\hfill \end{array}$$ (4.11)

$${|K_1(t,S)-K_1(t,S_1)|}^2\le r_3^2{\left|\right(S-S_1\left)\right|}^2$$ (4.12)

$${|K_2(t,I)-K_1(t,I_1)|}^2\le (d+2\delta +{\varphi }_1){\left|\right(I-I_1\left)\right|}^2$$ (4.13)

$${|K_3(t,D)-K_3(t,D_1)|}^2\le (d+\frac{3\delta }{2}){\left|\right(D-D_1\left)\right|}^2$$ (4.14)

$${|K_4(t,R)-K_3(t,R_1)|}^2\le {\left(\frac{3}{2}\right)}^2{\left|\right(R-R_1\left)\right|}^2$$ (4.15)

Finally

$${|K_5(t,P)-K_5(t,P_1)|}^2\le {(K+d)}^2{\left|\right(P-P_1\left)\right|}^2$$ (4.16)

5. Equilibrium point and stability analysis

We derive first the disease free equilibrium for the Eq. (3.1)

$$S=\frac{\Lambda }{d},I=0,R=0,P=0$$

$$E_0=(\frac{\Lambda }{d},0,0,0)\text{Since}\lambda =0$$

Now we derive the endemic equilibrium by setting the left hand to be zero

$$\Lambda -(\lambda +d)S^{*}=0$$ (5.1)

$$\lambda S-(d+\delta +{\varphi }_1)I^{*}=0$$ (5.2)

$$D=\frac{d+\delta }{ϵ}{I}^{*},R=\frac{{\varphi }_1}{d}{I}^{*}$$

$$\begin{array}{cc}{P}^{*}\hfill & {\displaystyle =\frac{{\displaystyle \varpi +\xi I^{*}+\theta \frac{d+\delta }{ϵ}{I}^{*}}}{\kappa }}\hfill \\ & ={\displaystyle \frac{{\displaystyle \varpi +(\xi +\theta \frac{d+\delta }{ϵ})I^{*}}}{\kappa }}\hfill \end{array}$$ (5.3)

$$\begin{array}{cc}S\hfill & {\displaystyle =\frac{\Lambda }{{\displaystyle d+{\beta }_1{I}^{*}+{\beta }_2\frac{d+\delta }{ϵ}{I}^{*}+\psi \left({\displaystyle \frac{{\displaystyle \varpi +\xi I^{*}+\theta \frac{d+\delta }{ϵ}{I}^{*}}}{\kappa }}\right)}}}\hfill \\ & {\displaystyle =\frac{\Lambda }{{\displaystyle d+({\beta }_1+{\beta }_2\frac{d+\delta }{ϵ}+\frac{\psi \xi }{\kappa }+\theta \psi \frac{d+\delta }{\kappa ϵ})I^{*}+\frac{\psi \varpi }{\kappa }}}}\hfill \end{array}$$ (5.4)

$$\begin{array}{cc}{S}^{*}\hfill & {\displaystyle =\frac{(d+\delta +\varphi )I^{*}}{{\displaystyle {\beta }_1{I}^{*}+{\beta }_2\frac{d+\delta }{ϵ}{I}^{*}+\psi {\displaystyle \frac{{\displaystyle \varpi +(\xi +\theta \frac{d+\delta }{ϵ})I^{*}}}{\kappa }}}}}\hfill \\ & {\displaystyle =\frac{d+\delta +\varphi }{{\displaystyle {\beta }_1+{\beta }_2\frac{d+\delta }{ϵ}+\frac{\psi }{\kappa }\left({\displaystyle \frac{\varpi }{I^{*}}+\xi +\theta \frac{d+\delta }{ϵ}}\right)}}}\hfill \end{array}$$ (5.5)

we now present the reproductive number to achieve this, we consider the following equations:

$$\frac{dI}{dt}=\lambda S-(d+\delta +{\varphi }_1)I$$

$$\frac{dP}{dt}=\varpi +\xi I+\theta D-\kappa P$$

here we define the function F and V

$$F=\left(\begin{array}{cc}{\beta }_1& \psi \\ 0& 0\end{array}\right)$$

$$V=\left(\begin{array}{cc}d+\delta +{\varphi }_1& \psi \\ -\xi & \kappa \end{array}\right)$$

$$F{V}^{-1}=\left(\begin{array}{cc}{\displaystyle \frac{{\beta }_1\kappa +\psi \xi }{(d+\delta +{\varphi }_1)\kappa +\psi \xi }}& {\displaystyle \frac{-\psi {\beta }_1+\psi (d+\delta +{\varphi }_1)}{(d+\delta +{\varphi }_1)+\psi \xi }}\\ 0& 0\end{array}\right)$$

Thus the reproductive number be expressed as

$$R_0=\frac{{\beta }_1\kappa +\psi \xi }{(d+\delta +{\varphi }_1)\kappa +\psi \xi }$$ (5.6)

we present the global asymptotic stability of disease-free and endemic. But first we prove the endemic possibility by assuming $\frac{dI}{dt}>0$ and $\frac{dD}{dt}>0$

$$\lambda S-(d+\delta +{\varphi }_1)I>0$$ (5.7)

$$\varpi +\xi I+\theta D-\kappa P>0$$ (5.8)

Such that

$$\lambda S>(d+\delta +{\varphi }_1)I$$ (5.9)

$$\varpi +\xi I+\theta D>\kappa P$$ (5.10)

However, we have that

$$(d+\delta )I-ϵD>0\to D<\frac{d+\delta }{ϵ}I$$

such that at least we should have death from the disease thus

$$\frac{({\beta }_{1}I+{\beta }_2\left(\frac{d+\delta }{ϵ}\right)I+\psi P)S}{d+\delta +{\varphi }_1}>I$$ (5.11)

$$\varpi +\xi I+\theta \left(\frac{d+\delta }{ϵ}\right)I>\kappa P$$ (5.12)

$$\left(\frac{\left({\displaystyle {\beta }_{1}I+{\beta }_2\frac{d+\delta }{ϵ}I+\psi \frac{(\varpi +\xi I+\theta \left(\frac{d+\delta }{ϵ}\right)I)}{\kappa }}\right)S}{d+\delta +{\varphi }_1}\right)>I$$ (5.13)

$$\left(\frac{({\beta }_1+{\beta }_2\frac{d+\delta }{ϵ}+\frac{\psi }{\kappa }(\frac{\varpi }{I}+\xi +\theta \left(\frac{d+\delta }{ϵ}\right)))S}{d+\delta +{\varphi }_1}\right)>1$$ (5.14)

Thus one can conclude that

$$R_0>1$$

we consider the following Lyapunov

$$L=\frac{1}{d+\delta +{\varphi }_1}I+\frac{P}{\kappa }\Rightarrow \frac{dL}{dt}=\frac{1}{d+\delta +{\varphi }_1}\frac{dI}{dt}+\frac{1}{\kappa }\frac{dP}{dt}$$ (5.15)

$$\begin{array}{cc}\frac{dL}{dt}\hfill & =\left({\displaystyle \frac{1}{d+\delta +{\varphi }_1}(\lambda S-(d+\delta +{\varphi }_1)I)+\frac{1}{\kappa }(\varpi +\xi I+\theta D)-\kappa P}\right)\hfill \\ & {\displaystyle =\frac{\lambda S}{(d+\delta +{\varphi }_1)}-I+\frac{1}{\kappa }(\varpi +\xi I+\theta D)-P}\hfill \\ & =\left[{\displaystyle \left\{{\displaystyle \frac{\lambda S}{(d+\delta +{\varphi }_1)}+\frac{1}{\kappa }(\varpi +\xi I+\theta D)}\right\}\frac{1}{I+P}-1}\right][I+P]\hfill \\ & \le \left\{{\displaystyle \frac{\lambda S}{(d+\delta +{\varphi }_1)}+\frac{1}{\kappa }(\varpi +\xi I+\theta D-1)}\right\}[I+P]\hfill \\ & \le \left\{{\displaystyle \frac{{\beta }_1\kappa +\psi \xi }{(d+\delta +{\varphi }_1)\kappa +\psi \xi }-1}\right\}[I+P]\hfill \\ & \le (R_0-1)[I+P]\hfill \end{array}$$ (5.16)

$$\frac{dL}{dt}\le 0\Rightarrow R_0<1.$$

we now consider the Lyapunov function for endemic case

$$\begin{array}{cc}L(S^{*},I^{*},R^{*},P^{*})\hfill & =(S-S^{*}-S^{*}\log \frac{S}{S^{*}})+(I-I^{*}-I^{*}\log \frac{I}{I^{*}})\hfill \\ & +(R-R^{*}-R^{*}\log \frac{R}{R^{*}})+(P-P^{*}-P^{*}\log \frac{P}{P^{*}})\hfill \end{array}$$ (5.17)

$$\begin{array}{cc}{\displaystyle \frac{dL}{dt}}\hfill & {\displaystyle =\left({\displaystyle \frac{S-S^{*}}{S}}\right)\frac{dS}{dt}+\left({\displaystyle \frac{I-I^{*}}{I}}\right)\frac{dI}{dt}+\left({\displaystyle \frac{R-R^{*}}{R}}\right)\frac{dR}{dt}+\left({\displaystyle \frac{P-P^{*}}{P}}\right)\frac{dP}{dt}}\hfill \\ & =\left({\displaystyle \frac{S-S^{*}}{S}}\right)(\Lambda -\lambda S-ds)+\left({\displaystyle \frac{I-I^{*}}{I}}\right)(\lambda S-(d+\delta +{\varphi }_1)I)\hfill \\ & +\left({\displaystyle \frac{R-R^{*}}{R}}\right)({\varphi }_{1}I-dR)+\left({\displaystyle \frac{P-P^{*}}{P}}\right)(\phi -\xi I+\theta D-\kappa P)\hfill \end{array}$$ (5.18)

$$\begin{array}{cc}{\displaystyle \frac{dL}{dt}}\hfill & =\left({\displaystyle \frac{S-S^{*}}{S}}\right)\left(\Lambda \right)-(\lambda (S-S^{*})-d(S-S^{*}))+\left({\displaystyle \frac{I-I^{*}}{I}}\right)(\lambda (S-S^{*})-(d+\delta +{\varphi }_1))(I-I^{*})\hfill \\ & +\left({\displaystyle \frac{R-R^{*}}{R}}\right)({\varphi }_1(I-I^{*})-d(R-R^{*}))+\left({\displaystyle \frac{P-P^{*}}{P}}\right)(\phi +ϵ(I-I^{*})+\theta (P-D)-\kappa (P-P^{*}))\hfill \\ & {\displaystyle =-(\lambda +d)\frac{{(S-S^{*})}^2}{S}-\frac{{(I-I^{*})}^2}{I}(d+\delta +{\varphi }_1)-d\frac{{(R-R^{*})}^2}{R}-\kappa \frac{{(P-P^{*})}^2}{P}}\hfill \\ & {\displaystyle +\Lambda -\frac{S^{*}}{S}\Lambda +\lambda S-\lambda S^{*}-\frac{\lambda S{I}^{*}}{I}+\frac{\lambda S^{*}{I}^{*}}{I}+{\varphi }_{1}I-{\varphi }_1{I}^{*}-\frac{R^{*}\varphi I}{R}+\frac{\varphi R^{*}{I}^{*}}{R}+\varpi -\frac{\varpi P^{*}}{P}}\hfill \\ & {\displaystyle +ϵI-ϵI^{*}-\frac{P^{*}}{P}ϵI+\frac{P^{*}ϵI^{*}}{P}}\hfill \\ & ={\psi }_1-{\psi }_2\hfill \end{array}$$ (5.19)

where

$$\begin{array}{cc}{\psi }_2\hfill & {\displaystyle =(\lambda +d)\frac{{(S-S^{*})}^2}{S}+\frac{{(I-I^{*})}^2}{I}(d+\delta +{\varphi }_1)+d\frac{{(R-R^{*})}^2}{R}+\kappa \frac{{(P-P^{*})}^2}{P}}\hfill \\ & {\displaystyle +\frac{S^{*}}{S}\Lambda +\lambda S^{*}+\frac{\lambda S{I}^{*}}{I}+{\varphi }_1{I}^{*}+\frac{R^{*}\varphi I}{R}+\frac{\varpi P^{*}}{P}ϵI^{*}+\frac{P^{*}}{P}ϵI}\hfill \end{array}$$ (5.20)

$${\displaystyle {\psi }_1=\Lambda +\lambda S+\frac{\lambda S^{*}{I}^{*}}{I}+{\varphi }_{1}I+\frac{\varphi R^{*}{I}^{*}}{R}+\varpi +ϵI+\frac{P^{*}ϵI^{*}}{P}}$$ (5.21)

Thus

$${\displaystyle \frac{dL}{dt}={\psi }_1-{\psi }_2,\frac{dL}{dt}>0}$$

if ψ ₁ > ψ ₂

$$\frac{dL}{dt}=0,\text{if}{\psi }_1={\psi }_2$$

and

$$\frac{dL}{dt}<0,\text{if}{\psi }_1<{\psi }_2$$

6. Positive solutions

Since the solutions of this system describe a real world situation as they representing numbers as functions of time, it is worth showing that ∀t ≥ 0 those solution are positive or Zero. Λ is positive thus

$$\frac{dS}{dt}=\Lambda -(\lambda +d)S>-(\lambda +d)S$$ (6.1)

thus

$$S\left(t\right)\ge S\left(0\right)\exp [-(\lambda +d\left)t\right]\forall t\ge 0$$ (6.2)

Since δ(t) ≥ 0     ∀t ≥ 0

$$\frac{dI}{dt}=\lambda S-(d+\delta +{\varphi }_1)I\ge -(d+\delta +{\varphi }_1)I$$ (6.3)

Thus

$$I\left(t\right)\ge I\left(0\right)\exp [-(d+\delta +{\varphi }_1)t]\forall t\ge 0$$ (6.4)

$$\frac{dR}{dt}={\varphi }_1-dR\ge -dR$$ (6.5)

This leads to

$$R\left(t\right)\ge R\left(0\right)\exp [-dt]\forall t\ge 0$$ (6.6)

Also

$$D\left(t\right)\ge D\left(0\right)\exp [-ϵt]\forall t\ge 0$$ (6.7)

finally I(t), D(t) and R(t) are positive ∀t ≥ 0 thus

$$P\left(t\right)\ge P\left(0\right)\exp [-\kappa t]\forall t\ge 0$$ (6.8)

therefore all solutions are positive.

7. Numerical solution

In this section, we construct a numerical scheme for fractional model based on the Caputo fractional derivative, CF fractional derivative and Atangana-Baleanu fractional derivative [6]. On applying this scheme we first consider the following non-linear fractional ODE:

7.1. Numerical method for Caputo fractional derivative

In this section, we concern with the following Cauchy problem

$$\begin{array}{c}\{\begin{array}{cc}& {}_0^C{D}_t^{\Theta }y\left(t\right)=f(t,y\left(t\right)),\hfill \\ & y\left(0\right)=y_0\hfill \end{array}\hfill \end{array}$$ (7.1)

where the derivative is Caputo fractional derivative. Here we aim to present a numerical scheme to solve the above equation. For this, firstly we transform the above equation into

$$y\left(t\right)-y\left(0\right)=\frac{1}{\Gamma \left(\Theta \right)}{\int }_0^{t}f(\tau ,y\left(\tau \right)){(t-\tau )}^{\Theta -1}d\tau .$$ (7.2)

At the point $t_{n+1}=(n+1)\Delta t,$ we have

$$y\left(t_{n+1}\right)-y\left(0\right)=\frac{1}{\Gamma \left(\Theta \right)}{\int }_0^{t_{n+1}}f(\tau ,y\left(\tau \right)){(t_{n+1}-\tau )}^{\Theta -1}d\tau .$$ (7.3)

Also we have

$$y\left(t_{n+1}\right)=y\left(0\right)+\frac{1}{\Gamma \left(\Theta \right)}\sum _{j=2}^n{\int }_{t_j}^{t_{j+1}}f(\tau ,y\left(\tau \right)){(t_{n+1}-\tau )}^{\Theta -1}d\tau .$$ (7.4)

Replacing Newton polynomial into the above equation, we have

$$\begin{array}{cc}{y}^{n+1}-y^0\hfill & =\frac{1}{\Gamma \left(\Theta \right)}\sum _{j=2}^n{\int }_{t_j}^{t_{j+1}}\left\{\begin{array}{c}+f(t_{j-1},y^{j-2})\\ +\frac{f(t_{j-1},y^{j-1})-f(t_{j-2},y^{j-2})}{\Delta t}(\tau -t_{j-2})\\ +\frac{f(t_j,y^j)-2f(t_{j-1},y^{j-1})+f(t_{j-2},y^{j-2})}{2{\left(\Delta t\right)}^2}\\ \times (\tau -t_{j-2})(\tau -t_{j-1})\end{array}\right\}{(t_{n+1}-\tau )}^{\Theta -1}d\tau .\hfill \end{array}$$ (7.5)

Thus we can write the following

$$\begin{array}{cc}{y}^{n+1}\hfill & =y^0+\frac{1}{\Gamma \left(\Theta \right)}\sum _{j=2}^n\left\{\begin{array}{cc}& +{\int }_{t_j}^{t_{j+1}}f(t_{j-2},y^{j-2}){(t_{n+1}-\tau )}^{\Theta -1}d\tau \\ & +{\int }_{t_j}^{t_{j+1}}\frac{f(t_{j-1},y^{j-1})-f(t_{j-2},y^{j-2})}{\Delta t}{\int }_{t_j}^{t_{j+1}}(\tau -t_{j-2}){(t_{n+1}-\tau )}^{\Theta -1}d\tau \\ & +{\int }_{t_j}^{t_{j+1}}\frac{f(t_j,y^j)-2f(t_{j-1},y^{j-1})+f(t_{j-2},y^{j-2})}{2{\left(\Delta t\right)}^2}\\ & \times (\tau -t_{j-2})(\tau -t_{j-1}){(t_{n+1}-\tau )}^{\Theta -1}d\tau \end{array}\right\}.\hfill \end{array}$$ (7.6)

and rearrange such as

$$\begin{array}{cc}{y}^{n+1}\hfill & =y^0+\frac{1}{\Gamma \left(\Theta \right)}\sum _{j=2}^{n}f(t_{j-2},y^{j-2}){\int }_{t_j}^{t_{j+1}}{(t_{n+1}-\tau )}^{\Theta -1}d\tau \hfill \\ & +\frac{1}{\Gamma \left(\Theta \right)}\sum _{j=2}^n\frac{f(t_{j-1},y^{j-1})-f(t_{j-2},y^{j-2})}{\Delta t}{\int }_{t_j}^{t_{j+1}}(\tau -t_{j-2}){(t_{n+1}-\tau )}^{\Theta -1}d\tau \hfill \\ & +\frac{1}{\Gamma \left(\Theta \right)}\sum _{j=2}^n\frac{f(t_j,y^j)-2f(t_{j-1},y^{j-1})+f(t_{j-2},y^{j-2})}{2{\left(\Delta t\right)}^2}\hfill \\ & \times {\int }_{t_j}^{t_{j+1}}(\tau -t_{j-2})(\tau -t_{j-1}){(t_{n+1}-\tau )}^{\Theta -1}d\tau .\hfill \end{array}$$ (7.7)

For the above integrals, we can have as follows

$$\begin{array}{cc}& {\int }_{t_j}^{t_{j+1}}{(t_{n+1}-\tau )}^{\Theta -1}d\tau =\frac{{\left(\Delta t\right)}^{\Theta }}{\Theta }[{(n-j+1)}^{\Theta }-{(n-j)}^{\Theta }]\hfill \\ & {\int }_{t_j}^{t_{j+1}}(\tau -t_{j-2}){(t_{n+1}-\tau )}^{\Theta -1}d\tau =\frac{{\left(\Delta t\right)}^{\Theta +1}}{\Theta (\Theta +1)}\left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }(n-j+3+2\Theta )\\ & \hfill -{(n-j)}^{\Theta }(n-j+3+3\Theta )\end{array}\right]\hfill \\ & {\int }_{t_j}^{t_{j+1}}(\tau -t_{j-2})(\tau -t_{j-1}){(t_{n+1}-\tau )}^{\Theta -1}d\tau =\frac{{\left(\Delta t\right)}^{\Theta +2}}{\Theta (\Theta +1)(\Theta +2)}\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+\left(3\Theta +10\right)(n-j)\\ & \hfill +2{\Theta }^2+9\Theta +12\end{array}\right]\\ \hfill & \hfill -{(n-j)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+(5\Theta +10)(n-j)\\ & \hfill 6{\Theta }^2+18\Theta +12\end{array}\right]\end{array}\right]\hfill \end{array}$$ (7.8)

If we put them into above equality, we obtain the following scheme

$$\begin{array}{cc}{y}^{n+1}\hfill & =y^0+\frac{{\left(\Delta t\right)}^{\vartheta }}{\Gamma (\vartheta +1)}\sum _{j=2}^{n}f(t_{j-2},y^{j-2})[{(n-j+1)}^{\vartheta }-{(n-j)}^{\vartheta }]\hfill \\ & +\frac{{\left(\Delta t\right)}^{\vartheta }}{\Gamma (\vartheta +2)}\sum _{j=2}^{n}f(t_{j-1},y^{j-1})-f(t_{j-2},y^{j-2})\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\vartheta }(n-j+3+2\vartheta )\\ & \hfill -{(n-j)}^{\vartheta }(n-j+3+3\vartheta )\end{array}\right]\hfill \\ & +\frac{{\left(\Delta t\right)}^{\vartheta }}{2\Gamma (\vartheta +3)}\sum _{j=2}^{n}f(t_j,y^j)-2f(t_{j-1},y^{j-1})+f(t_{j-2},y^{j-2})\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\vartheta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+\left(3\vartheta +10\right)(n-j)\\ & \hfill +2{\vartheta }^2+9\vartheta +12\end{array}\right]\\ \hfill & \hfill -{(n-j)}^{\vartheta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+(5\vartheta +10)(n-j)\\ & \hfill 6{\vartheta }^2+18\vartheta +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (7.9)

So we can write the (3.1) with caputo derivative as

$$\begin{array}{cc}& {}_0^C{D}_t^{\kappa }S=\wedge -\lambda S-dS\hfill \\ & {}_0^C{D}_t^{\kappa }I=\lambda S-(d+\delta +{\varphi }_1)I\hfill \\ & {}_0^C{D}_t^{\kappa }R={\varphi }_{1}I-dR\hfill \\ & {}_0^C{D}_t^{\kappa }D=((d+\delta )I-ϵD),\hfill \\ & {}_0^C{D}_t^{\kappa }P=\varpi +\xi I+\theta D-\kappa P\hfill \end{array}$$ (7.10)

These come with the initial conditions

$$S\left(0\right)=s_0,I\left(0\right)=I_0,R\left(0\right)=R_0,D\left(0\right)=D_0,P\left(0\right)=P_0.$$ (7.11)

For simplicity, we write above Eq. (7.10) as follows;

$$\begin{array}{cc}& {}_0^C{D}_t^{\Theta }S\left(t\right)=S_1(t,S,I,R,D,P)\hfill \\ & {}_0^C{D}_t^{\Theta }I\left(t\right)=I_1(t,S,I,R,D,P)\hfill \\ & {}_0^C{D}_t^{\Theta }R\left(t\right)=R_1(t,S,I,R,D,P)\hfill \\ & {}_0^C{D}_t^{\Theta }D\left(t\right)=D_1(t,S,I,R,D,P)\hfill \\ & {}_0^C{D}_t^{\Theta }P\left(t\right)=P_1(t,S,I,R,D,P)\hfill \end{array}$$ (7.12)

where

$$\begin{array}{cc}& S_1(t,S,I,R,D,P)=\wedge -\lambda S-dS\hfill \\ & I_1(t,S,I,R,D,P)=\lambda S-(d+\delta +{\varphi }_1)I\hfill \\ & R_1(t,S,I,R,D,P)={\varphi }_{1}I-dR\hfill \\ & D_1(t,S,I,R,D,P)=((d+\delta )I-ϵD),\hfill \\ & P_1(t,S,I,R,D,P)=\varpi +\xi I+\theta D-\kappa P\hfill \end{array}$$ (7.13)

We can have the following solution for this model

$$\begin{array}{cc}& S^{n+1}=S^0+\frac{{\left(\Delta t\right)}^{\Theta }}{\Gamma (\Theta +1)}\sum _{j=2}^n\left(S_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)[{(n-j+1)}^{\Theta }-{(n-j)}^{\Theta }]\hfill \\ & +\frac{{\left(\Delta t\right)}^{\Theta }}{\Gamma (\Theta +2)}\hfill \\ & \times \sum _{j=2}^n\left(S_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)-\left(S_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }(n-j+3+2\Theta )\\ & \hfill -{(n-j)}^{\Theta }(n-j+3+3\Theta )\end{array}\right]+\frac{{\left(\Delta t\right)}^{\Theta }}{2\Gamma (\Theta +3)}\hfill \\ & \times \sum _{j=2}^n[\left(S_1(t_n,S^n,I^n,R^n,D^n,P^n)\right)-2\left(S_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)\hfill \\ & +\left(S_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)]\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+\left(3\Theta +10\right)(n-j)\\ & \hfill +2{\Theta }^2+9\Theta +12\end{array}\right]\\ \hfill & \hfill -{(n-j)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+(5\Theta +10)(n-j)\\ & \hfill 6{\Theta }^2+18\Theta +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (7.14)

$$\begin{array}{cc}& I^{n+1}=I^0+\frac{{\left(\Delta t\right)}^{\Theta }}{\Gamma (\Theta +1)}\sum _{j=2}^n\left(I_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)[{(n-j+1)}^{\Theta }-{(n-j)}^{\Theta }]\hfill \\ & +\frac{{\left(\Delta t\right)}^{\Theta }}{\Gamma (\Theta +2)}\hfill \\ & \times \sum _{j=2}^n\left(I_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)-\left(I_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }(n-j+3+2\Theta )\\ & \hfill -{(n-j)}^{\Theta }(n-j+3+3\Theta )\end{array}\right]+\frac{{\left(\Delta t\right)}^{\Theta }}{2\Gamma (\Theta +3)}\hfill \\ & \times \sum _{j=2}^n[\left(I_1(t_n,S^n,I^n,R^n,D^n,P^n)\right)-2\left(E_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)\hfill \\ & +\left(I_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)]\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+\left(3\Theta +10\right)(n-j)\\ & \hfill +2{\Theta }^2+9\Theta +12\end{array}\right]\\ \hfill & \hfill -{(n-j)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+(5\Theta +10)(n-j)\\ & \hfill 6{\Theta }^2+18\Theta +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (7.15)

$$\begin{array}{cc}& R^{n+1}=R^0+\frac{{\left(\Delta t\right)}^{\Theta }}{\Gamma (\Theta +1)}\sum _{j=2}^n\left(R_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)[{(n-j+1)}^{\Theta }-{(n-j)}^{\Theta }]\hfill \\ & +\frac{{\left(\Delta t\right)}^{\Theta }}{\Gamma (\Theta +2)}\hfill \\ & \times \sum _{j=2}^n\left(R_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)-\left(R_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }(n-j+3+2\Theta )\\ & \hfill -{(n-j)}^{\Theta }(n-j+3+3\Theta )\end{array}\right]+\frac{{\left(\Delta t\right)}^{\Theta }}{2\Gamma (\Theta +3)}\hfill \\ & \times \sum _{j=2}^n[\left(R_1(t_n,S^n,I^n,R^n,D^n,P^n)\right)-2\left(R_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)\hfill \\ & +\left(R_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)]\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+\left(3\Theta +10\right)(n-j)\\ & \hfill +2{\Theta }^2+9\Theta +12\end{array}\right]\\ \hfill & \hfill -{(n-j)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+(5\Theta +10)(n-j)\\ & \hfill 6{\Theta }^2+18\Theta +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (7.16)

$$\begin{array}{cc}& D^{n+1}=D^0+\frac{{\left(\Delta t\right)}^{\Theta }}{\Gamma (\Theta +1)}\sum _{j=2}^n\left(D_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)[{(n-j+1)}^{\Theta }-{(n-j)}^{\Theta }]\hfill \\ & +\frac{{\left(\Delta t\right)}^{\Theta }}{\Gamma (\Theta +2)}\hfill \\ & \times \sum _{j=2}^n\left(D_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)-\left(D_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }(n-j+3+2\Theta )\\ & \hfill -{(n-j)}^{\Theta }(n-j+3+3\Theta )\end{array}\right]+\frac{{\left(\Delta t\right)}^{\Theta }}{2\Gamma (\Theta +3)}\hfill \\ & \times \sum _{j=2}^n[\left(D_1(t_n,S^n,I^n,R^n,D^n,P^n)\right)-2\left(D_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)\hfill \\ & +\left(D_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)]\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+\left(3\Theta +10\right)(n-j)\\ & \hfill +2{\Theta }^2+9\Theta +12\end{array}\right]\\ \hfill & \hfill -{(n-j)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+(5\Theta +10)(n-j)\\ & \hfill 6{\Theta }^2+18\Theta +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (7.17)

$$\begin{array}{cc}& P^{n+1}=P^0+\frac{{\left(\Delta t\right)}^{\Theta }}{\Gamma (\Theta +1)}\sum _{j=2}^n\left(P_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)[{(n-j+1)}^{\Theta }-{(n-j)}^{\Theta }]\hfill \\ & +\frac{{\left(\Delta t\right)}^{\Theta }}{\Gamma (\Theta +2)}\hfill \\ & \times \sum _{j=2}^n\left(P_1(t_{n-1},S^{n-1},I^{n-1},Rn-1,D^{n-1},P^{n-1})\right)-\left(P_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }(n-j+3+2\Theta )\\ & \hfill -{(n-j)}^{\Theta }(n-j+3+3\Theta )\end{array}\right]+\frac{{\left(\Delta t\right)}^{\Theta }}{2\Gamma (\Theta +3)}\hfill \\ & \times \sum _{j=2}^n[\left(P_1(t_n,S^n,I^n,R^n,D^n,P^n)\right)-2\left(P_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)\hfill \\ & +\left(P_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)]\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+\left(3\Theta +10\right)(n-j)\\ & \hfill +2{\Theta }^2+9\Theta +12\end{array}\right]\\ \hfill & \hfill -{(n-j)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+(5\Theta +10)(n-j)\\ & \hfill 6{\Theta }^2+18\Theta +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (7.18)

7.2. Numerical method for Caputo-Fabrizio fractional derivative

In this section, we handle the following Cauchy problem with Caputo-Fabrizio fractional derivative

$$\{\begin{array}{cc}& {}_0^{CF}{D}_t^{\Theta }y\left(t\right)=f(t,y\left(t\right)),\hfill \\ & y\left(0\right)=y_0\hfill \end{array}$$ (7.19)

where the function f is non-linear. To present a numerical scheme for solution of our equation, we can reformulate the above equation as

$$y\left(t\right)-y\left(0\right)=\frac{1-\Theta }{M\left(\Theta \right)}f(t,y\left(t\right))+\frac{\Theta }{M\left(\Theta \right)}{\int }_0^{t}f(\tau ,y\left(\tau \right))d\tau .$$ (7.20)

At the point $t_{n+1}=(n+1)\Delta t,$ we have

$$y\left(t_{n+1}\right)-y\left(0\right)=\frac{1-\Theta }{M\left(\Theta \right)}f(t_n,y\left(t_n\right))+\frac{\Theta }{M\left(\Theta \right)}{\int }_0^{t_{n+1}}f(\tau ,y\left(\tau \right))d\tau .$$ (7.21)

at the point $t_n=n\Delta t,$ we have

$$y\left(t_n\right)-y\left(0\right)=\frac{1-\Theta }{M\left(\Theta \right)}f(t_{n-1},y\left(t_{n-1}\right))+\frac{\Theta }{M\left(\Theta \right)}{\int }_0^{t_n}f(\tau ,y\left(\tau \right))d\tau .$$ (7.22)

If we take the difference of this equations, we obtain

$$\begin{array}{cc}y\left(t_{n+1}\right)-y\left(t_n\right)\hfill & =\frac{1-\Theta }{M\left(\Theta \right)}[f(t_n,y\left(t_n\right))-f(t_{n-1},y\left(t_{n-1}\right))]\hfill \\ & +\frac{\Theta }{M\left(\alpha \right)}{\int }_{t_n}^{t_{n+1}}f(\tau ,y\left(\tau \right))d\tau .\hfill \end{array}$$ (7.23)

and

$$\begin{array}{cc}y\left(t_{n+1}\right)-y\left(t_n\right)\hfill & =\frac{1-\Theta }{M\left(\Theta \right)}[f(t_n,y\left(t_n\right))-f(t_{n-1},y\left(t_{n-1}\right))]\hfill \\ & +\frac{\Theta }{M\left(\Theta \right)}\sum _{j=2}^n{\int }_{t_j}^{t_{j+1}}f(\tau ,y\left(\tau \right))d\tau .\hfill \end{array}$$ (7.24)

Using the Newton polynomial, we can write the approximation of the function f(t, y(t)) as follows

$$\begin{array}{cc}{P}_n\left(\tau \right)\hfill & {\displaystyle =f(t_{n-2},y\left(t_{n-2}\right))+\frac{f(t_{n-1},y\left(t_{n-1}\right))-f(t_{n-2},y\left(t_{n-2}\right))}{\Delta \left(t\right)}(\tau -t_{n-2})}\hfill \\ & {\displaystyle \frac{f(t_n,y\left(t_n\right))-2f(t_{n-1},y\left(t_{n-1}\right))+f(t_{n-2},y\left(t_{n-2}\right))}{2{\left(\Delta t\right)}^2}}\hfill \\ & \times (\tau -t_{n-2})(\tau -t_{n-1}).\hfill \end{array}$$ (7.25)

Thus putting this polynomial into the above equation, we write the following

$$\begin{array}{cc}{y}^{n+1}-y^n\hfill & {\displaystyle =\frac{1-\Theta }{M\left(\Theta \right)}[f(t_n,y\left(t_n\right))-f(t_{n-1},y\left(t_{n-1}\right))]}\hfill \\ & {\displaystyle +\frac{\Theta }{M\left(\Theta \right)}\sum _{j=2}^n{\int }_{t_j}^{t_{j+1}}\left\{\begin{array}{c}+f(t_{j-2},y^{j-2})\\ {\displaystyle +\frac{f(t_{j-1},y^{j-1})-f(t_{j-2},y^{j-2})}{\Delta t}(\tau -t_{j-2})}\\ {\displaystyle +\frac{f(t_j,y^j)-2f(t_{j-1},y^{j-1})+f(t_{j-2},y^{j-2})}{2{\left(\Delta t\right)}^2}}\\ \times (\tau -t_{j-2})(\tau -t_{j-1})\end{array}\right\}d\tau .}\hfill \end{array}$$ (7.26)

and reorder as follows

$$\begin{array}{cc}{y}^{n+1}-y^n\hfill & {\displaystyle =\frac{1-\Theta }{M\left(\Theta \right)}[f(t_n,y\left(t_n\right))-f(t_{n-1},y\left(t_{n-1}\right))]}\hfill \\ & {\displaystyle +\frac{\Theta }{M\left(\Theta \right)}\sum _{j=2}^n\left\{\begin{array}{cc}& +f(t_{j-2},y^{j-2})\\ & {\displaystyle +\frac{f(t_{j-1},y^{j-1})-f(t_{j-2},y^{j-2})}{\Delta t}{\int }_{t_j}^{t_{j+1}}(\tau -t_{j-2})d\tau }\\ & {\displaystyle +\frac{f(t_j,y^j)-2f(t_{j-1},y^{j-1})+f(t_{j-2},y^{j-2})}{2{\left(\Delta t\right)}^2}}\\ & \times {\int }_{t_j}^{t_{j+1}}(\tau -t_{j-2})(\tau -t_{j-1})d\tau \end{array}\right\}.}\hfill \end{array}$$ (7.27)

We can have the following calculations for the above integrals

$${\int }_{t_j}^{t_{j+1}}(\tau -t_{j-2})d\tau =\frac{5}{2}{\left(\Delta t\right)}^2$$ (7.28)

$${\int }_{t_j}^{t_{j+1}}(\tau -t_{j-2})(\tau -t_{j-1})d\tau =\frac{23}{6}{\left(\Delta t\right)}^3$$ (7.29)

If we replace them into above scheme, we obtain the following scheme

$$\begin{array}{cc}{y}^{n+1}\hfill & =y^n+\frac{1-\Theta }{M\left(\Theta \right)}[f(t_n,y\left(t_n\right))-f(t_{n-1},y\left(t_{n-1}\right))]\hfill \\ & +\frac{\Theta }{M\left(\Theta \right)}\sum _{j=2}^n\left\{\begin{array}{cc}& +f(t_{j-2},y^{j-2})\Delta t+[f(t_{j-1},y^{j-1})-f(t_{j-2},y^{j-2})]\frac{5}{2}\Delta t\\ & +[f(t_j,y^j)-2f(t_{j-1},y^{j-1})+f(t_{j-2},y^{j-2})\frac{23}{6}\Delta t\end{array}\right\}.\hfill \end{array}$$ (7.30)

and we can rearrange as

$$\begin{array}{cc}{y}^{n+1}\hfill & {\displaystyle =y^n+\frac{1-\Theta }{M\left(\Theta \right)}[f(t_n,y\left(t_n\right))-f(t_{n-1},y\left(t_{n-1}\right))]}\hfill \\ & {\displaystyle +\frac{\Theta }{M\left(\Theta \right)}\sum _{j=2}^n\left\{{\displaystyle -\frac{4}{3}f(t_{j-1},y^{j-1})\Delta t+\frac{5}{12}f(t_{j-2},y^{j-2})\Delta t+\frac{23}{12}f(t_j,y^j)\Delta t}\right\}}\hfill \end{array}$$ (7.31)

For simplicity, we write above Eq. (7.10) with Caputo-Fabrizio fractional derivative as follows;

$$\begin{array}{cc}& {}_0^{CF}{D}_t^{\Theta }S\left(t\right)=S_1(t,S,I,R,D,P)\hfill \\ & {}_0^{CF}{D}_t^{\Theta }I\left(t\right)=I_1(t,S,I,R,D,P)\hfill \\ & {}_0^{CF}{D}_t^{\Theta }R\left(t\right)=R_1(t,S,I,R,D,P)\hfill \\ & {}_0^{CF}{D}_t^{\Theta }D\left(t\right)=D_1(t,S,I,R,D,P)\hfill \\ & {}_0^{CF}{D}_t^{\Theta }P\left(t\right)=P_1(t,S,I,R,D,P)\hfill \end{array}$$ (7.32)

After applying Caputo-Fabrizio fractional derivative we have the following

We can have the following solution for this model

$$\begin{array}{cc}S\left(t_{n+1}\right)\hfill & {\displaystyle =S\left(t_n\right)+\frac{1-\Theta }{M\left(\Theta \right)}[S_1(t_n,S\left(t_n\right),I\left(t_n\right),R\left(t_n\right),D\left(t_n\right),P\left(t_n\right))}\hfill \\ & -S_1(t_{n-1},(S\left(t_{n-1}\right),I\left(t_{n-1}\right),R\left(t_{n-1}\right),D\left(t_{n-1}\right),P\left(t_{n-1}\right))]\hfill \\ & {\displaystyle +\frac{\Theta }{M\left(\Theta \right)}\sum _{j=2}^n\{{\displaystyle -\frac{4}{3}{S}_1(t_{n-1},S\left(t_{n-1}\right),I\left(t_{n-1}\right),R\left(t_{n-1}\right),D\left(t_{n-1}\right),P\left(t_{n-1}\right))\Delta t}}\hfill \\ & {\displaystyle +\frac{5}{12}{S}_1(t_{n-2},S\left(t_{n-2}\right),I\left(t_{n-2}\right),R\left(t_{n-2}\right),D\left(t_{n-2}\right),P\left(t_{n-2}\right))\Delta t}\hfill \\ & {\displaystyle +\frac{23}{12}{S}_1(t_n,S\left(t_n\right),I\left(t_n\right),R\left(t_n\right),D\left(t_n\right),P\left(t_n\right))\Delta t}\}\hfill \end{array}$$ (7.33)

$$\begin{array}{cc}I\left(t_{n+1}\right)\hfill & {\displaystyle =I\left(t_n\right)+\frac{1-\Theta }{M\left(\Theta \right)}[I_1(t_n,S\left(t_n\right),I\left(t_n\right),R\left(t_n\right),D\left(t_n\right),P\left(t_n\right))}\hfill \\ & -I_1(t_{n-1},S\left(t_{n-1}\right),I\left(t_{n-1}\right),R\left(t_{n-1}\right),D\left(t_{n-1}\right),P\left(t_{n-1}\right))]\hfill \\ & {\displaystyle +\frac{\Theta }{M\left(\Theta \right)}\sum _{j=2}^n\{{\displaystyle -\frac{4}{3}{I}_1(t_{n-1},S\left(t_{n-1}\right),I\left(t_{n-1}\right),R\left(t_{n-1}\right),D\left(t_{n-1}\right),P\left(t_{n-1}\right))\Delta t}}\hfill \\ & {\displaystyle +\frac{5}{12}{I}_1(t_{n-2},S\left(t_{n-2}\right),I\left(t_{n-2}\right),R\left(t_{n-2}\right),D\left(t_{n-2}\right),P\left(t_{n-2}\right))\Delta t}\hfill \\ & {\displaystyle +\frac{23}{12}{I}_1(t_n,S\left(t_n\right),I\left(t_n\right),R\left(t_n\right),D\left(t_n\right),P\left(t_n\right))\Delta t}\}\hfill \end{array}$$ (7.34)

$$\begin{array}{cc}R\left(t_{n+1}\right)\hfill & {\displaystyle =R\left(t_n\right)+\frac{1-\Theta }{M\left(\Theta \right)}[R_1(t_n,S\left(t_n\right),I\left(t_n\right),R\left(t_n\right),D\left(t_n\right),P\left(t_n\right))}\hfill \\ & -R_1(t_{n-1},S\left(t_{n-1}\right),I\left(t_{n-1}\right),R\left(t_{n-1}\right),D\left(t_{n-1}\right),P\left(t_{n-1}\right))]\hfill \\ & {\displaystyle +\frac{\Theta }{M\left(\Theta \right)}\sum _{j=2}^n\{{\displaystyle -\frac{4}{3}{R}_1(t_{n-1},S\left(t_{n-1}\right),I\left(t_{n-1}\right),R\left(t_{n-1}\right),D\left(t_{n-1}\right),P\left(t_{n-1}\right))\Delta t}}\hfill \\ & {\displaystyle +\frac{5}{12}{R}_1(t_{n-2},S\left(t_{n-2}\right),I\left(t_{n-2}\right),R\left(t_{n-2}\right),D\left(t_{n-2}\right),P\left(t_{n-2}\right))\Delta t}\hfill \\ & {\displaystyle +\frac{23}{12}{R}_1(t_n,S\left(t_n\right),I\left(t_n\right),R\left(t_n\right),D\left(t_n\right),P\left(t_n\right))\Delta t}\}\hfill \end{array}$$ (7.35)

$$\begin{array}{cc}D\left(t_{n+1}\right)\hfill & {\displaystyle =D\left(t_n\right)+\frac{1-\Theta }{M\left(\Theta \right)}[D_1(t_n,S\left(t_n\right),I\left(t_n\right),R\left(t_n\right),D\left(t_n\right),P\left(t_n\right))}\hfill \\ & -D_1(t_{n-1},S\left(t_{n-1}\right),I\left(t_{n-1}\right),R\left(t_{n-1}\right),D\left(t_{n-1}\right),P\left(t_{n-1}\right))]\hfill \\ & {\displaystyle +\frac{\Theta }{M\left(\Theta \right)}\sum _{j=2}^n\{{\displaystyle -\frac{4}{3}{D}_1(t_{n-1},S\left(t_{n-1}\right),I\left(t_{n-1}\right),R\left(t_{n-1}\right),D\left(t_{n-1}\right),P\left(t_{n-1}\right))\Delta t}}\hfill \\ & {\displaystyle +\frac{5}{12}{D}_1(t_{n-2},S\left(t_{n-2}\right),I\left(t_{n-2}\right),R\left(t_{n-2}\right),D\left(t_{n-2}\right),P\left(t_{n-2}\right))\Delta t}\hfill \\ & {\displaystyle +\frac{23}{12}{D}_1(t_n,S\left(t_n\right),I\left(t_n\right),R\left(t_n\right),D\left(t_n\right),P\left(t_n\right))\Delta t}\}\hfill \end{array}$$ (7.36)

$$\begin{array}{cc}P\left(t_{n+1}\right)\hfill & {\displaystyle =P\left(t_n\right)+\frac{1-\Theta }{M\left(\Theta \right)}[P_1(t_n,S\left(t_n\right),I\left(t_n\right),R\left(t_n\right),D\left(t_n\right),P\left(t_n\right))}\hfill \\ & -P_1(t_{n-1},S\left(t_{n-1}\right),I\left(t_{n-1}\right),R\left(t_{n-1}\right),D\left(t_{n-1}\right),P\left(t_{n-1}\right))]\hfill \\ & {\displaystyle +\frac{\Theta }{M\left(\Theta \right)}\sum _{j=2}^n\{{\displaystyle -\frac{4}{3}{P}_1(t_{n-1},S\left(t_{n-1}\right),I\left(t_{n-1}\right),R\left(t_{n-1}\right),D\left(t_{n-1}\right),P\left(t_{n-1}\right))\Delta t}}\hfill \\ & {\displaystyle +\frac{5}{12}{P}_1(t_{n-2},S\left(t_{n-2}\right),I\left(t_{n-2}\right),R\left(t_{n-2}\right),D\left(t_{n-2}\right),P\left(t_{n-2}\right))\Delta t}\hfill \\ & {\displaystyle +\frac{23}{12}{P}_1(t_n,S\left(t_n\right),I\left(t_n\right),R\left(t_n\right),D\left(t_n\right),P\left(t_n\right))\Delta t}\}\hfill \end{array}$$ (7.37)

7.3. Numerical method for Atangana-Baleanu fractional derivative

Now we deal with the following Cauchy problem with AtanganaBaleanu fractional derivative

$$\{\begin{array}{cc}& {}_0^{ABC}{D}_t^{\Theta }y\left(t\right)=f(t,y\left(t\right)),\hfill \\ & y\left(0\right)=y_0\hfill \end{array}$$ (7.38)

In this section, we provide a numerical scheme to solve this equation. Applying Atangana-Baleanu integral, we convert the above equation into

$${\displaystyle y\left(t\right)-y\left(0\right)=\frac{1-\Theta }{AB\left(\Theta \right)}f(t,y\left(t\right))+\frac{\Theta }{AB\left(\Theta \right)\Gamma \left(\Theta \right)}{\int }_0^{t}f(\tau ,y\left(\tau \right)){(t-\tau )}^{\Theta -1}d\tau .}$$ (7.39)

At the point $t_{n+1}=(n+1)\Delta t,$ we have

$$y\left(t_{n+1}\right)-y\left(0\right)=\frac{1-\Theta }{AB\left(\Theta \right)}f(t_n,y\left(t_n\right))+\frac{\Theta }{AB\left(\Theta \right)\Gamma \left(\Theta \right)}{\int }_0^{t_{n+1}}f(\tau ,y\left(\tau \right)){(t_{n+1}-\tau )}^{\Theta -1}d\tau .$$ (7.40)

at the point $t_n=n\Delta t,$ we have

$$y\left(t_{n+1}\right)-y\left(0\right)=\frac{1-\Theta }{AB\left(\Theta \right)}f(t_n,y\left(t_n\right))+\frac{\Theta }{AB\left(\Theta \right)\Gamma \left(\Theta \right)}\sum _{j=2}^n{\int }_j^{t_{j+1}}f(\tau ,y\left(\tau \right))d\tau .$$ (7.41)

Here, for the approximation of the function f(t, y(t)), we use the Newton polynomial which is given by

$$\begin{array}{cc}{P}_n\left(\tau \right)\hfill & {\displaystyle =f(t_{n-2},y\left(t_{n-2}\right))+\frac{f(t_{n-1},y\left(t_{n-1}\right))-f(t_{n-2},y\left(t_{n-2}\right))}{\Delta \left(t\right)}(\tau -t_{n-2})}\hfill \\ & {\displaystyle \frac{f(t_n,y\left(t_n\right))-2f(t_{n-1},y\left(t_{n-1}\right))+f(t_{n-2},y\left(t_{n-2}\right))}{2{\left(\Delta t\right)}^2}}\hfill \\ & \times (\tau -t_{n-2})(\tau -t_{n-1}).\hfill \end{array}$$ (7.42)

Thus if we write this polynomial in (7.41), we have the following

$$\begin{array}{cc}{y}^{n+1}\hfill & {\displaystyle =y^0+\frac{1-\Theta }{AB\left(\Theta \right)}f(t_n,y\left(t_n\right))}\hfill \\ & {\displaystyle +\frac{\Theta }{AB\left(\Theta \right)\Gamma \left(\Theta \right)}\sum _{j=2}^n{\int }_{t_j}^{t_{j+1}}\left\{\begin{array}{c}+f(t_{j-2},y^{j-2})\\ {\displaystyle +\frac{f(t_{j-1},y^{j-1})-f(t_{j-2},y^{j-2})}{\Delta t}(\tau -t_{j-2})}\\ {\displaystyle +\frac{f(t_j,y^j)-2f(t_{j-1},y^{j-1})+f(t_{j-2},y^{j-2})}{2{\left(\Delta t\right)}^2}}\\ \times (\tau -t_{j-2})(\tau -t_{j-1})\end{array}\right\}{(t_{n+1}-\tau )}^{\Theta -1}d\tau .}\hfill \end{array}$$ (7.43)

and we can reorganize

$$\begin{array}{cc}{y}^{n+1}\hfill & {\displaystyle =y^0+\frac{1-\Theta }{AB\left(\Theta \right)}f(t_n,y\left(t_n\right))}\hfill \\ & {\displaystyle +\frac{\Theta }{AB\left(\Theta \right)\Gamma \left(\Theta \right)}\sum _{j=2}^n\left\{\begin{array}{c}+{\int }_{t_j}^{t_{j+1}}f(t_{j-2},y^{j-2}){(t_{n+1}-\tau )}^{\Theta -1}d\tau \\ {\displaystyle +{\int }_{t_j}^{t_{j+1}}\frac{f(t_{j-1},y^{j-1})-f(t_{j-2},y^{j-2})}{\Delta t}(\tau -t_{j-2}){(t_{n+1}-\tau )}^{\Theta -1}d\tau }\\ {\displaystyle +{\int }_{t_j}^{t_{j+1}}\frac{f(t_j,y^j)-2f(t_{j-1},y^{j-1})+f(t_{j-2},y^{j-2})}{2{\left(\Delta t\right)}^2}}\\ \times (\tau -t_{j-2})(\tau -t_{j-1}){(t_{n+1}-\tau )}^{\Theta -1}d\tau \end{array}\right\}.}\hfill \end{array}$$ (7.44)

Thus we have

$$\begin{array}{cc}{y}^{n+1}\hfill & {\displaystyle =y^0+\frac{1-\Theta }{AB\left(\Theta \right)}f(t_n,y\left(t_n\right))}\hfill \\ & {\displaystyle +\frac{\Theta }{AB\left(\Theta \right)\Gamma \left(\Theta \right)}\sum _{j=2}^{n}f(t_{j-2},y^{j-2})\Delta t{\int }_{t_j}^{t_{j+1}}{(t_{n+1}-\tau )}^{\Theta -1}d\tau }\hfill \\ & {\displaystyle +\frac{\Theta }{AB\left(\Theta \right)\Gamma \left(\Theta \right)}\sum _{j=2}^n\frac{f(t_{j-1},y^{j-1})-f(t_{j-2},y^{j-2})}{\Delta t}}\hfill \\ & \times {\int }_{t_j}^{t_{j+1}}(\tau -t_{j-2})(\tau -t_{j-1}){(t_{n+1}-\tau )}^{\Theta -1}d\tau \hfill \\ & {\displaystyle +\frac{\Theta }{AB\left(\Theta \right)\Gamma \left(\Theta \right)}\sum _{j=2}^n\frac{f(t_j,y^j)-2f(t_{j-1},y^{j-1})+f(t_{j-2},y^{j-2})}{2{\left(\Delta t\right)}^2}}\hfill \\ & \times {\int }_{t_j}^{t_{j+1}}(\tau -t_{j-2})(\tau -t_{j-1}){(t_{n+1}-\tau )}^{\Theta -1}d\tau .\hfill \end{array}$$ (7.45)

When calculating the above integrals

$$\begin{array}{cc}& {\displaystyle {\int }_{t_j}^{t_{j+1}}{(t_{n+1}-\tau )}^{\Theta -1}d\tau =\frac{{\left(\Delta t\right)}^{\Theta }}{\Theta }[{(n-j+1)}^{\Theta }-{(n-j)}^{\Theta }]}\hfill \\ & {\displaystyle {\int }_{t_j}^{t_{j+1}}(\tau -t_{j-2}){(t_{n+1}-\tau )}^{\Theta -1}d\tau =\frac{{\left(\Delta t\right)}^{\Theta +1}}{\Theta (\Theta +1)}\left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }(n-j+3+2\Theta )\\ & \hfill -{(n-j)}^{\Theta }(n-j+3+3\Theta )\end{array}\right]}\hfill \\ & {\displaystyle {\int }_{t_j}^{t_{j+1}}(\tau -t_{j-2})(\tau -t_{j-1}){(t_{n+1}-\tau )}^{\Theta -1}d\tau =\frac{{\left(\Delta t\right)}^{\Theta +2}}{\Theta (\Theta +1)(\Theta +2)}}\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+\left(3\Theta +10\right)(n-j)\\ & \hfill +2{\Theta }^2+9\Theta +12\end{array}\right]\\ \hfill & \hfill -{(n-j)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+(5\Theta +10)(n-j)\\ & \hfill 6{\Theta }^2+18\Theta +12\end{array}\right]\end{array}\right]\hfill \end{array}$$ (7.46)

and putting this equalities into above scheme, we can obtain the following scheme

$$\begin{array}{cc}{y}^{n+1}\hfill & {\displaystyle =y^0+\frac{1-\Theta }{AB\left(\Theta \right)}f(t_n,y\left(t_n\right))}\hfill \\ & {\displaystyle +\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +1)}\sum _{j=2}^{n}f(t_{j-2},y^{j-2})[{(n-j+1)}^{\Theta }-{(n-j)}^{\Theta }]}\hfill \\ & {\displaystyle +\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +2)}\sum _{j=2}^{n}f(t_{j-1},y^{j-1})-f(t_{j-2},y^{j-2})}\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }(n-j+3+2\Theta )\\ & \hfill -{(n-j)}^{\Theta }(n-j+3+3\Theta )\end{array}\right]\hfill \\ & {\displaystyle +\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +3)}\sum _{j=2}^{n}f(t_j,y^j)-2f(t_{j-1},y^{j-1})+f(t_{j-2},y^{j-2})}\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+\left(3\Theta +10\right)(n-j)\\ & \hfill +2{\Theta }^2+9\Theta +12\end{array}\right]\\ \hfill & \hfill -{(n-j)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+(5\Theta +10)(n-j)\\ & \hfill 6{\Theta }^2+18\Theta +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (7.47)

we do the same routine for Atangana-Baleanu fractional derivative for the Eq. (3.1) as

$$\begin{array}{cc}& {}_0^{ABC}{D}_t^{\Theta }S\left(t\right)=S_1(t,S,I,R,D,P)\hfill \\ & {}_0^{ABC}{D}_t^{\Theta }I\left(t\right)=I_1(t,S,I,R,D,P)\hfill \\ & {}_0^{ABC}{D}_t^{\Theta }R\left(t\right)=R_1(t,S,I,R,D,P)\hfill \\ & {}_0^{ABC}{D}_t^{\Theta }D\left(t\right)=D_1(t,S,I,R,D,P)\hfill \\ & {}_0^{ABC}{D}_t^{\Theta }P\left(t\right)=P_1(t,S,I,R,D,P)\hfill \end{array}$$ (7.48)

Thus, we can present the following scheme for numerical solution of our above equation as

$$\begin{array}{cc}& {\displaystyle S^{n+1}=S^0+\frac{1-\Theta }{AB\left(\Theta \right)}\left(S_1(t_n,S^n,I^n,R^n,D^n,P^n)\right)}\hfill \\ & {\displaystyle +\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +1)}\sum _{j=2}^n\left(S_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)[{(n-j+1)}^{\Theta }-{(n-j)}^{\Theta }]}\hfill \\ & {\displaystyle +\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +2)}}\hfill \\ & \times \sum _{j=2}^n\left(S_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)-\left(S_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)\hfill \\ & {\displaystyle \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }(n-j+3+2\Theta )\\ & \hfill -{(n-j)}^{\Theta }(n-j+3+3\Theta )\end{array}\right]+\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +3)}}\hfill \\ & \times \sum _{j=2}^n[\left(S_1(t_n,S^n,I^n,R^n,D^n,P^n)\right)-2\left(S_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)\hfill \\ & +\left(S_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)]\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+\left(3\Theta +10\right)(n-j)\\ & \hfill +2{\Theta }^2+9\Theta +12\end{array}\right]\\ \hfill & \hfill -{(n-j)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+(5\Theta +10)(n-j)\\ & \hfill 6{\Theta }^2+18\Theta +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (7.49)

$$\begin{array}{cc}& {\displaystyle I^{n+1}=I^0+\frac{1-\Theta }{AB\left(\Theta \right)}\left(E_1(t_n,S^n,I^n,R^n,D^n,P^n)\right)}\hfill \\ & {\displaystyle +\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +1)}\sum _{j=2}^n\left(I_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)[{(n-j+1)}^{\Theta }-{(n-j)}^{\Theta }]}\hfill \\ & {\displaystyle +\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +2)}}\hfill \\ & \times \sum _{j=2}^n\left(I_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)-\left(I_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)\hfill \\ & {\displaystyle \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }(n-j+3+2\Theta )\\ & \hfill -{(n-j)}^{\Theta }(n-j+3+3\Theta )\end{array}\right]+\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +3)}}\hfill \\ & \times \sum _{j=2}^n[\left(I_1(t_n,S^n,I^n,R^n,D^n,P^n)\right)-2\left(E_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)\hfill \\ & +\left(I_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)]\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+\left(3\Theta +10\right)(n-j)\\ & \hfill +2{\Theta }^2+9\Theta +12\end{array}\right]\\ \hfill & \hfill -{(n-j)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+(5\Theta +10)(n-j)\\ & \hfill 6{\Theta }^2+18\Theta +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (7.50)

$$\begin{array}{cc}& {\displaystyle R^{n+1}=R^0+\frac{1-\Theta }{AB\left(\Theta \right)}\left(R_1(t_n,S^n,I^n,R^n,D^n,P^n)\right)}\hfill \\ & {\displaystyle +\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +1)}\sum _{j=2}^n\left(R_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)[{(n-j+1)}^{\Theta }-{(n-j)}^{\Theta }]}\hfill \\ & {\displaystyle +\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +2)}}\hfill \\ & \times \sum _{j=2}^n\left(R_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)-\left(R_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)\hfill \\ & {\displaystyle \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }(n-j+3+2\Theta )\\ & \hfill -{(n-j)}^{\Theta }(n-j+3+3\Theta )\end{array}\right]+\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +3)}}\hfill \\ & \times \sum _{j=2}^n[\left(R_1(t_n,S^n,I^n,R^n,D^n,P^n)\right)-2\left(R_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)\hfill \\ & +\left(R_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)]\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+\left(3\Theta +10\right)(n-j)\\ & \hfill +2{\Theta }^2+9\Theta +12\end{array}\right]\\ \hfill & \hfill -{(n-j)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+(5\Theta +10)(n-j)\\ & \hfill 6{\Theta }^2+18\Theta +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (7.51)

$$\begin{array}{cc}& {\displaystyle D^{n+1}=D^0+\frac{1-\Theta }{AB\left(\Theta \right)}\left(D_1(t_n,S^n,I^n,R^n,D^n,P^n)\right)}\hfill \\ & {\displaystyle +\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +1)}\sum _{j=2}^n\left(D_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)[{(n-j+1)}^{\Theta }-{(n-j)}^{\Theta }]}\hfill \\ & {\displaystyle +\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +2)}}\hfill \\ & \times \sum _{j=2}^n\left(D_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)-\left(D_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)\hfill \\ & {\displaystyle \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }(n-j+3+2\Theta )\\ & \hfill -{(n-j)}^{\Theta }(n-j+3+3\Theta )\end{array}\right]+\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +3)}}\hfill \\ & \times \sum _{j=2}^n[\left(D_1(t_n,S^n,I^n,R^n,D^n,P^n)\right)-2\left(D_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)\hfill \\ & +\left(D_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)]\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+\left(3\Theta +10\right)(n-j)\\ & \hfill +2{\Theta }^2+9\Theta +12\end{array}\right]\\ \hfill & \hfill -{(n-j)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+(5\Theta +10)(n-j)\\ & \hfill 6{\Theta }^2+18\Theta +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (7.52)

$$\begin{array}{cc}& {\displaystyle P^{n+1}=P^0+\frac{1-\Theta }{AB\left(\Theta \right)}\left(P_1(t_n,S^n,I^n,R^n,D^n,P^n)\right)}\hfill \\ & {\displaystyle +\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +1)}\sum _{j=2}^n\left(P_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)[{(n-j+1)}^{\Theta }-{(n-j)}^{\Theta }]}\hfill \\ & {\displaystyle +\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +2)}}\hfill \\ & \times \sum _{j=2}^n\left(P_1(t_{n-1},S^{n-1},I^{n-1},Rn-1,D^{n-1},P^{n-1})\right)-\left(P_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)\hfill \\ & {\displaystyle \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }(n-j+3+2\Theta )\\ & \hfill -{(n-j)}^{\Theta }(n-j+3+3\Theta )\end{array}\right]+\frac{\Theta {\left(\Delta t\right)}^{\Theta }}{AB\left(\Theta \right)\Gamma (\Theta +3)}}\hfill \\ & \times \sum _{j=2}^n[\left(P_1(t_n,S^n,I^n,R^n,D^n,P^n)\right)-2\left(P_1(t_{n-1},S^{n-1},I^{n-1},R^{n-1},D^{n-1},P^{n-1})\right)\hfill \\ & +\left(P_1(t_{n-2},S^{n-2},I^{n-2},R^{n-2},D^{n-2},P^{n-2})\right)]\hfill \\ & \times \left[\begin{array}{cc}& \hfill {(n-j+1)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+\left(3\Theta +10\right)(n-j)\\ & \hfill +2{\Theta }^2+9\Theta +12\end{array}\right]\\ \hfill & \hfill -{(n-j)}^{\Theta }\left[\begin{array}{cc}& \hfill 2{(n-j)}^2+(5\Theta +10)(n-j)\\ & \hfill 6{\Theta }^2+18\Theta +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (7.53)

8. Application to maximum likehood estimation on approximation solution

Now after obtaining the numerical solution of Ebola model including (S_N, I_N, R_N, D_N, P_N). The number of new infected susceptible death and other are available in the literature, we can now suppose that the data function Φ_I follows a given distribution for example Poisson distribution with parameters ${\pi }_I=P_1{I}_N.$ Thus

$${\Phi }_I=\text{Poisson}({\pi }_I=P_1{I}_N)$$

The parameter P ₁ is constant reflecting a combination of collected sampling efficiency also the detectability of infections, thus the likelihood can be defined as

$$\begin{array}{cc}L\left({\pi }_I\right)\hfill & ={\Pi }_{t=0}^{m}f({\varphi }_t,{\pi }_I)\hfill \\ & {\displaystyle ={\Pi }_{t=0}^m\frac{{\pi }_I^{{\varphi }_t}\exp (-{\pi }_I)}{{\Phi }_t}}\hfill \end{array}$$ (8.1)

Then the log  likelihood function is given as

$$\begin{array}{cc}\log L\left({\pi }_I\right)\hfill & =\sum _{t=0}^m\log \left[{\displaystyle \frac{{\pi }_I^{{\varphi }_t}\exp (-{\pi }_I)}{{\Phi }_t}}\right]\hfill \\ & =\sum _{t=0}^m[{\Phi }_t\log {\pi }_I-{\pi }_I-\log {\Phi }_t]\hfill \end{array}$$ (8.2)

Thus replacing ${\pi }_I=P_1{I}_N$ we have

$$\log L\left({\pi }_I\right)=\sum _{t=0}^m[\log {\left(P_1{I}_N\right)}^{{\Phi }_t}-P_1{I}_N-\log {\Phi }_t]$$

Using some collected data we can estimate $\xi ,\phi ,\nu ,\upsilon ,\theta$ and σ.

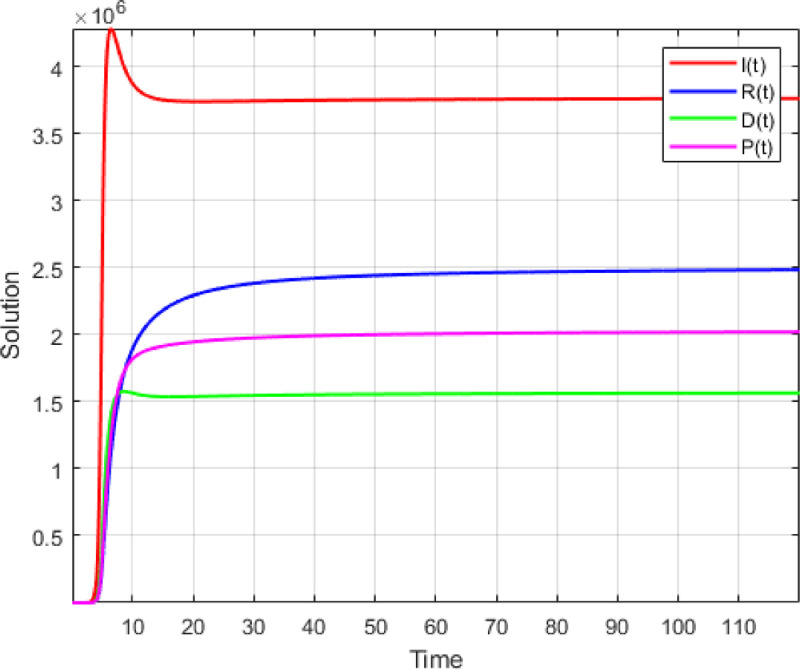
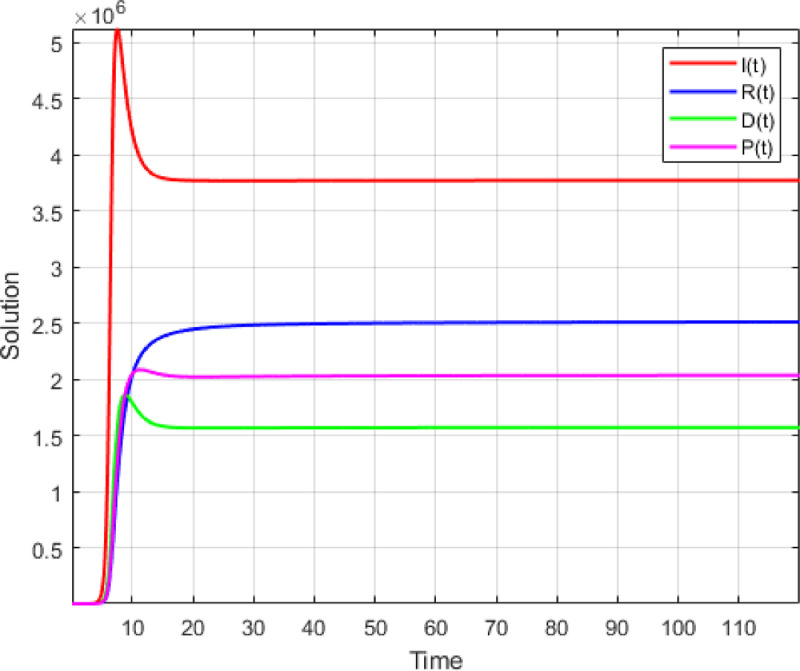
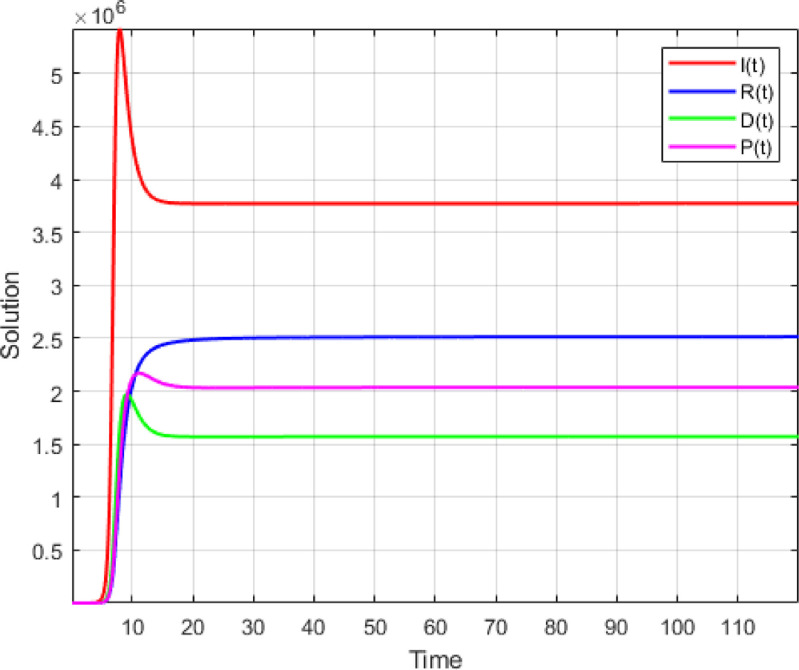
9. Numerical simulation

In this section using theoretical parameters, we present some numerical simulations for different values of fractional order. The obtained numerical solutions are therefore presented in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig. 7 .

Fig. 1.

Numerical Simulation For $\alpha =0.81$.

Fig. 2.

Numerical Simulation For $\alpha =0.85$.

Fig. 3.

Numerical Simulation For $\alpha =0.87$.

Fig. 4.

Numerical Simulation For $\alpha =0.92$.

Fig. 5.

Numerical Simulation For $\alpha =0.95$.

Fig. 6.

Numerical Simulation For $\alpha =0.98$.

Fig. 7.

Numerical Simulation For $\alpha =1$.

10. Conclusion

Ebola and Covid-19 are very strange infectious diseases that put worry around the globe as they biological and mode of transmissions are not fully understood. White their effects have been fatal around the globe especially the Covid-19, humans have taking serious measures to fight them back and possible eradicate them from the globe to insure security, peace and stability among humans. Mathematical models have been used helpful to at least warn humans for the severity of these fatal disease. In this paper, we consider a mathematical model that take into account the Ebola and Covid-19 virus pathogen in the environment. Stability analysis for disease-free and endemic equilibrium, we presented numerical solutions using a new trend of numerical scheme to derive approximate, additionally, we presented, the Likelihood formula for Poisson distribution was presented for parameters estimation.

CRediT authorship contribution statement

Zizhen Zhang: Conceptualization, Funding acquisition, Investigation, Project administration, Resources, Writing - original draft. Sonal Jain: Data curation, Formal analysis, Methodology, Software, Supervision, Validation, Visualization, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they do not have any financial or non- financial conflict of interests.