On forecasting the spread of the COVID-19 in Iran: The second wave

Highlights

• •A predictive COVID-19 model is considered.
• •The second wave of COVID-19 in Iran is studied.
• •Some predictive results of the peak epidemic outbreak are given.
• •Estimated times of the end of the epidemic in Iran in several scenarios are approximated in the plots.
• •The second wave of COVID-19 is predicated to happen between August and December 2020.

Abstract

One of the common misconceptions about COVID-19 disease is to assume that we will not see a recurrence after the first wave of the disease has subsided. This completely wrong perception causes people to disregard the necessary protocols and engage in some misbehavior, such as routine socializing or holiday travel. These conditions will put double pressure on the medical staff and endanger the lives of many people around the world. In this research, we are interested in analyzing the existing data to predict the number of infected people in the second wave of out-breaking COVID-19 in Iran. For this purpose, a model is proposed. The mathematical analysis corresponded to the model is also included in this paper. Based on proposed numerical simulations, several scenarios of progress of COVID-19 corresponding to the second wave of the disease in the coming months, will be discussed. We predict that the second wave of will be most severe than the first one. From the results, improving the recovery rate of people with weak immune systems via appropriate medical incentives is resulted as one of the most effective prescriptions to prevent the widespread unbridled outbreak of the second wave of COVID-19.

1. Introduction

COVID-19 was first identified in late December 2019 in Wuhan, Hubei Province, China, and quickly spread to all parts of the world. Nowadays, after near six months, a rapid surge in the number of new cases of COVID-19 has been reported across the globe. It seems that the prevalence of this disease has decreased for some time, which has led to the reduction and even elimination of restrictions. But the increase in public relations and travel, non-compliance with health precautions by a group of people, and in particular, the lack of seriousness on the part of various governments, brought closer what experts called a nightmare: The second wave of coronavirus spread!

The second wave of outbreaks of infectious diseases occurs when, after a relative decrease or decrease, the number of patients with the disease increases again. The second wave may be an increase in age groups or specific populations, or in particular areas of each country, or it may be as widespread as the first wave.

Concerns about COVID-19 second wave have escalated as many countries around the world move toward reopening and lifting traffic and quarantine restrictions. In almost all of these countries, experts warn that more contact with each other may lead to an increase in the number of patients and a higher prevalence of the disease. It is well known that respiratory infections, including influenza, are less common in the warmer months of the year. Even research on other types of coronavirus has shown that dry weather and sunlight in the summer make the virus unfavorable for the host’s body. However, some believe that the behavior of the new coronavirus is not yet known. Therefore, due to the contagious and unknown nature of the virus in the human immune system, appropriate weather conditions may not be necessary for the growth and proliferation of the disease. People over the age of 60 or those with a long-term history of heart disease, such as heart surgeries, lung disease, diabetes, cancer, or high blood pressure, as well as people with weakened immune systems, have a much higher risk of developing the disease if they have COVID-19 [1].

In recent months, many research works have been extensively conducted on studding various aspects of the disease. In [2], the author has presented a new fractional COVID-19 mathematical model with a lock-down effect. The authors of [3] have analyzed and forecasted the trend of COVID-19 spreading in China, Italy, and France. They have claimed that the infection rate needs to be cut down drastically and quickly to observe a considerable decrease in the epidemic peak and mortality rate. A mathematical model has been utilized in [4] to predict cases of COVID-19 in Mexico. A predictive analysis of the peak outbreak epidemic in South Africa, Turkey, and Brazil has been presented in [5]. The effectiveness of the social distancing measures on the spread of COVID-19 was studied in [6] different between the ten major countries affected by COVID-19. The authors of [7] have investigated some useful climatology parameters on the COVID-19 outbreak in Iran. The work of [8] has characterized the epidemic of COVID-19 in Heilongjiang province. For more works, interested readers are referred to [9], [10], [11], [12], [13], [14], [15].

A review of historical evidence suggests that the highest mortality rate in the Spanish pandemic-influenza in 1918 was also related to the second wave of the disease. This “second wave” of epidemic activity peaked by the end of October but was followed by yet another wave of disease in midwinter [16]. In the case of COVID-19, the study of the behavior and prevalence of the disease in the second and even later waves seems to be a significant point. This concern has been our main motivation for presenting this article.

The general structure of the content of this article is as follows. In Section 2, we will review the history of the disease in Iran from the beginning up to now. In the third section, we will introduce the mathematical model of the problem, which describes the behavior of four different groups of people in society affected by the disease. The mathematical analysis corresponded to the model is also presented in Section 4. This section includes the proof of the positiveness of the solutions, and analyzing the stability behavior of the equilibrium points for the model. Numerical simulations related to the model will be presented in the fifth section of this article. This chapter predicts the behavior of the virus in the coming months in the form of several scenarios, and by changing some of the parameters in the method. Finally, general conclusions will be drawn at the end of the article.

2. COVID-19 In Iran

The first cases of COVID-19 disease in Iran were announced by the authorities on February 19, 2020 in Qom, which is located 140 km to the south of Tehran. The disease was rapidly observed in other provinces of the country, and the number of victims of the virus was increasing every day. At this time, the authorities decided to take restrictive measures for people in the community and public places. From the beginning of April to the beginning of May, the severity of the disease in Iran was reduced by applying social distance, quarantine, and closing public places. The general belief of the people during this period was that the disease had subsided permanently. This misconception has led people to forget the issue of social distance and to remove the imposed travel restrictions one after another. With the reduction of imposed restrictions in April and the resumption of normal behavior in society, the disease resurfaced. The evolution of the spread of COVID-19 disease in Iran between 22/01/2020 and 20/06/2020 is shown in Fig. 1 , where necessary data has been taken from [17]. As can be seen, the recent growing trend of the disease has sounded a new alarm for the people and public health authorities in Iran.

Fig. 1.

The evolution of the spread of COVID-19 disease in Iran between 22/01/2020 and 20/06/2020.

During the coronavirus (COVID-19) pandemic, many people take precautions actions to stay healthy. Although it is important to wash your hands for 20 s and remain in lock-down to prevent the spread of the virus, having a strong immune system that resists the virus is the primary way to deal with the deadly effects of the disease. For example, stress reduces the body’s lymphocytes, which help fight infection. If the level of lymphocytes in the body drops, we will be more prone to viruses such as COVID-19. Also, people with immunodeficiency are at risk. People with severe immunodeficiency and who taking immunosuppressive drugs, including those undergoing bone marrow transplantation and receiving immunoglobulin therapy at hospitals monthly, are also at higher risk for respiratory infections, including coronavirus. Some categories of people with weakened immune systems include people with leukemia, lymphomas, myeloid plasma syndromes, organ recipients, and hematopoietic stem cells, people with primary or acquired immunodeficiency such as AIDS, and those currently undergoing chemotherapy or radiotherapy. And people who take high-dose corticosteroids for more than 20 mg of prednisone a day, or the equivalent for 14 days or more. The virus may cause severe complications in persons with immunodeficiency, the elderly, and persons with chronic diseases such as cancer, diabetes, and lung diseases. Table 1 shows the percentages of people with some chronic disease in Iran. The data has taken from Sepanlou et al. [18].

Table 1.

The percentage of individuals with chronic diseases in Iran.

Chronic disease	percentage
Heart disease	21.8%
Cancer	0.111%
Diabetes	0.0121%
Hypertension	25%

Due to the high percentage of people suffering from such diseases in Iran, it is necessary for infected people and health officials to comply with relevant protocols against COVID-19.

3. A mathematical representation of the model

In this manuscript, we consider a mathematical formulation that takes into account four major classes. We consider the following model:

$$\{\begin{array}{c}\frac{dS\left(t\right)}{dt}=-\tau \left(t\right)S\left(t\right)(I_1\left(t\right)+I_2\left(t\right)),\hfill \\ \frac{d{I}_1\left(t\right)}{dt}=\alpha \tau \left(t\right)S\left(t\right)(I_1\left(t\right)+I_2\left(t\right))-{\gamma }_1{I}_1\left(t\right),\hfill \\ \frac{d{I}_2\left(t\right)}{dt}=(1-\alpha )\tau \left(t\right)S\left(t\right)(I_1\left(t\right)+I_2\left(t\right))-({\gamma }_2+\mu )I_2\left(t\right),\hfill \\ \frac{dR\left(t\right)}{dt}={\gamma }_1{I}_1\left(t\right)+{\gamma }_2{I}_2\left(t\right),\hfill \end{array}$$ (1)

where S(t) represents the density of the susceptible population at time t. I ₁(t) is the density of the infected population with a strong immunity system. I ₂(t) is the density of the infected population with a weak immunity system or with a historical medical illness as diabetic, blood pressure, heart issue, and others. R(t) is the recovered individuals from the COVID-19 disease. Also, α is the percentage of individuals with a weak immunity system, and μ is the mortality rate of the infected individual. Moreover, ${\gamma }_i,i=1,2$ are the recover rates corresponding to the infected individuals I ₁, I ₂.

The transmission function is denoted by τ(t) which is assumed to take the following form:

$$\tau \left(t\right)=\{\begin{array}{c}{\tau }_0,fort\in [0,T],\hfill \\ {\tau }_0{\exp }^{-at},fort\in [T,T^{*}],\hfill \\ {\tau }_1,fort>T^{*}\hfill \end{array}$$ (2)

the reason behind choosing the transmission functional to be written in this special form for modeling the restriction given in Iran. In our simulations, we set $T=$1 April 2020 and $T^{*}=$1 May 2020.

4. The model analysis

This section is devoted to the mathematical analysis aspects of the model used in this paper.

4.1. The positiveness of the solutions

First, we need to prove that the solutions of the system are positive.

From the second equation in (1), one gets

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{I}_1\left(t\right)}{dt}}& =& \alpha \tau \left(t\right)S\left(t\right)(I_1\left(t\right)+I_2\left(t\right))-{\gamma }_1{I}_1\left(t\right),\hfill \\ & \ge & -{\gamma }_1{I}_1\left(t\right),\hfill \end{array}$$ (3)

which implies that

$$I_1\left(t\right)\ge I_1\left(0\right)exp[-{\gamma }_{1}t],\forall t\ge 0$$ (4)

Moreover, we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{I}_2\left(t\right)}{dt}}& =& (1-\alpha )\tau \left(t\right)S\left(t\right)(I_1\left(t\right)+I_2\left(t\right))-({\gamma }_2+\mu )I_2\left(t\right),\hfill \\ & \ge & -({\gamma }_2+\mu )I_2\left(t\right),\hfill \end{array}$$ (5)

For which we obtain

$$I_2\left(t\right)\ge I_2\left(0\right)exp[-({\gamma }_2+\mu )t],\forall t\ge 0$$ (6)

The last equation in (1) implies that

$$\frac{dR\left(t\right)}{dt}={\gamma }_1{I}_1\left(t\right)+{\gamma }_2{I}_2\left(t\right)$$ (7)

From (7) we get

$$R\left(t\right)=R\left(0\right)+{\int }_0^t{\gamma }_1{I}_1\left(u\right)+{\gamma }_2{I}_2\left(u\right)du$$ (8)

Since R(0) > 0, and for t ≥ 0 we have I ₁(t), I ₂(t) > 0, the positiveness of R(t) for t ≥ 0 is established.

Finally from

$$\frac{dS\left(t\right)}{dt}=-\tau \left(t\right)S\left(t\right)(I_1\left(t\right)+I_2\left(t\right))$$ (9)

we get

$$\frac{S^{\prime }\left(t\right)}{S\left(t\right)}=-\tau \left(t\right)(I_1\left(t\right)+I_2\left(t\right))$$ (10)

From definition for τ(t), we know that τ(t) > 0, I ₁(t), and I ₂(t) for t ≥ 0. Then we get

$$S\left(t\right)=S\left(0\right)exp[-\tau \left(t\right)(I_1\left(t\right)+I_2\left(t\right))].$$ (11)

The last equation implies that S(t) > 0 for t ≥ 0.

4.2. The basic reproduction number

In this part, we will calculate the basic reproduction number corresponding to the first and the second wave. Note that in the period t ∈ [0, T] and t > T* we obtain that the transmission rate becomes constant. So, at these intervals, we can use the next generation matrix. we consider the infectious part by the following system

$$\{\begin{array}{c}\dot{I_1}\left(t\right)=(1-\alpha )\tau S_0(I_1\left(t\right)+I_2\left(t\right))-{\gamma }_1{I}_1\left(t\right),\hfill \\ \dot{I_2}\left(t\right)=\alpha \tau S_0(I_1\left(t\right)+I_2\left(t\right))-({\gamma }_2+\mu )I_2\left(t\right),\hfill \end{array}$$ (12)

We consider the following two matrixes:

$$F=\left(\begin{array}{cc}(1-\alpha )\tau S_0\hfill & (1-\alpha )\tau S_0\hfill \\ \alpha \tau S_0\hfill & \alpha \tau S_0\hfill \end{array}\right)\text{and}V=\left(\begin{array}{cc}-{\gamma }_1\hfill & 0\hfill \\ 0\hfill & -({\gamma }_2+\mu )\hfill \end{array}\right)$$

Hence, the next-generation matrix is:

$$F{V}^{-1}=\left(\begin{array}{cc}\frac{(1-\alpha )\tau S_0}{\mu +{\gamma }_2}\hfill & \frac{(1-\alpha )\tau S_0}{{\gamma }_1}\hfill \\ \frac{\alpha \tau S_0}{\mu +{\gamma }_2}\hfill & \frac{\alpha \tau S_0}{{\gamma }_1}\hfill \end{array}\right)$$

then the basic reproduction number is given in the following form:

$$R_0=\frac{(1-\alpha )\tau S_0}{\mu +{\gamma }_2}+\frac{\alpha \tau S_0}{{\gamma }_1}$$ (13)

4.3. The equilibrium stability

The model presented in (1) has one equilibrium point corresponding to the disease-free and endemic equilibrium of

$$E^{*}=(0,0,0,0)$$

The model will exabit endemic features if

$$I_1\left(t\right),I_2\left(t\right)>0.$$ (14)

That is

$$\begin{array}{c}0<\alpha \tau \left(t\right)S\left(t\right)(I_1\left(t\right)+I_2\left(t\right))-{\gamma }_1{I}_1\left(t\right),\hfill \\ 0<(1-\alpha )\tau \left(t\right)S\left(t\right)(I_1\left(t\right)+I_2\left(t\right))-({\gamma }_2+\mu )I_2\left(t\right)>.\hfill \end{array}$$ (15)

Thus

$$I_1\left(t\right)>\frac{-{\tau }^{*}{s}^{*}+{\gamma }_1+\mu }{{\tau }^{*}{s}^{*}-{\gamma }_1}{I}_2\left(t\right)$$ (16)

Taking the norm of the two equations then replacing in Eq. (1), we have

$$(1-\alpha ){\tau }^{*}{s}^{*}(\frac{-{\tau }^{*}{s}^{*}+{\gamma }_1+\mu }{{\tau }^{*}{s}^{*}-{\gamma }_1}{I}_2\left(t\right)+I_2\left(t\right))>({\gamma }_1+\mu )I_2\left(t\right),$$ (17)

thus

$$(1-\alpha ){\tau }^{*}{s}^{*}(\frac{-{\tau }^{*}{s}^{*}+{\gamma }_1+\mu }{{\tau }^{*}{s}^{*}-{\gamma }_1}+1)>({\gamma }_1+\mu ),$$ (18)

Therefore if $S^{*}=S$ and $\tau =ta{u}^{*},$ one gets

$$(1-\alpha ){\tau }^{*}{s}^{*}(\frac{-{\tau }^{*}{s}^{*}+{\gamma }_1+\mu }{{\tau }^{*}{s}^{*}-{\gamma }_1}+1)>1,$$ (19)

In particular

$$\frac{(1-\alpha )\tau S_0}{{\gamma }_1+\mu }+\frac{\alpha \tau S_0}{{\gamma }_1}>1,$$ (20)

Hence from (13), we get R ₀ > 1.

4.4. Local and global asymptotic stability of equilibrium points

For local case, let us define the following Lyapunov function

$$L=\frac{1}{{\gamma }_1}{I}_1\left(t\right)+\frac{1}{{\gamma }_2+\mu }{I}_2\left(t\right).$$ (21)

Hence we have

$$\frac{dL}{dt}=\frac{1}{{\gamma }_1}{I}_1^{\prime }\left(t\right)+\frac{1}{{\gamma }_2+\mu }{I}_2^{\prime }\left(t\right).$$ (22)

Taking (1) into consideration, we obtain

$$\begin{array}{ccc}\hfill \frac{dL}{dt}& =& \frac{1}{{\gamma }_1}(\alpha \tau \left(t\right)S\left(t\right)(I_1\left(t\right)+I_2\left(t\right))-{\gamma }_1{I}_1\left(t\right))\hfill \\ & & +\frac{1}{{\gamma }_2+\mu }((1-\alpha )\tau \left(t\right)S\left(t\right)(I_1\left(t\right)+I_2\left(t\right))-({\gamma }_2+\mu )I_2\left(t\right)),\hfill \end{array}$$ (23)

Some straightforward manipulations give

$$\begin{array}{ccc}\hfill \frac{dL}{dt}& =& \frac{1}{{\gamma }_1}\left(\alpha \tau \left(t\right)S\left(t\right)\right(I_1\left(t\right)+I_2\left(t\right)\left)\right)\hfill \\ & & +\frac{1}{{\gamma }_2+\mu }\left((1-\alpha )\tau \left(t\right)S\left(t\right)\right(I_1\left(t\right)+I_2\left(t\right)\left)\right)-(I_2\left(t\right)+I_2\left(t\right)),\hfill \\ & =& (\frac{1}{{\gamma }_1}\left(\alpha \tau \right(t\left)S\right(t)+(1-\alpha \left)\tau \right(t\left)S\right(t\left)\right)-1)(I_2\left(t\right)+I_2\left(t\right))\hfill \\ & =& (R_0-1)(I_2\left(t\right)+I_2\left(t\right)),\hfill \end{array}$$ (24)

Since if R ₀ > 1 holds, then we have $\frac{dL}{dt}>0,$ and for R ₀ < 1 then $\frac{dL}{dt}<0$ is established. It is apparent that in case of $I_1=I2=0,$ then $\frac{dL}{dt}=0$.

For global stability analysis, let us define the following Lyapunov function

$$\begin{array}{ccc}\hfill L& =& (S-S^{*}-S^{*}log\frac{S}{S^{*}})+(I_1-I_1^{*}-I_1^{*}log\frac{I_1}{I_1^{*}})\hfill \\ & & +(I_2-I_2^{*}-I_2^{*}log\frac{I_2}{I_2^{*}})+(R-R^{*}-R^{*}log\frac{R}{R^{*}}).\hfill \end{array}$$ (25)

Consequently, we obtain

$$\frac{dL}{dt}=\frac{(S-S^{*})}{S}\frac{dS}{dt}+\frac{(I_1-I_1^{*})}{I_1}\frac{d{I}_1}{dt}+\frac{(I_2-I_2^{*})}{I_2}\frac{d{I}_2}{dt}+\frac{(R-R^{*})}{R}\frac{dR}{dt}.$$ (26)

Taking (1) into consideration, we obtain

$$\begin{array}{ccc}\hfill \frac{dL}{dt}& \ge & \frac{(S-S^{*})}{S}(-\tau \left(t\right)S\left(t\right)(I_1+I_2))+\frac{(I_1-I_1^{*})}{I_1}(\alpha \tau S(I_1+I_2)-{\gamma }_1{I}_1)\hfill \\ & & -\frac{I_1^{*}}{I_1}\alpha \tau S(I_1+I_2)-({\gamma }_2+\mu )I_2+\frac{(R-R^{*})}{R}({\gamma }_1{I}_1+{\gamma }_2{I}_2),\hfill \\ & \ge & -\tau \frac{{(S-S^{*})}^2}{S}(I_1+I_2)-{\gamma }_1\frac{{(I_1-I_1^{*})}^2}{I_1}-({\gamma }_2+\mu )\frac{{(I_2-I_2^{*})}^2}{I_2}\hfill \\ & & -\frac{\left(I_1^{*}\right)}{I_1}\alpha \tau S(I_1+I_2)+\alpha \tau S(I_1+I_2)\hfill \\ & & +(1-\alpha )\tau S(I_1+I_2)-(1-\alpha )\tau S(I_1+I_2)\frac{I_2^{*}}{I_2}-\frac{R^{*}}{R}({\gamma }_1{I}_1+{\gamma }_2{I}_2),\hfill \\ & \ge & {\Lambda }_1+{\Lambda }_2.\hfill \end{array}$$ (27)

where

$$\begin{array}{ccc}\hfill {\Lambda }_1& =& \alpha \tau S(I_1+I_2)+(1-\alpha )S\tau (I_1+I_2)+{\gamma }_1{I}_1+{\gamma }_2{I}_2\hfill \\ & =& \tau S(I_1+I_2)+{\gamma }_1{I}_1+{\gamma }_2{I}_2\hfill \\ \hfill {\Lambda }_2& =& \tau \frac{{(S-S^{*})}^2}{S}+{\gamma }_1\frac{{(I_1-I_1^{*})}^2}{I_1}+({\gamma }_2+\mu )\frac{{(I_2-I_2^{*})}^2}{I_2}\hfill \\ & & +\frac{I_1^{*}}{I_1}\alpha \tau S(I_1+I_2)+(1-\alpha )\tau S(I_1+I_2)\frac{I_2^{*}}{I_2}+\frac{R^{*}}{R}({\gamma }_1{I}_1+{\gamma }_2{I}_2).\hfill \end{array}$$ (28)

So, we conclude that

• • $\frac{dL}{dt}=0,$ whenever ${\Lambda }_1={\Lambda }_2,$
• • $\frac{dL}{dt}>0,$ whenever Λ₁ > Λ₂,
• • $\frac{dL}{dt}<0,$ whenever Λ₁ < Λ₂.

5. Numerical simulations

In this section, numerical simulations related to the model and description of the results obtained from it will be examined. We simulate the model system (1) using the fourth-order Runge Kutta method. To this end, let usdefine $\mathbb{X}\left(t\right)={\left[S\left(t\right)I_1\left(t\right)I_1\left(t\right)R\left(t\right)\right]}^T,$ we can rewrite the system (1), as

$${\mathbb{X}}^{\prime }\left(t\right)=\mathbb{F}(t,\mathbb{X}(t\left)\right),$$

where

$$\mathbb{F}(t,\mathbb{X}(t\left)\right)=\left[\begin{array}{c}-\tau \left(t\right)S\left(t\right)(I_1\left(t\right)+I_2\left(t\right))\\ \alpha \tau \left(t\right)S\left(t\right)(I_1\left(t\right)+I_2\left(t\right))-{\gamma }_1{I}_1\left(t\right)\\ (1-\alpha )\tau \left(t\right)S\left(t\right)(I_1\left(t\right)+I_2\left(t\right))-({\gamma }_2+\mu )I_2\left(t\right)\\ {\gamma }_1{I}_1\left(t\right)+{\gamma }_2{I}_2\left(t\right)\end{array}\right].$$

Now pick a step-size δt > 0 and define $t_{n+1}=t_n+\delta t$. As a result, successive approximations for the system response are determined as follows

$${\mathbb{X}}_{n+1}={\mathbb{X}}_n+\frac{\delta t}{6}(K_1+2K_2+2K_3+K_4),n\ge 0$$ (29)

where

$$\begin{array}{ccc}\hfill K_1& =& \mathbb{F}(t_n,{\mathbb{X}}_n),\hfill \\ \hfill K_2& =& \mathbb{F}(t_n+\frac{\delta t}{2},{\mathbb{X}}_n+\delta t\frac{K_1}{2}),\hfill \\ \hfill K_3& =& \mathbb{F}(t_n+\frac{\delta t}{2},{\mathbb{X}}_n+\delta t\frac{K_2}{2}),\hfill \\ \hfill K_4& =& \mathbb{F}(t_n+\delta t,{\mathbb{X}}_n+\delta t{K}_3).\hfill \end{array}$$

In this contribution, we use the COVID-19 real data starting from 22 January 2020 to 25 June 2020 in Iran for the calibration, and validation then of the COVID-19 model (1). The constant parameters in the model (1) are taken as

$$\begin{array}{ccc}\hfill \alpha & =& 0.47,{\gamma }_1=1/10,{\gamma }_2=1/15,\mu =1/50,{\tau }_0=2\times {10}^{-9},\hfill \\ \hfill {\tau }_1& =& 1.41\times {10}^{-9}.\hfill \end{array}$$ (30)

Also, we have set step-size as $\delta t=0.001,$ and following initial values for solutions are considered

$$\begin{array}{ccc}\hfill S\left(0\right)& =& 8.18\times {10}^7,I_1\left(0\right)=5.0604\times {10}^3,I_2\left(0\right)=4.4876\times {10}^3,\hfill \\ \hfill R\left(0\right)& =& 4590.\hfill \end{array}$$

Fig. 2 depicts the exact values obtained from valid sources for two functions I ₁(t) and I ₂(t) and the approximate values corresponding to them achieved by the model (1). As can be seen, there is an excellent agreement between these two categories of data. This confirms the validity of the model and its corresponding results.

Fig. 2.

The real and approximation of the first and the second wave of COVID-19 in Iran.

In Fig. 3 , we show the effect of α on both I ₁(t) and I ₂(t) solutions where all the parameters introduced in (30) remain fixed, and only the effect of the parameter α on the model changes. A closer look reveals that the maximum value for the density of the infected population with strong immunity I ₁(t) and weak immunity I ₂(t) will occur on 23 December 2020 and 25 December 2020 for $\alpha =0.5,$ respectively. As the α rate decreases, the peak value of the graphs decreases, and their occurrence time is delayed. The results confirm that the percentage of people with a weak system α will have a direct impact on increasing the number of patients with the disease. Because such people are the most susceptible people in society to be infected by the disease. Besides, the incidence of people with a strong immune system will increase at the same time as people with a weak immune system.

Fig. 3.

Impact of α on the dynamic of the system.

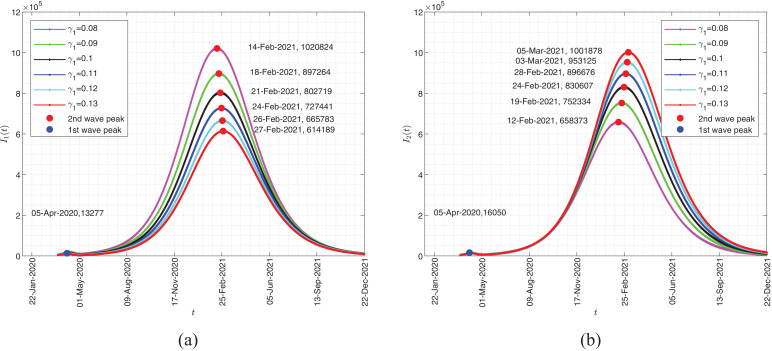
In Fig. 4 , we show the effect of γ ₁ on both I ₁(t) and I ₂(t) densities. In these scenarios, all the parameters introduced in the model, as reported in Table 1, are fixed and only the effect of the parameter γ ₁ on the model feedback is examined. The plot shows that the maximum values for I ₁(t) and I ₂(t) will occur on 14 February 2021 and 5 March 2021 for ${\gamma }_1=0.8,$ respectively. As γ ₁ decreases, the peak value of the graphs decreases and their occurrence time is delayed. The results confirm that the recovery rate corresponding to the infected individual I ₁ has a reverse impact on increasing the number of patients in two populations with a weak or strong immune system.

Fig. 4.

Impact of γ₁ on the dynamic of the system.

Now, we are going to study the effect of γ ₂ on both I ₁(t) and I ₂(t) solutions. Fig. 5 , shows that the maximum values for I ₁(t) and I ₂(t) will occur on 30 October 2020 and 4 November 2020 for ${\gamma }_2=0.05,$ respectively. As γ ₂ decreases, the peak value of the graphs decreases, and their occurrence time is delayed. The results confirm that the recovery rate corresponding to the infected individual I ₂ has a reverse impact on increasing the number of patients in two populations with a weak or strong immune system. Thus, by increasing the rate of the γ ₂, it is possible to control the disease to some extent and prevent more people from becoming infected and thus dying from the disease.

Fig. 5.

Impact of γ₂ on the dynamic of the system.

The effect of the mortality rate of the infected individual μ on both I ₁(t) and I ₂(t) solutions are displayed in Fig. 6 . It is apparent that the maximum predicted values for I ₁(t) and I ₂(t) will occur on 3 December 2020 and 7 December 2020 for $\mu =0.01,$ respectively. As μ decreases, the peak value of the graphs decreases, and their occurrence time is delayed. In all of the cases examined, it was found that if the number of illnesses reaches a peak earlier then the number of sick people in society decreases faster. Based on the performed numerical simulations, the highest incidence of the disease occurs simultaneously with changes in the parameter γ ₂. We observe that one of the essential strategies to prevent the incidence of fewer people in the community is to increase the recovery rate corresponding to the infected individuals with weak immune systems by applying necessary medical prescriptions. This point can be considered as one of significant achievements in the article.

Fig. 6.

Impact of μ on the dynamic of the system.

In all of the examined cases, we predict that the second wave will be hugely higher than the first wave.

6. Conclusion

Epidemiologists have come up with different theories about how Corona’s second wave works. Some believe that the second wave is likely to occur in the fall and winter, which is more severe than the first one. Failure to comply with social distances in public places from the middle of this year can lead to the second wave of COVID-19 between August and December. Therefore, preparation for the second wave of the disease is very important. In this article, we look at the problem from the framework of mathematical modeling of a system of differential equations. Then, the necessary conditions for local and global stability of the equilibrium points of this system have been investigated. The important thing about the second wave of COVID-19 depends mostly on our social behaviors. Using the simulations performed by considering the different values of the parameters in the method, the proposed scenarios have been provided in recent months in Iran. We remark that the second wave has less spread than the first, but the number of infection cases will continue rising. So an urgent public health intervention is needed. The results of this paper and similar articles can be used in future decision-making to control the disease and prevent further damages.

CRediT authorship contribution statement

Behzad Ghanbari: Writing - original draft, Conceptualization, Methodology, Software, Supervision, Writing - review & editing, Data curation, Visualization, Investigation.

Declaration of Competing Interest

The authors certify that they have NO affiliations with or involvement in any organization or entity with any financial interest (such as honoraria; educational grants; participation in speakers bureaus; membership, employment, consultancies, stock ownership, or other equity interest; and expert testimony or patent-licensing arrangements), or non-financial interest (such as personal or professional relationships, affiliations, knowledge or beliefs) in the subject matter or materials discussed in this manuscript. Also no funding was received for this work.