Transcranial focused ultrasound generates skull-conducted shear waves: Computational model and implications for neuromodulation

Abstract

Focused ultrasound (FUS) is an established technique for non-invasive surgery and has recently attracted considerable attention as a potential method for non-invasive neuromodulation. While the pressure waves in FUS procedures have been extensively studied in this context, the accompanying shear waves are often neglected due to the relatively high shear compliance of soft tissues. However, in bony structures such as the skull, acoustic pressure can also induce significant shear waves that could propagate outside the ultrasound focus. Here, we investigate wave propagation in the human cranium by means of a finite-element model that accounts for the anatomy, elasticity, and viscoelasticity of the skull and brain. We show that, when a region on the scalp is subjected to FUS, the skull acts as a waveguide for shear waves that propagate with a speed close to 1500 m/s, reaching off-target structures such as the cochlea. In particular, when a sharp onset of FUS is introduced in a zone proximal to the intersection of the parietal and temporal cranium, the bone-propagated shear waves reach the inner ear in about 40 $\mu s$, leading to cumulative displacements of about 1 $\mu \mathrm{m}$. We further quantify the effect of ramped and sharp application of FUS on the cumulative displacements in the inner ear. Our results help explain the off-target auditory responses observed during neuromodulation experiments and inform the development of mitigation and sham control strategies.

Focused ultrasound (FUS) is an established therapeutic modality taking advantage of the ability of sound waves to deliver energy to anatomically precise regions of organs such as the human brain.^1–3 In addition to previous medical applications,^4–10 low-intensity transcranial FUS has recently elicited growing interest as a tool for neuromodulation,^11–22 owing to its concurrent benefits of relative safety, non-invasiveness, and millimeter-scale precision. However, the underlying biophysical mechanisms that are responsible for eliciting neural activation are not well understood and constitute an active area of research. We refer the reader to Ref. 23 for a thorough review of the relevant literature. In particular, recent studies have documented off-target auditory responses to FUS neuromodulation in rodents^24,25 and humans.²⁶ To better understand these phenomena at both the tissue and cellular levels, computational models can play a useful role.^27,28

Modeling ultrasound wave propagation in the brain requires realistic models that accurately represent anatomical details and the mechanical response of the tissues. In recent years, detailed computational models have been successfully constructed from magnetic resonance (MR) images.^29–32 The constitutive modeling of soft biological tissues has also received considerable attention.^33–38 Due to the complexity of the mechanical response of the tissues, the material parameters reported in the literature differ by several orders of magnitude.^36,39 These uncertainties notwithstanding, the large contrast between the bulk and shear moduli is generally understood to result in widely disparate longitudinal and transverse wave speeds, with the former in the range of 1000–1500 m/s and the latter at most 10 m/s.^40–42 Moreover, shear waves are strongly attenuated in soft biological tissues.^40,42–45 This shear compliance and strong shear wave attenuation properties often allow soft tissues to be modeled as acoustic media.²⁷ By contrast, this assumption fails in the presence of hard structures such as bone, which can sustain shear waves of amplitude comparable to pressure waves and can act as waveguides by virtue of their extreme impedance contrast to soft tissues.

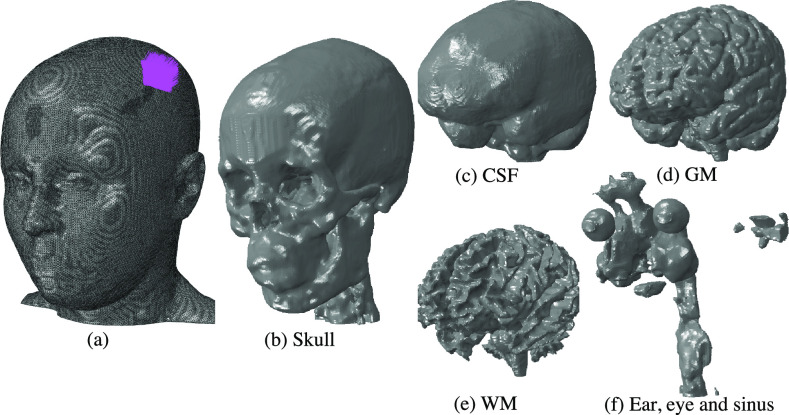
In the present work, we investigate wave propagation in the human cranium by means of a finite-element model that accounts for the anatomy, elasticity, and viscoelasticity of the skull and brain (Fig. 1). We employ a high-resolution solid model from the SCI Head Model project⁴⁶ constructed from T1-weighted MR images obtained from a 23-year old healthy female subject. The model comprises the scalp, skull, cerebrospinal fluid (CSF), gray matter (GM), white matter (WM), eyes, ears, and sinuses (Fig. 1).

FIG. 1.

High-resolution solid mechanical model of the human cranium from the SCI Head Model project.⁴⁵ (a) Total model with 8 512 657 nodes and 48 458 912 million linear tetrahedral elements. The region on the scalp subjected to ultrasound pressure as the traction boundary is shown by purple arrows. Inner parts of the model include the (b) skull, (c) cerebrospinal fluid (CSF), (d) gray matter (GM), (e) white matter (WM), and (f) combined ear, eye, and sinus.

On this domain, we solve the initial boundary-value problem of small-strain viscoelasticity. Finite elasticity models have been investigated³⁷ and found to be indistinguishable from small-strain Hookean models under the low-intensity FUS conditions of interest here, which amounts to displacements of the order of micrometers. The material parameters used in calculations for various tissue types in the model are taken from the literature^47,48 and collected in Table I. In this table, $\kappa$ is the bulk modulus, G is the shear modulus, and $\rho$ is the mass density. The six-order of magnitude contrast in the shear moduli of bone and soft cerebrospinal tissue is remarkable, as is the similar contrast between the bulk and shear moduli in the soft tissue. The discrepancy between bulk and shear moduli in the soft tissue is often taken as a basis for neglecting shear waves, accounting for pressure or sound waves only.²⁷ However, when the skull/brain system is considered in its entirety, shear stiffness and impedance mismatch strongly influence wave patterns. The viscoelastic properties of the soft tissues are modeled by means of the standard linear solid model⁴⁹ with the exponential relaxation function,

$$G\left(t\right)=1-g^{\prime }\left(1-e^{-\frac{t}{\tau }}\right),$$ (1)

where $g^{\prime }$ and $\tau$ denote the relaxation coefficient and characteristic relaxation time, respectively. The values of the relaxation parameters are taken from Refs. 47 and 48 and shown in Table I. The CSF is approximated as an elastic medium with an exceedingly small shear modulus but capable of transmitting pressure waves.

TABLE I.

Elastic and viscoelastic properties of different tissues of the head, where κ is the bulk modulus, G is the shear modulus, ρ is the mass density, $g^{\prime }$ is the relaxation coefficient, and $\tau$ is the characteristic relaxation time. Where $g^{\prime }$ and $\tau$ is left blank, viscoelasticity is not accounted for.

	$\kappa \hspace{0.17em}(\mathrm{Pa})$	G (Pa)	$\rho \hspace{0.17em}(N/{\mathrm{m}}^3)$	$g^{\prime }$	$\tau (s)$
Skull	4.76 × 109	3.28 × 109	1721	…	…
Scalp	3.36 × 109	6.7 × 105	1100	0.6	3e-5
GM	1.2 × 109	1.2 × 103	1060	0.8	80
WM	1.5 × 109	1.5 × 103	1060	0.8	80
CSF	1.33 × 109	20	1040	…	…
Ear/Sinus	8.33 × 105	3.85 × 105	1000	…	…
Eye	1.13 × 107	2.28 × 103	1078	…	…

The skull and brain geometry is discretized into a finite-element model comprising 48.4 million three-dimensional tetrahedral elements and 8.5 million nodes (Fig. 1). We subject a region of the scalp, proximal to the intersection of parietal and temporal cranium, shown in purple in Fig. 1, to sinusoidal pressure with a peak amplitude of 0.6 MPa and a frequency of 200 kHz. Transient pressure wave propagation results for other US frequencies are reported in the supplementary material. Acoustic focusing is modeled by imposing the applied pressure with a phase offset in the radial direction. The governing equations are integrated in time by means of the explicit Newmark algorithm, as implemented in the commercial code Abaqus/Explicit (Dassault Systemes Simulia, France).

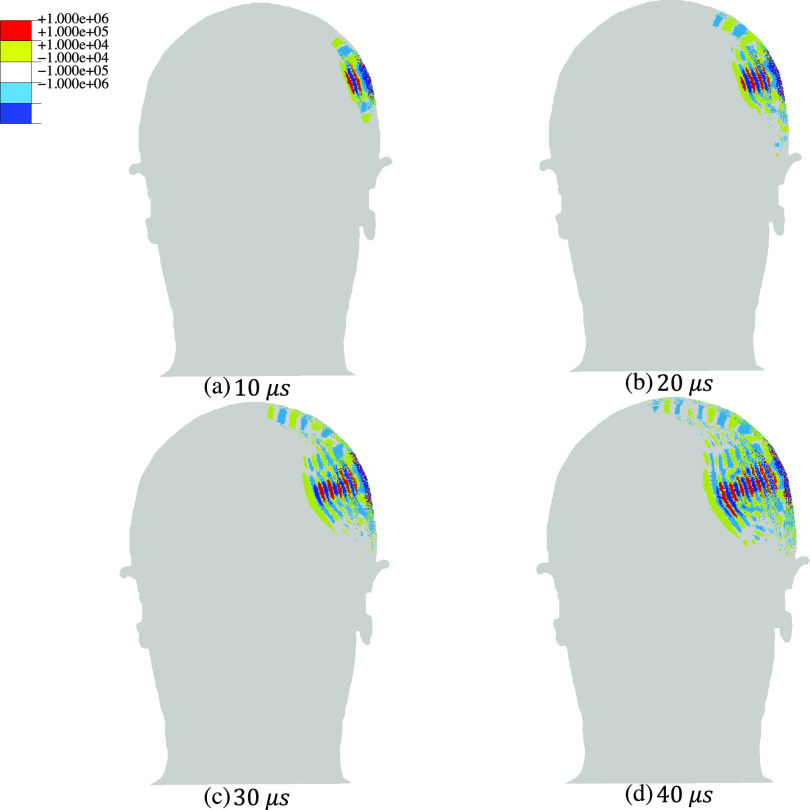
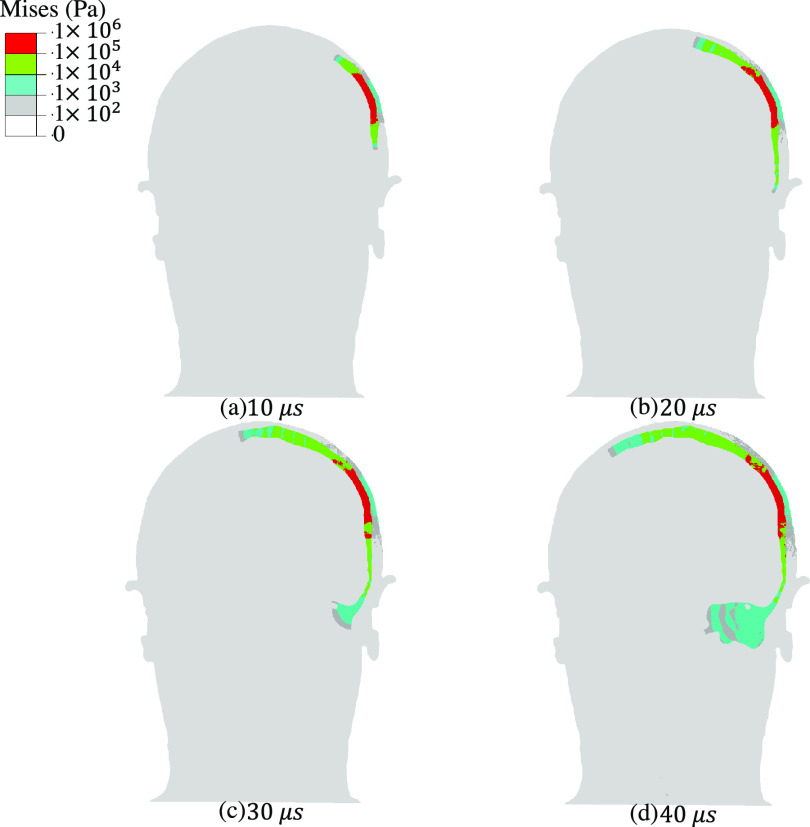
Representative computed transient pressure and shear wave patterns (Figs. 2 and 3, respectively) depict contours of pressure and von Mises stress at four different times after the onset of FUS. The results are shown in a coronal section of the head through the center of the area of application of FUS. These results show that the pressure wave is transmitted through the skull to the soft tissue and propagates through the brain, reaching peak positive and negative focal pressures of 0.95 MPa and 0.88 MPa, respectively. At the same time, shear stresses inside the brain have very low amplitudes, on the order of a few Pa, and propagate significantly more slowly. As expected for low-intensity FUS, the computed pressures are below the values reported for injury thresholds for pressure and shear stress.^34,50–53

FIG. 2.

Transient pressure wave propagation due to the application of continuous sinusoidal ultrasound with an amplitude of 0.6 MPa and a frequency of 200 kHz to a region proximal to the intersection of parietal and temporal cranium in the human head. The snapshots correspond to the pressure distribution in a coronal cross section of the head including the ultrasound focus at (a) 10 $\mu \mathrm{s}$, (b) 20 $\mu \mathrm{s}$, (c) 30 $\mu \mathrm{s}$, and (d) 40 $\mu \mathrm{s}$. For pressure results at other frequencies, 320 and 400 kHz, see Figs. S1 and S2 in the supplementary material.

FIG. 3.

Transient shear wave propagation due to the application of continuous sinusoidal ultrasound with an amplitude of 0.6 MPa and a frequency of 200 kHz to a region proximal to the intersection of parietal and temporal cranium in the human head. Bone conduction of shear waves through the skull and toward inner ear is observed. The snapshots correspond to the von Mises stress distribution in a coronal cross section of the head including the ultrasound focus at (a) 10 $\mu \mathrm{s}$, (b) 20 $\mu \mathrm{s}$, (c) 30 $\mu \mathrm{s}$, and (d) 40 $\mu \mathrm{s}$. For shear wave propagation results at other frequencies, 320 and 400 kHz, see Figs. S3 and S4 in the supplementary material.

In contrast to the transmission of pressure waves to the brain, our model shows that shear waves are guided by the skull (Fig. 3), suggesting that that the skull acts as a shear waveguide. This mechanism results in the conduction of shear waves to locations well outside the ultrasound beam path. By 30 μs after the start of FUS application, the shear waves reach the cochlea, applying stress on the order of 100 Pa to this auditory organ. Transient shear wave propagation results for two other US frequencies—320 kHz and 400 kHz—showed similar trends (supplementary material Figs. S1–S4). While higher-frequency simulations were not possible with our current computational platform, the frequency range of 200–400 kHz corresponds to parameters used in a large number of neuromodulation studies.^{18,19,21,22,25,54–56}

Our results suggest that propagation of shear waves through the skull is due to the extreme mismatch between the shear moduli of bone and brain matter. Moreover, we remark that, by maintaining the ultrasound excitation, the shear waves traverse the entire skull, which, in turn, leads to contralateral displacements. Figures S5 represents the von Mises stress distribution in the skull after 0.5 ms of ultrasound excitation. The rapid transmission of shear waves to the cochlea may help explain the off-target auditory responses recorded during neuromodulation experiments.^24–26 In particular, through ex vivo skull experiments, Braun et al.²⁶ demonstrate that the auditory response during neuromodulation in human subjects is caused by bone propagation of sound. We believe that our computational results are consistent with their findings.

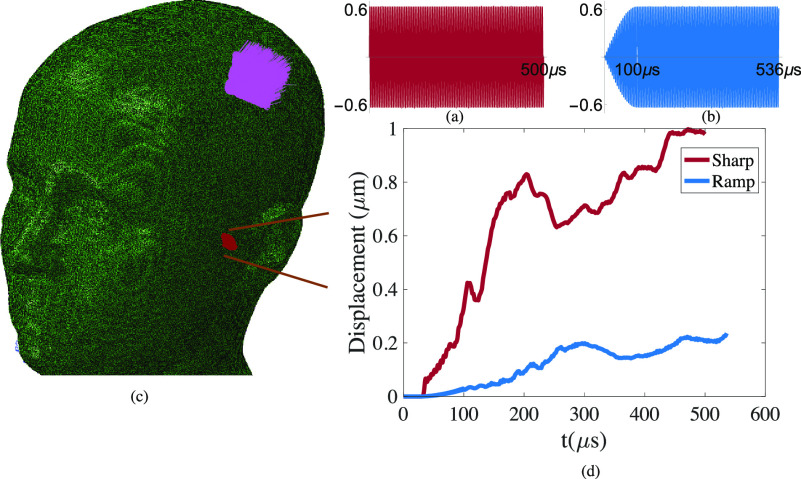
Several recent studies have argued that FUS waveforms can be designed to mitigate auditory side-effects. For example, gradual ramping of the applied wave amplitude is proposed to reduce the generation of audible frequencies in the ears.^54,55,57 To investigate this possibility while assessing the utility of our computational model in pulse waveform design, we subjected the model to two distinct FUS profiles. In the sharp profile, we applied a 200 kHz waveform with an immediate amplitude of 0.6 MPa for a stimulation time of 0.5 ms [Fig. 4(a)]. In a ramped profile, we gradually increase the amplitude, reaching a pressure of 0.6 MPa over 0.1 ms [(Fig. 4(b)]. The total stimulation time in the second waveform was extended such that the total pulse energy is identical in both cases. With recourse to the aforementioned methods, we computed the displacements in a zone of the inner ear for both cases [Fig. 4(c)]. The maximum envelope of a family of curves, where each curve corresponds to the displacement magnitude of a node in the inner as a function of time, is plotted for both scenarios in Fig. 4(d). In both the sharp and ramped scenarios, at a given point in time, the average displacement magnitude in the nodes in the inner ear is about half of the maximum values reported in Fig. 4(d). The maximum displacements resulting from sharply applied FUS reached a magnitude of 1 μm, coinciding with the displacement ranges in the Stapes and Basilar membrane needed for bone conduction hearing.⁵⁸ Obtaining the frequency content through bone propagation requires a much longer analysis.

FIG. 4.

Cumulative displacements in a zone in the inner ear resulting from sharp and ramped ultrasound application at 200 kHz to a region proximal to the intersection of parietal and temporal cranium in the human head. (a) The sharp waveform has an amplitude of 0.6 MPa, starting and ending abruptly after 0.5 ms. (b) In the ramped waveform, the maximum 0.6 MPa amplitude is reached gradually over 0.1 ms; it is then continued long enough (0.536 ms) so that both waveforms have the same total energy. (c) Model of the human cranium showing the location of FUS application and the zone of the inner ear where displacements are quantified. (d) Envelope of the family of displacement magnitude curves in the inner ear in response to sharp and ramped pulses.

Meanwhile, the ramped pulse produces a maximal displacement of 0.2 μm. This difference in displacements is consistent with the general response of an elastic system to step and ramp functions, pertinent to the theory of oscillations.⁵⁹ While we cannot conclude that the fivefold reduced magnitude of displacement in the ramped pulse is low enough to eliminate auditory effects, our finding provides support for ramping, in general, as an approach to reducing them. Due to computational limitations, the ramping time used here was shorter than those used in some neuromodulation studies.^54,57 Such more gradual ramps may be expected to further reduce the maximal shear-generated displacement. These results support the utility of this model for the design of FUS waveforms for neuromodulation. Furthermore, the existing model could be enhanced to capture other physical phenomena, for instance, by incorporating more complex microstructures into the skull or fluid models to account for the possibility of cavitation.

In summary, our results establish a computational modeling approach incorporating the solid mechanics of cranial tissues in addition to acoustics and show that this multi-physical combination is essential to fully capture the biophysical effects of transcranial FUS. In the scenario examined in this work, our model demonstrates that the skull can act as a waveguide conducting ultrasound-induced shear waves to the ear, explaining a potential source of auditory side effects in FUS neuromodulation. More generally, the ability of bone to serve as a naturally embedded waveguide for ultrasound-induced shear waves could have implications in multiple other biomedical uses of ultrasound.

See the supplementary material for additional results for transient pressure and shear wave propagation at FUS frequencies of 320 kHz and 400 kHz as well as Mises stress distributions after 0.5 ms of continuous FUS at 200 kHz.

DATA AVAILABILITY

The data that support the findings of this study are available within this article and references therein. The results of the calculations reported in this article and its supplementary material are available from the corresponding author upon reasonable request.