Highlights
-
•
The region-specific modulation of COVID-19 dynamicsis characterised with a reduced exponential model leveraging available data on sub-intensive and intensive care unit patientsmade available by all regional councils from the very onset of the disease.
-
•
This simple model provides a rather good fit of regional patient dynamics,particularly for regions where the affected population was large, highlightingimportant region-specific patterns of epidemic dynamics.
Keywords: COVID-19, Discrete-time model, Patients’ dynamics
Abstract
Italy has been one of the countries hardest hit by the coronavirus disease (COVID-19) pandemic. While the overall policy in response to the epidemic was to a large degree centralised, the regional basis of the healthcare system represented an important factor affecting the natural dynamics of the disease induced geographic specificities. Here, we characterise the region-specific modulation of COVID dynamics with a reduced exponential model leveraging available data on sub-intensive and intensive care unit patients made available by all regional councils from the very onset of the disease. This simple model provides a rather good fit of regional patient dynamics, particularly for regions where the affected population was large, highlighting important region-specific patterns of epidemic dynamics.
1. Introduction
Caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), the pandemic of coronavirus disease (COVID-19) emerged in December 2019 in Wuhan, China and rapidly spread globally [2], [27]. It was ex post confirmed to have reached Italy on 30 January 2020. An outbreak of COVID-19 infections was subsequently detected on 20 February 2020, in Codogno, in the province of Lodi, in the northern region of Lombardy [5]. On 21 February 2020, a resident of the municipality of Vo, a small town near Padua, in the Veneto region, died of pneumonia due to SARS-CoV-2 infection. This was the first COVID-19 death detected in Italy. In response, the regional authorities imposed a 14 day lockdown of the whole municipality. By the first week of March, the virus had spread to all Italian regions, most positive cases tracing back to the two original clusters. On 8 March 2020, Lombardy and 14 other northern provinces were put into quarantine, a policy extended to the whole country the following day. As of 28 June 2020, Italy had 16,681 active cases, with an overall 240,310 confirmed cases and 34,738 deaths [19].
The availability in almost real-time of data on the evolution of COVID [6], [29], something unprecedented in history, has allowed studying the patterns of disease propagation, and simulating how different contention policies may help keeping it under control [1], [7], [17], [20], [30]. These models have a long history, starting with the seminal work of Daniel Bernoulli [4], in which epidemic dynamics is described in terms of constitutive equations framed in the general theory of reaction-diffusion processes [28]. The spreading process is modelled by subdividing the studied population into subpopulations, e.g. susceptible, infected and recovered compartments in the SIR model [15], [25] - note that model acronyms usually reflect the names of the considered subpopulations. Epidemic dynamics is then modelled using difference equations (or their continuous limit) for the evolution of the average number of individuals in each compartment. The homogenous mixing approximation, whereby individuals are well mixed and interact in a random fashion, allows considering that individuals in a given subpopulation are indistinguishable. The spreading rate is then proportional to the number of infected individuals [3], [13]. While the space in which the spreading process takes place typically differs from a random uncorrelated network, and higher-order properties play an important role in theoretical models of epidemic spreading [22], [24], neglecting diffusion of individuals and assuming random and homogeneous mixing may be a reasonable approximation when studying single-region dynamics, with homogeneity forced but a common healthcare system.
It has long been known that the spatial homogeneity hypothesis incorrectly portrays real epidemic processes [26], and is in general not the rule [10], [11], [12]. The scale at which it is reasonable to assume this hypothesis is therefore non-trivial and context-dependent, the microscopic scale being determined by available data. In the case of Italy, the overall policy in response to the COVID-19 epidemic was to a large extent centralised and directed by the Health Ministry and the Civil Protection Department, the national body in charge of the prediction, prevention and management of emergency events. One could thus consider the entire territory as prima facie homogeneous. However, due to the regional basis of the healthcare system, health care management was decentralised and heterogeneous across the territory. Thus, administrative factors exogenous to the natural dynamics of the disease induced geographic specificities, justifying a region-based analysis of epidemic dynamics.
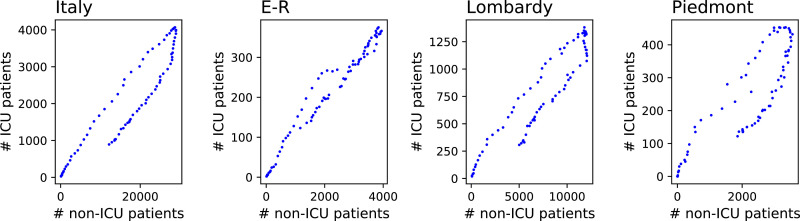
A major issue in the characterisation of epidemic dynamics is represented by the choice of the relevant variables and their reliability. Often, the chosen variable would be the number of positive cases. While this variable is essential to understanding the magnitude of the pandemic, it presents two disadvantages: it is not always easy to measure, due to different testing policies and the presence of asymptomatic patients; and it does not represent the pressure on the healthcare system. This latter point has been of special relevance in the case of COVID-19, as one of the major worries was the possibility of reaching intensive care unit saturation [14], [16], [18]. Data on hospitalised patients would offer an information-rich source of information on epidemic dynamics, which though inescapably noisy would be far more reliable (both quantitatively and temporally) than bare new case or even fatality statistics. While generally unavailable in real time, data on hospitalised patients were provided by all Italian regional councils from the very onset of the disease, making up for a data set almost unparalleled in other parts of the world. Importantly, the data set provides information on patients by case seriousness (see Section 2.2 for details). A simple scatterplot of hospitalised cases by seriousness (see Fig. 1 ) shows non-random region-specific patterns, suggesting that these two variables alone contain essential information to characterise geographic modulations of epidemic dynamics, providing a good proxy of regional healthcare system specificities.
Fig. 1.
Scatter plots of the evolution of the number of patients in Intensive Care Units (ICU), as a function of the number of patients in non-intensive care. From left to right, the four panels correspond to Italy as a whole, Emilia-Romagna (E-R), Lombardy and Piedmont. See main text for details, and especially Section 2.2 for a description of the data.
Here, we characterise the region-specific modulation of COVID-19 dynamics with a reduced exponential model. In this model, the population within a given Italian region is divided into three main compartments: non-hospitalised, hospitalised, deceased. The focus is on the second compartment, which is further divided into two sub-compartments, respectively sub-intensive and intensive care unit patients. We show that in spite of its simplicity and restrictive hypotheses, e.g. on the fluxes between compartments limited to nearest neighbour categories (see Section 2 for details), this exponential model provides a rather good fit of regional patient dynamics, particularly for regions where the affected population was large. We further show how this model is able to highlight differences between regions in the way patients are treated, specifically the time they spend in sub-intensive and intensive care units; and how these times have changed throughout the course of the pandemic. We additionally discuss some surprising results, as e.g. the fact that patients spent more time in intensive care units in regions with lower mortality. While the available data do not allow to disentangle the contribution of different virus strands vs. different healthcare policies, we believe that this model could serve as a foundation for future studies, and as an essential building block for detailed epidemics models.
2. Methods and data
In this section we describe the three main elements of the work here presented: the mathematical model of patient dynamics (Section 2.1), the data set of the regional evolution of COVID-19 in Italy (Section 2.2), and the procedure to fit the model to the data (Section 2.3).
2.1. Patient dynamics’ model
We consider that the dynamics of the relevant population in the influence area of an hospital can be described by four time series:
-
•
The number of recovered people per day, r(t), i.e. of the people who have left the hospital because their condition has improved.
-
•
The number of people in non-ICU condition in each day, n(t).
-
•
The number of people in ICU care in each day, i(t).
-
•
The number of people who have died each day in the hospital, d(t).
Using these four time series it is possible to define a fifth time series, describing the evolution of the change in the total number of cases per day: with δ representing the difference between day t and day .
We further base the model on the idea that patients move between these four groups according to a reduced set of transitions: new patients always enter as non-ICU; from non-ICU one can improve and recover, or get worse and move to ICU; and finally, ICU patients can either improve (and go back to non-ICU, or die in the hospital. Using these time series and these transition paths, we construct a discrete-time model linking them, and defined as:
| (1) |
| (2) |
| (3) |
| (4) |
In other words, the dynamics of the system is defined by four parameters:
-
•
the rate non-ICU patients improve and leave the hospital;
-
•
the rate non-ICU patients get worse and are moved to ICU;
-
•
the rate ICU patients improve and are moved to non-ICU care;
-
•
the rate ICU patients get worse and die in the hospital.
We further consider the possibility of these parameters to be time-dependent. For that, each one of them is defined by two values, respectively at time (initial step) and (last step); intermediate values are obtained through a linear interpolation. In what follows, these two values are denoted as and with * representing n → r, n → i, i → n or i → d. A synthesis of all the rates and corresponding symbols is reported in Table 1 .
Table 1.
Synthesis of all the rates here considered and of the corresponding symbols.
| Rate name | Symbol | Average value | Evolution | Initial value | Final value |
|---|---|---|---|---|---|
| Improvement of non-ICU patients | kn → r | Δkn → r | |||
| Worsening of non-ICU patients | kn → i | Δkn → i | |||
| Improvement of ICU patients | ki → n | Δki → n | |||
| Death of ICU patients | ki → d | Δki → d |
Note that, following the standard physical convention, transition rates are defined as 1/k; k then becomes the characteristic time of the system, i.e. it defines how much time patients spend in each state.
2.2. COVID evolution data
The data set here considered has been made available by the Italian Dipartimento della Protezione Civile, a department of the Consiglio dei Ministri (Council of Ministers), and has been downloaded from https://github.com/pcm-dpc/COVID-19. The data set is updated daily, and reports several quantities related to COVID-19 with a regional spatial resolution. Importantly, while inhomogeneities within regions did exist, no statistics by province were made available, thus we fixed the scale of the analysis at regional level. For this work the following variables have been considered: 1) number of people recovered with COVID-19, 2) number of patients in ICU, 3) number of patients discharged, and 4) number of daily deaths. In order to see a more stationary evolution of the disease, and exclude mayor policy changes, the first 50 days have been retained, from February 24th to April 13th 2020.
An inherent problem of this kind of data is their incompleteness and noisy nature. To illustrate, the assessment of the number of people recovered with COVID-19 related symptoms depends on how these symptoms are evaluated, which in turn depends on local policies and even personal (i.e. doctors’) perception. This number can also be adjusted a posteriori, i.e. when a patient is tested and the disease is finally confirmed or discarded. To alleviate this problem, we here have smoothed the data using a convolution function with a five-days uniform kernel. While deleting abnormal peaks and valleys, this filtering retains the global dynamics - calculating a linear correlation between the original and smoothed time series yields a median of 0.8011.
2.3. Model optimisation and parameter estimation
Given the time series of the number of daily new cases Δ(t), and an initial estimation of the eight parameters k (i.e. the four transition rates, each one defined by an initial and final value), the previous model has been executed to obtain three estimated time series and corresponding to the model estimation of n(t), i(t) and d(t). The error in the estimation of n(t) has then been calculated as
| (5) |
where σn is the standard deviation of the values of n(t). A similar error has also been calculated for i(t) and d(t), respectively yielding an error ei and ed. A total error has finally been calculated, by combining these three partial errors:
| (6) |
The best values of the eight parameters has been obtained using the Nelder-Mead algorithm [9], [23], with initial conditions drawn from a uniform distribution . In order to ensure a meaningful result, an additional condition k * > 1 is imposed. Due to the stochastic nature of the optimisation algorithm, 104 different attempts with random conditions have been performed, and the result of the attempt with lower e has been selected.
3. Results
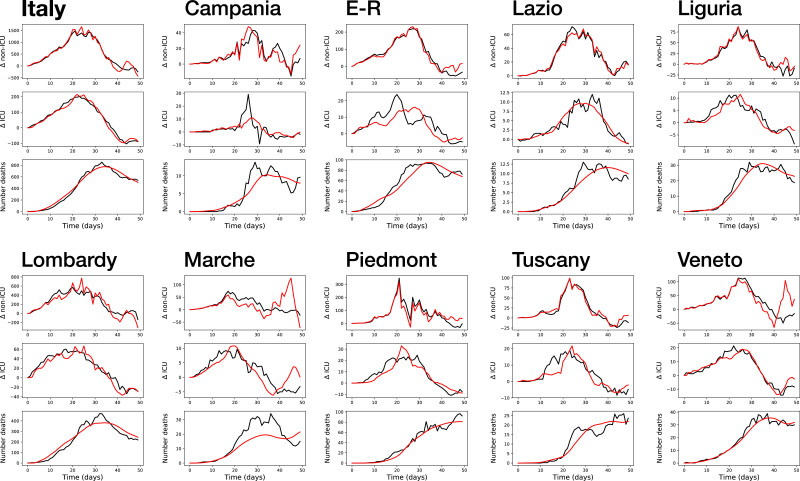
As a first result, Fig. 2 reports a comparison of the real and simulated time series, for Italy and the nine regions here considered. Within each panel, the three graphs, from top to bottom, correspond to the daily number of non-ICU, ICU and deaths. It can be appreciated that a generally good fit is obtained, in some cases even outstanding (as for Italy as a whole, first panel). On other cases, like Campania and Marche, the fit is substantially inferior, especially in the case of the time series of the number of daily deaths; yet, these two cases also present unusual behaviours in the real time series, as is the case of the central peak for the Campania’s number of ICU patients. Additionally, these cases correspond to the less populated regions, and with less COVID-19 cases; their evolution is thus intrinsically more noisy. This behaviour will further be discussed in the conclusions. Still, these results seem to suggest that the model is able to capture the most important part of the dynamics of hospital patients, with the exception of a few pathological cases.
Fig. 2.
Real (black lines) and modelled (red lines) time series of the variation in the daily number of non-ICU, ICU and deaths (respectively, top, middle and bottom graph in each panel), for Italy and the nine regions here considered. E-R: Emilia-Romagna. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
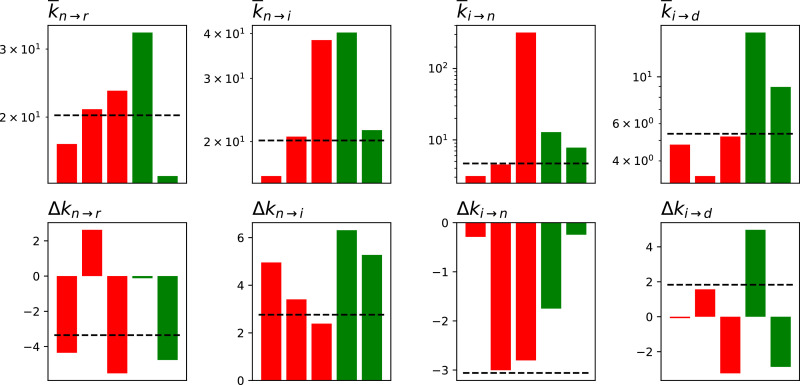
We secondly analyse the best parameters obtained by the optimisation algorithm. As they are time-dependent, we here synthesise two values: the average value of the parameter; and Δk, how much it changed from the beginning to the end of the considered time period - refer also to Table 1 for a synthesis. Specifically, Δk is defined as ; a value of (respectively, ) thus indicate a doubling (halving) of the value. Fig. 3 reports the results for the five regions for which the model yielded the best fit, divided in two groups: Liguria, Lombardy and Piedmont, red bars, i.e. regions with a high number of COVID-19 deaths (respectively 0.8942, 1.5569 and 0.8535 deaths per thousand); and Lazio and Veneto, green bars, characterised by a lower mortality (0.1100 and 0.3735 per thousand).
Fig. 3.
Values of the fitted parameters, in terms of their average ( top row) and variation (Δk, bottom row). The three red bars correspond to the three regions with higher mortality, i.e. Liguria, Lombardy and Piedmont; the two green ones, to the regions with lower mortality, i.e. Lazio and Veneto. The horizontal dashed lines correspond to the values for Italy as a whole. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
A few common patterns can be observed in Fig. 3. First of all, Δk n → i is always greater than zero: this means that k n → i always increases with time, and that patients move slower from non-ICU to ICU care - or, in other words, that less patients get worse while in the hospital. Secondly, Δk i → n is always lower than zero, thus patient conditions improve faster. Finally, is larger for regions with a lower mortality - as is to be expected, as k i → d defines the mortality rate. Beyond these patterns, a high heterogeneity is observed, with no clear rule discriminating between high- and low-mortality regions.
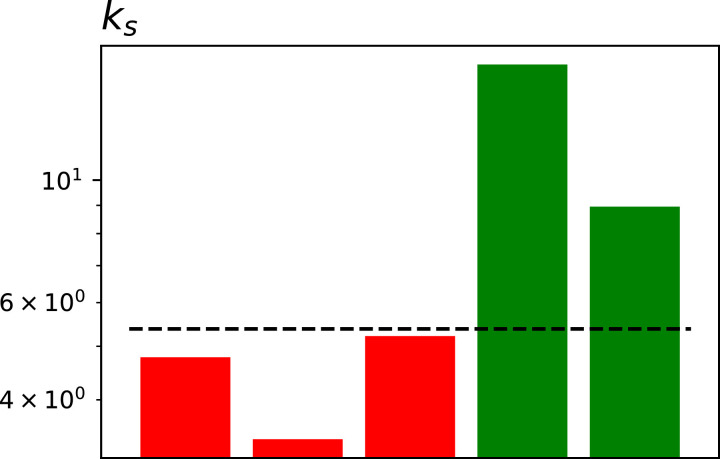
To further analyse the meaning of the variables, we here create a single synthetic metric for each region, defined as:
| (7) |
ks is thus the product of the two ks controlling the rate of improvement, divided by the two ks defining the rate according to which patients get worse or die. In the case of uncorrelated statistics of events, ks is thus the ratio between the probability rate to die divided by the rate to be discharged. As can be seen in Fig. 4 , ks is larger for the two regions with low mortality. Note that this is counterintuitive, as indicates that, on average, the positive ks are larger; or, in other words, that patients take more time to recover with respect to high-mortality regions. This may point towards several mechanisms. First of all, the virus may not be the same in all regions; patients may thus take more time to evolve, but they finally recover, as opposed to dying. Secondly, high-mortality regions also correspond to regions in which healthcare systems were subject to high pressure; patients may thus be moved faster to non-ICU, to leave space in ICU for more serious cases.
Fig. 4.
Values of ks for the five considered regions (coloured bars) and for Italy (horizontal dashed line). Bar colours as per Fig. 3. See main text for the definition of ks.
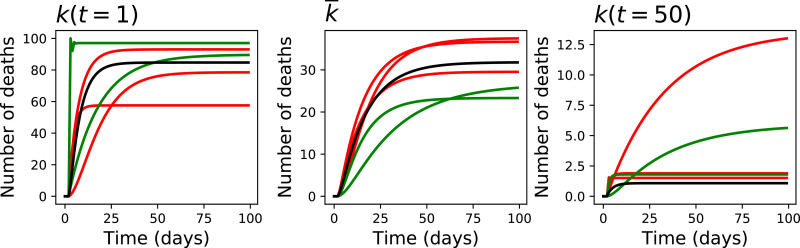
We finally analyse what is the steady-state solution of the model, for these five regions, considering three scenarios: an initial one, with ; the intermediate one, using the average s previously calculated; and the final one, with . Towards this aim, we executed the model during 100 days, supposing a constant number of new COVID-19 cases (specifically, 100 per day); and plotted the evolution in the number of deaths per day - see Fig. 5 . The main conclusion that can be drawn is the fast evolution of the system. Specifically, using the parameters of the beginning of the considered period yields a very high number of deaths (over 60% in all five regions); this then improves, until reaching a steady state of less than 2.5% in most regions.
Fig. 5.
Steady-state solution of the system. From left to right, the three graphs report the evolution in the number of daily deaths for and . Colours as per Fig. 3.
4. Discussion and conclusions
The dynamics of patients inside a hospital is a complex one, with each person evolving according to his/her condition and comorbidities, and requiring different cares to ensure the maximum survivability. This is especially true in the case of COVID-19, due to its heterogeneity and the initial lack of standard treatments and guidelines. In spite of this, we have here shown that a simple model, comprising only four parameters, is in general able to describe this dynamics in an effective way.
When applied to the data of nine Italian regions, this model allows to depict the heterogeneity in the way patients have evolved in each one of them. Two major conclusions can be drawn. First of all, and in a way opposite to what may be intuitive, patients in regions with a lower mortality are characterised by a slower rate of improvement. Whether this is due to differences in the virus or to a different way of managing patients cannot be decided with the data here available. Indeed, a possibility consistent with our results is that UCI saturation operated as a cut-off in patient treatment, and medical care was concentrated on patients in less serious conditions, on the one hand increasing mortality, while on the other decreasing the average time in the care units [8]. Secondly, improvement and worsening rates strongly vary between the beginning and the end of the considering period, with changes of over one order of magnitude. Once again, it is not possible to say if this is due to a change in the virus characteristics or to the applied treatments. In any case, these changes are of relevance for models trying to predict the pressure of a disease on the healthcare system, as what seen at the beginning of the epidemics may not be representative of the average situation. This may be the reason behind the failure of initial models trying to forecast the evolution of COVID-19 [21].
In spite of the good results here obtained, a note of caution should be raised. Specifically, the quality and reliability of any mathematical model of the kind here described strongly depend on the quality of the data used in the fit. In general, but especially in the case of COVID-19, it has been shown that different countries and regions followed different rules for reporting pandemic numbers, as e.g. when a death is considered due to COVID-19 or to other comorbidities. Additionally, the real number of cases is not known, as many patients are asymptomatic and tests have not always been performed. Finally, countries have tried to optimise the use of their healthcare infrastructures, by e.g. moving patients between regions, thus further biasing the time series. This implies that it is difficult to assess the reasons behind some abnormal behaviours, as these could be due to non-conventional protocols inside the hospitals, or simply to unreliable data. Still, the fact that a good fit has been obtained for eight out of ten regions supports the hypothesis that the proposed model is able to capture the most important elements of the dynamics.
Beyond the information here extracted about the evolution and treatment of COVID-19 in Italy, the model here described can have a major role in efforts aimed at defining the best strategies to control the pandemics. For instance, this model can be used in studies trying to optimise the scope of contention policies, as these require an estimation of the pressure on the healthcare system and of the evolution of such pressure over time.
Credit Author Statement
LF defined the problem; DP, MR, and FB built the model; MZ performed all computations; MZ and DP wrote the first draft of the manuscript. All authors contributed to the submitted version of the manuscript.
Declaration of Competing Interest
All authors declare that they have no conflict of interest.
Acknowlgedgements
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 851255).
M.Z. acknowledges the Spanish State Research Agency, through the Severo Ochoa and María de Maeztu Program for Centers and Units of Excellence in R&D (MDM-2017-0711).
References
- 1.Anastassopoulou C., Russo L., Tsakris A., Siettos C. Data-based analysis, modelling and forecasting of the covid-19 outbreak. PLoS ONE. 2020;15(3):e0230405. doi: 10.1371/journal.pone.0230405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Andersen K.G., Rambaut A., Lipkin W.I., Holmes E.C., Garry R.F. The proximal origin of sars-cov-2. Nat Med. 2020;26(4):450–452. doi: 10.1038/s41591-020-0820-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Anderson R.M., May R.M. Oxford university press; 1992. Infectious diseases of humans: dynamics and control. [Google Scholar]
- 4.Bernoulli D. Essai d’une nouvelle analyse de la mortalité causée par la petite vérole, et des avantages de l’inoculation pour la prévenir. Histoire de l’Acad, Roy Sci(Paris) avec Mem. 1760:1–45. [Google Scholar]
- 5.Cereda D., Tirani M., Rovida F., Demicheli V., Ajelli M., Poletti P., et al. The early phase of the covid-19 outbreak in lombardy, italy. arXiv preprint 2020; arXiv:2003.09320.
- 6.Dong E., Du H., Gardner L. An interactive web-based dashboard to track covid-19 in real time. Lancet infect disea. 2020;20(5):533–534. doi: 10.1016/S1473-3099(20)30120-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fanelli D., Piazza F. Analysis and forecast of covid-19 spreading in china, italy and france. Chaos, Solitons & Fractals. 2020;134:109761. doi: 10.1016/j.chaos.2020.109761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Favero C.A. Discussion paper. 2020. Why is covid-19 mortality in lombardy so high? evidence from the simulation of a seihcr model. [Google Scholar]
- 9.Gao F., Han L. Implementing the nelder-mead simplex algorithm with adaptive parameters. Comput Optim Appl. 2012;51(1):259–277. [Google Scholar]
- 10.Gupta S., Nguyen T.D., Rojas F.L., Raman S., Lee B., Bento A. Tech. Rep. National Bureau of Economic Research; 2020. Tracking public and private response to the covid-19 epidemic: Evidence from state and local government actions. [Google Scholar]
- 11.Haffajee R.L., Mello M.M. Thinking globally, acting locally-the us response to covid-19. N top N Engl J Med. 2020;382(22):e75. doi: 10.1056/NEJMp2006740. [DOI] [PubMed] [Google Scholar]
- 12.Hale T., Petherick A., Phillips T., Webster S.. Variation in government responses to covid-19. Blavatnik school of government working paper2020; 31.
- 13.Hethcote H.W. The mathematics of infectious diseases. SIAM Rev. 2000;42(4):599–653. [Google Scholar]
- 14.Ji Y., Ma Z., Peppelenbosch M.P., Pan Q. Potential association between covid-19 mortality and health-care resource availability. Lancet Glob Health. 2020;8(4):e480. doi: 10.1016/S2214-109X(20)30068-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proceed Roy Soc Lond Series A. 1927;115(772):700–721. [Google Scholar]
- 16.Legido-Quigley H., Asgari N., Teo Y.Y., Leung G.M., Oshitani H., Fukuda K. Are high-performing health systems resilient against the covid-19 epidemic? The Lancet. 2020;395(10227):848–850. doi: 10.1016/S0140-6736(20)30551-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Li L., Yang Z., Dang Z., Meng C., Huang J., Meng H. Propagation analysis and prediction of the covid-19. Infect Disea Model. 2020;5:282–292. doi: 10.1016/j.idm.2020.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Li R., Rivers C., Tan Q., Murray M.B., Toner E., Lipsitch M. The demand for inpatient and icu beds for covid-19 in the us: lessons from chinese cities. MedRxiv. 2020 [Google Scholar]
- 19.Livingston E., Bucher K. Coronavirus disease 2019 (covid-19) in italy. JAMA. 2020;323(14):1335. doi: 10.1001/jama.2020.4344. [DOI] [PubMed] [Google Scholar]
- 20.Mazzoli M., Mateo D., Hernando A., Meloni S., Ramasco J.J. Effects of mobility and multi-seeding on the propagation of the covid-19 in spain. medRxiv. 2020 [Google Scholar]
- 21.Mitjà O., Arenas À., Rodó X., Tobias A., Brew J., Benlloch J.M. Experts’ Request to the spanish government: move spain towards complete lockdown. The Lancet. 2020;395(10231):1193–1194. doi: 10.1016/S0140-6736(20)30753-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Moreno Y., Pastor-Satorras R., Vespignani A. Epidemic outbreaks in complex heterogeneous networks. Eur Phys J B-Conden Matter Compl Syst. 2002;26(4):521–529. [Google Scholar]
- 23.Nelder J.A., Mead R. A simplex method for function minimization. Comput J. 1965;7(4):308–313. [Google Scholar]
- 24.Pastor-Satorras R., Vespignani A. Epidemic dynamics and endemic states in complex networks. Phys Rev E. 2001;63(6):066117. doi: 10.1103/PhysRevE.63.066117. [DOI] [PubMed] [Google Scholar]
- 25.Pastor-Satorras R., Castellano C., Van Mieghem P., Vespignani A. Epidemic processes in complex networks. Rev Mod Phys. 2015;87(3):925. [Google Scholar]
- 26.Saccomandi G. The spatial diffusion of diseases. Math Comput Model. 1997;25(12):83–95. [Google Scholar]
- 27.Tang X., Wu C., Li X., Song Y., Yao X., Wu X. On the origin and continuing evolution of sars-cov-2. Natl Sci Rev. 2020 doi: 10.1093/nsr/nwaa036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Van Kampen N. Stochastic processes in chemistry and physics. Chaos. 1981 [Google Scholar]
- 29.Xu B., Kraemer M.U., Gutierrez B., Mekaru S., Sewalk K., Loskill A. Open access epidemiological data from the covid-19 outbreak. Lancet Infect Disea. 2020;20(5):534. doi: 10.1016/S1473-3099(20)30119-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zanin M., Papo D. Assessing functional propagation patterns in covid-19. Chaos, Solitons & Fractals. 2020;138:109993. doi: 10.1016/j.chaos.2020.109993. [DOI] [PMC free article] [PubMed] [Google Scholar]