Selective Characterization of Microsecond Motions in Proteins by NMR Relaxation

Abstract

The three-dimensional structures of macromolecules fluctuate over a wide range of time-scales. Separating the individual dynamic processes according to frequency is of importance in relating protein motions to biological function and stability. We present here a general NMR method for the specific characterization of microsecond motions at backbone positions in proteins even in the presence of other dynamics such as large-amplitude nanosecond motions and millisecond chemical exchange processes. The method is based on measurement of relaxation rates of four bilinear coherences and relies on the ability of strong continuous radio frequency fields to quench millisecond chemical exchange. The utility of the methodology is demonstrated and validated through two specific examples focusing on the thermo-stable proteins, ubiquitin and protein L, where it is found that small-amplitude microsecond dynamics are more pervasive than previously thought. Specifically, these motions are localized to α helices, loop regions, and regions along the rim of β sheets in both of the proteins examined. A third example focuses on a 28 kDa ternary complex of the chaperone Chz1 and the histones H2A.Z/H2B, where it is established that pervasive microsecond motions are localized to a region of the chaperone that is important for stabilizing the complex. It is further shown that these motions can be well separated from extensive millisecond dynamics that are also present and that derive from exchange of Chz1 between bound and free states. The methodology is straightforward to implement, and data recorded at only a single static magnetic field are required.

Introduction

Macromolecules such as proteins populate many microstates that differ in structure and energy. Molecular function is often dictated by the relative populations of these diverse states and their rates of interconversion, ranging from the nanosecond time-scale in the case of domain rearrangements to orders of magnitude slower for protein unfolding events.^1–4 Indeed, there is now increasing evidence to suggest that microsecond–millisecond (μs–ms) time-scale dynamics are used to navigate complex energy landscapes so as to connect various functional states.^5–7 A rigorous characterization of these dynamic processes is therefore a prerequisite for understanding protein function. Nuclear magnetic resonance (NMR) spectroscopy,^8,9 fluorescence spectroscopy (including fluorescence correlation spectroscopy),^10–13 and vibrational spectroscopy^14,15 have emerged as powerful techniques for characterizing the motions of macromolecules in solution. However, NMR spectroscopy is often the method of choice because site-specific dynamics information can be obtained at many positions throughout the molecule, often over a wide range of motional time-scales. Yet, it is precisely the sensitivity of the NMR method to this broad spectrum of time-scales that can make data analysis complex.

Consider the case of a protein tumbling in solution with an anisotropic diffusion tensor. Traditionally, backbone amide ¹⁵N R₁, R₂, and steady-state ¹H–¹⁵N NOE experiments¹⁶ are recorded, often at more than one static magnetic field strength, from which both site-specific internal “fast” dynamics (pico-to nanoseconds, ps–ns) parameters are extracted, as well as the principal components and orientation of the diffusion tensor. The obtained transverse relaxation rates are also sensitive to processes occurring on slower time-scales (μs–ms) that give rise to a contribution to R₂, R_ex, which is also fitted. In cases where μs–ms exchange is pervasive, such as for partially unfolded proteins, or even in certain regions of folded domains, it can be difficult to separate the different time-scale processes (ps–ns from μs–ms) in an accurate manner. Over the past decade, a number of NMR methods have been developed to address this issue. Original approaches were based on the measurement of ¹⁵N, ¹H dipole–¹⁵N chemical shift anisotropy cross-correlated relaxation interference^17–19 that is independent of chemical exchange. A more recent method, developed in our laboratory, measures the decay rates of four coherences, R₂(2H_xN_z), R₂(2H_zN_x), R₂(2H_xN_x), R₁(2H_zN_z) (see below), which can be combined in such a way so that contributions to relaxation from only pure dipolar interactions remain (that is, the effects of exchange are subtracted out). It is also possible, however, to take a separate linear combination of these four rates so that site-specific values for exchange contributions on the μs time-scale, R_ex,μs, are isolated, which forms the basis for the studies reported here.

There are a number of distinct advantages in using this (four-rate) approach to quantify exchange in proteins. First, the rates are already available as part of a larger study of ps–ns time-scale dynamics. Second, they can be recorded at only a single static magnetic field strength and with a single carrier offset. In contrast, other approaches such as those that extract exchange contributions from transverse relaxation rates are often based on measurements at multiple fields and assumptions about the time-scale of the chemical exchange process. Third, measurements such as off-resonance relaxation dispersion, which are complementary, require much longer measurement times because both the offset and the spin-lock field strength must be varied, with spin-lock field strengths that are significantly larger than the exchange process employed.

Herein, we establish the utility of this approach for measuring microsecond chemical exchange processes with a series of applications that quantify such dynamics in a pair of well-folded and thermally stabile proteins, human ubiquitin and the B1 immunoglobulin binding domain of peptostreptococcal protein L (protein L). We first cross-validate the methodology by comparing R_ex,μs rates measured on these proteins using two different approaches, emphasizing that the new measurements eliminate the limitations of previous experiments that focus on extraction of exchange contributions from quantification of the magnetic field dependence of transverse relaxation rates. A major conclusion of the present study is that, despite the fact that both ubiquitin and protein L have been thought of in the past as rigid entities, with little dynamics of interest, the work here establishes that microsecond time-scale motions are present in α helices, loop regions, and in the rims of β sheets in both of these molecules, emphasizing that such dynamics are a likely feature of all proteins. In this regard, the results are consistent with elegant studies of Griesinger and co-workers based on residual dipolar coupling measurements in ubiquitin that make clear the importance of motion in the function of this protein.² A second application is presented involving the characterization of microsecond motions in the histone chaperone Chz1²⁰ in complex with the variant histone H2A.Z-H2B. We show that such dynamics can be separated from pervasive contributions to ¹⁵N linewidths from millisecond time-scale motions that report on the association/dissociation process of the chaperone and from extensive nanosecond processes that vary significantly along the protein backbone.²¹

Results and Discussion

Isolation of Exchange Contributions

Molecular motions modulate the interactions between NMR active nuclei, leading to the relaxation of nuclear spins. Thus, accurate measurement of nuclear relaxation rates provides an avenue for probing molecular dynamics over a wide range of time-scales, from picoseconds to seconds. Micro- to millisecond time-scale chemical exchange processes (often referred to as “slow motions”) enhance transverse nuclear relaxation rates, while motions with time-constants from picoseconds to nanoseconds (“fast motions”) affect both longitudinal and transverse relaxation rates. A separation of different motional processes can be difficult in cases where large amplitude ps–ns and pervasive ms time-scale dynamics are present because contributions to the transverse relaxation rate from the slow motions (line broadening) and the fast motions (line narrowing) tend to cancel.

Previously, an approach for achieving this separation was described on the basis of recording four relaxation rates, corresponding to R₂(2H_xN_z), R₂(2H_zN_x), R₂(2H_xN_x), and R₁(2H_zN_z), where R_1,2(2H_νN_μ) is the autorelaxation rate of the coherence 2H_νN_μ and H_ν and N_μ are the canonical Cartesian product operator density elements.²² Two-dimensional NMR experiments for measuring these rates have been described in detail previously.²³ As described there, and below, the R₂(2H_xN_z) rate is derived from the related rotating frame relaxation rate R_1ρ(2H′_zN_z) that is measured in the presence of a continuous ¹H spin-lock radio frequency field, R₂(2H_zN_x) follows from R_1ρ(2H_zN′_z), while R₂(2H_xN_x) is determined from $R_{1{\rho }^2}\left(2{{\text{H}}^{\prime }}_z{{\text{N}}^{\prime }}_z\right)$ that is measured in the presence of a double {¹H,¹⁵N} spin-lock. The individual autorelaxation rates^24–26 of the four relevant coherences above are given by

$$R_1\left(2{\text{H}}_z{\text{N}}_z\right)=\frac{d_{\text{HN}}^2}{8}\left(6J\left({\omega }_{\text{N}}\right)+6J\left({\omega }_{\text{H}}\right)\right)+c_{\text{N}}^{2}J\left({\omega }_{\text{N}}\right)+{\lambda }_{\text{N}}+{\lambda }_{\text{H}}$$ (1)

$$\begin{gathered} R_2\left(2{\text{H}}_x{\text{N}}_z\right)=\frac{d_{\text{HN}}^2}{8}(4J(0)+J\left({\omega }_{\text{H}}-{\omega }_{\text{N}}\right)+3J\left({\omega }_{\text{H}}\right)+ \\ 6J\left({\omega }_{\text{H}}+{\omega }_{\text{N}}\right))+c_{\text{N}}^{2}J\left({\omega }_{\text{N}}\right)+{\vartheta }_{\text{H}}+{\lambda }_{\text{N}}+R_{\text{ex},\rho }\left({\text{H}}_x\right) \end{gathered}$$ (2)

$$\begin{gathered} R_2\left(2{\text{H}}_z{\text{N}}_z\right)=\frac{d_{\text{HN}}^2}{8}(4J(0)+J\left({\omega }_{\text{H}}-{\omega }_{\text{N}}\right)+3J\left({\omega }_{\text{N}}\right)+ \\ 6J\left({\omega }_{\text{H}}+{\omega }_{\text{N}}\right))+\frac{c_{\text{N}}^2}{6}\left(4J(0)+3J\left({\omega }_{\text{N}}\right)\right)+{\vartheta }_{\text{N}}+{\lambda }_{\text{H}}+ \\ {R}_{\text{ex},\rho }\left({\text{N}}_x\right) \end{gathered}$$ (3)

$$\begin{gathered} R_2\left(2{\text{H}}_x{\text{N}}_x\right)=\frac{d_{\text{HN}}^2}{8}(3J\left({\omega }_{\text{N}}\right)+J\left({\omega }_{\text{H}}-{\omega }_{\text{N}}\right)+3J\left({\omega }_{\text{H}}\right)+ \\ 6J\left({\omega }_{\text{H}}+{\omega }_{\text{N}}\right))+\frac{c_{\text{N}}^2}{6}\left(4J(0)+3J\left({\omega }_{\text{N}}\right)\right)+{\vartheta }_{\text{H}}+{\vartheta }_{\text{N}}+ \\ {R}_{\text{ex},\rho }\left(2{\text{H}}_x{\text{N}}_x\right) \end{gathered}$$ (4)

where $d_{\text{HN}}=\left({\mu }_0/4\pi \right)\hslash {\gamma }_{\text{H}}{\gamma }_{\text{N}}{r}_{\text{HN}}^{-3}$, $c_{\text{N}}=B_0{\gamma }_{\text{N}}\mathrm{\Delta }{\sigma }_{\text{N}}\sqrt{(}\left(1+{\eta }_{\text{N}}^2/3\right)/3)$, μ₀ is the permeability of free space, $\hslash$ is Planck’s constant divided by 2π, γ_H and γ_N are the magnetogyric ratios of ¹H and ¹⁵N, respectively, r_HN is the vibrationally averaged distance between ¹H and ¹⁵N nuclei, B₀ is the static magnetic field strength, Δσ_N = σ_11,N − (σ_22,N + σ_33,N)/2 (shift anisotropy), and η_N = (σ_22,N − σ_33,N)/(σ_11,N − σ_iso,N) (reduced asymmetry), where σ_11,N, σ_22,N, and σ_33,N are the principal components of the nitrogen CSA tensor^24,27 and σiso,N = 1/3(σ11,N + σ22,N + σ33,N). The power spectral density function, J(ω), describes the frequency distribution of the stochastic motions that modulate both the ¹H–¹⁵N dipole-dipole and the ¹⁵N CSA interactions and in its simplest form is given by^28,29

$$J(\omega )=\frac{2}{5}\frac{S^2{\tau }_{\text{C}}}{1+{\omega }^2{\tau }_{\text{C}}^2}+\frac{2}{5}\frac{\left(1-S^2\right){{\tau }^{\prime }}_{\text{e}}}{1+{\omega }^2{\tau }_{\text{e}}^{\prime 2}},1/{{\tau }^{\prime }}_{\text{e}}=1/{\tau }_{\text{C}}+1/{\tau }_{\text{e}}$$ (5)

where S is an order parameter describing the amplitude of ps–ns motions occurring on the time-scale τ_e, and τ_C is the correlation time for the assumed isotropic motion. In what follows, the specific form of J(ω) is arbitrary, that is, the dynamics could be more complex than what is “captured” by eq 5; this has no effect on the robustness of the extracted exchange contributions because the only assumption about the spectral density function made below is that J(ω) ∝ 1/ω² for ω > ω_H + ω_N.^30,31 The contributions to the longitudinal relaxation of the ¹H (¹⁵N) spin from interactions with external spins are given by λ_H (λ_N), while ϑ_H and ϑ_N are additions to ¹H and ¹⁵N transverse relaxation rates, respectively, that result from interactions with proximal external spins and from other magnetization leaking mechanisms, such as exchange with the solvent. Finally, R_ex,ρ(H_x) and R_ex,ρ(N_x) are contributions to the R₂(2H_xN_z) and R₂(2H_zN_x) relaxation rates, respectively, which originate from chemical exchange processes that are measured in the presence of ¹H and ¹⁵N spin-lock fields (see above). The corresponding contribution to the rate R_ex,ρ(2H_xN_x) can be written to very good approximation as R_ex,ρ(H_x) + R_ex,ρ(N_x) that follows directly from the fact that relaxation rates are measured under spin-locking conditions (see Supporting Information). In eqs 1–4, we have neglected contributions to relaxation from ¹H CSA; however, these subtract out in what follows below.

Previously, we showed that it is possible to isolate a pure dipole–dipole “chemical exchange-free” measure of ¹⁵N backbone transverse relaxation, R_dd:

$$\begin{gathered} R_{\text{dd}}=(1/2)[R_2\left(2{\text{H}}_x{\text{N}}_z\right)+R_2\left(2{\text{H}}_z{\text{N}}_x\right)-R_2\left(2{\text{H}}_x{\text{N}}_x\right)- \\ {R}_1\left(2{\text{H}}_z{\text{N}}_z\right)] \end{gathered}$$ (6)

with small systematic errors due to cross-relaxation between amide protons and proximal proton spins minimized by recording spectra on proteins with deuteration levels of 50% or higher. We now turn our attention to quantification of the chemical exchange contribution to nitrogen transverse relaxation, R_ex,ρ(N_x), that reports on micro-millisecond time-scale motions in proteins.^32–34 A linear combination of eqs 1–4 is constructed that isolates R_ex,ρ(N_x) according to (see Supporting Information):

$$\begin{gathered} R_{\text{ex},\rho }\left({\text{N}}_x\right)+{\vartheta }_{\text{N}}=\frac{1}{2}\{R_1\left(2{\text{H}}_z{\text{N}}_z\right)\left(-1+\frac{4c_{\text{N}}^2}{3d_{\text{HN}}^2}\right)+R_2\left(2{\text{H}}_z{\text{N}}_x\right)\times \\ \left(1-\frac{4c_{\text{N}}^2}{3d_{\text{HN}}^2}\right)+R_2\left(2{\text{H}}_x{\text{N}}_z\right)\left(-1-\frac{4c_{\text{N}}^2}{3d_{\text{HN}}^2}\right)+R_2\left(2{\text{H}}_x{\text{N}}_x\right)\times \\ \left(1+\frac{4c_{\text{N}}^2}{3d_{\text{HN}}^2}\right)\}+{\lambda }_{\text{N}}-0.035\left(3d_{\text{HN}}^2-4c_{\text{N}}^2\right)J\left(0.87{\omega }_{\text{H}}\right) \end{gathered}$$ (7)

with each of the terms defined above and where the high frequency spectral density elements, J(ω_Η + ω_Ν), J(ω_Η), and J(ω_Η − ω_Ν), have been combined using the relation J(εω) ≈ (0.87/ε)²J(0.87ω_H).^17,25,30 For macromolecules, $0.035(3d_{\text{HN}}^2-4c_{\text{N}}^2)J\left(0.87{\omega }_{\text{H}}\right)$ and λ_N can be neglected; for example, in the case of ubiquitin at 298 K, for which τ_C ≈ 5 ns (278 K; τ_C ≈ 9 ns), $0.035\left(3d_{\text{HN}}^2-4c_{\text{N}}^2\right)J\left(0.87{\omega }_{\text{H}}\right)=1.6\times {10}^{-3}{\text{s}}^{-1}\pm 7\times {10}^{-4}{\text{s}}^{-1}\left(9\times {10}^{-4}{\text{s}}^{-1}\pm 5\times {10}^{-4}{\text{s}}^{-1}\right)$ on average, and this term will only get smaller with proteins of increasing size. Contributions to transverse relaxation of ¹⁵N from external spins ϑ_N can be minimized by using highly deuterated samples (discussed previously in the context of measuring R_dd).²³ From the X-ray structure of protein L and using a value of S² = 0.85 for all ¹⁵N-distal proton interactions, a maximum value of ϑ_N = 0.05 (0.1) s⁻¹ is calculated at 298 (278 K), assuming that the protein is deuterated at all positions other than amides, well below the accuracy of measurement of μs exchange contributions (see Supporting Information). In principle, ϑ_N can be separated from R_ex,ρ(N_x) if measurements are carried out at multiple static magnetic fields and if the field dependencies of the individual contributions are known and are different. For example, for both ubiquitin and protein L considered here, R_ex,ρ(N_x) ∝ B₀² (see below), while remote dipolar contributions are field independent. In what follows, we have assumed ϑ_N = 0.

From the above discussion, it follows that to excellent approximation:

$$\begin{gathered} R_{\text{ex},\rho }\left({\text{N}}_x\right)=\frac{1}{2}\{R_1\left(2{\text{H}}_z{\text{N}}_z\right)\left(-1+\frac{4c_{\text{N}}^2}{3d_{\text{HN}}^2}\right)+ \\ {R}_2\left(2{\text{H}}_z{\text{N}}_x\right)\left(1-\frac{4c_{\text{N}}^2}{3d_{\text{HN}}^2}\right)+R_2\left(2{\text{H}}_x{\text{N}}_z\right)\left(-1-\frac{4c_{\text{N}}^2}{3d_{\text{HN}}^2}\right)+ \\ {R}_2\left(2{\text{H}}_x{\text{N}}_x\right)\left(1+\frac{4c_{\text{N}}^2}{3d_{\text{HN}}^2}\right)\} \end{gathered}$$ (8)

It is worth reemphasizing that eq 8 is derived under the assumption that R_ex,ρ(2H_xN_x) is very well approximated by R_ex,ρ(H_x) + R_ex,ρ(N_x). That this is the case under the spin-locking conditions used experimentally is established in the Supporting Information. From eq 8, it is clear that accurate values of both c_N and d_HN are required to obtain meaningful R_ex,ρ rates. So long as the “correct” values are used, it is straightforward to show directly from eq 8 that R_ex,ρ isolated from the four R_1,2(2H_νN_μ) rates is independent of molecular tumbling and fast internal dynamics. That is, exchange contributions are completely isolated from ps–ns time-scale motions. However, values of Δσ_Ν are known to vary between residues with Δσ_avg = −172 ppm,^27,35–37 rmsd (Δσ_Ν) ≈ 10 ppm, leading to some uncertainty in calculated R_ex,ρ(N_x) rates. In general, if a value of c_N is used in eq 8, while the correct value is c, then the error in the calculated R_ex,ρ rate, ΔR_ex,ρ(N_x) = R_ex,ρ(c_N) − R_ex,ρ(c), is given by

$$\mathrm{\Delta }{R}_{\text{ex},\rho }\left({\text{N}}_x\right)=\frac{1}{6}\left(c_{\text{N}}^2-c^2\right)\left(3J\left({\omega }_{\text{N}}\right)-4J(0)\right)$$ (9)

so that slightly negative values of ΔR_ex,ρ(N_x) are derived when the assumed |Δσ_Ν| is larger than the actual value, for example. Thus, R_ex,ρ rates may have some dependence on molecular tumbling that reflects the errors in CSA and bond lengths used in the analysis. It is thus conceivable that even in the absence of chemical exchange, nonzero values of R_ex,ρ could be obtained (see below). It is worth noting that the same situation occurs, of course, in the measurement of exchange contributions to relaxation from R₁, R_1ρ, and ¹H–¹⁵N NOE data sets, where uncertainties in constants result in a “mixing” of ps–ns and exchange dynamics as well.

In principle, information about residue-specific variations in Δσ_Ν can be obtained from experiments based on dipole-CSA cross-correlated relaxation,³⁸ such as those that measure η_xy, for example, and subsequently used in analyses that quantify exchange. However, small variations in the angle between the axial component of the CSA tensor and the ¹H–¹⁵N bond vector, and differences in intrinsic dynamics on a per-residue basis, prevent an accurate determination of residue-specific Δσ_Ν from this experiment alone. Rather than attempting to obtain residue-specific Δσ_Ν values and incorporate these into the calculation, we prefer to estimate the uncertainty in R_ex,ρ(N_x) values based on the rmsd of experimentally determined Δσ_Ν and the known dynamics parameters of each protein using eq 9. In what follows, we have used Δσ_avg = −172 ppm, r_HN = 1.02 Å.

As described above, R₂(2H_zN_x) and R₂(2H_xN_x) relaxation rates used to quantify R_ex,ρ(N_x) are recorded in the presence of a nitrogen spin-lock field that quenches contributions from exchange processes with rate constants smaller than the spin lock field strength.³⁹ Typically, a 2 kHz ¹⁵N spin lock field is applied, so that the resulting exchange contribution calculated from eq 8 is only sensitive to exchange processes faster than ~2000 s⁻¹. More quantitatively, for the case of a system undergoing exchange between two sites, A ⇌ B, with forward rate k_A and reverse rate k_B, this contribution is given by⁴⁰

$$R_{\text{ex},\rho }\left({\text{N}}_x\right)\approx \frac{p_{\text{A}}{p}_{\text{B}}\mathrm{\Delta }{\omega }^2{k}_{\text{ex}}}{{\mathrm{\Omega }}_{\text{B}}^2+{\omega }_{\text{SL}}^2+k_{\text{ex}}^2}$$ (10)

where Δω = Ω_B − Ω_A, with Ω_A and Ω_B the offsets of the ¹⁵N resonance frequencies of sites A and B (rad/s) from the nitrogen spin-lock carrier, ω_SL is the field strength of the spin-lock field (rad/s), k_ex = k_A + k_B is the rate of exchange, and the population of the minor state is p_B = k_A/k_ex and p_A = 1 − p_B. Thus, in concert with eq 8, the four relaxation rates R_1,2(2H_νN_μ) provide a way to measure contributions from exchange on the order of or faster than ~ω_SL. The time-scale of the processes contributing to R_ex,ρ can be estimated in a number of ways. For exchange events with frequencies on the order of ω_SL/(2π), relaxation dispersion experiments are powerful for quantifying the exchange time-scale.^41,42 In cases were both μs and ms processes are present, the exchange parameters isolated from fits of relaxation dispersion profiles can be used to estimate the small contributions to measured R_ex,ρ(N_x) rates from the ms time-scale process (via eq 10) and subtracted from measured R_ex,ρ values to “isolate” contributions from μs exchange exclusively, as described later in the text. Further insight can be obtained by measuring R_ex,ρ(N_x) for different offsets of the nitrogen rf-carrier (Ω_B) and/or different nitrogen spin-lock strengths (ω_SL) to extract k_ex in cases where k_ex ≲ 25 000 s⁻¹.⁴³ Note that only R₂(2H_xN_x) and the R₂(2H_zN_x) must be measured as a function of {Ω_B, ω_SL}, because R₁(2H_zN_z) and R₂(2H_xN_z) rates are independent of the nitrogen spin-lock strength and carrier offset. If no variation is observed in R_ex,ρ(N_x), then it follows that $k_{\text{ex}}^2\gg {\omega }_{\text{SL}}^2+{\mathrm{\Omega }}_{\text{B}}^2$, and exchange parameters k_ex, p_b, and Δω are unfortunately inseparable. If it can be argued that a range of residues are all affected by the same chemical exchange process, as seen previously,^33,44 then the observed R_ex,ρ(N_x), which is proportional to Δω², can be used to obtain qualitative information on the structural changes that are involved in the transition. Below we have not attempted to determine the individual exchange parameters, but rather show that accurate R_ex,ρ(N_x) can indeed be obtained.

Validation of the Methodology

In what follows, we consider a pair of proteins, protein L and human ubiquitin, where the exchange contribution R_ex,ρ(N_x) can be quantified both from the measurement of the rates described above (eq 8) and from an independent set of experiments, outlined below. It is known from previous studies that chemical exchange processes for both of these proteins are in the fast-exchange regime, that is, k_ex. ≫ Δω. For ubiquitin, residues 23–25, 55, and 70 undergo exchange with a rate constant k_ex ≈ 25 000 s⁻¹ at 280 K;⁴⁵ thus, ω_SL² + k_ex² ≫ Ω_B² so that R_ex,ρ(N_x) ∝ B₀². Moreover, we have used amide proton R_1ρ experiments⁴³ to probe exchange in protein L. A pair of exchange processes are found, including one affecting the relaxation of residues 4–7 and a second in the vicinity of residues 51–53, with rates of ~8000 and ~37 000 s⁻¹, respectively (see Supporting Information), so that R_ex,ρ ∝ B₀² in this case as well.

Because the fast exchange condition applies for both ubiquitin and protein L (although not in general for all proteins, see below), R_ex,ρ(N_x) can be measured using a second approach for these proteins distinct from the one described above, in which the exchange contribution is extracted from ¹⁵N R₁, R_1ρ relaxation rates and steady-state ¹H–¹⁵N NOE values measured at multiple magnetic fields,²³ using the relation R_ex,ρ(N_x) ∝ B₀² (see below). The rotating frame relaxation rate is given by

$$R_{1\rho }\left({\text{N}}_x\right)=R_1\left({\text{N}}_z\right){\cos }^2\theta +R_2\left({\text{N}}_x\right){\sin }^2\theta$$ (11)

where tan θ = ω_SL/Ω and Ω = p_ΑΩ_Α+ p_ΒΩ_Β is the offset of the exchange averaged resonance position from the carrier (rad/s). In eq 11,

$$\begin{gathered} R_2\left({\text{N}}_x\right)=\left(\frac{d_{\text{HN}}^2}{8}+\frac{c^2}{6}\right)\left(4J(0)+3J\left({\omega }_{\text{N}}\right)\right)+ \\ 1.349d_{\text{HN}}^{2}J\left(0.87{\omega }_{\text{H}}\right)+R_{\text{ex},\rho }\left({\text{N}}_x\right)+{\vartheta }_{\text{N}} \end{gathered}$$ (12)

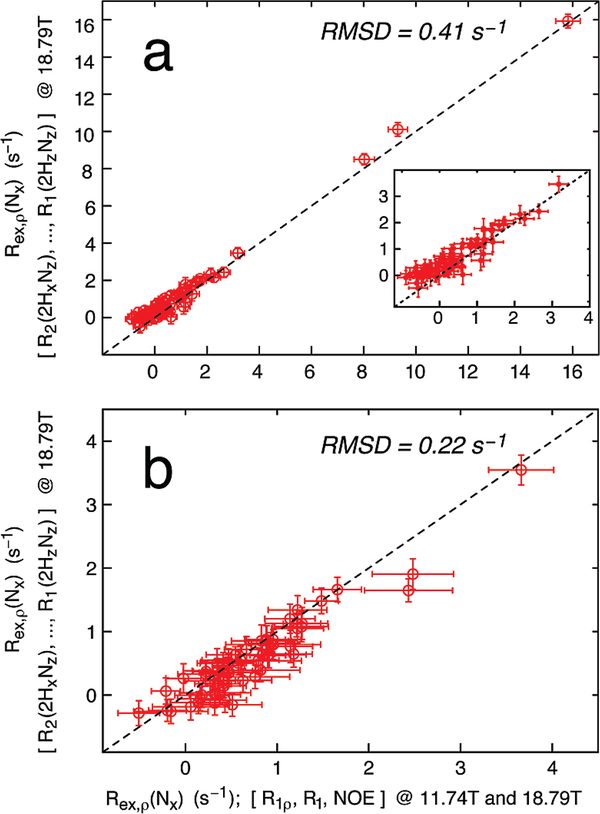
where the high-frequency spectral density terms, J(ω_Η + ω_Ν), J(ω_H), and J(ω_Η − ω_Ν), have been combined into a term proportional to J(0.87ω_H), as described above. A spectral density mapping of R₁, R_1ρ, and ¹H–¹⁵N NOE values measured at static magnetic fields of 11.7 and 18.8 T (six measurables) into five discrete values of the power spectral density function {J(0), J(ω_N,11.7T), J(ω_N,18.8T), J(0.87ω_H,11.7T), J(0.87ω_H,18.8T)} and an additional parameter that accounts for the exchange, ξ, where R_ex,ρ(N_x) = ξB₀², is performed that then allows the determination of R_ex,ρ(N_x) from the relaxation data. Figure 1 illustrates the comparison of R_ex,ρ(N_x) values derived from the four R_1,2(2H_νN_μ) relaxation rates measured at 18.8 T (eq 8) and from spectral density mapping of R₁, R_1ρ, and ¹H–¹⁵N NOE data recorded at 11.7 and 18.8 T for both ubiquitin (Figure 1a) and protein L (Figure 1b). Overall, there is a very good correlation between R_ex,ρ(N_x) rates derived by the two different methods, cross-validating the present approach. A similar plot is shown in the Supporting Information where R_ex,ρ(N_x) rates derived from R_1,2(2H_νN_μ) values measured at 11.7 T are compared to the corresponding R_ex rates derived from spectral density mapping of R₁, R_1ρ, and ¹H–¹⁵N NOE data. Remarkably, even very small R_ex,ρ(N_x) contributions are determined accurately, and the agreement between the two methods is high once again. What then is the advantage of measuring {R_1,2(2H_νN_μ)}? First, the four R_1,2(2H_νN_μ) values need be acquired at only one static magnetic field strength, in this case 18.8 T (Figure 1, or 11.7 T as in the Supporting Information), obviating the need for data at two or more fields that are necessary in the spectral density mapping approach. This is a considerable benefit because it avoids errors associated with different spectrometer usage (temperature differences, slight differences in ω_SL values between the measurements at different fields) that can become important for the quantification of small exchange contributions. In addition, assumptions about the dependence of R_ex,ρ(N_x) on B₀ are not needed (here we have shown that the quadratic dependence is justified, but this will not be the case in general²³). One might argue that an appropriate spin-lock field strength, ω_SL, can be chosen in a conventional R_1ρ experiment to ensure that R_1ρ is always proportional to B₀² (see eq 10). However, because in practice chemical shifts of the excited state are likely not to be available, strong spin-lock fields (3 kHz) must be used to ensure that R_ex,ρ follows a quadratic B₀ dependence. Of course, the application of such strong fields would exacerbate the difficulties in ensuring identical sample temperatures for experiments recorded at the multiple magnetic fields, a requirement for the R_1ρ analysis. Moreover, very strong fields lead to efficient quenching of the exchange effect that is to be measured in the first place. The approach described here where four R_1,2(2H_νN_μ) rates are measured at a single field avoids these issues.

Figure 1.

Exchange contributions R_ex,ρ(N_x) obtained from measurement of residue-specific R₂(2H_xN_z), R₂(2H_zN_x), R₂(2H_xN_x), and R₁(2H_zN_z) relaxation rates at a magnetic field strength of 18.8 T (y-axis) agree with the corresponding values isolated from ¹⁵N R₁, ¹⁵N R_1ρ, and ¹H–¹⁵N NOE measurements at two static magnetic fields (11.7 and 18.8 T) for U-²H,¹⁵N-labeled human ubiquitin (a) and U-²H,¹⁵N-labeled protein L (b), 278 K. A ¹⁵N spin-lock field strength of 2 kHz was used for all experiments. The dashed lines correspond to y = x, and the rmsd is calculated as $\surd (\mathrm{\Sigma }{(x_i-y_i)}^2/N)$. The inset in (a) shows an expansion of the region corresponding to small R_ex,ρ(N_x) rates. A similar plot is shown in the Supporting Information where R_ex,ρ(N_x) was obtained from R₂(2H_xN_z), R₂(2H_zN_x), R₂(2H_xN_x), and R₁(2H_zN_z) relaxation rates measured at a magnetic field strength of 11.7 T.

Studies of Ubiquitin and Protein L Establish Significant Microsecond Fluctuations Even in These Thermostable Proteins

Residue-specific R_ex,ρ(N_x) rates, obtained from measured R_1,2(2H_νN_μ) values, are shown for ubiquitin (at 278 K, Figure 2a; and 298 K, Figure 2c) and for protein L (278 K, Figure 2b). The error introduced due to the uncertainty in the magnitude of the CSA, δ_CSA (site-specific variation in Δσ_Ν of ±10 ppm^27,35–37), is combined with each residue-specific experimental error in R_ex,ρ(N_x), δ_Exp (red vertical bars), to generate the total error ${\delta }_{\text{Total}}=\surd ({\delta }_{\text{Exp}}^2+{\delta }_{\text{CSA}}^2)$, shown as light blue error bars in Figure 2. From eq 9, it is clear that δ_CSA depends on the rotational correlation time. Herein, we have assumed that δ_CSA corresponds to an error in the assumed Δσ_Ν value of 10 ppm so that δ_CSA ≈ 0.4 s⁻¹ for ubiquitin at 278 K (Figure 2a), ≈ 0.5 s⁻¹ for protein L at 278 K (Figure 2b), and ≈ 0.25 s⁻¹ for ubiquitin at 298 K (Figure 2c). Only those residues for which R_ex,ρ(N_x) − δ_Total > 0 are considered to show exchange.

Figure 2.

Residue-specific microsecond chemical exchange contributions, R_ex,ρ(N_x), derived from the four relaxation rates R₂(2H_xN_z), R₂(2H_zN_x), R₂(2H_xN_x), and R₁(2H_zN_z) for (a) human ubiquitin at 278 K, (b) protein L at 278 K, and (c) ubiquitin at 298 K. The inset in (c) is a comparison of R_ex,ρ(N_x) derived at 278 K versus R_ex,ρ(N_x) derived at 298 K for ubiquitin. An ¹⁵N spin-lock field strength of 2 kHz was used to monitor the R₂(2H_zN_x) and R₂(2H_xN_x) rates. The red error bars correspond to the experimental error in the determination of R_ex,ρ(N_x), while the blue error bars include both experimental errors and errors introduced by the uncertainty in Δσ_Ν (±10 ppm), as described in the text.

Several residues of human ubiquitin have previously been identified to exhibit chemical exchange (e.g., 23–25, 43, 45, 55, and 70), and clearly these residues show large R_ex,ρ(N_x) contributions in Figure 2a. However, many more residues show significant exchange contributions, such as 9–14. Similarly, many significant R_ex,ρ(N_x) values are observed for protein L (Figure 2b), in particular for residues in the α helix region that includes amino acids 25–42. Thus, for both of these proteins, microsecond chemical exchange seems to be localized to α helical and loop regions and is certainly much more extensive than observed before.

It is worth noting that the derived exchange contributions cannot be due to simple exchange of amide protons with solvent, because such contributions will rigorously cancel in the linear combination of eqs 7 and 8. Neither can protein aggregation be a factor because R_ex,ρ(N_x) is independent of overall protein concentration over the 3–4-fold concentration range examined for both ubiquitin and protein L (see Supporting Information). Large site-specific variations of Δσ_Ν suggested earlier^46–48 could explain some of the chemical exchange contributions observed in Figure 2; however, to account for all of the residues not previously identified as undergoing exchange,⁴⁵ an average value of 〈Δσ〉 = −179 ppm (ubiquitin) and 〈Δσ〉 = −186 ppm (protein L) must be used, at variance with previous solid-state^36,37 and solution-state NMR studies.²⁷ Further evidence that the elevated R_ex,ρ(N_x) rates are interpreted correctly in terms of microsecond exchange comes from a temperature-dependent study of ubiquitin where R_ex,ρ(N_x) is measured at 298 and 278 K. At the higher temperature, the exchange contributions are attenuated as shown in a comparison of Figure 2a and c, likely reflecting an increase in k_ex (eq 10). That exchange must be present can be “visualized” in an alternate manner, as shown in the inset to Figure 2c. Recall that the derived R_ex,ρ(N_x) rates from eq 8 are nonzero when the value of Δσ_Ν used differs from the actual residue-specific CSA value, even in the absence of chemical exchange. That is, $R_{\text{ex},\rho }^{\text{measured}}=R_{\text{ex},\rho }^{\text{correct}}+1/6\left(c_{\text{N}}^2-c^2\right)\left(3J\left({\omega }_{\text{N}}\right)-4\text{J}(0)\right)$, eq 9. Moreover, assuming only very small changes in internal dynamics with temperature, it follows that

$$\langle \frac{{\left[4J(0)-3J\left({\omega }_{\text{N}}\right)\right]}_{298\text{K}}}{{\left[4J(0)-3J\left({\omega }_{\text{N}}\right)\right]}_{278\text{K}}}\rangle =0.47\pm 0.02$$ (13)

so that $R_{\text{ex},\rho }^{\text{measured},298}=0.47R_{\text{ex},\rho }^{\text{measured},278}$ in the absence of exchange and when c_N² ≠ c². Those residues for which R_ex,298K/R_ex,278K values significantly differ from 0.47 (Figure 2c, inset) must experience microsecond exchange, and site-specific variation of Δσ_Ν cannot explain the observed deviations. Indeed, R_ex,ρ(N_x)₂₉₈ < 0.47R_ex,ρ(N_x)₂₇₈ for many of the ubiquitin residues with statistically significant R_ex,ρ(N_x) (Figure 2a,c, numbered residues). It is worth noting that while R_ex,ρ(N_x)₂₉₈ < 0.47R_ex,ρ(N_x)₂₇₈ implies exchange, residues for which R_ex,ρ(N_x)₂₉₈ = 0.47R_ex,ρ(N_x)₂₇₈ may also undergo exchange because contributions from exchange and overall tumbling could scale approximately the same way with temperature.

Color-coded values of R_ex,ρ(N_x) calculated from measured R_1,2(2H_νN_μ) rates using eq 8 are plotted on the structures of ubiquitin (Figure 3) and protein L (Figure 4). It is clear that residues with microsecond chemical exchange include those in α-helices, loops, and to some extent on the strands that define the “rim” of β sheets. By contrast, very limited μs exchange is present for amide nitrogens located in the core of β sheets. Of interest, residues 9–14 in ubiquitin, which are shown here to have elevated R_ex,ρ(N_x) values, have been identified in a previous study based on residual dipolar couplings to have enhanced dynamics² and play a role in a conformational selection process, which facilitates the binding of this protein to its many targets.⁵¹ This study makes clear that even thermo-stable proteins that have been thought previously to be very rigid, such as ubiquitin and protein L, can have rather pervasive μs dynamics. Indeed, such a result must have been anticipated by the early pioneers in the biomolecular NMR field,^52–54 who showed that aromatic groups in proteins can undergo a wide range of motions on very different time-scales that must involve significant structural rearrangements.

Figure 3.

Microsecond chemical exchange contributions for human ubiquitin depicted on the 3D structure (pdb 1D3Z).⁴⁹ The rims of the β sheet, the α helix, and in particular the loop regions show significant R_ex,ρ(N_x) contributions due to microsecond molecular fluctuations, which are absent from the protein core. The orientation in (a) is similar to that presented previously in a study focusing on dynamics based on residual dipolar couplings,² while (b) is a view from a different angle. Residues with large R_ex,ρ(N_x) are indicated on the structure. No data are available for residues depicted with gray color.

Figure 4.

Microsecond chemical exchange contributions for protein L shown on the 3D structure (pdb 1HZ6).⁵⁰ The loop regions and the α helix between K28 and K41 show significant R_ex,ρ(N_x) rates, which are absent in the core of the β sheet. No data are available for residues depicted with gray color.

Microsecond Time-Scale Motions in a Histone–Chaperone Complex

Many molecular complexes are dynamic over a wide range of time-scales, and it is often of interest to separate the different motional processes according to their frequencies. One such complex involves the histone chaperone Chz1 that transports and delivers the variant histone H2A.Z to the nucleosomal remodeling complex,²⁰ which, in turn, inserts H2A.Z into nucleosomes to alter levels of gene expression in eukaryotic cells. The binding kinetics and in particular the stability and dynamics of the Chz1:H2A.Z-H2B complex may be key for understanding both the delivery process and the function of this chaperone. Previous studies of the association/dissociation reaction:²¹

$$\text{H}2\text{A}.\text{Z}-\text{H}2\text{B}:\text{Chz}1\underset{k_{\text{off}}}{\overset{k_{\text{on}}}{\rightleftharpoons }}\text{H}2\text{A}.\text{Z}-\text{H}2\text{B}+\text{Chz}1$$ (14)

have established that k_off = 22 ± 2 s⁻¹, k_on = 10⁸ ± 10⁷ M⁻¹ s⁻¹, and K_D = 0.22 ± 0.02 μM, 35 °C. These values were obtained by CPMG relaxation dispersion measurements that are sensitive to the millisecond time-scale association/dissociation that occurs when a near 1:1 mixture of chaperone and histone is present. In addition to this process, there are significant “fast” local fluctuations over a range extending from 100 ps to 2 ns,⁵⁵ overall rotation of the complex (~12 ns), and, as we show below, extensive μs dynamics. The pico–nanosecond fluctuations cause line narrowing of NMR signals, with both the millisecond and the microsecond time-scale processes leading to line broadening. The entanglement of these various processes makes their separation challenging.

As described above, the key to the separation of μs from ms exchange events lies in the use of kHz spin-lock fields that suppress contributions from the ms time-scale process. For ¹⁵N experiments that monitor the fate of Chz1 during the binding reaction of eq 14, the exchange rate is given by k_ex = k_on × [H2A.Z-H2B] + k_off, and previous studies have shown that for (total) concentrations of Chz1 and H2A.Z-H2B ≈ 1 mM employed presently, k_ex ≈ k_on[H2A.Z-H2B] = 1500 s⁻¹ at 35 °C. Thus, contributions to R_ex,ρ(N_x) from ligand association/dissociation, R_ex,ass, will be largely quenched by the 2 kHz ¹⁵N spin-lock field (ω_SL,N) used to record R₂(2H_νN_x) rates, because k_ex < ω_SL,N. More quantitatively,

$$R_{\text{ex},\text{ass}}\approx \frac{p_{\text{Chz}1}\mathrm{\Delta }{\omega }_{\text{ass}/\text{diss}}^2{k}_{\text{ass}}}{{\mathrm{\Omega }}_{\text{Chz}1}^2+{\omega }_{\text{SL}}^2+k_{\text{ass}}^2}$$ (15)

where Δω_ass/diss = Ω_Chz1 − Ω_{Chz1:H2A.Z-H2B}, with Ω_Chz1 and Ω_{Chz1:H2A.Z-H2B} the offsets of ¹⁵N resonance frequencies of probes in free and bound Chz1 from the spin-lock carrier (rad/s), k_ass is the pseudo first-order rate constant for the reaction, k_on[H2A.Z-H2B], and p_Chz1 ≪ 1 is the population of free Chz1. Values of R_ex,ass were calculated for all residues of Chz1 using measured chemical shift changes |Δω_CPMG|, p_Chz1 = 1.5%, and k_ass = 1500 s⁻¹ derived earlier from relaxation dispersions experiments.²¹ For all residues of Chz1, R_ex,ass < 3.5 s⁻¹, with R_ex,ass < 1.1 s⁻¹ for 96% of the ¹⁵N sites. Thus, even though it is a reasonable approximation to assume that millisecond processes are quenched effectively by the spin-lock, the “pure” contribution from microsecond dynamics can be calculated as R_ex,μs = R_ex,ρ(N_x) − R_ex,ass.

Large microsecond exchange contributions are observed for residues 94–115 of Chz1, encompassing the CHZ recognition motif that plays an important role in stabilizing the Chz1:H2A.Z-H2B ternary complex,⁵⁵ Figure 5. By contrast, R_ex,μs values are much smaller for the N- and C-terminal helices. Although the time-scale(s) of the microsecond motions cannot be calculated directly from the R_ex,μs rates, estimates can be made. Microsecond processes must be of the same order of or faster than the nitrogen spin-lock frequency (2000 Hz) used in the R_ex,ρ(N_x) measurements to avoid quenching by the spin-lock field (see above), but sufficiently slow so that self-quenching does not occur (note that R_ex,ρ becomes small for large k_ex, eq 10). Assuming two-site exchange with a limiting scenario of p_B = 50% and Δω_Ν = 10 ppm, ω_SL = 2 kHz, then k_ex must be less than 4 × 10⁵ s⁻¹ to account for the R_ex,μs values observed in Figure 5. Thus, our experiments establish that the CHZ motif of Chz1 bound to histones H2A.Z-H2B is dynamic on a microsecond time-scale, ranging between 2.5 and 500 μs. Such motion may well affect the stability of the complex and may play a role in regulating dissociation of chaperone that is strongly anchored to H2A.Z-H2B by a large interaction surface and strong electrostatic attractive forces.

Figure 5.

Exchange contributions to ¹⁵N transverse relaxation rates, R_ex,ρ(N_x), of Chz1 in the ternary Chz1:H2A.Z-H2B complex from dynamic processes with time-scales faster than |0.5 ms. The secondary structure elements are shown on the top of the plot. The thick pale red line is a “running average” calculated as R_ex,avg(i) = 0.25R_ex(i − 1) + 0.5R_ex(i) + 0.25R_ex(i + 1). Large R_ex,ρ(N_x) values are primarily observed for residues 94–115 (the CHZ motif), whereas the N-cap and C-cap helices only show small contributions from microsecond dynamics. The red error bars correspond to the experimental error, whereas the blue error bars are calculated to take into account both the variability of CSA values (from −182 to −162 ppm^27,35–37) and the experimental error (see text and legend of Figure 2).

In summary, we have presented a new approach for quantifying microsecond time-scale dynamics in proteins from chemical exchange contributions, R_ex,μs, to amide nitrogen transverse relaxation rates. The method is based on the measurement of four relaxation rates that can be combined in a straightforward manner to isolate exchange contributions on a per-residue basis. Notably, the influence of millisecond (k_ex < 2000 s⁻¹) motions is effectively eliminated by recording individual relaxation rates in the presence of a nitrogen spin-lock field of approximately 2 kHz. Perhaps surprisingly, rather extensive microsecond time-scale dynamics have been detected in both human ubiquitin and protein L, two molecules that are thermo-stable and that are likely more rigid than many other proteins. Such motions are located exclusively in α helices, loops, and on the rim of β sheets, with the β sheet core much less dynamic. The results from the present work suggest, therefore, that microsecond dynamics are likely to be more pervasive in proteins than previously thought. Finally, it has also been shown that microsecond motions can be separated from other chemical exchange processes, as demonstrated in the context of a histone-chaperone complex. Relaxation data measured at only a single static magnetic field are required. The described method will provide a very useful addition to a growing body of backbone spin-relaxation measurements that quantify dynamics over a wide range of time-scales and that provide insight into the relation between motion and protein function.

Material and Methods

Sample Preparation

U-[¹⁵N,²H] human ubiquitin was expressed with a cleavable His-tag and purified by standard methods.⁵⁶ A pair of protein samples with concentrations of 2.2 and 0.7 mM were prepared using a 20 mM Na₃PO₄, 10 mM NaCl, 0.03% NaN₃, 90%/10% H₂O/D₂O, pH 5.5 buffer. U-[¹⁵N,²H]-protein L was produced as described previously.⁵⁷ Two protein L samples were obtained with protein concentrations of 2.7 and 0.5 mM in 50 mM Na₃PO₄, 20 μM EDTA, 0.05% NaN₃, 90%/10% H₂O/D₂O, pH 6.0 buffer. An approximate 1:1 mixture of U-[¹⁵N,²H] Chz1 (~1 mM) and U-[¹⁵N,²H] single-chain H2A.Z-H2B (~1 mM) was prepared as described previously⁵⁵ in a buffer consisting of 25 mM MES, 200 mM NaCl, 1 mM EDTA, pH 6.0, and 10% D₂O.

NMR Spectroscopy

The four relaxation rates R₂(2H_xN_z), R₂(2H_zN_x), R₂(2H_xN_x), and R₁(2H_zN_z) were derived for human ubiquitin ((278 K; 0.7 mM), (278 K; 2.2 mM), and (298 K; 2.2 mM)), for protein L ((278 K; 0.5 mM) and (278 K; 2.3 mM),) and for Chz1 in the Chz1:H2A.Z-H2B ternary complex (308 K) at a static magnetic field strength of 18.8 T (800 MHz proton frequency), using pulse schemes for measuring the rotating frame relaxation rates, R_1ρ(2H′_zN_z), R_1ρ(2H_zN′_z), $R_{1{\rho }^2}\left(2{{\text{H}}^{\prime }}_z{{\text{N}}^{\prime }}_z\right)$, and R₁(2H_zN_z), that have been published previously.²³ Briefly, the rotating frame antiphase relaxation rate, R_1ρ(2H′_zN_z), was measured with ¹H magnetization spin-locked⁵⁸ along an effective field that is given by the vector-sum of the spin-lock field (ω_SL,H ≈ 13 kHz, along x) and the offset of the ¹H nucleus from the ¹H radio frequency (rf) carrier (Ω_H, along z), ${\overrightarrow{\omega }}_{\text{eff},\text{H}}={\overrightarrow{\omega }}_{\text{SL},\text{H}}+{\overrightarrow{\mathrm{\Omega }}}_{\text{H}}$. The proton carrier was placed at 9.5 ppm as suggested previously.²³ It follows directly that 2H′_zN_z = sin(θ_H)2H_xN_z + cos(θ_H)2H_zN_z, where tan θ_H = ω_SL,H/Ω_H, and consequently it can be shown that

$$R_{1\rho }\left(2{{\text{H}}^{\prime }}_z{\text{N}}_z\right)=R_2\left(2{\text{H}}_x{\text{N}}_z\right){\sin }^2{\theta }_{\text{H}}+R_1\left(2{\text{H}}_z{\text{N}}_z\right){\cos }^2{\theta }_{\text{H}}$$ (16)

Similarly, R_1ρ(2H_zN′_z) was measured with the ¹⁵N magnetization spin-locked along an effective nitrogen field so that

$$R_{1\rho }\left(2{\text{H}}_z{{\text{N}}^{\prime }}_z\right)=R_2\left(2{\text{H}}_z{\text{N}}_x\right){\sin }^2{\theta }_{\text{N}}+R_1\left(2{\text{H}}_z{\text{N}}_z\right){\cos }^2{\theta }_{\text{N}}$$ (17)

where tan θ_N = ω_SL,N/Ω_N, ω_SL,N is the strength (rad/s) of the ¹⁵N spin-lock field, and Ω_N is the offset (rad/s) of the ¹⁵N nucleus from the ¹⁵N radio frequency carrier placed at 119 ppm. Finally, the “double-rotating frame” rate, $R_{1{\rho }^2}\left(2{{\text{H}}^{\prime }}_z{{\text{N}}^{\prime }}_z\right)$, was measured with ¹H and ¹⁵N magnetization spin-locked along their respective fields so that

$$\begin{gathered} R_{1{\rho }^2}\left(2{{\text{H}}^{\prime }}_z{{\text{N}}^{\prime }}_z\right)=R_2\left(2{\text{H}}_x{\text{N}}_x\right){\sin }^2{\theta }_{\text{H}}{\sin }^2{\theta }_{\text{N}}+ \\ {R}_2\left(2{\text{H}}_x{\text{N}}_z\right){\sin }^2{\theta }_{\text{H}}{\cos }^2{\theta }_{\text{N}}+R_2\left(2{\text{H}}_z{\text{N}}_x\right){\cos }^2{\theta }_{\text{H}}{\sin }^2{\theta }_{\text{N}}+ \\ {R}_1\left(2{\text{H}}_z{\text{N}}_z\right){\cos }^2{\theta }_{\text{H}}{\cos }^2{\theta }_{\text{N}} \end{gathered}$$ (18)

The transverse relaxation rates R₂(2H_xN_z), R₂(2H_zN_x), and R₂(2H_xN_x) were derived from the four measured relaxation rates R_1ρ(2H′_zN_z), R_1ρ(2H_zN′_z), $R_{1{\rho }^2}\left(2{{\text{H}}^{\prime }}_z{{\text{N}}^{\prime }}_z\right)$, and R₁(2H_zN_z) via eqs 16–18 and used in subsequent analyses.

The relaxation rates R_1,2(2H_νN_μ) were measured with delays of 2.5, 5.3, 8.3, 11.5, 15.1, 19.2, 23.7, 28.8, 35 ms (ubiquitin and protein L) and 2, 3.8, 5.9, 8, 10.4, 12.8, 15.5, 18.4, 21.5 ms for the histone-chaperone complex. ¹H and ¹⁵N continuous wave (CW) spin-lock field strengths varied between 11.5 and 13.7 kHz for ¹H (depending on the sample) and were very close to 1.9 kHz for ¹⁵N. Nitrogen R₁ and R_1ρ relaxation rates along with steady-state ¹H–¹⁵N NOE values⁵⁹ were obtained for the backbone amides of ubiquitin (298 and 278 K) and protein L (278 K) at static magnetic field strengths of 11.7 and 18.8 T. Relaxation delays of 0.01, 0.1, 0.21, 0.34, 0.49, 0.67, 0.67, and 0.9 s were used for the R₁ measurements, while the R_1ρ rates were quantified from experiments recorded with delays of 2, 9.5, 20, 32, 60, 78, and 100 ms. In all cases, the ¹⁵N field strength applied during the spin-lock period in the R_1ρ experiments was very close to 1.9 kHz, with fine-power adjustments to ensure that identical spin-lock powers were used for a given sample at both static magnetic fields. ¹H–¹⁵N NOE values were quantified from two spectra, with and without proton presaturation. The spectrum with presaturation was recorded with a prescan delay of 9 s followed by 6 s of proton saturation, while the spectrum without proton presaturation was recorded with a 15 s prescan delay.

Data Processing

Data sets were processed with the NMRPipe program⁶⁰ and analyzed with UCSF Sparky.⁶¹ Signal intensities were determined using the program FuDA (flemming@pound.med.utoronto.ca; http://pound.med.utoronto.ca/software) by fitting a mixed Gaussian/Lorentzian line-shape to each correlation and assuming a common line-shape for a given cross-peak within a relaxation series (i.e., line-shape and peak positions are independent of relaxation delay). All relaxation rates were determined by fitting a single exponential decay function, I(T_relax) = A exp(−RT_relax), to the measured intensity versus T_relax profile. Microsecond chemical exchange contributions, R_ex,ρ, were calculated using eq 8. Uncertainties in relaxation rates were obtained from the covariance matrix method⁶² and propagated with a Monte Carlo procedure.