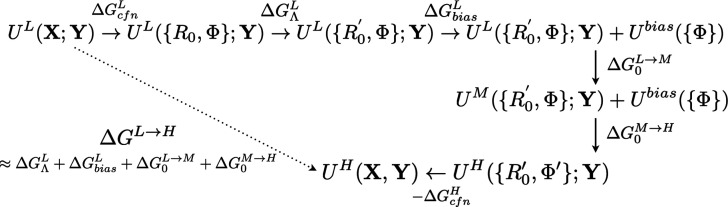Abstract
Combining multiple levels of theory in free energy simulations to balance computational accuracy and efficiency is a promising approach for studying processes in the condensed phase. While the basic idea has been proposed and explored for quite some time, it remains challenging to achieve convergence for such multi-level free energy simulations as it requires a favorable distribution overlap between different levels of theory. Previous efforts focused on improving the distribution overlap by either altering the low-level of theory for the specific system of interest or ignoring certain degrees of freedom. Here, we propose an alternative strategy that first identifies the degrees of freedom that lead to gaps in the distributions of different levels of theory and then treats them separately with either constraints or restraints or by introducing an intermediate model that better connects the low and high levels of theory. As a result, the conversion from the low level to the high level model is done in a staged fashion that ensures a favorable distribution overlap along the way. Free energy components associated with different steps are mostly evaluated explicitly, and thus, the final result can be meaningfully compared to the rigorous free energy difference between the two levels of theory with limited and well-defined approximations. The additional free energy component calculations involve simulations at the low level of theory and therefore do not incur high computational costs. The approach is illustrated with two simple but non-trivial solution examples, and factors that dictate the reliability of the result are discussed.
I. INTRODUCTION
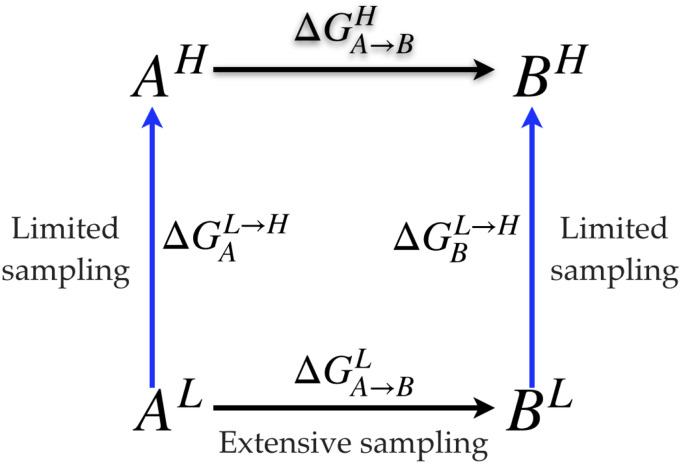
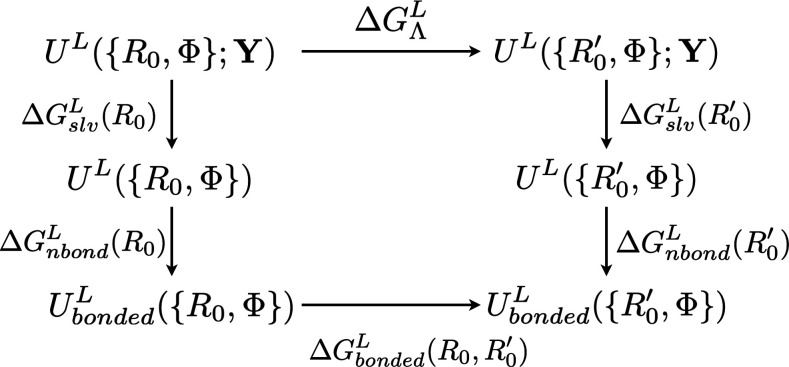
Hybrid quantum mechanical/molecular mechanical (QM/MM) methods1–9 have become an established technique in computational chemistry, biochemistry, and biophysics as well as materials science.7,9–16 One of the remaining challenges for predictive applications for condensed phase systems is to compute reliable free energy changes. As discussed in numerous studies,17–20 this requires, in principle, an accurate QM/MM potential function and adequate sampling, which is difficult to accomplish for most condensed phase studies at this stage. Therefore, a potentially attractive alternative is to conduct multi-level free energy simulations20–29 in which a low-level QM/MM potential (e.g., using a semi-empirical QM method) is used to conduct extensive sampling, while a higher-level QM/MM potential (e.g., with a density functional theory or a correlated wavefunction method as QM) is used to improve the free energy estimate; if the process of interest is not reactive in nature, the low-level method can be a classical MM model as well. A commonly discussed free energy cycle is shown in Fig. 1; due to the state function nature of free energy, , where “L” and “H” indicate the low and high levels of theory, respectively. For the quantities on the rhs of the equation, is obtained with a low-level of theory and therefore can be computed with extensive sampling using, for example, umbrella sampling30 or its more modern variants.31 The “vertical” components, , are needed only for the end-states, A/B; for the multi-level free energy simulation to be computationally worthwhile, calculations of should rely mostly (if not exclusively) on sampling at the low-level, and high-level single point energy calculations are done only at a limited number of uncorrelated snapshots. The most naïve estimator, for example, is the one-step free energy perturbation, , which, in principle, requires sampling only at the low level.
FIG. 1.
A thermodynamic cycle that uses the low-level (L) method as a reference potential to indirectly compute the free energy difference between states A and B at the high (H) level. In this work, we focus on a single vertical leg and discuss the computation of ΔGL→H.
While this is an intuitive idea and has been explored for quite a few times in previous studies in slightly different forms,20–29 reaching converged results, in practice, for based on low-level sampling alone has been difficult, except for relatively simple or structurally rigid systems. This is not unexpected since it has been well-known in the free energy simulation literature that a single step perturbation gives reasonable results only if the two end-states (in this case, low- and high-level potential energies) are sufficiently similar such that the standard deviation of energy difference (in our case, ) is on the order of several kBT.32–35 More quantitative metrics for the distribution overlap between the two end-states have been developed by several authors,32,33,36,37 but most of them are not straightforward to use for the case of multi-level free energy simulations in which high-level sampling is to be avoided as much as possible. Accordingly, based on the work of Kofke and co-workers,38–40 Boresch and Woodcock developed an approximate version41 of the Π score38,39 to estimate the degree of distribution overlap between two levels of theory; a value of >0.5 was recommended as the indicator of the minimal overlap for the meaningful one-step free energy estimate. It was found that the approximate Π score correlates reasonably well with the width of the ΔUL→H distribution, which can also be an instructive factor for monitoring the convergence of one-step free energy estimates.33,34,41
The test of a range of small molecules in both gas phase and solution using CHARMM22/36 as the low-level and DFTB342,43 as the high-level indicated that the overlap Π score is favorable for rigid molecules.44 For more flexible molecules, such as a serine amino acid in the gas phase, the overlap is poor with a negative Π score.45 To improve the convergence behavior, several strategies have been developed. If the main difference between the two levels of theory concerns the bonded degrees of freedom, one approach is to conduct non-equilibrium free energy simulations by rapidly switching the potential function; since the bonded degrees of freedom (especially bond stretch and angle bending) tend to be highly localized, rapid switching at the picosecond time scale appeared effective, although many trajectories (on the order of thousands or more) are usually required for stringent numerical convergence, which is a well-documented feature for non-equilibrium free energy simulations46 based on the Jarzynski equality47 or the fluctuation theorem.48
When more general degrees of freedom are responsible for the deviation between different levels of theory, it seems necessary to modify the low-level of theory such that the distribution overlap with the high-level method is improved. This has been done by several authors in the broader context of free energy simulations. For example, Rossi and Truhlar49 pioneered reaction-specific-parameters to improve the semi-empirical QM method for the specific system of interest; this has been adapted in the framework of the string method with force matching by Zhou et al.50 for effective reaction free energy simulations. Similarly, Shen andYang51 reported an approach in which a neural network is used to iteratively improve the low-level QM method in reaction free energy simulations. Plotnikov et al. developed “para-dynamics,”52 which iteratively improves the reference potential in the empirical valence bond (EVB) framework using ab initio QM single point energies. Specifically, in the context of multi-level free energy simulation based on the thermodynamic cycle in Fig. 1, Heimdal and Ryde advocated for the parameterization of better force fields as the reference approach.19 Similarly, Woodcock and co-workers45,53 as well as York and co-workers54,55 proposed to use force-matching to improve the low-level potential based on single-point high-level force calculations; for relatively rigid small molecules in solution or a protein active site, encouraging results have been reported. For rigid molecules, another possibility is to compute only the QM/MM interaction energies,56 although this is clearly an approximation and may lead to considerable errors as the flexibility of molecules increases.57
Despite this progress, it is worthwhile exploring alternative strategies for connecting different levels of theory in quantitative free energy simulations. For example, while the non-equilibrium approach can benefit from “embarrassingly parallel” simulations,53 conducting thousands of picosecond scale trajectories that involve explicitly mixing low- and high-levels of potentials is computationally demanding when the QM region is large; moreover, conducting many fast non-equilibrium switching simulations likely entangles the free energy difference due to the stiff bonded degrees of freedom with that arising from incomplete sampling of other degrees of freedom. Similarly, improving a low-level method with force matching or even a neural network may not be straightforward for large systems.
Motivated by these considerations, we explore an approach in which the low-level theory is not modified explicitly; instead, the transformation from the low-level to the high-level potential function is done in a staged fashion such that a favorable distribution overlap is always maintained. Although the transformation is carried out in multiple stages and thus involves more computations, most of these computations are done at the low-level of theory, and therefore, the approach still offers a significant gain in computational efficiency compared to brute-force free energy simulations that explicitly mix low and high level potential functions in multiple windows.
In the following, we first describe the fundamental consideration behind our development and then present the staged transformation approach. Next, as a proof of concept, we study two small but non-trivial molecules in solution and discuss technical choices that are likely important to the effectiveness of our specific thermodynamic path. We end with a few concluding remarks, including our perspective regarding future developments.
II. METHOD
In the following discussion, we focus on a single vertical leg of the thermodynamic cycle in Fig. 1. To simplify nomenclature, we make the assumption that the A/B conversion depicted in the generic thermodynamic cycle in Fig. 1 involves the entire QM region only, which will also be simply referred to as the “solute.”
A. Fundamental considerations
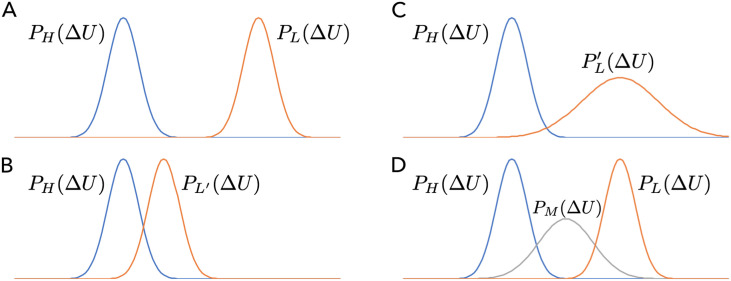
As shown schematically in Fig. 2, different strategies can be used to improve the distribution overlap between L and H levels of theory [panel (a)]. The most natural approach, as mentioned above in the Introduction, is to modify the low level of theory [L → L′, panel (b)]. Since this may not be straightforward, one could consider other alternatives. One possibility is to artificially broaden the distribution at the low level of theory (i.e., sample rather than PL with, for example, a higher temperature or Tsallis statistics58) so as to develop the distribution overlap with H; to complete the thermodynamic cycle, however, one has to either reweight or compute the free energy difference between the original and broadened distributions. In fact, panel (c) can be considered as a special case for panel (d) in which an intermediate distribution PM is introduced to bridge the otherwise separated PL and PH; PM can be sampled using a different level of theory, using L in a different thermodynamic state, or using L in the presence of additional constraints/restraints (see below). The fundamental philosophy is that instead of modifying L explicitly, efforts are spend to bridge the distributions of L and H, provided that the computational costs of L and H are sufficiently different, including additional steps that require sampling with L or a comparable level of theory does not significantly reduce the computational advantage of the multi-level free energy approach.
FIG. 2.
Different strategies for improving the energy difference (ΔU) distribution overlap between L and H levels of theory, which is critical to the convergence of free energy simulations that rely on sampling at either one end-state or both end-states.32,33,36,40 (a) The two end-states have a gap in the ΔU distribution. (b) One can modify the low-level method (L → L′) to improve the ΔU distribution based on, for example, force-matching45,55 or a neural network.51 (c) One can modify the distribution of the same low level method (PL → ), with, for example, Tsallis sampling,58 to improve the ΔU distribution. (d) One can introduce an intermediate level of method (or distribution) PM to bridge the distributions at the L and H levels. The staged protocol described here falls into this category.
Given the fundamental aim of our approach, the key is then to identify the degrees of freedom responsible for creating the gap in the distributions of L and H. This is certainly not a trivial problem and can benefit from innovative approaches such as machine learning (see discussion in Sec. IV). For the case of integrating low-level and high-level QM potentials, which is the major motivation for our work, the likely situation is that they differ mainly in bonded degrees of freedom,19,45,55 such as bond lengths, bond angles, and selected dihedrals. While low-level QM methods generally suffer from inadequate electronic polarization59–61 and inaccurate multiple moments,62,63 it is unlikely that the charge distribution is grossly misrepresented as compared to a high-level QM description; nevertheless, the impact of different non-bonded terms on the distribution is also explored in the following test cases. Denoting the degrees of freedom that cause a poor overlap between L and H as X and the rest (QM) degrees of freedom as Y, our strategy is then to treat them differently when converting between the L and H levels of theory.
B. A staged transformation approach
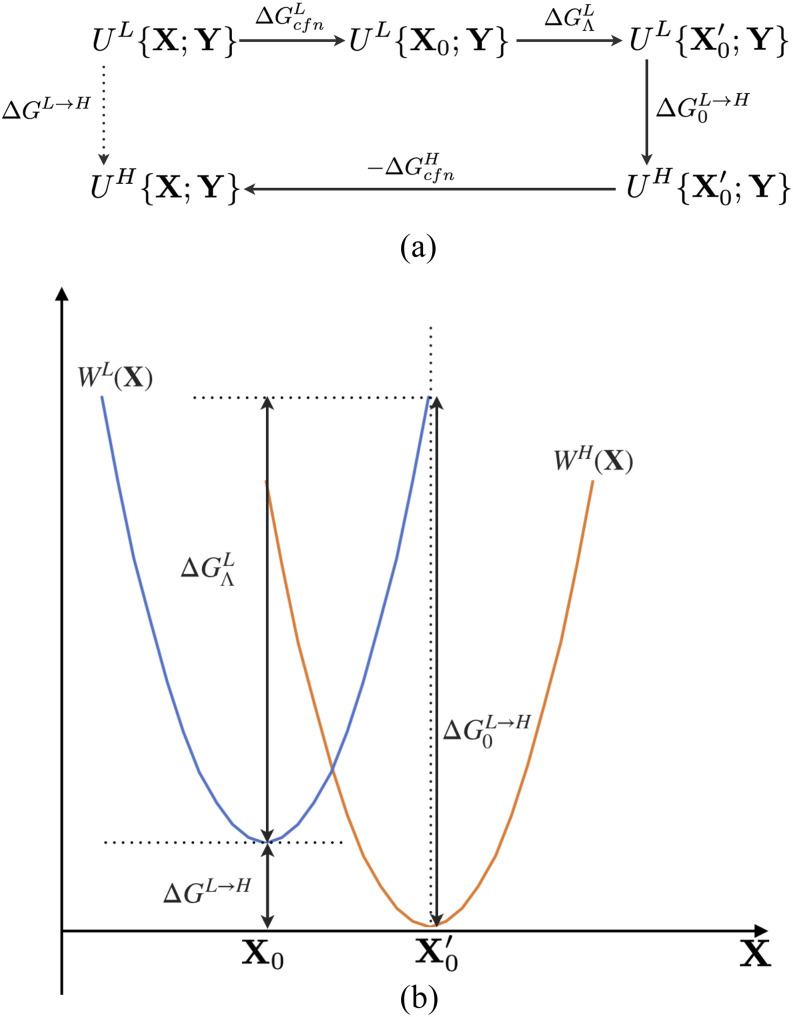
Recognizing that different “solute” degrees of freedom X, Y feature different distribution overlaps between L and H and that X tends to be more local in nature, the basic thermodynamic path that we propose is shown in Fig. 3(a) in which the system is transformed from L to H in a staged fashion: first, imagine turning on a confinement potential to restrain/constrain X to the free energy minimum on the L level (X0), then evaluate the “reorganization free energy cost” () of changing X0 to , the free energy minimum at the H level of theory, with X restrained/constrained to , evaluate the free energy change associated with changing the potential function from L to H, , and finally, imagine turning off the confinement potential on X on the H level. Formally, the total free energy change is written as the sum of contributions from all stages (Fig. 3),
| (1) |
If we approximate that the confinement free energies evaluated at the L and H levels are comparable (vide infra), then the expression can be simplified into the sum of only two contributions,
| (2) |
FIG. 3.
A simple staged transformation approach for computing the free energy difference at two levels (L/H) of theory, ΔGL→H. (a) The staged thermodynamic path treats the selected degrees of freedom (X) separately from the rest (Y); X represents the degrees of freedom that lead to a large gap in the ΔULH distribution. Assuming that the free energy costs for confining X to values at (or near) the free energy minima are similar at the L and H levels, ΔGL→H, is given by the sum of , which converges readily since the sampling involves only Y, and the “reorganization free energy,” , which is the free energy cost of changing X0 to at the low level of theory. (b) A simple one-dimensional illustration for the staged transformation approach: W(X) is the potential of mean force and the key approximation is that the configurational entropies for X are comparable at the L and H levels.
The staging strategy can be better illustrated with a simple example where X is one-dimensional, as shown in Fig. 3(b). Define the potential of mean force in X at different levels (L/H) as
| (3) |
we can express the free energy difference between L and H in terms of W at the free energy minimum and the entropic contributions associated with X (),
| (4) |
and here, the entropic contributions can be regarded as the confinement free energies in Eq. (1). If the entropic contributions at the L and H levels are comparable, this can be simplified and rearranged as
| (5) |
The significance of this simple rearrangement is that is evaluated by sampling along the Y degrees of freedom, which feature a favorable overlap between L and H; the “reorganization” in the X degrees of freedom, , is evaluated at the low-level of theory.
Before discussing the evaluation of and in detail in Subsection II C, we note that in these basic schemes discussed so far, we approximate that the confinement free energies (), which are mostly entropic in nature, are similar at the L and H levels of theory and therefore do not need to be evaluated explicitly. If the “solute” is structurally rigid, it is possible to explicitly evaluate the confinement free energies with normal mode analysis.8,64,65 As the region of interest becomes large and/or flexible, either ignoring the difference between and harmonic approximations becomes unreliable. Instead, it is preferable to limit X to a small number of bonded degrees of freedom for which free energy contributions can be evaluated using approximate analytic expressions66 while treating differences in specific dihedral angles and/or non-bonded terms differently. Accordingly, we imagine a more general staged transformation path as illustrated in Fig. 4.
FIG. 4.
A more general staging strategy for transforming from the L to H level of theory with the controlled distribution overlap along the path. Here, X = {R, Φ}; the general aim is to minimize the number of degrees of freedom that are constrained ({R}) such that the approximation of similar “confinement free energies” at the L/H levels is expected to hold; any difference in softer degrees of freedom, such as selected dihedrals ({Φ}), can be controlled with a biasing potential and the corresponding free energy can be evaluated as commonly done in ligand-binding simulations.67 To further improve the distribution overlap, an intermediate level of model with improved partial charges, for instance, can be introduced (see Sec. III).
Along this more general transformation path, the difference in specific dihedral terms can be considered by turning on restraining potentials at the L level so that the corresponding dihedral distribution overlaps favorably with that at the H level; the free energy contribution of turning on the restraining potential can be evaluated explicitly as commonly done in binding free energy simulations.67 In the event that the distribution overlap between L and H is also impacted by difference in non-bonded interactions, such as partial charge distributions, it is also possible to introduce an intermediate level of model M to bridge the distributions (see Sec. III).
C. Evaluation of and
In this subsection, we discuss in more detail the calculations of and . The former is done with X constrained at , while the latter involves changing from X0 to ; thus, both calculations rely on the determination of free energy minima on the L and H free energy surfaces. Provided that X includes only localized degrees of freedom such as bond-stretches and angle-bending or stiff torsions, X0 and are expected to be well-defined and straightforward to determine with relatively short equilibrium MD simulations (see Sec. III B for a discussion of impacts of choosing different X0 and values and Sec. III C for a discussion of sampling requirement).
Once X0 and are determined, and can be computed using the well-established simulation methodologies. Specifically, for , since sampling along Y is expected to feature a favorable distribution overlap between L and H, it is possible that 1-step free energy perturbation that relies on sampling only at the L level is sufficient for practical convergence. On the other hand, it is always more robust to conduct some sampling at the H level so that the distribution overlap can be explicitly assessed, including sampling at the H level also enables more reliable free energy estimates using techniques such as the linear response approximation (LRA)18,20,68 or Bennet acceptance ratio (BAR).69–71
For the computation of , which involves sampling only at the L level, different strategies can be employed. The most straightforward approach is to use the dual topology free energy perturbation to convert the solute/QM region from X0 to . One could pursue an alternative thermodynamic path (see Fig. 6) in which the solute, while adopting structure X0 and , is first decoupled from the environment; then, the conversion from X0 to can be done with free energy perturbation in the gas phase, which is expected to converge rapidly. The important point is that regardless of the chosen path, all simulations require sampling at the L level only and therefore are computationally inexpensive.
FIG. 6.
A sample thermodynamic cycle used to compute the reorganization free energy, , in which the solute is first decoupled from the environment and then removed of any non-bonded interactions; finally, the difference in the bonded free energies is evaluated, leading to . Note that all calculations are done at the low level of theory, and most steps are done in the gas phase; thus, the computational cost is modest.
D. Computational setup of test systems
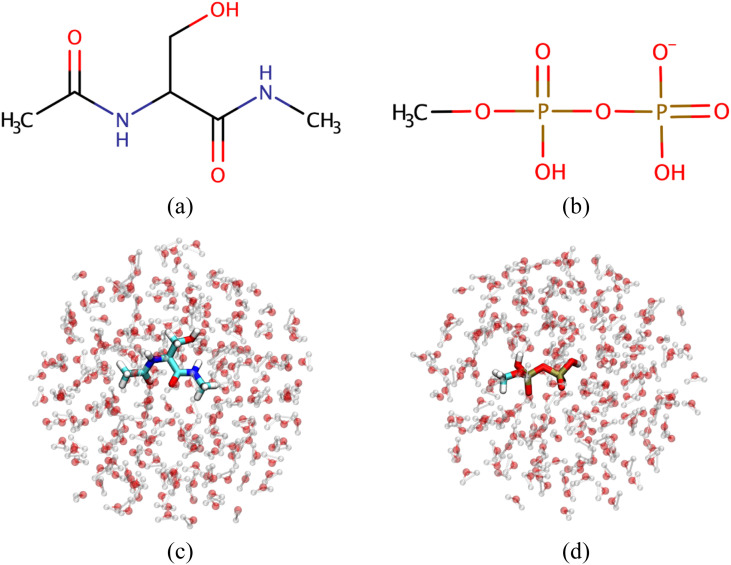
As a proof of concept, we illustrate the staged transformation approach with two simple but non-trivial examples in a water droplet (Fig. 5) and we examine a single vertical leg of the thermodynamic cycle in Fig. 1. For the purpose of this work, we mainly focus on the choice of CHARMM3672 as the low (L) level and DFTB3/3OB/MM73 as the high (H) level; we also study the case in which L is DFTB3/3OB/MM and H is B3LYP/6-31G(d)/MM.
FIG. 5.
Test systems explored in this work: (a) blocked serine: N-acetyl-serine-methyl-amide (Ser) and (b) methyl di-phosphate (MDP). [(c) and (d)] A water droplet of radius 12 Å that contains a Ser or MDP.
1. System setup
The small molecule solute is weakly restrained to be at the center of a 12 Å radius water droplet, which is not subject to any special solvent boundary potential. Non-bonded interactions at the pure MM level are computed with extended electrostatics74 available in CHARMM,75 which computes electrostatic interactions with group-based multipoles beyond the cutoff (12 Å) distance; this option is consistent with the fact that QM/MM electrostatic interactions are computed without any cutoff.
For simulations aimed at probing the distribution overlap between L = MM (CHARMM36) and H = DFTB3/3OB/MM, the molecular dynamics simulations are typically NVT simulations at 300 K with ∼100 ps of sampling. For L = DFTB3/3OB/MM and H = B3LYP/MM, the sampling is ∼50 ps. For the integration time step, it is 0.5 fs for simulations with a completely unrestrained solute. With the bonded degrees of freedom constrained (SHAKE76), the integration time step is 2.0 fs. For simulations that also probe the effect of restraining angular degrees of freedom, the force constant used is 300 kcal/mol rad2.
2. Free energy simulations
With L = MM (CHARMM36) and H = DFTB3/3OB/MM, it is possible to compute the ΔGL→H with “brute-force” thermodynamic integration using multiple λ windows that connect the L and H levels. We have done so for the cases of unrestrained solutes and for each solute, 11 λ windows (0.0, 0.05, 0.15, …, 0.95, 1.0) are used with each window sampled by 350 ps of production runs followed by 60 ps of equilibration. For the more approximate free energy estimators: 1-λ FEP, LRA, and BAR, 100 ps of production run is used for the relevant windows; 1-λ FEP employs only the L-level sampling, while the other estimators employ sampling with both end-states (L and H). The lengths of these simulations are chosen such that they represent the typically affordable level of computations using QM potentials such as DFT. In addition to unrestrained solutes, we have also examined the consistency among these approximate free energy estimators for cases where the solute is either completely frozen or partially constrained/restrained (see Tables for details); the sampling is also 100 ps of production run for the relevant windows. Finally, for L = DFTB3/3OB/MM and H = B3LYP/MM, we also computed ΔGL→H using the various approximate free energy estimators with 50 ps of production for the relevant windows.
For the exploration of the staged transformation protocol, we focus on the case of unrestrained solutes with L = MM (CHARMM36) and H = DFTB3/3OB/MM. For the “confinement step,” we apply both bond constraint (SHAKE) and angle restraint using a large force constant of 300 kcal/mol rad2 with the reference structures collected from free 1 ns L (i.e., X0) and H (i.e., ) simulations (see Sec. III B for a discussion of selection criteria); to test the sensitivity of the results to the choice of the reference, we choose five X0 and five , leading to 25 possible combinations. As discussed below, even with the constraints/restraints on the bonded degrees of freedom, the overlap between the L and H distributions is not optimal. Therefore, we take the advantage of the flexibility of the staged transformation approach (Fig. 4) and include an additional intermediate (M) level, which differs only from L in terms of the partial charges; instead of the standard CHARMM36 charges, we use the Mulliken charges at the DFTB3/3OB level calculated for a random snapshot collected from the aforementioned DFTB3/3OB/MM simulations.
For the computation of , since L = CHARMM36, we use the specific thermodynamic cycle outlined in Fig. 6, which involves five separate sets of free energy simulations in either the water droplet [ and ] or in the gas phase [, , and ]. Since all these simulations are at the low-level, they are readily conducted with multi-λ thermodynamic integration with 11 λ windows (0.0, 0.05, 0.15, …, 0.95, 1.0), with each window sampled for at least 100 ps.
3. Scores used to evaluate distribution overlap
To help characterize the distribution overlap between the L and H levels, we follow the discussions of Kofke and co-workers.37–40,77,78 In particular, we have computed the following two sets of scores. The first set is based on the total energy distributions at different levels of theories. As discussed in Refs. 38 and 39, we define the following energy distributions:
-
•
ρLL(UL) ≡ ρL: sample with L, examine the distribution of UL;
-
•
ρHH(UH) ≡ ρH: sample with H, examine the distribution of UH;
-
•
ρLH(UH): sample with L, examine the distribution of UH; and
-
•
ρHL(UL): sample with H, examine the distribution of UL.
Then, one can define the following overlap integrals, which range between 0 and 2 depending on the degree of overlap: (a) H in L,
| (6) |
(b) L in H,
| (7) |
The second set of scores is based on the Kullback–Leibler (KL) divergence of total energy distributions,
| (8) |
| (9) |
These can be shown to be related to the dissipative work associated with the L → H conversion,
| (10) |
| (11) |
where W is the work; for FEP, it is just the energy gap ΔUHL. These relative entropies can be used to define the Π scores,
| (12) |
| (13) |
where M is the sample size, WL(x) is the Lambert W function, defined as the solution for w in the equation x = wew. It was proposed that good sampling is expected if Π > 0. Woodcock and Boresch explored a simplified version of the Π score that assumes sL = sH.41
III. RESULTS AND DISCUSSION
In the following, we first illustrate the impact of separately treating X degrees of freedom on the distribution overlap between L and H, then we demonstrate that the staged transformation approach indeed leads to the expected free energy difference between L and H by comparing to brute-force thermodynamic integration for ΔGL→H, which involves explicitly mixing the L and H potential functions in multiple-λ windows. Finally, we briefly comment on the issue of sampling on both the L and H levels of potential energy surfaces. While the work was motivated by conducting multi-level QM/MM simulations, the L level is taken to be CHARMM36 in most analyses, with DFTB3/3OB/MM being the H level; nevertheless, we also include results on the combination of DFTB3/3OB/MM as L and B3LYP/6-31G(d)/MM as H.
A. Improvement of distribution overlap with confinement of X degrees of freedom
As discussed extensively in the literature,32,40 free energy simulation results depend critically on the ΔU distribution overlap of the two end-states. The challenge of establishing the good distribution overlap is well illustrated in Figs. 7(a) and 7(c): without any conformational restraint, there is essentially no ΔU overlap between the CHARMM36 (L) and DFTB3/3OB/MM (H) simulations for both a serine and a methyl diphosphate (MDP) in solution. The overlap is even smaller for the case of MDP with an apparent gap in the ΔU distribution of ∼25 kcal/mol. The lack of overlap is well captured by the various overlap scores reported in Tables I and II, for example, the Π scores are large and negative with values ∼−4.
FIG. 7.
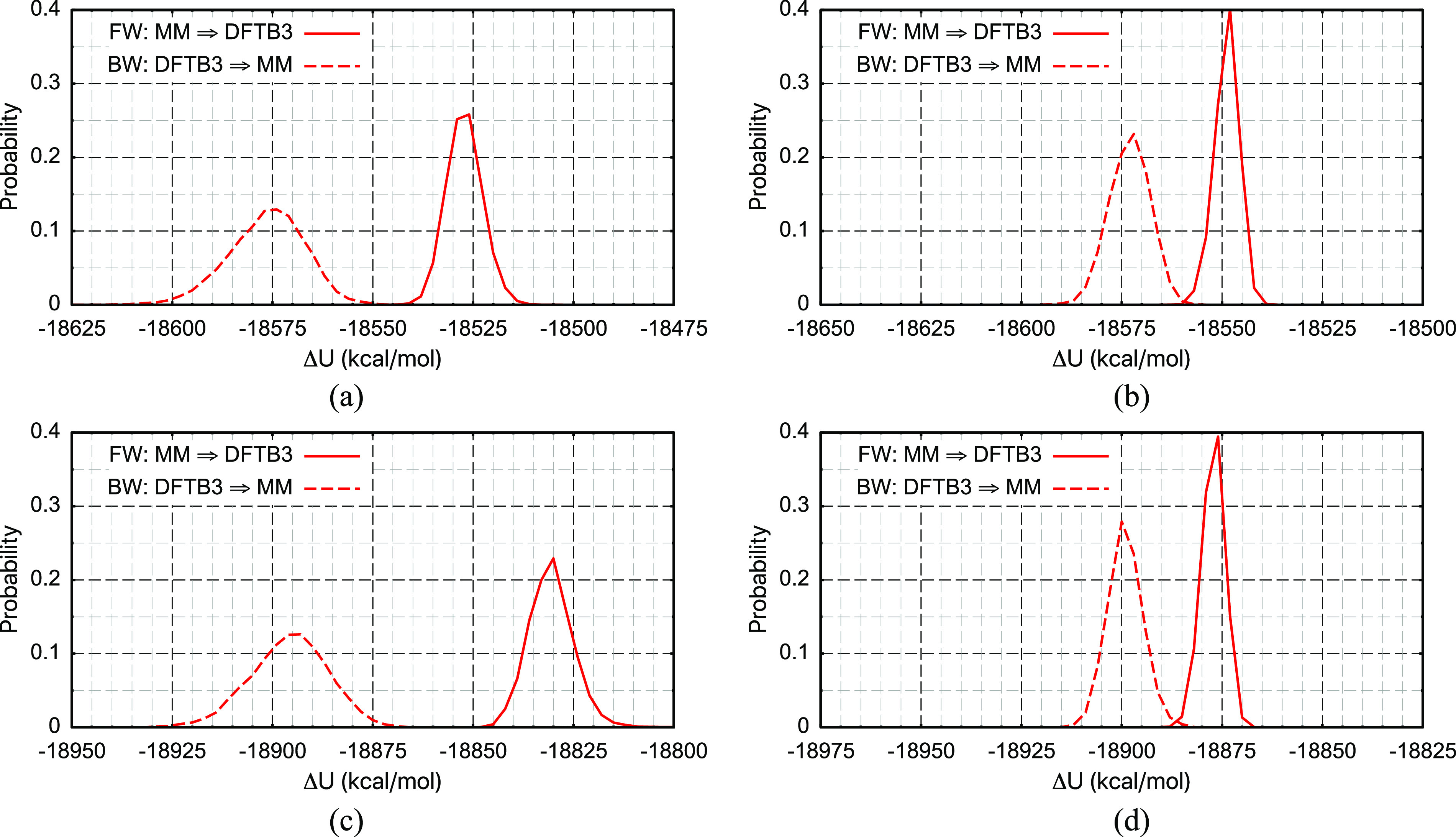
Energy difference (ΔULH) distribution for L = CHARMM36 and H = DFTB3/3OB/MM. The solid lines are for the “forward (FW)” distribution (i.e., sampling with L), and the dashed lines are for the “backward (BW)” distribution (i.e., sampling with H). The four solution cases are (a) a fully unrestrained blocked serine, (b) a blocked serine with a frozen structure, (c) a fully unrestrained methyl diphosphate (MDP), and (d) a MDP with a frozen structure.
TABLE I.
Computed ΔGL→H values (in kcal/mol) and distribution overlap scores for a blocked serine in water.a
| ΔGb | Overlap scoresc | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Low | High | Constraints | M-λ TI | 1-λ FEP | LRA | BAR | Staged | ΠLH | ΠHL | Overlap (%) | KHL | KLH |
| C36 | DFTB3 | Free | −18 545.3 | −18 541.2 | −18 545.5 | … | −18 545.4 | −4.04 | −4.09 | 0.01 | 0.58 | 0.30 |
| (0.6) | (0.5) | (2.9/1.2) | ||||||||||
| C36 | DFTB3 | Frozen | … | −18 557.1 | −18 559.1 | −18 559.1 | … | −2.03 | −1.64 | 0.22 | 0.79 | 0.55 |
| (0.6) | (0.5) | … | ||||||||||
| MULL | DFTB3 | Bond | … | −18 484.5 | −18 485.4 | −18 485.9 | … | −0.89 | 0.34 | 2.01 | 0.95 | 0.70 |
| (0.3) | (0.2) | … | ||||||||||
| MULL | DFTB3 | Frozen | … | −18 483.6 | −18 483.7 | −18 483.6 | … | 1.66 | 1.42 | 31.67 | 0.92 | 0.82 |
| (0.2) | (0.2) | (0.2) | ||||||||||
| DFTB3 | B3LYP | Free | … | −339 808.6 | −339 809.1 | −339 809.0 | … | −0.17 | −0.68 | 2.75 | 0.73 | 0.43 |
| (0.6) | (0.5) | … | ||||||||||
C36 = CHARMM36; DFTB3 = DFTB3/3OB/MM; and in MULL, the partial charges of the solute are taken as Mulliken charges from a DFTB3 calculation and held fixed during each MULL simulation.
M-λ TI: 11-λ window thermodynamic integration; 1-λ FEP: single window FEP based on L sampling; LRA: linear response approximation based on sampling with both end-states (L and H) windows; BAR: Bennet-Acceptance-Ratio based on the same sampling data from LRA; and Staged: staged transformation protocol introduced here. The statistical errors are estimated based on block averaging and are less than 0.1 kcal/mol for M-λ TI. For the staged transformation, the uncertainty is estimated based on 25 different choices of X0, combinations (see Table III for detailed data).
TABLE II.
Computed ΔGL→H values (in kcal/mol) and distribution overlap scores for a methyl diphosphate in water.a
| ΔG | Overlap scores | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Low | High | Constraints | M-λ TI | 1-λ FEP | LRA | BAR | Staged | ΠLH | ΠHL | Overlap % | KHL | KLH |
| C36 | DFTB3 | Free | −18 857.3 | −18 845.1 | −18 858.2 | … | −18 858.0 | −3.92 | −3.92 | 0.00 | 0.22 | 0.45 |
| (0.5) | (0.6) | (1.9) | ||||||||||
| C36 | DFTB3 | Frozen | … | −18 885.0 | −18 885.9 | −18 885.9 | … | −2.00 | −1.52 | 0.70 | 0.75 | 0.68 |
| (0.7) | (0.6) | … | ||||||||||
| MULL | DFTB3 | B + A | … | −18 813.3 | −18 814.9 | −18 814.9 | … | −0.22 | 0.88 | 2.11 | 0.77 | 0.93 |
| (0.3) | (0.3) | … | ||||||||||
| MULL | DFTB3 | Frozen | … | −18 820.4 | −18 820.3 | −18 820.3 | … | 2.69 | 2.95 | 84.75 | 0.81 | 0.83 |
| (0.1) | (0.1) | … | ||||||||||
| DFTB3 | B3LYP | Free | … | −765 491.4 | −765 494.1 | −765 493.8 | … | −1.20 | −1.63 | 0.17 | 0.33 | 0.02 |
| (0.3) | (0.3) | … | ||||||||||
| DFTB3 | B3LYP | B + A | … | −765 501.7 | −765 502.6 | −765 502.3 | … | 0.66 | 0.09 | 5.36 | 0.80 | 0.90 |
| (0.2) | (0.2) | (0.2) | ||||||||||
To reveal whether the lack of overlap is largely dominated by the intra-solute degrees of freedom or by the non-bonded parameters at the low (CHARMM36) level, we first reexamine the ΔU distributions with simulations in which the solute structure is frozen. As shown in Figs. 7(b) and 7(d), freezing the intra-solute degrees of freedom improves the ΔU overlap for both cases analyzed; the improvement is visibly more transparent for MDP, suggesting that the CHARMM36-CGENFF79 model leads to considerably different conformations for MDP compared to DFTB3/3OB. Examination of snapshots suggests that the difference largely lies in the bond angles and several dihedrals. Correspondingly, various overlap scores improve significantly; the Π scores, for example, increase from ∼−4 for the unconstrained simulations to ∼−2 for the frozen-solute simulations.
Even with the solute structure entirely frozen (thus fully consistent between L and H simulations), the ΔU distribution overlap is minimal, suggesting that there are significant differences in the non-bonded interactions between the solute and the solvent in the L and H simulations. The situation can be substantially improved by replacing the MM partial charges at the L level with Mulliken charges calculated at the DFTB3/3OB/MM level based on a single random snapshot, as shown in Figs. 8(a) and 8(b) for serine and MDP, respectively; the Π scores are now positive and in the range of ∼1.5 to 3. Since the Mulliken charges in these intermediate models are not updated during the simulation, the excellent ΔU overlaps suggest that the lack of electronic polarization per se is not a major factor that impacts the distribution overlap, even for a highly charged and polarizable solute such as MDP. However, the overlap deteriorates significantly when the solute structure is no longer frozen with only bonds constrained with SHAKE [Figs. 8(c) and 8(d)], highlighting the importance of capturing the structural dependence of charge distribution. In the case of MDP, constraining the covalent bonds and restraining the bond angles help improve the ΔU distribution overlap considerably.
FIG. 8.
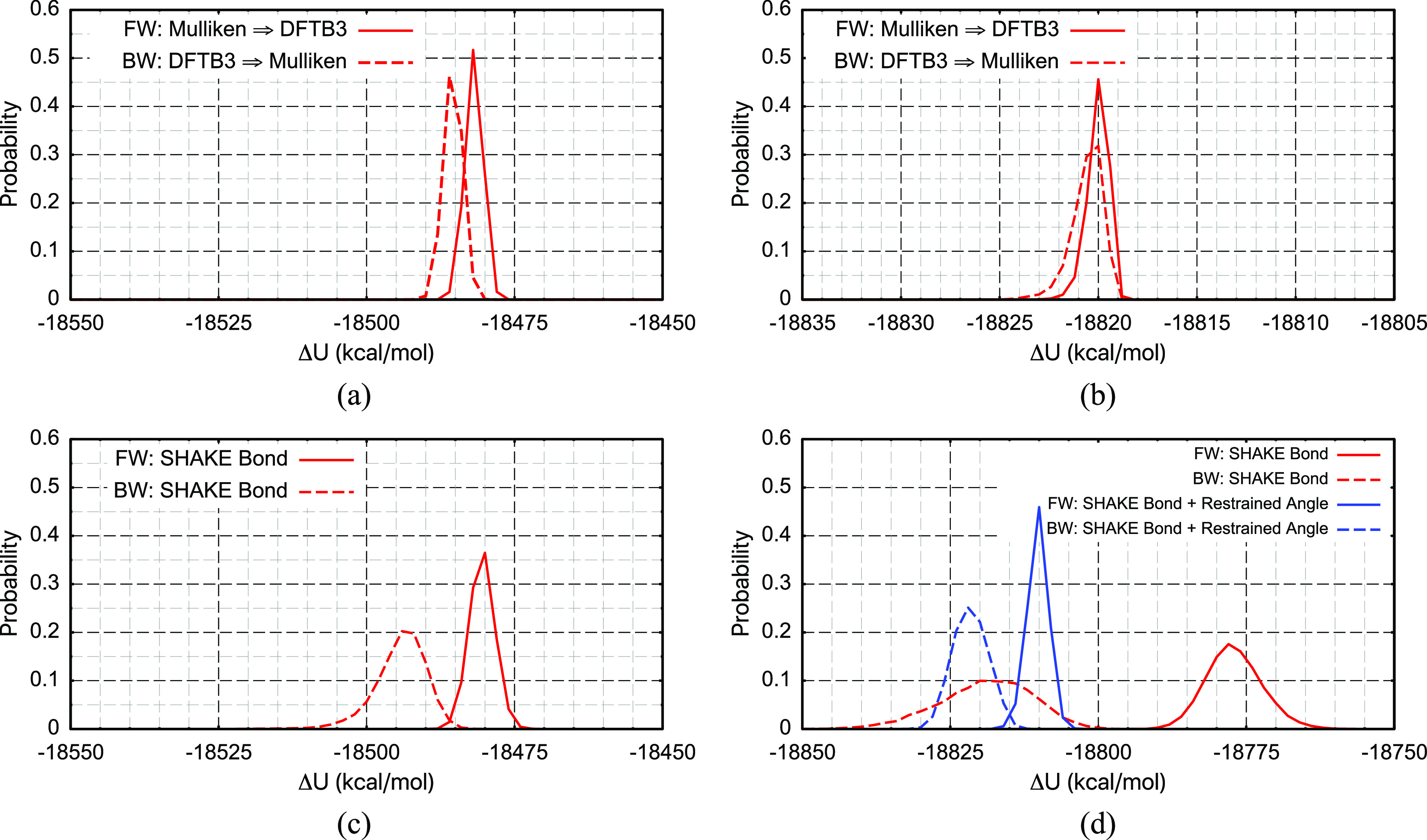
Similar to Fig. 7, but the partial charges on the MM solute are replaced by Mulliken charges from a DFTB3/3OB/MM calculation; note that these Mulliken charges are held fixed in each trajectory. The four solution cases are (a) a blocked serine with a frozen structure, (b) a MDP with a frozen structure, (c) a blocked serine with all covalent bonds constrained with SHAKE, and (d) a MDP with all covalent bonds constrained using SHAKE and free (red) or restrained (blue) bond angles.
When the L is DFTB3/3OB/MM and H is B3LYP/6-31G(d)/MM, there is a decent (∼3%) overlap in ΔU distribution for serine in water, but the overlap is minimal (∼0.17%) for MDP [Figs. 9(a) and 9(b)]; the Π scores are small negative values and ∼−1, respectively. With constrained bond length and restrained bond angles, as shown in Fig. 9(c), the overlap improves substantially for MDP to ∼5.4%; the Π scores also become positive (Table II).
FIG. 9.
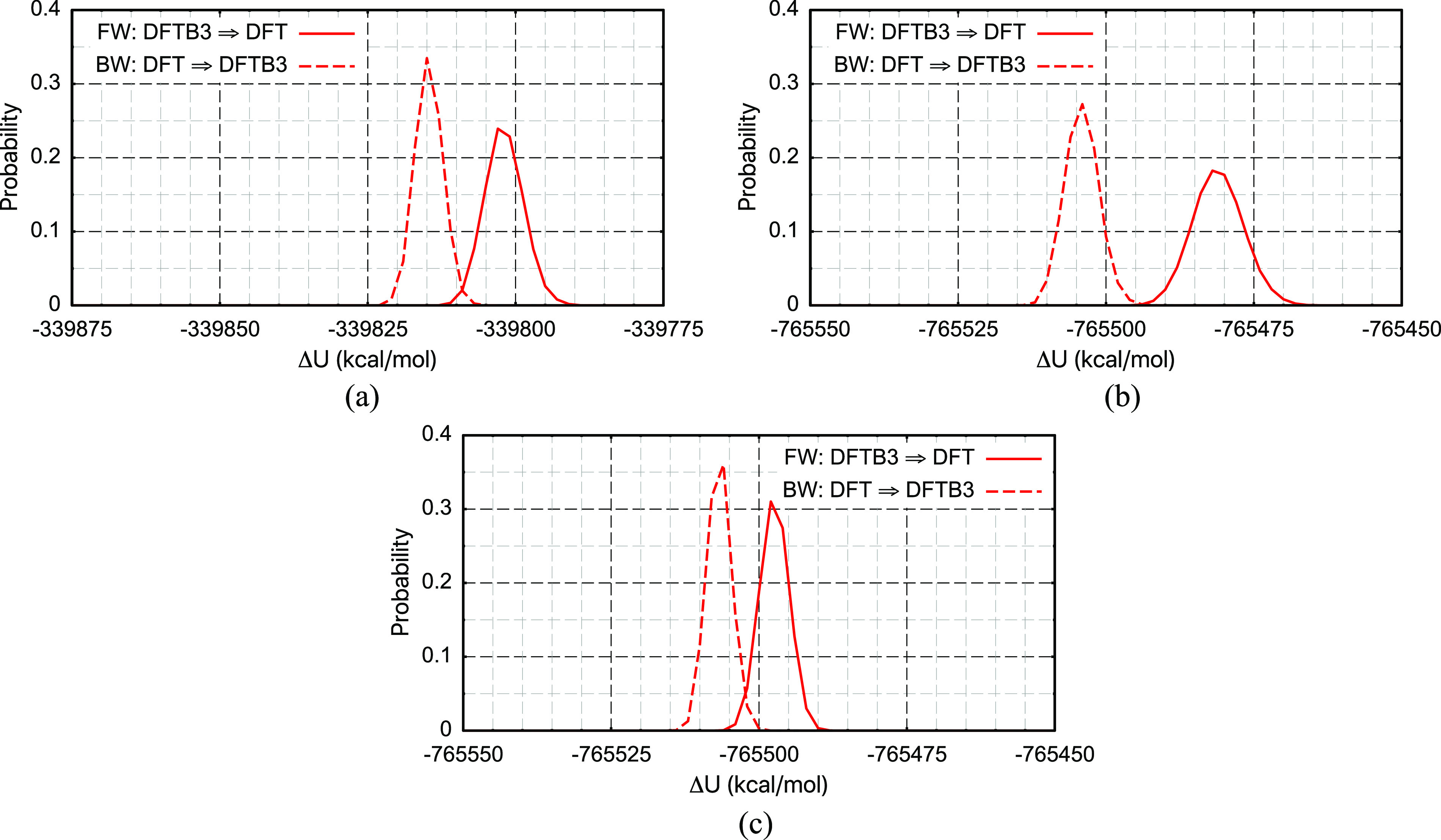
Similar to Fig. 7 but with L = DFTB3/3OB/MM and H = B3LYP/6-31G(d)/MM. The three solution cases studied are (a) a fully unrestrained blocked serine, (b) a fully unrestrained MDP, and (c) a MDP with covalent bonds constrained using SHAKE and bond angles restrained.
In short, the results in this subsection indicate that both bonded and non-bonded degrees of freedom may contribute to modulate the distribution overlap between L and H levels of theory. With a decent QM level as L, it is expected that the overall charge distribution is reasonably represented compared to H, even for a highly charged and polarizable molecule such as MDP. Small differences in stiff bonded degrees of freedom such as bond stretch and bond angle can lead to a poor distribution overlap, which can be improved with constraints/restraints. When the L level is MM, the non-bonded interactions might be sufficiently different from the H level, and thus, constraining/restraining stiff intra-solute degrees of freedom alone may not be sufficient for improving the distribution overlap to a satisfactory level. For the test cases studied here, replacing the MM charges with a single set of Mulliken charges improves the overlap significantly, especially when combined with constraining/restraining stiff intra-solute degrees of freedom.
B. Staged transformation is able to complete the thermodynamic cycle
In Sec. III A, we examine whether the staged transformation approach is able to reproduce the ΔGL→H result of brute-force multi-λ thermodynamic integration for free serine and MDP in solution. Prior to the discussion, we first compare ΔGL→H computed with various approximations for the different simulations used to explore the ΔU overlap in the last subsection; this helps better illustrate the impact of the distribution overlap on the reliability of estimated ΔGL→H.
With a free solute in water, the distribution overlap is poor for serine and MDP for both L/H combinations tested here; accordingly, the simple 1-λ FEP result is significantly different from other estimators (Tables I and II). For a free serine in water, L = CHARMM36 and H = DFTB3/3OB/MM, the 1-λ FEP value differs by ∼4 kcal/mol from the multi-λ TI result; the difference is even larger, ∼13 kcal/mol for MDP. With L = DFTB3/3OB/MM and H = B3LYP/6-31G(d)/MM, the overlap is minimal for MDP in water; thus, 1-λ FEP differs from a linear response approximation (LRA) estimator by ∼3 kcal/mol. By contrast, the overlap is appreciable (∼2.75%) for a free serine in water, and 1-λ FEP agrees with LRA to ∼0.5 kcal/mol.
For all other cases explored here, which involves either changing the MM charges or confining/restraining stiff intra-solute degrees of freedom, improvement of the ΔU overlap is highly correlated with the level of consistency among 1-λ FEP, LRA, and BAR estimators. As far as the percentile of the overlap is higher than 1%, the three estimators are within 1 kcal/mol (see Tables I and II). Another observation is that the LRA estimator is robust for the two test systems studied here. Even for the cases of free solutes in water for which the distribution overlap between L/H is poor, the LRA estimator is ∼1 kcal/mol from the brute-force multi-λ simulation; this is rather remarkable considering that the error for 1-λ FEP can be as large as 13 kcal/mol. This observation resonates with several previous studies that also highlighted the significant gain in conducting sampling on the H level,18,20,68 even in cases where BAR has difficulty in convergence.
To examine the effectiveness and limitations of the staged transformation approach, we study the cases of fully unrestrained small solutes (serine and MDP) in water with L = CHARMM36 and H = DFTB3/3OB/MM for which the reference ΔGL→H values are readily computed using brute-force multi-λ TI simulations. From the results shown in Tables I and II, the staged transformation approach indeed gives an average result consistent with the multi-λ TI reference value for both Ser and MDP in water; the difference appears to be less than 1 kcal/mol. However, we note that the staged transformation approach requires the determination of equilibrium or representative structures at the L (X0) and H () levels in the “confinement step.” Therefore, it is important to understand the sensitivity of the result to the choice of these reference structures, especially if the confinement free energies are not explicitly computed, i.e., the approximation is that they cancel out perfectly between the L and H levels.
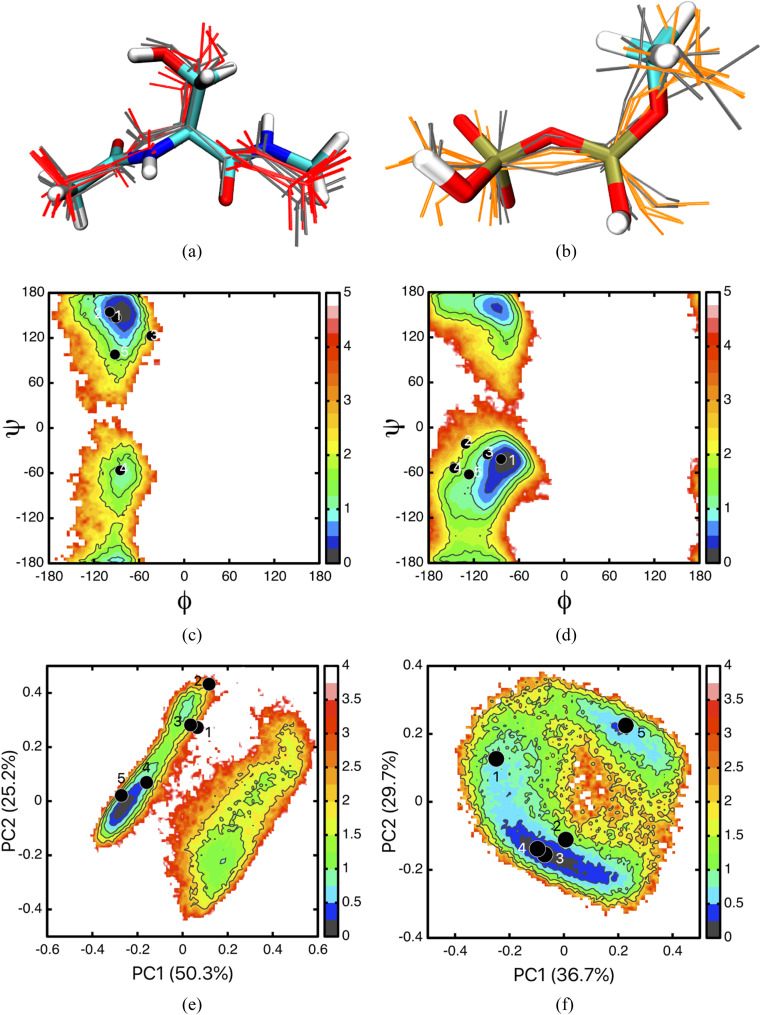
To this end, for each test case, we have sampled 25 different combinations of X0 and by choosing five reference structures at each level of theory. Ideally, X0 and should be selected by identifying structures near the free energy minima at L and H levels of theory [Fig. 3(b)], which requires projecting the free energy surface onto different dimensions using, for example, principal component analysis.80 In this work, to test the robustness of the result, we chose X0 and by simply identifying structures that have the lowest potential energies for the solute, including both intra-solute and solute–solvent interactions. As illustrated in Figs. 10(c)–10(f), some of the selected structures are indeed close to the free energy minima, while others are not. The spread of the conformations, as shown by the superpositions in Figs. 10(a) and 10(b), is more modest for the blocked serine than MDP; the root mean squared difference (RMSD) among the different structures is ∼0.05 Å, with some dihedral angles differing by ∼20° for the blocked serine and ∼40° for MDP. In principle, the staged transformation approach ought to be applicable to any reference structure (X0 and ) combinations, although the assumption of canceled is expected to work better for X0 and close to the respective free energy minimum.
FIG. 10.
Distribution of X0, for a blocked serine and MDP. (a) and(b) illustrate the superposition of the structures; one X0 is shown in licorice and colored based on element, the rest X0 shown in gray lines; structures are shown in a different color in line form. [(c) and (d)] Φ − Ψ free energy surfaces of a blocked serine in solution with (c) CHARMM36 and (d) DFTB3-Mulliken charges, the latter better resembles the DFTB3/3OB/CHARMM result (see, e.g., Ref. 53). [(e) and (f)] Free energy map projected onto the first two principal components for a MDP in solution using (e) CHARMM36 and (f) DFTB3/3OB/CHARMM. The dots indicate the locations of X0, , and the labels correspond to those used in Table III.
The results for these 25 combinations are shown in Tables III and IV, which illustrate several points worth noting. First, without considering the free energy components associated with changing the confined degrees of freedom from X0 to , the free energy quantity is sensitive to the choice of ; the magnitude of variation is ∼6 kcal/mol for serine and ∼8 kcal/mol for MDP. More importantly, the magnitude of can be substantially different from the true ΔGL→H value, by as much as ∼20 kcal/mol for MDP. Indeed, the “reorganization free energy,” , ranges from 3 kcal/mol to 11 kcal/mol for the blocked serine, and 12 kcal/mol to 25 kcal/mol for MDP (see numbers before slashes in Tables III and IV). Second, for the combination of X0, that are close to the free energy minima (highlighted in bold in Tables III and IV), at least based on the 2D projection in Fig. 10, the computed ΔGL→H values are indeed close to the m-λ TI results (−18 545.3 kcal/mol for serine and −18 857.3 kcal/mol for MDP), although the difference can be as large as 3 kcal/mol. Finally, comparing the ΔGL→H values for the 25 combinations, we see that the results are mixed. On one hand, the results are largely consistent, for example, while the values may differ by as much as 8 kcal/mol, once is included, the estimated ΔGL→H values are closer in magnitude with a standard deviation of 1.9 kcal/mol. On the other hand, for the serine case, one particular choice of leads to consistently different ΔGL→H values compared to the other 20 combinations by as much as ∼6 kcal/mol. As shown in Fig. 10(d), the location of this reference structure (labeled 5) is not much different from the other four reference structures in the ϕ, ψ plane. On the other hand, the five reference structures differ in all degrees of freedom (they were collected from a fully unrestrained simulation), and projection in Fig. 10(d) reflects only two dihedral angles. Evidently, additional studies are required to develop better ways to determine optimal reference structures, such as using an efficient clustering analysis. Nevertheless, the current analysis highlights the importance of collecting multiple reference structures at both L and H levels to explicitly evaluate the robustness of the free energy results.
TABLE III.
Computed ΔGL→H values (in kcal/mol) for a fully unrestrained blocked serine in solution from the staged transformation approach using different combinations of confined reference structures (i.e., X0, ).a
| sample 1 | sample 2 | sample 3 | sample 4 | sample 5 | |
|---|---|---|---|---|---|
| −18 550.6 ± 0.3 | −18 551.9 ± 0.2 | −18 553.9 ± 0.3 | −18 556.3 ± 0.5 | −18 550.2 ± 0.2 | |
| X0 sample 1 | 4.5/−18 546.1b | 5.0/−18 546.8 | 9.6/−18 544.3 | 11.1/−18 545.2 | 11.1/−18 539.0 |
| X0 sample 2 | 2.4/−18 548.2 | 2.9/−18 548.9 | 7.6/−18 546.3 | 9.0/−18 547.3 | 9.1/−18 541.1 |
| X0 sample 3 | 3.9/−18 546.7 | 4.5/−18 547.4 | 9.1/−18 544.8 | 10.6/−185 45.7 | 10.6/−18 539.6 |
| X0 sample 4 | 3.1/−18 547.5 | 3.7/−18 548.2 | 8.3/−18 545.7 | 9.7/−18 546.5 | 9.8/−18 540.4 |
| X0 sample 5 | 3.0/−18 547.6 | 3.5/−18 548.3 | 8.2/−18 545.8 | 9.6/−18 546.7 | 9.6/−18 540.5 |
| Avg.c | −18 545.4 ± 2.9 | (−18 546.7 ± 1.2) |
See text for the discussion of the selection of the confined structures. The first row lists the values of , which depends only on the choices of R0′, as discussed in Sec. II D 2, we introduced an intermediate level of model (M) that uses the CHARMM36 force field, except that the partial charges are replaced by DFTB3/3OB Mulliken charges computed for a single snapshot in solution; thus, , where the L/M conversion is done with multi-λ TI due to the low computational cost, and M/H conversion is done with 1-λ FEP due to the favorable distribution overlap illustrated in Fig. 8. For other entries, the value before the slash is , and the value after the slash is .
For this specific combination, the confined structures (X0, ) are close to the minima on the L/H free energy surface based on the 2D projection [see Figs. 10(c) and 10(d)].
The average ΔGL→H value is reported as the “Stage” entry in Table I; values with parentheses are the results without including data from R0′ sample 5 [see Fig. 10(d)], which leads to consistently different values (see text).
TABLE IV.
Computed ΔGL→H values (in kcal/mol) for a fully unrestrained methyl diphosphate in solution from the staged transformation approach using different combinations of confined reference structures (i.e., X0, ).a
| sample 1 | sample 2 | sample 3 | sample 4 | sample 5 | |
|---|---|---|---|---|---|
| −18 878.6 ± 0.3 | −18 878.6 ± 0.2 | −18 876.4 ± 0.2 | −18 872.8 ± 0.2 | −18 880.5 ± 0.3 | |
| X0 sample 1 | 23.7/−18 854.8 | 21.6/−18 857.0 | 17.7/−18 858.7 | 16.0/−18 856.8 | 24.7/−18 855.8 |
| X0 sample 2 | 22.9/−18 855.7 | 20.8/−18 857.8 | 16.9/−18 859.5 | 15.2/−18 857.6 | 23.9/−18 856.6 |
| X0 sample 3 | 20.0/−18 858.6 | 17.8/−18 860.7 | 13.9/−18 862.4 | 12.3/−18 860.5 | 20.9/−18 859.6 |
| X0 sample 4 | 23.2/−18 855.3 | 21.1/−18 857.5 | 17.2/−18 859.1 | 15.5/−18 857.2 | 24.2/−18 856.3 |
| X0 sample 5 | 21.7/−18 856.9 | 19.6/−18 859.0 | 15.7/−18 860.7b | 14.0/−18 858.8b | 22.6/−18 857.8 |
| Avg. | −18 858.0 ± 1.9 |
See footnote a of Table III for the format of the entries. The average ΔGL→H value is reported as the “Stage” entry in Table II.
For these specific combinations, the confined structures (X0, ) are close to the minima on the L/H free energy surface based on the 2D projection [see Figs. 10(e) and 10(f)].
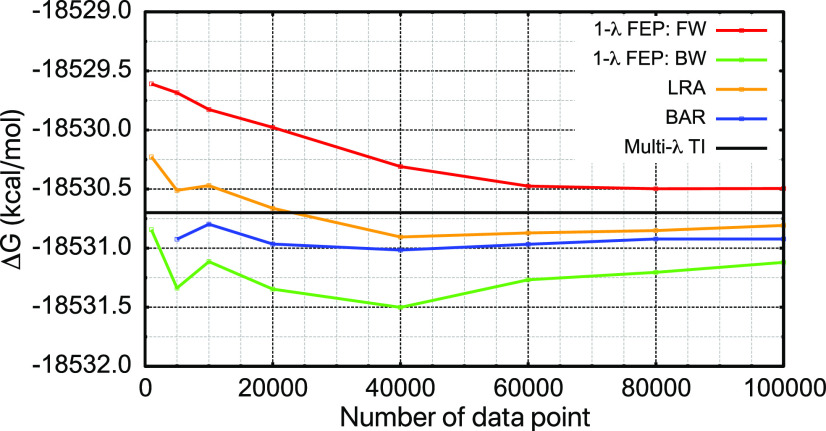
C. Length of sampling at the low- and high-level of theory
Finally, we briefly comment on the minimal amount of sampling needed at the L and H levels of theory for the test systems examined here. For sampling at the low level, we use the example of a frozen Ser in water, which exhibits the adequate distribution overlap between L = CHARMM36 and H = DFTB3/3OB/MM [Fig. 7(b)]. We examine the convergence of various free energy estimators for with respect to the number of data points included. As shown in Fig. 11, even for this favorable case, at least 20 000 data points are necessary for good statistical convergence; this is in line with previous analysis.20,25,34,53 As expected, the convergence behavior for BAR and LRA, which involve sampling at both L and H levels, is superior to the one-step FEP using either L or H sampling alone.
FIG. 11.
Convergence behavior of different free energy estimators for a blocked serine with a frozen structure in water with respect to the number of data points included. The L is CHARMM36, and the H is DFTB3/3OB/MM. Note that the reference M-λ TI value is different from that shown in Table I because a different serine structure is adopted in this set of calculations.
Another relevant question for multi-level free energy simulation is the time required to equilibrate at the H level, provided that adequate equilibration has already been done at the L level. For the computationally expensive H level, minimizing the amount of sampling is crucial to the practical efficiency. Here, we advocate the use of time-dependent Stokes shift, a quantity borrowed from the condensed phase spectroscopy literature.81,82 The normalized dynamic Stokes shift is defined as
| (14) |
where ΔU(t) is the energy difference between the L/H levels at time t in the H level simulation that started (i.e., t = 0) with an equilibrated snapshot from the L level simulation. The quantity S(t) reflects the time scale for the environment to respond to the change of the solute potential function from L to H.
Specifically, for the two test systems examined here, we examine the combination of L = CHARMM36 and H = DFTB3/3OB/MM and we compare the situation of free solutes and frozen solutes, which are expected to correspond to the limiting behaviors of the solvent response. To compute S(t), we conduct 30 independent H level trajectories for each case examined.
As shown in Fig. 12, with a fully flexible solute, solvent response to the change of the solute potential function from CHARMM36 to DFTB3/3OB involves at least two time scales, and the longer time scale is on the order of 20 ps. Although MDP tends to exhibit a poorer distribution overlap between L and H as compared to Ser (see Fig. 7), the solvent response time is similar for the two solutes. With a frozen solute, the solvent response to the change of the solute potential function is much faster, even the longer time scale is merely a few picoseconds. These calculations suggest that with adequately equilibrated simulations at the L level for modest size solutes (QM regions), the amount of equilibration at the H level is likely limited to tens of picoseconds, which are readily affordable nowadays. Whether this is the case for a heterogeneous environment such as the active site of proteins remains to be examined in the future.
FIG. 12.
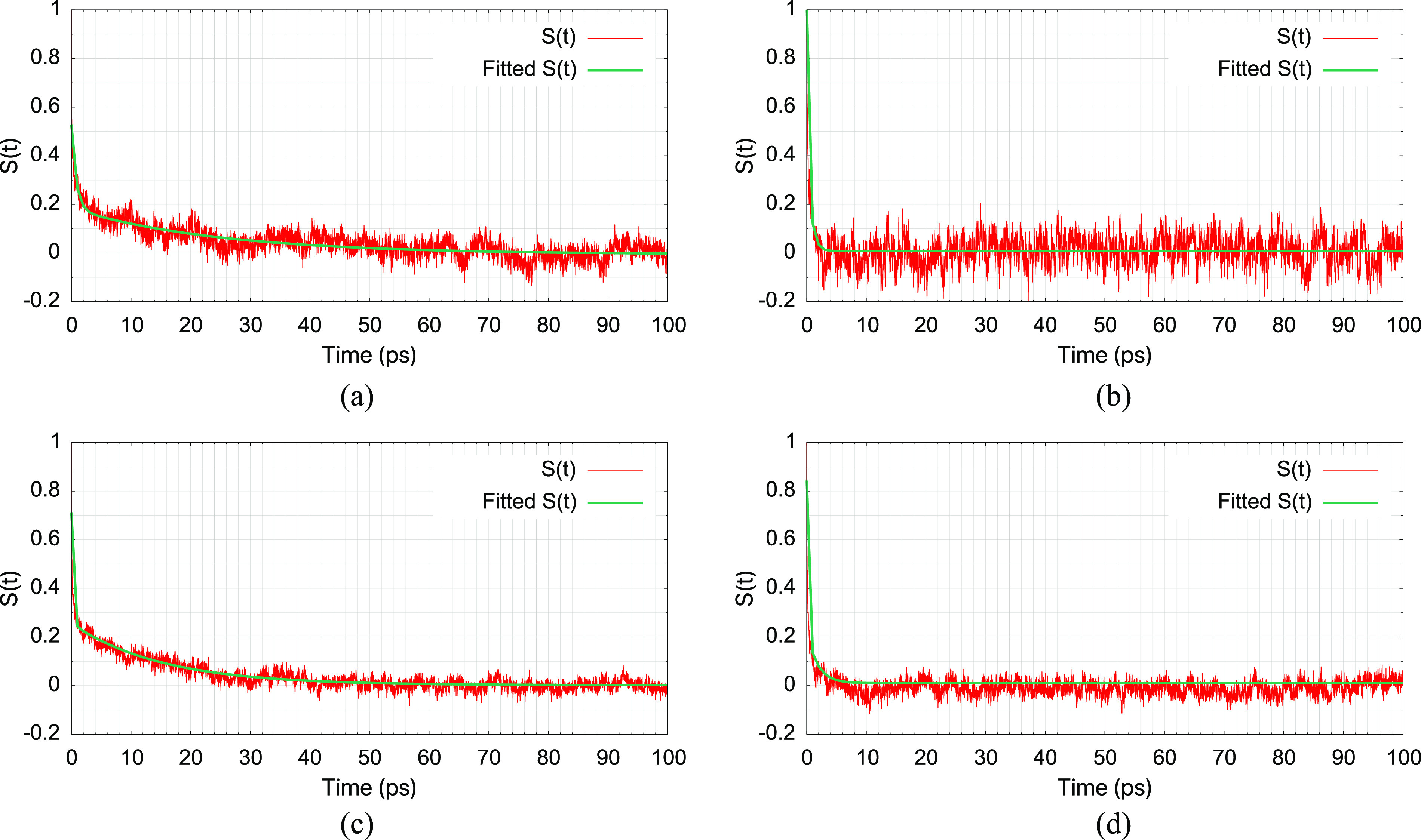
Normalized dynamic Stokes shift computed for L = CHARMM36 and H = DFTB3/3OB/MM simulations. The four solution cases examined are (a) a fully unrestrained blocked serine, (b) a blocked serine with a frozen structure, (c) a fully unrestrained methyl diphosphate (MDP), and (d) a MDP with a frozen structure. The longer time constants from bi-exponential fits are 25.1 ps, 0.7 ps, 15.2 ps, and 1.8 ps for (a)–(d)], respectively. Similar results are found for L = DFTB3/3OB/MM and H = B3LYP/6-31G(d)/MM for the cases of frozen solutes.
IV. CONCLUDING REMARKS
There has been tremendous interest in combining different levels of theory to obtain reliable thermodynamic properties for condensed phase systems. It has widely been recognized that the key to such multi-level free energy simulations is to ensure a favorable distribution overlap between different levels of theory. Therefore, the fundamental challenge is to identify the major degrees of freedom that lead to gaps in the distributions at the L and H levels of theory and then develop approaches that circumvent convergence difficulties due to the lack of adequate distribution overlap.
In this work, we have explored a strategy that converts from the L to H level of theory in a staged fashion, so as to ensure a favorable distribution overlap between different models along the way. The key philosophy behind the strategy is to treat the problematic degrees of freedom (denoted as X in this work), which lead to distribution gaps, differently from the rest; the stiff degrees of freedom in X are treated with constraints (for bond lengths) or hard restraints (for bond angles), softer degrees of freedom (e.g., dihedrals) are treated with biasing potentials, and non-bonded degrees of freedom (e.g., partial charges) are treated by introducing an intermediate level of model (e.g., replacing MM charges with Mulliken/ESP charges).
Importantly, different models are connected through well-defined steps in a thermodynamic cycle, and corresponding free energy components are evaluated explicitly; this is an essential difference between our approach with more approximate schemes that compute, for example, only interaction energies. Test calculations using model compounds in solution indicate that the free energy components for connecting different levels of theory (e.g., for the X0/ transformation) can be large in magnitude (∼20 kcal/mol) and therefore essential to evaluate explicitly. While the staged transformation approach introduces additional steps, most of the free energy component calculations are done at the low level of theory and therefore do not significantly increase the computational cost. In fact, one way of describing our approach is starting with the L level conformational ensemble, progressively building up the optimal conformational ensemble that exhibits a favorable distribution overlap with the high-level of theory such that the amount of expensive H calculations is kept at a minimum.
As a proof of concept, two simple but non-trivial solution model systems are used to demonstrate that the staged transformation scheme is able to reproduce brute-force multi-window thermodynamic integration results for the L to H conversion with encouraging accuracy. For example, for a charged molecule (methyl diphosphate) in solution, free energy perturbation using only L level trajectories has a large error of ∼13 kcal/mol, the staged transformation scheme leads to results within 1 kcal/mol–2 kcal/mol from M-λ TI calculations. We note that in the current implementation, we do make the approximation that confining the stiff degrees of freedom in X has similar free energy costs at the L and H levels of theory (i.e., ); considering the localized nature of these degrees of freedom, the errors of the approximation are likely small, as supported by the favorable results for the staged transformation calculations, although this needs to be quantitatively evaluated for more complex systems in the future.
To apply the staged approach to more complex systems with a large number of atoms treated at multiple levels, the two major bottlenecks concern the systematic identification of the X degrees of freedom and the selection of appropriate reference structures at different levels of theory (i.e., X0, ). For the former issue, creative solutions likely involve combining multiple short simulations with machine learning algorithms for identifying variables that lead to large distribution gaps between different levels of theory, similar in spirit to the problem of optimizing collective variables in free energy simulations.83 In fact, it is conceivable that machine learning approaches can be used to simultaneously learn the difference between the different levels of theory and the key coordinates responsible for the distribution gaps. In this way, the staged transformation approach and Δ-learning51 can be integrated so that convergence in ΔGL→H can be achieved with only modest improvement of the low-level method based on a limited amount of high-level data. For the issue of choosing reference structures, efficient clustering algorithms and dimensional reduction schemes should be explored and compared; test calculations illustrate the importance of sampling multiple reference structures to evaluate the robustness of the result. For cases that involve multiple free energy basins, it is natural to employ a divide-and-conquer strategy that requires evaluating free energy difference at the L/H levels of theory for the different basins separately.84
Finally, we stress the importance of conducting some degree of sampling at the H level of theory. This helps to explicitly evaluate the distribution overlap between the different models, and even a simple LRA model can be a substantial improvement over free energy perturbation that relies on the L level sampling alone, as shown by the model systems studied here. Along this line, monitoring the energy gap correlation function (i.e., the dynamic Stokes shift) can be an effective way to evaluate equilibration at the expensive H level, starting with a well-equilibrated L level ensemble.
DATA AVAILABILITY
The data that support the findings of this study are available from the corresponding author upon reasonable request.
ACKNOWLEDGMENTS
This work was supported by a grant from the NIH to QC (Grant No. R01 GM106443). Computational resources from the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the NSF (Grant No. OCI-1053575), are greatly appreciated; part of the computational work was performed on the Shared Computing Cluster, which is administered by Boston University’s Research Computing Services (www.bu.edu/tech/support/research/).
Note: This paper is part of the JCP Special Topic on Classical Molecular Dynamics (MD) Simulations: Codes, Algorithms, Force Fields, and Applications.
REFERENCES
- 1.Warshel A. and Levitt M., “Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme,” J. Mol. Biol. 103, 227–249 (1976). 10.1016/0022-2836(76)90311-9 [DOI] [PubMed] [Google Scholar]
- 2.Field M. J., Bash P. A., and Karplus M., “A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations,” J. Comput. Chem. 11, 700–733 (1990). 10.1002/jcc.540110605 [DOI] [Google Scholar]
- 3.Lipkowitz K. B. and Boyd D. B., in Reviews in Computational Chemistry VII, edited by Gao J. (VCH, New York, 1995), p. 119. [Google Scholar]
- 4.Monard G. and Merz K. M., “Combined quantum mechanical/molecular mechanical methodologies applied to biomolecular systems,” Acc. Chem. Res. 32, 904–911 (1999). 10.1021/ar970218z [DOI] [Google Scholar]
- 5.Friesner R. A. and Guallar V., “Ab initio QM and QM/MM methods for studying enzyme catalysis,” Annu. Rev. Phys. Chem. 56, 389–427 (2005). 10.1146/annurev.physchem.55.091602.094410 [DOI] [PubMed] [Google Scholar]
- 6.Riccardi D., Schaefer P., Yang Y., Yu H., Ghosh N., Prat-Resina X., König P., Li G., Xu D., Guo H., Elstner M., and Cui Q., “Development of effective quantum mechanical/molecular mechanical (QM/MM) methods for complex biological processes,” J. Phys. Chem. B 110, 6458–6469 (2006). 10.1021/jp056361o [DOI] [PubMed] [Google Scholar]
- 7.Senn H. M. and Thiel W., “QM/MM studies of enzymes,” Curr. Opin. Chem. Biol. 11, 182–187 (2007). 10.1016/j.cbpa.2007.01.684 [DOI] [PubMed] [Google Scholar]
- 8.Hu H. and Yang W., “Free energies of chemical reactions in solution and in enzymes with ab initio quantum mechanics/molecular mechanics methods,” Annu. Rev. Phys. Chem. 59, 573–601 (2008). 10.1146/annurev.physchem.59.032607.093618 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Brunk E. and Rothlisberger U., “Mixed quantum mechanical/molecular mechanical molecular dynamics simulations of biological systems in ground and electronically excited states,” Chem. Rev. 115, 6217–6263 (2015). 10.1021/cr500628b [DOI] [PubMed] [Google Scholar]
- 10.Gao J. and Truhlar D. G., “Quantum mechanical methods for enzyme kinetics,” Annu. Rev. Phys. Chem. 53, 467–505 (2002). 10.1146/annurev.physchem.53.091301.150114 [DOI] [PubMed] [Google Scholar]
- 11.Gao J., Ma S., Major D. T., Nam K., Pu J., and Truhlar D. G., “Mechanisms and free energies of enzymatic reactions,” Chem. Rev. 106, 3188–3209 (2006). 10.1021/cr050293k [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pu J., Gao J., and Truhlar D. G., “Multidimensional tunneling, recrossing, and the transmission coefficient for enzymatic reactions,” Chem. Rev. 106, 3140–3169 (2006). 10.1021/cr050308e [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ryde U., “QM/MM calculations on proteins,” in Methods in Enzymology (Academic Press, 2016), Vol. 577, pp. 119–158. [DOI] [PubMed] [Google Scholar]
- 14.Shaik S., Cohen S., Wang Y., Chen H., Kumar D., and Thiel W., “P450 enzymes: Their structure, reactivity, and selectivity-modeled by QM/MM calculations,” Chem. Rev. 110, 949–1017 (2010). 10.1021/cr900121s [DOI] [PubMed] [Google Scholar]
- 15.Lonsdale R. and Mulholland A., “QM/MM modelling of drug-metabolizing enzymes,” Curr. Top. Med. Chem. 14, 1339–1347 (2014). 10.2174/1568026614666140506114859 [DOI] [PubMed] [Google Scholar]
- 16.Bernstein N., Kermode J. R., and Csányi G., “Hybrid atomistic simulation methods for materials systems,” Rep. Prog. Phys. 72, 026501 (2009). 10.1088/0034-4885/72/2/026501 [DOI] [Google Scholar]
- 17.Claeyssens F., Harvey J. N., Manby F. R., Mata R. A., Mulholland A. J., Ranaghan K. E., Schütz M., Thiel S., Thiel W., and Werner H.-J., “High-accuracy computation of reaction barriers in enzymes,” Angew. Chem., Int. Ed. 45, 6856–6859 (2006). 10.1002/anie.200602711 [DOI] [PubMed] [Google Scholar]
- 18.Rosta E., Klähn M., and Warshel A., “Towards accurate ab initio QM/MM calculations of free-energy profiles of enzymatic reactions,” J. Phys. Chem. B 110, 2934–2941 (2006). 10.1021/jp057109j [DOI] [PubMed] [Google Scholar]
- 19.Heimdal J. and Ryde U., “Convergence of QM/MM free-energy perturbations based on molecular-mechanics or semiempirical simulations,” Phys. Chem. Chem. Phys. 14, 12592 (2012). 10.1039/c2cp41005b [DOI] [PubMed] [Google Scholar]
- 20.Lu X., Fang D., Ito S., Okamoto Y., Ovchinnikov V., and Cui Q., “QM/MM free energy simulations: Recent progress and challenges,” Mol. Simul. 42, 1056–1078 (2016). 10.1080/08927022.2015.1132317 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Luzhkov V. and Warshel A., “Microscopic models for quantum mechanical calculations of chemical processes in solutions: LD/AMPAC and SCAAS/AMPAC calculations of solvation energies,” J. Comput. Chem. 13, 199–213 (1992). 10.1002/jcc.540130212 [DOI] [Google Scholar]
- 22.Gao J., “Absolute free energy of solvation from Monte Carlo simulations using combined quantum and molecular mechanical potentials,” J. Phys. Chem. 96, 537–540 (1992). 10.1021/j100181a009 [DOI] [Google Scholar]
- 23.Martí S., Moliner V., and Tuñón I., “Improving the QM/MM description of chemical processes: A dual level strategy to explore the potential energy surface in very large systems,” J. Chem. Theory Comput. 1, 1008–1016 (2005). 10.1021/ct0501396 [DOI] [PubMed] [Google Scholar]
- 24.Retegan M., Martins-Costa M., and Ruiz-López M. F., “Free energy calculations using dual-level Born–Oppenheimer molecular dynamics,” J. Chem. Phys. 133, 064103 (2010). 10.1063/1.3466767 [DOI] [PubMed] [Google Scholar]
- 25.König G., Hudson P. S., Boresch S., and Woodcock H. L., “Multiscale free energy simulations: An efficient method for connecting classical MD simulations to QM or QM/MM free energies using non-Boltzmann Bennett reweighting schemes,” J. Chem. Theory Comput. 10, 1406–1419 (2014). 10.1021/ct401118k [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Polyak I., Benighaus T., Boulanger E., and Thiel W., “Quantum mechanics/molecular mechanics dual Hamiltonian free energy perturbation,” J. Chem. Phys. 139, 064105 (2013). 10.1063/1.4817402 [DOI] [PubMed] [Google Scholar]
- 27.Li P., Jia X., Pan X., Shao Y., and Mei Y., “Accelerated computation of free energy profile at ab initio quantum mechanical/molecular mechanics accuracy via a semi-empirical reference potential. I. Weighted thermodynamics perturbation,” J. Chem. Theory Comput. 14, 5583–5596 (2018). 10.1021/acs.jctc.8b00571 [DOI] [PubMed] [Google Scholar]
- 28.Li P., Liu F., Jia X., Shao Y., Hu W., Zheng J., and Mei Y., “Efficient computation of free energy surfaces of Diels–Alder reactions in explicit solvent at ab initio QM/MM level,” Molecules 23, 2487 (2018). 10.3390/molecules23102487 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wang M., Mei Y., and Ryde U., “Host-guest relative binding Affinities at density-functional theory level from semiempirical molecular dynamics simulations,” J. Chem. Theory Comput. 15, 2659–2671 (2019). 10.1021/acs.jctc.8b01280 [DOI] [PubMed] [Google Scholar]
- 30.Torrie G. M. and Valleau J. P., “Non-physical sampling distributions in Monte-Carlo free-energy estimation: Umbrella sampling,” J. Comput. Phys. 23, 187–199 (1977). 10.1016/0021-9991(77)90121-8 [DOI] [Google Scholar]
- 31.Barducci A., Bonomi M., and Parrinello M., “Metadynamics,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. 1, 826–843 (2011). 10.1002/wcms.31 [DOI] [Google Scholar]
- 32.Pohorille A., Jarzynski C., and Chipot C., “Good practices in free energy calculations,” J. Phys. Chem. B 114, 10235–10253 (2010). 10.1021/jp102971x [DOI] [PubMed] [Google Scholar]
- 33.Zuckerman D. M. and Woolf T. B., “Theory of a systematic computational error in free energy differences,” Phys. Rev. Lett. 89, 180602 (2002). 10.1103/physrevlett.89.180602 [DOI] [PubMed] [Google Scholar]
- 34.Ryde U., “How many conformations need to be sampled to obtain converged QM/MM energies? The curse of exponential averaging,” J. Chem. Theory Comput. 13, 5745–5752 (2017). 10.1021/acs.jctc.7b00826 [DOI] [PubMed] [Google Scholar]
- 35.Wood R. H., Mühlbauer W. C. F., and Thompson P. T., “Systematic errors in free energy perturbation calculations due to a finite sample of configuration space: Sample-size hysteresis,” J. Phys. Chem. 95, 6670–6675 (1991). 10.1021/j100170a054 [DOI] [Google Scholar]
- 36.Kofke D. A., “Free energy methods in molecular simulation,” Fluid Phase Equilib. 228-229, 41–48 (2005). 10.1016/j.fluid.2004.09.017 [DOI] [Google Scholar]
- 37.Lu N., Singh J. K., and Kofke D. A., “Appropriate methods to combine forward and reverse free-energy perturbation averages,” J. Chem. Phys. 118, 2977–2984 (2003). 10.1063/1.1537241 [DOI] [Google Scholar]
- 38.Wu D. and Kofke D. A., “Phase-space overlap measures. I. Fail-safe bias detection in free energies calculated by molecular simulation,” J. Chem. Phys. 123, 054103 (2005). 10.1063/1.1992483 [DOI] [PubMed] [Google Scholar]
- 39.Wu D. and Kofke D. A., “Phase-space overlap measures. II. Design and implementation of staging methods for free-energy calculations,” J. Chem. Phys. 123, 084109 (2005). 10.1063/1.2011391 [DOI] [PubMed] [Google Scholar]
- 40.Kofke D. A., “On the sampling requirements for exponential-work free-energy calculations,” Mol. Simul. 104, 3701–3708 (2006). 10.1080/00268970601074421 [DOI] [Google Scholar]
- 41.Boresch S. and Woodcock H. L., “Convergence of single-step free energy perturbation,” Mol. Phys. 115, 1200–1213 (2017). 10.1080/00268976.2016.1269960 [DOI] [Google Scholar]
- 42.Gaus M., Cui Q., and Elstner M., “DFTB3: Extension of the self-consistent-charge density-functional tight-binding method (SCC-DFTB),” J. Chem. Theory Comput. 7, 931–948 (2011). 10.1021/ct100684s [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gaus M., Cui Q., and Elstner M., “Density functional tight binding: Application to organic and biological molecules,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. 4, 49–61 (2014). 10.1002/wcms.1156 [DOI] [Google Scholar]
- 44.Kearns F., Warrensford L., Boresch S., and Woodcock H., “The good, the bad, and the ugly: “HiPen”, a new dataset for validating (S)QM/MM free energy simulations,” Molecules 24, 681 (2019). 10.3390/molecules24040681 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hudson P. S., Boresch S., Rogers D. M., and Woodcock H. L., “Accelerating QM/MM free energy computations via intramolecular force matching,” J. Chem. Theory Comput. 14, 6327–6335 (2018). 10.1021/acs.jctc.8b00517 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hummer G., “Fast-growth thermodynamic integration: Error and efficiency analysis,” J. Chem. Phys. 114, 7330–7337 (2001). 10.1063/1.1363668 [DOI] [Google Scholar]
- 47.Jarzynski C., “Nonequilibrium equality for free energy differences,” Phys. Rev. Lett. 78, 2690–2693 (1997). 10.1103/physrevlett.78.2690 [DOI] [Google Scholar]
- 48.Crooks G. E., “Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences,” Phys. Rev. E 60, 2721–2726 (1999). 10.1103/physreve.60.2721 [DOI] [PubMed] [Google Scholar]
- 49.Rossi I. and Truhlar D. G., “Parameterization of NDDO wave-functions using genetic algorithms. An evolutionary approach to parameterizing potential-energy surfaces and direct dynamics calculations for organic-reactions,” Chem. Phys. Lett. 233, 231–236 (1995). 10.1016/0009-2614(94)01450-a [DOI] [Google Scholar]
- 50.Zhou Y., Ojeda-May P., Nagaraju M., and Pu J., “Toward determining ATPase mechanism in ABC transporters: Development of the reaction path-force matching QM/MM method,” in Methods in Enzymology (Academic Press, 2016), Vol. 577, pp. 185–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Shen L. and Yang W., “Molecular dynamics simulations with quantum mechanics/molecular mechanics and adaptive neural networks,” J. Chem. Theory Comput. 14, 1442–1455 (2018). 10.1021/acs.jctc.7b01195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Plotnikov N. V., Kamerlin S. C. L., and Warshel A., “Paradynamics: An effective and reliable model for ab initio QM/MM free-energy calculations and related tasks,” J. Phys. Chem. B 115, 7950–7962 (2011). 10.1021/jp201217b [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kearns F. L., Hudson P. S., Woodcock H. L., and Boresch S., “Computing converged free energy differences between levels of theory via nonequilibrium work methods: Challenges and opportunities,” J. Comput. Chem. 38, 1376–1388 (2017). 10.1002/jcc.24706 [DOI] [PubMed] [Google Scholar]
- 54.König G., Brooks B. R., Thiel W., and York D. M., “On the convergence of multi-scale free energy simulations,” Mol. Simul. 44, 1062–1081 (2018). 10.1080/08927022.2018.1475741 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Giese T. J. and York D. M., “Development of a robust indirect approach for MM → QM free energy calculations that combines force-matched reference potential and Bennett’s acceptance ratio methods,” J. Chem. Theory Comput. 15, 5543–5562 (2019). 10.1021/acs.jctc.9b00401 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Olsson M. A., Söderhjelm P., and Ryde U., “Converging ligand-binding free energies obtained with free-energy perturbations at the quantum mechanical level,” J. Comput. Chem. 37, 1589–1600 (2016). 10.1002/jcc.24375 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Hudson P. S., Woodcock H. L., and Boresch S., “Use of interaction energies in QM/MM free energy simulations,” J. Chem. Theory Comput. 15, 4632–4645 (2019). 10.1021/acs.jctc.9b00084 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Andricioaei I. and Straub J. E., “Generalized simulated annealing algorithms using Tsallis statistics: Application to conformational optimization of a tetrapeptide,” Phys. Rev. E 53, R3055–R3058 (1996). 10.1103/physreve.53.r3055 [DOI] [PubMed] [Google Scholar]
- 59.Giese T. J. and York D. M., “Charge-dependent model for many-body polarization, exchange, and dispersion interactions in hybrid quantum mechanical/molecular mechanical calculations,” J. Chem. Phys. 127, 194101 (2007). 10.1063/1.2778428 [DOI] [PubMed] [Google Scholar]
- 60.Kaminski S., Giese T. J., Gaus M., York D. M., and Elstner M., “Extended polarization in 3rd-order SCC-DFTB from chemical potential equilization,” J. Phys. Chem. A 116, 9131–9141 (2012). 10.1021/jp306239c [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Christensen A. S., Elstner M., and Cui Q., “Improving intermolecular interactions in DFTB3 using extended polarization from chemical-potential equalization,” J. Chem. Phys. 143, 084123 (2015). 10.1063/1.4929335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Giese T. J., Chen H., Dissanayake T., Giambaşu G. M., Heldenbrand H., Huang M., Kuechler E. R., Lee T.-S., Panteva M. T., Radak B. K., and York D. M., “A variational linear-scaling framework to build practical, efficient next-generation quantum force fields,” J. Chem. Theory Comput. 9, 1417–1427 (2013). 10.1021/ct3010134 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Christensen A. S., Kubař T., Cui Q., and Elstner M., “Semi-empirical quantum mechanical methods for non-covalent interactions for chemical and biochemical applications,” Chem. Rev. 116, 5301–5337 (2016). 10.1021/acs.chemrev.5b00584 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Cui Q. and Karplus M., “Molecular properties from combined QM/MM methods. I. Analytical second derivative and vibrational calculations,” J. Chem. Phys. 112, 1133–1149 (2000). 10.1063/1.480658 [DOI] [Google Scholar]
- 65.Woodcock H. L., Zheng W., Ghysels A., Shao Y., Kong J., and Brooks B. R., “Vibrational subsystem analysis: A method for probing free energies and correlations in the harmonic limit,” J. Chem. Phys. 129, 214109 (2008). 10.1063/1.3013558 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.König G. and Brooks B. R., “Correcting for the free energy costs of bond or angle constraints in molecular dynamics simulations,” Biochim. Biophys. Acta 1850, 932–943 (2015). 10.1016/j.bbagen.2014.09.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Deng Y. and Roux B., “Computations of standard binding free energies with molecular dynamics simulations,” J. Phys. Chem. B 113, 2234–2246 (2009). 10.1021/jp807701h [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Cui Q., “Quantum mechanical methods in biochemistry and biophysics,” J. Chem. Phys. 145, 140901 (2016). 10.1063/1.4964410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Bennett C. H., “Efficient estimation of free energy difference from Monte Carlo data,” J. Comput. Phys. 22, 245–268 (1976). 10.1016/0021-9991(76)90078-4 [DOI] [Google Scholar]
- 70.Shirts M. R. and Pande V. S., “Comparison of efficiency and bias of free energies computed by exponential averaging, the Bennett acceptance ratio, and thermodynamic integration,” J. Chem. Phys. 122, 144107 (2005). 10.1063/1.1873592 [DOI] [PubMed] [Google Scholar]
- 71.Bruckner S. and Boresch S., “Efficiency of alchemical free energy simulations. I. A practical comparison of the exponential formula, thermodynamic integration, and Bennett’s acceptance ratio method,” J. Comput. Chem. 32, 1303–1319 (2011). 10.1002/jcc.21713 [DOI] [PubMed] [Google Scholar]
- 72.Best R. B., Zhu X., Shim J., Lopes P. E. M., Mittal J., Feig M., and MacKerell A. D., “Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone ϕ, ψ and side-chain χ1 and χ2 dihedral angles,” J. Chem. Theory Comput. 8, 3257–3273 (2012). 10.1021/ct300400x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Gaus M., Goez A., and Elstner M., “Parametrization and benchmark of DFTB3 for organic molecules,” J. Chem. Theory Comput. 9, 338–354 (2013). 10.1021/ct300849w [DOI] [PubMed] [Google Scholar]
- 74.Stote R., States D., and Karplus M., “On the treatment of electrostatic interactions in biololecular simulation,” J. Chim. Phys. 88, 2419–2433 (1991). 10.1051/jcp/1991882419 [DOI] [Google Scholar]
- 75.Brooks B. R., Brooks C. L. III, Mackerell A. D., Nilsson L., Petrella R. J., Roux B., Won Y., Archontis G., Bartels C., Boresch S., Caflisch A., Caves L., Cui Q., Dinner A. R., Feig M., Fischer S., Gao J., Hodoscek M., Im W., Kuczera K., Lazaridis T., Ma J., Ovchinnikov V., Paci E., Pastor R. W., Post C. B., Pu J. Z., Schaefer M., Tidor B., Venable R. M., Woodcock H. L., Wu X., Yang W., York D. M., and Karplus M., “CHARMM: The biomolecular simulation program,” J. Comput. Chem. 30, 1545–1614 (2009). 10.1002/jcc.21287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Ryckaert J.-P., Ciccotti G., and Berendsen H. J. C., “Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes,” J. Comput. Phys. 23, 327–341 (1977). 10.1016/0021-9991(77)90098-5 [DOI] [Google Scholar]
- 77.Lu N. and Kofke D. A., “Accuracy of free-energy perturbation calculations in molecular simulation. I. Modeling,” J. Chem. Phys. 114, 7303–7311 (2001). 10.1063/1.1359181 [DOI] [Google Scholar]
- 78.Lu N. and Kofke D. A., “Accuracy of free-energy perturbation calculations in molecular simulation. II. Heuristics,” J. Chem. Phys. 115, 6866–6875 (2001). 10.1063/1.1405449 [DOI] [Google Scholar]
- 79.Vanommeslaeghe K., Hatcher E., Acharya C., Kundu S., Zhong S., Shim J., Darian E., Guvench O., Lopes P., Vorobyov I., and Mackerell A. D., “CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields,” J. Comput. Chem. 31, 671–690 (2010). 10.1002/jcc.21367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Sittel F. and Stock G., “Perspective: Identification of collective variables and metastable states of protein dynamics,” J. Chem. Phys. 149, 150901 (2018). 10.1063/1.5049637 [DOI] [PubMed] [Google Scholar]
- 81.Stratt R. M. and Maroncelli M., “Nonreactive dynamics in solution: The emerging molecular view of solvation dynamics and vibrational relaxation,” J. Phys. Chem. 100, 12981–12996 (1996). 10.1021/jp9608483 [DOI] [Google Scholar]
- 82.Thompson W. H., “Solvation dynamics and proton transfer in nanoconfined liquids,” Annu. Rev. Phys. Chem. 62, 599–619 (2011). 10.1146/annurev-physchem-032210-103330 [DOI] [PubMed] [Google Scholar]
- 83.Wang Y., Lamim Ribeiro J. M., and Tiwary P., “Machine learning approaches for analyzing and enhancing molecular dynamics simulations,” Curr. Opin. Struct. Biol. 61, 139–145 (2020). 10.1016/j.sbi.2019.12.016 [DOI] [PubMed] [Google Scholar]
- 84.Hodel A., Simonson T., Fox R. O., and Brünger A. T., “Conformational substrates and uncertainty in macromolecular free energy calculations,” J. Phys. Chem. 97, 3409–3417 (1993). 10.1021/j100115a054 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.