Set Size Effects on Working Memory Precision Are Not Due to an Averaging of Slots

Abstract

Visual working memory is often characterized as a discrete system, where an item is either stored in memory or it is lost completely. As this theory predicts, increasing memory load primarily affects the probability that an item is in memory. However, the precision of items successfully stored in memory also decreases with memory load. The prominent explanation for this effect is the “slots-plus-averaging” model, which proposes that an item can be stored in replicate across multiple memory slots. Here, however, precision declined with set size even in iconic memory tasks that did not require working memory storage, ruling out such storage accounts. Moreover, whereas the slots-plus-averaging model predicts that precision effects should plateau at working memory capacity limits, precision continued to decline well beyond these limits in an iconic memory task, where the number of items available at test was far greater than working memory capacity. Precision also declined in tasks that did not require study items to be encoded simultaneously, ruling out perceptual limitations as the cause of set size effects on memory precision. Taken together, these results imply that set size effects on working memory precision do not stem from working memory storage processes, such as an averaging of slots, and are not due to perceptual limitations. This rejection of the prominent slots-plus-averaging model has implications for how contemporary models of discrete capacities theories can be improved, and how they might be rejected.

Visual working memory underlies our ability to remember visual information over periods of seconds. This storage system is severely capacity-limited: whereas a few items can be held in mind with very high accuracy, as the number of to-be-remembered items increases, memory accuracy declines precipitously (Luck & Vogel, 1997). This limitation is often characterized as a discrete capacity limit, such that a discrete number of studied items can be retained with very high precision, but information about all other items fails to be stored. The idea of a discrete working memory capacity limit has a long history (e.g. Cowan, 1995; Luck & Vogel, 1997; Miller, 1956), and recent evidence for such a limit has been observed in studies of receiver operating characteristic curves (Rouder et al., 2008), reaction time distributions (Donkin, Nosofsky, Gold, & Shiffrin, 2013; Nosofsky & Donkin, 2016), distributions of confidence ratings (Pratte, 2019), and distributions of memory errors (Adam, Vogel, & Awh, 2017; Nosofsky & Gold, 2017; Rouder, Thiele, Province, Cusumano, & Cowan, submitted).

Zhang and Luck (2008) provided what has been taken as some of the most compelling evidence for the existence of a discrete, item-based capacity limit. In their experiments participants studied various numbers of colored squares and, after a brief delay, reported the color of a probed square on a continuous color scale. Discrete capacity theories predict that when the set size of a study array is below a person’s memory capacity, performance on this delayed-estimation task should be high and should not depend on how many items are to be remembered. When the set size surpasses a person’s capacity limit, only a subset of the items will be successfully stored. Consequently, the theory predicts that responses will follow a mixture of accurate in-memory responses, and random guesses. Zhang and Luck (2008) developed a mixture model that estimated the probability of items being stored successfully, and the precision of responses based on the memory representations of those items. Whereas some manipulations affected the precision of responses from memory, such as adding external noise to study stimuli, other manipulations affected the storage rate. Critically, increasing set size produced decreases in the proportion of in-memory responses in a manner predicted by discrete capacity theory.

However, Zhang and Luck (2008) also observed a small but consistent effect of set size on the precision of responses generated from memory: Precision initially decreased as set size increased from one to three items, but reached an asymptote and remained constant at set sizes above three. This effect was not anticipated by existing discrete capacity theories, but Zhang & Luck proposed an elegant elaboration of the discrete capacity model to account for it. According their “slots-plus-averaging” model, when set size is below a person’s capacity limit, multiple copies of an item will be stored in replicate across the free memory slots. For example, if your capacity is three, then when shown a single item you will store three copies of the item. If these copies are independent of one another, and the reported value is based on their average, then the standard deviation of memory representations will increase with the square root of set size, until set size equals the capacity limit, where it will asymptote as now each item can only be assigned a single slot. Zhang & Luck found that the square-root function provided a good characterization of how standard deviation increased with set size, and this pattern has been taken as evidence for the idea that visual memories are stored in multiple memory slots when the memory load is below capacity, and that these representations are averaged when making a response.

Following Zhang & Lucks’s proposal of the slot-plus-averaging model, precision effects as predicted by the model were explicitly built into mathematical instantiations of discrete capacity models. These developments included models of change-detection (Cowan & Rouder, 2009) and of the delayed estimation task (van den Berg, Shin, Chou, George, & Ma, 2012). These formal slots-plus-averaging models have since often served as the de facto models of discrete capacity theory. They have been pivotal in formal model comparison studies, several of which have found that this model does not account for data as well as other models that do not assume a discrete capacity limit (e.g. van den Berg, Awh, & Ma, 2014; van den Berg et al., 2012). However, the notion of averaging slots is not a necessary feature of discrete capacity theory, but was an addendum to the theory proposed by Zhang & Luck (2008) as an account of set size effects on precision. Consequently, any rejection of the formal slots-plus-averaging model may be a rejection of the idea of a discrete capacity limit (“slots”) as is often claimed, or it may be a rejection of the notion that items are stored in replicate and averaged (“plus averaging”). Although Zhang and Luck (2008) found that a square root function provided a good description of how standard deviation increased with set size, the idea that multiple copies of an item are independently stored in memory, and that these copies can be averaged to produce a response, has not been directly tested.

In Experiment 1 we tested a more general question: Are set size effects on precision due to limitations in working memory storage at all, such as an averaging of working memory slots, or might they instead reflect limitations at some other stage of processing? Set size effects on precision were measured in a working memory condition, and in conditions in which retention intervals were brief (33 and 50 ms) such that responses could be made using iconic memory (Sperling, 1960). According to standard memory models (e.g., Atkinson & Shiffrin, 1968), in the iconic memory conditions the cued item can be loaded from iconic into working memory at the time of the cue. Performance in this condition should therefore not be limited by the need to concurrently store multiple items in working memory. If the effect of set size on precision reflects an averaging of slots in working memory, then set size should not affect precision in these iconic memory conditions, as the working memory load is effectively 1.0 regardless of how many items are studied. Alternatively, if set size effects on precision stem from processes other than working memory storage limitations, then precision should decline with set size in the iconic memory conditions, just as it does in working memory conditions.

Experiments 1a-c

Method

Participants.

All participants were undergraduate students at Mississippi State University who participated in exchange for course credit. Forty-eight students participated in Experiment 1a (32 female, mean age 20 years), forty-five participated in Experiment 1b (26 female, mean age 20), and forty-five participated in Experiment 1c (34 female, mean age 20 years). Data from participants who did not complete the study were not analyzed (two, one and one in Experiments 1a, 1b and 1c, respectively). Each experiment lasted approximately one hour. Participants in all studies provided informed consent prior to participation, and all studies were approved by the institutional review board at Mississippi State University.

Stimuli & Design.

Experiments 1a, 1b and 1c were 2×2 within-subject factorial designs, counterbalanced across conditions of set size and retention interval. Each experiment included set size two and set size eight conditions. Although the set size effect on precision is largest when comparing set size one to higher set sizes, the single-item condition may be fundamentally different than all others because there is no need to store the item’s location as there is at higher set sizes (Bae & Flombaum, 2013). We therefore used set size two to rule out such differences as an explanation for observed effects. Each experiment included a working memory retention interval (1000 ms), and an additional brief retention interval of 0 ms (Exp. 1a), 33 ms (Exp. 1b) or 50 ms (Exp. 1c). Including both the 1000 ms condition and a brief-interval condition within each experiment allowed for within-subject comparisons between working memory conditions and each of the brief-interval conditions. Each participant completed 150 trials per condition (600 total).

Trials began with an array of colored squares presented for 200 ms on a gray background (Figure 1). Stimuli subtended 1° visual angle, and each was located at one of eight evenly spaced polar angles along an invisible circle (7° diameter) centered around a central fixation point (.4° diameter). The color of each square was chosen randomly from 180 possible colors, generated from a circle in the Lab color space (L=70, a=−10, b=30, radius=40). LCD Displays were gamma corrected and color calibrated using the Cambridge Research Systems ColorCAL MKII colorimeter. For all conditions with a non-zero retention interval (Figure 1A), a fixation period (33, 50 or 1000 ms) followed the study display, followed by a line cue which pointed to a randomly chosen stimulus (1.5° long, 500 ms in duration). A color wheel was then shown (spanning from 6° to 7° in diameter, and rotated by a random amount on each trial), and participants used the mouse cursor to indicate the color of the cued item. During this response period a square was shown at fixation with color that matched that at the location of the mouse cursor, and upon making a response (via mouse click) the studied stimulus was shown at its original study location and color to provide performance feedback. This 500 ms feedback period was followed by a 1000 ms inter-trial interval.

Figure 1.

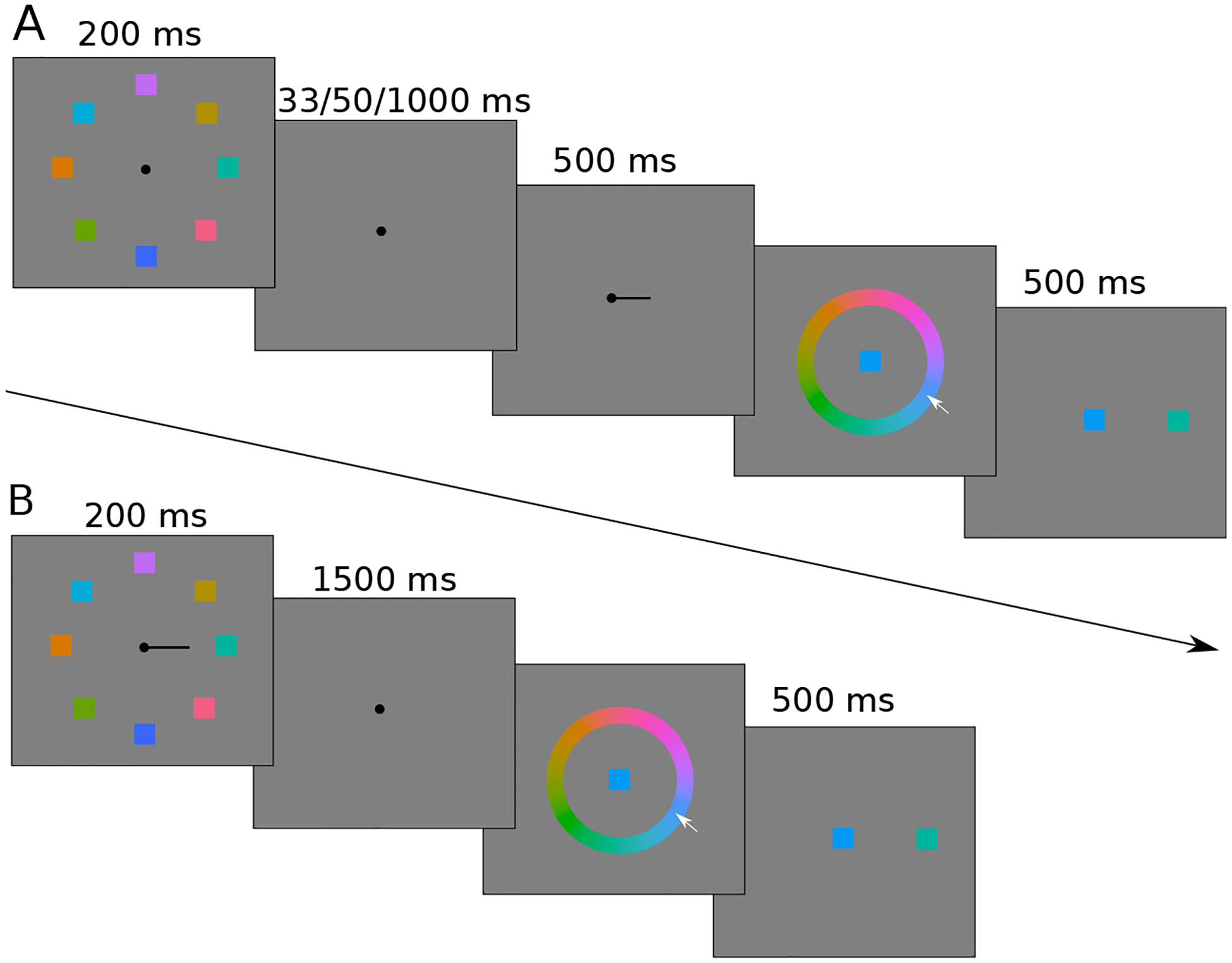
Trial structure of Experiments 1a–c. A) Experiments 1a–c each included a 1000 ms retention interval condition. Experiment 1b additionally included a 33 ms retention interval, and Experiment 1c a 50 ms retention interval. B) For the 0 ms retention condition in Experiment 1a, the location cue was presented simultaneously with the study array.

In the “0 ms” retention interval condition of Experiment 1a, the study array and line cue were presented simultaniously for 200 ms (Figure 1B). Whereas this timing makes it difficult to make a saccade toward the cued stimulus (Walker, Walker, Husain, & Kennard, 2000), there is ample time for attention to be directed to the item while it is still visible (Posner, 1980). Following a 1500 ms retention interval participants indicated the color of the cued item and received feedback in the same manner as in other conditions. This longer retention interval served to maintain the same stimulus onset asynchrony between the study array and the response period, across the 0 ms and 1000 ms conditions in Experiment 1a.

Results

Figure 2 shows response error distributions from Experiment 1b, for the 33 ms (top) and 1000 ms (bottom) conditions for each set size. The data were analyzed by fitting the Zhang and Luck (2008) two-component mixture model using standard maximum likelihood procedures. The mixture model assumes that responses arise from a mixture of random guesses, which necessarily follow a uniform distribution for circular variables such as color, and in-memory responses that follow a von Mises distribution, the circular analogue of the normal distribution. The model is governed by two free parameters: the proportion of responses that come from memory as opposed to guessing, and the precision of responses arising from memory (κ). The lines in Figure 2 show model fits to the data aggregated over participants. Although such aggregating can distort the shapes of error distributions when participants vary from one another in precision (e.g. the aggregate distribution will be more peaked than any individual), the mixture model nonetheless provides an excellent fit across conditions.

Figure 2.

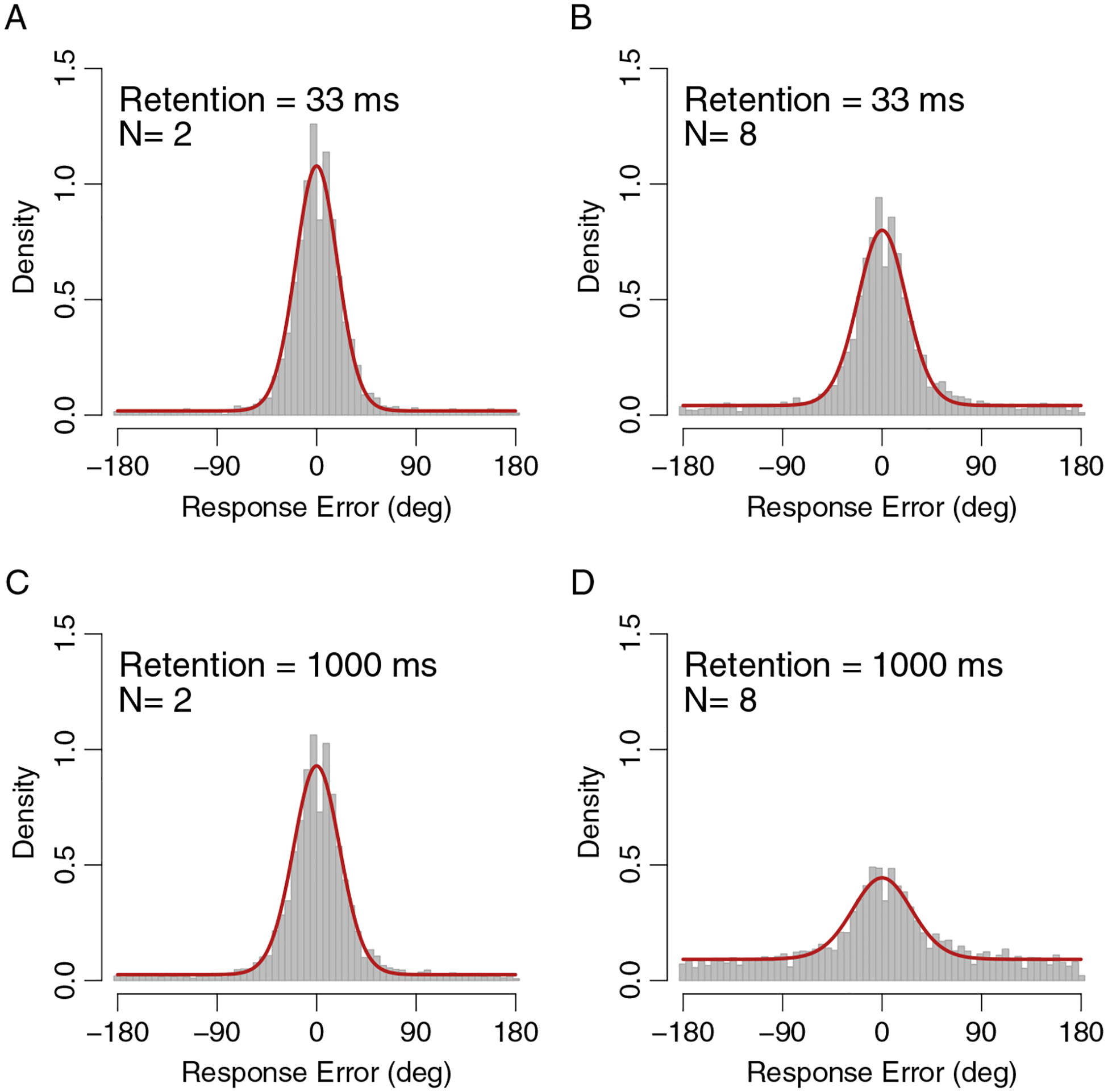
Response error distributions from Experiment 1b, aggregated across participants. Top panels show errors for the 33 ms conditions for set size 2 (A) and set size 8 (B). Bottom panels show response errors for the 1000 ms conditions for set size 2 (C) and set size 8 (D). Red lines show mixture model fits to the aggregated data.

For the main analyses the model was fit separately to each condition and participant. Average estimates of memory precision from Experiments 1a-c are shown in Figure 3A. The precision of working memory, as measured at the 1000 ms retention interval, was lower at set size 8 than set size 2 in Experiment 1a (t(45) = 4.34, p < .001, d = 0.64), Experiment 1b (t(43) = 5.65, p < .001, d = 0.85) and Experiment 1c (t(43) = 8.64, p < .001, d = 1.30), replicating previous results. Memory precision did not decline with set size in the 0 ms condition of Experiment 1a (t(45) = 0.55, p = .58, d = 0.08), in which the item cue was presented simultaneously with the study display. This lack of an effect was confirmed by using a Bayes Factor analogue of the paired t-test (Rouder, Speckman, Sun, Morey, & Iverson, 2009, using default scale of $\sqrt{2}/2$), which suggested that the set size effect on precision in the 0 ms condition was 5.41 times more likely to be observed under the null model. Critically, however, precision did decline with set size in the iconic memory conditions, for both the 33 ms retention interval (Exp. 1b, t(43) = 6.47, p < .001, d = 0.97) and the 50 ms retention interval (Exp. 1c, t(43) = 11.42, p < .001, d = 1.72).

Figure 3.

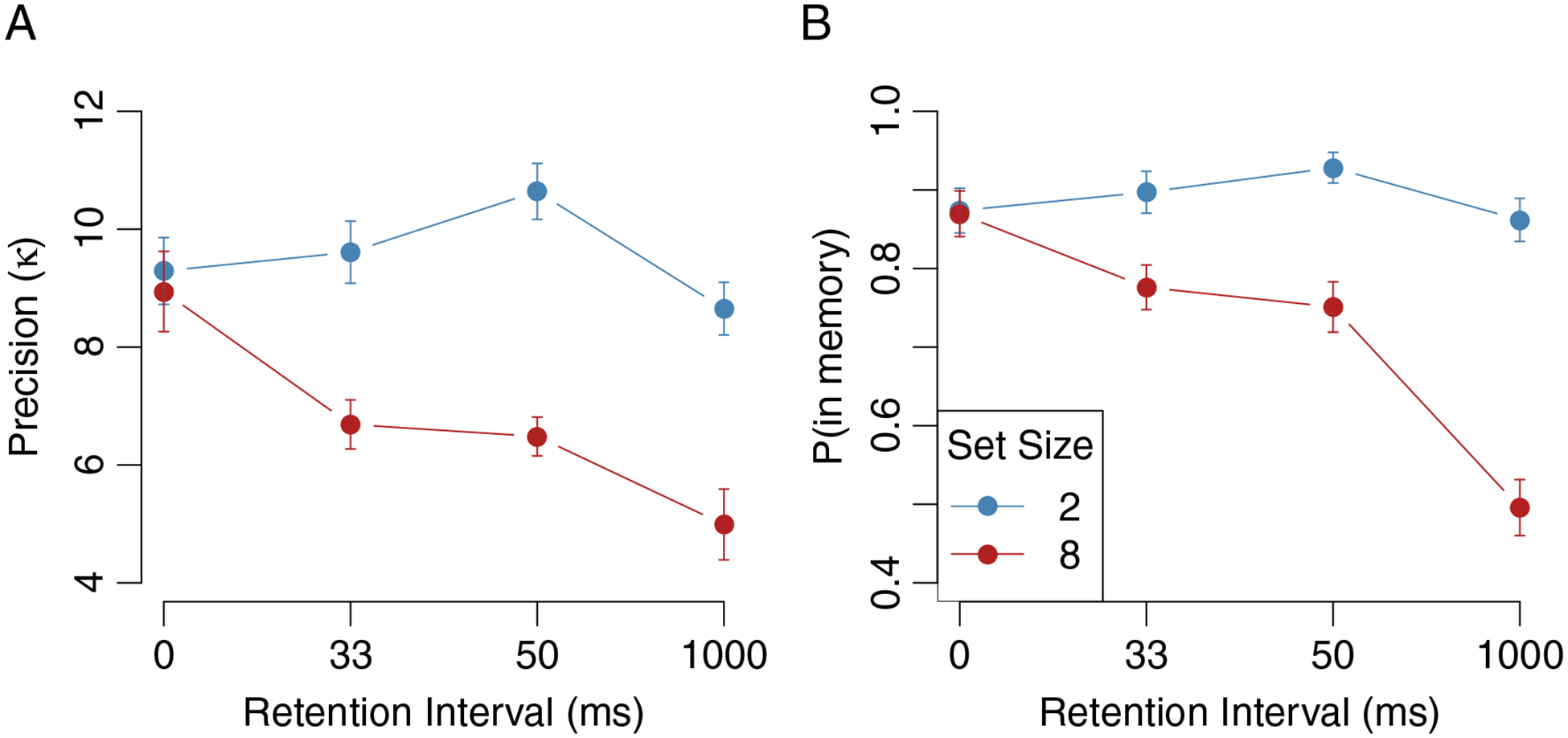
Parameter estimates from Experiment 1. (A) Average precision for each retention interval and set size condition. (B) Average probabilities that items are in memory for each retention interval and set size condition. Results from the three 1000 ms conditions were highly similar across experiments, and are averaged in this figure. All error bars are standard errors.

A 2×2 repeated-measures ANOVA was also applied within each experiment to examine whether the effects of set size and retention interval on memory precision might interact. In Experiment 1a, a significant interaction between set size and retention condition (F (1, 45) = 9.15, p < .01, ${\eta }_p^2=.17$) reflects the presence of a set size effect in the 1000 ms but not the 0 ms condition. However, whereas in Experiment 1b there were significant main effects of set size (2 vs. 8, F (1, 43) = 61.4, p < .001, ${\eta }_p^2=.59$) and retention interval (33 vs. 1000 ms, F (1, 43) = 22.18, p < .001, ${\eta }_p^2=.34$), the interaction was not significant (F (1, 43) ≈ 0, p = .99, ${\eta }_p^2\approx 0$). This lack of an interaction implies that the effect of set size on precision is not significantly different across the 33 ms and 1000 ms conditions. To more rigorously assess evidenced for the lack of an interaction, precision values were subtracted across set size conditions and the resulting effects subtracted across retention conditions. If there is no interaction then the mean of these interaction terms should not differ from zero, and a Bayes Factor t-test suggests that these effects are 6.13 times more likely to have come from a model with no interaction. The results are similar if a full Bayesian ANOVA is applied to these data (Rouder, Morey, Speckman, & Province, 2012, using default priors), according to which the data were 4.5 times as likely to have come from a model with only main effects than from a model that also allowed for an interaction.

Similar results were found for Experiment 1c, with significant main effects of set size (2 vs. 8, F (1, 43) = 160.4, p < .001, ${\eta }_p^2=.79$) and retention interval (50 vs. 1000 ms, F (1, 43) = 15.5, p < .001, ${\eta }_p^2=.26$), but no interaction (F (1, 43) = 0.58, p = .45, ${\eta }_p^2=.01$). A Bayes Factor t-test on interaction terms suggests that the data were 4.67 times more likely under a model with no interaction. Likewise, the full Bayesian ANOVA suggests that the data were 3.95 times more likely under a model with only main-effects. The lack of an interaction in both Experiments 1b and 1c suggests that the effect of set size on precision is of the same magnitude in iconic and working memory conditions. It is important to note that this lack of an interaction is “removable” (Loftus, 1978), such that the interaction could become significant under some non-linear transformations of the precision space. However, because the main effect of retention interval on precision is extremely small, most transformations will do little to change the pattern of results.

Set size and retention interval also affected the probability that items were successfully stored in memory (Figure 3B), but in a substantially different way than the effects on precision. Repeated measures ANOVAs on these rates within each experiment revealed significant interactions between set size and retention interval in Experiment 1a (F (1, 45) = 125.8, p < .001, ${\eta }_p^2=.74$), Experiment 1b (F (1, 43) = 83.09, p < .001, ${\eta }_p^2=.54$) and Experiment 1c (F (1, 43) = 25.34, p < .001, ${\eta }_p^2=.50$). These interactions suggest that set size effects on memory rates are larger in the 1000 ms condition than in each of the shorter interval conditions. Although there is a significant effect of set size on memory rate in the 33 ms (Exp. 2b, t(43) = 4.93, p =< .001, d = 0.74) and 50 ms conditions (Exp. 2c, t(43) = 9.60, p =< .001, d = 1.45), set size had no effect on the probability of items being in memory in the 0 ms condition, when the item cue appeared simultaneously with the study array (Exp 2a, t(45) = 0.68, p = .50, d = 0.10, BF = 5.02). Taken together, these results imply that the capacity of iconic memory is larger than that of working memory (e.g. Pratte, 2018; Sperling, 1960), and is larger still if attention can be directed to the probed item while it remains in view.

The probability of an item being in memory at set size two was high and fairly constant across conditions, but was not 100%. This less-than-perfect rate of memory storage in such easy conditions is likely due to something like attentional lapses, rather than true memory failures (e.g. Rouder et al., 2008). Therefore, performance in the 0 ms is likely as high as it can be at both set size 2 and set size 8, suggesting that memory capacity is at least 8 items when attention can be directed toward an item while it remains in view. Likewise, if performance at set size two is taken as an estimate of how often participants attended to the task, then capacity estimates from set size 8 can be corrected for the probability of attending being less than 1.0 (capacity = 8 * p(memory)/p(attending)). The results suggest that the capacity of iconic memory is 6.9 items at 33 ms and 6.5 items at 50 ms, and the capacity of working memory is 4.6 items (averaged over the 1000 ms conditions). Critically, although memory capacity is substantially higher in iconic than in working memory conditions, the set size effects on precision were highly similar across these conditions.

Discussion

In working memory conditions (1000 ms retention interval) precision decreased with increasing set size, replicating previous results which have been assumed to reflect mechanisms of working memory storage (Zhang & Luck, 2008). However, decrements in precision were also observed with very brief 33 ms and 50 ms retention intervals, where responses could be based on iconic memory, and need not rely on the concurrent storage of multiple items in working memory. That the effects of set size on precision were similar in the iconic memory and working memory conditions suggests that this effect does not arise from working memory storage processes, such as an averaging of slots in working memory.

Although the set size effect on precision was present even after a mere 33 ms retention interval, the effect was alleviated by cuing an item while the study display was still visible in the 0 ms condition (Exp. 1a). This result rules out several low-level perceptual effects as causes for the set size effect on precision. For example, although attending to a target can reduce visual crowding, crowding effects are still large even if attention is directed toward a crowded item (Yeshurun & Rashal, 2010). If the set size effect on precision reflected more crowding at higher set sizes, then attending to the study item should not have eliminated the effect. However, in the 0 ms condition only a single item needed to be attended, encoded, stored, and retrieved from memory, such that the lack of a set size effect in this condition does not rule out contributions from at any of these processing stages.

Previous evidence for the slots-plus-averaging model rests not only on the existance of a set size effect on precision, but also on the nature by which working memory precision declines as set size increases. In particular, Zhang and Luck (2008) and others have found that the effect of set size on precision plateaus near the typical working memory capacity limit of three items. They interpreted this plateau as evidence for the slots-plus-averaging model: at set sizes beyond one’s capacity all slots are filled, such that multiple items can not be stored in replicate, and the precision effect will level off. Subsequent studies have argued against this interpretation, showing for example that the location of the plateau for an individual is not predicted by that individual’s particular working memory capacity limit, as would be expected by a slots-plus-averaging model (Bays, 2018). Others have failed to find a plateau when using a change-detection paradigm (Salmela & Saarinen, 2013), or have argued that it is difficult to know whether set size effects on precision actually plateau, or merely follow a non-linear function that decelerates but does not necessary stop decreasing (van den Berg & Ma, 2014). However, even if set size effects on working memory precision do plateau near three items, mechanisms other than an averaging of slots can anticipate such a pattern. In particular, if a maximum of three items can be encoded, then a precision effect stemming from limitations in encoding, storage or retrieval processes would be expected to level off near working memory capacity, as there are never more than three items processed at any of these stages.

In Experiment 1 the set size effect on precision was similar in iconic and working memory conditions. However, only two set sizes were examined, so it is not clear how precision declines with set size when iconic memory is available. For example, if the plateau occurs at the capacity of whatever memory system produces the response, then precision should level off at a set size well above three items when iconic memory is available. Alternatively, if the precision effect plateaus at set size three regardless of what memory systems are being used, such a pattern would implicate working memory as playing a role in the effect, even in iconic memory conditions. For example, it may be the case that even when a single item is probed in the iconic memory conditions, other items in the display are automatically encoded and stored as well, until working memory capacity limits are reached (e.g., Lavie, 1995). Experiment 2 was designed to investigate how precision declines with set size when iconic memory can be leveraged, by measuring memory performance across set sizes 2, 4, 6, 8 and 10, with a brief 100 ms retention interval. If some limitation in working memory is what’s causing precision to decline with set size, then the precision effect should still plateau near three items, even in iconic memory conditions.

Experiment 2

Participants

The goal of Experiment 2 was to measure memory performance at several set sizes, necessitating several conditions per participant. We therefore utilized a design with fewer participants but more trials per participant than Experiment 1, achieved by running each participant in several experimental sessions. Seven people (2 female, average age 21 years) each participated in three 1-hour sessions, on three different days, in exchange for monetary compensation ($10/hr).

Stimuli & Design

Experiment 2 was identical to Experiment 1 with the following exceptions. A retention interval of 100 ms (stimulus offset to cue onset) was used throughout the experiment, and set size conditions included 2, 4, 6, 8 or 10 items. Item locations were randomly chosen from 10 evenly spaced locations along an invisible circle. Set size conditions were randomized within each session. Each participant completed a total of 300 trials at each set size condition across the three experimental sessions.

Results

Estimates of precision are shown in Figure 4A. An ANOVA on precision estimates suggests that set size had an overall effect on precision (F (4, 24) = 49.02, p < .001, ${\eta }_p^2=.89$). Follow-up t-tests indicate that precision declined from each set size to the next, from set sizes 2 to 4 (t(6) = 4.19, p = .006, d = 1.58), 4 to 6 (t(6) = 5.09, p = .002, d = 1.92), 6 to 8 (t(6) = 3.53, p = .012, d = 1.33) and 8 to 10 (t(6) = 3.66, p = .011, d = 1.38). This monotonic decline across set sizes 2 to 10 stands in contrast to the pattern predicted by a slots-plus-averaging model, according to which set size should have no effect on precision in these iconic memory conditions, especially beyond the typical plateau observed near working memory capacity limits of three or four items.

Figure 4.

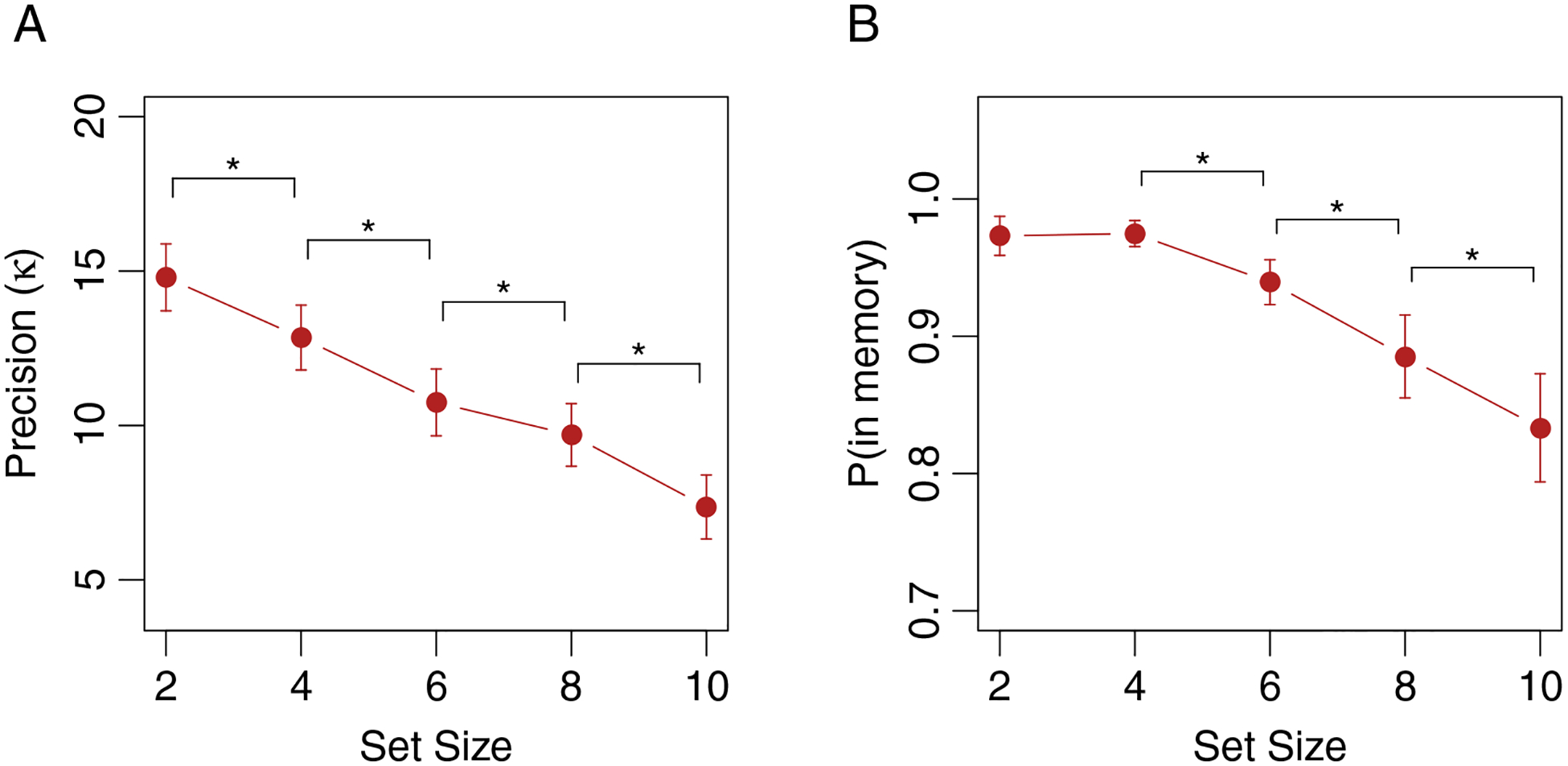
Experiment 2 results. Parameter estimates of A) memory precision, and B) the probability that an item is in memory. Stars denote significant pairwise differences between successive conditions.

The probability of an item being in memory (Figure 4B) was also affected by set size (F (4, 24) = 10.96, p < .001, ${\eta }_p^2=.65$). Follow-up t-tests indicate that this measure of memory capacity did not differ between set size 2 and set size 4 (t(6) = .17, p = .87, d = .07), however it did decrease from set sizes 4 to 6 (t(6) = 4.32, p = .005, d = 1.63), 6 to 8 (t(6) = 2.88, p = .028, d = 1.09) and 8 to 10 (t(6) = 2.78, p = .032, d = 1.05). Approximately 83% of responses in the set size 10 condition were from memory, implying that memory capacity was about 8.6 items (after correcting for attentional lapses), consistent with previous estimates of iconic memory capacity for color (Bradley & Pearson, 2012; Pratte, 2018). Unfortunately, this high capacity means that conditions with more than 10 items may be needed to thoroughly determine whether precision asymptotes near the capacity limit of iconic memory in iconic memory tasks, or perhaps continues to decline. However, extensive work would be needed to study memory at such high set sizes, where effects such as visual crowding (Tamber-Rosenau, Fintzi, & Marois, 2015) and errors in interpreting the location cue (Bays, Catalao, & Husain, 2009) would likely affect task performance.

Discussion

In Experiment 2, where a brief retention interval allowed iconic memory to support memory reports, precision declined monotonically with set size up to a set size of 10 items. The plateau in precision near set size three observed in working memory tasks is therefore not a fundamental property of set size effects on precision. Moreover, the lack of a plateau in Experiment 2 implies that set size effects on precision in iconic memory conditions are not due to working memory limitations. This result lends further support to the conclusion that set size effects on precision do not reflect working memory processes, such as an averaging of memory slots slots.

There are many stages of processing other than working memory storage that may give rise to the set size effects on precision. For example, precision effects may stem from a limitation in our ability to perceive multiple items simultaneously at study. For example, inter-item competition occurs when multiple stimuli are presented simultaneously, perhaps due to a limitation in attending to multiple items at the same time (Desimone & Duncan, 1995). Results from the 0 ms condition of Experiment 1, in which a study item was probed while still visible, are in line with the idea that set size effects on precision stem from limitations in visual perception: when a single item could be attended to at study, there was no longer a set size effect on precision. However, this results does not provide strong evidence that perceptual limitations cause the set size effect. Although in this condition only a single item needed to be attended to during study, it is also the case that only a single item needed to be subsequently encoded, stored, retrieved, and reported at test. Therefore, the lack of a precision effect in this condition could have resulted from alleviating the multi-item burden from any of several processes subsequent to perception.

Experiments 3a–c were designed to directly test the hypothesis that set size effects on precision arise from limitations in our ability to perceive multiple items simultaneously during study. Study items were presented sequentially, one at a time, in order to minimize interference that might result from the need to perceive multiple items simultaneously. Several studies have examined working memory under sequential presentation conditions (e.g. Ahmad et al., 2017; Gorgoraptis, Catalao, Bays, & Husain, 2011; Kool, Conway, & Turk-Browne, 2014; Smyth & Scholey, 1996), but none have examined the conditions required to determine whether sequential presentations mitigate set size effects on precision, as measured by the Zhang and Luck (2008) mixture model. Sequential presentations are thought to minimize the inter-item competition that occurs when multiple stimuli are presented simultaneously by eliminating competitive interactions within receptive fields of neurons in early visual areas (see Beck & Kastner, 2009). If such perceptual limitations are what cause memory precision to decline with set size, then presenting items sequentially should eliminate the effect of set size on precision.

Experiments 3a-c

Method

Participants.

In Experiments 3a, 3b and 3c, 30 , 34 and 64 undergraduate students (82 female, mean age 19 years), respectively, participated in exchange for course credit. Target enrollment was doubled for Experiment 3c as there were fewer trials per participant in this experiment, and to increase our ability to find positive evidence for a null effect with the Bayesian analysis, which was anticipated by the results of Experiments 3a and 3b. Three participants in Experiment 3b and one in Experiment 3c did not complete the experiment and their data were excluded from analysis.

Stimuli & Design.

Experiments 3a-c were similar to Experiment 1 with the following exceptions. Each experiment was a 2×2 within-subject factorial design with a set size of two or four items, and study items were either presented simultaneously as in Experiment 1, or sequentially such that each item was presented one at a time (see Figure 5). Experiments 3a-c differed from one another in the presentation timing of study items. In the simultaneous condition of Experiment 3a stimuli were presented simultaneously for 50 ms, each in one of 8 possible locations, and the test probe was presented after a 1000 ms retention period. In the sequential condition each study stimulus was presented for 50 ms one after another, and the test probe was presented 1000 ms after the offset of the final study stimulus. Stimulus timing for this sequential presentation was modeled after Kool et al. (2014), who failed to find set size effects on precision, but did not test set sizes less than three, and did not directly compare simultaneous and sequential presentation conditions. We worried, however, that with such a rapid presentation the sequential condition may not fully alleviate competition between items. In Experiment 3b the stimulus duration was therefore increased to 200 ms. In Experiment 3c the presentation was further slowed by inserting a 500 fixation interval between successive 200 ms stimulus presentations in the sequential presentation condition (shown in Figure 5). Ahmad et al. (2017) recently suggested that this relatively slow design is necessary in order for sequential presentations to alleviate inter-item competition at encoding (they did compare sequential and simultaneous conditions, but only for a set size of two). In addition, in Experiment 3c stimuli were presented in only four possible locations (45, 135, 225 or 315°) rather than eight, in order to minimize potential uncertainty regarding the location probe, and the number of trials was reduced from 600 to 480 (120 per condition) to account for the added study time.

Figure 5.

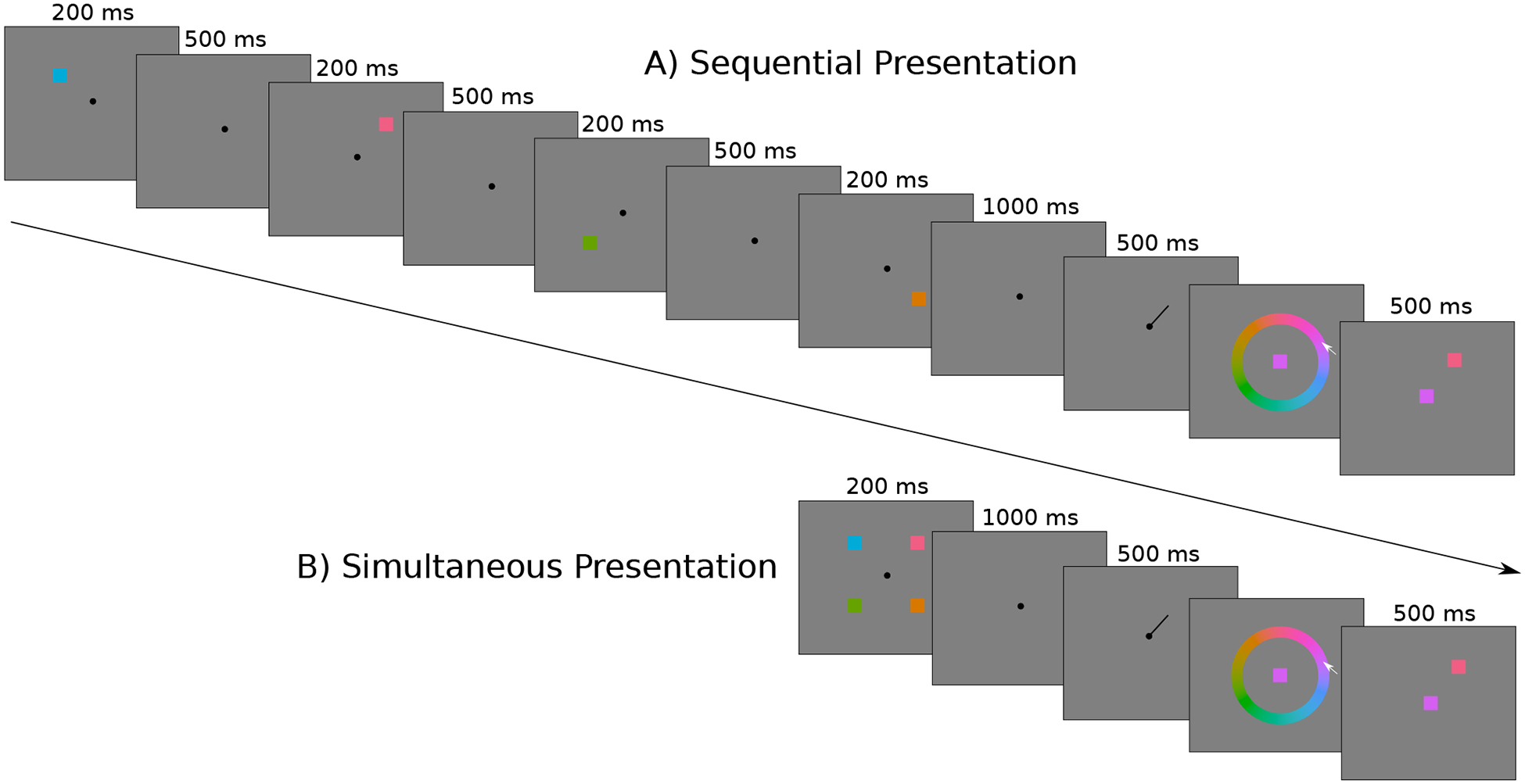
Trial structure of Experiment 3c. A) In the sequential-presentation condition each item was presented one at a time. B) In the simultaneous-presentation condition all items were presented simultaneously, as in a typical working memory experiment. In each condition the set size could be two, or four as shown here.

Results

Precision estimates from Experiments 3a-c are shown in Figure 6A. The typical set size effect on precision was observed in the simultaneous presentation conditions of Experiment 3a (t(29) = 4.81, p < .001, d = .88), Experiment 3b (t(30) = 3.23, p < .005, d = .58) and Experiment 3c (t(62) = 5.53, p < .001, d = .70). Critically, there were also significant set size effects on precision in the sequential presentation conditions of Experiment 3a (t(29) = 4.85, p < .001, d = .89), Experiment 3b (t(30) = 2.38, p < .05, d = .43) and Experiment 3c (t(62) = 2.56, p < .05, d = .32). The presence of set size effects on precision in the sequential conditions suggests that these effects do not result from a limitation in our ability to perceive and encode multiple items simultaneously.

Figure 6.

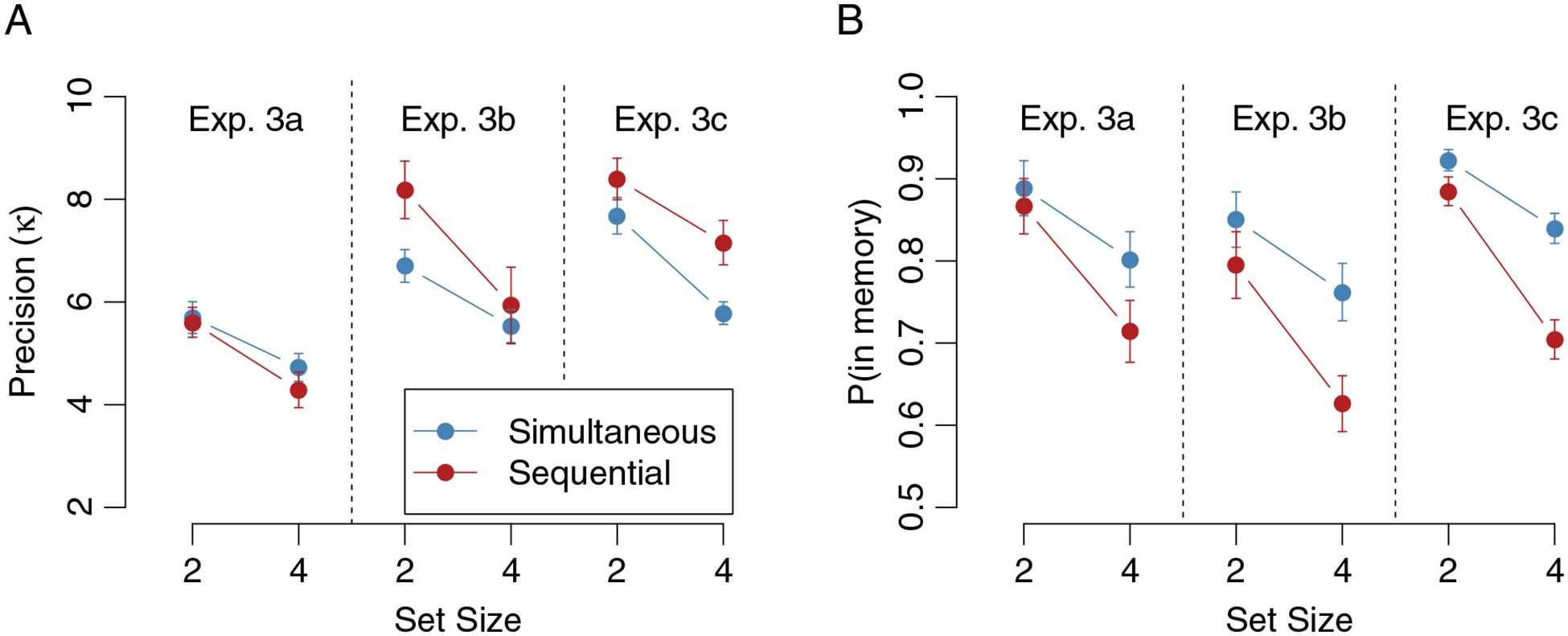
Parameter estimates from Experiments 3a–c. A) Estimates of precision for each experiment. B) Estimates of the probability that items were successfully stored in memory.

Repeated-measures ANOVAs were used within each experiment to further examine how the set size effect in precision may depend on the sequential vs. simultaneous presentation of study items. In Experiment 3a there was a main effect of set size (F (1, 29) = 45.25, p < .001, ${\eta }_p^2=.61$), no difference between the simultaneous and sequential presentation conditions (F (1, 29) = 2.00, p = .17, ${\eta }_p^2=.06$), and no interaction (F (1, 29) = 1.05, p = .31, ${\eta }_p^2=.03$). This lack of an interaction was supported by the Bayesian t-test on interaction terms (data were 3.19 times more likely under the null model) and the fully Bayesian ANOVA (data were 2.54 times more likely under the main-effects model). Whereas in the sequential condition of Experiment 3a items were presented for 50 ms each, in Experiment 3b presentation was slowed to 200 ms per item to further alleviate inter-item competition at encoding. Nonetheless, the results were highly similar: precision decreased significantly with set size (F (1, 30) = 11.34, p < .005, ${\eta }_p^2=.27$), and was marginally lower in the simultaneous than sequential condition (F (1, 30) = 2.97, p = .10, ${\eta }_p^2=.09$), but there was again no interaction between set size and simultaneous/sequential presentation (F (1, 30) = 1.14, p = .29, ${\eta }_p^2=.04$). This lack of an interaction was again supported by the Bayesian t-test on interaction terms (data were 3.10 times more likely under the null model) and the fully Bayesian ANOVA (data were 2.39 times more likely under the main-effects model). In Experiment 3c the sequential presentation rate was further slowed to 500 ms per item, and a 200 ms inter-stimulus interval was inserted between each item. In addition to a main effect of set size (F (1, 62) = 27.99, p < .001, ${\eta }_p^2=.31$), this extremely slow design produced a main effect of simultaneous vs. sequential presentation conditions on precision (F (1, 62) = 12.0, p < .001, ${\eta }_p^2=.16$). Overall higher memory precision in this slow sequential presentation condition suggests that this design effectively alleviated some of the cost of perceiving and encoding multiple items simultaneously. However, the interaction between set size and simultaneous/sequential condition was again not significant (F (1, 62) = 1.21, p = .28, ${\eta }_p^2=.02$). And again, the lack of an interaction was supported by the Bayesian t-test on interaction terms (data were 4.08 times more likely under the null model) and the fully Bayesian ANOVA (data were 3.12 times more likely under the main-effects model). In each of Experiments 3a-c, presenting items sequentially rather than simultaneously did nothing to alleviate the effect of set size on memory precision.

Figure 6B shows estimates of the probability that items were in memory for each condition in Experiments 3a-c. A repeated-measures ANOVA on the rates from Experiment 3a suggests a main effect of set size (F (1, 29) = 48.12, p < .001, ${\eta }_p^2=.62$), a main effect of simultaneous verses sequential presentation (F (1, 29) = 26.87, p < .001, ${\eta }_p^2=.48$), and an interaction (F (1, 29) = 9.45, p < .005, ${\eta }_p^2=.25$). The smaller number of remembered items in the sequential condition replicates previous results, and may reflect a loss of early items as later ones are stored (Kool et al., 2014). This pattern of main effects and an interaction was replicated in Experiments 3b and 3c.

Discussion

Studying stimuli one at a time should minimize interference that results from having to perceive multiple items simultaneously. Indeed, the sequential presentation of study items led to significantly higher precision in Experiment 3c and a marginally significant increase in Experiment 3b. If the effect of set size on precision was due to limitations in perceiving or encoding multiple items simultaneously, then presenting items sequentially should have eliminated these set size effects. However, the results of Experiments 3a, 3b and 3c suggest that the effect of set size on precision is present, and is of similar magnitude, regardless of whether stimuli are studied simultaneously or one at a time. Taken together, the results of Experiments 3a-c rule out limitations in perceiving multiple items simultaneously as a viable explanation for the effect of set size on precision.

General Discussion

Zhang and Luck (2008) found that increasing set size primarily led to increased guessing in visual working memory. However, when set sizes were below the typical working memory capacity limit of 4 items, the precision of items successfully stored in memory also declined as set size was increased. Zhang & Luck accounted for this pattern by proposing that when the number of to-be-remembered items is below capacity, multiple independent copies of each item can be stored and then averaged at retrieval, producing increased precision at small set sizes. Whereas this “slots plus averaging” model has since served as the standard discrete-capacity model of working memory in many formal model comparison studies (e.g. Cowan & Rouder, 2009; Pratte, Park, Rademaker, & Tong, 2017; Taylor & Bays, 2018; van den Berg et al., 2014; van den Berg et al., 2012), here we considered the possibility that precision effects do not reflect working memory storage at all. In Experiment 1 precision declined with set size in iconic memory conditions that did not require multiple items to be concurrently stored in working memory. In the iconic memory task of Experiment 2, in which more than 8 items were in memory at the time of retrieval, precision decline monotonically up to set size 10, well past typical working memory capacity limits. The manner by which precision declines with set size therefore depends on the retention interval, and the often-observed plateau near three or four items is not a fundamental feature of how precision declines with set size. Taken together, these results suggest that precision effects are not due to working memory storage processes, such as an averaging of working memory slots.

The results of Experiment 1 futher suggest that precision declines with set size by the same amount under iconic and working memory conditions. One possible explination for this result is that these set size effects result from limitations in simultaneously perceiving multiple items at study, as such limitations would affect performanace on any subsequent test that relied on the initial perception. Such inter-item competition can be observed in both behavior and neural activity, and is often attributed to a limited pool of attention resources (Desimone & Duncan, 1995). In Experiments 3a-c the need to perceive multiple items simultaneously was alleviated by presenting study items one at a time. However, this sequential presentation did nothing to mitigate the set size effect on precision. It is posslble that there are perceptual effects that are not alleviated by sequential presentation, such as the perception of a later item in the sequence being influenced by the current contents of memory. However, a recent study suggests that a stimulus in memory and one viewed during the retention interval do not impact one another as they do when both stimuli are viewed simultaniously (Bloem, Watanabe, Kibbe, & Ling, 2018). A sequential presentation should therefore be sufficient to mitigate perceptual phenomenon that occur with multi-item displays. Consequently, set size effects on precision can not be explained by low-level perceptual effects during study.

The results of Experiments 1–3 provide boundary conditions on what might be causing precision to decline with set size. However, even within a discrete capacity framework there remain numerous possible causes for these effects on precision. For example, Nassar, Helmers, and Frank (2018) recently showed that participants can use a chucking strategy whereby similar colors in a display are grouped together in memory, and that under some conditions this strategy might cause precision to decline with set size. It is not clear why such a strategy would be used in iconic memory conditions, where we nonetheless observe a set size effect on precision. It is possible that automatic chunking processes also exist and cause precision to decline with set size in iconic memory conditions, however, the sequential presentation in Experiment 3 should have at least lessened the influence of such processes. In addition to limitations at encoding, retrieval processes may play a role. When the item probe appears, it must be interpreted and used to select one of several items currently held in iconic or working memory. There are known costs associated with the process of withdrawing attention from irrelevant information in an effort to focus attention on a cued item (e.g. Posner, 1980). It is also clear that attention plays a central role in working memory (Fougnie, 2008; Gaspar, Christie, Prime, Jolicœur, & McDonald, 2016) and iconic memory (Mack, Erol, & Clarke, 2015; Persuh, Genzer, & Melara, 2012), and attending to an item in memory may employ similar mechanisms as selecting a viewed target among distractors. Such a retrieval limitation would explain why set size effects plateau in working memory but not iconic memory conditions: in working memory conditions there are only a few items available to retrieve regardless of set size, whereas there are far more in iconic memory conditions, such that interference continues to grow well past set sizes near three. This account does not, however, explain why precision declines only marginally across the iconic memory and working memory conditions in Experiments 1b and 1c, replicating previous findings that longer retention intervals primarily affect the probability that items are stored in memory at all (Pratte, 2018, 2019). Although there may be limitations at perception, encoding, storage and retrieval that play a role in causing precision to decline with set size, no one process seems an obvious candidate to fully explain the observed effects.

Here we tested the idea that memory precision, as measured by the Zhang & Luck (2008) mixture model, decreases with set size due to an averaging of working memory slots. Our results provide evidence against the notion of slot-averaging, but the degree to which it is nonetheless important to characterize these precision effects depends on whether precision, as measured by the Zhang & Luck mixture model, provides a meaningful measure of memory performance. For example, whereas the Zhang & Luck mixture model assumes that responses from memory follow a Von Mises distribution, a circular analogue of the normal distribution, it has been argued that other distributions provide a more accurate account. For example, even if responses on any particular trial follow a von Mises, the existance of trial-to-trial variability in the precision of that distribution, such as due to differences in stimulus properties across trials (Bae, Allred, Wilson, & Flombaum, 2014; Pratte et al., 2017), fluctuations in available resources (van den Berg et al., 2012), or variabilty in memory decay (Fougnie, Suchow, & Alvarez, 2012), will produce aggregate disributions that deviate substantially from a von Mises distribution. It has also been suggest that in-memory distributions deviate so much from normality that non-parametric approaches, which make few assumptions about the distributional form, should be used (Bays, 2016). Critically, such alternative distributional assumptions will yield different estimates of precision across conditions, such that attempting to characterize how precision varies with set size will require careful consideration of other ongoing questions, such as how to best measure memory precision in the first place.

In addition to critiques of particular distributional assumptions within the Zhang & Luck mixture model, it has been argued that the entire notation of a discrete working memory capacity limit is incorrect, and that the mixture model is therefore altogether misguided. A prominent alternative proposes that working memory is limited not by a fixed number of items, but by a limited pool of memory resources that must be shared across items (Bays & Husain, 2008; van den Berg et al., 2012; Wilken & Ma, 2004). These continuous resource theories propose that memory performance should only be characterized by a unitary measure, and that estimated mixture model parameters (precision and guess rate) provide uninterpretable estimates of this single construct. The debate between continuous resource and discrete capacity theories is ongoing (Luck & Vogel, 2013; Ma, Husain, & Bays, 2014), and we believe it is premature to take any particular statistical measure of working memory performance too seriously. However, examining whether predictions of a particular theory (slots-plus-averaging) hold when using that theory’s own analysis tools (the mixture model) provides a powerful way to test the theory. This approach has recently been referred to as assessing the “self-consistancy” of a theory and its coressponding mathematical instantition (Bays, 2018). When the theoretical predictions fail to hold, as is the case here, then either the particular aspects of the theory that led to the predictions, or the entire theory, should be rejected. The results here suggest that the plus-averaging aspect of the slots-plus-averaging model should be rejected. However, our results do not necessarily imply a rejection of the broader idea of a discrete capacity limit.

Rejecting the “plus-averaging” component of the slots-plus-averaging model has implications for previous attempts to compare discrete capacity theory with continuous resource theories. Formal instantiations of the Zhang and Luck (2008) slots-plus-averaging model are remarkably parsimonious, accounting for data across any number of set size conditions with only two parameters: capacity, and the precision of a single memory slot. However, if precision decrements do not result from an averaging of slots or other memory storage processes, then there is little reason to expect the standard deviation of in-memory responses to follow a square root function of set size as these models assume (c.f. Smith, Corbett, Lilburn, & Kyllingsbaek, 2018). On one hand, abandoning the “plus averaging” aspect of the model does away with some of the parsimony that may have played an important role in cases where it was successful (e.g. Cowan & Rouder, 2009). On the other hand, these formal slots-plus-averaging models have therefore been inappropriately constrained by the “plus averaging” assumption, such that evidence against them (e.g. van den Berg et al., 2012) might have reflected this incorrect assumption rather than core tenets of discrete capacity theories. The idea of a discrete working memory capacity limit has a long history (Miller, 1956), and Zhang and Luck (2008) added the “plus averaging” assumption to this more general theory in light of new data. If the slots-plus-averaging model is rejected due to the “plus averaging” assumption, but not necessarily the “slots” part of the model, then such results do not necessarily say anything about the core prediction of discrete capacity theory: that there is pure guessing when set sizes are greater than a person’s capacity.

To meaningfully compare memory theories by comparing formal mathematical models, it is necessary that the models faithfully represent their respective theories, and that rejections of a model are due to reasons that are central to the theory, and not to a rejection of ancillary assumptions. Unfortunately, however, if slots are not averaged then the slots-plus-averaging model does not provide a good instantiation of the more general discrete capacity theory. Moreover, previous rejections of the slots-plus-averaging model may reflect rejections of the ancillary assumption of slot-averaging, rather than core tenants of discrete capacity theory. Going forward, comparing discrete-capacity and continuous-resource models may continue to be a critical avenue toward understanding working memory. Doing so fruitfully, however, will require a continued development of both discrete and continuous models, to ensure that they are well specified and represent the theories upon which they are based.