Guidelines for Reporting of Figures and Tables for Clinical Research in Urology

Abstract

In an effort to improve the presentation of and information within tables and figures in clinical urology research, we propose a set of appropriate guidelines. We introduce six principles: (1) include graphs only if they improve the reader’s ability to understand the study findings; (2) think through how a graph might best convey information, do not just select a graph from preselected options on statistical software; (3) do not use graphs to replace reporting key numbers in the text of a paper; (4) make sure that graphs give an immediate visual impression of the data; (5) make the figure beautiful; and (6) make the labels and legend clear and complete. We present a list of quick “dos and don’ts” for both tables and figures. Investigators should feel free to break any of the guidelines if it would result in a beautiful figure or a clear table that communicates data effectively. That said, we believe that the quality of tables and figures in the medical literature would improve if these guidelines were to be followed.

Patient summary

A set of guidelines were developed for presenting figures and tables in urology research. The guidelines were developed by a broad group of statistical experts with special interest in urology.

1. Introduction

Graphical representation of data is a cornerstone of medical research. It is hard to imagine the history of medicine without John Snow’s map of cholera cases, Doll and Peto’s plots of the cumulative incidence of lung cancer by smoking status, or the recent Centers for Disease Control plots of opioid deaths with time (Fig. 1). The funnel plot demonstrating publication bias in magnesium clinical trials, also shown in Figure 1, is an example of a single graph that explained what had previously been a mystifying finding, a large trial with opposite conclusions to a prior meta-analysis. It is similarly difficult to imagine the medical literature without well-presented tables of data.

Fig. 1 –

Four classic medical research images: (A) John Snow’s map of cholera cases clustered around the Broad Street pump; (B) Doll and Peto’s plot of lung cancer incidence against smoking; (C) a funnel plot of randomized trials of magnesium for cardiovascular prevention, where the lack of symmetry suggests a publication bias; and (D) opioid deaths in the USA over time.

Yet graphs and tables presented in the medical literature are often of poor quality and risk obscuring rather than illuminating the underlying research findings. Our view is that investigators might benefit from a guide to graphical presentation of data, as well as a guide to presenting data in tables, comparable with our guide on the presentation of statistics [1,2].

In this paper, we provide guidelines for the presentation of data in graphs and tables for clinical research in urology [3]. The guidelines and examples were based on a review of over 400 papers. This set of guidelines is not intended to be completely comprehensive, but to inform submitting authors of common comments that we have provided on prior submissions. Statistical reviewers in these journals will be using the guidelines as a reference when reviewing submitted manuscripts, and will direct submitting authors to read and implement these guidelines or, if deviating, to provide substantial support for their decision about not to do so. There are two parts to the guidelines on figures: a set of principles and some specific “dos and don’ts”. This is followed by guidelines on tables. Note that in the following sections, references to the “statistical reporting guidelines” refer to the “Guidelines for Reporting of Statistics for Clinical Research in Urology” [1] that were copublished by the four major urology journals and which have been adopted more widely since.

2. Introductory remarks

Tables and figures should complement, rather than duplicate, the text in a manuscript. Salient points should be described in both the text and a table and/or graph. The order of tables and figures should allow a reader to flow seamlessly between these and the text. Tables are predominately used to report numerical findings in greater detail than would be appropriate in the text. Figures are generally used to give an immediate impression of the data that is not easy to convey with words or numbers. It takes time and thought to develop tables and figures that enhance a paper. This is time well spent, as their content and appearance can be critical to the acceptance of that paper in the scientific community.

3. Principles for graphical presentation of data

3.1. Include figures only if they improve notably the reader’s ability to understand the study findings

Investigators commonly include graphical representations that add little to the paper [4]. An example is shown in Figure 2. It is hard to know what the figure adds beyond a simple tabulation of results (shown in Table 1). Authors should carefully evaluate each proposed figure and ask themselves whether it materially aids in the understanding, perhaps by considering whether omission of the figure would weaken the paper. One example is Kaplan-Meier plots: the current default seems to be for authors to include a survival curve for any analysis of time-to-event data. Such plots do not always add important information to a paper: consider a case where the event rate was low and most patients were followed for a long time. Authors need to think through exactly why they are including such a plot.

Fig. 2 –

A bar chart showing volume of patients presenting with different stages of cancer. Comment: this is an example of a graph that is not useful because it does not importantly improve readers’ understanding of the data compared with a table.

Table 1 –

The data underlying Figure 2

Cancer state	Number (%)
I	1055 (14)
II	2531 (33)
III	2559 (34)
IV	1491 (20)

Number (%) of patients presenting with different stages of cancer.

3.2. Think through how a graph might best convey information, do not just select a graph from preselected options

One suspects that many figures in scientific papers result from authors selecting options from a dropdown menu within analytical software. For example, in Figure 3, it is hard to imagine an investigator sitting down, carefully thinking through the problem, and concluding that the best way of illustrating the effects of a drug treatment would be a three-dimensional set of blocks. The figure was created probably because this type of graph is one of the standard options in Microsoft Excel. We recommend instead that investigators think through ways of illustrating their data completely independently of their software, mocking up possibilities using a whiteboard. The appropriate graphical representation of data can then be programmed in the statistical software. In our experience, it is rare that preset graphical defaults can be used outside of standard plots such as a calibration plot, decision curve analysis, forest plot, or survival curve. Figure 4 shows the same data as in Figure 3 but based on a carefully thought through plan as to how best to illustrate the findings of the study. Creation of Figure 4 involved writing additional code in Stata statistical software, rather than simple use of one or other presets. Note how Figure 4 shows data on individual patients and provides a clear visual impression that older patients tended to have larger changes in kidney function scores and that the drug use was associated with a larger increase in kidney function, although the impact of the drug was not seen in younger patients.

Fig. 3 –

A bar chart showing change in kidney function scores in a trial of drug versus placebo, separately by age group. Comment: this sort of three-dimensional bar chart is often presented simply because it is a standard option in spreadsheet packages (such as Microsoft Excel), but it is difficult to read and including a third dimension does not improve our understanding of the data. Note also that the x-axis text is difficult to read.

Fig. 4 –

Age at treatment versus change in kidney function scores for drug (blue) and placebo (red). Dots represent individual patients; the regression lines show change in function by age for placebo and drug group separately. Comment: the graph is from the same data set as Figure 3, but shows individual patient data and illustrates the relationship between age, treatment, and outcome much more clearly.

3.3. Do not use graphs to replace reporting key numbers in the text of a paper

A figure is a graphical representation of data. As such, inclusion of numbers on a graph is sometimes duplicative and can distract the reader from the visual impression. More critically, key estimates cannot be reported in a graphical form only. Figure 5, for instance, shows pain scores over time in a randomized trial. It would be inappropriate for the “Results” section of the paper to state merely that “the results of the trial are shown in Figure 5,” as this would require the reader to read across from a line to a value on the y-axis to obtain exact values. Figure 5 would need to be accompanied by a table such as that shown in Table 2, which gives the data plus key estimates such as the difference between groups and a 95% confidence interval (CI).

Fig. 5 –

Mean pain scores (95% confidence intervals) at baseline, after treatment, and at long-term follow-up in groups A and B. CI = confidence interval. Comment: this sort of graph is reasonable to present but should not be used instead of reporting the numerical results of a randomized trial (eg, means and standard deviations at each time point; differences between groups along with a 95% CI).

Table 2 –

Mean and mean differences in pain scores at various points of follow-up, the data for Figure 5

	Placebo (N = 50)	Drug (N = 50)	Difference	95% CI	p value
Baseline	6.0 (0.47)	5.9 (0.59)	0.1	−0.2, 0.3	0.6
1 mo	3.1 (0.44)	2.0 (0.55)	1.0	0.8, 1.2	<0.0001
6 mo	4.0 (0.43)	3.9 (0.55)	0.1	−0.1, 0.3	0.2

CI = confidence interval.

The difference is calculated as the mean pain score in the drug arm subtracted from the mean pain score in the placebo arm. The p values are generated from the Wald test.

3.4. Ensure that graphs give an immediate visual impression

The adage “a picture is worth a thousand words” expresses the idea that a graph expresses information in a manner not easy to replicate with text. One only has to glance at the graphs shown in Figure 1 to know immediately that cholera cases are clustered, that smoking dramatically increases the risk of lung cancer, that we have an opioid crisis, or that the results of magnesium trials are subject to a publication bias. Moreover, none of those graphs could be replaced with a short sentence or table that could give a comparable impression. On the contrary, consider Figure 6, a boxplot: it is true that this shows a median age of 65 yr, with quartiles of 58–71 yr, and that few patients are <40 or above 90 yr. However, the time it takes to work that out from the inspection of the figure is not much different from the time it takes to read the one-sentence description of the findings. Figure 2 similarly fails to give a visual impression that is stronger or quicker than presenting the numbers in Table 1; Figure 3 gives no strong visual impression at all. We note that there are examples of graphs that do not necessarily give an immediate impression but reward concentrated attention with detailed and nuanced information. However, these are rare, especially in the medical research literature, and we hold that giving an “immediate impression” is a good general rule of thumb.

Fig. 6 –

A box plot of age for patients with csPCa at biopsy. csPCa = clinically significant prostate cancer. Comment: this is an example of a box plot that does not give much additional information compared with standard descriptive statistics such as the median and interquartile range. For where it is useful to show a distribution visually, good alternatives to box plots include violin plots, spike histograms, and ridgeline plots, such as that shown in Figure 9.

3.5. Make the figure beautiful

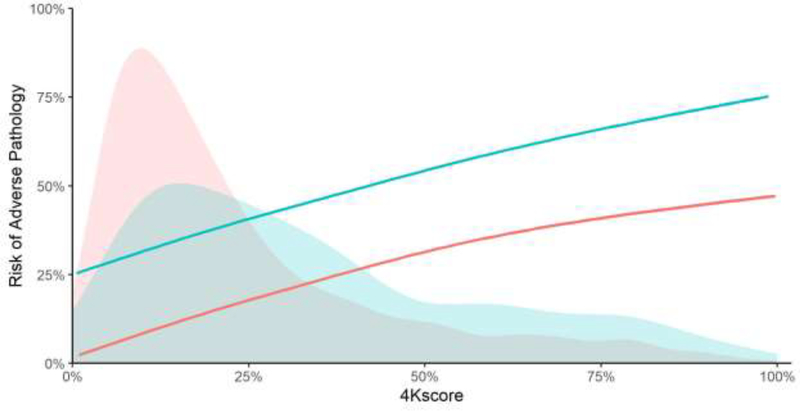
All too often, figures are not visually attractive. Take Figure 7, which is a standard print out of a Kaplan-Meier plot from R; note how the censoring hash marks obscure the survival curve. Additionally, Figure 8 is visually unattractive, as there are too many gridlines and axis labels making the graph appear cluttered, unusual plot marks, and an ugly color scheme. Figures 9 and 10 are attractive to look at: clean lines, uncluttered, and clear space. In Figure 9, we see the distribution of intact-to-free prostate-specific antigen (PSA) ratios separately for eight different cohorts in one condensed figure. We can easily see that the mean intact-to-free PSA ratio is higher in the Southern Community Cohort and also that the distribution is different from that of the other cohorts. Figure 10 shows predicted risks of adverse pathology for different values of a marker, as well as the distribution of marker scores, separately for two different groups. It shows that, although risks are higher in one group, risk distributions are largely overlapping. It also allows the reader to get an idea of the risk associated with particular marker scores.

Fig. 7 –

Kaplan-Meier curve for overall survival. Dotted lines represent 95% confidence intervals and the hash marks represent censoring times. Comment: this is an example of a graph that is visually unattractive, particularly due to the use of dotted lines for the 95% CI and the inclusion of censoring marks, which makes it difficult to follow the curve. Figure 12 shows a more attractive version of a survival plot.

Fig. 8 –

Scatterplot of age versus total PSA at treatment. PSA = prostate-specific antigen. Comment: this is an example of a visually unattractive graph due to the use of excessive gridlines, dense axis numbering, capitals on axis labels, uncommon plot marks, and ugly colors.

Fig. 9 –

Distributions of intact-to-free PSA ratio separately by cohort. AA = African American; MDC = Malmö Diet and Cancer study; MEC = multiethnic cohort; Opko = Opko validation study; PLCO = Prostate, Lung, Colorectal, Ovarian screening study; PSA = prostate-specific antigen; SCC = Southern Community Cohort. Comment: an example of a visually attractive graph that provides a great deal of information and an immediate visual impression, namely, that the data from the SCC cohort are quite different from the others.

Fig. 10 –

Risk of adverse pathology against 4Kscore for men with Gleason grade 3 + 3 (pink) or Gleason grade 3 + 4 (blue) disease on biopsy. The shaded areas give the distributions of 4Kscore for patients with respective Gleason scores. The lines give the association between the predicted risk of high-grade disease on biopsy, represented by the 4Kscore, and the observed risk of adverse pathology. Comment: a visually attractive graph that provides a good deal of information.

3.6. Make the labels and legend clear and complete

Legends and labels on graphs should be fully self-explanatory. Acronyms should be avoided unless these are widely used. Legends can be lengthy if required; indeed, they should be sufficient to understand the graph without a reader needing to refer to the text. As examples of some common errors, Figure 5 refers to groups A and B in the legend rather than referring to drug and placebo, the legend for Figure 6 refers to “clinically significant prostate cancer,” whereas it would be preferable to state “age for patients with clinically significant prostate cancer, defined as primary Gleason pattern 4 or clinical stage T2b or higher”, and the x-axis for Figure 11 is labeled as “analysis time” rather than months or years. That said, it is not always preferable to rely on legends where, for instance, a label can be placed inside the graph in proximity to the curve being labeled (see Fig. 1 for two examples).

Fig. 11 –

Kaplan-Meier curve for metastasis-free survival by treatment group. The gray line represents those who underwent RT and the black line those who underwent RP (log-rank p < 0.0001). CI = confidence interval; HR = hazard ratio; RP = radical prostatectomy; RT = radiotherapy. Comment: this is a graph that is not visually attractive, includes results from a different analysis (ie, a Cox model), and has a vague label (time from when? unit of measurement) that is not capitalized and does not show number of patients at risk. Figure 12 shows an example of an attractively presented survival curve.

A list of dos and don’ts for graphical presentation of data is as follows:

1. Label all axes and ensure that the entire text is readable easily. Figures from software often include default labels that are unreadable or squashed up against an axis. Use an appropriate font size so that numbers and letters are easy to read. If use of abbreviations is unavoidable, these should be explained in the caption.

2. Include leading “0”s (eg, “0.5” rather than “.5”).

3. Consider reporting percentages rather than proportions (eg, “50%” rather than “0.5”) when reporting rates or probabilities.

4. Be consistent across figures in a paper. Use similar fonts, color schemes, and labels. If there is text on a graph, make sure that it is in a consistent place on each figure.

5. Consider adding distributions to line plots. For example, in Figure 10, distribution of the marker score in each grade group is easily identifiable and color coordinated with the corresponding regression line within each subgroup. This gives an immediate impression to the reader that the regression line for grade 3 + 3 is based on a majority of data in the ranges of the 4Kscore under 25%, whereas in grade 3 + 4, we have more data in the higher ranges of the 4Kscore.

6. Report the number at risk per arm in a risk table below Kaplan-Meier figures and consider including CIs. For example, in Figure 12, the number of patients at risk at various follow-up times is clearly indicated within each treatment arm. If this is done, then censoring marks should be avoided.

7. Use numbers and text added to a figure sparingly. Numbers and text should explain the figure (eg, labeling axis or line) and should not add information such as a p value or estimate. For example, in Figure 11, we have a Kaplan-Meier figure that superimposes a table onto the graph. The analysis in the table corresponds to a multivariable model when what is presented in the figure is unadjusted cumulative probabilities. The estimate and p value could be indicated in the figure legend, where it would be possible to explain that they are from an adjusted analysis and would not clutter the figure.

8. Provide an adequate description to explain the meaning of error bars in graphs (eg, 95% CI vs reference range vs standard deviation).

9. Do not use subfigures merely to condense the figure count if the graphs are unrelated. Subfigures should be closely related.

10. Do not present receiver operating characteristic (ROC) curves. They rarely, if ever, tell us more than the area under the ROC curve (see 5.7 in the statistical reporting guidelines).

11. Do not include values that are undefined for the outcome. For example, a plot of predicted risk should include values only in the range of (0, 1). If a CI is extending past these bounds, consider alternative means of estimation.

12. Do not use pie charts. Pie charts have a low “data-to-ink” ratio, and rarely give a visual impression of the data that is more immediate or informative than a table of proportions. Moreover, pie charts are difficult to read if some categories are of low prevalence.

13. Do not use bar charts. Figure 13 shows a bar chart of adverse events from a chemotherapy trial. The same data are presented using a dot plot in Figure 14. Note how the dot plot is less cluttered, with a better “data to ink” ratio, and gives a better immediate impression of the data.

14. Consider the ratio of white space to informative data. Truncating axes in order to avoid excessive white space and focus in on key parts of a figure can improve figures.

15. Be mindful about tails. Presenting data in tail areas of sparsity can be misleading, and inclusion of outliers can obscure visualization of the data.

16. Truncate follow-up for Kaplan-Meier figures when the number at risk is low. The tail of a Kaplan-Meier distribution can be very unstable. A good rule of thumb is to truncate follow-up when the number at risk in any group falls below 5 (or even 10).

17. Do not use three-dimensional (3D) plots to represent 2D data. In Figure 3, for instance, the extra dimension in the 3D plot does not provide additional information. Two-dimensional plots are cleaner and easier to read.

18. Do not use colored or dark backgrounds. Use white or light gray and keep the image clean.

19. Do not use hatching or patterned shading. Fills such as dots or diagonal lines are often visually unattractive, particularly when different types of fills are used in the same plot.

20. Draw the graph to scale. When the underlying distribution of a categorical variable is continuous, the distance between categories must represent the actual difference. For instance, if data were collected on patients at 1, 3, 6, and 12 mo after treatment, the gap between 6 and 12 on the x-axis must be twice of that between 3 and 6; do not use even spacing for all four time points.

21. Do not use box and whisker plots unless there is a good reason. Box plots do not provide a sense of where observations are clustered; it simply provides information on the minimum, maximum, quartile 1, median, and quartile 3, and on potential outliers. For example, the 25% of patients represented in the upper whisker could be uniformly distributed within this whisker ranging from quartile 3 to the maximum value, or all 25% of patients could have the maximum value. Good alternatives to box plots include violin plots, spike histograms, and ridgeline plots such as the one shown in Figure 9.

22. Distinguish between multiple lines using different dashes, clearly different shades of gray (eg, very pale, medium, and black), or different colors.

23. Refer to all figures in the text.

24. Include an informative figure title. The figure title does not need to entirely spell out all findings, but an interpretation of the figure and a citation within the text is required. For example, in reference to Figure 4, the following is an example of interpretation that is included in the text: “Older patients tended to have larger changes in kidney function scores. The drug was associated with a larger increase in kidney function, although benefit was not seen in younger patients.” The title of the graph is much simpler.

25. Use figures to illustrate the association between a continuous predictor and the outcome (see guideline 4.8 of the statistical reporting guidelines).

26. Turn off legends and labels automatically created by software. These tend to be clunky (eg, a blue box labeled “x = 1” and a red box labeled “x = 0”). Either add labeling to the graph (eg, labeling curves at the point of maximum separation) or use the figure caption to provide appropriate information.

27. Use appropriate wording for the x-axis of a Kaplan-Meier plot, including units of time and the definition of time zero. Too often, the x-axis is labeled as “time” or “months” rather than “years from diagnosis” or “months from surgery”. Avoid using days as the unit unless events occur over a brief period of time; it is better, for instance, to have a survival probability given at 5 yr than at 1750 d.

28. Use appropriate labeling for the y-axis of a Kaplan-Meier plot. See guideline 4.13 from the statistical reporting guidelines that describes differences between, for instance, “disease-free survival” and “disease-specific survival.”

29. Consider cumulative incidence curves instead of truncating the axis of a Kaplan-Meier plot. For instance, if the survival probability at the maximum follow-up time was 0.92, instead of showing the y-axis from 0.9 to 1, it would be preferable to show a cumulative incidence curve with a y-axis of 0 to 0.1.

30. Do not show separate CIs for patient groups if the study was designed to make inferences about group differences. This is guideline 4.5 in the statistical reporting guidelines. For instance, Figure 5 shows data from a randomized trial with 95% CI shown for each group separately. However, the study question here concerns differences between groups, and so the estimate and associated 95% CI should, accordingly, be for group differences. See section 6 (“Taking it further”) below for ideas on how to present group differences graphically.

Fig. 12 –

Kaplan-Meier curves for recurrence-free survival in stage I (blue line) versus stage II (red line) disease, with 95% confidence interval illustrated with corresponding gray lines. Comment: a good example of well-presented Kaplan-Meier plot.

Fig. 13 –

A bar chart of adverse events in a randomized trial with two treatments, stratified by treatment and region. Ab = abdominal; COAD = chronic obstructive airway disease; GI = gastrointestinal; Resp = respiratory; URTI = upper respiratory tract infection; UTI = urinary tract infection. Pairs of bars correspond to standard chemotherapy (blue) compared with a novel regimen (red). Data are modified from those provided in the work of Heiberger and Holland [7].Comment: bar widths convey no information and take up space that could be used to include more categories. Proportions of zero are problematic since they have bar heights of zero so that bars disappear. It is not easy to see key differences between groups or to compare the European and North American setting.

Fig. 14 –

A dot chart of the same data used in Figure 13. This follows the work of Cleveland [6] and is arranged horizontally for easy viewing of category labels. Red dots are for standard chemotherapy and blue dots for a novel chemotherapy regimen. Ab = abdominal; COAD = chronic obstructive airway disease; GI = gastrointestinal; Resp = respiratory; URTI = upper respiratory tract infection; UTI = urinary tract infection. Comment: superpositioning of two treatment estimates on the same line saves space and allows for easy treatment comparisons. Adverse event categories are sorted in the order of the treatment differences in proportions, ignoring the region. One can see more easily which events are with the largest differences in incidences between treatments, and larger differences in proportions occur for more common adverse events. In addition, adverse events are sorted in descending order of differences between treatments in North America, making it easy to compare between the two geographical locations.

4. Guidelines for presenting tables

1. Avoid repeating in the text the results reported in the tables. Refer to all tables in the text by providing a general summary or overall interpretation. For example, avoid text such as the following: “Baseline characteristics are shown in Table 1, in cohort 1 median age was 64 (quartiles 58, 68) and 36% had a prior negative biopsy.” A better alternative would “Baseline characteristics by study cohort are shown in Table 1. The cohort is generally typical of men undergoing biopsy other than the high rate of prior negative biopsy, related to the study site being a tertiary referral center.”

2. Avoid inclusion of columns or rows that can be derived easily based on the data already provided. This is given as guideline 4.2 in the statistical reporting guidelines. Common errors include presenting data for groups both separately and combined (eg, if median age is 64 yr in cohort 1 and 69 yr in cohort 2, we do not need to be told that the median age in all the cohorts as a whole is close to 67 yr), providing two proportions for binary variables (eg, 53% with a family history and 47% with no family history) and providing data in two different ways (eg, giving number with extraprostatic extension and seminal vesicle invasion, and also giving pathological stage).

3. Avoid reporting p values in tables unless you have carefully considered the hypothesis. In many cases, either it is known that the groups are or are not different, or, alternatively, it is not important to know whether they are different or not. In a randomized trial, p values testing baseline characteristics between groups are testing a hypothesis that is known to be true; in short, any apparent differences are due to chance. Conversely, in comparisons of patients receiving different procedures, it is often known that they will differ (eg, Gleason grade in patients managed by surgery vs active surveillance). In the case of large population-based data sets, such as Surveillance, Epidemiology and End Results (SEER) Medicare data, sample sizes are often enormous so that almost any difference will be highly significant and p values are redundant.

4. Be clear about the null hypothesis when reporting p values in tables. One common problem is when there are three groups in a table, and it is unclear whether the p value addresses the null hypothesis that all three groups are the same or a pairwise comparison between two key groups. Similarly, do not report more than one p value in one column without being 100% clear about which p value tests which hypothesis.

5. Keep it simple. Tables with multiple subcolumns or rows can make it difficult for the reader to find information.

6. For categorical variables, a single hypothesis test is preferable to multiple tests at each level of the category. Take, for instance, a table giving demographic characteristics of patients receiving different treatments, where patient education level was categorized into less than high school, high school graduate, college, and postgraduate. It is more appropriate to address the question “is there an association between educational status and treatment?” than multiple questions such as the following: “Compared with patients who did not graduate from high school, do patients who graduated from high school but did not go to college receive different treatments? Is there a difference between no high school education and college education? What about patients who did postgraduate studies?”

7. Avoid unnecessary repetition or tables with empty cells. A typical example would be a table comparing two groups for five different variables, and with an entire column of p values <0.0001. Having a column with “p < 0.0001” repeated five times would be redundant. Instead, a note could be added to the caption stating “all differences statistically significant at p < 0.0001”. Similarly, avoid repeating text such as “standard deviation” (SD) or “95% CI”. Instead, use column headers such as “Proportion (95% CI)” or “Mean (SD)”. Empty cells across rows can be avoided by techniques such as specifying the reference category with an asterisk rather than by having a row specifying the reference group. As pointed out in the statistical reporting guidelines [1], it is also important to avoid table rows or columns if the reported data can be deduced readily from other rows or columns. For instance, there is no need to have any of the following: a column giving data for the full cohort if there are already columns for the treatment and control groups, rows for both the binary options (eg, 60% of the cohort were men and 40% were women), and rows using different categorizations of the same variable (eg, frequency and percentage both for stages T1, T2, T3, and T4 and separately for localized vs advanced disease).

8. Indicate the number of patients and missing data. If missing data are found in only a subset of variables, the number of patients can be indicated in column headers. Missing data can be indicated in several different ways: in row headers (eg, “Total PSA at diagnosis [ng/ml; N = 992]” in Table 1), as a row title (eg, “T1, T2, T3, T4, Missing” as a separate row under clinical stage), or with footnotes (eg, “Clinical stage *. Footnote: * Clinical stage data missing on two patients”). Be clear as to the statistics reported. The title of a table should indicate which statistics are reported, stating, for instance, “median (interquartile range) or number (%)”. Statistics should be kept consistent within the table (eg, avoid switching from Fisher’s to χ² or from median to mean). If there is a good reason to switch between different statistics in the same table, include a footnote to indicate the values that deviate from the standard and give the rationale.

9. Follow the statistical reporting guidelines for the statistics presented in tables. For instance, for descriptive statistics, medians and quartiles are preferred to means and standard deviations, range is to be avoided, appropriate levels of precision has to be used, and predictors have to be rescaled so that statistics such as odds ratios are interpretable (eg, giving an odds ratio per 10-yr increase in age so as to avoid an odds ratio per 1 yr, such as 1.01, 95% CI 1.00, 1.01).

10. Include clear labels, specify units, and make the reference group clear when reporting odds or hazard ratios. If use of abbreviations is unavoidable, spell out the abbreviations in the table footnotes.

11. Avoid splitting categorical variables into too many separate categories. For instance, there are nine different clinical stages for prostate cancer, but it is rarely, if ever, worth having nine separate rows for each stage in a table. Far more common is to group stages into five categories: T1a, b, or c; T2a; T2b; T2c; and T3a, T3b, or T4).

12. Use formatting that makes tables easy to read for the reviewer. The row specifier (left hand) column should be left justified, while the columns containing data should be centered. Use indents for subcategories (eg, left justify “Gleason grade group” and then use indents on the next lines for groups 1, 2, 3, and 4–5) as in Table 2. It can be helpful to use bolding for the column headers.

13. Avoid using the “±” notation. Specify standard deviation or 95% CI.

14. Avoid including too much data in a single table. Split a long or wide table into two tables. For instance, if an author wants to describe 25 different baseline variables, it would be better to have two separate tables for disease versus demographic variables rather than one table with 25 rows. Considering how a table fits on a page in a wordprocessing program often gives a clue as to how it would look on a journal page.

15. Present detailed information in tables when there is a likelihood that a reader will need such details. Tables are not meant for quick impressions but for looking up information. There is obviously a balance between, on the one hand, providing a wide variety of statistics that could be of interest, and, on the other hand, providing so many numbers that it is difficult to find key statistics. However, unlike the text of a scientific paper, which is meant to summarize key findings, tables are the correct places in a paper to include detailed information.

5. Example tables

Note how Table 3 demonstrates guideline 2 (there is no column for the “entire cohort”; similarly, percentages are not given separately for prior vs no prior negative biopsy), guideline 6 (p values given comparing stage and grade overall by cohort, rather than individual grades and stages being compared), guideline 8 (number of patients and missing data clearly indicated), guideline 9 (follows the statistical reporting guidelines, including appropriate levels of precision), guideline 10 (labels and units are clear), guideline 11 (grouping of some stage or grade categories), and guideline 12 (the table is well formatted). Table 4 demonstrates guideline 5 (p values given comparing stage and grade overall by cohort, rather than individual grades and stages being compared), guideline 9 (follows the statistical reporting guidelines, including appropriate levels of precision and rescaling predictors so that the odds ratio is interpretable), guideline 10 (labels and units are clear), and guideline 12 (the table is well formatted).

Table 3 –

Characteristics of participants by cohort

Characteristic	Cohort 1 (N = 501; 50%)	Cohort 2 (N = 499; 50%)	p value *
Age	64 (62, 66)	69 (67, 71)	<0.0001
Family history, n (%)	26 (5.2)	27 (5.4)	0.9
Prior negative biopsy, n (%)	128 (26)	153 (31)	0.079
Total PSA at diagnosis (ng/ml; N = 992)	4.5 (3.5, 5.5)	6.5 (5.5, 7.5)	<0.0001
Clinical T stage, n (%)
T1a/b/c	273 (54)	266 (53)	0.7
T2a	72 (14)	78 (16)
T2b	42 (8.4)	33 (6.6)
T2c	21 (4.2)	28 (5.6)
T3/4	19 (3.8)	16 (3.2)
Missing, n (%)	74 (15)	78 (16)
Gleason grade group, n (%)
1	85 (17)	99 (20)	0.5
2	180 (36)	187 (37)
3	142 (28)	129 (26)
4–5	94 (19)	84 (17)
Education, n (%)
Less than high school	96 (19)	109 (22)	0.8
High school	147 (29)	147 (29)
College	155 (31)	153 (31)
Postgraduate	74 (15)	70 (14)
Missing	29 (5.8)	20 (4.0)

PSA = prostate-specific antigen.

Estimates were given as median (quartile 1, quartile 3) or frequency (percentage).

^*p values were calculated using Wilcoxon rank-sum test for continuous and Fisher’s exact test for categorical variables.

Table 4 –

Multivariable logistic regression to predict locally advanced disease among men with clinical T2 prostate cancer (n = 287)

Variable	Odds ratio	95% Confidence interval	p value
Age at RP (increase per 5 yr)	1.16	0.95, 1.41	0.14
Preoperative PSA (ng/ml) a	NA	NA	0.0009
Clinical T stage			0.038
T2A	Reference	–
T2B	2.03	0.89, 4.63
T2C	3.34	1.08, 9.98
Gleason grade group			<0.0001
1–2	Reference	–
3	1.99	0.96, 4.12
4	3.85	2.01, 7.37
BRCA1	1.72	0.76, 3.91	0.2

NA = not available; PSA = prostate-specific antigen; RP = radical prostatectomy.

^aNonlinear terms (cubic splines) used.

6. Taking it further

This paper aimed only to help authors avoid the most common errors in the presentation of figures and tables. Interested readers may want to take it further and think about how they could present their research findings using innovative approaches. The senior author Frank Harrell has created a web page of graphical ideas (at datamethods.org/t/journal-graphics). This resource, best accessed using Firefox, Chrome, or Safari browser, describes enhanced scatter and line plots, extended box plots, spike histograms, CIs for differences in survival curves, use of interactive graphics in online supplements, and more. We invite readers to add their own suggestions, ideas, questions, and links to that site. The site also has links to course handouts, videos, and presentations listing principles for designing high-quality graphs and demonstrating how to apply these principles in practice, including R code in many examples. Co-author Daniel Sjoberg has created gtsummary, a suite of widely used R functions for presenting data in tables that follow these guidelines. The package is available from CRAN. Readers are also advised to see the work of Tufte [5] and Cleveland [6].

7. Concluding remarks

These guidelines and examples are meant as a resource for investigators submitting clinical research in urology for publication, to assess whether their submissions can be improved. Investigators should feel free to break any of these guidelines if it would result in a beautiful figure or a table that communicates data effectively. That said, we believe that the quality of figures and tables in the medical literature would improve if submitting authors were to incorporate the guidelines when considering how to present data.