Control of Solvent Dynamics around the B₁₂-Dependent Ethanolamine Ammonia-Lyase Enzyme in Frozen Aqueous Solution by using Dimethyl Sulfoxide Modulation of Mesodomain Volume

Abstract

The temperature-dependent structure and dynamics of two concentric solvent phases, the protein-associated domain (PAD) and mesodomain, that surround the protein, ethanolamine ammonia-lyase (EAL) from Salmonella typhimurium in frozen polycrystalline aqueous solution are addressed by using electron paramagnetic resonance (EPR) spectroscopy of the paramagnetic nitroxide spin probe, TEMPOL, over the temperature (T) range, 195–265 K. Dimethyl sulfoxide (DMSO; added at 0.5, 2.0 and 4.0 % v/v), and present at the maximum freeze concentration at T≤245 K, varies the volume of the interstitial aqueous-DMSO mesodomain (V_meso), relative to a fixed PAD volume (V_PAD). The increase in V_meso/V_PAD from 0.8 to 6.0 is quantified by the partitioning of TEMPOL between the two phases. As V_meso/V_PAD is increased, Arrhenius parameters for activated TEMPOL rotational motion in the mesodomain remain uniform, while the parameters for TEMPOL in the PAD show a progressive transformation toward the mesodomain values (higher-mobility). An order-disorder transition (ODT) in the PAD is detected by exclusion of TEMPOL from the PAD into the mesodomain. The ODT T value is systematically lowered by increased V_meso/V_PAD (from 215 to 200 K), and PAD ordering kinks the mesodomain Arrhenius dependence. Thus, there is reciprocity in PAD-mesodomain solvent coupling. The results are interpreted as a dominant influence of ice-boundary confinement on PAD solvent structure and dynamics, that is transmitted through the mesodomain, and which decreases with mesodomain volume at increased added DMSO. The systematic tuning of PAD and mesodomain solvent dynamics by variation of added DMSO is an incisive approach for resolution of contributions of protein-solvent dynamical coupling to EAL catalysis.

Graphical Abstract

INTRODUCTION

The configurational states characteristic of a native, folded protein monomer or subunit at room temperature (T) are linked by a hierarchy of fluctuations among positions of the polypeptide backbone, and amino acid side chains and substituents.^1–2 The presence of solvent water is necessary to enable the native protein configurational fluctuations.³ In the dehydrated state, amplitudes of protein motions are severely suppressed.⁴ Study of partially hydrated protein powder samples by using scattering techniques and dielectric spectroscopy indicate that graded addition of water up to a hydration level (h, g water/g protein) of ~0.5 increases the amplitudes of a broad spectrum of collective and local motions,^4–5 that are akin to the α- and β-fluctuations, respectively, that are described for glass-forming solutions. At h~2, a two water molecule-thick, “protein hydration layer” (~6 Å) surrounds the protein, which is sufficient to support basic native protein functions, such as small-molecule migration through the interior.¹ The presence of additional, “bulk” water around the hydration layer enables larger-scale configurational fluctuations of the protein, which allow small molecule ingress/egress.¹ Reciprocally, unique structural and dynamical characteristics of the protein hydration water extend into the bulk phase.^6–7 Understanding the interplay of protein, hydration and bulk solvent dynamics is essential for molecular-mechanistic description of the chemical steps,^8–9 and conformational steps that bracket them,^10–11 in enzyme catalysis. Here, we address the dynamics of two distinct solvent components that surround the protein, ethanolamine ammonia-lyase (EAL; EC 4.3.1.7),¹² from Salmonella typhimurium, by using electron paramagnetic resonance (EPR) spectroscopy of the paramagnetic nitroxide (aminoxyl) spin probe, TEMPOL,¹³ in a frozen polycrystalline aqueous solution system¹⁴ over the wide temperature (T) range of 195–265 K. Dimethyl sulfoxide (DMSO) cosolvent (added prior to freezing at 0.5, 1.0,¹⁴ 2.0, and 4.0 % v/v) is used to manipulate the solvent dynamics.

During freezing of the low-concentration DMSO solutions, an interstitial mesodomain^15–17 is created by the exclusion of DMSO from the growing ice crystallite domains. TEMPOL is also excluded from the ice domains.^{14, 18} As T descends, the cosolvent concentration in the mesodomain is elevated to the maximum freeze-concentration, which corresponds to the eutectic point in the melting temperature-composition dependence.¹⁵ For aqueous-DMSO solutions, the maximum freeze-concentration is 65% v/v.¹⁹ The aqueous-DMSO in the low-T mesodomain forms a high-viscosity (η) fluid in the T-range of 195–265 K.²⁰ Values of η of 14 – 340 cP over 263 – 218 K, and a calorimetrically-determined glass transition temperature of T_g=145 K, are reported for bulk aqueous 65% v/v DMSO solutions.²⁰ Previous measurements of the T-dependence of TEMPOL spin probe rotational mobility in frozen solutions in the presence and absence of EAL and added 1% v/v DMSO resolved two solvent components that surround the protein:¹⁴ (1) a protein-associated domain (PAD; proposed to correspond to the protein hydration layer), characterized by relatively low TEMPOL mobility, and (2) an aqueous-DMSO mesodomain phase that concentrically envelops the PAD, characterized by relatively high TEMPOL mobility. The assignment of the PAD solvent phase was based on the direct dependence of its volume on varied EAL concentration, with no PAD component observed in the absence of EAL.¹⁴ The mesodomain solvent phase assignment reflected the near-identical T-dependence of TEMPOL mobility in the absence and presence of EAL.¹⁴

The X-band EPR spin probe approach has previously been used to characterize structure and dynamics of mesodomains in frozen, bulk polycrystalline aqueous–sucrose,¹⁸ aqueous-glycerol,²¹ and sub-phases in other solvent mixtures,²² in the absence of protein. TEMPOL rotational motion leads to averaging of the unpaired electron (S=1/2) g- and electron-¹⁴N (I=1) dipolar hyperfine- anisotropies, and a consequent narrowing of the EPR lineshape,¹³ which is quantified by the rotational correlation time (τ_c) obtained from spectral simulations. X-band, continuous wave-EPR is sensitive to TEMPOL tumbling motion in the τ_c range of ~10⁻¹¹ (rapid limit) to 10⁻⁷ s (defined as the rigid limit).²²

Here, we use added DMSO concentrations of 0.5, 2.0 and 4.0 % v/v to vary the volume of the mesodomain (V_meso), relative to a fixed PAD volume (V_PAD) over a range of V_meso/V_PAD from 0.8 to 6.0. TEMPOL rotational motion for each condition is addressed by EPR spectrscopy and simulations over the T-range of 200 – 265 K. The increase in V_meso/V_PAD is characterized by a simple partitioning relation for TEMPOL between the two phases, which supports the model of concentric PAD and mesodomain solvent layers around EAL. An order-disorder transition (ODT) in the PAD is detected, based on exclusion of TEMPOL from the PAD and into the mesodomain. The T-dependent TEMPOL rotational motion in the PAD is facilitated, and the transition T value for the ODT is lowered, by increased V_meso/V_PAD. The results are accounted for in a model of the protein-PAD-mesodomain-ice system, in which solvent-ordering confinement effects^23–25 of the ice boundary and the sub-ODT hydration layer are modulated by the volume of the intervening mesodomain, which is systematically dependent on the amount of added DMSO. The evidenced persistence of local and collective solvent fluctuations in the mesodomain into the cryo-T regime rationalizes the native catalytic performance of EAL under comparable conditions in frozen aqueous solutions.^26–29 The systematic tuning of PAD and mesodomain solvent dynamics by variation of added DMSO is an incisive approach that can be applied to resolve contributions of protein-solvent dynamical coupling to EAL catalysis.

EXPERIMENTAL METHODS

Sample preparation.

All chemicals were purchased from commercial sources, including DMSO (purity, ≥99.9%; EMD Chemical), and deionized water was used (resistivity, 18.2 MΩ·cm; Nanopure system, Siemens). The EAL protein from S. typhimurium was obtained from an Escherichia coli overexpression systems and purified as described,^30–31 with modifications.²⁹ The specific activity of purified EAL with aminoethanol as substrate was 20 μmol/min/mg (T=298 K, P=1 atm), as determined by using the coupled assay with alcohol dehydrogenase and NADH.³² Protein samples included 10 mM potassium phosphate buffer (pH 7.5), 20 μM EAL protein, and 0.2 mM TEMPOL spin probe (4-hydroxy-TEMPO, Sigma-Aldrich; added from a freshly-prepared stock solution in water) in a final volume of 0.3 ml. When present, DMSO was added to 0.5, 2.0, and 4.0% v/v, respectively, relative to the final, 0.3 ml volume of the EPR sample. The EPR samples were prepared aerobically, on ice in small vials, mixed, and loaded into 4 mm outer diameter EPR tubes (Wilmad-LabGlass). The samples were frozen by immersion in isopentane solution at T=140 K. This method has a characteristic cooling rate of 10 K/s.²⁹ Samples were transferred to liquid nitrogen for storage. Samples without EAL protein were prepared by the same methods, in 2 mm outer diameter EPR tubes.

Continuous-wave EPR spectroscopy.

Continuous-wave EPR measurements were performed by using a Bruker E500 ElexSys EPR spectrometer and ER4123SHQE X-band cavity resonator as described.¹⁴ EPR acquisition parameters: Microwave frequency, 9.45 GHz; microwave power, 0.2 mW; magnetic field modulation, 0.2 mT; modulation frequency, 100 kHz; acquisition number, 4–8 spectra were averaged at each T value.

EPR Spectrum Simulations.

The EPR spectrum of TEMPOL in the random-orientation samples arises from the electron Zeeman interaction (defined by the g tensor) and the interaction of the unpaired electron spin (S=1/2) with the nitroxide ¹⁴N nucleus (I =1), which produces three dominant spectral features, that correspond to electron spin-spin transitions between the m_s=±1/2 electron spin energy levels, among m_I=0, ± 1 nuclear spin energy levels.¹³ Simulations of the continuous-wave-EPR spectra were performed by using the Chili algorithm in the program, EasySpin,³³ with a common set of g tensor and ¹⁴N hyperfine tensor parameters, as described.¹⁴ Briefly, simulations required one component for solution-only (-EAL) samples and two components for samples with EAL. For the solution-only samples, the simulations were performed by variation of the rotational correlation time (τ_c) and the corresponding intrinsic line width (“lw” parameter, in EasySpin). The two-component simulations were performed by variation of the correlation times and weights for the slow-motional (τ_c,s; normalized weight, W_s) and fast-motional (τ_c,f; normalized weight, W_f) components, and the corresponding intrinsic line widths. Comparisons of one- and two-component simulations for representative types of line shapes are shown in Figure S1. The X-band, CW-EPR spin probe approach is sensitive to TEMPOL reorientational motion in the τ_c range of ~10⁻¹¹ (rapid reorientation limit) to 10⁻⁷ s (defined as the rigid limit).²²

RESULTS

Temperature dependence of the TEMPOL EPR line shape in frozen aqueous solution with EAL.

The effect of T on the EPR line shape of the TEMPOL spin probe at different representative values from the complete addressed range of 200–265 K is shown in Figure 1 for the EAL, added 0.5, 2.0 and 4.0% v/v DMSO conditions. For all DMSO concentrations, the rigid-limit, powder pattern line shape is observed at the lowest T value, and at the highest T values, the widths of the m_I lines narrow, and the overall spectral width approaches twice the value of the ¹⁴N isotropic hyperfine coupling constant (2A_iso=3.4 mT=96 MHz). The transition from the rigid-limit, powder pattern line shape to initial motional-narrowed spectra, that represent averaging of the g-tensor and electron-nuclear dipolar anisotropy by rotational, tumbling motion of the TEMPOL, occurs at different T values, that decrease with added DMSO concentration. Likewise, the T values at which significant line-narrowing occurs, owing to rapid tumbling, also decrease with added DMSO concentration. Therefore, the line shapes in Figure 1 qualitatively show that increased added DMSO shifts the onset and trend of increased tumbling rate to lower T values.

Figure 1.

Temperature dependence of the TEMPOL EPR spectrum (black), in the presence of EAL, at different added % v/v DMSO, and overlaid two-component EPR simulations (dashed, red). (A) 0.5%. (B) 2%. (C) 4%. The spectra are normalized to the central peak-to-trough amplitude. Alignment along the magnetic field axis corresponds to the microwave frequency at 200 K.

Temperature dependence of the TEMPOL rotational correlation times and normalized component weights in frozen aqueous solution with EAL.

The EPR spectra were simulated³³ to quantify the temperature dependence of the rotational mobility in terms of the τ_c and normalized W values of TEMPOL mobility components (Table I). The T-dependence of τ_c in the presence of EAL at 0.5, 2.0, and 4.0 % v/v DMSO displays two-component behavior, where the two components are characterized by a relatively small τ_c value (denoted as the “fast” tumbling component, τ_c,f) and a relatively large τ_c value (denoted as the “slow” tumbling component, τ_c,s). The dependence of logτ_c on T in Figure 2 (data are presented in Tables S1–S3) is divided into four regions, as follows: Region I: Both logτ_c values lie above the tumbling detection criterion, of logτ_c>−7.0. Region II: A fast-tumbling population is present, with logτ_c,f≤–7.0 and decreasing with T, along with a rigid population (simulated logτ_c,s>–7.0). The T value, at which the logτ_c,f and logτ_c,s values meet the criterion for detectable tumbling of ≤–7.0, T_II/III, marks the boundary of Region II and Region III. The T_II/III value decreases with increasing % v/v DMSO, as previously reported for 1.0 versus 0% v/v DMSO.¹⁴ Region III: Both fast- and slow-tumbling populations are present, with logτ_c,f and logτ_c,s continuing to decrease with T. Figure 2 shows that, for all % v/v DMSO conditions, the normalized weights of the slow component (W_s) and fast component (W_f) display a transition, that is centered near the boundary of Region II and Region III (at T_II/III), at which W_s joins W_f as a detectable tumbling component (Table 1). With increasing T across the transition, there is a shift in population from W_f to W_s. At T>T_II/III, W_f and W_s are constant in Region III. Region IV: The T dependence displays a kink, followed by a subtle trend of increased proportion of W_f, for all DMSO concentrations for T>245 K.

Table 1.

Arrhenius parameters obtained from the temperature-dependence of the rotational correlation times of TEMPOL at 0.5, 1.0, 2.0 and 4.0 % v/v DMSO, in Region III.

Ea (kcal/mol)
DMSO (% v/v)	+EAL PAD	+EAL mesodomain	-EAL mesodomain
0.5	13 ±0.61	8.5 ±0.20	8.6 ±0.39
1.0	11 ±0.73	9.0 ±0.32	8.7 ±0.28
2.0	9.2 ±0.40	7.9 ±0.23	9.0 ±0.42
4.0	9.0 ±0.31	8.5 ±0.12	8.5 ±0.22
-log[τc,0 (s)]
DMSO (% v/v)	+EAL PAD	+EAL Mesodomain	-EAL Mesodomain
0.5	20 ±0.57	17 ±0.19	17 ±0.37
1.0	19 ±0.70	17 ±0.30	17 ±0.27
2.0	17 ±0.39	16 ±0.22	17 ±0.40
4.0	17 ±0.31	17 ±0.12	16 ±0.21

Figure 2.

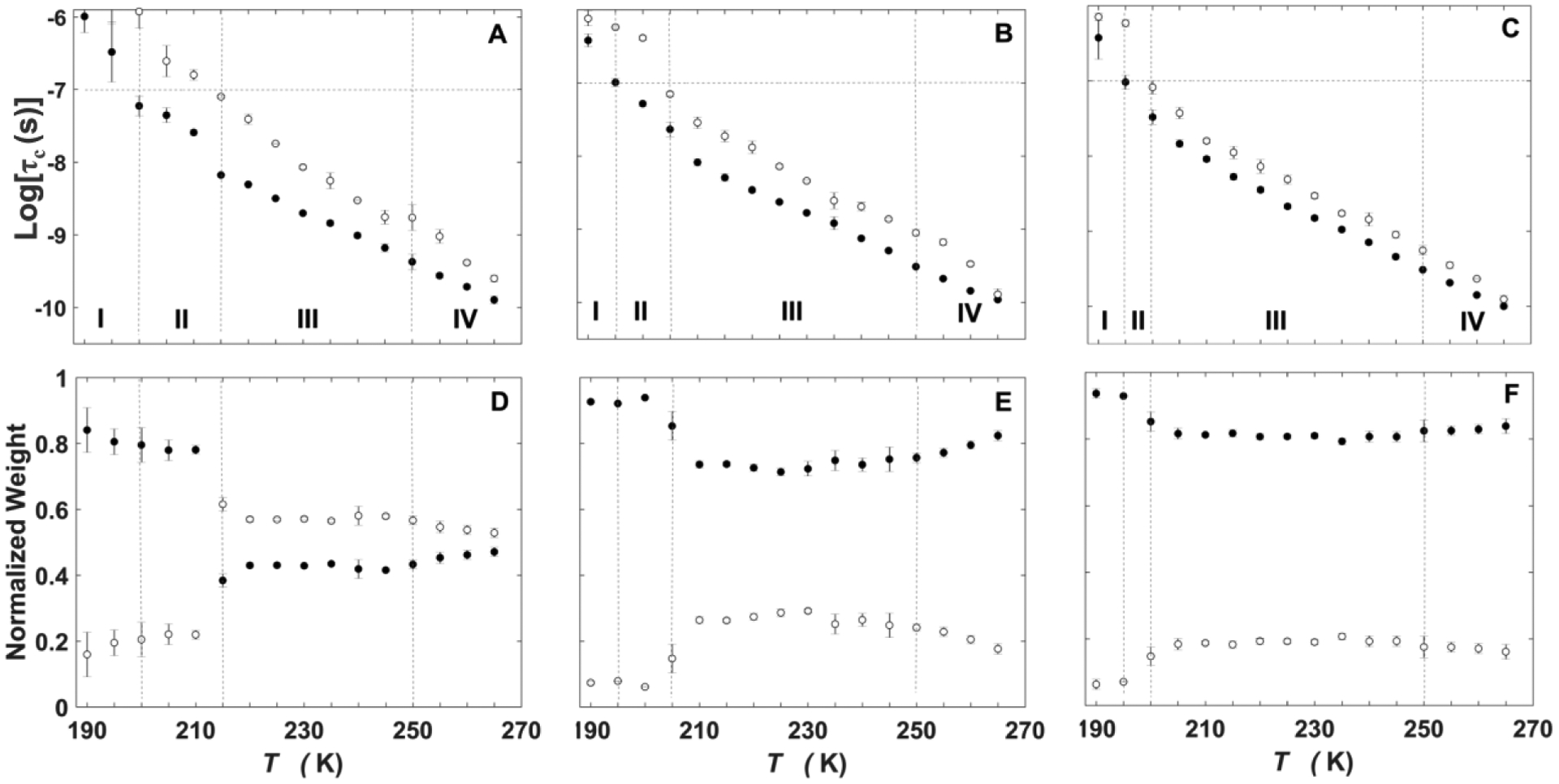
Temperature dependence of the rotational correlation time of TEMPOL and normalized mobility component weights, in the presence of EAL, at different added % v/v DMSO. Rotational correlation time: (A) 0.5%. (B) 2%. (C) 4%. Horizontal line represents upper limit of logτ_c = −7.0 for detection of tumbling motion. Normalized component weight: (D) 0.5%. (E) 2%. (F) 4%. In each panel, solid circles represent the fast component (logτ_c,f, W_f) and open circles represent the slow component (logτ_c,s, W_s). Error bars represent standard deviations for three separate determinations.

Temperature dependence of the TEMPOL spectral line shape in the absence of EAL: 0.5, 2.0 and 4.0 % v/v DMSO.

Frozen aqueous solutions with 0.5, 2.0 and 4.0 % v/v DMSO, in the absence of EAL (–EAL condition), yielded characteristic three-line TEMPOL EPR spectra at all T values (Figure 3). A single component is observed, as reported previously for 1.0% v/v DMSO in the absence of EAL.¹⁴ For all DMSO concentrations, the trend of transformation of the rigid-limit, powder pattern line shape to the motionally-averaged spectrum at higher T values, that was observed for the +EAL samples, is reproduced.

Figure 3.

Temperature dependence of the TEMPOL EPR spectrum (black), in the absence of EAL, at different added % v/v DMSO, and overlaid EPR simulations (dashed red lines). (A) 0.5%. (B) 2%. (C) 4%. The spectra are normalized to the central peak-to-trough amplitude. Alignment along the magnetic field axis corresponds to the microwave frequency at 200 K.

Temperature dependence of the TEMPOL rotational correlation times and normalized component weights in solution, in the absence of EAL.

The EPR spectra for 0.5, 2.0 and 4.0 % v/v DMSO in the –EAL condition (Figure 3) were simulated by using a single mobility component (single τ_c value; data are presented in Tables S4–S6). As shown in Figure 4, the T-dependences of logτ_c,f (+EAL) and logτ_c (-EAL) are comparable for each condition. The results indicate that the W_f components in the 0.5, 2.0 and 4.0 % v/v DMSO, +EAL conditions are associated with a DMSO-aqueous mesodomain phase, as concluded previously for the 1.0% v/v DMSO condition.¹⁴ The logτ_c,s values are distinct from the monotonic logτ_c values obtained for the –EAL condition (Figure 4), indicating that W_s represents a different TEMPOL environment. This pattern has been previously reported in 1.0% v/v DMSO solution in the presence and absence of EAL, where it was established, from the linear dependence of W_s on EAL concentration, that the W_s component originates from the PAD.¹⁴

Figure 4.

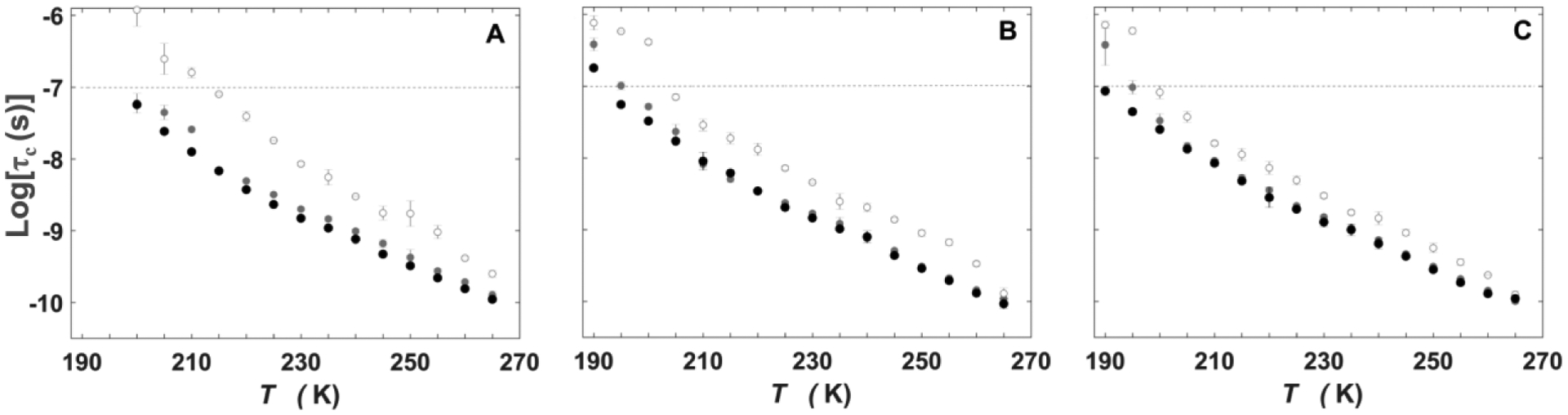
Temperature dependence of the rotational correlation time of TEMPOL, in the absence and presence of EAL, at different added % v/v DMSO. (A) 0.5%. (B) 2%. (C) 4%. In each panel, black solid circles represent the single component, –EAL (logτ_c), and grey solid (fast, logτ_c,f) and open (slow, logτ_c,s) represent components, +EAL. Horizontal line represents upper limit of τ_c for detection of tumbling motion. Error bars represent standard deviations for three separate determinations.

DISCUSSION

Added DMSO resides in the mesodomain.

The W_f and W_s values are constant in Region III at each value of added % v/v DMSO (Figure 2). As the added DMSO increases, the constant value of W_f increases, as W_s compensatorially decreases. This indicates that V_meso increases with added DMSO, relative to V_PAD. Previously, V_PAD was shown to be linearly dependent on EAL concentration, and thus, independent of the relative value of V_meso, at added 1.0 % v/v DMSO_.¹⁴ This is consistent with the previouly characterized exclusion of DMSO from the protein hydration layer, promoting the “preferential hydration” condition, which favors the native state of folded proteins.³⁴ A folded state of EAL in the DMSO-mesodomain system is supported by native cofactor-protein interactions³⁵ and function^36–37 at low T values in fluid, bulk aqueous-DMSO (41 and 50 % v/v) solution. Based on these considerations, we propose that V_meso increases relative to V_PAD, as the added DMSO is increased, and that the larger reservoir of mesodomain recruits a higher proportion of TEMPOL, by mass-action. This model is quantified by using the following expression, that relates the measured W_f and W_s values to the partition coefficient (P) of TEMPOL between the mesodomain and PAD, and the volumes of the two solvent components:

$$\frac{W_s}{W_f}=P\frac{V_{PAD}}{V_{\mathit{\text{meso}}}}$$ (1)

The volume of the mesodomain is dependent on the volume of added DMSO (V_DMSO) as:

$$V_{\mathit{\text{meso}}}={\gamma }_{\mathit{\text{meso}}}{V}_{\mathit{\text{DMSO}}}$$ (2)

where γ_meso is a proportionality constant, that accounts for the hydration of DMSO in the mesodomain. Combination of eq 1 and eq 2 gives:

$$\frac{W_s}{W_f}=P\frac{V_{PAD}}{{\gamma }_{\mathit{\text{meso}}}{V}_{\mathit{\text{DMSO}}}}$$ (3)

A linear relation between W_s/W_f and 1/V_DMSO, consistent with eq 3, is verified (Figure 5). Therefore, a negligible proportion of the added DMSO resides in the PAD, and added DMSO contributes primarily to an increase in V_meso. From the slope of the linear relation, PV_PAD/γ_meso=1.9 μL. The value of γ_meso is related to the maximum freeze-concentration of aqueous-DMSO solution, which is 65% v/v.¹⁹ Thus, for γ_meso=1/0.65, PV_PAD=2.9 μL.

Figure 5.

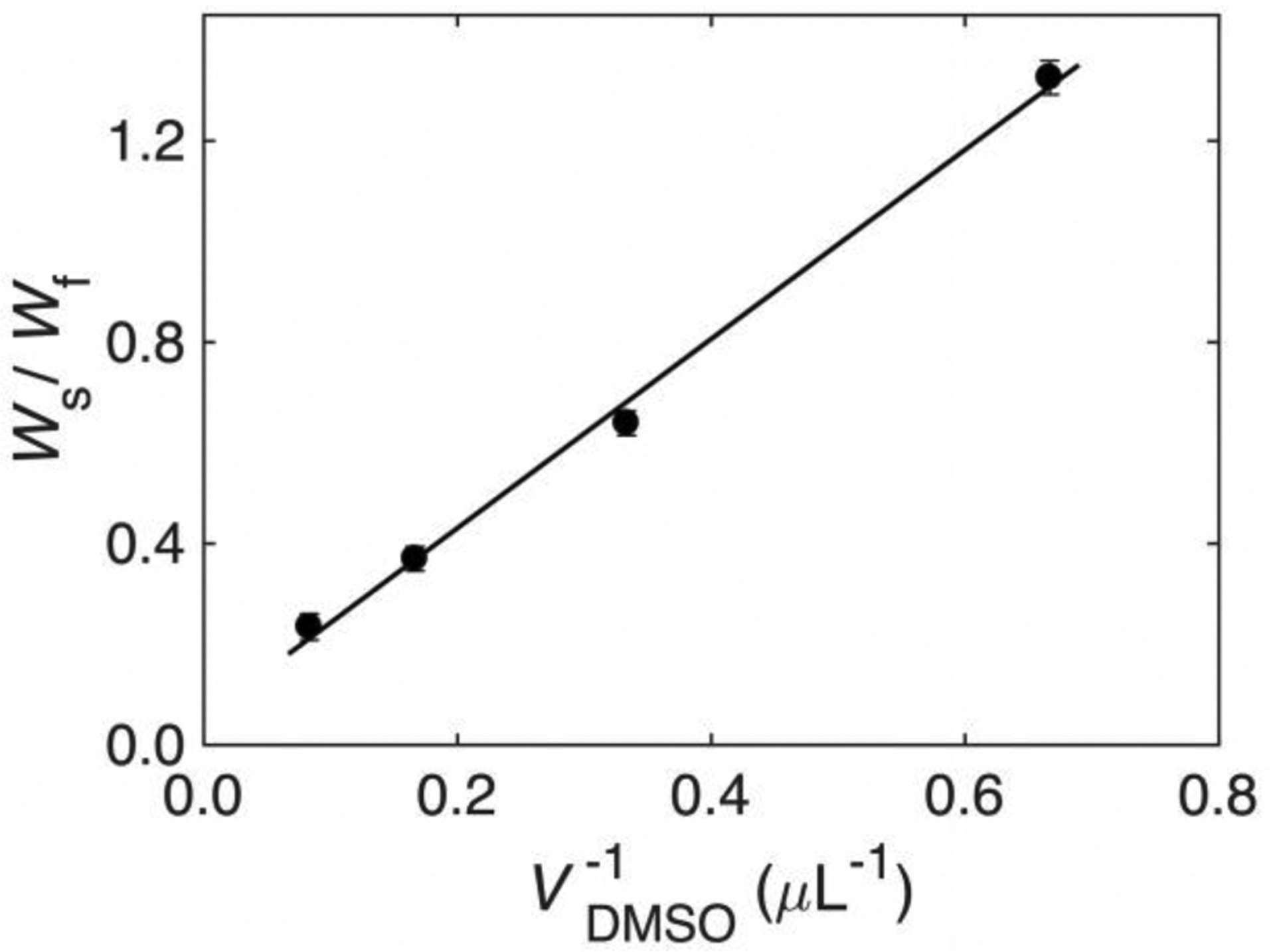
Dependence of the ratio of the slow- and fast-tumbling component weights on the inverse concentration of added DMSO in Region III, and overlaid best-fit linear relation. Error bars represent standard deviations for three data sets. Parameters: slope, 1.89 ±0.17 μL; y-intercept, 0.051 ±0.067 (R²=0.9963).

Estimation of the relative dimensions of mesodomain and PAD.

The demonstrated association of PAD with EAL, and the facile exchange of TEMPOL between PAD and mesodomain, led to the model of concentric PAD and mesodomain layers around EAL.¹⁴ We now refine this model, and estimate the mean thickness, t, of these layers. For the representative condition of added 2.0% v/v DMSO, a value of V_meso=6.0 μL/0.65, or 9.2 μL is obtained from eq 2. The accessible surface area of the EAL oligomer of 1.3×10⁵ Ų is calculated³⁸ by using the X-ray crystallographic structure³⁹ –based model for the S. typhimurium oligomer.⁴⁰ The experimental condition of 20 μM EAL oligomer (3.0 mg per EPR sample), corresponds to 4.0×10¹⁵ EAL, based on a molecular mass, 4.88×10⁵ g/mol⁴¹.³⁸ An assumed thickness of the protein hydration layer of approximately two water molecules, or t_PAD=6 Å,¹ leads to an estimated V_PAD=3.1 μL for a planar equivalent of the accessible surface area.¹⁴ Thus, from the relation, PV_PAD=2.9 μL, P is near unity. The estimated mean mesodomain thicknesses, t_meso, for added 0.5, 1.0,¹⁴ 2.0, and 4.0 % v/v DMSO are approximately 5, 9, 18 and 36 Å, respectively, thus covering a range from t_meso<t_PAD to t_meso>t_PAD. The simple, uniform thickness, planar layer model captures global features of the solvent environment around EAL, but ignores the topography and heterogeneous properties (e.g., polarity, charge, hydrogen-bonding) of the EAL protein surface,^39–40 which might lead to solvent clustering and regions of varying layer thickness.

Resolution of an order-disorder transition in the protein-associated domain.

The abrupt decrease in W_s and compensating increase in W_f, in the direction of decreasing T at the Region II/III boundary, is proposed to represent a transition from a disordered to ordered state of the PAD. (This type of transition is most commonly referred to as an “order-disorder transition,” and thus, in the sense of word sequence, it is defined for the direction of change from ordered to disordered. We thus refer to the proposed transition in the PAD as an order-disorder transition, ODT. In the direction of decreasing T, the PAD changes from a disorded to an ordered state. In the direction of increasing T, the PAD changes from an ordered to a disordered state.). The change in W values is not expected from extrapolation of the constant, Region III values of W_s and W_f across T_II/III into Region II, and it occurs over a T-range for which both logτ_c,s and logτ_c,f are ≤−7.0 (Figure 2). Detectability of τ_c,f extends into Region II. Therefore, the change in W values is not an artifact of exceeding the mobility-detection bandwidth of the spin-probe EPR technique at X-band. We propose that the change in weights, quantified as ΔW_s=W_s,II – W_s,III, where W_s,II and W_s,III are the slow component weights in Regions II (ordered PAD) and III (disordered PAD), arises from partial exclusion⁴² of TEMPOL from the PAD, owing to increased solvent order in the PAD. The change in weight can be expressed as:

$$\epsilon =\Delta W_{\text{s}}/W_{\text{s,III}}$$ (4)

where the exclusion coefficient, ε, represents the normalized weight component of TEMPOL that is excluded from the PAD and transferred into the mesodomain. Values of ΔW_s, W_s,II, W_s,III, and ε are collected in Table S7. The mean value of ε for the different % v/v DMSO conditions is 0.70 ±0.07. Thus, 70% of the TEMPOL in the disordered PAD is excluded, upon decreasing T through the ODT at T_II/III. Independence of the value of ε from added DMSO provides additional support for a constant PAD volume and properties at the different added % v/v DMSO.

Mechanism of coupling of TEMPOL rotational motion to solvent motions.

The rotational correlation time of a probe molecule in a bulk solution of smaller solvent molecules typically displays a high-T regime characterized by direct dependence on the solvent viscosity, η (Debye-Stokes-Einstein behavior).^43–44 As T decreases, the exponential T-dependence of η⁴⁵ leads to a rapid increase in η, and Arrhenius (logτ_c versus 1/T) plots over the full T-range display concave-up curvature. At high η values, decoupling of probe rotation and collective solvent motions leads to independence of τ_c and η.^43–44 This breakdown of Debye-Stokes-Einstein behavior is signalled by a linear Arrhenius dependence. For nitroxide and other small spin probes in bulk aqueous-cosolvent fluids, divergence from Debye-Stokes-Einstein behavior begins at logτ_c ≈ −8.5.^43–44 The large η values (>10 cP) for aqueous-DMSO at the maximum freeze-concentration for the T values of Region III (Figure S2) are consistent with the T values associated with Debye-Stokes-Einstein behavior breakdown.²⁰ Confinement can also suppress η-coupled collective solvent motions, which could lead to deviations from Debye-Stokes-Einstein behavior.⁴⁶ Figures 6 and 7 show that the logτ_c versus 1/T dependences in Region III for TEMPOL in the PAD and mesodomain in the presence of EAL are linear. Therefore, τ_c is independent of η in each phase in Region III, in accord with expectation. Although collective solvent motions, similar to α-fluctuations observed in super-cooled fluids,⁴⁷ exist in confined systems,⁴⁸ the η-independent TEMPOL rotational motion does not represent collective solvent motions on the time-scale corresponding to the X-band EPR detection bandwidth, τ_c ~10⁻¹¹–10⁻⁷ s. Rather, TEMPOL rotational motion reports on mesodomain and PAD solvent structure and dynamics through their effects on localized motions of single solvent molecules (β-fluctuations),^{1, 45} or small clusters (Johari-Goldstein β-fluctuations),^49–50 that influence the properties of the solvent “cage,” that surrounds TEMPOL.

Figure 6.

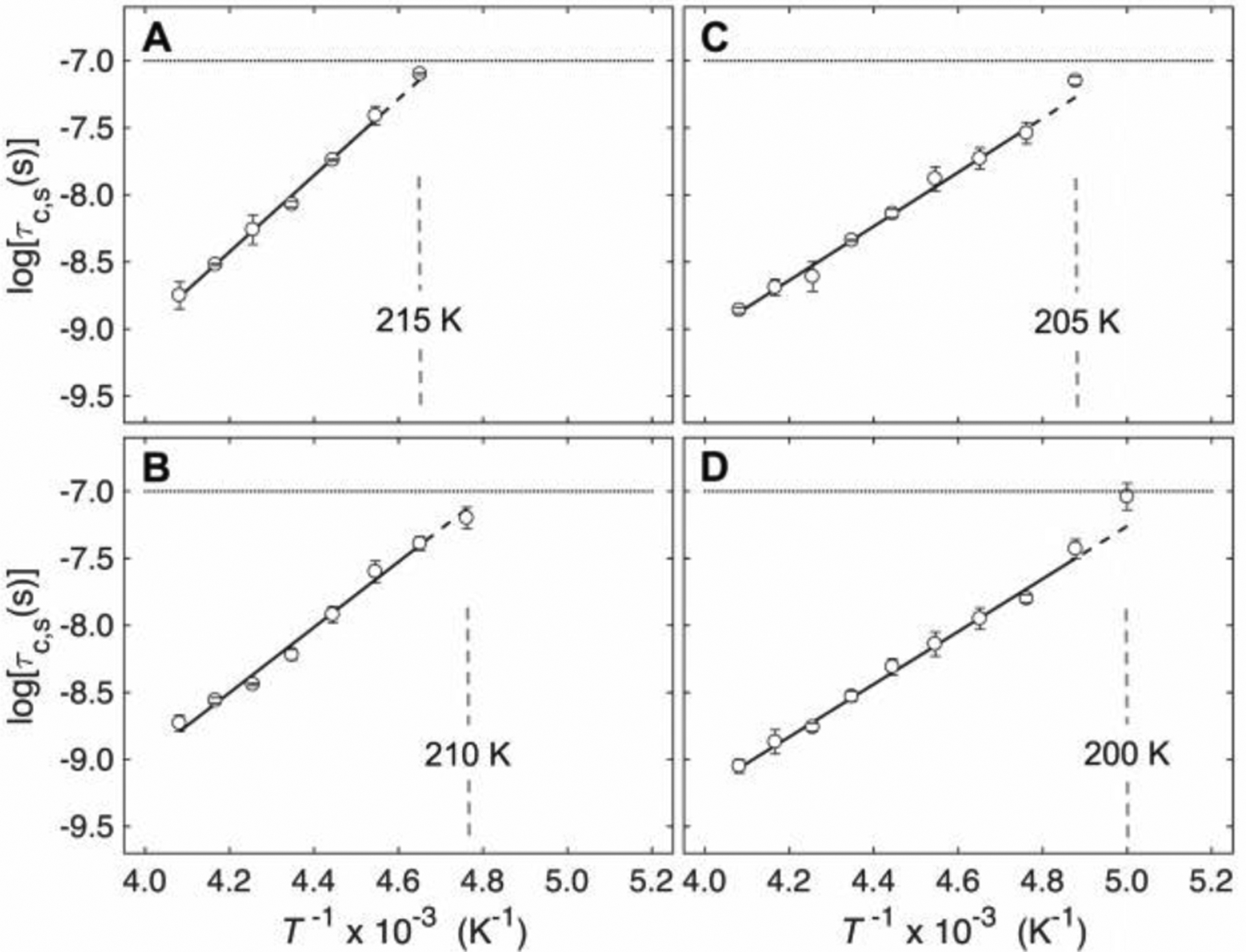
Arrhenius dependence of rotational correlation times for TEMPOL in the PAD (τ_c,s) at different added % v/v DMSO. (A) 0.5%. (B) 1.0%.¹⁴ (C) 2%. (D) 4%. Vertical dashed line represents T_II/III for the ODT. Linear fit for Region III (solid line) and extrapolation into Region II (T<T_II/III; dashed line) are shown. Horizontal line represents upper limit of τ_c for detection of tumbling motion. Error bars correspond to standard deviations for three separate experiments at each temperature. R² values for linear fit: 0.5 (0.9955), 1.0 (0.9871), 2.0 (0.9923), 4.0 (0.9939).

Figure 7.

Arrhenius dependence of rotational correlation times for TEMPOL in the mesodomain in the presence of EAL (τ_c,f) at different added % v/v DMSO. (A) 0.5%. (B) 1.0%.¹⁴ (C) 2%. (D) 4%. Vertical dashed line represents T_II/III for the ODT. Linear fit for (Region III, solid line) and extrapolation into Region II (T<T_II/III; dashed line) are shown. Horizontal line represents upper limit of τ_c for detection of tumbling motion. Error bars correspond to standard deviations for three separate experiments at each temperature. R² values for linear fit: 0.5 (0.9988), 1.0 (0.9963), 2.0 (0.9966), 4.0 (0.9990).

Temperature-dependence of spin probe mobility in mesodomain and PAD in Region III.

To quantify the T-dependences of τ_c under the different conditions, the Arrhenius equation is used to fit the data in Region III (Figures 6, 7 and 8):

$$\text{log}({\tau }_{\text{c}})=\text{log}({\tau }_{\text{c,0}})-\left[\frac{E_a}{2.3RT}\right]$$ (5)

The PAD and mesodomain data and fits are also presented in a combined plot (Figure S3). In eq 5, τ_c,0 is the correlation time in the high-T limit, R is the gas constant, and E_a represents a mean energy barrier to probe reorientation. The logτ_c,0 and E_a values from linear fits of the Region III data in Figure 6 (PAD, τ_c,s) and Figure 7 (mesodomain, τ_c,f) are provided in Table 1. The Arrhenius parameters for TEMPOL rotational motion in the mesodomain are essentially independent of % v/v DMSO (E_a=8.5 ±0.50 kcal/mol; logτ_c,0= −16.8 ±0.45). In contrast, E_a for the PAD decreases with increasing % v/v DMSO, and approaches the value for the mesodomain. The kink and increase in slope at T≤T_II/III for the mesodomain in Figure 7 reveals a correlation between the ODT in the PAD and the rotational dynamics of TEMPOL in the mesodomain.

Figure 8.

Arrhenius dependence of rotational correlation times for TEMPOL in the mesodomain in the absence of EAL (τ_c) at different added % v/v DMSO. (A) 0.5%. (B) 1.0%.¹⁴ (C) 2%. (D) 4%. Vertical dashed arrows denote position of T_II/III in the +EAL system. Linear fit for Region III (solid line) and extrapolation into Region II (T<T_II/III; dashed line) are shown. Horizontal line represents upper limit of τ_c for detection of tumbling motion. Error bars correspond to standard deviations for three separate experiments at each temperature. R² values for linear fit: 0.5 (0.9957), 1.0 (0.9968), 2.0 (0.9914), 4.0 (0.9968).

Arrhenius plots for TEMPOL in the aqueous-DMSO mesodomain in the absence of EAL are shown in Figure 8 (parameters, Table 1). The Arrhenius parameters for the –EAL condition at each % v/v DMSO value in Region III, and the mean values (E_a =8.7 ±0.2 kcal/mol; logτ_c,0= −17.1 ±0.20), are the same as for the +EAL condition, to within one standard deviation. The linear Region III relations continue into Region II for 2.0 and 4.0 % v/v DMSO, which confirms that the abrupt kink at T_II/III and sharp slope increase at T < T_II/III in the presence of EAL arise from an effect on the mesodomain from the ODT in the PAD. The slight increase in slope observed in Region II for 0.5 and 1.0 % v/v DMSO is explained as arising from an ice boundary confinement effect, which is amplified by the proximity of TEMPOL to the ice boundary, owing to a larger ice-mesodomain interfacial area to mesodomain volume ratio for the lower % v/v DMSO conditions, in the absence of EAL.

The mean values for E_a of 8.7 and 8.9 kcal/mol for the +EAL and –EAL mesodomain are comparable to Arrhenius activation energies of 8–10 kcal/mol, that have been assigned to solvent β-fluctuations in other aqueous solvent systems.^{47, 51} This is consistent with the enabling of TEMPOL rotational motion by localized fluctuations of the caging solvent.

Conclusions

Model for the protein-PAD-mesodomain-ice system.

The interpretation of the TEMPOL-detected structural and dynamical properties of the protein-PAD-mesodomain-ice system in Regions II and III as a function of added DMSO and T leads to a model, that is depicted in Figure 9. Three key features of this model are: (1) The rigid ice boundary exerts the dominant solvent-structuring (ordering) confinement effect in the system, in Region III. This confinement effect is mediated through the mesodomain. The confinement effect on the PAD decreases with increased distance from the ice boundary, as the mesodomain thickness increases from an estimated 5 to 36 Å for 0.5 to 4.0 % v/v DMSO. This is quantified by the decreases in E_a and logτ_c,0 for TEMPOL in the PAD (corresponding to τ_c,s), with increasing added DMSO. At added 4.0% v/v DMSO, the E_a and logτ_c,0 values for the PAD and mesodomain are the same, to within two standard deviations. This suggests that the ice boundary confinement of the PAD is vanishing at 4.0% v/v DMSO, and further, that the solvent structure and motions in PAD and mesodomain, that enable TEMPOL reorientation, have common features. (2) TEMPOL rotational motion in the viscous aqueous-DMSO mesodomain is decoupled from solvent viscosity in Regions II and III (beyond the Debye-Stokes-Einstein limit). (3) TEMPOL, free in the mesodomain, migrates to regions of lowest solvent ordering, in Region III. Therefore, the mean position of TEMPOL in Region III is closer to the disordered PAD interface, than to the ice boundary. These three features of the model are depicted in Figure 9. As a consequence of model features (2) and (3), the TEMPOL logτ_c,f (+EAL) values in the mesodomain in Region III are comparable, and thus relatively independent of the ice boundary confinement effects, at the different added % v/v DMSO. Features (2) and (3) also account for the same values of E_a and logτ_c,0 for TEMPOL reorientation in the +EAL and –EAL mesodomains. Although the sensitivity of mesodomain TEMPOL rotational motion (logτ_c,f) to the degree of ice-boundary confinement propagated through the mesodomain is relatively low, the influence of the confinement is detected, through the effects on TEMPOL rotational motion (logτ_c,s) in the PAD, and the change in T_II/III of the ODT.

Figure 9.

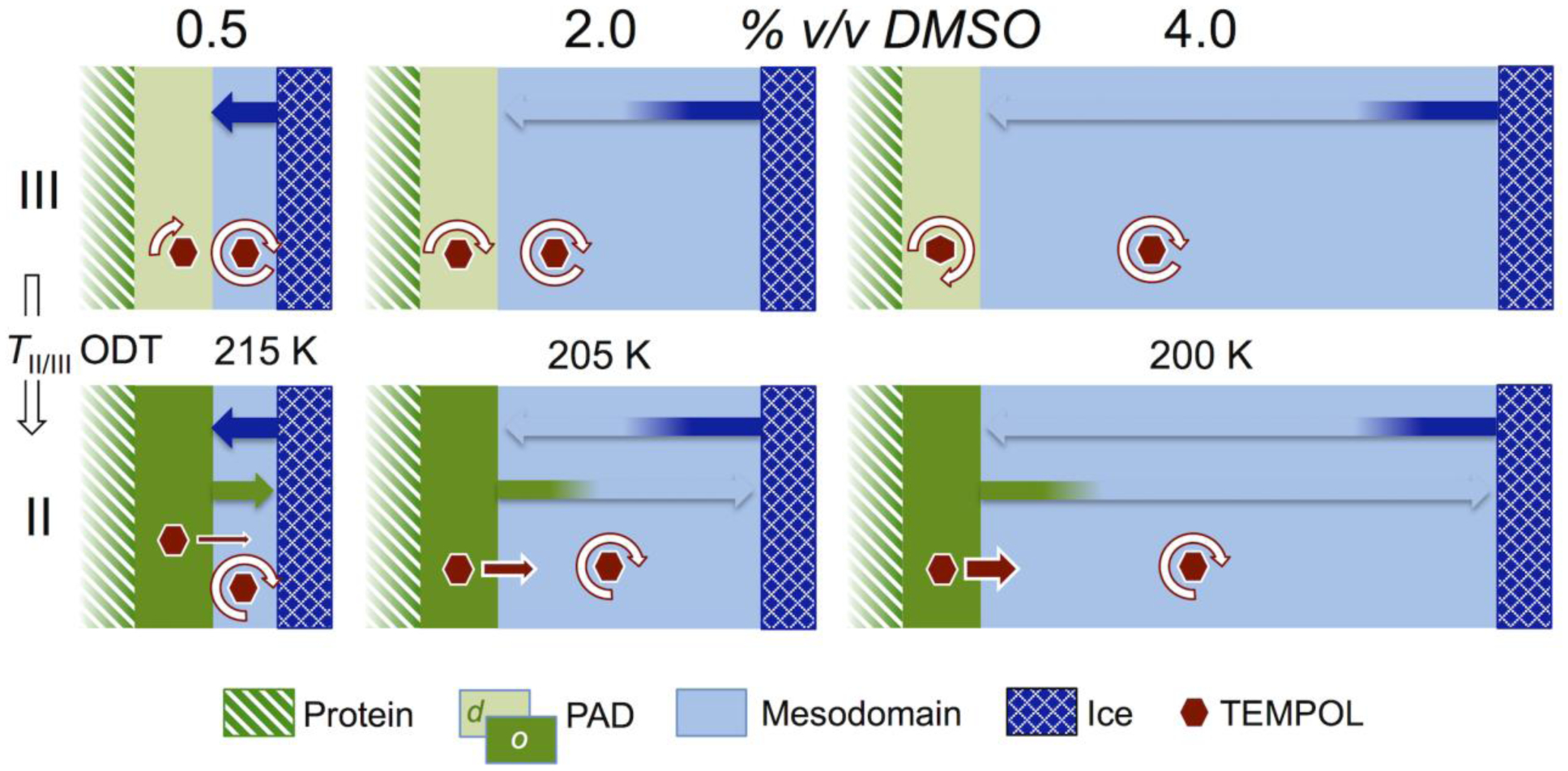
Model for the temperature-dependence of solvent dynamical and confinement effects in the protein-PAD-mesodomain-ice system, that give rise to the observed TEMPOL EPR spin probe rotational mobility and phase partitioning, as a function of added % v/v DMSO, in Regions II and III, and effect of the ODT at T_II/III. Key shows color-pattern identification of phases and ordered-disordered state of the PAD. Broad arrows depict the spatial extent of confinement effects, from the ice boundary and the PAD, that are mediated through the mesodomain. The relative rotational mobility of TEMPOL is depicted by length of circular white arrows. Exclusion of TEMPOL from the PAD at the ODT is depicted by linear red arrows, whose size represents amount of TEMPOL excluded.

Origin of the ODT.

TEMPOL exclusion from the PAD at the ODT in the direction of decreasing T suggests that the PAD undergoes a change in structure. The decrease in T_II/III with increasing added DMSO is consistent with the increase in mesodomain volume, and consequent diminishing confinement, from the receding ice boundary. The estimated spatial extent of strong ice boundary confinement, which must be propagated over mean mesodomain shell t-values of ≤9 Å, suggests the existence of collective solvent motions. This is consistent with the length scale of a few tens of Ångströms for cooperatively-rearranging solvent domains, that are involved in the α-process in molecular liquids.⁵² The range of T_II/III of 200–215 K is comparable to values of a liquid-liquid phase transition (LLT), observed for water at a confinement dimension of ~20 Å.⁵³ By analogy with the proposal for the mechanistic origin of the LLT,⁵³ the ODT may arise from protein surface-induced ordering of the water in the PAD, through an increase in water-water hydrogen bond order.

Two-way transmission of solvent structure and dynamics at the PAD-mesodomain boundary.

At T≤T_II/III, the ordering of the PAD introduces a relatively strong, local structuring effect on the mesodomain, which is manifested as a kink and increased Arrhenius plot slope for τ_c,f (Figure 7). Our model proposes that this relatively strong, local effect is revealed, because TEMPOL in the mesodomain is localized, on average, relatively near to the PAD/mesodomain boundary. The reciprocal confinement effect of PAD on mesodomain, relative to the mesodomain-mediated ice boundary confinement effect on the PAD, demonstrates a two-way coupling of solvent structure and dynamics, across the PAD-mesodomain interface.

Relation to EAL enzyme catalysis.

The persistence of EAL-mediated reactions with native kinetic parameters at the T values that correspond to Regions II and III and below,^26–28 is consistent with the results presented here: The mesodomain maintains a reservoir of solvent fluctuations, that couple to PAD and protein fluctuations, to enable the reactions that take place in the protein interior. In the case of the EAL activity measurements in frozen solutions at cryogenic-T values,^26–28 the mesodomain is created by the added substrates, aminoethanol or 2-aminopropanol, which like DMSO, behave as cryo-cosolvents.⁵⁴ The nuanced control of PAD and mesodomain solvent structure and dynamics, and their mutual coupling, by added DMSO will be used to further characterize the coupling of solvent structure and dynamics to the kinetics of individual reaction steps in EAL catalysis.