Abstract
The relation of surface polarity and conformational preferences is decisive for cell permeability and thus bioavailability of macrocyclic drugs. Here, we employ grid inhomogeneous solvation theory (GIST) to calculate solvation free energies for a series of six macrocycles in water and chloroform as a measure of passive membrane permeability. We perform accelerated molecular dynamics simulations to capture a diverse structural ensemble in water and chloroform, allowing for a direct profiling of solvent-dependent conformational preferences. Subsequent GIST calculations facilitate a quantitative measure of solvent preference in the form of a transfer free energy, calculated from the ensemble-averaged solvation free energies in water and chloroform. Hence, the proposed method considers how the conformational diversity of macrocycles in polar and apolar solvents translates into transfer free energies. Following this strategy, we find a striking correlation of 0.92 between experimentally determined cell permeabilities and calculated transfer free energies. For the studied model systems, we find that the transfer free energy exceeds the purely water-based solvation free energies as a reliable estimate of cell permeability and that conformational sampling is imperative for a physically meaningful model. We thus recommend this purely physics-based approach as a computational tool to assess cell permeabilities of macrocyclic drug candidates.
Introduction
Macrocycles are a potent new class of molecules for drug discovery.1,2 Approximately 75% of disease relevant proteins still cannot be targeted, neither with small molecules nor with biopharmaceuticals.3 A major portion of these yet undruggable targets are intracellular protein–protein interfaces (PPIs), including several notorious cancer-associated targets.4 Biologics, such as antibodies, are the prime class of pharmaceuticals to target extracellular PPIs with uncontested specificities and affinities.5,6 However, with a few exceptions, they are generally not able to cross through the cell membrane.7 Small-molecule drugs, on the other hand, are extremely well-studied, and clear models and guidelines to achieve oral bioavailability and membrane permeability are well-established.8 However, they mostly require deep apolar binding pockets to achieve the desired affinities and physiological effects, which are lacking in typical PPIs with extensive flat surface areas.3 Macrocycles bridge these two medication strategies in terms of physicochemical and pharmacological features.9−12
Macrocyclic compounds have repeatedly been established as drugs without fulfilling all or even any of Lipinski’s rule of 5 for bioavailability of small-molecule drugs. Nevertheless, it has been shown that they can be designed to achieve cell permeability and even oral bioavailability.3,13−18 As they are substantially larger than typical small molecules, macrocycles are able to target the characteristic shallow and broad surfaces of protein–protein interaction sites.16,19−21 Furthermore, their proteolytic stability and thus bioavailability are increased due to the cyclic scaffold.16,22,23 Compared to their non-cyclic analogues, the cyclization additionally decreases the entropic loss upon binding, which can enhance their binding affinity to magnitudes that are usually only achievable by biopharmaceuticals.24−26 However, despite the continuous advancement in experimental strategies, the synthesis of macrocyclic compounds is still challenging.27−30 Reliable computational tools to identify and optimize promising scaffolds are thus paramount for the efficient design of macrocyclic drugs.31−36
Substantial scientific efforts in this field have led to a fast-growing number of theoretical methodologies for characterizing physicochemical properties of macrocycles.9,37,38 A major aspect of these approaches is concerned with the development and testing of conformational sampling algorithms suitable for macrocyclic molecules.35,36,39 The development of specialized strategies for conformer generation is imperative as the conformational restraints introduced by the ring closure entails unique structural characteristics to this compound class, which are generally not captured by conventional conformer generators.34,40 Furthermore, cyclization can also induce a strain energy within the ring leading to high energetic barriers between relevant conformational states.41 Numerous of the proposed sampling algorithms for macrocycles are force-field based.36,38,42−44 While classical molecular dynamics (MD) simulations have often failed to overcome the energetic barriers between the diverse conformational states of macrocycles within a feasible simulation time, several enhanced sampling strategies have been shown to capture structurally accurate ensembles.31 These more sophisticated sampling techniques, such as replica exchange MD,45 multicanonical MD,43 metadynamics,46,47 and accelerated MD,31 allow comprehensive and efficient profiling of the conformational space of macrocycles.
As described above, a particularly intriguing feature of macrocycles is their ability to cross the cell membrane.15,48 While high passive membrane permeability has been demonstrated for a multitude of macrocycles, not all macrocyclic scaffolds are inherently membrane-permeable.17,49 In order to achieve permeability, macrocyclic compounds have to also balance an intricate interplay of physicochemical properties to ensure solubility in the polar extra- and intracellular environments as well as within the mostly apolar membrane.50,51 The surprisingly high permeability of these large molecules is commonly explained based on solvent-dependent conformational rearrangements ( e.g., cyclosporin A).38,43,52 The fundamental idea is that macrocycles with high passive membrane permeabilities are able to adapt to different solvent polarities via a population shift in their conformational ensembles: In aqueous solution, the most favorable conformational state is “open” with polar groups turned outward to interact with the polar solvent. Upon entering a less polar environment, the conformational ensemble shifts toward a “closed” conformational state. Here, polar groups are turned inward increasing the number of intramolecular hydrogen bonds, while apolar groups rearrange to maximize the apolar surface area. Several comprehensive studies, including extensive enhanced sampling and Markov state modeling, have fostered this hypothesis and also extended it to more generalized multistate models.53−55
To quantify conformational preferences in polar and apolar environments, most of these studies perform simulations in water and an apolar solvent, such as chloroform.18,38,43 In previous studies, atomistic models for membranes led to promising results in estimating permeability of small molecules. However, this approach is still challenging and computationally costly.56 Despite its striking simplicity, the approximation of a membrane by organic solvents has repeatedly demonstrated its suitability to estimate cell permeability in a multitude of approaches.17,51,57,58
In this study, we use accelerated MD (aMD) simulations59,60 to capture the diverse conformational ensembles of a series of six macrocyclic compounds in water and chloroform (Figure 1).61 We have previously shown the reliability of aMD simulations in characterizing the structural ensemble and thermodynamic quantities of macrocycles consistent with experiments.31 Here, we perform aMD simulations to profile and quantify solvent-induced shifts of ensemble populations. Furthermore, we track how structural rearrangements translate into changes in surface properties by calculating solvation free energies with grid inhomogeneous solvation theory (GIST).62,63 The fundamental idea of this approach is to estimate thermodynamic solvation properties of the solvent in the vicinity of the solute by tracing the solvent distribution in MD simulations. We have demonstrated previously that GIST solvation free energies can be used to describe surface hydrophobicity.64,65 Furthermore, we have recently reimplemented this approach on the GPU achieving superior computational performance. Although, compared to the calculation of polar surface area values, GIST analysis is still computationally noticeably more demanding and estimating surface polarity via solvation free energies offers several convincing advantages. First, GIST accounts for non-additive effects, for example, polar atoms, which are solvent-exposed but form intramolecular hydrogen bonds, show fewer interactions with the solvent and thus contribute less to surface polarity. Second, the latest reimplementation of the GIST algorithm introduces the possibility to calculate solvation free energies in chloroform. Hence, while previous GIST studies estimate differences in hydration free energy referenced to the solute in vacuum,62,64,66−69 we now are able to compare differences between solvation in water and in chloroform.70 In a preceding study, we demonstrated the accuracy of the approach in estimating partition coefficients, i.e., differences in solvation free energies, between water and chloroform for a set of rigid small molecules.70
Figure 1.
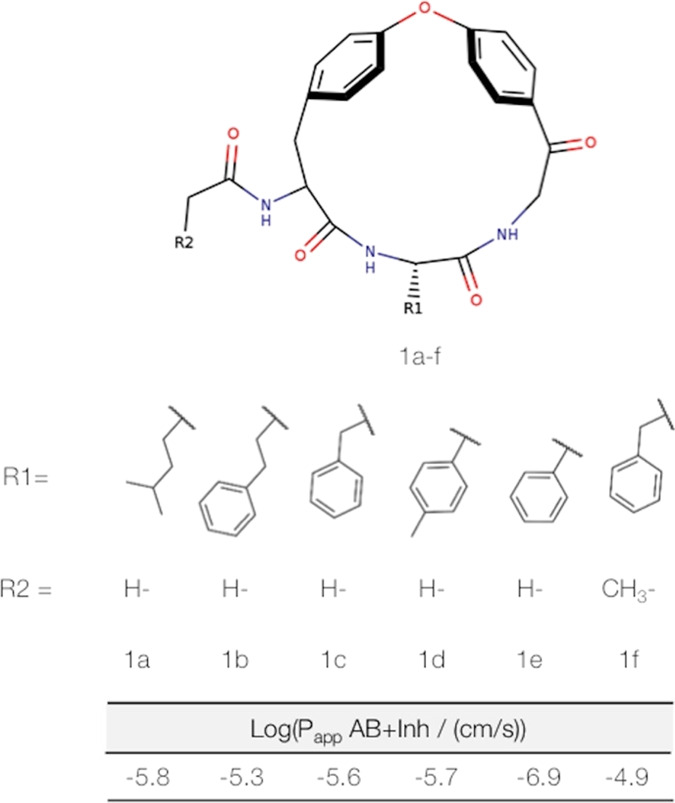
Series of macrocyclic model systems.61 The model compounds share a common ring scaffold but vary in their side chains. These modifications were specifically designed to achieve different conformational preferences and cell permeabilities. Reprinted with permission from ref (61). Copyright 2018 American Chemical Society.
For the present study, we extend this approach by further incorporating conformational aspects into the calculations of solvation free energy differences. By combining information on the state populations in chloroform and water with the respective solvation free energies, we derive an estimate of the transfer free energy of each compound. We evaluate the reliability of this approach against the experimentally measured cell permeabilities and analyze contributions of conformational sampling and solvation free energies from both solvents.
Theory and Methods
Grid Inhomogeneous Solvation Theory
GIST calculates thermodynamic properties of a solvent around a solute. Calculation of the free energy around the solute can be split into an energetic and an entropic part. These two parts are then calculated individually (eq 1). Here, we aim at a short summary of the fundamental theory of GIST. For a comprehensive overview of GIST62,63,71,72 as well as of the underlying concepts from Lazaridis et al.,73,74 we want to refer the reader to the original literature.
| 1 |
For the calculation of the energetic contribution, the force field of the simulation is used. At each grid voxel where a water molecule is found, the total energy of this molecule is calculated. This total energy consists of two parts (eq 2), the solvent–solvent interaction energy and the solute–solvent interaction energy (ΔEuv(rk)). To avoid double counting, the total solvent–solvent energy is divided by two, and we denote the result of this division as ΔEvv(rk).62
| 2 |
Finally, the entropic contribution only considers the two-body term. This two-body term is approximated via a nearest neighbor method, which estimates the translational and the orientational contributions to the entropy together (ΔSuvsix). The nearest neighbor is calculated by an l2 norm of the distance in translational and orientational space, resulting in eq 3. Finally, the translational distance is calculated as a simple Euclidean distance and the orientational distance is calculated as a quaternion distance.
| 3 |
Transfer Free Energies from GIST Calculations in Water and Chloroform
The transfer free energy between two different solvents can be readily computed from GIST using the thermodynamic cycle.70 The transition from chloroform into water can be partitioned into the transition from chloroform into vacuum and then from vacuum into water. The first transition is the solvation free energy of the compound in chloroform. The second transition is simply the negative hydration free energy of the compound. Both values can be calculated using GIST.
For the calculation of the solvation free energies, GIST analyses were performed on simulation trajectories of the various macrocycles. For this analysis, the reference density for water was set according to the values in the AMBER manual (0.0329 Å−3),75 and the reference density for chloroform was set to the same value as found by Kraml et al. (0.00768 Å−3).70
The values for the solvation free energy were then derived from the GIST calculations. In a first step, the reference solvent–solvent energy was subtracted. For the TIP3P water model, the value present in the AMBER manual was used, and for chloroform, the value found by Kraml et al. was used.70 In the second step, the two energy contributions were summed up, following eq 2. Then, the entropic contribution was subtracted, following eq 1, to yield the solvation free energy in the respective solvent.
For the calculation of the transfer free energy (ΔAtransfer), the two solvation free energies were subtracted from each other, following eq 4.
| 4 |
Studied Series of Macrocyclic Compounds
We test the reliability of our approach on six macrocyclic molecules introduced by Tyagi et al., which were inspired by natural products.61 This series was specifically designed to investigate molecular determinants of passive membrane permeability, in particular, the role of shielding NH−π interactions. Within their comprehensive work, Tyagi et al. provide high-quality experimental data including cell permeabilities, log POW values, and a crystal structure. Despite their high similarities, the six macrocycles in this series, 1a to 1f, show clear distinction in their passive membrane permeability (Figure 1). Macrocycle 1e clearly exhibits the lowest permeability followed by the macrocycles 1a, 1c, and 1d, which are nearly identical in their permeabilities. The highest permeabilities are observed for the macrocycles 1b and 1f. Hence, the permeability distribution for these six is not spread evenly but rather represents three to four clusters. Nevertheless, the high quality and consistency of the available experimental data render these molecules an ideal test set for the presented study.
Structure Preparation and Simulation Setup
We performed our calculation using a set of macrocyclic compounds published by Tyagi et al.61 The single available crystal structure (compound f in the terminology of Tyagi et al.; CCDC identifier 1853494) was used directly, while all other studied compounds were modeled based on this structure with the molecular operating environment (MOE).76 All compounds were parameterized using the AMBER ff14SB77 and GAFF78 force fields. Missing parameters were derived with the antechamber module of AmberTools 18.79 We assigned partial charges using Gaussian1680 and the RESP81 procedure using the HF/6-31G* basis set. Subsequently, topology and coordinate files were generated with the tLEaP module of AmberTools 18.75 All compounds were solvated in a cubic box of TIP3P water82 and chloroform83 with a minimum wall distance of 12 Å for both solvents. Before production simulations, all systems were equilibrated following an extensive heating and cooling protocol.84 The conformational space was sampled with the accelerated molecular dynamics (aMD) framework, as implemented in AMBER 18, using the dual boost approach.59,85−87 Boosting parameters were obtained from short cMD simulations following a procedure adapted from Pierce et al.60 For each macrocycle, 10 aMD simulations with random starting velocities were performed in both solvents to maximize conformational sampling. The simulations were run for 100 ns each, resulting in an aggregate simulation time of 1 μs/system. We used a Langevin thermostat88 with a collision frequency of 2 ps–1 to keep the system at 300 K, together with a Berendsen barostat89 with a relaxation time of 2 ps to keep the system at atmospheric pressure. All bonds involving hydrogen were constrained with the SHAKE algorithm, which enabled the use of a 2 fs time step for the water simulations.90 Chloroform simulations were run with a 1 fs time step. All simulations were carried out with the GPU implementation of the PMEMD module in AMBER.91,92
Clustering and GIST Calculations
To determine representative structures and their population in each solvent, we performed a hierarchical cluster analysis based on the polar surface area (PSA) using cpptraj from AmberTools 18.93 We estimate the PSA as the solvent-accessible surface area of polar heavy atoms, oxygen and nitrogen, for the concatenated trajectories in water and chloroform for each model system. We then applied the implemented average linkage clustering algorithm with a cutoff distance of 12 Å2 on the resulting data. This clustering strategy resulted in three to five representative structures per macrocycle. To reweight the respective population of each conformational cluster, we adapt a strategy proposed by Miao et al. in which we approximate the Boltzmann factor with a Maclaurin expansion up to the 20th order.94,95
To perform subsequent GIST analysis, we solvated each representative structure in a cubic box of TIP3P waters and chloroform molecules, ensuring a minimum distance of 20 Å for each solute atom to the box faces. We equilibrate the solvent as described above. Subsequently, we performed restrained simulations with a weight of 100 kcal/(mol·Å2) to fix the solute heavy atoms. Furthermore, all bonds involving hydrogen atoms were restrained following the SHAKE algorithm.90 As described above, we employed the Langevin thermostat with a collision frequency of 2 ps–1 to ensure a temperature of 300 K and used the CUDA implementation of the particle mesh Ewald MD (pmemd.cuda) module of AMBER 18 to perform simulation in the NVT ensemble.91,92 For each macrocycle/solvent combination, we performed 100 ns of restrained MD simulations where frames were collected every 2 ps, resulting in 50,000 frames per trajectory.
Conformational Space Characterization
To characterize the captured conformational space of each compound in water and chloroform, we performed principal component analysis (PCA) based on the dihedrals along the ring atoms using cpptraj.93 To represent the common and deviating structural preferences in each solvent, we calculated the principal components based on the concatenated trajectories. In order to compare the structural data in water and chloroform, we project the respective data on the two first eigenvectors (with the highest eigenvalues) of the matrix with the combined features. To retrieve the unbiased population from the aMD simulations, we applied a Boltzmann reweighting scheme described above94 (Figure S1). For the two macrocycles with the highest and lowest permeability, i.e., 1f and 1e, we performed a density-based clustering of the PC space to visualize structural differences corresponding to the free energy minima (Figures S3 to S5). Furthermore, we profiled the conformational space using a more global measure based on ratios of the principal moments of inertia (Figure S6).
As an additional measure of solvent-dependent structural rearrangements, we calculated PSAs, i.e., solvent-accessible surface areas of oxygen and nitrogen atoms. In order to remove the bias introduced by the aMD approach, we again reweighted the individual distributions as described above (Figure S7).
Results
We characterize the captured conformational space of six macrocyclic compounds using PCA (Figure S2). Projecting the structural data captured in each solvent onto the combined PCA space allows a direct comparison of structural preferences. In Figure 2, we depict the conformational ensembles of the macrocycles 1e and 1f, which show the largest difference in cell permeability. For both systems, we clearly observe a solvent-dependent shift of ensemble populations. While the covered conformational space is similar in chloroform and water, the maxima in population are clearly shifted. These maxima in the probability density directly translate into minima in free energy to which we will further refer as favorable conformational states. For macrocycle 1e, we find four highly populated areas in chloroform of which the most favorable conformational state is located around [2, −0.5] in the PCA space shown in Figure 2A. On the other hand, in water, the same macrocycle populates seven to eight distinguishable areas and the most favorable conformational states are found in areas around [−1.8, −1] and [−1, −0.5] (Figure 2B). The conformational space of macrocycle 1f in chloroform is clearly less restricted than that of 1e, showing a large number of highly populated areas in the space spanned by PC1 and PC2 (Figure 2C). The ensemble of the same macrocycle in water shows significantly fewer favorable conformational states and is overall shifted toward areas with more positive PC2 values (Figure 2D).
Figure 2.
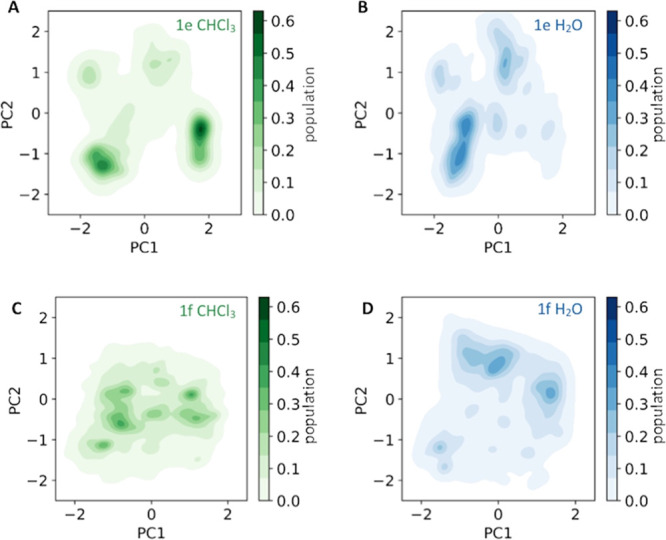
Solvent-dependent ensemble shift of macrocycles 1e and 1f. The structural ensembles of macrocycles 1e (A, B; top) and 1f (C, D; bottom) in chloroform (green) and water (blue) are projected onto the first two PC eigenvectors and color-coded according to their reweighted populations.
Furthermore, we profile distinctions between the ensembles captured in the polar and apolar environments in terms of intramolecular hydrogen bonds (IMHBs) and surface properties. It has been shown before that the structural differences of several peptidic macrocycles in varying solvents relate to changes in the pattern of IMHBs and in the polar surface area (PSA).43 In Figure 3, we show the ensemble distributions of both descriptors for the most permeable macrocycle in our series, 1f, compared to the least permeable compound 1e. We clearly find that, for both systems, the number of IMHBs is higher in chloroform, while the polar surface area shifts toward smaller values in the apolar environment. However, for the least permeable macrocycle 1e, the average number of IMHBs observed during the simulation is significantly smaller than for 1f. Furthermore, we find that the distribution of PSA in chloroform is clearly skewed toward higher values for 1e, which is not observed for 1f. This observation suggests that 1e is not able to bury or shield its polar moieties as well as 1f.
Figure 3.
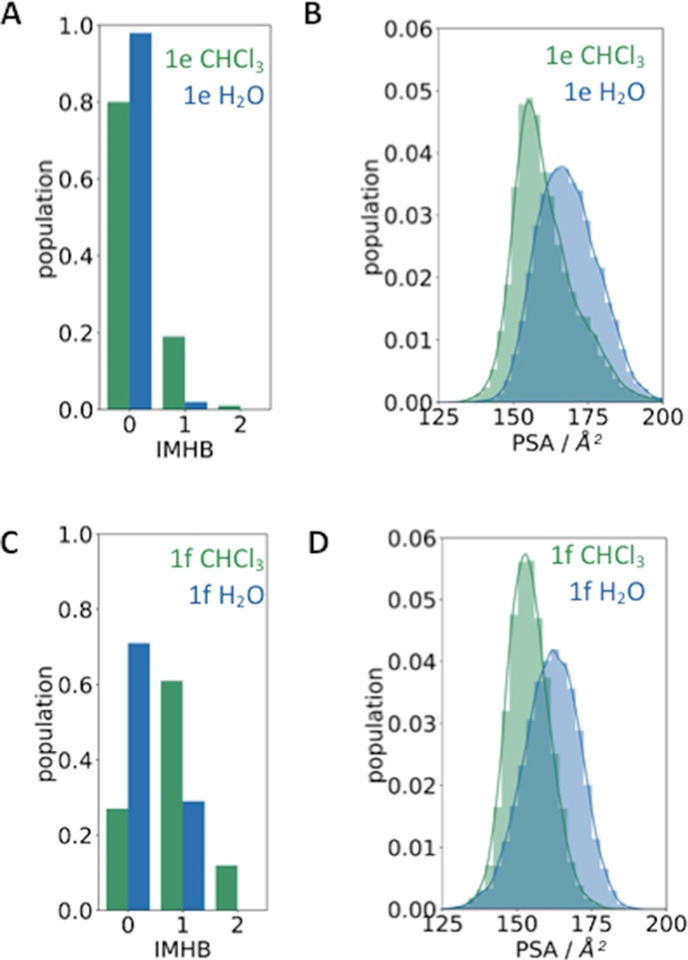
Ensemble distributions of conformational descriptors in water and chloroform. (A, C) Histograms of the number of intramolecular hydrogen bonds (IMHB), and (B, D) the polar surface areas (PSAs) of macrocycles 1e and 1f are depicted in blue for simulations in water and in green for simulations in chloroform.
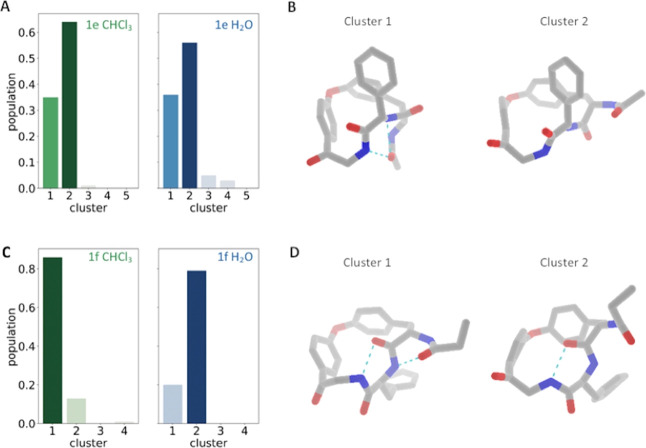
To achieve a more detailed analysis of the surface properties, we calculate solvation free energies using GIST. To do so, we determine representative structures using the PSA-based clustering strategy described in the Theory and Methods section. From the GIST solvation free energies in chloroform and water, we can then calculate transfer free energies ΔAtransfer for each representative structure. In Figure 4, we show the cluster populations and representative structures for the macrocycles with the highest and lowest membrane permeability, 1f and 1e, respectively. As described above, we find a more widespread PSA distribution in both solvents for macrocycle 1e than for 1f (Figure 3B,D). This trend translates into a higher number of clusters and a slightly broader distribution in terms of cluster populations for macrocycle 1e (Figure 4A). Furthermore, the cluster with the highest probability in water and chloroform is the same one for 1e. This is an additional result of the substantial overlap of 1e’s PSA distributions in water and chloroform. For macrocycle 1f, on the other hand, the ensemble probabilities shift from cluster 1, being most favorable in chloroform, toward cluster 2 when simulated in water (Figure 4C). Comparing representatives for the highest populated clusters of 1f in water and chloroform, we find that the conformation favored in chloroform shows a higher number of intramolecular hydrogen bonds (cyan dotted lines) (Figure 4D).
Figure 4.
Conformational preferences in water and chloroform. (A, C) Cluster populations of macrocycles 1e (top row) and 1f (bottom row) are depicted in blue for simulations in water and in green for simulations in chloroform. (B, D) Representative structures from the respective clustering of macrocycles 1e and 1f.
To obtain a quantitative measure of the transfer free energy for each compound, we use the solvent-dependent populations of all representative structures and weight the transfer free energies accordingly, resulting in an ensemble average. In Figure 5A, we compare the resulting transfer free energies with the experimentally determined cell permeabilities and report a striking value of 0.92 for the Pearson correlation coefficient r. We find that the predicted ordering is perfectly in line with the experiment, as indicated by the Spearman correlation coefficient ρ of 1.0. If we follow the exact same sampling strategy but solely consider the solvation free energy in water, we obtain r = 0.71 and ρ = 0.49 (Figure 5B). Comparing the solvation free energy of chloroform alone with experimental cell permeabilities, we find similar agreement as quantified by r = −0.71 and ρ = −0.77 (Figure S10).
Figure 5.
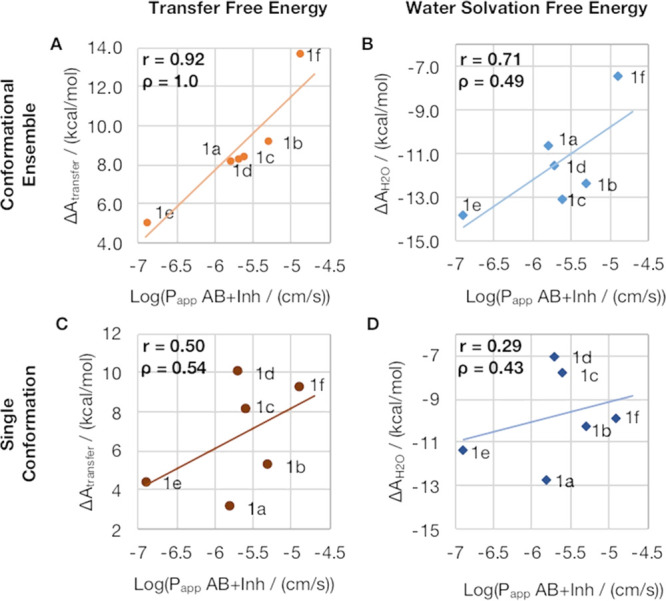
Impact of conformational sampling and contributions from both solvents on prediction accuracy. The top row depicts the cell permeabilities compared to (A) transfer free energies and (B) water solvation free energies considering the conformational ensemble of each macrocycle. The bottom row shows the results of the same calculations when only a single conformation is included (C - transfer free energy, D - water solvation free energy).
Furthermore, we obtain substantially lower agreement with the experiment if we do not consider the conformational variability of each macrocycle but only use the single starting structure of each compound for the GIST calculations (Figure 5C,D). By calculating transfer free energies from a single structure of each compound, we find r = 0.50 and ρ = 0.49 (Figure 5C). Calculating water solvation free energies of the single conformations lowers the correlation further, resulting in r = 0.29 and ρ = 0.43 (Figure 5D). Considering only contributions from chloroform solvation free energies of the single conformations also results in moderate agreement with the experiment with r = −0.58 and ρ = −0.43.
Discussion
Macrocyclic drugs could become a powerful alternative to biopharmaceutical drugs since they show superior membrane permeability while offering similar binding affinities.25 However, their membrane permeability strongly depends on the interplay between surface polarity and conformational preferences.51,96 In this study, we incorporate both of these aspects in our calculation of transfer free energies using ensemble-averaged solvation free energies.
We perform accelerated molecular dynamics simulations to capture the conformational diversity of six macrocycles in water and chloroform (Figure S1). We find that, for all model systems, the conformational space in water and chloroform overlaps to a varying extent. However, the change in solvent polarity consistently alters the population of the captured conformational states. Hence, we find a solvent-dependent shift of ensemble probabilities. This observation is consistent with current literature describing similar behavior for a broad range of peptidic and non-peptidic macrocycles.38,43,57
Comparing the conformational landscapes for the two macrocycles 1e and 1f, which vary most in their cell permeabilities, implies that the core scaffold of 1e has to undergo major structural rearrangements upon membrane penetration, which could translate into a significant cost in terms of free energy. The ring atoms in 1f (highest permeability) on the other hand are likely to pre-organize in conformations favorable in both solvents, which facilitates membrane crossing. This finding is perfectly in line with a model proposed by Witek et al. on the mechanism of cell permeability of macrocycles.38,97 The authors propose that the traditional hypothesis of a macrocycle switching from one (open) conformation that is favorable in water to another (closed) conformation favorable in chloroform is too simplistic. Based on exhaustive sampling, they suggest a more generalized model, which includes one or more congruent conformational states. These congruent conformational states are significantly populated in both solvents and allow the compound to pass through the membrane.
However, the cost of conformational rearrangements is only one contribution to the transfer free energy, which determines the water membrane partition coefficient. While the PCA projections capture differences based on dihedral conformations, these analyses are not designed to reflect distinctions of surface properties. Since surface polarity is decisive for the solvation free energies involved in the membrane crossing, we calculate the PSA for the ensemble of each compound in both solvents (Figure S7). We find that, for all compounds, the PSA distribution is shifted toward smaller values in chloroform. This observation is consistent with several studies from Kihlberg and co-workers on the conformational ensembles of macrocycles in different environments.96 Based on results from NMR, X-ray crystallography, and computational sampling, these studies report an increase of intramolecular hydrogen bonds and a decrease of the polar surface area for macrocyclic systems in an apolar environment compared to water.51,57
To assess structural aspects associated with the observed variations in surface polarity, we retrieve representative conformations using a PSA-based clustering (Figure 4A,C). For macrocycle 1f, we find the expected trend. In the PSA-based clustering of macrocycle 1e, however, the predominant conformational state of the 1e ensemble in chloroform does not show the typical features promoting cell permeability. This qualitative observation could be another contribution to the lower cell permeability of macrocycle 1e compared to 1f.
The results from the PSA-based clustering might appear counterintuitive compared to the trend captured with PCA. Hence, we emphasize that these two analyses focus on different aspects of conformational dynamics. The dihedral PCA depicted in Figure 2 captures the structural preferences at the core of the macrocycles, i.e., the ring atoms. However, this representation does not consider motions of the macrocycles’ side chains. In Figures S2 to S5, we highlight that distinctly separated minima in the dihedral PCA space can be very similar in terms of heavy-atom RMSD and surface polarity. In contrast, the PSA-based clustering shown in Figure 2 identifies structures based on their difference in surface polarity. Hence, by definition, we retrieve representative structures with clearly distinct surface polarity (Figures S8 and S9), which is dictated by the flexible side chains. Thus, the analyses presented in Figures 2 and 4 elucidate complementary aspects of the underlying mechanism and molecular determinants of membrane permeability.
For a thorough quantification of the properties on the surface, we then compute the transfer free energies for each conformation using GIST. By calculating the respective ensemble averages, we find a striking agreement of GIST transfer free energies with cell permeability, resulting in a Pearson correlation coefficient of r of 0.92 and a Spearman correlation coefficient ρ of 1.0 (Figure 5A). This result becomes even more intriguing considering that the experimental log POW, i.e., the octanol–water partition coefficient, for the same compounds shows an r of 0.89 and ρ of 0.77 with cell permeabilities (Figure S11). The proposed workflow hence is comparable with experimental log POW values in accuracy and could thus tremendously reduce the costs at the stage of macrocycle design and optimization.
Furthermore, we profile the impact of individual aspects of the applied methodology. As described in the Introduction, we have previously shown that water solvation free energy relates to a molecule’s hydrophobicity. Therefore, we tested for the benefits of incorporating contributions from chloroform solvation. In Figure 5B, we use the captured conformational ensembles and the respective populations in both solvents to calculate the ensemble average of the water solvation free energy of each macrocycle. Thus, we apply the same workflow for Figure 5A but only consider solvation free energies from water (Figure 5B) or chloroform (Figure S10). The results are clearly inferior to the transfer free energies that consider the contributions from both water and chloroform solvation.
This finding is in line with our latest work, in which we introduce transfer free energies to estimate partition coefficients between water and chloroform. In this preceding study, we deliberately only considered rigid small molecules to avoid inaccuracies resulting from insufficient sampling. Here, we describe transfer free energies as an ensemble property. Consequently, we also benchmark whether conformational sampling has a beneficial impact. In Figure 5C,D, we again calculate transfer free energies and water solvation free energies, yet we only consider a single conformation of each macrocycle. We consistently find that ensemble averages lead to substantially higher agreement with the experiment than single conformations.
We want to note that, in recent years, several workflows have been established that achieve exhaustive and reliable sampling of macrocycle conformational ensembles.32,35,36,38−40 Here, we perform aMD simulations as their computational demand is comparable to classic MD simulations while the conformational sampling is significantly enhanced.98,99 Furthermore, we have previously benchmarked the high reliability of this technique in providing conformational state populations.31 However, the presented GIST calculations are independent of the aMD approach and can be applied to ensembles from any sampling technique. We thus deem the proposed workflow as a highly generalizable and reliable tool to estimate cell permeabilities of macrocyclic drug candidates.
Conclusions
We present an approach to estimate cell permeabilities of macrocycles where we use aMD simulations and GIST to derive ensemble-averaged transfer free energies. We profile the conformational space in water and chloroform of a set of six macrocycles, which were designed to exhibit varying cell permeabilities and structural preferences.61
By applying our proposed approach, we find a remarkable correlation to the experimental membrane permeability with an r of 0.92 and ρ of 1.0, which is comparable with experimental log POW values. Furthermore, we find that exhaustive conformational sampling is an indispensable step to retrieve physically meaningful predictions for the physicochemical properties of macrocycles. Additionally, we show that incorporation of the contributions from chloroform considerably increases the reliability of our descriptor compared to the solely water-based approach.
Thus, we highlight the significance of reliable conformational sampling in macrocycle design. Additionally, we demonstrate the benefits of our recent re-implementation of the GIST algorithm, which now also allows us to employ chloroform as a solvent. We thus demonstrate a powerful workflow that provides extremely reliable estimates of macrocycle membrane permeabilities to enhance their design and optimization process.
The latest GPU implementation of GIST (GIGIST) is available free of charge from the github page of the Liedl Lab (https://github.com/liedllab/gigist.git).
Acknowledgments
This work was supported by the Austrian Science Fund (FWF) via the grant nos. P30737 “Protein Dynamics and Proteolytic Susceptibility” and P30565 “Characterization of Promiscuity and Specificity of Proteases” and the Erwin Schrödinger fellowship no. J-4150 (granted to M.S.). This project has further received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement no. 764958.
Glossary
Abbreviations
- GIST
grid inhomogeneous solvation theory
- PPIs
protein–protein interfaces
- MD
molecular dynamics
- aMD
accelerated molecular dynamics
- GPU
graphical processing unit
- PCA
principle component analysis
- PSA
polar surface area
- IMHB
intramolecular hydrogen bond
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.0c00280.
PCA projections of all six model compounds in water and chloroform (Figure S1), PCA projections including representative structures for macrocycles 1e and 1f (Figures S2 to S5), a representation of the conformational space of all macrocycles in terms of their global shape (Figure S6), PSA distributions of the entire series in water and chloroform (Figure S7), all representative structures from SASA-based clustering of macrocycles 1e and 1f (Figures S8 and S9), solvation free energies in chloroform for all compounds (Figure S10), and the correlation of experimental log POW values and cell permeabilities (Figure S11) (PDF)
Author Contributions
‡ A.S.K. and J.K. contributed equally. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
The authors declare no competing financial interest.
Supplementary Material
References
- Driggers E. M.; Hale S. P.; Lee J.; Terrett N. K. The Exploration of Macrocycles for Drug Discovery--an Underexploited Structural Class. Nat. Rev. Drug Discov. 2008, 7, 608–624. 10.1038/nrd2590. [DOI] [PubMed] [Google Scholar]
- Engelhardt H.; Böse D.; Petronczki M.; Scharn D.; Bader G.; Baum A.; Bergner A.; Chong E.; Dobel S.; Egger G.; Engelhardt C.; Ettmayer P.; Fuchs J. E.; Gerstberger T.; Gonnella N.; Grimm A.; Grondal E.; Haddad N.; Hopfgartner B.; Kousek R.; Krawiec M.; Kriz M.; Lamarre L.; Leung J.; Mayer M.; Patel N. D.; Simov B. P.; Reeves J. T.; Schnitzer R.; Schrenk A.; Sharps B.; Solca F.; Stadtmuller H.; Tan Z.; Wunberg T.; Zoephel A.; McConnell D. B. Start Selective and Rigidify: The Discovery Path toward a Next Generation of Egfr Tyrosine Kinase Inhibitors. J. Med. Chem. 2019, 62, 10272–10293. 10.1021/acs.jmedchem.9b01169. [DOI] [PubMed] [Google Scholar]
- Dougherty P. G.; Sahni A.; Pei D. Understanding Cell Penetration of Cyclic Peptides. Chem. Rev. 2019, 119, 10241–10287. 10.1021/acs.chemrev.9b00008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazo J. S.; Sharlow E. R. Drugging Undruggable Molecular Cancer Targets. Annu. Rev. Pharmacol. Toxicol. 2016, 56, 23–40. 10.1146/annurev-pharmtox-010715-103440. [DOI] [PubMed] [Google Scholar]
- Carter P. J. Potent Antibody Therapeutics by Design. Nat. Rev. Immunol. 2006, 6, 343–357. 10.1038/nri1837. [DOI] [PubMed] [Google Scholar]
- Leavy O. Therapeutic Antibodies: Past, Present and Future. Nat. Rev. Immunol. 2010, 10, 297. 10.1038/nri2763. [DOI] [PubMed] [Google Scholar]
- Slastnikova T. A.; Ulasov A. V.; Rosenkranz A. A.; Sobolev A. S. Targeted Intracellular Delivery of Antibodies: The State of the Art. Front Pharmacol. 2018, 9, 1208. 10.3389/fphar.2018.01208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hannesschlaeger C.; Horner A.; Pohl P. Intrinsic Membrane Permeability to Small Molecules. Chem. Rev. 2019, 119, 5922–5953. 10.1021/acs.chemrev.8b00560. [DOI] [PubMed] [Google Scholar]
- Yudin A. K. Macrocycles: Lessons from the Distant Past, Recent Developments, and Future Directions. Chem. Sci. 2015, 6, 30–49. 10.1039/C4SC03089C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marsault E.; Peterson M. L. Macrocycles Are Great Cycles: Applications, Opportunities, and Challenges of Synthetic Macrocycles in Drug Discovery. J. Med. Chem. 2011, 54, 1961–2004. 10.1021/jm1012374. [DOI] [PubMed] [Google Scholar]
- Zorzi A.; Deyle K.; Heinis C. Cyclic Peptide Therapeutics: Past, Present and Future. Curr. Opin. Chem. Biol. 2017, 38, 24–29. 10.1016/j.cbpa.2017.02.006. [DOI] [PubMed] [Google Scholar]
- Giordanetto F.; Kihlberg J. Macrocyclic Drugs and Clinical Candidates: What Can Medicinal Chemists Learn from Their Properties?. J. Med. Chem. 2014, 57, 278–295. 10.1021/jm400887j. [DOI] [PubMed] [Google Scholar]
- Doak B. C.; Over B.; Giordanetto F.; Kihlberg J. Oral Druggable Space Beyond the Rule of 5: Insights from Drugs and Clinical Candidates. Chem. Biol. 2014, 21, 1115–1142. 10.1016/j.chembiol.2014.08.013. [DOI] [PubMed] [Google Scholar]
- Matsson P.; Doak B. C.; Over B.; Kihlberg J. Cell Permeability Beyond the Rule of 5. Adv. Drug Delivery Rev. 2016, 101, 42–61. 10.1016/j.addr.2016.03.013. [DOI] [PubMed] [Google Scholar]
- Over B.; Matsson P.; Tyrchan C.; Artursson P.; Doak B. C.; Foley M. A.; Hilgendorf C.; Johnston S. E.; Lee M. D. IV; Lewis R. J.; McCarren P.; Muncipinto G.; Norinder U.; Perry M. W.; Duvall J. R.; Kihlberg J. Structural and Conformational Determinants of Macrocycle Cell Permeability. Nat. Chem. Biol. 2016, 12, 1065–1074. 10.1038/nchembio.2203. [DOI] [PubMed] [Google Scholar]
- Fouché M.; Schäfer M.; Berghausen J.; Desrayaud S.; Blatter M.; Piéchon P.; Dix I.; Martin Garcia A.; Roth H. J. Design and Development of a Cyclic Decapeptide Scaffold with Suitable Properties for Bioavailability and Oral Exposure. ChemMedChem 2016, 11, 1048–1059. 10.1002/cmdc.201600082. [DOI] [PubMed] [Google Scholar]
- Rand A. C.; Leung S. S.; Eng H.; Rotter C. J.; Sharma R.; Kalgutkar A. S.; Zhang Y.; Varma M. V.; Farley K. A.; Khunte B.; Limberakis C.; Price D. A.; Liras S.; Mathiowetz A. M.; Jacobson M. P.; Lokey R. S. Optimizing Pk Properties of Cyclic Peptides: The Effect of Side Chain Substitutions on Permeability and Clearance. MedChemComm 2012, 3, 1282–1289. 10.1039/C2MD20203D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bockus A. T.; Lexa K. W.; Pye C. R.; Kalgutkar A. S.; Gardner J. W.; Hund K. C.; Hewitt W. M.; Schwochert J. A.; Glassey E.; Price D. A.; Mathiowetz A. M.; Liras S.; Jacobson M. P.; Lokey R. S. Probing the Physicochemical Boundaries of Cell Permeability and Oral Bioavailability in Lipophilic Macrocycles Inspired by Natural Products. J. Med. Chem. 2015, 58, 4581–4589. 10.1021/acs.jmedchem.5b00128. [DOI] [PubMed] [Google Scholar]
- Villar E. A.; Beglov D.; Chennamadhavuni S.; Porco J. A. Jr.; Kozakov D.; Vajda S.; Whitty A. How Proteins Bind Macrocycles. Nat. Chem. Biol. 2014, 10, 723–731. 10.1038/nchembio.1584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krüger D. M.; Glas A.; Bier D.; Pospiech N.; Wallraven K.; Dietrich L.; Ottmann C.; Koch O.; Hennig S.; Grossmann T. N. Structure-Based Design of Non-Natural Macrocyclic Peptides That Inhibit Protein-Protein Interactions. J. Med. Chem. 2017, 60, 8982–8988. 10.1021/acs.jmedchem.7b01221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doak B. C.; Zheng J.; Dobritzsch D.; Kihlberg J. How Beyond Rule of 5 Drugs and Clinical Candidates Bind to Their Targets. J. Med. Chem. 2016, 59, 2312–2327. 10.1021/acs.jmedchem.5b01286. [DOI] [PubMed] [Google Scholar]
- Fairlie D. P.; Tyndall J. D. A.; Reid R. C.; Wong A. K.; Abbenante G.; Scanlon M. J.; March D. R.; Bergman D. A.; Chai C. L. L.; Burkett B. A. Conformational Selection of Inhibitors and Substrates by Proteolytic Enzymes: Implications for Drug Design and Polypeptide Processing. J. Med. Chem. 2000, 43, 1271–1281. 10.1021/jm990315t. [DOI] [PubMed] [Google Scholar]
- Passioura T.; Katoh T.; Goto Y.; Suga H. Selection-Based Discovery of Druglike Macrocyclic Peptides. Annu. Rev. Biochem. 2014, 83, 727–752. 10.1146/annurev-biochem-060713-035456. [DOI] [PubMed] [Google Scholar]
- Madala P. K.; Tyndall J. D.; Nall T.; Fairlie D. P. Update 1 Of: Proteases Universally Recognize Beta Strands in Their Active Sites. Chem. Rev. 2010, 110, PR1–PR31. 10.1021/cr900368a. [DOI] [PubMed] [Google Scholar]
- Millward S. W.; Fiacco S.; Austin R. J.; Roberts R. W. Design of Cyclic Peptides That Bind Protein Surfaces with Antibody-Like Affinity. ACS Chem. Biol. 2007, 2, 625–634. 10.1021/cb7001126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J.; Talibov V. O.; Peintner S.; Rhee C.; Poongavanam V.; Geitmann M.; Sebastiano M. R.; Simon B.; Hennig J.; Dobritzsch D.; Danielson U. H.; Kihlberg J. Macrocyclic Peptides Uncover a Novel Binding Mode for Reversible Inhibitors of Lsd1. ACS Omega 2020, 5, 3979–3995. 10.1021/acsomega.9b03493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu X.; Sun D. Macrocyclic Drugs and Synthetic Methodologies toward Macrocycles. Molecules 2013, 18, 6230–6268. 10.3390/molecules18066230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hugelshofer C. L.; Magauer T. A Divergent Approach to the Marine Diterpenoids (+)-Dictyoxetane and (+)-Dolabellane V. Chemistry 2016, 22, 15125–15136. 10.1002/chem.201603061. [DOI] [PubMed] [Google Scholar]
- Donald J. R.; Unsworth W. P. Ring-Expansion Reactions in the Synthesis of Macrocycles and Medium-Sized Rings. Chemistry 2017, 23, 8780–8799. 10.1002/chem.201700467. [DOI] [PubMed] [Google Scholar]
- Turner R. A.; Oliver A. G.; Lokey R. S. Click Chemistry as a Macrocyclization Tool in the Solid-Phase Synthesis of Small Cyclic Peptides. Org. Lett. 2007, 9, 5011–5014. 10.1021/ol702228u. [DOI] [PubMed] [Google Scholar]
- Kamenik A. S.; Lessel U.; Fuchs J. E.; Fox T.; Liedl K. R. Peptidic Macrocycles - Conformational Sampling and Thermodynamic Characterization. J. Chem. Inf. Model. 2018, 58, 982–992. 10.1021/acs.jcim.8b00097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coutsias E. A.; Lexa K. W.; Wester M. J.; Pollock S. N.; Jacobson M. P. Exhaustive Conformational Sampling of Complex Fused Ring Macrocycles Using Inverse Kinematics. J. Chem. Theory Comput. 2016, 12, 4674–4687. 10.1021/acs.jctc.6b00250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Appavoo S. D.; Huh S.; Diaz D. B.; Yudin A. K. Conformational Control of Macrocycles by Remote Structural Modification. Chem. Rev. 2019, 119, 9724–9752. 10.1021/acs.chemrev.8b00742. [DOI] [PubMed] [Google Scholar]
- Hosseinzadeh P.; Bhardwaj G.; Mulligan V. K.; Shortridge M. D.; Craven T. W.; Pardo-Avila F.; Rettie S. A.; Kim D. E.; Silva D.-A.; Ibrahim Y. M.; Webb I. K.; Cort J. R.; Adkins J. N.; Varani G.; Baker D. Comprehensive Computational Design of Ordered Peptide Macrocycles. Science 2017, 358, 1461–1466. 10.1126/science.aap7577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sindhikara D.; Spronk S. A.; Day T.; Borrelli K.; Cheney D. L.; Posy S. L. Improving Accuracy, Diversity, and Speed with Prime Macrocycle Conformational Sampling. J. Chem. Inf. Model. 2017, 57, 1881–1894. 10.1021/acs.jcim.7b00052. [DOI] [PubMed] [Google Scholar]
- Chen I.-J.; Foloppe N. Tackling the Conformational Sampling of Larger Flexible Compounds and Macrocycles in Pharmacology and Drug Discovery. Bioorg. Med. Chem. 2013, 21, 7898–7920. 10.1016/j.bmc.2013.10.003. [DOI] [PubMed] [Google Scholar]
- Glas A.; Wamhoff E.-C.; Krüger D. M.; Rademacher C.; Grossmann T. N. Increased Conformational Flexibility of a Macrocycle-Receptor Complex Contributes to Reduced Dissociation Rates. Chemistry 2017, 23, 16157–16161. 10.1002/chem.201702776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witek J.; Keller B. G.; Blatter M.; Meissner A.; Wagner T.; Riniker S. Kinetic Models of Cyclosporin a in Polar and Apolar Environments Reveal Multiple Congruent Conformational States. J. Chem. Inf. Model. 2016, 56, 1547–1562. 10.1021/acs.jcim.6b00251. [DOI] [PubMed] [Google Scholar]
- Watts K. S.; Dalal P.; Tebben A. J.; Cheney D. L.; Shelley J. C. Macrocycle Conformational Sampling with Macromodel. J. Chem. Inf. Model. 2014, 54, 2680–2696. 10.1021/ci5001696. [DOI] [PubMed] [Google Scholar]
- Bonnet P.; Agrafiotis D. K.; Zhu F.; Martin E. Conformational Analysis of Macrocycles: Finding What Common Search Methods Miss. J. Chem. Inf. Model. 2009, 49, 2242–2259. 10.1021/ci900238a. [DOI] [PubMed] [Google Scholar]
- Suarez D.; Diaz N. Ligand Strain and Entropic Effects on the Binding of Macrocyclic and Linear Inhibitors: Molecular Modeling of Penicillopepsin Complexes. J. Chem. Inf. Model. 2017, 57, 2045–2055. 10.1021/acs.jcim.7b00355. [DOI] [PubMed] [Google Scholar]
- Labute P. Lowmodemd--Implicit Low-Mode Velocity Filtering Applied to Conformational Search of Macrocycles and Protein Loops. J. Chem. Inf. Model. 2010, 50, 792–800. 10.1021/ci900508k. [DOI] [PubMed] [Google Scholar]
- Ono S.; Naylor M. R.; Townsend C. E.; Okumura C.; Okada O.; Lokey R. S. Conformation and Permeability: Cyclic Hexapeptide Diastereomers. J. Chem. Inf. Model. 2019, 59, 2952–2963. 10.1021/acs.jcim.9b00217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jain A. N.; Cleves A. E.; Gao Q.; Wang X.; Liu Y.; Sherer E. C.; Reibarkh M. Y. Complex Macrocycle Exploration: Parallel, Heuristic, and Constraint-Based Conformer Generation Using Forcegen. J. Comput.-Aided Mol. Des. 2019, 33, 531–558. 10.1007/s10822-019-00203-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakefield A. E.; Wuest W. M.; Voelz V. A. Molecular Simulation of Conformational Pre-Organization in Cyclic Rgd Peptides. J. Chem. Inf. Model. 2015, 55, 806–813. 10.1021/ci500768u. [DOI] [PubMed] [Google Scholar]
- McHugh S. M.; Rogers J. R.; Yu H.; Lin Y.-S. Insights into How Cyclic Peptides Switch Conformations. J. Chem. Theory Comput. 2016, 12, 2480–2488. 10.1021/acs.jctc.6b00193. [DOI] [PubMed] [Google Scholar]
- Slough D. P.; Yu H.; McHugh S. M.; Lin Y.-S. Toward Accurately Modeling N-Methylated Cyclic Peptides. Phys. Chem. Chem. Phys. 2017, 19, 5377–5388. 10.1039/C6CP07700E. [DOI] [PubMed] [Google Scholar]
- Bell I. M.; Gallicchio S. N.; Abrams M.; Beese L. S.; Beshore D. C.; Bhimnathwala H.; Bogusky M. J.; Buser C. A.; Culberson J. C.; Davide J.; Ellis-Hutchings M.; Fernandes C.; Gibbs J. B.; Graham S. L.; Hamilton K. A.; Hartman G. D.; Heimbrook D. C.; Homnick C. F.; Huber H. E.; Huff J. R.; Kassahun K.; Koblan K. S.; Kohl N. E.; Lobell R. B.; Lynch J. J.; Robinson R.; Rodrigues A. D.; Taylor J. S.; Walsh E. S.; Williams T. M.; Zartman C. B. 3-Aminopyrrolidinone Farnesyltransferase Inhibitors: Design of Macrocyclic Compounds with Improved Pharmacokinetics and Excellent Cell Potency. J. Med. Chem. 2002, 45, 2388–2409. 10.1021/jm010531d. [DOI] [PubMed] [Google Scholar]
- Nielsen D. S.; Hoang H. N.; Lohman R.-J.; Hill T. A.; Lucke A. J.; Craik D. J.; Edmonds D. J.; Griffith D. A.; Rotter C. J.; Ruggeri R. B.; Price D. A.; Liras S.; Fairlie D. P. Improving on Nature: Making a Cyclic Heptapeptide Orally Bioavailable. Angew. Chem. Int. Ed. 2014, 53, 12059–12063. 10.1002/anie.201405364. [DOI] [PubMed] [Google Scholar]
- Schwochert J.; Lao Y.; Pye C. R.; Naylor M. R.; Desai P. V.; Gonzalez Valcarcel I. C.; Barrett J. A.; Sawada G.; Blanco M.-J.; Lokey R. S. Stereochemistry Balances Cell Permeability and Solubility in the Naturally Derived Phepropeptin Cyclic Peptides. ACS Med. Chem. Lett. 2016, 7, 757–761. 10.1021/acsmedchemlett.6b00100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danelius E.; Poongavanam V.; Peintner S.; Wieske L. H. E.; Erdélyi M.; Kihlberg J. Solution Conformations Explain the Chameleonic Behaviour of Macrocyclic Drugs. Chemistry 2020, 26, 5231–5244. 10.1002/chem.201905599. [DOI] [PubMed] [Google Scholar]
- Ahlbach C. L.; Lexa K. W.; Bockus A. T.; Chen V.; Crews P.; Jacobson M. P.; Lokey R. S. Beyond Cyclosporine A: Conformation-Dependent Passive Membrane Permeabilities of Cyclic Peptide Natural Products. Future Med. Chem. 2015, 7, 2121–2130. 10.4155/fmc.15.78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riniker S. Toward the Elucidation of the Mechanism for Passive Membrane Permeability of Cyclic Peptides. Future Med. Chem. 2019, 11, 637–639. 10.4155/fmc-2018-0429. [DOI] [PubMed] [Google Scholar]
- Witek J.; Mühlbauer M.; Keller B. G.; Blatter M.; Meissner A.; Wagner T.; Riniker S. Interconversion Rates between Conformational States as Rationale for the Membrane Permeability of Cyclosporines. ChemPhysChem 2017, 18, 3309–3314. 10.1002/cphc.201700995. [DOI] [PubMed] [Google Scholar]
- Rezai T.; Yu B.; Millhauser G. L.; Jacobson M. P.; Lokey R. S. Testing the Conformational Hypothesis of Passive Membrane Permeability Using Synthetic Cyclic Peptide Diastereomers. J. Am. Chem. Soc. 2006, 128, 2510–2511. 10.1021/ja0563455. [DOI] [PubMed] [Google Scholar]
- Dickson C. J.; Hornak V.; Pearlstein R. A.; Duca J. S. Structure-Kinetic Relationships of Passive Membrane Permeation from Multiscale Modeling. J. Am. Chem. Soc. 2017, 139, 442–452. 10.1021/jacs.6b11215. [DOI] [PubMed] [Google Scholar]
- Peng C.; Atilaw Y.; Wang J.; Xu Z.; Poongavanam V.; Shi J.; Kihlberg J.; Zhu W.; Erdélyi M. Conformation of the Macrocyclic Drug Lorlatinib in Polar and Nonpolar Environments: A Md Simulation and Nmr Study. ACS Omega 2019, 4, 22245–22250. 10.1021/acsomega.9b03797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen D. S.; Lohman R.-J.; Hoang H. N.; Hill T. A.; Jones A.; Lucke A. J.; Fairlie D. P. Flexibility Versus Rigidity for Orally Bioavailable Cyclic Hexapeptides. ChemBioChem 2015, 16, 2289–2293. 10.1002/cbic.201500441. [DOI] [PubMed] [Google Scholar]
- Hamelberg D.; Mongan J.; McCammon J. A. Accelerated Molecular Dynamics: A Promising and Efficient Simulation Method for Biomolecules. J. Chem. Phys. 2004, 120, 11919–11929. 10.1063/1.1755656. [DOI] [PubMed] [Google Scholar]
- Pierce L. C. T.; Salomon-Ferrer R.; de Oliveira C. A. F.; McCammon J. A.; Walker R. C. Routine Access to Millisecond Time Scale Events with Accelerated Molecular Dynamics. J. Chem. Theory Comput. 2012, 8, 2997–3002. 10.1021/ct300284c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyagi M.; Poongavanam V.; Lindhagen M.; Pettersen A.; Sjö P.; Schiesser S.; Kihlberg J. Toward the Design of Molecular Chameleons: Flexible Shielding of an Amide Bond Enhances Macrocycle Cell Permeability. Org. Lett. 2018, 20, 5737–5742. 10.1021/acs.orglett.8b02447. [DOI] [PubMed] [Google Scholar]
- Nguyen C. N.; Young T. K.; Gilson M. K. Grid Inhomogeneous Solvation Theory: Hydration Structure and Thermodynamics of the Miniature Receptor Cucurbit[7]Uril. J. Chem. Phys. 2012, 137, 044101 10.1063/1.4733951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen C.; Gilson M. K.; Young T.. Structure and Thermodynamics of Molecular Hydration Via Grid Inhomogeneous Solvation Theory; arXiv preprint arXiv:1108.48762011. [DOI] [PMC free article] [PubMed]
- Kraml J.; Kamenik A. S.; Waibl F.; Schauperl M.; Liedl K. R. Solvation Free Energy as a Measure of Hydrophobicity: Application to Serine Protease Binding Interfaces. J. Chem. Theory Comput. 2019, 15, 5872–5882. 10.1021/acs.jctc.9b00742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schauperl M.; Podewitz M.; Waldner B. J.; Liedl K. R. Enthalpic and Entropic Contributions to Hydrophobicity. J. Chem. Theory Comput. 2016, 12, 4600–4610. 10.1021/acs.jctc.6b00422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loeffler J. R.; Schauperl M.; Liedl K. R. Hydration of Aromatic Heterocycles as an Adversary of Pi-Stacking. J. Chem. Inf. Model. 2019, 59, 4209–4219. 10.1021/acs.jcim.9b00395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balius T. E.; Fischer M.; Stein R. M.; Adler T. B.; Nguyen C. N.; Cruz A.; Gilson M. K.; Kurtzman T.; Shoichet B. K. Testing Inhomogeneous Solvation Theory in Structure-Based Ligand Discovery. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, E6839–E6846. 10.1073/pnas.1703287114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Podewitz M.; Wang Y.; Quoika P. K.; Loeffler J. R.; Schauperl M.; Liedl K. R. Coil-Globule Transition Thermodynamics of Poly(N-Isopropylacrylamide). J. Phys. Chem. B 2019, 123, 8838–8847. 10.1021/acs.jpcb.9b06125. [DOI] [PubMed] [Google Scholar]
- Hüfner-Wulsdorf T.; Klebe G. Protein-Ligand Complex Solvation Thermodynamics: Development, Parameterization, and Testing of Gist-Based Solvent Functionals. J. Chem. Inf. Model. 2020, 60, 1409–1423. 10.1021/acs.jcim.9b01109. [DOI] [PubMed] [Google Scholar]
- Kraml J.; Hofer F.; Kamenik A. S.; Waibl F.; Kahler U.; Liedl K. R. Solvation Thermodynamics in Different Solvents – Water Chloroform Partition Coefficients from Grid Inhomogeneous Solvation Theory. J. Chem. Theory Comput. 2020, submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen C. N.; Cruz A.; Gilson M. K.; Kurtzman T. Thermodynamics of Water in an Enzyme Active Site: Grid-Based Hydration Analysis of Coagulation Factor Xa. J. Chem. Theory Comput. 2014, 10, 2769–2780. 10.1021/ct401110x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsey S.; Nguyen C.; Salomon-Ferrer R.; Walker R. C.; Gilson M. K.; Kurtzman T. Solvation Thermodynamic Mapping of Molecular Surfaces in Ambertools: Gist. J. Comput. Chem. 2016, 37, 2029–2037. 10.1002/jcc.24417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazaridis T. Inhomogeneous Fluid Approach to Solvation Thermodynamics. 1. Theory. J. Phys. Chem. B 1998, 102, 3531–3541. 10.1021/jp9723574. [DOI] [Google Scholar]
- Lazaridis T. Inhomogeneous Fluid Approach to Solvation Thermodynamics. 2. Applications to Simple Fluids. J. Phys. Chem. B 1998, 102, 3542–3550. 10.1021/jp972358w. [DOI] [Google Scholar]
- Case D.; Ben-Shalom I.; Brozell S.; Cerutti D.; Cheatham T. III; Cruzeiro V.; Darden T.; Duke R.; Ghoreishi D.; Gilson M.. Amber 2018, 2018.
- MOE Moe (Molecular Operating Environment), 2019.1; Chemical Computing Group (CCG): 2019
- Maier J. A.; Martinez C.; Kasavajhala K.; Wickstrom L.; Hauser K. E.; Simmerling C. Ff14sb: Improving the Accuracy of Protein Side Chain and Backbone Parameters from Ff99sb. J. Chem. Theory Comput. 2015, 11, 3696–3713. 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Wang J.; Wang W.; Kollman P. A.; Case D. A. Automatic Atom Type and Bond Type Perception in Molecular Mechanical Calculations. J. Mol. Graphics Modell. 2006, 25, 247–260. 10.1016/j.jmgm.2005.12.005. [DOI] [PubMed] [Google Scholar]
- Frisch M.; Trucks G.; Schlegel H.; Scuseria G.; Robb M.; Cheeseman J.; Scalmani G.; Barone V.; Petersson G.; Nakatsuji H.. Gaussian 16, Revision rev. D01; Gaussian, Inc.: Wallingford, CT, 2016. [Google Scholar]
- Bayly C. I.; Cieplak P.; Cornell W.; Kollman P. A. A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges: The Resp Model. J. Chem. Phys. 1993, 97, 10269–10280. 10.1021/j100142a004. [DOI] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Fox T.; Kollman P. A. Application of the RESP Methodology in the Parametrization of Organic Solvents. J. Phys. Chem. B 1998, 102, 8070–8079. 10.1021/jp9717655. [DOI] [Google Scholar]
- Wallnoefer H. G.; Liedl K. R.; Fox T. A Challenging System: Free Energy Prediction for Factor Xa. J. Comput. Chem. 2011, 32, 1743–1752. 10.1002/jcc.21758. [DOI] [PubMed] [Google Scholar]
- de Oliveira C. A. F.; Hamelberg D.; McCammon J. A. On the Application of Accelerated Molecular Dynamics to Liquid Water Simulations. J. Phys. Chem. B 2006, 110, 22695–22701. 10.1021/jp062845o. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doshi U.; Hamelberg D. Improved Statistical Sampling and Accuracy with Accelerated Molecular Dynamics on Rotatable Torsions. J. Chem. Theory Comput. 2012, 8, 4004–4012. 10.1021/ct3004194. [DOI] [PubMed] [Google Scholar]
- Hamelberg D.; de Oliveira C. A. F.; McCammon J. A. Sampling of Slow Diffusive Conformational Transitions with Accelerated Molecular Dynamics. J. Chem. Phys. 2007, 127, 155102. 10.1063/1.2789432. [DOI] [PubMed] [Google Scholar]
- Adelman S. A.; Doll J. D. Generalized Langevin Equation Approach for Atom/Solid-Surface Scattering: General Formulation for Classical Scattering Off Harmonic Solids. J. Chem. Phys. 1976, 64, 2375–2388. 10.1063/1.432526. [DOI] [Google Scholar]
- Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; DiNola A.; Haak J. R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
- Ciccotti G.; Ryckaert J. P. Molecular-Dynamics Simulation of Rigid Molecules. Comput. Phys. Rep. 1986, 4, 346–392. 10.1016/0167-7977(86)90022-5. [DOI] [Google Scholar]
- Götz A. W.; Williamson M. J.; Xu D.; Poole D.; Le Grand S.; Walker R. C. Routine Microsecond Molecular Dynamics Simulations with Amber on Gpus. 1. Generalized Born. J. Chem. Theory Comput. 2012, 8, 1542–1555. 10.1021/ct200909j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salomon-Ferrer R.; Götz A. W.; Poole D.; Le Grand S.; Walker R. C. Routine Microsecond Molecular Dynamics Simulations with Amber on Gpus. 2. Explicit Solvent Particle Mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. 10.1021/ct400314y. [DOI] [PubMed] [Google Scholar]
- Roe D. R.; Cheatham T. E. III 3rd, Ptraj and Cpptraj: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput. 2013, 9, 3084–3095. 10.1021/ct400341p. [DOI] [PubMed] [Google Scholar]
- Miao Y.; Sinko W.; Pierce L.; Bucher D.; Walker R. C.; McCammon J. A. Improved Reweighting of Accelerated Molecular Dynamics Simulations for Free Energy Calculation. J. Chem. Theory Comput. 2014, 10, 2677–2689. 10.1021/ct500090q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamenik A. S.; Kahler U.; Fuchs J. E.; Liedl K. R. Localization of Millisecond Dynamics: Dihedral Entropy from Accelerated Md. J. Chem. Theory Comput. 2016, 12, 3449–3455. 10.1021/acs.jctc.6b00231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poongavanam V.; Danelius E.; Peintner S.; Alcaraz L.; Caron G.; Cummings M. D.; Wlodek S.; Erdelyi M.; Hawkins P. C. D.; Ermondi G.; Kihlberg J. Conformational Sampling of Macrocyclic Drugs in Different Environments: Can We Find the Relevant Conformations?. ACS Omega 2018, 3, 11742–11757. 10.1021/acsomega.8b01379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witek J.; Wang S.; Schroeder B.; Lingwood R.; Dounas A.; Roth H. J.; Fouché M.; Blatter M.; Lemke O.; Keller B.; Riniker S. Rationalization of the Membrane Permeability Differences in a Series of Analogue Cyclic Decapeptides. J. Chem. Inf. Model. 2019, 59, 294–308. 10.1021/acs.jcim.8b00485. [DOI] [PubMed] [Google Scholar]
- Miao Y.; Nichols S. E.; McCammon J. A. Free Energy Landscape of G-Protein Coupled Receptors, Explored by Accelerated Molecular Dynamics. Phys. Chem. Chem. Phys. 2014, 16, 6398–6406. 10.1039/c3cp53962h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markwick P. R. L.; Cervantes C. F.; Abel B. L.; Komives E. A.; Blackledge M.; McCammon J. A. Enhanced Conformational Space Sampling Improves the Prediction of Chemical Shifts in Proteins. J. Am. Chem. Soc. 2010, 132, 1220–1221. 10.1021/ja9093692. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.