Abstract
In recent years, we have witnessed the explosion of large-scale data in various fields. Classical statistical methodologies such as linear regression or generalized linear regression often show inadequate performance on heterogeneous data because the key homogeneity assumption fails. In this paper, we present a flexible framework to handle heterogeneous populations that can be naturally grouped into several ordered subtypes. A local model technique utilizing ordinal class labels during the training stage is proposed. We define a new “progression score” that captures the progression of ordinal classes, and use a truncated Gaussian kernel to construct the weight function in a local regression framework. Furthermore, given the weights, we apply sparse shrinkage on the local fitting to handle high dimensionality. In this way, our local model is able to conduct variable selection on each query point. Numerical studies show the superiority of our proposed method over several existing ones. Our method is also applied to the Alzheimer’s Disease Neuroimaging Initiative (ADNI) data to make predictions on the longitudinal clinical scores based on different modalities of baseline brain image features.
Keywords: Heterogeneity, local models, ordinal classification, random forests
I. Introduction
ALZHEIMER’S disease (AD) is one of the most common forms of chronic neurodegenerative diseases characterized by memory loss and behavioural issues. In 2015, there were about 29.8 million people in the world diagnosed with AD [1]. The widespread incidence of AD makes it an inevitable issue and it creates severe financial burden to both patients and governments. Therefore, accurate AD diagnosis is critical for public health. To identify behavioral and mental abnormalities associated with the disease, several neuropsychological tests have been proposed such as Mini-Mental State Examination (MMSE) [2] and Alzheimer’s Disease Assessment Scale-Cognitive Subscale (ADAS-Cog) [3]. The scores obtained from the tests can be considered as the quantitive measurements of the disease progression. Recently, several studies based on regression methods have been conducted to estimate clinical scores based on extracted features from different modalities of biomarkers, e.g., structural brain atrophy delineated by structural magnetic resonance imaging (MRI) [4], [5], [6], and metabolic alterations characterized by fluorodeoxyglucose positron emission tomography (FDG-PET) [7]. In this paper, we mainly focus on estimating longitudinal clinical scores from baseline brain modality features to better understand the relationship between them and gain further insight about AD.
Our key motivation for the proposed method is to handle data heterogeneity to improve interpretation in terms of feature selection and prediction. One important characteristic of brain image features is that the data can be very heterogeneous [8]. In this paper, heterogeneity refers to that data can be neither independent identically distributed (i.i.d.) nor stationary observations from a distribution [9]. Classical statistical methodologies that give a global fit such as linear regression or generalized linear regression often show inadequate performance on heterogeneous data because the key homogeneity asssumption fails. For example, homogeneity in linear regression assumes that the regression coefficient is the same for the whole population and the errors are i.i.d. In particular, linear regression assumes the following probability distribution for response yi given feature xi:
with ϵi being the noise term. To make statistical inference, one often assumes normality. If ϵi are i.i.d. N(0, σ2), then the homogeneity assumption holds. A similar concept is homoscadescity, which assumes the equality of the variances on the errors. If we have different variances , then the errors are heteroscadastic and the homogeneity assumption fails. A typical way to relax the homoscedasticity assumption is weighted regression if we have some information about the variances. The scope of this paper is beyond heteroscedastic errors. Our proposed framework is more flexible to model heterogeneous data such as brain image data.
In this paper, we are interested in the regression setting with clinical scores as the continuous response, where the population can be naturally grouped into several ordered subtypes. The ordered subtypes indicate that the groups underlying the population are ordinal, which can be seen in many applications, especially in the biomedical research studies. For example, in the study of AD, subjects are diagnosed into Normal Control (NC), Mild Cognitive Impairment (MCI) or AD, where the three groups are ordered by the disease severity. The underlying relationship between the responses and input variables can vary among different ordered groups. Since there is inherent relationship between the class label information and clinical scores [10], [11], it would be useful to incorporate the class information during the training stage to improve the prediction performance. A natural way of handling this is the clusterwise regression models [12], where the idea behind is to determine the class membership and then apply linear regression within each class. However by training separate models within each class, the training sample size will be decreased dramatically and at the same time information across different groups may not be sufficiently captured. Furthermore, in many applications, close classes often share a similar distribution or a smoothly changing behavior [9]. The mixed effect model or latent mixed effect model [13] is another possible solution. Despite the improvement over fixed effect models, the model assumption is still not flexible enough and may not be well suited for the case with ordinal classes. In addition, it is typically computationally intensive with EM type algorithms that need multiple steps to converge.
To utilize the class label information, we define a new “progression score” that captures the progression of ordinal classes on a continuous spectrum. For example, in the AD study, instead of labeling the subjects with discrete labels NC, MCI and AD, a continuous scalar variable could be assigned. In this way, the severity of the disease is naturally characterized by the ordering of real numbers. In the literature, [14], [15] developed progression scores on a longitudinal trajectory by assuming a linear or nonlinear link from progression scores to seven selected cognitive biomarkers, where their progression scores are modeled as affine transformations from subjects’ ages. Utilizing similar longitudinal frameworks, [16], [17], [18] proposed longitudinal models using voxel-wise biomarkers as the responses. EM-type algorithms were used, which can be time-consuming to predict progression scores using high-dimensional brain biomarkers as input. For example, [16] took 30 minutes per iteration and [18] took 15 hours. To reduce the dimensionality, [17] used a clustering algorithm for voxel-wise biomarkers before fitting the longitudinal model. [13] proposed a composite cognitive performance measure based on four types of existing clinical scores. In contrast to existing progression scores, in this paper, our new progression score is not defined as a longitudinal measure along the time course, but as a disease severity measure, which is characterized by the natural ordering the disease stages: NC, MCI and AD. Another major difference is that our progression scores are obtained from modeling the relationship between brain modality features (as inputs) and class labels (as responses), while the progression scores from existing longitudinal models are estimated from modeling the relationship between ages (as inputs) and cognitive biomarkers such as clinical scores and other brain modality features (as responses).
We propose the use of ordinal logistic regression to define our progression score. Being known as a classification method dealing with ordinal population, the class assignment is accomplished by maximizing the likelihood of an ordinal logistic regression model for predicting class. Our choice of progression scores is based on linear transformation of the logistic regression output, which quantifies the disease severity on a continuous scale.
The information from the estimated progression scores is utilized by fitting a flexible local model [19]. [20] proposed a local framework with applications to classification in ADNI studies. In general, local methods can be formulated within the nonparametric regression framework as local weighted averages for prediction, using kernel functions as weights. More specifically, these types of local kernel methods fit a different but simple model separately at each query point to achieve the flexibility. The kernel weight function can control the contribution of each training point according to its distance to the query point. As a result, such local kernel methods can handle heterogeneity since separate models are used in the local neighborhood of every query point. For example, the method of K nearest neighbors (KNN) [21] is a special case of such local kernel methods. The local fitting step in the traditional kernel methods can be challenged by the high dimensionality, which motivates us to apply shrinkage techniques to prevent overfitting.
We propose to use a truncated Gaussian kernel with the estimated progression scores as input to construct the weight function in our local model framework. The prediction on each query point can borrow the strength of samples both within the same class and across different classes. As a result, our method can be more robust to incorrect classification results even if we apply a classification model in our first step. By doing so, we are able to map the high dimensional large-scale data onto a one-dimensional space that characterizes the class progression, where the Euclidean distance can work well. A truncation parameter is automatically selected by cross-validation to remove samples that are far away from the query point in the local fitting.
In addition to the kernel function from ordinal logistic regression that forms part of our sample weights, we also include random forests [22] sample weights [23] adaptively for the kernel function in our framework. The weights from random forests circumvent the use of the Euclidean distance in high dimensional data in the nonparametric setting. By doing so, our method inherits the benefits from random forests such as robustness to outliers and the good performance on large-scale data. Depending on the effectiveness of random forests, we allow our algorithm to automatically determine whether the sample weights from random forests are absorbed into the kernels by cross-validation. Once the adaptive weights are determined, we fit the local shape of the regression surface using these weights.
There are two main new contributions on our proposed weight function: its capability to capture the ordinal population structure and the utilization of the random forest weights to improve performance. Furthermore, given the weights, we apply shrinkage on the local fitting to handle high dimesionality. For the local fitting, we apply a penalty to achieve the goal of variable selection. We have shown that applying the penalty in the local fitting generalizes the methods of kernel smoothing, i.e., local weighted averaging. Our numerical studies show the superiority of our proposed method over random forests and penalized regression techniques.
The rest of the paper is organized as follows. In Section II, we introduce the general penalized local model framework and develop our own sample weight functions, tailored to the ordinal heterogeneous population. In Section III, we perform some simulation studies and show the superiority of our work over several other existing methods. In Section IV, we apply our method onto the ADNI data to make predictions on the longitudinal clinical scores based on different modalities of baseline brain image features. Some discussions are provided in Section V.
II. Supervised Neighborhoods for Ordinal Subgrouped Population
There are two key ingredients in our local model framework. First, we have a regularization step embedded in the local linear fitting. Second, we construct local kernel weights by adaptively combining weights from truncated Gaussian kernel with weights from random forests. The Gaussian kernel functions are defined on a newly defined progression score space, on which the scores are given by the ordinal logistic regression to capture the heterogeneity in the ordinal population. Besides the progression score, the sample weights from random forests are adaptively included in the local weights to make our method more flexible than global methods.
We now introduce some notations for the paper. Suppose there are n training samples and p predictive variables. Let X = (X1, · · ·, Xp) = (x1, · · ·, xn)T denote the n×p training data matrix of prediciting variables. Let y = (y1, · · · , yn)T denote response vector of length n. Suppose there are K ordered groups in the population and let c = (c1, · · · , cn)T denote the observation vector of class labels for the n subjects, where ci takes discrete values from the set {1, · · · ,K}.
In order to discuss our proposed method, we first introduce the general penalized local linear models in Section II-A. Then, we describe how the progression score is established based on ordinal logistic regression and applied to build the kernel function in Section II-B. Finally, we describe an additional type of local weights trained from random forests that can possibly be absorbed in the weights to enhance the model performance in Section II-C.
A. Penalized Local Linear Models
Local models are very flexible and have the potential to be robust to heterogeneity. In this paper, we fit a different local model that uses a squared error loss and takes linear functions in the function space at each query point . Moreover, we apply a penalty to the weighted squared loss to overcome the high dimensionality in the large-scale data. Denote the weight function as , a mapping that is determined by the distance between two points in . The smaller the distance is, the larger the weight will be. For now we assume that the weights are given and will discuss the choice of weights in Sections II-B and II-C.
We use a toy example to better illustrate the idea of local models. As in Figure 1, we simulate the heterogeneous population with 3 classes such as NC, MCI and AD and one covariate. The 3 ordinal classes are separated by 2 dashed lines. Within each class, the reponse seems to be roughly linear with respect to the covariate with small variations while there is a steeper change across neighboring classes. A global model will not be optimal for such a heterogeneous population. In particular, as is shown in the plot, we fit a global linear model for the data. This global model is not sufficient to capture the local variability in the population due to its heterogeneity. On the other hand, we can fit the data more efficiently with a local model. For the query point x0 marked by blue color in the plot, the red bell-shaped shading area symetrically around x0 represents the local Gaussian kernel weight function. The estimate utilizes only the data points covered by the kernel. The height of the kernel function represents the weight of the observations for calculation of . The red curve is the corresponding response function estimated from the local Gaussian smoothing method. As we can see from Figure 1, the local method indeed captures the local variability and better recover the heterogeneity in the population.
Fig. 1.
A toy example to illustrate heterogeneity and local models.
For a given query point , we denote wi(xi, x0) to be the weight given by the training sample i and use the notation wi in this section for simplicity. Then local linear coefficients associated with xi are estimated from solving the following penalized weighted least square problem:
| (1) |
where ∥ · ∥1 denotes the L1-penalty, as in the Lasso [24], denotes the L2-penalty, as in the ridge regression [25], λ is a tuning parameter, and α is the parameter that balances between the L1-penalty and L2-penalty. The linear combination of the L1- and L2-penalties forms the Elastic Net penalty [26]. The weighted penalized framework we proposed can be implemented in the R programming language under the R package “glmnet”. Note that in our tuning procedure, we determine the λ candidate set based on x0. Given x0, we compute the largest candidate λmax that vanishes the corresponding estimated , based on Section 2.5 in [27]. Our λ candidate set for x0 is chosen using the same strategy with [27], by selecting a minimum value λmin = 0.001λmax and constructing a sequence of 100 values of λ decreasing from λmax to λmin on the log scale. We choose α = 0,0.5 or 1 in the simulation study and real data applications and the choice depends on problem. We tune the parameter λ by cross-validation. With the estimated local linear coefficients, the response of the query point x0 is given by
| (2) |
which is the estimated intercept term.
Our key contribution of this paper is the construction of the local weights for every training sample given any query point. We next describe the construction of the weight function using ordinal logistic regression in Section II-B. Besides the weights defined by the continuous class progression, our weight function can also be flexibly enhanced by random forests depending on the model performance during cross-validation, which will be described in Section II-C.
B. Progression Scores for Local Weights Using Ordinal Logistic Regression
In an ordinal heterogeneous population, the responses tend to have clustering effects among different groups. Hence, it can be helpful to utilize the information from the class labels. Instead of discretizing the population into different nonoverlapping classes, we model the change of the ordinal class label as a continuous progress. We define a progression score to quantify the degree to which the subject progresses on the class evolution spectrum. There are K − 1 latent thresholds on the spectrum being set as the ordinal class bounds. Then, based on the progression score, we develop a sample weight function so that not only the samples from the same class but also the samples from different but close classes will be utilized in the local fitting.
Let Ci = 1, · · · , K denote the class label random variable from the K ordered classes and ci the realization of this random variable. Consider the ordinal logistic regression model [28]. The cumulative probability of Ci is modeled as the logistic function,
| (3) |
where j = 1, · · · , K − 1, and i = 1, · · · , n. Here , are vectors of parameters and ϕ is defined as the logistic function ϕ(t) = 1/(1+exp(−t)). In addition, θ is constrained to be non-decreasing (−∞ = θ0 < θ1 ≤ θ2 ≤ · · · ≤ θK−1 < θK = +∞) to characterize the ordinal structure of the K classes.
The overall likelihood function based on the ordinal logistic model can be expressed as
As in the local weighted least squares, we apply shrinkage to tackle the high dimensional problem. The parameters θ and η can be estimated by minimizing the penalized negative log-likelihood, defined as
| (4) |
Here we impose an L2-penalty on η due to its simplicity and its effectiveness on dealing with multicollinearity in the heterogeneous dataset. We use γ as the tuning parameter. The optimization problem can be solved by gradient methods [29]. Detail calculation can be found in Section S.I in the supplementary material.
From the ordinal logistic regression, we want to define a quantity to capture the continuous progression of ordinal classes. For example, in the ADNI studies, we want to characterize how the disease progresses from the very healthy brain in the NC group to the most severe case of AD. One natural idea is to utilize the estimated posterior probability of one class, but it can only interpret the closeness to this specific class. More specifically, if we let the probability of a subject being an AD quantify the disease progression, then a low probability will not give us information on whether this subject is closer to the state of NC or MCI. On the other hand, the affine function ηTx naturally quantifies the disease progression since there exists a latent vector , such that Ci = j if . The threshold vector determines the class assignments in the ordinal logistic model. However, the score ηTx provides more detailed information on disease severity of all subjects.
Motivated by the discussion of the disease progression, we define the progression score si for subject i to be the estimated affine function
| (5) |
If the query point and a training sample are in different classes, the distance between their progression scores can still be small, and hence the weight given from this training sample to the query point should be large. If the distance between the query point and a training sample is too large, then it would be reasonable to make the weight from this training sample small or even zero. In the literature, Gaussian kernel is a commonly used kernel when the dimension is relatively low. The kernel gets larger when the Euclidean distance between two points gets smaller, indicating that more information should be drawn from each other during the local fitting process. This motivates us to build a truncated Gaussian kernel. For a query point x0 and training sample xi, we define
| (6) |
where and are the estimated progression scores for the training sample i and query point x0 respectively. Here is the indicator function that only allows for those observations whose progression scores’ gaps from the query’s point are less than D to contribute the weights, where D is the cutting off threshold parameter. The function is a univariate Gaussian kernel with the bandwidth parameter . As we can see in Figure 1, the red bell-shaped is a truncated Gaussian kernel. Parameter determines the flatness or sharpeness of the kernel. Parameter D determines how far its truncated tail can reach from the center x0. In our framework, the choice of D is tuned together with λ, and is estimated from the Silverman’s Rule of Thumb [30]
where is the standard error taken over the set and n0,D is the number of samples in the set.
The weight function defined above gives a query-specific weight function for the local fitting. The cut off D gives a uniform cutting off threshold while is specifically computed for each query point x0. By using ws(·, ·), we can adaptively choose the local neighborhood for x0 depending on its location on the class progression spectrum. More weights are added to the sample points closer to the query point.
C. Weights Using Random Forests
The weight ws(·, ·) developed in Section II-B efficiently uses the ordinal label information. In this section, we introduce a sample weight trained from random forests. Depending on the cross-validation results, we adaptively absorb the random forests sample weights into our existing kernel.
Random forests enjoy several benefits such as its robustness to outliers and its good performance on large-scale datasets. [23] utilized the random forests [22] to train a local linear regression model for each query point, which has an effect of correcting local imbalances in the design. Motivated by this, we aim to exploit the advantage from random forests based on our current framework, which can be naturally done by absorbing the random forests weights into our current kernel. To make it more flexible, we provide two choices on our kernel depending on the cross-validation performance, which will be introduced in Section II-D.
Next we briefly describe the random forests framework in terms of local fitting. Given a random forest consisting of J trees, let ρ be the random parameter vector that determines the growth of a tree. Denote the tree built with ρ as T(ρ). For a given query point , let be the rectangle with respect to the terminal node of T(ρ) that contains x0. Denote n(xi, ρ) as the number of times (with replacement) for the training sample xi to be used, e.g., in-bag in the random forests terminology, while building the tree T(ρ). With the notation introduced, the prediction of the response from a random forest at query point can be written as
where
| (7) |
For a query point x0 and a training sample xi, we define the local weight absorbing the random forests weight as
| (8) |
Then we can conduct a cross-validation procedure to determine whether to use ws(·, ·) or w(·, ·). The details will be introduced in Section II-D.
D. Parameters Tuning and Weight Selection
In our experiment, we use M-fold cross-validation to tune the parameters. We also use cross-validation to determine whether to use ws(·, ·) and w(·, ·), depending on the performance.
It is worth noting that in our model, there are three parameters to tune: γ in the ordinal logistic regression model, D as the thresholding parameter, and λ in the penalized local linear models. Theoretically, the three parameters can be tuned together using one cross-validation procedure to achieve a global optimum. Tuning three parameters together is practically difficult and computationally expensive, hence we decide to tune γ and D, λ separately by two cross-validation procedures in two separate training processes. Since the ordinal logistic regression model (4) and the local linear model (1) are trained separately, γ, D, and λ can be tuned separately as well. Denote the sizes of candidate sets for γ, D and λ as nγ, nD and nλ, respectively. Tuning these three parameters together will computationally cost O(MnγnDnλ). If tuned seperately, the total computational cost will be proportional to O(Mnγ) + O(MnDnλ).
Let n(−m) denote the number of all samples excluding the mth segment (also referred to as the mth segment of training samples) and n(m) denote the number of samples in the mth segment (also referred to as the mth validation samples). Denote the data in the mth segment as , and the data excluding the mth segment as .
Let be the parameters estimated from the mth training samples and tuning parameter γ in the penalized ordinal logistic model. Then the estimated progression score vector for the mth validation set is given by . We select the optimal tuning parameter to maximize the Pearson’s correlation coefficient between the predicted progression scores and the true response, since we assume that the progression score is correlated to the responses. Specifically, we select γ to maximize CV (γ) as follows
| (9) |
After determining the optimal , we can get the estimated progression score . Given , let denote the response trained from fitting the training samples in (1) with the threshold parameter D and tuning parameter λ, using sample weights given by (6). Let denote the response estimated with the same parameters D and λ and with sample weights enhanced by random forests given by (8). Define the following two cross-validation estimation errors with respect to the two weight functions as
| (10) |
Let and denote the sets of parameters that minimize CV1(·, ·) and CV2(·, ·) respectively. Then we determine the weight function by choosing the one that minimizes . More specificallly, if , then we select (6) as our weight function. Otherwise, if , then we select (8) as our weight function.
We summarize the algorithm of the procedure of our framework in Section S.II the supplementary material.
III. Simulation Study
We conduct numerical studies using simulated examples. The methods that we compare include the Lasso regression, ridge regression, elastic net regression with α = 0.5 and random forests (RF). All our simulations in this section and real data applications in Section IV are implemented under R programming language. We utilize the R package “glmnet” to implement the baseline methods Lasso, ridge and elastic net and “randomForest” to implement random forest algorithm. Five-fold cross validation is utilized for parameter tuning for our framework and Lasso, ridge and elestic net. For the choice of parameters in random forests, we fix the number of trees to be 100 and let the trees grow to the maximum possible depth subject to the minimum size of terminal nodes 5.
To simulate the data, we use a simulation setting similar to the mixture models in [9]. Here we generate the known groups by ordinal logistic regression and define the smoothness structure by the affine function in the ordinal logistic regression framework. One characteristic of heterogeneity is that the set of important features might differentiate across different groups. To capture that, we consider the following setting with 3 ordinal classes:
| (11) |
where , j = 1,2,3, are independent and identically distributed (i.i.d.) multivariate normal with mean and covariance matrix Σj. We fix n = 150 and vary the choices of Σj. The predictors are the group j specific important features. In particular, are also generated from i.i.d. multivariate normal with mean 0 and covariance Σc. Since the distribution is the same for all groups, the features in xic are important for all 3 groups. Finally, we generate from i.i.d. multivariate normal with mean 0 and covariance Σ0, which represents the unimportant features that have zero coefficients β0 = 0. In (11), si is the affine function that defines the progression score for the sample i in the ordinal logistic setting. Given si, βi1, βi2, βi3, βc are model coefficients that capture the group differences.
To determine the class label, we use the ordinal logistic regression model in Section II-B and let θ1 = −4 and θ2 = 4. We define the linear predictor θj − ηTxi in (3) to be
| (12) |
where for j = 1, 2, 3 and and to represent the coefficients for the covariates that are unrelated to the classification. The latter equality in (12) defines the true progression score . Then the class label ci for the sample i is determined by the largest posterior probability
| (13) |
Now we introduce how the coefficients are defined. Define to be 1 if ci = 1 and 0 otherwise; define to be 1 if ci = 2 and 0 otherwise; define to be 1 if ci = 3 and 0 otherwise. Here corresponds to the group specific important features. Let the coefficients corresponding to the common important features be 1 if ci = 1, 1.5 if ci = 2, and 2 if ci = 3.
Example 3.1. for j = 0, · · ·, 3.
Example 3.2. with , for j = 0, · · ·, 3.
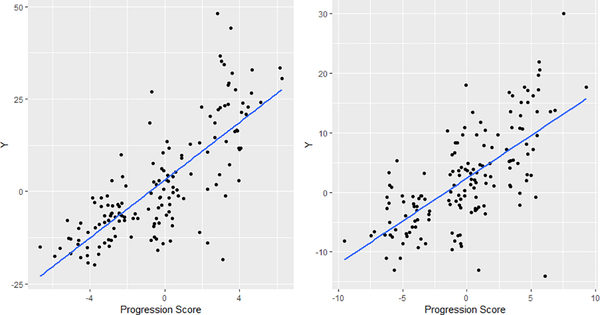
In our simulated examples, we fix the parameters p1 = p2 = p3 = 10 and pc = 20. The parameter p0 takes values 50,100 or 200 to control the sparsity in both examples. We have generated the plots for the simulated heterogeneous response in Figure 2. In Figure 3, we plot the estimated progression score as a function of clinical score for both simulation settings. There exists a strong correlation between the two scores, which further validates the usefulness of the progression scores in our framework. The simulated results are summarized in Tables I and III for the case p0 = 50, 200. Results for p0 = 100 is given in the supplementary material in Tables SI and SIV. The results show that our LWPR methods outperform other methods. Among different penalties for LWPR, the ridge penalty appears to achieve the best performance. As its dimension increases, the estimation error gets larger as well. Note that our LWPR methods achieve better performance than the corresponding linear regression methods with the same penalties. This implies that the local weights defined in our framework work well. Another interesting fact to note here is that, even though random forests generally perform the worst in these examples, our LWPR method still achieve the best performance, indicating that our cross-validation procedure indeed works well to adaptively determine the inclusion or exclusion of the sample weights from random forests.
Fig. 2.
The distributions of simulated responses in Example 3.1 (top) and Example 3.2 (bottom) with p0 =200.
Fig. 3.
Plots of simulated response against estimated progression score in Example 3.1 (left) and Example 3.2 (right) with p0 =50.
TABLE I.
Simulation results from Example 3.1.
| p0 | Methods | MAE | CC |
|---|---|---|---|
| RF | 7.339 (0.073) | 0.269 (0.012) | |
| Ridge | 6.334 (0.082) | 0.617 (0.008) | |
| Elastic Net | 6.399 (0.092) | 0.545 (0.014) | |
| p0 = 50 | Lasso | 6.426 (0.093) | 0.531 (0.015) |
| LWPR+Ridge | 5.162 (0.051) | 0.698 (0.008) | |
| LWPR+EN | 5.602 (0.055) | 0.651 (0.007) | |
| LWPR+Lasso | 5.676 (0.057) | 0.644 (0.008) | |
| RF | 7.598 (0.068) | 0.180 (0.012) | |
| Ridge | 7.570 (0.071) | 0.419 (0.010) | |
| Elastic Net | 7.338 (0.081) | 0.354 (0.018) | |
| p0 = 200 | Lasso | 7.376 (0.077) | 0.357 (0.015) |
| LWPR+Ridge | 6.715 (0.079) | 0.465 (0.011) | |
| LWPR+EN | 6.975 (0.086) | 0.421 (0.013) | |
| LWPR+Lasso | 7.018 (0.086) | 0.413 (0.013) | |
“MAE” stands for the mean absolute error and “CC” stands for the correlation coefficient. RF: random forests. The values in the parentheses are standard errors.
TABLE III.
Simulation results from Example 3.2.
| p0 | Method | MAE | CC |
|---|---|---|---|
| RF | 11.301 (0.112) | 0.480 (0.009) | |
| Ridge | 8.858 (0.104) | 0.756 (0.006) | |
| Elastic Net | 9.051 (0.111) | 0.713 (0.009) | |
| p0 = 50 | Lasso | 9.133 (0.117) | 0.702 (0.009 |
| LWPR+Ridge | 6.508 (0.098) | 0.832 (0.006) | |
| LWPR+EN | 7.538 (0.104) | 0.769 (0.008) | |
| LWPR+Lasso | 7.859 (0.105) | 0.751 (0.009) | |
| RF | 11.653 (0.114) | 0.422 (0.010) | |
| Ridge | 11.016 (0.128) | 0.677 (0.007) | |
| Elastic Net | 9.605 (0.126) | 0.677 (0.008) | |
| p0 = 200 | Lasso | 9.673 (0.126) | 0.663 (0.009) |
| LWPR+Ridge | 8.359 (0.108) | 0.722 (0.008) | |
| LWPR+EN | 8.777 (0.097) | 0.689 (0.008) | |
| LWPR+Lasso | 9.012 (0.116) | 0.672 (0.009) | |
“MAE” stands for the mean absolute error and “CC” stands for the correlation coefficient. RF: random forests. The values in the parentheses are standard errors.
We underline the performance measures from the methods that achieve the best performance among the baseline methods and make bold the performance measures from the methods that perform the best among our LWPR methods. To test the superiority of our method over other methods, we conduct one-sided two-sample t-tests to check if the performance measures given by our method are statistically significantly better than others. All tests on the underlined values and the corresponding bold values give p-values smaller than the magnitude of 10−3, indicating a statistically significant improvement of our method over the baseline methods.
Misdiagnosis can be an important issue in practice. Under this setting, subjects can be assigned with incorrect labels. We conduct modified simulations on Examples 3.1 and 3.2 to test our model robustness. Keeping all the parameters and simulation schemes (11) and (12) to be the same, we randomly select 10% and 20% simulated samples and assign them with the wrong labels. If the original label of a selected sample is 1 or 3, we relabel this sample with 2. If the original label of a selected sample is 2, we randomly relabel this sample with 1 or 3 with equal probabilities. Table II, IV and Table SII, SIII, SVI, SV in the supplementary material summarize the simulation results with misdiagnosis probability 10% and 20% respectively. Comparing with the performances given by the baseline method in Tables I and III, our methods are still better despite incorrect labels. The differences with the ones given the true labels are not significant compared with improvement over the baseline methods.
TABLE II.
Simulation results from Example 3.1 with misdiagnosis probability 10%.
| p0 | Method | MAE | CC |
|---|---|---|---|
| LWPR+Ridge | 5.627 (0.068) | 0.634 (0.010) | |
| p0 = 50 | LWPR+EN | 6.058 (0.076) | 0.579 (0.010) |
| LWPR+Lasso | 6.130 (0.086) | 0.567 (0.011) | |
| LWPR+Ridge | 6.766 (0.081) | 0.443 (0.011) | |
| p0 = 200 | LWPR+EN | 7.081 (0.098) | 0.396 (0.014) |
| LWPR+Lasso | 7.062 (0.096) | 0.393 (0.014) | |
“MAE” stands for the mean absolute error and “CC” stands for the correlation coefficient.
TABLE IV.
Simulation results from Example 3.2 with misdiagnosis probability 10%.
| p0 | Method | MAE | CC |
|---|---|---|---|
| LWPR+Ridge | 7.011 (0.084) | 0.812 (0.007) | |
| p0 = 50 | LWPR+EN | 8.094 (0.095) | 0.744 (0.008) |
| LWPR+Lasso | 8.247 (0.096) | 0.731 (0.009) | |
| LWPR+Ridge | 8.637 (0.105) | 0.701 (0.008) | |
| p0 = 200 | LWPR+EN | 9.156 (0.125) | 0.659 (0.011) |
| LWPR+Lasso | 9.203 (0.128) | 0.653 (0.012) | |
“MAE” stands for the mean absolute error and “CC” stands for the correlation coefficient. The values in the parentheses are standard errors.
IV. Applications on ADNI Clinical Score Prediction
We apply our method to the ADNI data (data aquired from http://adni.loni.usc.edu/). All the subjects are from ADNI 1 phase of study. We are interested in predicting the longitudinal ADAS-Cog scores at 0 month, 12 and 24 months, from two brain image modalities, MRI and PET, together with the class labels (NC, MCI and AD), all of which were acquired at the baseline. This is not an easy task, as most existing literatures use additional inputs such as clinical scores at the previous time points to achieve this goal [6]. MRI images were acquired from structural magnetic resonance imaging scans and PET images were acquired from fluorodeoxyglucose positron emission tomography scans. The images for both modalities were preprocessed. For MRI, the preprocessing steps include anterior commissure (AC) posterior commissure (PC) correction, intensity inhomogeneity correction, skull stripping, cerebellum removal based on registration with atlas, spatial segmentation and registration. After registration, we obtain the subject-labeled image based on the Jacob template with 93 manually labeled regions of interest (ROIs). For each of the 93 ROIs in the labeled MRI, we compute the volume of gray matter as a feature. For each PET image, we first align the PET image to its respective MRI using affine registration. Then, we obtain the skull-stripping image using the corresponding brain mask of MRI and compute the average standardized uptake value ratio (SUVR) of every ROI in the PET image as a feature. For each subject, we finally obtain 93 MRI features and 93 PET features.
Table SVII in the supplementary material summarizes the complete subject demography and the clinical score statistics. There were 803 subjects tested on their ADAS-cog scores at the baseline. In addition, 90 and 176 subjects missed the follow-up visits at 12 months and 24 months respectively, which are not included in our analysis at those time points. The baseline PET images were not acquired for all 803 subjects. For simplicity, we impute the missing values in the PET features with the group medians. Imputation can be superior to case deletion, because it utilizes all the observed data [31]. Despite its simplicity, median imputation can distort the distribution of the missing variables, leading to underestimates of the standard deviation and bias on the mean. We have maximized the variation in the imputed data by computing the group medians on the missing variables. Moreover, the localized framework and the penalty imposed on the coefficients in (1) can compensate for the imputation effects by giving weights to different samples.
To take into consideration of the dependence of the 186 features, we construct the pairwise interaction terms in our analysis [32], which is often utilized in the categorical data analysis [33]. In other words, we include the following constructed features into our model (1):
There are in total as many as 17205 interaction terms, and 17391 features including the “original” 186 features. To reduce the dimensionality, we utilize the technique of distance correlation for screening of noise variables [34], [35]. Distance correlation is a measure to quantify the linear and nonlinear dependence between two paired random vectors. We select the top 200 features that share the largest distance correlations with the responses to be included in the model. The names of the ROIs that have been selected 50 times are given in the supplementary material. Table SVIII in the supplementary material summarizes the percentages of the selected features as interaction features vs original features. Over half of the 200 selected features are interactions, which justifies the inclusion of interaction features for prediction. Out of the selected interaction features, the percentages of MRI-only, PET-only, and MRI-PET interaction features are summarized in Table SIX. As shown in the tables, interestingly, the MRI-PET interactions are the most common ones being selected among all interactions. This indicates the strong association between the two modalities.
We plot our estimated progression scores against the three ordinal classes (NC, MCI, AD) and ADAS-cog scores in Figure 4. The overall progression scores tend to increase from the class NC to the class AD. There are overlaps on the estimated progression scores across the neighboring classes. This further validates our motivation to locally predict the query point’s clinical score by including points both from the same and neighboring classes. In addition, we have also plotted the scatterplot between the predicted progression scores against the clinical scores, and such a plot shows a strong positive correlation between the two.
Fig. 4.
Plots of estimated progression scores vs class labels (left) and progression scores vs clinical scores (right) at 0 month.
We randomly partition 75% of the dataset into the training dataset and the rest into the testing dataset. We train our model on the training dataset and test the performance on the testing dataset. The performance measures we use here are mean absolute error (MAE) and Pearson’s correlation coefficient (CC). The procedure is repeated 50 times and we take the means of the performance measures. The standard errors are also provided, which are calculated by dividing the standard deviation of the performance measures by square root of number of replications (50 in our case).
Table V summarizes the performances of different methods. At each time point, our method always achieves the best performance in terms of mean absolute errors and correlations, shown in bold values. We conduct one-sided two-sample t-tests to statistically demonstrate the performance improvement of our method. At each time point, we test the null hypothesis that the measures from our method (bold values) are smaller (for MAE) / larger (for CC) than the measures from the method that achieves the best performance among baseline methods (underlined values). The p-values for the tests are summarized in Table SX in the supplementary material. We use Bonferroni correction to control the family-wise error rate for multiple testing. For an overall significance level of 0.05, our p-values are compared to the adjusted criteria 0.017(0.05/3). Both of the adjusted tests on MAE and CC are rejected.
TABLE V.
Comparison of the prediction performance on the ADNI dataset.
| Month | Method | MAE | CC |
|---|---|---|---|
| RF | 3.635 (0.029) | 0.660 (0.005) | |
| Ridge | 3.751 (0.028) | 0.622 (0.010) | |
| EN | 3.647 (0.026) | 0.672 (0.005) | |
| 0 | Lasso | 3.652 (0.026) | 0.671 (0.004) |
| LWPR+Ridge | 3.528 (0.024) | 0.698 (0.004) | |
| LWPR+EN | 3.527 (0.024) | 0.700 (0.004) | |
| LWPR+Lasso | 3.528 (0.024) | 0.700 (0.004) | |
| RF | 4.455 (0.045) | 0.701 (0.005) | |
| Ridge | 4.632 (0.049) | 0.657 (0.009) | |
| EN | 4.420 (0.046) | 0.697 (0.006) | |
| 12 | Lasso | 4.420 (0.046) | 0.698 (0.006) |
| LWPR+Ridge | 4.280 (0.040) | 0.730 (0.005) | |
| LWPR+EN | 4.275 (0.040) | 0.732 (0.005) | |
| LWPR+Lasso | 4.274 (0.039) | 0.733 (0.005) | |
| RF | 5.367 (0.058) | 0.705 (0.006) | |
| Ridge | 5.508 (0.074) | 0.688 (0.010) | |
| EN | 5.464 (0.071) | 0.690 (0.008) | |
| 24 | Lasso | 5.480 (0.051) | 0.688 (0.008) |
| LWPR+Ridge | 5.161 (0.0.053) | 0.735 (0.007) | |
| LWPR+EN | 5.133 (0.052) | 0.741 (0.005) | |
| LWPR+Lasso | 5.140 (0.052) | 0.740 (0.006) | |
“MAE” stands for the mean absolute error and “CC” stands for the correlation coefficient. The values in the parentheses are standard errors.
In real applications, it is of great interest to accurately predict clinical scores among NC and MCI patients for early detection of MCI patients, since diagnosis on the AD patients is a relatively easy task for a neurologist. We have retrained our model on the NC/MCI subjects and Table VI summarizes the performance of our proposed method on the NC/MCI subjects. By comparing the predictive MAEs and the standard deviations among MCI subjects, our method achieves some improvement. With more precise predicted clinical scores, our proposed method can be more useful for the prodromal purpose.
TABLE VI.
Predictive MAE on the NC/MCI subjects on the ADNI dataset.
| Month | Method | MAE |
|---|---|---|
| LWPR+Ridge | 3.032 (0.024) | |
| 0 | LWPR+EN | 3.041 (0.023) |
| LWPR+Lasso | 3.038 (0.023) | |
| LWPR+Ridge | 3.619 (0.037) | |
| 12 | LWPR+EN | 3.609 (0.036) |
| LWPR+Lasso | 3.600 (0.036) | |
| LWPR+Ridge | 4.121 (0.053) | |
| 24 | LWPR+EN | 4.120 (0.054) |
| LWPR+Lasso | 4.123 (0.053) | |
The values in the parentheses are standard errors.
Our method has an unique advantage in the sense that it can detect the most discriminative brain regions for each individual subject because it is inherently a local method. When we use a Lasso penalty, the most discrimative ROIs will be selected as features with nonzero coefficients. To summarize the result, we group the testing samples into 5 subgroups according to the magnitudes of their progression scores. We selected the 20th, 40th, 60th and 80th percentiles as the grouping thresholds. In more details, sample i is grouped into subgroup 1 if the estimated progression score ; subgroup 2 if ; subgroup 3 if ; subgroup 4 if ; subgroup 5 if . Table VII summarizes the average number of NC, MCI and AD subjects in the 5 groups out of 50 experiments. Table VII summarizes the distribution of the class labels across subgroups 1–5 in the revised manuscript. There is a clear shift from NC to AD among these five subgroups with highest percentage of NC in subgroup 1 and highest percentage of AD in subgroup 5. Within each subgroup, in each iteration, we count the number of times for each ROI that has been estimated with nonzero coefficients. After 50 iterations, we sum up the total number of the count for each ROI, and select the 10 mostly chosen ROIs within each subgroup. Figure 5 shows the top 10 most selected regions by LWPR with the Lasso penalty and MRI as the modality input at the baseline. The brighter the color, the more frequent the corresponding ROI is chosen. The names of the 10 mostly selected regions among the 5 groups are summarized in Table SXI in the supplementary material.
TABLE VII.
Average numbers of NC, MCI and AD subjects in the 5 different groups determined by progression score
| Index | NC | MCI | AD |
|---|---|---|---|
| 1 | 32.26 | 7.74 | 0.00 |
| 2 | 19.04 | 20.22 | 0.74 |
| 3 | 2.90 | 35.50 | 1.60 |
| 4 | 1.66 | 27.56 | 10.78 |
| 5 | 0.14 | 6.98 | 32.88 |
Fig. 5.
Ten most discriminative regions detected by LWPR.
Interestingly, in Figure 5, as the disease gets more severe (going in direction of group 1 to group 5), some regions are detected to be brighter, meaning that the role played by them are getting more significant as AD develops. For instance, thalamus left in Figure 5 is marked brighter and brighter over the first three subgroups, corresponding to the early stage of AD development. [36] studied the thalamic pathology along with the early development of AD, in which they reported that thalamic dysfunctions may contribute or even be responsible for some of the earliest cognitive symptoms of MCI and AD. In Figure 5, the role played by thalamus detected by LWPR is more and more significant over the first three subgroups, which coincides with the finding in the previous study. As the disease progresses, more regions in the medial temporal lobe appears to be detected at the later stage of AD, such as hippocampal formation left and fornix right. Moreover, we note that the patterns of the marked regions seem to be generally consistent within the first three subgroups, and they become more diversed in the fourth and fifth subgroups where the subjects’ disease become more severe. This further validates our assumption on the heterogeneity of the population, especially when AD progresses into a more serious stage. Table SXI reveals asymmetry in the ROIs selected by LWPR, which is a common phenomenon of human brain with neurodegeneration. For example, asymmetry on the hippocampal volume has been investigated in [37] and a consistent left-less-than-right asymmetry pattern is found. One possible reason for the asymmetry on the brain structure deterioration related to AD is that most language- and motor-dominant regions are on the left hemisphere, hence it is believed that the left side of the brain suffers more from the gray matter loss in AD. In [38] it is reported that rightward-biased asymmetries appear in a cluster comprising the middle and superior temporal gyri, and leftward-biased asymmetries are found in hippocampal GM. Our result agrees with the latter by giving similar asymmetry pattern in the 5th subgroup. According to [39], AD pathology tends to affect brain lobes to different extents in an asymmetric manner, where asymmetry can be derived from temporal, parietal, and occipital lobe. This is also consistent with our findings on the five subgroups.
V. Conclusion
In this paper we propose a flexible local framework to predict clinical scores in the ADNI study based on subjects’ brain image features. Our method is superior in that it can deal with subjects’ heterogeneity by modeling their disease progression into a progression score and utilizing the defined score in a truncated Gaussian kernel. We also adaptively include random forests sample weights into the kernel function to improve performance. We apply the elastic penalty in the local fitting step to handle relatively high dimensionality. Numerical studies show that our method can achieve better performance than random forests, and Elastic Net type penalized regression. Results of applications on ADNI real data also agree with several previous scientific findings.
Supplementary Material
Acknowledgments
This work was supported in part by NIH grants (EB008374, AG041721, AG049371, AG042599, AG053867, EB022880, R01GM126550) and NSF grants (IIS1632951, DMS-1821231).
Contributor Information
Peiyao Wang, Department of Statistics and Operations Research, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA.
Yufeng Liu, Department of Statistics and Operations Research, Department of Genetics, Department of Biostatistics, Carolina Center for Genome Sciences, Lineberger Comprehensive Cancer Center, University of North Carolina at Chapel Hill, Chapel Hill, NC, USA.
Dinggang Shen, Department of Radiology and Biomedical Research Imaging Center, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599 USA, and is also with Department of Brain and Cognitive Engineering, Korea University, Seoul 02841, South Korea.
References
- [1].Vos T, Allen C, Arora M, Barber RM, Bhutta ZA, Brown A, Carter A, Casey DC, Charlson FJ, Chen AZ et al. , “Global, regional, and national incidence, prevalence, and years lived with disability for 310 diseases and injuries, 1990–2015: a systematic analysis for the global burden of disease study 2015,” The Lancet, vol. 388, no. 10053, pp. 1545–1602, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Tombaugh TN and McIntyre NJ, “The mini-mental state examination: a comprehensive review,” Journal of the American Geriatrics Society, vol. 40, no. 9, pp. 922–935, 1992. [DOI] [PubMed] [Google Scholar]
- [3].Graham DP, Cully JA, Snow AL, Massman P, and Doody R, “The alzheimer’s disease assessment scale-cognitive subscale: normative data for older adult controls,” Alzheimer Disease & Associated Disorders, vol. 18, no. 4, pp. 236–240, 2004. [PubMed] [Google Scholar]
- [4].Fan Y, Gur RE, Gur RC, Wu X, Shen D, Calkins ME, and Davatzikos C, “Unaffected family members and schizophrenia patients share brain structure patterns: a high-dimensional pattern classification study,” Biological psychiatry, vol. 63, no. 1, pp. 118–124, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Stonnington CM, Chu C, Klöppel S, Jack CR Jr, Ashburner J, Frackowiak RS, Initiative ADN et al. , “Predicting clinical scores from magnetic resonance scans in alzheimer’s disease,” Neuroimage, vol. 51, no. 4, pp. 1405–1413, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Huang L, Jin Y, Gao Y, Thung K-H, Shen D, Initiative ADN et al. , “Longitudinal clinical score prediction in alzheimer’s disease with soft-split sparse regression based random forest,” Neurobiology of aging, vol. 46, pp. 180–191, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Cheng B, Zhang D, Chen S, and Shen D, “Predicting clinical scores using semi-supervised multimodal relevance vector regression,” in International Workshop on Machine Learning in Medical Imaging Springer, 2011, pp. 241–248. [Google Scholar]
- [8].Ye J, Chen K, Wu T, Li J, Zhao Z, Patel R, Bae M, Janardan R, Liu H, Alexander G et al. , “Heterogeneous data fusion for alzheimer’s disease study,” in Proceedings of the 14th ACM SIGKDD international conference on Knowledge discovery and data mining ACM, 2008, pp. 1025–1033. [Google Scholar]
- [9].Bühlmann P and Meinshausen N, “Magging: maximin aggregation for inhomogeneous large-scale data,” arXiv preprint arXiv:1409.2638, 2014. [Google Scholar]
- [10].Yu G, Liu Y, and Shen D, “Graph-guided joint prediction of class label and clinical scores for the alzheimer?s disease,” Brain Structure and Function, vol. 221, no. 7, pp. 3787–3801, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Zhu X, Suk H-I, Wang L, Lee S-W, Shen D, Initiative ADN et al. , “A novel relational regularization feature selection method for joint regression and classification in ad diagnosis,” Medical image analysis, vol. 38, pp. 205–214, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].DeSarbo WS and Cron WL, “A maximum likelihood methodology for clusterwise linear regression,” Journal of classification, vol. 5, no. 2, pp. 249–282, 1988. [Google Scholar]
- [13].Donohue MC, Sperling RA, Salmon DP, Rentz DM, Raman R, Thomas RG, Weiner M, and Aisen PS, “The preclinical alzheimer cognitive composite: measuring amyloid-related decline,” JAMA neurology, vol. 71, no. 8, pp. 961–970, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Jedynak BM, Lang A, Liu B, Katz E, Zhang Y, Wyman BT, Raunig D, Jedynak CP, Caffo B, Prince JL et al. , “A computational neurodegenerative disease progression score: method and results with the alzheimer’s disease neuroimaging initiative cohort,” Neuroimage, vol. 63, no. 3, pp. 1478–1486, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Li D, Iddi S, Thompson WK, Donohue MC, and Initiative ADN, “Bayesian latent time joint mixed effect models for multicohort longitudinal data,” Statistical methods in medical research, p. 0962280217737566, 2017. [DOI] [PubMed] [Google Scholar]
- [16].Bilgel M, Prince JL, Wong DF, Resnick SM, and Jedynak BM, “A multivariate nonlinear mixed effects model for longitudinal image analysis: Application to amyloid imaging,” Neuroimage, vol. 134, pp. 658–670, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Marinescu RV, Eshaghi A, Lorenzi M, Young AL, Oxtoby NP, Garbarino S, Shakespeare TJ, Crutch SJ, Alexander DC, Initiative ADN et al. , “A vertex clustering model for disease progression: application to cortical thickness images,” in International Conference on Information Processing in Medical Imaging Springer, 2017, pp. 134–145. [Google Scholar]
- [18].Koval I, Schiratti J-B, Routier A, Bacci M, Colliot O, Allassonniere S, and Durrleman S, “Spatiotemporal propagation of the cortical atrophy: Population and individual patterns,” Frontiers in Neurology, vol. 9, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Cleveland WS, Devlin SJ, and Grosse E, “Regression by local fitting: methods, properties, and computational algorithms,” Journal of econometrics, vol. 37, no. 1, pp. 87–114, 1988. [Google Scholar]
- [20].XiaofengvZhu H-I, Lee S-W, and Shen D, “Subspace regularized sparse multi-task learning for multi-class neurodegenerative disease identification,” 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Altman NS, “An introduction to kernel and nearest-neighbor nonparametric regression,” The American Statistician, vol. 46, no. 3, pp. 175–185, 1992. [Google Scholar]
- [22].Breiman L, “Random forests,” Machine learning, vol. 45, no. 1, pp. 5–32, 2001. [Google Scholar]
- [23].Bloniarz A, Talwalkar A, Yu B, and Wu C, “Supervised neighborhoods for distributed nonparametric regression,” in Artificial Intelligence and Statistics, 2016, pp. 1450–1459. [Google Scholar]
- [24].Tibshirani R, “Regression shrinkage and selection via the lasso,” Journal of the Royal Statistical Society. Series B (Methodological), pp. 267–288, 1996. [Google Scholar]
- [25].Hoerl AE and Kennard RW, “Ridge regression: Biased estimation for nonorthogonal problems,” Technometrics, vol. 12, no. 1, pp. 55–67, 1970. [Google Scholar]
- [26].Zou H and Hastie T, “Regularization and variable selection via the elastic net,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), vol. 67, no. 2, pp. 301–320, 2005. [Google Scholar]
- [27].Friedman J, Hastie T, and Tibshirani R, “Regularization paths for generalized linear models via coordinate descent,” Journal of statistical software, vol. 33, no. 1, p. 1, 2010. [PMC free article] [PubMed] [Google Scholar]
- [28].Bender R and Grouven U, “Ordinal logistic regression in medical research,” Journal of the Royal College of physicians of London, vol. 31, no. 5, pp. 546–551, 1997. [PMC free article] [PubMed] [Google Scholar]
- [29].Bertsekas DP, Nonlinear programming. Athena scientific Belmont, 1999. [Google Scholar]
- [30].Sheather SJ et al. , “Density estimation,” Statistical Science, vol. 19, no. 4, pp. 588–597, 2004. [Google Scholar]
- [31].Acuna E and Rodriguez C, “The treatment of missing values and its effect on classifier accuracy,” in Classification, clustering, and data mining applications. Springer, 2004, pp. 639–647. [Google Scholar]
- [32].Ai C and Norton EC, “Interaction terms in logit and probit models,” Economics letters, vol. 80, no. 1, pp. 123–129, 2003. [Google Scholar]
- [33].Agresti A and Kateri M, “Categorical data analysis,” in International encyclopedia of statistical science. Springer, 2011, pp. 206–208. [Google Scholar]
- [34].Székely GJ, Rizzo ML, and Bakirov NK, “Measuring and testing dependence by correlation of distances,” The annals of statistics, pp. 2769–2794, 2007. [Google Scholar]
- [35].Li R, Zhong W, and Zhu L, “Feature screening via distance correlation learning,” Journal of the American Statistical Association, vol. 107, no. 499, pp. 1129–1139, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Aggleton JP, Pralus A, Nelson AJ, and Hornberger M, “Thalamic pathology and memory loss in early alzheimers disease: moving the focus from the medial temporal lobe to papez circuit,” Brain, vol. 139, no. 7, pp. 1877–1890, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Shi F, Liu B, Zhou Y, Yu C, and Jiang T, “Hippocampal volume and asymmetry in mild cognitive impairment and alzheimer’s disease: Meta-analyses of mri studies,” Hippocampus, vol. 19, no. 11, pp. 1055–1064, 2009. [DOI] [PubMed] [Google Scholar]
- [38].Minkova L, Habich A, Peter J, Kaller CP, Eickhoff SB, and Klöppel S, “Gray matter asymmetries in aging and neurodegeneration: A review and meta-analysis,” Human brain mapping, vol. 38, no. 12, pp. 5890–5904, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Derflinger S, Sorg C, Gaser C, Myers N, Arsic M, Kurz A, Zimmer C, Wohlschläger A, and Mühlau M, “Grey-matter atrophy in alzheimer’s disease is asymmetric but not lateralized,” Journal of Alzheimer’s Disease, vol. 25, no. 2, pp. 347–357, 2011. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.