Highlights
-
•
From the pandemic scenario of COVID-19 disease cases in all over the world, the outbreak prediction becomes very complex for the emerging scientifically research.
-
•
Several epidemiological mathematical models of spread are increasing day by day to forecast correctly.
-
•
Here, the classical SIR modelling approach is carried out to study the different parameters of this model in case of India county.
-
•
This type of approach analyzed by considering different governmental lock down measures in India.
-
•
The outcome results showed the extreme interventions should be taken to tackle this type of pandemic situation in near future.
Keywords: COVID-19, India, Lockdown, Python, SIR Model
Abstract
Owing to the pandemic scenario of COVID-19 disease cases all over the world, the outbreak prediction has become extremely complex for the emerging scientific research. Several epidemiological mathematical models of spread are increasing daily to forecast the predictions appropriately. In this study, the classical susceptible-infected-recovered (SIR) modeling approach was employed to study the different parameters of this model for India. This approach was analyzed by considering different governmental lockdown measures in India. Some assumptions were considered to fit the model in the Python simulation for each lockdown scenario. The predicted parameters of the SIR model exhibited some improvement in each case of lockdown in India. In addition, the outcome results indicated that extreme interventions should be performed to tackle this type of pandemic situation in the near future.
Graphical abstract
1. Introduction
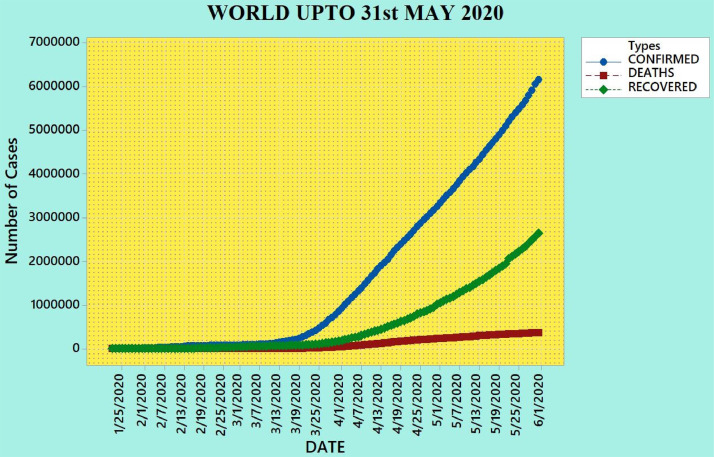
On December 3, 2019, a new virus emerged, affecting 41 patients with a mysterious pneumonia, in the large seafood market area of Wuhan, China [1]. Initially, this virus was called the SARS-CoV version 2; however, WHO named it COVID-19 and declared it as a global pandemic on March 11, 2020 [2]. COVID-19 is an infectious disease caused by the severe acute respiratory syndrome-novel coronavirus-2 (SARS-CoV-2) [3]. Currently, almost all parts of the world are exposed to this virus, and because the infectivity of this virus is high, an immense number of people have already become victims of it [4]. The SARS-CoV-2 infection represents one of the greatest challenges for humanity. India first reported a positive COVID-19 case, a student who returned from Wuhan, the capital of Hubei province, China, on January 30, 2020 [5]. Fig. 1 shows the COVID-19 scenario of the world until May 31, 2020 by considering confirmed, death, and recovered cases.
Fig. 1.
Scenario of the world until May 31, 2020.
Dhanwant and Ramanathan [6] employed a susceptible-infected-recovered (SIR) approach to forecast the outbreak of COVID-19 cases in India using the SciPy platform. Rodrigues et al. [7] proposed an epidemiological model by combining the SIR model with a genetic algorithm consisting of three types of networks. Elhia et al. [8] optimized the SIR epidemic model with time variation and controlled measures of H1N1 data in Morocco. They considered five parameters, namely recruitment rate of susceptible, effective contact rate, natural mortality rate, recovery rate, and disease-induced death rate, for modeling. Chaves et al. [9] determined the reproduction number (R0) and time-varying reproduction number (Rt) for Costa Rica, Panama, and Uruguay using the SIR model with three types of phases. Singh and Adhikari [10] studied the age-structured impact of India, China, and Italy using a hybrid SIR model. Das [11] predicted the COVID-19 disease progression in India and China using an SIR and statistical machine learning approach by considering the data obtained until April 6, 2020. Arif et al. [12] analyzed the COVID-19 data of Pakistan up to May 10, 2020 using an SIR model. Boudrioua and Boudrioua [13] predicted the daily cases of COVID-19 in Algeria using an SIR approach and the data obtained from February 25–April 24, 2020. Deo et al. [14] predicted the dynamics of COVID-19 epidemic data obtained from March 2–April 30, 2020 in India based on a time-series SIR model. Hazem et al. [15] analyzed the COVID-19 cases in the USA, Germany, UK, Italy, Spain, and Canada using a SIR approach from January 20–May 15, 2020 by considering lockdown measures. Jakhar et al. [16] predicted the COVID-19 epidemic cases in 24 different states of India using an SIR model by considering the data up to May 12, 2020. Mujallad and Khoj [17] forecasted COVID-19 cases in Makkah, Saudi Arabia by using an SIR model by considering the data obtained from March 16–May 9, 2020. de Oliveira et al. [18] forecasted the COVID-19 cases in Brazil by introducing a Bayesian methodology into the SIR model and using the data obtained from February 26–May 20, 2020. Postnikov [19] employed an SIR model with a Verhulst (logistic) equation to predict the COVID-19 outbreak in different countries using the Matlab software. Rojas-Gallardo et al. [20] analyzed the phylodynamic SIR trajectories of COVID-19 cases in Latin America using the data up to May 13, 2020 using two epidemiological surveillances.
Lopez and Rodo [21] predicted the outbreaks in Spain and Italy until March 31, 2020 using a SEIR (Susceptible-Exposed-Infectious-Removed) model by employing multiple scenarios. Yang et al. [22] employed a modified SEIR and artificial intelligence approach to predict the COVID-19 outbreaks under certain public interventions in China using the time-slice data. Engbert et al. [23] predicted the dynamics of COVID-19 cases in Germany using a stochastic SEIR model by employing different scenarios. Berger et al. [24] investigated the role of sample testing and case-dependent quarantine measures in the USA using an SEIR epidemic model. Hou et al. [25] employed a well-mixed approach of the SEIR model to predict the COVID-19 cases in Wuhan, China, with suggestions for interventions such as quarantine and isolation. Saito et al. [26] applied the SEIR model to cases of the H1N1 influenza pandemic in Japan and detected the immigration effect. Godio et al. [27] employed a generalized SEIR model for COVID-19 cases in Italy and compared the outcome results with those of Spain and South Korea using the Matlab software. Feng et al. [28] analyzed the COVID-19 outbreak using the SEIR model by considering strict social distancing initiatives to slow down the spread of disease. Gupta et al. [29] employed an SEIR and regression approach to predict the COVID-19 cases in India by training the data available up to March 30, 2020. Pandey et al. [30] predicted the COVID-19 cases in India using an SEIR and regression model by involving the data obtained from January 30–March 30, 2020 and determined the R0 value. Goswami et al. [31] highlighted the effective contact rate of COVID-19 cases in India using an SEIR model and compared the results with those of six other countries. Bonnasse-Gahot et al. [32] employed an SEIR model with an incubation compartment and emphasized the monitoring of bed availability during the pandemic in France. Dixit et al. [33] forecasted the COVID-19 cases up to May 25, 2020 in India using regression, exponential smoothing, and compartmental age structured SEIR modeling. Kohanovski et al. [34] fitted an SEIR model to COVID-19 cases using the data obtained from 12 countries along with extreme non-pharmaceutical interventions (NPIs). Teles [35] studied the SARS-COVID-2 epidemic outbreak cases in Portugal using a time-dependent SEIR model. Wagh et al. [36] studied the epidemic peak of COVID-19 cases in India until May 9, 2020 by using an auto-regressive integrated moving average model coupled with SEIR compartmental epidemiological model.
Ray et al. [37] studied the short- and long-term impacts of an initial 21-day lockdown on March 25, 2020 using an extended SIR model by considering the data obtained from March 1–April 7, 2020 and employing RShiny package. da Cruz and Cruz [38] analyzed the COVID-19 outbreak in the State of São Paulo, Brazil using a SEIR-A (Susceptible-Exposed-Infected-Recovered-Asymptomatic concentration) model. Kobayashi et al. [39] studied the intervention effect on COVID-19 cases in Japan by considering the data up to May 18, 2020 using a SS-SIR (State-Spate-Susceptible-Infected-Recovered) model. de Leon et al. [2] forecasted the outbreak in Mexico using a SEIARD (Susceptible-Exposed-Infected-Asymptomatic-Recovered-Dead) model and determined the R0 value using the Matlab 2016b software, which is based on the Runge-Kutta formula. Rajesh et al. [40] analyzed the COVID-19 data obtained from March 22–April 17, 2020 using an SIR(D) dynamical model in India. Khatua et al. [3] presented a dynamic optimal SEIAR model for COVID-19 cases in India along with a sensitivity analysis and recommended that consecutive 40 days might be able to control the pandemic influence. Jia et al. [41] studied the SEIRQAD (Susceptible-Exposed-Infectious-Recovered-Quarantined-Asymptomatic-Diagnosed) model involving control stages of different regions of China with some meteorological influences. Chatterjee et al. [42] applied a stochastic SEIQRD (Susceptible-Exposed-Infected-Quarantined-Recovered-Dead) model to COVID-19 cases in India by considering the data of March 30, 2020. Singh et al. [43] predicted the COVID-19 data of India and its states until May 12, 2020 using a mathematical approach. Hao [44] used an MSIR (Modified-Susceptible-Infectious-Recovered) and MSEIR (Modified-Susceptible-Exposed-Infectious-Recovered) model to predict the outbreak of COVID-19 cases from January 21–February 17, 2020 in China. Mandal et al. [45] analyzed the COVID-19 cases in three provinces/states of India using five time-dependent classes: susceptible S(t), exposed E(t), hospitalized infected I(t), quarantine Q(t), and recovered/removed R(t). Khan and Hossain [46] conducted an empirical analysis on COVID-19 outbreaks using a projection technique called the infection trajectory-pathway strategy in Bangladesh.
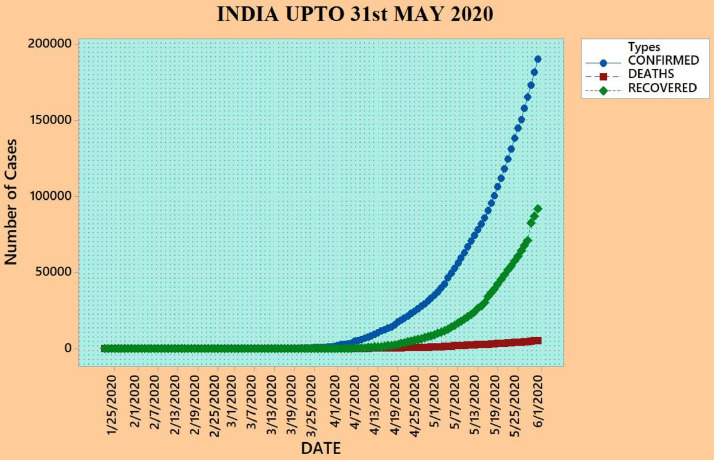
Pinter et al. 2020 [47] employed a hybrid machine learning approach to predict the outbreak of COVID-19 cases in Hungary using the data obtained from March 4–April 19, 2020. Fernández-Villaverde and Jones [48] estimated the parameters of several countries, states, and cities using a standard epidemiological SIRDC (Susceptible-Infectious-Resolving-Dead-reCovered) model of COVID-19. de-Camino-Beck [49] employed a modified confinement compartment SEICRS (Susceptible-Exposed-Infectious-Compartment-Recovered-Strategy) model to study the COVID-19 cases from February 3–May 14, 2020 in Costa Rica using the Mathematica 12 software with governmental NPIs. Gupta [50] forecasted the COVID-19 cases for India, Italy, USA, and UK until May 18, 2020. Lyra et al. [51] modeled the COVID-19 cases for Brazil using an SEIR(+CAQH) approach and found that the fatality rate of disease appears to be higher among the elderly population (particularly 60 and beyond). Rustam et al. [52] forecasted the COVID-19 cases for different countries using four machine learning regression models: linear regression, lasso regression, support vector machine, and exponential smoothing. Gupta et al. [53] analyzed the COVID-19 outbreaks in India and several states using the exponential modeling and considering several lockdown measures. Fig. 2 shows the COVID-19 scenario of India until May 31, 2020 by considering the confirmed, death, and recovered cases.
Fig. 2.
Scenario of India until May 31, 2020.
2. Estimation of parameters of SIR model of India using an actual data set
For the epidemical mathematical model, basic models that are based on compartments, as shown in the following, were used:
-
i
(Susceptible->Infectible) SI model,
-
ii
(Susceptible->Infectible-> Susceptible) SIS model, and
-
iii
(Susceptible->Infectible-> Recovery/Removed) SIR model.
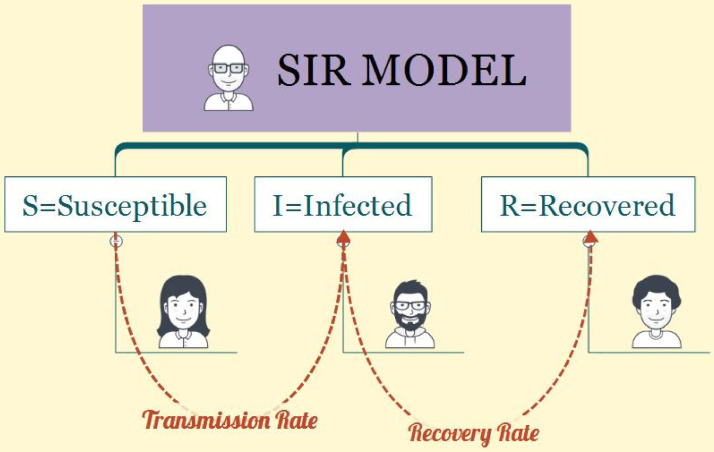
In 1927, Kermack and McKendrick [54] first proposed a class of compartmental models that simplified the mathematical modeling of infectious disease transmission. The SIR model is a set of general equations that explain the dynamics of an infectious disease spreading through a susceptible population. Fig. 3 shows the schematic of division of population based on the SIR model.
Fig. 3.
Division of population based on the SIR model.
Essentially, the standard SIR model is a set of differential equations that can be categorized as susceptible (if previously unexposed to the pandemic disease), infected (if currently colonized by the pandemic disease), and removed (either by death or recovery) as follows:
| (1) |
| (2) |
| (3) |
Here, N=S+I+R is independent of time t and denotes the total population size [8], [18], [55], [56], [69]. The population of India in 2020 is estimated as 1,380,004,385 people at mid-year according to the UN data [57]. Therefore, the value of population size (N) was considered as 1,380,004,385 for the SIR modeling of India. Fig. 4 describes the basic structure of SIR mathematical model.
Fig. 4.
Basic structure of the SIR model.
When there is no infection or I+R=0, then by substituting S≈N into Eq. (2), we obtain the following equation:
| (4) |
Then, by integrating Eq. (4), we obtained the following equation:
| (5) |
2.1. Determination of β and m values
At the onset of infection, almost all of the population is susceptible; i.e., S≈N. Therefore, I(t) first grows exponentially.
| (6) |
where m=β-γ is a constant term that represents the difference between transmission and recovery rates.
| (7) |
| (8) |
The m value can be estimated from the log-plot data and by using, for example, least squares to obtain the best-line fit.
In this study, the dataset was taken from the 2019 Novel Coronavirus Visual Dashboard operated by the Johns Hopkins University Center for Systems Science and Engineering (JHU-CSSE) database (JHU, 2020) [58]. The Python code [59] of the SIR model, based on the dataset of India, was simulated on the Google Colab platform, and the estimated futuristic dates were determined using the online date calculator [60]. In addition, the scenarios of the world and India, based on the actual JHU-CSSE dataset, was computed using the Minitab software (JHU-CSSE data set for World and India, 2020) [57].
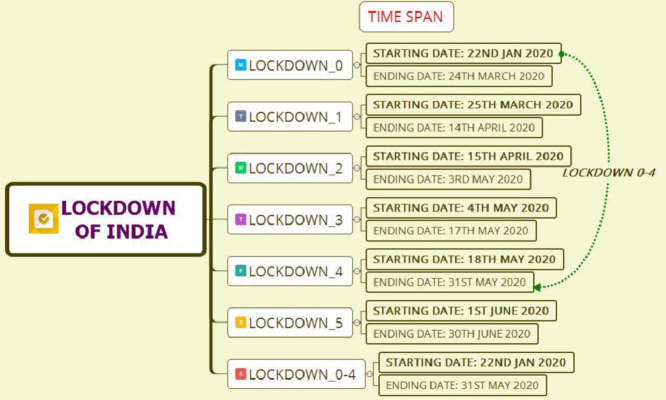
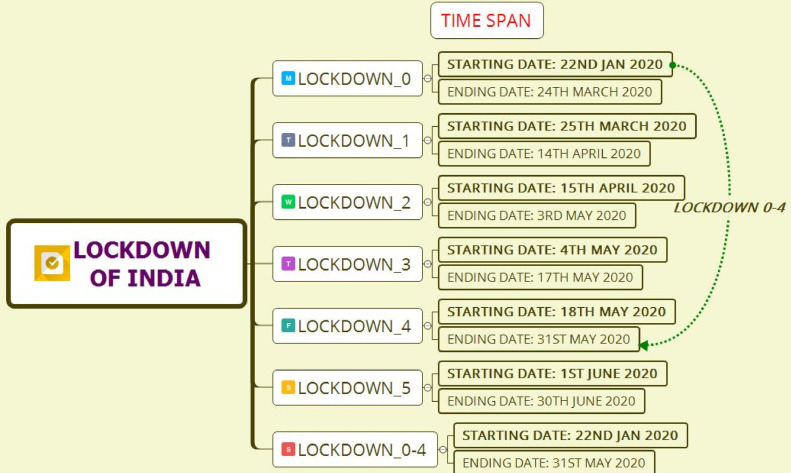
In this study, we assume that the governmental protocols of each lockdown measure are homogeneously implemented across the country. However, because of significant differences in various socio-economic, demographic, cultural, and administrative level factors, actual transmission rates are bound to differ from region to region. Hence, the parameters estimated in our study are only valid for the overall prediction of cases in India, on an average, and they may fail to trace the dynamics of the epidemic in sub-regions; e.g., districts or states [61]. The uncertainty in our predictions is large because of several unknown reasons arising from model assumptions, population demographics, the number of COVID-19 diagnostic tests administered per day, testing criteria, accuracy of the test results, and heterogeneity in implementation of different government-initiated interventions and community-level protective measures across the country. We have neither accounted for the age structure, contact patterns, or spatial information to finesse our predictions nor considered the possibility of a latent number of true cases, only a fraction of which are ascertained and observed. The COVID-19 hotspots in India are not uniformly spread across the country, and state-level forecasts may be more meaningful for state-level policymaking. Regardless of the caveats in our study, our analyses show the impact and necessity of lockdown and suppressed activity post-lockdown in India. One ideological limitation of considering only the epidemiological perspective of controlling the COVID-19 transmission in our model is the inability to count the excess deaths due to other causes during this period, or the flexibility to factor in reduction in mortality/morbidity due to other infectious or flu-like illnesses, traffic accidents, or health benefits of reduced air pollution levels. A more expansive framework of a cost-benefit analysis is required to gather more data and build an integrated landscape of population attributable risks [62]. Fig. 5 shows the time span of lockdowns in India during the COVID-19 pandemic situation.
Fig. 5.
Time span of lockdown in India.
Using the COVID-19 dataset of India, we obtained the values presented in Table 1 .
Table 1.
Obtained values of average γ, β and m.
| Sl. no. | Lockdown | Starting date | Ending date | AVG. (γ) | AVG. (β) | m |
|---|---|---|---|---|---|---|
| 1 | LD_0 | Jan 22, 2020 | March 24, 2020 | 0.0195558 | 0.240961 | 0.221405 |
| 2 | LD_1 | March 25, 2020 | April 14, 2020 | 0.0263881 | 0.128706 | 0.102318 |
| 3 | LD_2 | April 15, 2020 | May 3, 2020 | 0.086535 | 0.086535 | 0.051772 |
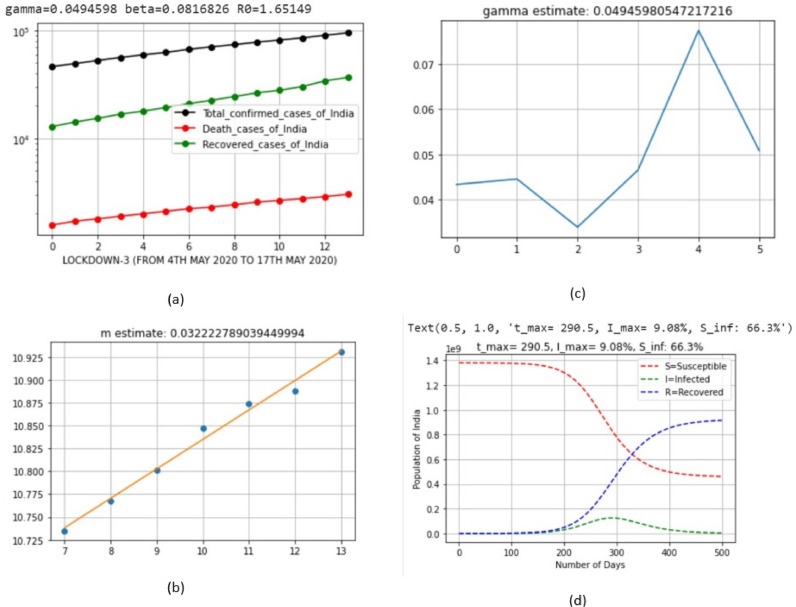
| 4 | LD_3 | May 4, 2020 | May 17, 2020 | 0.0494598 | 0.0816826 | 0.032222 |
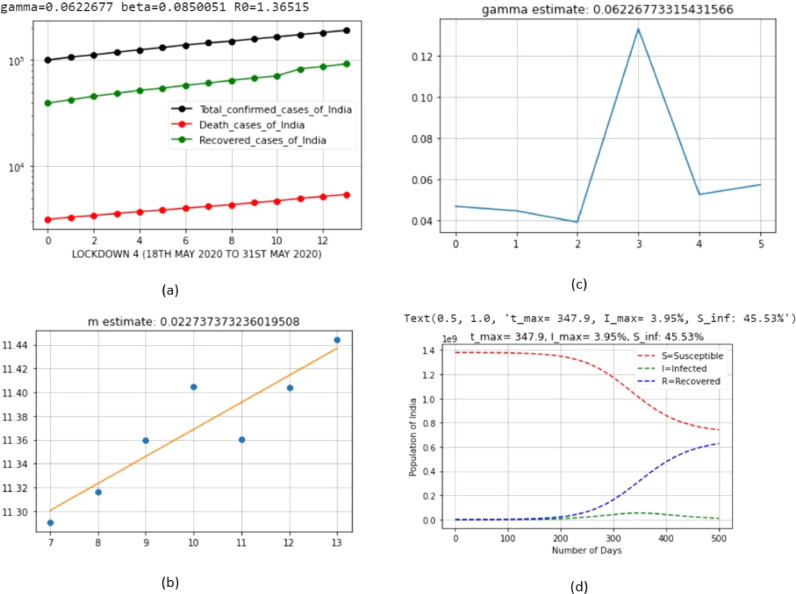
| 5 | LD_4 | May 18, 2020 | May 31, 2020 | 0.0622677 | 0.0850051 | 0.022737 |
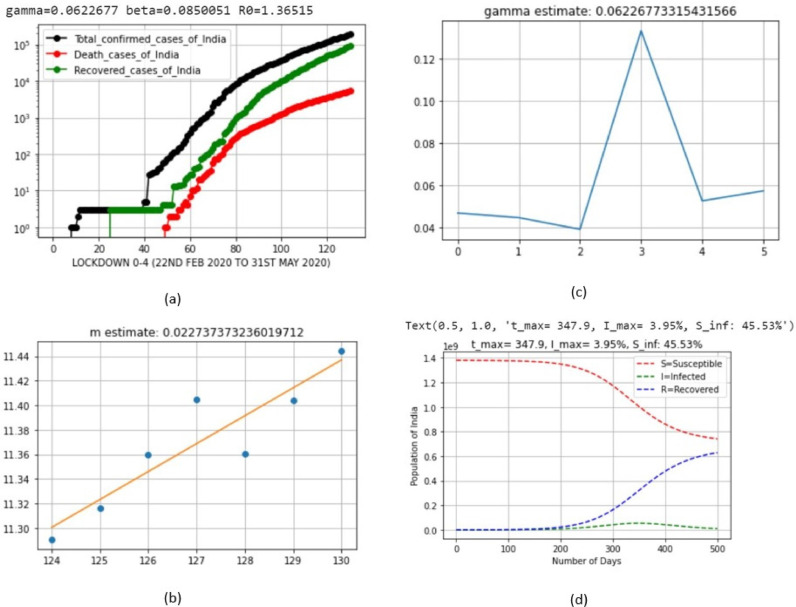
| 6 | LD_0–4 | Jan 22, 2020 | May 31, 2020 | 0.0622677 | 0.0850051 | 0.022737 |
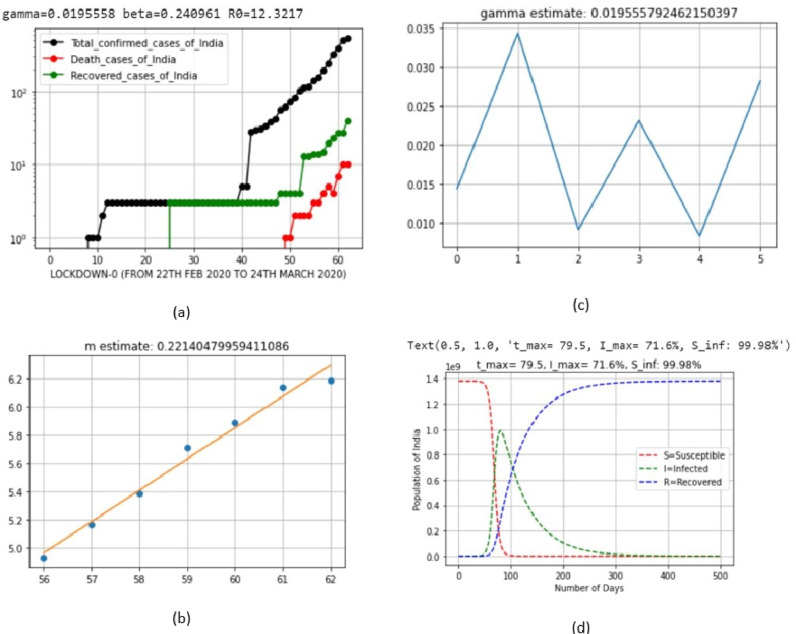
Here, lockdown 4 exhibited the minimum value; this means that severe control measures were taken to control the spread of virus.
2.2. Determination of γ value
Suppose I(t)=I0 (constant), then we obtain the following equation:
| (9) |
Then, by integrating Eq. (9), we obtained the following equation:
| (10) |
If it takes t=T days to recover, then, R(T)=I0, or γT=1.
Thus, we obtained the following equation:
| (11) |
where T is the recovery period.
From Eq. (3), for a change in time of dt=a, we obtained the following equation:
| (12) |
or
| (13) |
By estimating directly from the dataset of India, we obtained the values presented in Table 2 .
Table 2.
Obtained values of average γ.
| Sl. no. | Lockdown | Starting date | Ending date | AVG. (γ) |
|---|---|---|---|---|
| 1 | LD_0 | Jan 22, 2020 | March 24, 2020 | 0.0195558 |
| 2 | LD_1 | March 25, 2020 | April 14, 2020 | 0.0263881 |
| 3 | LD_2 | April 15, 2020 | May 3, 2020 | 0.086535 |
| 4 | LD_3 | May 4, 2020 | May 17, 2020 | 0.0494598 |
| 5 | LD_4 | May 18, 2020 | May 31, 2020 | 0.0622677 |
| 6 | LD_0–4 | Jan 22, 2020 | May 31, 2020 | 0.0622677 |
Here, lockdown 2 exhibited the maximum value; this means that the recovery rate of population in this period was better than those in other lockdown periods.
2.3. Determination of Imax and Sinf
By dividing Eq. (2) by Eq. (1), we obtained the following equation:
| (14) |
or
| (15) |
Then, by integrating both sides, we obtained the following equation:
| (16) |
where C=constant.
At the onset of infection, the value of I in Eq. (16) is extremely low, and S≈N (total population size).
Therefore, at t=0, I∼0 and S∼N.
Thus, by substituting these values into Eq. (16), we obtained the following equation:
| (17) |
or
| (18) |
By substituting the value of C, shown in Eq. (18), into Eq. (16), we obtained the following equation:
| (19) |
This equation is valid for all times. Generally, the I initially increases exponentially, reaches a peak, and then gradually decreases back to zero. We, now, need to find out the percentage of sick people at the peak of infection (Imax) and susceptible people remaining after the infection of COVID-19 virus has passed. The Eqs. (2) and (19) are the differential equation of infection rate and its solution respectively.
To simplify, assume S=Ns, I=Ni, and R=Nr. Here, s, i, and r represent the fraction of total susceptible, infected, and recovery/removed populations. Thus, we obtained the following equations:
| (20) |
and
| (21) |
During peak infection at di/dt=0, s is obtained by the following equation:
| (22) |
By substituting Eq. (22) into Eq. (21), we obtained the following equation:
| (23) |
From the dataset of India, we obtained the values presented in Table 3 .
Table 3.
Obtained values of Imax.
| Sl. no. | Lockdown | Starting date | Ending date | Imax (in %) | Tentative peak date |
|---|---|---|---|---|---|
| 1 | LD_0 | Jan 22, 2020 | March 24, 2020 | 71.6 | April 11, 2020 (Saturday) |
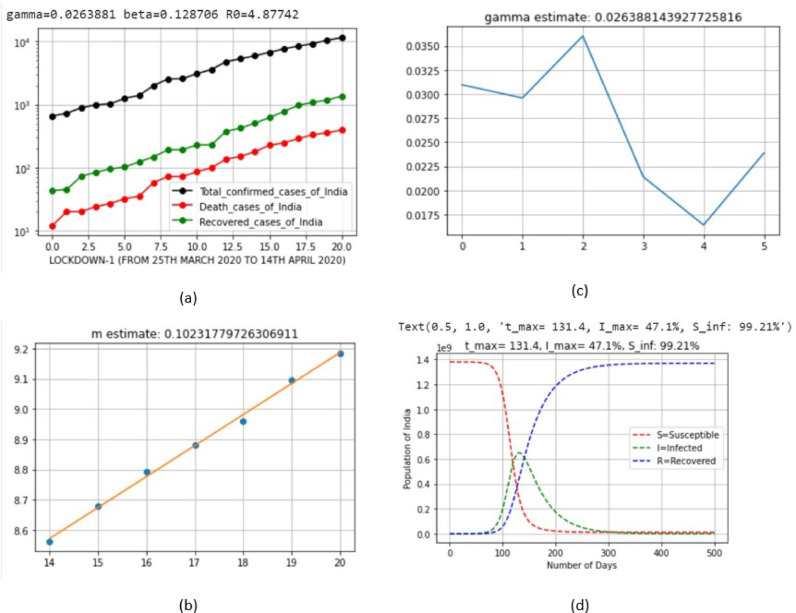
| 2 | LD_1 | March 25, 2020 | April 14, 2020 | 47.1 | Aug 3, 2020 (Monday) |
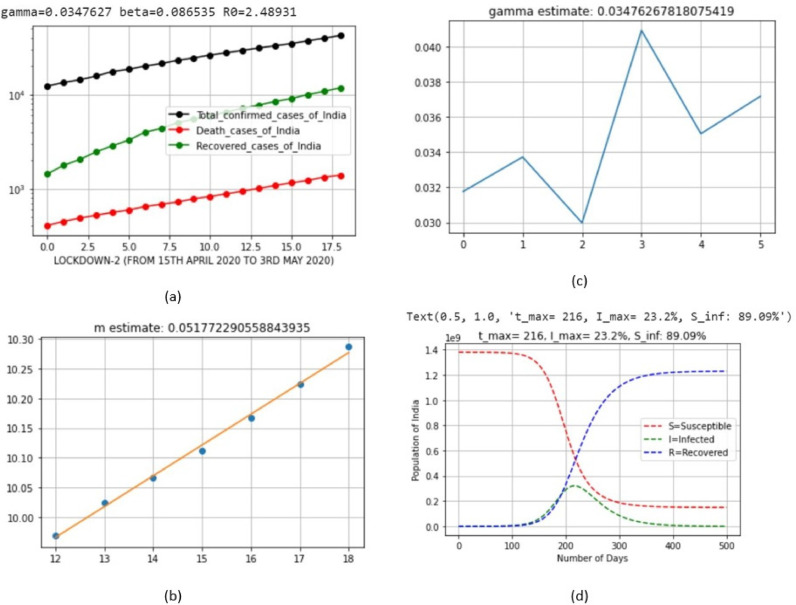
| 3 | LD_2 | April 15, 2020 | May 3, 2020 | 23.2 | Nov 17, 2020 (Tuesday) |
| 4 | LD_3 | May 4, 2020 | May 17, 2020 | 9.08 | Feb 19, 2021 (Friday) |
| 5 | LD_4 | May 18, 2020 | May 31, 2020 | 3.95 | May 1, 2021 (Saturday) |
| 6 | LD_0–4 | Jan 22, 2020 | May 31, 2020 | 3.95 | Feb 4, 2021 (Thursday) |
The percentage of sick people at the peak of infection drastically reduced in each lockdown period of India. We, now, need to find out Sinf=; i.e., the percentage of susceptible people remaining after the infection has passed. We note that i=0 because t tends to infinity (∞) at the end of infection; thus, Eq. (21) can be rewritten as follows:
| (24) |
Eq. (24) can be solved numerically to obtain the s value. From the data set of India, we obtained the values of Sinf for every lockdown stage, as shown in Table 4 .
Table 4.
Obtained values of Sinf.
| Sl. no. | Lockdown | Starting date | Ending date | Sinf |
|---|---|---|---|---|
| 1 | LD_0 | Jan 22, 2020 | March 24, 2020 | 99.98 |
| 2 | LD_1 | March 25, 2020 | April 14, 2020 | 99.21 |
| 3 | LD_2 | April 15, 2020 | May 3, 2020 | 89.09 |
| 4 | LD_3 | May 4, 2020 | May 17, 2020 | 66.3 |
| 5 | LD_4 | May 18, 2020 | May 31, 2020 | 45.53 |
| 6 | LD_0–4 | Jan 22, 2020 | May 31, 2020 | 45.53 |
The percentage of sick people at the end of infection decreased because of the strict procedures of lockdown, and this can be further decreased in future lockdown implementations.
2.4. Determination of R0
The basic reproduction number, R0, is the ratio of transmission and recovery rates.
| (25) |
It represents the number of individuals (on average) infected by a single individual [7], [18], [22], [63], [64], [65], [66], [67], [68], [70]. In terms of R0, the following equation can be obtained:
| (26) |
and
| (27) |
From the dataset of India, we obtained the values presented in Table 5 .
Table 5.
Obtained values of R0.
| Sl. no. | Lockdown | Starting date | Ending date | R0 |
|---|---|---|---|---|
| 1 | LD_0 | Jan 22, 2020 | March 24, 2020 | 12.3217 |
| 2 | LD_1 | March 25, 2020 | April 14, 2020 | 4.87742 |
| 3 | LD_2 | April 15, 2020 | May 3, 2020 | 2.48931 |
| 4 | LD_3 | May 4, 2020 | May 17, 2020 | 1.65149 |
| 5 | LD_4 | May 18, 2020 | May 31, 2020 | 1.36515 |
| 6 | LD_0–4 | Jan 22, 2020 | May 31, 2020 | 1.36515 |
The basic reproduction number decreased because of the strict procedures of lockdown, and this can be further decreased. The simulation results of the Python code of SIR model, based on the India COVID-19 dataset, are shown in Fig. 6, Fig. 7, Fig. 8, Fig. 9, Fig. 10, Fig. 11 for each lockdown case.
Fig. 6.
Output parameters of SIR model for lockdown 0.
Fig. 7.
Output parameters of SIR model for lockdown 1.
Fig. 8.
Output parameters of SIR model for lockdown 2.
Fig. 9.
Output parameters of SIR model for lockdown 3.
Fig. 10.
Output parameters of SIR model for lockdown 4.
Fig. 11.
Output parameters of SIR model for lockdown periods 0–4.
3. Conclusion
From the study of the SIR model for India, several points could be concluded, which are considered as the betterment of each lockdown measure that is to be incorporated. The recovery rate increased and the transmission rate decreased. Thus, the value of basic reproduction number decreased, flattening the curve of epidemic spread of COVID-19. Similarly, the percentage of susceptible people remaining after the infection had passed decreased, and it should be checked in the near future. In addition, the peak percentage value of infectious people decreased and exhibited better values. In the case of India, further strict governmental interventions should be performed, and, of course, the pandemic cases can be drastically decreased by spreading awareness among the residing people.
Supplementary material
The Python scripts used in this study, which include the code of SIR model used to derive parameters, will be made available with this manuscript.
Data availability statement
https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data/csse_covid_19_time_series
[59] https://www.dropbox.com/sh/akc525jjq3dp485/AADgo6WsT1RBpZqahmj_k-v_a/SIR/italy_fit.py?dl=0
Author contributions
Mr. Dilip Kumar Bagal monitored the research works from starting to ending process, Ms. Arati Rath simulated the SIR model through Python code, Mr. Abhishek Barua and Dr. Dulu Patnaik both drafted the manuscript as per the requirements.
Funding
There is no funding for this study.
Declaration of Competing Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Authors wish to thank the Ministry of Health & Family Welfare, Government of India for helping with the data collection in this study.
Footnotes
Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.chaos.2020.110154.
Appendix. Supplementary materials
References
- 1.Patrikar S., Poojary D., Basannar D., Kunte R. Projections for novel coronavirus (COVID-19) and evaluation of epidemic response strategies for India. Med J Armed Forces India. 2020 doi: 10.1016/j.mjafi.2020.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.de León, U.A.-.P., ÁG, P., Avila-Vales, E.. An SEIARD epidemic model for COVID-19 in Mexico: mathematical analysis and state-level forecast. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.11.20098517. [DOI] [PMC free article] [PubMed]
- 3.Khatua, D., De, A., Kar, S., Samanta, E., Mandal, S.M.. A dynamic optimal control model for SARS-CoV-2 in India. Available at SSRN 3597498. 2020. DOI: 10.2139/ssrn.3597498. [DOI]
- 4.Bhattacharyya, A., Bhowmik, D., Mukherjee, J.. Forecast and interpretation of daily affected people during 21 days lockdown due to COVID 19 pandemic in India. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.04.22.20075572. [DOI]
- 5.Ranjan, R.Predictions for COVID-19 outbreak in India using epidemiological models. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.04.02.20051466. [DOI]
- 6.Dhanwant, J.N., Ramanathan, V.Forecasting COVID 19 growth in India using susceptible-infected-recovered (SIR) model. arXiv:200400696 [Preprint]. 2020.
- 7.Rodrigues R.F., da Silva A.R., da Fonseca Vieira V., Xavier C.R. International Conference on computational science and its applications. 2018. Springer; 2018. Optimization of the choice of individuals to be immunized through the genetic algorithm in the sir model; pp. 62–75. in: International Conference on Computational Science and Its Applications. [DOI] [Google Scholar]
- 8.Elhia M., Rachik M., Benlahmar E. Optimal control of an SIR model with delay in state and control variables. ISRN Biomath. 2013;2013 doi: 10.1155/2013/403549. [DOI] [Google Scholar]
- 9.Chaves L.F., Hurtado L.A., Rojas M.R., Friberg M.D., Rodríguez R.M., Avila-Aguero M.L. COVID-19 basic reproduction number and assessment of initial suppression policies in Costa Rica. Math Model Nat Phenom. 2020;15:32. doi: 10.1051/mmnp/2020019. [DOI] [Google Scholar]
- 10.Singh, R., Adhikari, R.. Age-structured impact of social distancing on the COVID-19 epidemic in India. arXiv:200312055 [Preprint]. 2020.
- 11.Das, S.. Prediction of covid-19 disease progression in India: under the effect of national lockdown. arXiv:200403147 [Preprint]. 2020.
- 12.Arif, M., Kakar, A., Larik, E.. Estimation of the final size of the COVID-19 epidemic in Balochistan, Pakistan. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.22.20110064. [DOI]
- 13.Boudrioua, M.S., Boudrioua, A.. Predicting the COVID-19 epidemic in Algeria using the SIR model. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.04.25.20079467. [DOI]
- 14.Deo, V., Chetiya, A.R., Deka, B., Grover, G.. Forecasting transmission dynamics of COVID-19 epidemic in India under various containment measures-a time-dependent state-space SIR approach. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.08.20095877. [DOI]
- 15.Hazem, Y., Natarajan, S., Berikaa, E.. Hasty reduction of COVID-19 lockdown measures leads to the second wave of infection. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.23.20111526. [DOI]
- 16.Jakhar, M., Ahluwalia, P., Kumar, A.. COVID-19 epidemic forecast in different states of India using SIR model. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.14.20101725. [DOI]
- 17.Mujallad, A., Khoj, H.. Is there hope for the Hajj? Using the SIR model to forecast COVID-19 progression in the city of Makkah. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.23.20105643. [DOI]
- 18.de Oliveira, A.C.S., Morita, L.H.M., da Silva, E.B., Granzotto, D.C.T., Zardo, L.A.R., Fontes, C.J.F.. Bayesian modeling of COVID-19 cases with a correction to account for under-reported cases. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.24.20112029. [DOI] [PMC free article] [PubMed]
- 19.Postnikov E.B. Estimation of COVID-19 dynamics “on a back-of-envelope”: does the simplest SIR model provide quantitative parameters and predictions? Chaos Solitons Fractals. 2020;135 doi: 10.1016/j.chaos.2020.109841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rojas-Gallardo, D.M., Garzon-Castano, S.C., Millan, N., Jimenez-Posada, E.V., Cardona-Ospina, J.A.. COVID-19 in Latin America: contrasting phylodynamic inference with epidemiological surveillance. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.23.20111443. [DOI]
- 21.López, L., Rodo, X. A modified SEIR model to predict the COVID-19 outbreak in Spain and Italy: simulating control scenarios and multi-scale epidemics. Available at SSRN 3576802. 2020. DOI: 10.1101/2020.03.27.20045005. [DOI] [PMC free article] [PubMed]
- 22.Yang Z., Zeng Z., Wang K., Wong S.-S., Liang W., Zanin M. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J Thorac Dis. 2020;12(3):165. doi: 10.21037/jtd.2020.02.64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Engbert, R., Rabe, M.M., Kliegl, R., Reich, S.. Sequential data assimilation of the stochastic SEIR epidemic model for regional COVID-19 dynamics. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.04.13.20063768. [DOI] [PMC free article] [PubMed]
- 24.Berger D.W., Herkenhoff K.F., Mongey S. NBER Working Paper No. 26901. National Bureau of Economic Research; 2020. An SEIR infectious disease model with testing and conditional quarantine. [DOI] [Google Scholar]
- 25.Hou C., Chen J., Zhou Y., Hua L., Yuan J., He S. The effectiveness of quarantine of Wuhan city against the Corona Virus Disease 2019 (COVID‐19): a well‐mixed SEIR model analysis. J Med Virol. 2020 doi: 10.1002/jmv.25827. [DOI] [PubMed] [Google Scholar]
- 26.Saito M.M., Imoto S., Yamaguchi R., Sato H., Nakada H., Kami M. Extension and verification of the SEIR model on the 2009 influenza A (H1N1) pandemic in Japan. Math Biosci. 2013;246(1):47–54. doi: 10.1016/j.mbs.2013.08.009. [DOI] [PubMed] [Google Scholar]
- 27.Godio A., Pace F., Vergnano A. A. SEIR modeling of the Italian epidemic of SARS-CoV-2 using computational swarm intelligence. Int J Environ Res Public Health. 2020;17(10) doi: 10.3390/ijerph17103535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Feng, Z., Damon-Feng, H., Zhao, H.. Sustaining social distancing policies to prevent a dangerous second peak of COVID-19 outbreak. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.04.17.20069351. [DOI]
- 29.Gupta, R., Pandey, G., Chaudhary, P., Pal, S.K.. SEIR and Regression model based COVID-19 outbreak predictions in India. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.04.01.20049825. [DOI]
- 30.Pandey, G., Chaudhary, P., Gupta, R., Pal, S.. SEIR and regression model based COVID-19 outbreak predictions in India. arXiv:200400958 [Preprint]. 2020. DOI: 10.1101/2020.04.01.20049825. [DOI]
- 31.Goswami, G., Prasad, J., Dhuria, M.. Extracting the effective contact rate of COVID-19 pandemic. arXiv:200407750 [Preprint]. 2020.
- 32.Bonnasse-Gahot, L., Dénès, M., Dulac-Arnold, G., Girgin, S., Husson, F., Iovene, V., et al. ICU bed availability monitoring and analysis in the Grand Est region of France during the COVID-19 epidemic. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.18.20091264. [DOI]
- 33.Dixit, A., Vishnoi, S., Paul, S.B.. Adding structure to statistics: a study on COVID-19 dynamics in India. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.26.20113522. [DOI]
- 34.Kohanovski, I., Obolski, U., Ram, Y.. Inferring the effective start dates of non-pharmaceutical interventions during COVID-19 outbreaks. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.24.20092817. [DOI] [PMC free article] [PubMed]
- 35.Teles, P.. A time-dependent SEIR model to analyse the evolution of the SARS-CoV-2 epidemic outbreak in Portugal. arXiv:200404735 [Preprint]. 2020.
- 36.Wagh, C.S., Mahalle, P.N., Wagh, S.J.. Epidemic peak for COVID-19 in India, 2020. Preprints 2020 [Preprint]. 2020. DOI: 10.20944/preprints202005.0176.v1. [DOI]
- 37.Ray, D., Salvatore, M., Bhattacharyya, R., Wang, L., Mohammed, S., Purkayastha, S., et al. Predictions, role of interventions and effects of a historic national lockdown in India's response to the COVID-19 pandemic: data science call to arms. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.04.15.20067256. [DOI] [PMC free article] [PubMed]
- 38.da Cruz P.A., Cruz L.C.C. Mathematical modeling and epidemic prediction of COVID-19 of the State of São Paulo, Brazil. Int J Adv Eng Res Sci. 2020;7(5) doi: 10.22161/ijaers.75.41. [DOI] [Google Scholar]
- 39.Kobayashi G., Sugasawa S., Tamae H., Ozu T. Predicting intervention effect for COVID-19 in Japan: state space modeling approach. BioScience Trends. 2020;14(3):174–181. doi: 10.5582/bst.2020.03133. [DOI] [PubMed] [Google Scholar]
- 40.Rajesh, A., Pai, H., Roy, V., Samanta, S., Ghosh, S.. CoVID-19 prediction for India from the existing data and SIR (D) model study. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.05.20085902. [DOI]
- 41.Jia, J., Ding, J., Liu, S., Liao, G., Li, J., Duan, B., et al. Modeling the control of COVID-19: impact of policy interventions and meteorological factors. arXiv:200302985 [Preprint]. 2020.
- 42.Chatterjee K., Chatterjee K., Kumar A., Shankar S. Healthcare impact of COVID-19 epidemic in India: a stochastic mathematical model. Med J Armed Forces India. 2020 doi: 10.1016/j.mjafi.2020.03.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Singh, J., Ahluwalia, P., Kumar, A.. Mathematical model based COVID-19 prediction in India and its different states. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.16.20104232. [DOI]
- 44.Hao, T.. Infection dynamics of coronavirus disease 2019 (Covid-19) modeled with the integration of the eyring rate process theory and free volume concept. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.02.26.20028571. [DOI]
- 45.Mandal M., Jana S., Nandi S.K., Khatua A., Adak S., Kar T. A model based study on the dynamics of COVID-19: prediction and control. Chaos Solitons Fractals. 2020 doi: 10.1016/j.chaos.2020.109889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Khan, M.H.R., Hossain, A.. COVID-19 outbreak situations in Bangladesh: an empirical analysis. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.04.16.20068312. [DOI]
- 47.Pinter G., Felde I., Mosavi A., Ghamisi P., Gloaguen R. Mathematics-2020. 6th. Vol. 8. Molecular Diversity Preservation International (MDPI); 2020. COVID-19 pandemic prediction for Hungary; a hybrid machine learning approach; pp. 1–20. [DOI] [Google Scholar]
- 48.Fernández-Villaverde J., Jones C.I. National Bureau of Economic Research; 2020. Estimating and simulating a SIRD model of COVID-19 for many countries, states, and cities. National Bureau of Economic Research. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.de-Camino-Beck, T.. A modified SEIR model with Confinement and lockdown of COVID-19 for Costa Rica. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.19.20106492. [DOI]
- 50.Gupta, P.K.. Would India really touch the peak of SARS COVID 19 cases or deaths in near future?medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.21.20109728. [DOI]
- 51.Lyra, W., do Nascimento, J.D., Belkhiria, J., de Almeida, L., Chrispim, P.P., de Andrade, I.. COVID-19 pandemics modeling with SEIR (+ CAQH), social distancing, and age stratification. The effect of vertical confinement and release in Brazil. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.04.09.20060053. [DOI] [PMC free article] [PubMed]
- 52.Rustam F., Reshi A.A., Mehmood A., Ullah S., On B., Aslam W. COVID-19 future forecasting using supervised machine learning models. IEEE Access. 2020;4:1–12. doi: 10.1109/access.2020.2997311. [DOI] [Google Scholar]
- 53.Gupta, R., Pal, S.K., Pandey, G.. A comprehensive analysis of COVID-19 outbreak situation in India. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.04.08.20058347. [DOI]
- 54.Kermack W.O., McKendrick AG. Proceedings of the royal society of London series A, containing papers of a mathematical and physical character. Vol. 115. 1927. A contribution to the mathematical theory of epidemics; pp. 700–721. [DOI] [Google Scholar]
- 55.Fornaciari G., Borghi E.J.A., Vieira M.L., Aguiar R.L., Holtz A.M., Filho A.C.V. Survey of potentially host weeds of Planococcus spp. in coffee crops. Int J Adv Eng Res Sci. 2020;7(5):333–337. doi: 10.22161/ijaers.75.41. [DOI] [Google Scholar]
- 56.Moorthy V., Henao Restrepo A.M., Preziosi M.P., Swaminathan S. Data sharing for novel coronavirus (COVID-19) Bull World Health Organ. 2020;98(3):150. doi: 10.2471/BLT.20.251561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Population based on UN data for India Country. 2020; (Online) Available at:https://www.worldometers.info/world-population/india-population/.
- 58.Center for systems science and engineering (CSSE) at Johns Hopkins University (JHU) time series data set for COVID-19 cases. 2020; (Online) Available at:https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data/csse_covid_19_time_series.
- 59.SIR model Python code. 2020; (Online) Available at:https://www.dropbox.com/sh/akc525jjq3dp485/AADgo6WsT1RBpZqahmj_k-v_a/SIR/italy_fit.py?dl=0.
- 60.Date Calculator. 2020; (Online) Available at:http://date.bizcalcs.com/Calculator.asp?Calc=Find-Future-Date.
- 61.Deo, V., Chetiya, A.R., Deka, B., Grover, G.. Forecasting transmission dynamics of COVID-19 epidemic in India under Various containment measures- a time-dependent state-space SIR approach. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.08.20095877. [DOI]
- 62.Ray, D., Salvatore, M., Bhattacharyya, R., Wang, L., Mohammed, S., Purkayastha, S., et al. Predictions, role of interventions and effects of a historic national lockdown in India's response to the COVID-19 pandemic: data science call to arms. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.04.15.20067256. [DOI] [PMC free article] [PubMed]
- 63.Boldog P., Tekeli T., Vizi Z., Denes A., Bartha F.A., Rost G. Risk assessment of novel coronavirus COVID-19 outbreaks outside China. J Clin Med. 2020;9(2) doi: 10.3390/jcm9020571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Chatterjee, S., Sarkar, A., Chatterjee, S., Karmakar, M., Paul, R.. Studying the progress of COVID-19 outbreak in India using SIRD model. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.11.20098681. [DOI] [PMC free article] [PubMed]
- 65.Liu, X., Hewings, G.J.D., Wang, S., Qin, M., Xiang, X., Zheng, S., et al. Modelling the situation of COVID-19 and effects of different containment strategies in China with dynamic differential equations and parameters estimation. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.03.09.20033498. [DOI]
- 66.Singhal T. A review of coronavirus disease-2019 (COVID-19) Indian J Pediatr. 2020:1–6. doi: 10.1007/s12098-020-03263-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Tang, Z., Li, X., Li, H.. Prediction of new coronavirus infection based on a modified SEIR model. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.03.03.20030858. [DOI]
- 68.Tuite A.R., Fisman D.N. Reporting, epidemic growth, and reproduction numbers for the 2019 novel coronavirus (2019-nCoV) epidemic. Ann Inter Med. 2020;172(8):567–568. doi: 10.7326/M20-0358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Yang, P., Qi, J., Zhang, S., g, Bi, Wang, X., Yang, Y., et al. The effect of multiple interventions to balance healthcare demand for controlling COVID-19 outbreaks: a modelling study. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.05.19.20107326. [DOI] [PMC free article] [PubMed]
- 70.Zhou, X., Ma, X., Hong, N., Su, L., Ma, Y., He, J., et al. Forecasting the worldwide spread of COVID-19 based on logistic model and SEIR model. medRxiv [Preprint]. 2020. DOI: 10.1101/2020.03.26.20044289. [DOI]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data/csse_covid_19_time_series
[59] https://www.dropbox.com/sh/akc525jjq3dp485/AADgo6WsT1RBpZqahmj_k-v_a/SIR/italy_fit.py?dl=0