Abstract
The novel coronavirus (COVID-19) pandemic is causing devastating demographic, social, and economic damage globally. Understanding current patterns of the pandemic spread and forecasting its long-term trajectory is essential in guiding policies aimed at curtailing the pandemic. This is particularly important in regions with weak economies and fragile health care systems such as West Africa. We formulate and use a deterministic compartmental model to (i) assess the current patterns of COVID-19 spread in West Africa, (ii) evaluate the impact of currently implemented control measures, and (iii) predict the future course of the pandemic with and without currently implemented and additional control measures in West Africa. An analytical expression for the threshold level of control measures (involving a reduction in the effective contact rate) required to curtail the pandemic is computed. Considering currently applied health control measures, numerical simulations of the model using baseline parameter values estimated from West African COVID-19 data project a 67% reduction in the daily number of cases when the epidemic attains its peak. More reduction in the number of cases will be achieved if additional public health control measures that result in a reduction in the effective contact rate are implemented. We found out that disease elimination is difficult when more asymptomatic individuals contribute in transmission or are not identified and isolated in a timely manner. However, maintaining a baseline level of asymptomatic isolation and a low transmission rate will lead to a significant reduction in the number of daily cases when the pandemic peaks. For example, at the baseline level of asymptomatic isolation, at least a 46% reduction in the transmission rate is required for disease elimination. Additionally, disease elimination is possible if asymptomatic individuals are identified and isolated within 5 days (after the incubation period). Combining two or more measures is better for disease control, e.g., if asymptomatic cases are contact traced or identified and isolated in less than 8 days, only about 29% reduction in the disease transmission rate is required for disease elimination. Furthermore, we showed that the currently implemented measures triggered a 33% reduction in the time-dependent effective reproduction number between February 28 and June 26, 2020. We conclude that curtailing the COVID-19 pandemic burden significantly in West Africa requires more control measures than those that have already been implemented, as well as more mass testing and contact tracing in order to identify and isolate asymptomatic individuals early.
Keywords: Public health control measures, SARS-CoV-2 pandemic, Mathematical model, Reproduction number, Contact tracing, Asymptomatic transmission
Highlights
-
•
The time-dependent reproduction number is reduced by 33% with current measures.
-
•
Disease elimination is difficult if asymptomatic cases are not isolated timely.
-
•
At least, 46% reduction in the transmission rate is required for disease elimination.
-
•
Combining two or more measures is better for disease control.
-
•
Mass testing and contact tracing are key in curtailing the burden of the pandemic.
1. Introduction
A new strain of coronavirus (SARS-CoV-2), that emerged from Wuhan, China is the cause of the COVID-19 pandemic that is currently ravaging the world [1], [2], [3]. As of June , , about confirmed cases of COVID-19 infections and 491,128 deaths were reported worldwide [4], [5], [6], [7]. Most of these reported COVID-19 cases (approximately ) and deaths (approximately 124,161 deaths) were from the United States of America. The epicenter of the pandemic is expected to shift to sub-Saharan Africa, which as of June , had reported about 170,843 confirmed cases and 1915 deaths. Of these, about 73,624 confirmed cases and 1352 deaths were from West Africa. The first confirmed West African case was in Nigeria on February 27,2020, i.e., approximately two months after the first case was officially announced in China [1]. The highest burden of the disease in West Africa by June , was in Nigeria (about 23,298 cases and deaths) [5]. This is in line with a multilayered-risk assessment (based on nine risk factors) in [8] that identified Nigeria as the West African country with the highest COVID-19 risk. Another study by Martinez-Alvarez et al. [9] projected that some West African countries, e.g., Burkina Faso and Senegal might experience sharp increases in the number of COVID-19 cases that are similar to those observed in European countries in March and April, 2020.
Humans can acquire the novel coronavirus when they come into contact with contaminated surfaces or from droplets released by infectious symptomatic and asymptomatic individuals [10]. Mild to moderate infection symptoms of the disease include fever, cough, sore throat, nasal congestion, malaise, headache, muscle pain, and shortness of breath (or tachypnea in children). In severe cases, fever is associated with severe dyspnea, respiratory distress, and tachypnea [11]. Currently, there is no vaccine or widely accepted drug for COVID-19. Therefore, governments and individuals are forced to rely on public health preventive measures such as basic hygiene, travel or movement restrictions, social-distancing, wearing masks, etc. Current control measures being implemented in West Africa include regular hand washing with hydroalkolic solutions, quarantine of suspected cases, isolation of confirmed cases, social distancing (e.g., travel restrictions, school closures, and banning of gatherings involving more than 10 people), contact tracing, and testing and treating identified cases. Additionally, wearing of masks in public was recently recommended as another control measure in many countries in this region. Unfortunately, it is difficult to implement these basic public health measures effectively in some West African countries due to wide-spread poverty and poor investment in health care (staff, equipment, and infrastructure) [9]. For example, in thirteen of the sixteen West African countries, less than two medical doctors are allocated to every group of 10,000 inhabitants [9], [12]. In particular, only Nigeria, Côte d’Ivoire, and Cape Verde have or more medical doctors per 10,000 inhabitants [12]. Another possible explanation for this low doctor to population ratio is alternative medicine (especially traditional medicine) that is widely practiced in the West African region. The World Health Organization estimates that about of the population of West Africa rely on traditional medicine for their health care needs both in rural and urban areas [13]. On the other hand, the annual per capita spending on health for about half of the countries in the region (Gambia, Niger, Benin, Mali, Guinea, Togo, Burkina Faso, and Mauritania) is less than US$50. Only Cape Verde spends more than US$100 per capita, i.e., about times below the average per capita health spending in countries like Italy and Spain–two European countries that experienced high COVID-19 burden [14]. As a result of poor investment in health care and health care systems, the region has been an epidemic hotspot for emerging and neglected tropical diseases including the Ebola virus (EBOV), Lassa virus (LASV), and Buruli ulcers in recent years [15], [16]. With such inadequate healthcare systems and personnel in the region, the impact of COVID-19 might be catastrophic. To compound matters, some countries in West Africa are still not well prepared to tackle this pandemic despite the observed devastating impacts and trend of the pandemic in the US, Europe, and Asia [9].
There is, therefore, the need to exploit every existing tool and/or develop new tools that can be useful in guiding public health decision-making in the fight against the pandemic. This includes developing and using new qualitative and quantitative methods such as mathematical models. There has been an influx of mathematical models to assess the impact of COVID-19 and to guide public health response in different cities, countries and regions of the world (see, for example,[17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27]). Few of these mathematical model frameworks have focused on the COVID-19 pandemic situation in West Africa as a whole. Among these few models, some have focused only on one or two countries, e.g. Nigeria and Ghana, while others have used basic regression or exponential growth models to analyze and predict disease trends[25], [26]. Martinez-Alvarez et al. [9] used a simple graph-plot based comparative analysis of observed COVID-19 data for the first 23 days of the pandemic to examine the future trajectory of the epidemic in six West African countries (Burkina Faso, Senegal, Nigeria, Côte d’Ivoire, Ghana, and The Gambia). This far, only one study has considered the entire region of West Africa [27]. In this study, a co-variate-based instrumental variable regression framework was used to predict the number of disease cases (2.8 million by June 30, 2020) and to assess the epidemiological, socio-economic and health system readiness of the region to the pandemic.
In this study, we develop a new susceptible–exposed–infectious–recovered (SEIR)-type mathematical model for COVID-19 in West Africa and use it to (i) study the current transmission pattern of COVID-19, (ii) evaluate the impact of currently implemented public health control measures such contact tracing, social distancing and use of face masks on COVID-19 transmission, and (iii) predict the future course of the pandemic with and without currently implemented and additional control measures in West Africa. In addition to incorporating various basic public health control measures, our model accounts for asymptomatic infectious individuals – a class of individuals that render disease control more difficult since they do not exhibit clinical disease symptoms, although they contribute to disease transmission [21]. To our knowledge, this is the first study that has used an explicit SEIR-type compartmental model together with data for the West African pandemic period (from February 28, 2020 to June 26, 2020) to study the spread of the COVID-19 pandemic in the region, assess the impact of current control measures, and discuss further control measures that might be required to better control the pandemic in the region.
2. Methods
2.1. Model framework
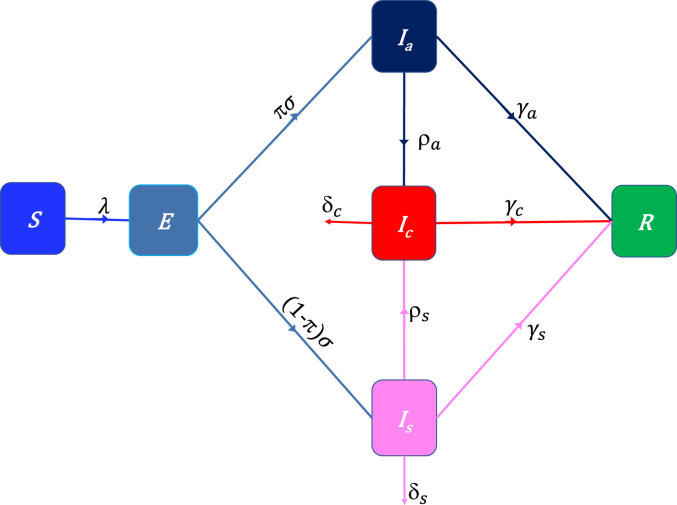
We develop a deterministic -type model framework, where the total population () is subdivided in four categories: Susceptible (), Exposed (), Infectious asymptomatic (), infectious symptomatic (), infectious at treatment or isolation centers (), and Recovered (). That is, . The model accounts for public health control measures that lead to a reduction in the force of infection , such as social distancing and face mask use. Following the approach in Ngonghala et al. [17], we model the force of infection by the functional form , where () is the disease transmission rate by individuals in the class and is the percentage reduction in disease transmission due to public health control measures such as social distancing and face masks use. Note that implies that no public health control measure leading to a reduction in disease transmission is applied and that implies that implemented public health control measures are efficient enough to stop disease transmission. After the average incubation period , a proportion of the exposed population does not develop symptoms, i.e., joins the compartment, while the remaining proportion () join the class. Identification and isolation of infectious asymptomatic individuals, e.g., through contact tracing occurs at rate , i.e., is the average time it takes for an infectious asymptomatic individual to be identified and isolated. Isolation or hospitalization of symptomatic cases occurs at rate , i.e., is the average time it takes for an infectious symptomatic individual to be isolated. Humans from the , and classes recover at rates , and , respectively, while individuals in the and classes die due to COVID-19 at respective rates and . Using the flow diagram Fig. 1 and above description we obtain the following system of equations:
Fig. 1.
Flow-chart of COVID-19 model showing the flow of humans between different compartments. The susceptible population is denoted by , the exposed population is denoted by , the infectious asymptomatic population is denoted by , the infectious symptomatic population is denoted by , the isolated infectious population is denoted by , and the recovered population is denoted by . The parameters of the model are described in the text.
| (2.1) |
where is the actively mixing population, i.e., . Since individuals in the class are in some form of confinement or isolation, we assume that they are not part of the actively mixing population and so they do not contribute in disease transmission. We denote the initial conditions of the model (2.1) by , , , , , , where for the pandemic to take off, at least one of the infected populations must be greater zero.
2.2. West African COVID-19 data and parameter estimation
West Africa comprises sixteen countries: Benin, Burkina-Faso, Cape Verde, Ghana, Guinea, Côte d’Ivoire, Mali, Mauritania, Niger, Nigeria, Senegal, Togo, Sierra Leone, Liberia, Guinea-Bissau and Gambia. Based on the latest United Nations estimates, the current population of West Africa is , i.e., about of the world population [28]. The region includes nine of the 25 poorest countries in the world [29]. Application of basic public health control measures against COVID-19 spread in most West African countries started on March , , i.e., about days after the outbreak in the region. The data considered for this analysis spans the period from February 28, 2020, i.e., one day after the first case until June 26, 2020. In West Africa, the reported confirmed cases are infectious symptomatic individuals who have been tested at a treatment center or infectious asymptomatic individuals who have been detected through contact-tracing or systematic testing on target groups and then tested at a treatment center. Hence, we assume that confirmed disease cases correspond to individuals isolated infectious individuals in isolation or at treatment centers ().
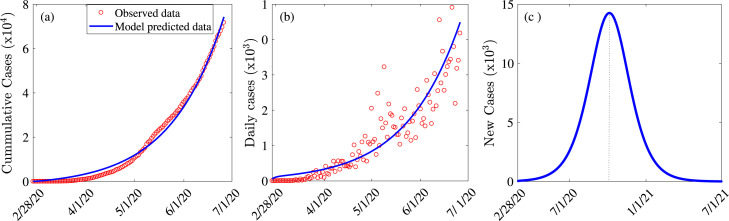
We use the cumulative number of cases in West Africa, downloaded from the Global Rise of Education website [30] to fit our model and estimate some of the key parameters presented in Table 1. The fitting that was carried out using a nonlinear least squares method in MATLAB version (R2017a) involved finding the best set of parameter values that minimizes the root mean square differences between the observed cumulative COVID-19 confirmed cases in West Africa and the predicted cumulative COVID-19 cases from our model (2.1). The minimization was achieved through the built-in constraint minimization algorithm “fmincon” in MATLAB. We repeated this procedure 1000 times for each of the parameters and used the normal distribution to compute the mean values of the parameters together with a confidence interval (CI). The goodness of fit of our model assessed using the Root Mean Squared Error (RMSE) was 188.45. The fitted and known parameter values are presented in Table 1 and the model fit is illustrated in Fig. 2(a). It is worth noting that the choice of parameters to estimate from the data or to extract from the literature was motivated by its importance to the transmission dynamics of the disease. A plot of the observed confirmed daily cases and the predicted daily cases from system (2.1) using the fitted and known parameters is presented in Fig. 2(b), while an extended plot of the new daily cases illustrating when the West African pandemic might peak (October 06, 2020) and the corresponding number of new cases (14,250) is depicted in Fig. 2(c).
Table 1.
Fitted parameter values and initial conditions of Model (2.1) together with known parameter values extracted from the literature.
| Parameter | Value | Confidence interval | Source |
|---|---|---|---|
| 0.373 | [0.364–0.381] | Fitted | |
| 0.197 | [0.178–0.216] | Fitted | |
| 0.059 | [0.048–0.069] | Fitted | |
| 0.103 | [0.094–0.110] | Fitted | |
| 0.057 | [0.053–0.060] | Fitted | |
| 0.361 | [0.315–0.406] | Fitted | |
| (baseline) | 0.261 | [0.240–0.281] | Fitted |
| 0.026 | – | Calculated | |
| 1/9.5 | – | [31] | |
| 1/10 | – | [32] | |
| 1/5.1 | – | [33] | |
| 0.780 | – | [34] | |
| Initial condition | Value | Confidence interval | Source |
| 10228231 | [10228149–10228311] | Fitted | |
| 1965 | [1956–1974] | Fitted | |
| 240 | [233–246] | Fitted | |
| 150 | [140–160] | Fitted | |
| 1 | – | [30] | |
| 22 | [22.0–22.5] | Fitted | |
Fig. 2.
Model fit and prediction. (a) Model fit using cumulative confirmed COVID-19 case data for West Africa for the period from February 28 to June 26, 2020. (b) Observed confirmed daily cases (red circles) and the predicted daily cases from Model (2.1) (solid blue line). (c) Number of new daily cases as a function of time depicting the peak of COVID-19 in West Africa. The initial conditions and the parameters used for the simulations are presented in Table 1.
3. Results
3.1. Analytical results (reproduction number and final size relation)
In this section, we derive the basic reproduction number of the model, which is defined as the average number of new infections generated by a typical infectious individual introduced in a population where everybody is susceptible [35]. For endemic models, i.e., models with vital dynamics (births and narural deaths), the basic reproduction number denoted by provides a condition under which a disease can invade a population (when ), or can be contained (when ), while for epidemic models like the one in this study, it serves as a threshold for determining whether the disease under consideration will spread. Using the next generation matrix approach in [35], [36], the basic reproduction number is:
| (3.1) |
where
Observe from Eq. (3.1) that the reproduction number , is the sum of two components, which represent the contribution of the infectious asymptomatic class and the infectious symptomatic class . For system (2.1) that already include some control efforts, the control reproduction number , is given by . The approach in[35], [36] also assures us that the family of disease-free equilibrium of system (2.1) is locally and asymptotically stable whenever the reproduction number is less than one. Another useful quantity that is associated with the reproduction number is the time-dependent effective reproduction number, which for model (2.1) is given by . It is worth mentioning that the epidemic grows when the effective reproduction number is greater than unity, peaks when the effective reproduction number equals unity and declines when the effective reproduction number is below unity. To derive the threshold reduction in the disease transmission , required to reduce the control reproduction number to one, we set , i.e., in Eq. (3.1) and solve for . This yields:
| (3.2) |
Note that the fraction in the right hand side of the threshold value of is greater than zero and less than or equal to one since . Note also that , which corresponds to the case in which now serves as a threshold for an outbreak or the disease dying out. In particular, disease elimination is possible if (since ). If , which corresponds to , the infected population increases, attains a peak, and declines to zero as . In particular, the pandemic peaks when the effective reproduction number is one. The epidemiological implication of this is that massive adherence to control measures that reduce COVID-19 transmission, e.g., social distancing can lead to disease elimination, while low adherence to such measures will reduce disease burden, but might not lead to elimination soon enough. To compute the final size relation, we follow the method in [37]. In addition to the final size relation calculation, this approach provides an alternative method for calculating the basic reproduction number of the model (2.1). To apply the method, we first identify the vector of COVID-19 infections, i.e., . Then, we identify the vectors and of the susceptible and recovered classes, respectively, i.e., and . With this notation, the system (2.1) can now be expressed in the compact form:
| (3.3) |
where is a row vector consisting of the proportions of susceptible individuals who progress to specific infected classes upon infection, is a diagonal matrix with leading diagonal elements the relative susceptibilities of individuals in the susceptible classes, is the force of infection, i.e., , is a row vector of relative horizontal transmissions, is a transition matrix (as in the next generation matrix approach), and is vector of recovery rates. For Model (2.1), , , and is the transition matrix
By Theorem 2.1 of [37], the basic reproduction number is
and by Theorem 5.1 of [37], the basic reproduction number is given by
, and . This final size relation can be used to approximate the number of individuals who remain uninfected, and consequently the number of individuals who were infected during the pandemic.
3.2. Numerical simulation results
3.2.1. Current patterns of COVID-19 transmission
In this section, we use the parameters presented in Table 1 to simulate system (2.1) and to investigate the impact of control measures on key model outputs such as the control and effective reproduction numbers and , respectively. The basic reproduction number , and the control reproduction number computed using this baseline parameter regime in Table 1 are 1.854 () and 1.37 (), respectively. The control reproduction number corresponds to an approximately reduction in the basic reproduction number due to implemented control measures. This calls for more effective control measures to limit the spread of the disease. All simulations were carried out using the computational software MATLAB (version R2017a). When it was necessary to solve the system of ordinary differential equations (2.1) we used the inbuilt MATLAB function “”.
3.3. Impact of control measures in West Africa
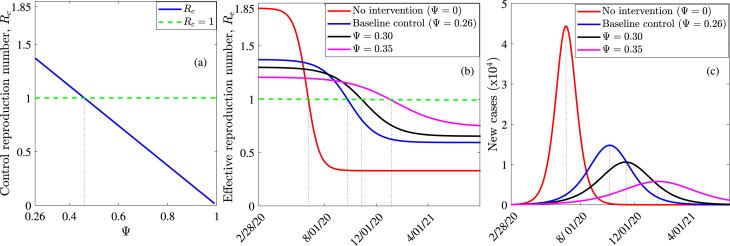
The first analysis involves evaluating the impact of the percentage reduction in the effective contact rates due to the implementation of public health control measures such as lockdowns, social distancing, the use of masks in public, washing of hands, etc., denoted by on the control and effective reproduction numbers, as well as the pandemic peak and the time to peak. Here, we fixed all the parameters at the baseline values provided in Table 1 and varied only the parameter . Changes in the control reproduction number as a function of , depicted in Fig. 3 show that about reduction in the disease transmission is required to reduce to one and possibly bring the pandemic under control. This value () corresponds to the numerical value of from Eq. (3.2) computed using the baseline parameter values from Table 1 and a increase from the baseline value of . Furthermore, our results show that there will be a reduction in the effective reproduction number by July 01, 2020 if no control measures are applied and a reduction by the same date if there is a reduction in disease transmission, i.e., an additional reduction of in (Fig. 3(b)).
Fig. 3.
Impact of control measures assessed through a reduction in the disease transmission rates on the control reproduction number, the effective reproduction number, and the epidemic peak. (a) Plot of the control reproduction number against the percentage reduction in disease transmission () showing the threshold level of required to eliminate the disease. (b) Evolution of the effective reproduction number of COVID-19 in West Africa for different values of . (c) Prediction and sensitivity of COVID-19 peak date and size to different values of . The initial conditions and parameters are presented in Table 1.
We also simulated the system (2.1) to explore the impact of public health control measures on the timing and size of the pandemic peak in West Africa (Fig. 3(c). The results of our simulations show that in the absence of any control measure that results in a reduction in the effective transmission rates, i.e., if , the COVID-19 pandemic in West Africa will peak by July , with about 44,350 people infected on the day of the peak (red curve in Fig. 3(c)). It is worth noting that this is the worst case scenario. Applying control measures at the baseline level, i.e., will bring about a reduction in the number of cases (from 44,350 in the worst case scenario to 14,780 at the baseline control measures) when the pandemic peaks and also delay the peak to October , (blue curve in Fig. 3(c)). Improved control measures resulting in and reduction in disease transmission, will lead to reductions of and , respectively, in the number of daily confirmed cases when the epidemic attains its peak (black and magenta curves in Fig. 3(c)). Thus, improved control measures that are related to reducing disease transmission have a significant effect in reducing the number of cases and flattening the epidemic curve—an outcome that will prevent the already fragile health care systems in West Africa from being overwhelmed by a high COVID-19 burden.
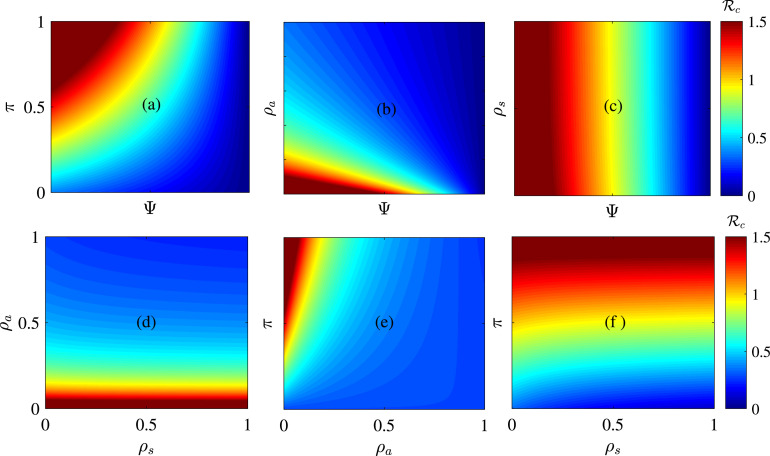
Other basic public health control measures include isolating symptomatic infectious humans and contact tracing and isolating asymptomatic humans. In our model we assume that isolating symptomatic infectious humans is at rate and contact tracing and systematic testing and isolating asymptomatic infectious humans is at rate . Heat maps were plotted to investigate the individual and combined effects of pairs of control measures such as contact tracing, isolation, and using control measures that lead to a reduction in disease transmission, e.g., lockdowns, social and physical distancing, mask use, etc., on COVID-19 in West Africa (Fig. 4). Our analyses show that the spread of the disease decreases with a higher reduction in the disease transmission rate and a decreasing proportion of exposed humans who do not develop clinical disease symptoms (i.e., become asymptomatic) after the incubation period, (Fig. 4(a)). Thus, if a higher proportion of exposed humans do not develop clinical disease symptoms after the incubation period, a higher reduction in the disease transmission rate will be required to eliminate the disease. In particular, if half of the exposed individuals develop symptoms at the end of the incubation period, i.e., , then only a reduction in the disease transmission rate is required to eliminate the disease. But, if of the exposed become asymptomatic after the incubation period, then a reduction in the disease transmission rate is required to eliminate the disease (Fig. 4(a)). The combined impact of detection and isolation of asymptomatic humans (by contact tracing or mass testing) together with a reduction in the disease transmission rate is explored in Fig. 4(b). If asymptomatic individuals are detected and isolated fast enough, e.g., within days, i.e., , then a reduction in the disease transmission rate would suffice for elimination, while if it takes a long time to detect and isolate asymptomatic individuals, e.g., within days, a reduction on the disease transmission rate is required to contain the pandemic in West Africa (Fig. 4(b)). In particular, we found out that disease elimination is possible even if detection and isolation of asymptomatic humans is not complemented with any additional measure (maintaining ). But such identification and isolation must occur in a timely manner, e.g., within days, i.e., (Fig. 4(b)). If only of humans fail to develop symptoms at the end of the incubation period, then asymptomatic humans must be identified and isolated within days for disease elimination to be possible (Fig. 4(e)). Thus, disease control is more difficult if it takes long to contact trace and isolate asymptomatic humans.
Fig. 4.
Sensitivity of COVID-19 control reproduction number , to different pairs of basic public health control measures. (a) Sensitivity of to the proportion of exposed humans who develop COVID-19 symptoms at the end of the incubation period () and the percentage reduction , in the disease transmission rate. (b) Sensitivity of to the identification and isolation rate of asymptomatic infectious humans () and . (c) Sensitivity of to the identification and isolation rate of symptomatic infectious humans () and . (d) Sensitivity of to and . (e) Sensitivity of to and . (f) Sensitivity of to and . The other parameter values are given in Table 1.
Our results also show that timely isolation of symptomatic cases is important in reducing the disease burden in West Africa but not enough as asymptomatic isolation do, although disease elimination is only possible if isolation of infectious symptomatic cases is complemented with another control measure (Fig. 4(c), (d)). In particular, if symptomatic humans are identified and isolated within days, i.e., , then a reduction in the disease transmission rate is required for disease elimination, while if it takes a long time to isolate symptomatic infectious individuals, e.g., within days (i.e., ), a reduction on the disease transmission rate is required to contain the pandemic in West Africa (Fig. 4(c)). When isolation of symptomatic infectious disease cases is complemented with identification and isolation of asymptomatic infectious cases, disease elimination is only possible through timely identification and isolation of asymptomatic cases (Fig. 4(d)). Thus, identifying and isolating asymptomatic individuals in a timely manner contributes more in curtailing the pandemic in West Africa than isolating symptomatic infectious individuals. Furthermore, if more exposed humans develop disease symptoms at the end of the incubation period and more symptomatic infectious individuals are identified and isolated in a timely manner, disease elimination is possible (Fig. 4(f)). In particular, if of exposed humans develop clinical disease symptoms at the end of the incubation period (i.e. , then symptomatic infectious humans must be isolated within days in order to eliminate the disease.
4. Discussion
Mathematical models have been useful in understanding disease-outbreaks and in informing policy aimed at curtailing such diseases in a timely manner [17], [18], [19], [23], [24], [38]. In the context of the COVID-19 pandemic that is currently spreading around the world, mathematical models have been very useful in predicting the course of the disease and in assessing the impacts of basic public health control measures[17], [18], [19], [23], [39]. In this study, we developed a mathematical model to inform the COVID-19 trend and possible course of control measures in West Africa. The model is trained with COVID-19 data from West Africa for the period from February 28, 2020 to June 26, 2020, and used to compute the reproduction number, as well as to assess the impact of basic public health control measures on the disease.
We obtained a basic reproduction number of 1.854 (CI ), which is relatively low compared to values recently reported for two West African countries—Nigeria (2.29) and Senegal (2.36) [40]. Also, a basic reproduction number of 2.083 (CI ) was reported for India in [41]. The control reproduction number obtained for West Africa was 1.37 (CI: ], which is close to the value reported for South Korea (1.5) [42] but lower than the value reported for Wuhan one week before travel restrictions were introduced (2.35) [43]. Hence, although the disease is still spreading () in West Africa, the spread is slow compared to other parts of world. This low transmission in the region can be attributed to the fact that there is limited movement of individuals within the region and between the region and the rest of the world [8]. Furthermore, the low number of confirmed cases in West Africa might result from under-reporting of cases as was the case in Peru [44]. This is supported by the growing number of asymptomatic infectious individuals observed in our study. De Leon et al. [21] observed a similar trend in Mexico, where over of the infectious population was asymptomatic [21]. In the absence of sufficient test kits in many West African countries, and with the limitations in health care facilities and personnel, identifying cases is difficult [45]. Irrespective of the current trend, the COVID-19 pandemic is still a more serious health problem in West-Africa compared to previous outbreaks like the 2014 Ebola outbreak () [46], [47] or the Lassa fever outbreak in Nigeria () [48].
Although most countries in West Africa started implementing basic control measures since March , , our simulation results indicate that improvements are necessary to control the pandemic effectively in the region. Because there is currently no safe and effective vaccine or drugs against the novel coronavirus, basic public health control measures have been used to curtail the pandemic in many parts of the world including West Africa. These measures include contact tracing, isolation, and measures that lead to a reduction in disease transmission, e.g., lockdowns, social or physical distancing, mask use, etc [17]. In the absence of such measures, the worst case scenario prediction for West Africa from our model would have recorded around 44,350 confirmed COVID-19 cases by July 01, when the epidemic peaks. This projection is lower than the 517,489- confirmed cases predicted by Achoki et al. [27] for the same West African region. The higher value in [27] might be linked to the fact that the authors used linear models and considered the rate of infection between the first and second weeks of the epidemic in countries in which the number of cases might have been overestimated. However such prediction was not true since the control measures implemented in many West African countries back in March 2020 reduced the disease transmission. In fact, we found out that basic public health control measures, especially those associated with a reduction in the disease transmission rate such as lockdowns, social distancing, and mask use have a significant effect on reducing the burden of the disease, e.g, at baseline values, control measures reduce the number of cases when the epidemic peaks in October , by about . Also, improving control measures so that an estimated reduction in the disease transmission is attained, will reduce the number of confirmed cases when the epidemic attains its peak by approximately and shift the peak date to November , . Such interventions are useful in reducing the disease spread and ensuring that the already limited and fragile health care systems are not overwhelmed by the COVID-19 burden [19].
Studies have shown that asymptomatic, i.e., pre-symptomatic and asymptomatic infectious individuals and symptomatic individuals contribute in COVID-19 transmission. Asymptomatic cases might contribute more in disease spread since they are not even aware of the fact that they are infected with COVID-19. For example, on the Diamond Princess, % of all infections were due to asymptomatic individuals [49]. Similarly, the proportion of pre-symptomatic transmission varied between % and % in a study in Singapore and in Tianjin (China) [50]. Although, we do not have any documented information on COVID-19 spread by pre-symptomatic and asymptomatic infectious individuals in West Africa, we believe these groups contribute more in COVID-19 transmission in West Africa. Our parameter estimation confirms the fact that asymptomatic transmission in the region is higher than symptomatic transmission—a result that is consistent with recent findings in [39]. It is also worth mentioning that many symptomatic cases might not be identified in the region, especially if they do not seek medical attention [51] or if they prefer alternative traditional medicine—a common practice in the region [13]. Our results suggest that early identification and isolation of both symptomatic and asymptomatic infectious individuals is an important step towards curtailing the burden of the pandemic. In particular, identifying and isolating asymptomatic individuals early enough, e.g., within 5–6 days after the end of the incubation period can result in a significant reduction in disease burden, even without any other control measure. The same is not true with identifying and isolating symptomatic individuals or when it takes a longer time to identify and isolate infectious asymptomatic individuals. In this case, the measure must be complemented with another measure that involves a reduction in the disease transmission rate in order to achieve a significant reduction in disease burden. Asymptomatic infectious individuals can be identified through contact-tracing and diagnostic RT-PCR testing. However, since mass testing in most West African countries only started during the last week of April, the primary way in which asymptomatic individuals were identified in West Africa before the start of mass testing was through contact tracing and then testing the contacts suspected to have the virus. One way in which contact tracing has been used successfully to identify and isolate both pre-symptomatic and asymptomatic infectious individuals is through mobile phone applications, see for example, Ferretti et al. [52]. We showed that a higher reduction in the disease transmission rate, e.g., through social distancing or using masks will be required to eliminate the disease if a higher proportion of exposed humans do not develop clinical disease symptoms after the incubation period. These results highlight the importance of early identification of disease cases and are consistent with the results of previous studies on Ebola virus and Lassa Fever virus in West Africa [47], [53]. The results are also consistent with those of a study by Hellewell et al. [54] on Covid-19, who used simulated data to illustrate that contact tracing and isolation is highly effective in controlling the pandemic and can lead to disease elimination within 3 months. Similarly, studies on COVID-19 by Ngonghala et al. [39] for three US states and the entire US and Gupta et al. [41] for India suggest that increased detection through testing can reduce the burden of the disease. Although, contact tracing is already being implemented in West Africa, the measure is not very effective due to the lack of resources and high community transmission in the region. For example, as of June 26, 2020, almost all the reported cases in the region resulted from community transmission [5]. Therefore increased compliance with measures like social distancing and mask use is very important for the region.
Since the disease can be transmitted from one human to the other through droplets from infected individuals that can travel though a few meters in air [23], [55], using masks and social distancing are very important in the fight against the pandemic. Masks are useful in reducing the risk of both uninfected individuals wearing them from contracting the virus and infected individuals wearing masks from spreading the virus to others [17], [23]. It is worth mentioning that the efficacy of N95 masks is about (), while the efficacy of surgical and cloth are () and (), respectively [23]. A study in US [23] suggested that the higher the number of infected asymptomatic people in a population, the more beneficial the use of masks by the general public. Both mask-use and social distancing are ongoing in many West African countries. However, the effectiveness of these measures in reducing the spread of the virus is linked to the extent to which they are applied, the compliance level by the public, and how long they will last [17], [21]. Our analyses show that COVID-19 can be reduced significantly in West Africa through social distancing and using masks if about of the population complies with these measures. This is consistent with recent results in [17], [23], [56], where strict compliance with social distancing and mask use can lead to a significant reduction disease burden. Some West African countries, e.g., Benin have implemented measures involving isolating some densely populated portions of the country, especially overcrowded urban areas with dilapidated sanitary facilities and limited basic amenities like clean water [28]. This has a positive effect on reducing the spread of the virus.
Finally, our study suggests that mass application of control measures coupled with appropriate testing and timely isolation of asymptomatic humans will go a long way in keeping disease numbers low, which is consistent with results in [41]. However, with the fragile economic conditions and health care systems in the region, interventions like complete lock-down as was there in some European countries, most US states, and China for a couple of months is not feasible [40] and can be more catastrophic than the disease itself. Therefore, the choice of interventions by public policy makers in the region should aim at balancing the prevention of the epidemic with the need for maintaining livelihoods and social cohesion.
5. Conclusion
Our study confirms the fact that the novel coronavirus (COVID-19) is highly contagious and that infectious humans who do not show clinical disease symptoms (asymptomatic or unreported cases) contribute significantly in disease transmission. This study also indicates that early identification of these unreported cases through contact tracing or systematic testing on target groups, and then isolating individuals who test positive plays a significant role in diminishing the burden of COVID-19 in West Africa. Furthermore, this study suggests that social distancing measures such as stay-at-home orders, closing educational institutions, limiting mass gatherings, etc., and using masks can reduce the spread of the disease significantly, with the possibility of disease-elimination if about one in every two people in West Africa respect these control measures. To enhance, the study shows that implementing more than one measure at the same time is better for disease control, and that under current control measures, the disease might not be disappearing from the region any time soon, unless there are improvements in these control measures. We conclude that systematic testing on target group, contact tracing and isolation of confirmed disease cases, as well as improvements to the other existing basic public health measures (e.g., social distancing and mask use) in the region, are required to better manage the pandemic. Due to uncertainties and disparities between the economies and health care systems of countries within the region, we conclude that country-level studies are necessary and will provide more insights into disease dynamics and control in the region.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
HBT acknowledges the support of the Graduate Research Assistantships in Developing Countries (GRAID) Program from the International Mathematical Union (IMU), USA. KVS acknowledges the support of the Wallonie-Bruxelles International Post-doctoral Fellowship for Excellence, Belgium (Fellowship # SUB/2019/443681). CNN acknowledges the support of the Simons Foundation, USA (Award #627346). RGK acknowledges the support from the Alexander von Humboldt Foundation, Germany. The Authors acknowledge assistance from Sacla Edmond, Kotanmy Brezesky, and Agbovoedo Robert for collecting the initial data used for the project.
References
- 1.World Health Organization . 2020. Coronavirus disease (COVID-19) technical guidance, WHO. https://www.who.int/emergencies/diseases/novel-coronavirus-2019/technical-guidance. (Accessed 4 March 2020) [Google Scholar]
- 2.World Health Organization . 2020. Emergencies, preparedness, response. Pneumonia of unknown origin – China, disease outbreak news. https://www.who.int/csr/don/05-january-2020-pneumonia-of-unkown-cause-china/en/. (Accessed 5 March 2020) [Google Scholar]
- 3.Li Q., Guan X., Wu P., Wang X., Zhou L., Tong Y., Ren R., Leung K.S., Lau E.H., Wong J.Y. Early transmission dynamics in wuhan, china, of novel coronavirus–infected pneumonia. New Engl. J. Med. 2020 doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Dong E., Du H., Gardner L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 2020 doi: 10.1016/S1473-3099(20)30120-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.World Health Organization . 2020. Coronavirus disease (COVID-2019) situation reports 159, WHO. https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200627-covid-19-sitrep-159.pdf?sfvrsn=93e027f6_2 (Accessed 27 June 2020) [Google Scholar]
- 6.Center for Disease Control Prevention, Coronavirus disease 2019 (COVID-19), National Center for Immunization and Respiratory Diseases (NCIRD), Division of Viral Diseases, 2020. https://www.cdc.gov/coronavirus/2019-ncov/index.html. (Accessed 4 March 2020).
- 7.Worldometer . 2020. Coronavirus data. https://www.worldometers.info/coronavirus/#countries (Accessed 27 March 2020) [Google Scholar]
- 8.Africa Center for Strategic Studies . 2020. Mapping risk factors for the spread of COVID-19 in africa. https://africacenter.org/spotlight/mapping-risk-factors-spread-covid-19-africa/. (Accessed 9 April 2020) [Google Scholar]
- 9.Martinez-Alvarez M., Jarde A., Usuf E., Brotherton H., Bittaye M., Samateh A.L., Antonio M., Vives-Tomas J., D’Alessandro U., Roca A. 2020. COVID-19 pandemic in west africa. lancet glob health. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bai Y., Yao L., Wei T., Tian F., Jin D.-Y., Chen L., Wang M. Presumed asymptomatic carrier transmission of covid-19. JAMA. 2020;323(14):1406–1407. doi: 10.1001/jama.2020.2565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lai C.C., Shih T.P., Ko W.C., Tang H.J., Hsueh P.R. Severe acute respiratory syndrome coronavirus 2(SARS-CoV-2) and corona virus disease-2019 (COVID-19): the epidemic and the challenges. Int. J. Antimicro. Ag. 2020 doi: 10.1016/j.ijantimicag.2020.105924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.World Health Organization (WHO) 2020. Global health observatory data. https://apps.who.int/gho/data/node.main.HWFGRP_0020?lang=en. (Accessed 10 April 2020) [Google Scholar]
- 13.West African Health Organization, West African Herbal Pharmacopoeia. Kumasi, Ghana, 2013, 260 pages.
- 14.World Health Organization, et al. Global Spending on Health: A World in Transition. WHO/HIS/HGF/HFWorkingPaper/19.4, 2019.
- 15.World Health Organization (WHO), Health Situation Analysis in the African Region: Atlas of Health Statistics, 2011, 2011.
- 16.Prescott J.B., Marzi A., Safronetz D., Robertson S.J., Feldmann H., Best S.M. Immunobiology of Ebola and Lassa virus infections. Nat. Rev. Immunol. 2017;17(3):195–207. doi: 10.1038/nri.2016.138. [DOI] [PubMed] [Google Scholar]
- 17.Ngonghala C.N., Iboi E., Eikenberry S., Scotch M., MacIntyre C.R., Bonds M.H., Gumel A.B. Mathematical assessment of the impact of non-pharmaceutical interventions on curtailing the 2019 novel coronavirus. Math. Biosci. 2020 doi: 10.1016/j.mbs.2020.108364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ferguson N., Laydon D., Nedjati G.G., Imai N., Ainslie K., Baguelin M., Bhatia S., Boonyasiri Z.U.L.M.A., Cucunuba Perez G., Cuomo-Dannenburg A., Dighe A. 2020. Report 9: Impact of non-pharmaceutical interventions (NPIs) to reduce COVID19 mortality and healthcare demand. [DOI] [Google Scholar]
- 19.Anderson R.M., Heesterbeek H., Klinkenberg D., Hollingsworth T.D. How will country-based mitigation measures influence the course of the COVID 19 epidemic? Lancet. 2020;395(10228):931–934. doi: 10.1016/S0140-6736(20)30567-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhou X., Ma X., Hong N., Su L., Ma Y., He J., Jiang H., Liu C., Shan G., Zhu W. Forecasting the worldwide spread of COVID-19 based on logistic model and SEIR model. medRxiv. 2020 doi: 10.1101/2020.03.26.20044289. [DOI] [Google Scholar]
- 21.De Leon U.A.P., Perez A.G., Avila-Vales E. 2020. A data driven analysis and forecast of an SEIARD epidemic model for COVID-19 in Mexico. arXiv, arXiv:2004.08288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Roda W.C., Varughese M.B., Han D., Li M.Y. Why is it difficult to accurately predict the COVID-19 epidemic? Infect. Dis. Model. 2020 doi: 10.1016/j.idm.2020.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Eikenberry S.E., Mancuso M., Iboi E., Phan T., Eikenberry K., Kuang Y., Kostelich E., Gumel A.B. To mask or not to mask: Modeling the potential for face mask use by the general public to curtail the COVID-19 pandemic. Infect. Dis. Model. 2020;2020 doi: 10.1016/j.idm.2020.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.COVID I., Murray C.J. Forecasting the impact of the first wave of the COVID-19 pandemic on hospital demand and deaths for the USA and european economic area countries. medRxiv. 2020 https://www.medrxiv.org/content/10.1101/2020.04.21.20074732v1.full.pdf. [Google Scholar]
- 25.Otitoloju A.A., Okafor I.P., Fasona M., Bawa-Allah K.A., Isanbor C., Onyeka C.S., Folarin O.S., Adubi T.O., Sogbanmu T.O., Ogbeibu A.E. COVID-19 pandemic: examining the faces of spatial differences in the morbidity and mortality in sub-Saharan Africa, Europe and USA. medRxiv. 2020 doi: 10.1101/2020.04.20.20072322. [DOI] [Google Scholar]
- 26.Adegboye O., Adekunle A.I., Gayawan E. Novel coronavirus in Nigeria: Epidemiological analysis of the first 45 days of the pandemic. medRxiv. 2020 doi: 10.1101/2020.04.14.20064949. [DOI] [Google Scholar]
- 27.Achoki T., Alam U., Were L., Gebremedhin T., Senkubuge F., Lesego A., Lius S., Wamai R., Kinfu Y. COVID-19pandemic in the african continent: forecasts of cumulative cases, new infections, and mortality. medRxiv. 2020 doi: 10.1101/2020.04.09.20059154. [DOI] [Google Scholar]
- 28.Worldometers, Population data. https://www.worldometers.info/world-population/western-africa-population/ (Accessed 8 April 2020).
- 29.World Bank, World Bank national accounts data and OECD National Accounts data files https://data.worldbank.org/indicator/NY.GDP.PCAP.CD?most_recent_value_desc=fals. (Accessed 10 April 2020).
- 30.Roser M., Ritchie H., Ortiz-Ospina E., Hasell J. Coronavirus pandemic (COVID-19), our world in data. 2020. https://ourworldindata.org/global-rise-of-education
- 31.Hu Z., Song C., Xu C., Jin G., Chen Y., Xu X., Ma H., Chen W., Lin Y., Zheng Y., Wang J. Clinical characteristics of 24 asymptomatic infections with COVID-19 screened amongclose contacts in nanjing. China. Sci. China Life Sci. 2020;63(5):706–711. doi: 10.1007/s11427-020-1661-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.N.M. Ferguson, D. Laydon, G. Nedjati-Gilani, N. Imai, K. Ainslie, M. Baguelin, S. Bhatia, A. Boonyasiri, Z. Cucunuba, G. Cuomo-Dannenburg, et al. Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand, London: Imperial College COVID-19 Response Team, March 16, 2020.
- 33.Lauer S.A., Grantz K.H., Bi Q., Jones F.K., Zheng Q., Meredith H.R., Azman A.S., Reich N.G., Lessler J. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: Estimation and application. Ann. Intern. Med. 2020;172(9):577–582. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Day M. Covid-19: four fifths of cases are asymptomatic, China figures indicate. Br. Med. J. 2020;369:m1375. doi: 10.1136/bmj.m1375. [DOI] [PubMed] [Google Scholar]
- 35.Van den Driessche P., Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002;180(1–2):29–48. doi: 10.1016/S0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
- 36.Dieckmann U., Metz J., Sabelis M., K. Sigmund K. Pursuit of Virulence Management. C.U.P; New York: 2005. Adaptive dynamics of infectious diseases. [Google Scholar]
- 37.Arino J., Brauer F., Van Den Driessche P., Watmough J., Wu J. A final size relation for epidemic models. Math. Biosci. Eng. 2007;4(2):159. doi: 10.3934/mbe.2007.4.159. [DOI] [PubMed] [Google Scholar]
- 38.Lipsitch M., Cohen T., Cooper B., Robins J.M., Ma S., James L., G.Gopalakrishna A.S., Chew S.K., Tan C.C., Samore M.H., Fisman D. Transmission dynamics and control of severe acute respiratory syndrome. Science. 2003;300(5627):1966–1970. doi: 10.1126/science.1086616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ngonghala C.N., Iboi E.A., Gumel A.B. Could masks curtail the post-lockdown resurgence of COVID-19 in the US? medRxiv. 2020 doi: 10.1016/j.mbs.2020.108452. https://www.medrxiv.org/content/10.1101/2020.07.05.20146951v3.full.pdf. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhao Z., Li X., Liu F., Zhu G., Ma C., Wang L. Prediction of the COVID-19 spread in african countries and implications for prevention and controls: A case study in South Africa, Egypt, Algeria, Nigeria, Senegal and Kenya. Sci. Total Environ. 2020 doi: 10.1016/j.scitotenv.2020.138959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gupta M., Mohanta S.S., Rao A., Parameswaran G.G., Agarwal M., Arora M., Mazumder A., Lohiya A., Behera P., Bansal A., Kumar R., Meena V.P., Tiwari P., Mohan A., Bhatnagar S. Transmission dynamics of the COVID-19 epidemic in India and modelling optimal lockdown exit strategies. medRxiv. 2020 doi: 10.1101/2020.05.13.20096826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Shim E., Tariq A., Choi W., Lee Y., Chowell M., G M. Transmission potential and severity of COVID-19 in South Korea. Int. J. Infect. Dis. 2020 doi: 10.1016/j.ijid.2020.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kucharski A.J., Russell T.W., Diamond C., Liu Y., Edmunds J., Funk S., Eggo R.M., Davies N. Early dynamicsof transmission and control of COVID-19: a mathematical modelling study. Lancet. Infect. Dis. 2020 doi: 10.1016/S1473-3099(20)30144-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Machicao J.C. 2020. Monitoring the covid-19 pandemic in peru with highly uncertain data. gestio din amica lima, peru. Published April 14th, 2020. https://www.researchgate.net/profile/Jose_Machicao/publication/340644468_Monitoring_the_Covid-19_pandemic_in_Peru_with_highly_uncertain_data/links/5e967be3a6fdcca789189e0c/Monitoring-the-Covid-19-pandemic-in-Peru-with-highly-uncertain-data.pdf. [Google Scholar]
- 45.Paintsil E. COVID-19 threatens health systems in sub-saharan africa: the eye of the crocodile. J. Clin. Invest. 2020 doi: 10.1172/JCI138493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Althaus C.L. Estimating the reproduction number of Ebola virus (EBOV) during the 2014 outbreak in west africa. PLoS Curr. 2014;6 doi: 10.1371/currents.outbreaks.91afb5e0f279e7f29e7056095255b288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Dénes A., Gumel A.B. Modeling the impact of quarantine during an outbreak of ebola virus disease. Infect. Dis. Model. 2019;4:12–27. doi: 10.1016/j.idm.2019.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Zhao S., Musa S.S., Fu H., He D., Qin J. Large-scale lassa fever outbreaks in Nigeria: quantifying the association between disease reproduction number and local rainfall. Epidemiol. Infect. 2020;148 doi: 10.1017/S0950268819002267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Emery J.C., Russel T.W., Liu Y., Hellewell J., Pearson C.A., Knight G.M., Eggo R.M., Kucharski A., Funk S., Flasche S., Houben R.M.G.J. The contribution of asymptomatic SARS-CoV-2 infections to transmission-a model-based analysis of the diamond princess outbreak. medRxiv. 2020 doi: 10.1101/2020.05.07.20093849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ganyani T., Kremer C., Chen D., Torneri A., Faes C., Wallinga J., Hens N. Estimating the generation interval for COVID-19 based on symptom onset data. Eurosurveillance. 2020;25(17):2000257. doi: 10.2807/1560-7917.ES.2020.25.17.2000257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Nishiura H., Kobayashi T., Yang Y., Hayashi K., Miyama T., Kinoshita R. The rate of underascertainment of novel coronavirus (2019-nCoV) infection: estimation using japanese passengers data on evacuation flights. J. Clin. Med. 2020;9(2) doi: 10.3390/jcm9020419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ferretti L., Wymant C., Kendall M., Zhao L., Nurtay A., Abeler-Dörner L., Parker M., Bonsall D., Fraser C. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science. 2020;368(6491) doi: 10.1126/science.abb6936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Obabiyi O.S., Onifade A.A. Mathematical model for lassa fever transmission dynamics with variable human and reservoir population. Int. J. Differ. 2017;16(1):67–91. doi: 10.12732/ijdea.v16i1.4703. [DOI] [Google Scholar]
- 54.Hellewell J., Abbott S., Gimma A., Bosse N.I., Jarvis C.I., Russell T.W., Munday J.D., Kucharski A.J., Edmunds W.J., Sun F., Flasche S. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob. Health. 2020;8(4):488–496. doi: 10.1016/S2214-109X(20)30074-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Morawska L., Cao J. Airborne transmission of SARS-CoV-2: the world should face the reality. Environ. Int. 2020 doi: 10.1016/j.envint.2020.105730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Chang S.L., Harding N., Zachreson C., Cliff O.M., Prokopenko M. 2020. Modelling transmission and control of the COVID-19 pandemic in Australia. arXiv arXiv:2003.10218. [DOI] [PMC free article] [PubMed] [Google Scholar]