Spatio-temporal simulation of the novel coronavirus (COVID-19) outbreak using the agent-based modeling approach (case study: Urmia, Iran)

Abstract

The ongoing outbreak of the COVID-19 as the current global concern threatens lives of many people around the world. COVID-19 is highly contagious so that it has infected more than 1,848,439 people until April 14, 2020 and killed more than 117,217 people. The main aim of this study is to develop an agent-based model (ABM) that simulates the spatio-temporal outbreak of COVID-19. The main innovation of this research is investigating the impacts of various strategies of school and educational center closures, heeding social distancing, and office closures on controlling the COVID-19 outbreak in Urmia city, Iran. In this research, the outbreak of COVID-19 disease was simulated with the help of ABM so that all agents considered in the ABM along with their attributes and behaviors as well as the environment of the ABM were described. Besides, the transmission of COVID-19 between human agents was simulated based on the SEIRD model, and finally, all control strategies applied in Urmia city along with corresponding actions of each control strategy were implemented in the ABM. The results of the ABM indicated that school and educational center closures in Urmia city, reduced the number of infected people by 4.96% each week on average and 49.61% in total from February 21 until May 10. Heeding social distancing by 30% and 70% of people of Urmia city from March 27, led to decrease the number of infected people by 5.24% and 10.07% each week, on average and 31.46% and 60.44% in total, respectively, and if 30% and 70% of civil servants of Urmia city did not go to work, the number of infected people would be decreased by 3.30% and 5.25% each week, on average and 32.98% and 52.48% in total from February 21 until May 10, respectively. As a result of this research, heeding social distancing by the majority of people is recommended for Urmia city in the current situation. The main advantages of disease modeling are to investigate how the disease is likely to evolve amongst the population of society and also assess the impacts of control strategies on controlling the outbreak of disease.

1. Introduction

COVID-19 is a member of Betacoronaviruses like the Severe Acute Respiratory Syndrome Human coronavirus (SARS HCoV) and the Middle-East Respiratory Syndrome Human coronavirus (MERS HCoV) [1]. Preliminary results of Chinese patients indicated that although the mortality rate of COVID-19 is lower than the SARS-HCoV (10%) and the MERS-HCoV (37%), it seems that the COVID-19 is severely contagious [2,3] so that its spread increases rapidly (exponentially and logarithmic) [4,5]. Although, many efforts have been made to produce the vaccine of COVID-19, no successful vaccine or antiviral drug for the novel coronavirus has been clinically confirmed.

A newly emerged human coronavirus (COVID-19) for the first time was reported in December 2019 in Wuhan, China [6,7]. Since the beginning of the COVID-19 outbreak until April 14, 1,848,439 people throughout the world have been infected with the COVID-19, of which 117,217 have died [8,9]. Following the epidemic of COVID-19 in different parts of the world, its epidemic was officially confirmed on February 19, 2010, in Iran [5] so that in mid-February, Iran became the second focal point of COVID-19 in the world after China. According to the world health organization (WHO), until April 14, 74,877 cases have been identified in the country, of which 4683 (6.25%) have died [8,9]. In addition, Iran has had the highest number of deaths due to COVID-19 after the United States, Italy, Spain, France, and the United Kingdom [8,9].

Nowadays, although various precautions and control strategies have been taken throughout the world, the ongoing outbreak of COVID-19 is the major challenge that many countries confront as well as Iran [10,11]. In that way, since the identification of the first case of COVID-19 in Iran, numerous proceedings and strategies have been implemented in order to control the COVID-19 outbreak that include: closing schools, universities, all educational centers, cinemas, concerts, theaters, national competitions, and sports leagues, as well as implementing the social distancing plan throughout the country.

Evaluations of the impacts of such control strategies as well as predictions of the future outbreak of COVID-19 can play important roles in controlling the COVID-19 outbreak [4,12]. Traditional decision-making methods generally use the experience of experts to estimate the efficiency of applied strategies. However, an assessment of COVID-19 with novel approaches is essential to the global debate [13]. Although accurate evaluation of the efficiency of strategies is determined over time, in modern management methods, experts' opinions can be combined with new methods of modeling in order to have a better prediction of future conditions and impacts of control strategies [14]. Therefore, the simulation of the COVID-19 outbreak as well as investigating the effects of diverse strategies on controlling its outbreak have attracted the interests of many scientists and researchers recently.

It is obvious that the exact simulation of phenomena is impossible due to their complexities and detail; therefore, in order to simulate phenomena, lots of simplifications must be considered in the model [14,15]. On the other hand, due to the ambiguity of the new emerged COVID-19 disease, the way it spreads, its complexity, as well as all other unknown characteristics of the COVID-19 disease [16,17], the simulated model must be flexible and capable to dynamically take into account the new information obtained.

Computational models are effective and robust tools in simulating complex and dynamics phenomena [15,18]. In addition, spatial analyses are of great help in understanding the spread of contagious diseases and are the key to the spatial spread during the early stages of the COVID-19 pandemic [12,19]. There are several computational models for simulating dynamics phenomena of which the agent-based model (ABM) is one of the most popular and widely used models that is able to be integrated with geospatial information science (GIS) and consequently, spatial modeling of phenomena, as well [15]. On the other hand, ABMs are models, in which it is possible to examine and analyze different strategies, optimize decision-making, and ultimately reduce losses. These models can be a powerful tool in simulating operations and strategic management. ABMs can be used to find optimal strategies in large-scale incidents and to manage the situation. In addition, the use of ABMs regarding their flexibility and bottom-up structure, allows decision-makers to combine space and time [20].

There are three epidemiological modeling approaches including the ordinary differential equation (ODE) model [[21], [22], [23], [24], [25]], cellular automata (CA) model [26,27], and ABM [15,[28], [29], [30], [31], [32]]. ODE models simulate phenomena by greatly simplifying them. These models do not take into account the heterogeneity of the population and assumed the population mixed. Although CA models are capable of overcoming the heterogeneity of the population, the movements and interactions of people are not considered in CA models, as well. Despite ODE and CA models, ABM has high ability and flexibility in simulating the interactions among individuals as well as the movements of individuals [15] that the outbreak of the COVID-19 is highly dependent on these two parameters. ABM has been used in simulating the spread of many diseases including COVID-19 [[33], [34], [35], [36], [37], [38], [39]], malaria [15], Cutaneous Leishmaniasis [32], smallpox [40], tuberculosis [41], hepatitis A [28], avian influenza [30], measles [29], mumps [31] and its effectiveness has been proven.

In the field of COVID-19 disease, most research has examined clinical and epidemiological features of COVID-19, whereas spatio-temporal modeling of COVID-19 has been performed just in limited research. Kang et al. [19] described the spatio-temporal pattern and also measured the spatial association of the early stages of the COVID-19 epidemic in the mainland, China. They explored the spatial epidemic dynamics of COVID-19 by Moran's I spatial statistic with various definitions of neighbors. They revealed that with the exception of medical-care-based connection models, a significant spatial association of COVID- 19 infections were indicated in most of the models. Guliyev [42] utilized spatial panel data models to investigate the propagation power and effects of the COVID-19 disease, examine the factors affecting COVID-19 along with the spatial effects, as well as determine the relationship among the variables including their spatial effects. Chatterjee et al. [12] created an early stochastic mathematical simulation approach of the COVID-19 epidemic in India with the objective of determining its magnitude, assessing the impact on health care resources, and studying the effect of certain Non-Pharmacological Interventions (NPI) on the epidemic. The results of their research indicated that the epidemic is likely to cross 3 million cases by May 25, 2020, and overwhelm the available healthcare resources. Liang [43] compared the spread rules of the COVID-19, SARS, and MERS with the help of the mathematical model. They established their propagation growth model by considering the growth rate as well as the inhibition constant of infectious diseases. The results of their research indicated that the growth rate of COVID-19 is approximately twice that of the SARS and MERS. Prem et al. [44] simulated the ongoing trajectory of the COVID-19 outbreak in Wuhan with the help of an age-structured susceptible-exposed-infected-removed (SEIR) model for several physical distancing measures. They estimated the impacts of physical distancing measures on the COVID-19 epidemic progression using synthetic location-specific contact patterns and adapting them in the presence of school closures, extended workplace closures, and a reduction in mixing in the general community. Their results indicated that physical distancing measures were most effective so that it is able to reduce the median number of infections by more than 92% and 24% in mid-2020 and end-2020.

From a modeling viewpoint, although ODE models have been utilized in simulating of COVID-19 outbreak in some research (e.g. Ref. [24,25,45]), ABMs have been utilized in the majority of research. Cuevas [35] evaluated the transmission risks of COVID-19 in facilities with the help of an ABM. Chang et al. [34] compared the impacts of several intervention strategies, including restrictions on international air travel, case isolation, home quarantine, social distancing with varying levels of compliance, and school closures in an ABM in Australia. In order to estimate the virus spreading in the closed built environment, D'Orazio et al. [36] provided an ABM which adopts a probabilistic approach to jointly simulate occupants’ movement and virus transmission according to proximity-based and exposure-time-based rules. Kai et al. [38] investigated the impact of universal face mask-wearing upon the spread of COVID-19 once by employing a stochastic dynamic network-based compartmental SEIR (susceptible-exposed-infectious-recovered) approach, and the other time by employing individual ABM. Bouchnita and Jebrane [33] designed a multi-scale ABM that simulates the transmission of COVID-19 by considering the motion of individual agents with the help of a social force model. German et al. [37] presented two commonly used epidemiological models of extended SEIR models formulated both as System Dynamics and Agent-Based Simulation in order to study the disease dynamics of the COVID-19. Kerr et al. [39] developed an open-source model entitled COVASIM (COVID-19 Agent-based Simulator) in order to explore the epidemic trends, estimate resource needs, and investigate the impacts of interventions including non-pharmaceutical interventions, such as physical distancing, hygiene measures, and protective equipment; and testing interventions, such as symptomatic and asymptomatic testing, isolation, contact tracing, and quarantine. As aforementioned, although there are various studies on the use of ABM to simulate COVID-19 outbreak, the impacts of three strategies of school and educational center closures, heeding social distancing, and office closures on controlling COVID-19 outbreak have not been yet investigated using a spatio-temporal agent-based model that constructs the main innovation of this research. In addition, there are several highlights in this research included as following:

• •The environment of the ABM is made up of a variety of spatial data so that humans' movements as well as interactions were performed in a similar way to reality.
• •The number of human agents created as well as the process of distributing human agents were performed with regard to the demographic condition of Urmia city.
• •Human agents were discriminated based on their occupations as well as whether having vehicles or using public transportations so that their movements and interactions were affected by these parameters.
• •The Susceptible-Exposed-Infected-Recovered-Dead (SEIRD) model was used to simulate the transmission of COVID-19 among human agents.
• •All strategies applied in the study area along with their exact dates were considered in the ABM.

The organization of this paper is as follows: materials and methods are described in section 2. In that way, first, the study area is introduced, then, the spatial dataset used in this research are described, and finally, the proposed ABM for modeling the outbreak of COVID-19 is explained in detail. In section 3, the outputs of the ABM and also the evaluation of the ABM are presented. In addition, applying three control strategies of school and educational center closures, heeding social distancing, and office closures are completely explained and their impacts on controlling the COVID-19 outbreak are explicitly discussed, and finally, in section 4, the conclusions of this research are presented.

2. Materials and methods

2.1. Study area

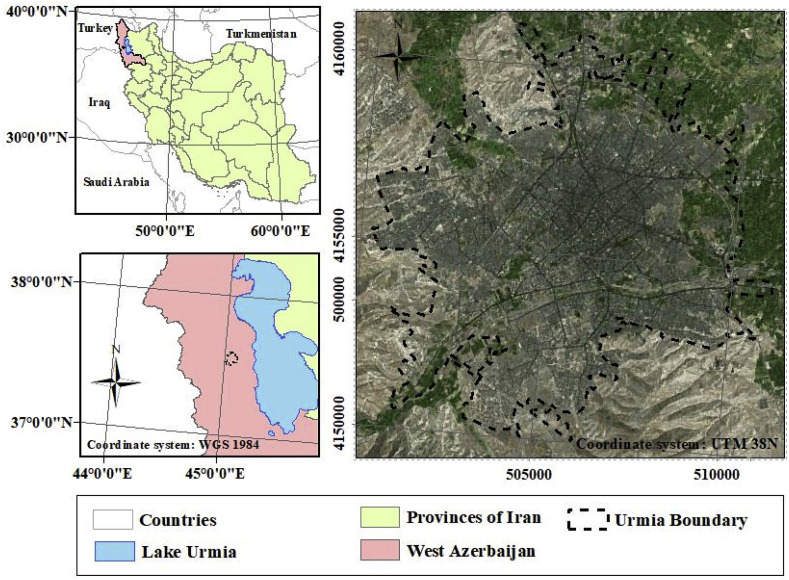
The city of Urmia, one of the metropolises of Iran and the capital of West Azerbaijan province, is located in northwestern of Iran. According to the 2017 census, it is the tenth-most populous city in Iran and the second-most populous city in the northwestern region of Iran with a population of 750,805. The city of Urmia is known as the city with the first modern hospital, the first medical training center, and the second-most crowded (high traffic) city in Iran. Although the present study is capable of implementation for different cities, Urmia city due to the existence and also the availability of its daily data on the number of infected cases was chosen as the study area (Fig. 1 ).

Fig. 1.

The geographical location of Urmia city in West Azerbaijan province, Iran (Study area).

2.2. Spatial data used

The spread of the COVID-19 disease is highly dependent on people's movements as well as their interactions with each other. Regarding this fact, the locations of people are immensely important and must be correctly determined in the simulation. Therefore, in order to dynamics simulation of the COVID-19 outbreak, the actual geographical data of the study area is required. The combination of ABM with GIS allows agents to be situated in their actual geographic locations. In addition, this integration improves the ABMs' ability to correctly simulate agents' behaviors, movements, as well as interactions.

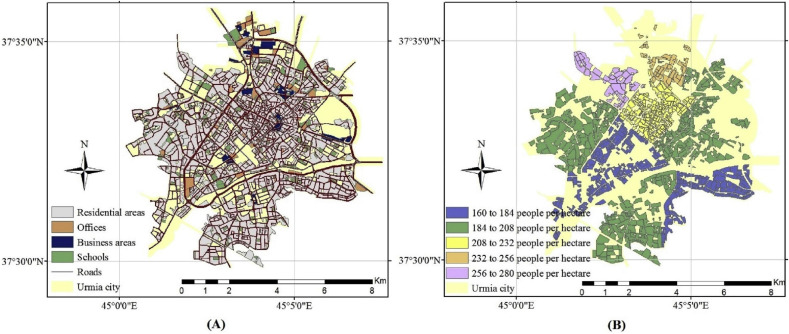
In this research, the spatial data utilized consist of residential areas, offices, business areas, schools, roads, as well as the boundary of Urmia city (Fig. 2 A), and the population density of residential areas (Fig. 2B). These spatial data together provide the environment of the proposed ABM in this study (see section 2.3.1).

Fig. 2.

All spatial data used in this research: residential areas, offices, business areas, schools, roads, and the boundary of Urmia city (A), and the population density of residential areas (B).

2.3. The proposed agent-based model

Agent-based modeling, as a widely used computational modeling approach, is a successful approach in simulating the simultaneous operations and interactions of multiple individual actors (agents), in order to recreate and predict the appearance of complex phenomena [15]. Simulation of phenomena with the help of an ABM is performed by creating the environment and agents, assigning attributes, distributing of agents, and also modeling agents' interactions with each other as well as with the environment.

An ABM is made up of two main components of the environment and a group of agents situated within the environment [46]. Agents can be representations of any type of autonomous entity such as people, insects, and etc. The environment is also an important contributor to ABMs that involves a set of cells on which agents are situated (more detail about ABMs can be found in Crooks and Heppenstall [46]). In the remainder of this section, the environment of the proposed ABM will be explicitly described as well as the agents considered.

2.3.1. The environment of the ABM

As it is obvious, the outbreak of a contagious disease such as COVID-19 highly depends on the location of the people as well as their movements. For this reason, the environment of the ABM should encompass the spatial data concerned with people's residential places as well as the places where people are likely to move. Therefore, the environment of the proposed ABM encompasses all constructed areas related to either people's occupations or their living places. The environment of the proposed ABM includes residential areas, schools, offices, and business areas. Besides, the outbreak of contagious disease, particularly COVID-19 is so likely in the areas with a high number of population; therefore, the environment of our ABM also involves the population density of residential areas. Moreover, the movements of people are performed through the roads. All in all, the environment of ABM involves the boundary of Urmia city, residential areas, schools, offices, business areas, the population density of residential areas, and roads.

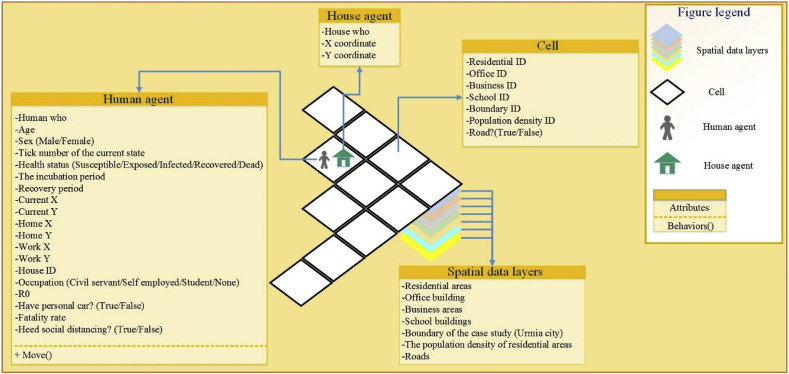
For cells of the ABM's environment, an attribute was defined with regard to each spatial data and its value was correspondingly initialized according to the spatial data layers. In Fig. 3 , the components of the proposed ABM along with their all detail are shown.

Fig. 3.

The component of the proposed ABM along with their detail.

2.3.2. Agents of the ABM

COVID-19 is transmitted directly from the infected person to uninfected person and so far there is not any document which demonstrates other alternative hosts like alive animals play a role in the transmission of COVID-19; therefore, in the simulation of COIVD-19 outbreak, only humans were considered as mobile agents so that each one represents one person in the real world. Even though house agents also were considered in our ABM, they were taken into account static and just utilized in the distribution of human agents (see section 2.3.2.1). Two types of agents were considered in our ABM: mobile and static; mobile agents can move throughout the environment and their locations can change, whereas, static agents can not move and their locations are constant during the simulation. Regarding the issue of COVID-19 outbreak as well as the most important parameters affecting the outbreak of the COVID-19, several attributes as well as behaviors were taken into account for human agents that all of those were shown in Fig. 3. In the remainder of this section, the process of human agents’ distribution, as well as their movements are completely described.

2.3.2.1. Distribution of human agents

In Urmia city, since the number of households along with the number of their members are known (Table 1 ), human agents were distributed as groups (households). In this model, it was assumed that one house was assigned to each household. Therefore, first, house agents were created by the number of households and situated randomly in the cells defined as residential areas; then, in each house, human agents were created by the number of members in the household. It is possible to have a cell with several houses located in it since the distribution of houses was performed randomly. On the other hand, COVID-19 is so likely to be spread in places with a high number of the population rather than a low number; therefore, it is better to distribute human agents, or rather, house agents according to the population density patterns of the study area. To do so, house agents were situated randomly in one of the five considered regions (see Fig. 2B) according to the roulette wheel selection method; thus, house agents are so likely to be situated in regions with high population density.

Table 1.

The number of households in Urmia city based on the number of households’ members along with the total number of people living in each group of the household.

Number of members in the household	Number of households	Total number of people living in each group of the household
1	12,293	12,293
2	37,452	74,904
3	60,703	182,109
4	65,222	260,888
5	26,518	132,590
6	8789	52,734
7	5041	35,287
Total	216,018	750,805

2.3.2.2. Movement of human agents

It is obvious that people's movements are the cause of the COVID-19 outbreak. In this model, the movements of human agents were considered in two modes. They move either by their personal vehicles or public transportations. In this model, humans based on age were classified into four groups (Table 2 ): 5 and less, more than 5 to 24, more than 24 to 64, and more than 64. It was assumed that humans who are more than 24 years old (two last groups) can have personal vehicles, of which 63% were assumed to have personal vehicles according to the statistics of people having personal vehicles in Urmia city [47]. It should be noted that the rest of humans were assumed to move by public transportations. On the other hand, humans based on the occupation were classified into four classes of civil servants, self-employed, students, and the rest of the people who are not in any of the first three classes. In this ABM, it was assumed that students were assigned to human agents who are more than 5 and less than 24 years old, and civil servants, as well as self-employed employees, were assigned to human agents who are more than 24 years old. Similarly, the number of human agents in each group was determined according to the statistics of human resources in Urmia city [47].

Table 2.

The population of Urmia city based on age as well as gender.

Age	Gender
	Male	Female
5 and less	41,451	38,692
6 until 24	111,670	108,135
25–64	207,590	202,002
65 and more	19,722	21,543
Total	380,433	370,372

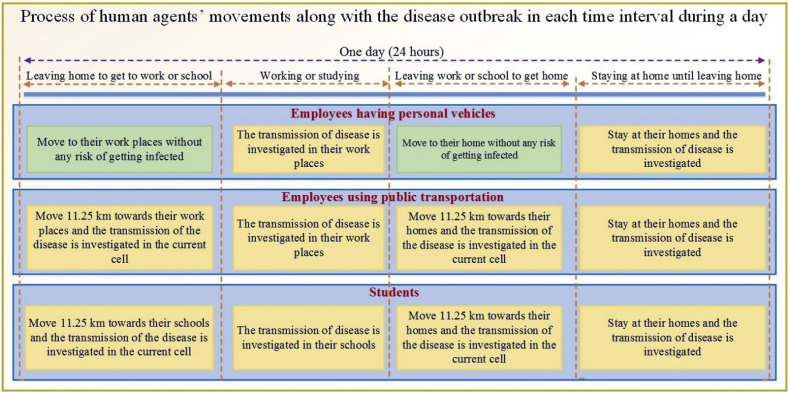
The selection of agents' workplaces was performed randomly among the office, business, or school cells on the basis of agents' occupations. During the simulation, for each human agent, a cell was assigned as the workplace and does not change. It should be noted that the same cell can be several human agents’ workplaces since the selection of the workplaces was done randomly. In this model, all employees (civil servants and self-employed) and students move between their houses and workplaces twice a day. To simulate the movements of human agents, one day was divided into four time intervals: in the first time interval, employee agents (civil servants and self-employed) who have personal vehicles move from their houses to their workplaces by their own vehicles and in this time interval, there is not any risk of becoming infected for these human agents. On contrary, employee agents who do not have personal vehicles as well as student agents in order to move from their houses to their workplaces, use public transportations and in this case, they are likely to become exposed if there is any exposed human agent on their way to work regarding the R0† value of the exposed human agent as well as the COVID-19 transmission probability. It should be noted that the speed of public transportations with regard to their stops in stations was considered 45 km an hour and according to this speed, it was assumed that human agents move about 11.25 km every 15 min; therefore, the movements of human agents are updated every 15 min and their health status (see section 2.3.3) are investigated every 15 min based on the existence of exposed human agents in the same cells with them. It should be noted that in order to transmit the COVID-19 indoors, people should be kept at a distance of fewer than 2 m for at least 15 min [8,9,48]; therefore, in this ABM, the time interval was considered 15 min and the dimension of the cells was taken into account 2 m. Human agents move between their houses and workplaces through road cells. All employees as well as students move to their own workplace cells in the second time interval and similarly, the probability of becoming exposed is investigated at their workplace cells. In the next time interval (the third time interval), employees and students come back from their workplaces to their houses in the same way described in the first time interval and the risk of disease transmission is investigated for employees who use public transportations as well as students; and in the last time interval, all employees and students move to their houses and in this time interval, the disease transmission is investigated among all members of the households. These processes are explicitly illustrated in Fig. 4 .

Fig. 4.

The process of human agents' movements along with the disease outbreak over different time intervals.

2.3.3. The SEIRD model used in the ABM

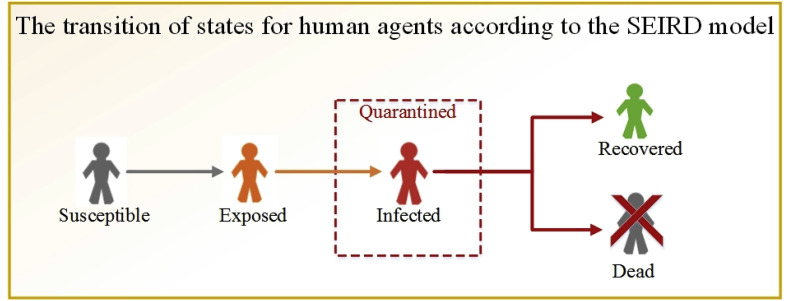
In our model, human agents at any moment of the simulation are in one of the susceptible, exposed, infected, recovered, or dead states and their states change regarding the SEIRD model [[49], [50], [51]]. The states of human agents change under certain conditions over time. They will remain susceptible until they coincide with at least one exposed human agent in the same cells. In this case, based on the transmission probability as well as the R0 value of the exposed human agent, COVID-19 might be transmitted from an exposed human to a susceptible human. If the human agent becomes exposed, it starts to transmit the disease and this trend lasts 2–14 days (COVID-19 incubation period) [48]. After passing the incubation period which is considered diverse for each human agent, the state of exposed human turns into infected, and in this case, it will be quarantined. In the infected state, human agents cannot move and consequently spread the disease because of the quarantine. In the state of infected, one of two events regarding the age of the human agent happens: first, the infected human agent becomes recovered after 2–4 weeks [52], or second, the infected human agent dies. In Fig. 5 , the transition of states for human agents was shown.

Fig. 5.

The transition of states for human agents.

In order to have an overview of the parameters of our ABM, input parameters of the model along with their values as well as the values assigned to the attributes of human agents were summarized in Table 3 . To initialize these values, previous studies and some of the most authoritative websites were used. For the parameters and attributes whose values were defined in a range, a normal distribution was considered. Moreover, for these parameters and attributes, the mean and standard deviation were also reported. It should be noted that the normal distribution was simply considered for these parameters and attributes due to the novelty of coronavirus as well as the lack of information on what distribution it follows (as a suggestion for future research, an investigation can be made on how these parameters (parameters defined in a range) are distributed; then, the values adjusted for these parameters would be based on the study of their changes in reality.).

Table 3.

Summary of the human agents’ attributes and all parameters considered in the model along with their values as well as resources.

Parameters		Value/range of value	Mean	Standard deviation	Reference/source
Duration of the exposed state (the incubation period)		2–14 days	8	(8/4) days	[48]
The recovery period		14–28 days	21 days	(21/8) days	[52]
R0		2.06–2.52 people	2.29 people	(2.29/32) people	[53]
Fatality rate (based on the age)	5 and less	0%	–	–	[54]
	6–24	0–0.2%	0.1%	(0.1/4) %
	25–64	0.2–3.6%	1.9%	(1.9/4) %
	65 and more	3.6–14.8%	9.2%	(9.2/4) %
Public transportations' speed		45 km/h	–	–	Authors' estimation
The COVID-19 transmission probability		2.5–4%	3.25%	(3.25/16) %	[55]
Cell size		2 m * 2 m	–	–	Authors' estimation
The maximum number of cells that human agents can move by public transportations in 15 min		5625 cells	–	–	Authors' estimation

2.3.4. Important dates along with all events which happened in the study area

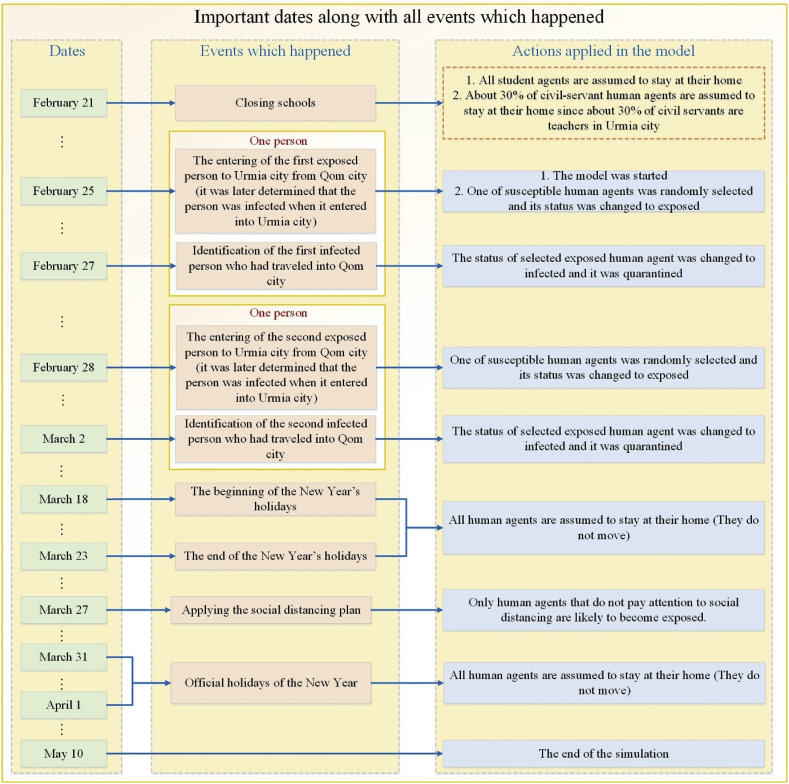
In this research, all happened events concerned with the COVID-19 outbreak in the Urmia city along with their exact dates were considered in our ABM. In Iran, COVID-19 disease was transmitted from China to the city of Qom (the first city in Iran where COVID-19 was observed) and subsequently, from Qom to all cities in Iran. The first case of COVID-19 in the city of Urmia was identified on February 27. According to the official government news, this person had traveled to Qom and returned to Urmia on February 25; therefore, the beginning of our ABM was scheduled for February 25. In addition, one human agent was randomly considered exposed at the beginning of the ABM. Precede the outbreak of COVID-19 from Qom to all cities in Iran, the Iranian government in order to reduce the rate of COVID-19 outbreak closed all schools and educational centers on February 21. For this reason, at the beginning of our ABM, it was assumed that all student agents do not move in the ABM as well as about 30% of civil servant agents (those who are teachers in the real world). Similar to the first detected case, the second infected case with COVID-19 disease in the Urmia city was identified on March 2. This person also became infected due to traveling to Qom city and returned to Urmia city on February 28; so, another susceptible human agent was randomly selected among all human agents, and its health status was changed to exposed. In Iran, the New Year's holidays begin on March 18 and continue until March 23. During this period of time in the model, it is assumed that all human agents stayed at their houses and did not move to their workplaces or any other places. On March 27, the Iranian government in order to reduce the outbreak of the COVID-19 imposed the social distancing plan on the population. Regarding this event, only human agents who did not pay attention to social distancing were likely to become exposed. The interval between March 31 and April 1 was the official holidays of the New Year and similarly, all human agents were assumed to stay at their houses and there were not any human agents' movements in this interval in the model. It should be noted that in Iran, one day a week is a holiday and these holidays were also considered in the ABM according to the exact dates of them. Similar to other holidays, on these holidays, it was assumed that human agents stay in their houses and do not move. Fig. 6 clearly illustrates all that happened in the study area from the beginning of the epidemic to May 10 (the end of the simulation).

Fig. 6.

Important dates of all events which happened as well as the actions applied in the proposed ABM regarding each event.

3. Results and discussion

In this section of research, first, the outputs of the ABM are expressed (section 3.1), then, the proposed ABM is evaluated according to the chi-square test (section 3.2), and finally, three control strategies are designed and implemented in the ABM and the number of infected people is investigated for different values of the parameters set in each strategy (section 3.3).

3.1. Model outputs

The main outputs of the proposed ABM encompass the number of human agents in infected and recovered states as well as the number of death. Regarding these outputs, the outbreak of COVID-19 can be traced in each day of the simulation throughout the study area. Fig. 7 illustrates the interface of the proposed ABM in the NetLogo 6.0.4 platform.

Fig. 7.

The interface of the proposed agent-based model in the NetLogo 6.0.4 platform.

It should be noted that in this research, although the values set for the parameters of the number of population by sex, age, and occupation (student, civil-servant, self-employed), percentage of people using public transportations, and percentage of people using personal vehicles according to the characteristics of the study area (Urmia city), all these parameters’ values were defined as changeable so that users are able to change them regarding their purposes. In addition, in this ABM, three various control strategies were designed that the parameters assigned to them are changeable, as well; therefore, the proposed ABM is very flexible as well as interactive so that not only it is able to predict the COVID-19 outbreak and consequently, help make decisions, but also the effects of the parameters as well as the impacts of various control strategies can be examined by increasing and decreasing the values of the parameters. In that way, the proposed ABM can be implemented for different scenarios, and consequently, the COVID-19 outbreak and the impacts of control strategies can be investigated in the study area for diverse conditions.

3.2. Comparison of the model's results with the actual observations

The results of the model (predicted values) must be compared with the real data (actual observed values) since simulation models are imitations of real-world systems. In order to investigate how close the model's predicted values are to the actual observed values, the chi-square test was used due to its appropriateness in examining the closeness of the two groups of predicted and actual observed values [15]. In the chi-square test, the null hypothesis ($H_0$) and the alternative hypothesis ($H_A$) are defined according to Eq. (1). In addition, the chi-square value is calculated according to Eq. (2).

$$\{\begin{array}{c}{H}_0:Thepredictedvaluesarecloseenoughtotheactualobservedvalues\\ H_A:Thepredictedvaluesarenotcloseenoughtotheactualobservedvalues\end{array}$$ (1)

$${\text{Χ}}^2=\sum _{i=1}^n\frac{{(P_i-O_i)}^2}{O_i}$$ (2)

Here, ${\text{Χ}}^2$ denotes the chi-square value, the average numbers of infected human agents in one hundred runs (the results of the ABM) are as predicted values ($P_i$), the real numbers of COVID-19 cases recorded are actual observed values ($O_i$), and n is the number of weeks that is equal to 10.

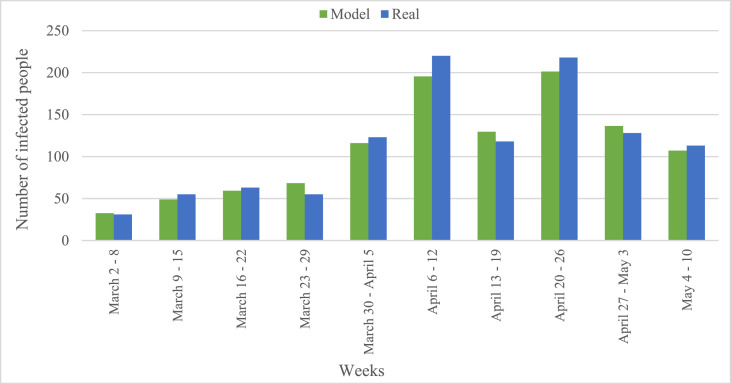
Both predicted and actual observed values for each week of the simulation are given in Fig. 8 . It should be noted that the proposed ABM for each scenario was run one hundred times since some random processes were considered in our ABM.

Fig. 8.

Comparison of the model's results with the real numbers of COIVD-19 cases in the Urmia city.

The value calculated for the chi-square based on predicted and actual observed values was 10.640. In addition, the critical value of ${\text{Χ}}_{0.05}^2(9)$ extracted from the chi-square table was achieved 16.919. According to the comparison of the chi-square value with the critical value, the null hypothesis ($H_0$) cannot be rejected; therefore, it can be concluded that the predicted values are close enough to the actual observed values.

The purpose of the simulation, as an imitation of the real world, is to simplify the real world in order to conclude about the behaviors of the real world over time. Even though simulations are implemented accurately, they cannot be completely consistent with reality since the phenomena occurring in the real world are so complicated and a variety of parameters might have influences on them. In addition, there are always some stochastic events in the real world that are not considered in models. The outbreak of COVID-19 is one of the complex phenomena so that diverse parameters affect it. It is obvious that taking into account all parameters affecting is not feasible. On the other hand, disease data always has a number of errors; for instance, people with the disease may not refer to health centers and this case may not be recorded. It is also possible that the place of becoming infected of people was recorded wrongly due to the lack of health facilities or other reasons; for example, people might become infected in the city other than the city where the disease was recorded. The actual observed data (daily infected cases) used in this research was the official data provided by the Ministry of Health and Medical Education, which was identified by the definitive diagnostic test method with the kit (laboratory-confirmed). It should be noted that sometimes, there are some postpones in the process of diagnosing infected cases in the laboratory that cause the number of positive recorded cases on each day is not quite exact. Therefore, regarding all these, in order to decrease the effects of mentioned issues on the evaluation of the model as well as all results of the research, the evaluation and also all results of the research were investigated based on the weekly cases of COVID-19 recorded and the weekly number of infected human agents obtained from the ABM. In addition, regarding the aforementioned reasons, although the model predicted value is sometimes higher and sometimes lower than the actual value, the trend of model's prediction is so similar to the trend of actual data that indicates the potential of our ABM in simulating the outbreak of the COVID-19.

3.3. Applying several COVID-19 control strategies in the proposed ABM

One of the purposes of this research is to investigate the effects of control strategies on reducing the number of infected people with COVID-19 and consequently, controlling the outbreak of the COVID-19. To do so, three COVID-19 control strategies that might have efficient impacts on preventing the COVID-19 outbreak were applied and investigated. In the remainder of this section, these three strategies are explicitly described and also their impacts on preventing of COVID-19 outbreak are investigated.

3.3.1. School and educational center closures

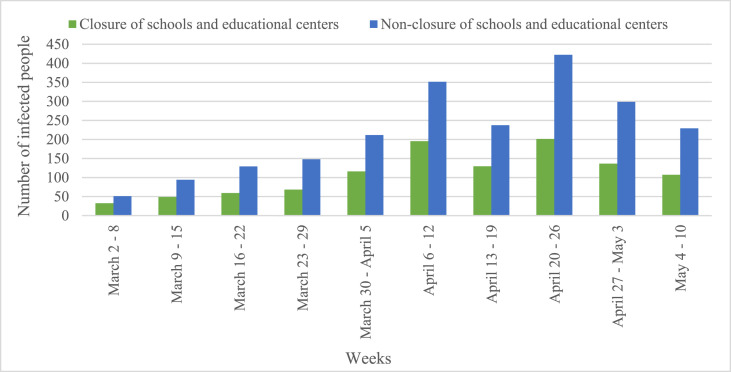
As it is obvious, the main causes of the COVID-19 outbreak are people's movements as well as their interactions with each other; therefore, one of the strategies that can help control the COVID-19 outbreak is the school and educational center closures. Therefore, the strategy of school and educational center closures was applied and investigated in the ABM. To do so, the ABM was implemented in two modes; once, when schools and educational centers were open, and another time when they were shut down. In order to investigate the impacts of this strategy on controlling the COVID-19 outbreak, the average number of infected human agents in one hundred runs was compared in both modes. In Fig. 9 , the average number of infected human agents in one hundred runs in both modes of closures and non-closures of schools and educational centers were shown.

Fig. 9.

Comparison of the average number of infected people in Urmia city in both modes of closures and non-closures of schools and educational centers.

According to Fig. 9, the results of the proposed ABM indicated how the COVID-19 would spread if schools and educational centers were not shut down in Urmia city until May 10. Therefore, the proposed ABM investigated how the COVID-19 has spread in Urmia city. The average number of infected people was determined in each week until May 10, in both modes of closure and non-closure of schools and educational centers. The results of the ABM indicated that applying school and educational center closures strategy decreased the number of infected people, 107.82 people (4.96%) a week, on average, and 1078.16 people (49.61%) in total. Regarding the results of the ABM in Fig. 9, it is concluded that if the schools and educational centers were not closed provided that the rest of the events happened according to Fig. 6, the number of people who will be infected by the COVID-19 was approximately 2173 people instead of 1095.

3.3.2. Heeding social distancing

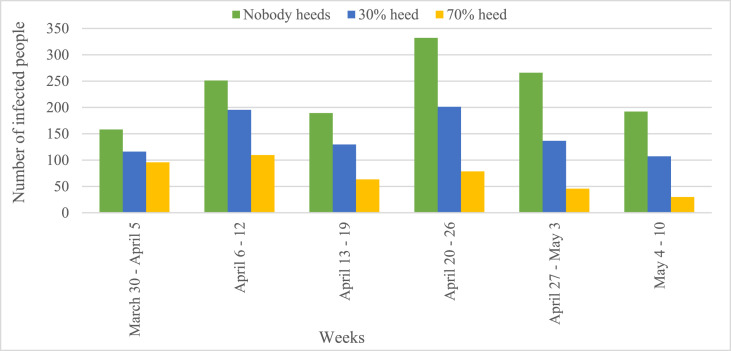
As mentioned in section 2.3.2.2, when an uninfected person is fewer than 2 m away from an infected person, the transmission of COVID-19 disease is likely to happen; therefore, one of the control strategies is heeding social distancing. According to this strategy as well as the cell size considered in this ABM (2 m), human agents do not move to the cell in which there is another human agent. In order to apply the strategy of heeding social distancing in the ABM, it was assumed that the transmission of disease does not happen for human agents heeding social distancing in their workplaces since the same cell can be the workplaces of several human agents. Similar to the previous strategy, in order to investigate the impacts of heeding social distancing on controlling the COVID-19 outbreak, the ABM was implemented in two modes: (i) when a number of people heed the social distancing, and (ii) when nobody heeds the social distancing; and then the average number of infected human agents obtained from the ABM in one hundred runs was investigated for two different values of percentage of human agents heeding social distancing as well as when nobody heeds social distancing (Fig. 10 ).

Fig. 10.

The average number of infected people in Urmia city for two different values of the percentage of human agents heeding social distancing as well as when nobody heeds.

With regard to the results of the model in Fig. 10, it can be concluded that heeding social distancing is one of the effective strategies in reducing the number of infected people, and consequently, the outbreak of the COVID-19. According to Fig. 10, the number of infected people resulted from the ABM until May 10, indicates that heeding social distancing strategy from March 27 (see Fig. 6), by 30% and 70% of the people of the study area reduced the number of infected people by 83.8 (5.24%) and 160.97 (10.07%) people a week on average, respectively. In addition, heeding social distancing from March 27, by 30% and 70% of the people of the study area led to a decrease of 502.8 (31.46%) and 965.83 (60.44%) infected people in total, respectively. Also, If nobody heeded social distancing strategy from March 27 in Urmia city, until May 10, approximately 1598 people will be infected by the COVID-19, instead of 1095 people.

3.3.3. Office closures

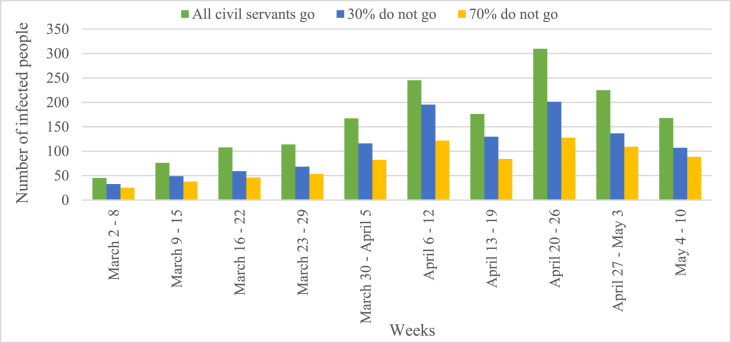
Due to the interactions of different people in offices, offices are one of the places that speed up the outbreak of the contagious diseases, especially COVID-19; therefore, one of the strategies that can lead to control the outbreak of the COVID-19 is office closures. For this reason, in the proposed ABM, the outbreak of COVID-19 was investigated for different values of the percentage of civil servant agents who do not go to their workplaces. The average number of infected human agents in one hundred runs for two different values of 30% and 70% for the percentage of civil servant agents who do not go to work as well as when all civil servants go to work are shown in Fig. 11 .

Fig. 11.

The average number of infected people in Urmia city for two different values of the percentage of civil servant agents who do not go to work as well as when all civil servants go to work.

The results of the model illustrated in Fig. 11 indicate that if instead of 30%, 70% of civil servants did not go to work provided that they stayed in their houses as well as all events happened according to Fig. 6, until May 10, the total number of infected people in the study area will be reduced by 318.7 people (29.10%) as well as 31.87 people (2.91%) each week on average. In addition, if all civil servants went to work, the number of people who will be infected by COVID-19 until May 10, was approximately 1634, instead of 1095 people. Therefore, when the 30% and 70% of civil servants do not go to work, the number of infected people is reduced by 53.89 (3.30%) and 85.76 (5.25%) people a week and 538.91 (32.98%) and 857.61 (52.48%) people in total, respectively.

It should be mentioned that the start date as well as the time periods are not consistent in three figures (Figs. 9, Fig. 10, and Fig. 11) since the starting dates of applying strategies were different in the study area. In addition, in the last two strategies, the values considered for the percentage of people heeding social distancing as well as the percentage of civil servants who do not go to work were defined as subjectively, without any specific investigation, and only in order to evaluate the impacts of strategies on controlling the outbreak of the COVID-19. In addition, the investigation of the impacts of these strategies was performed only based on the viewpoint of the COVID-19 outbreak.

According to the results of the model in Figs. 9, Fig. 10, and Fig. 11 it is concluded that movements of people are the main factor in spreading the COVID-19 so that the school and educational center closures, as well as office closures, extremely reduced the number of infected people until May 10. Civil servants and students are only a low proportion of the population, and although not moving this proportion reduces the number of infected people and slows down the spread of the COVID-19, it cannot lead to the elimination of the COVID-19 outbreak in the society. Elimination of the COVID-19 outbreak requires not moving of all members of society or a very high proportion of the population. The strategy of heeding social distancing not only does not damage the country from the economical viewpoint but also leads to an extreme reduction in the number of infected people and consequently, a decrease in the spread speed of COVID-19 in a society. In the current situation, the heeding social distancing strategy by the majority of people as a suggestion of this research can lead to a remarkable reduction in the number of infected people and consequently, the control of the COVID-19 outbreak in Urmia city.

4. Conclusions

At present, the epidemic of COVID-19 disease has emerged as the most important global health challenge and its outbreak has reached 210 countries and territories. Despite many efforts made to decrease the speed of COVID-19 outbreak around the world, it still spreads quickly and infects so many people daily. This rapid and widespread outbreak of COVID-19 has caused serious social, economic, cultural, and even political damage in the countries.

One of the most valuable aspects of simulation is the explanation of real-world phenomena that simulations of those phenomena either are not feasible in the real world or are costly to be performed. Modeling and simulation of the COVID-19 outbreak in a region as well as investigating the efficiency of control strategies can assist health policymakers in controlling and preventing the COVID-19 outbreak. This is the main contribution of this research.

In this research, the outbreak of the COVID-19 was simulated in Urmia city with the help of an agent-based model due to its capability in modeling people's movements as well as their interactions that are two main causes of the COVID-19 outbreak. In addition, three control strategies of school and educational center closures, heeding social distancing, and office closures were applied in the model and the impacts of each one on decreasing the speed of COIVD-19 outbreak as well as preventing its outbreak were investigated.

The results of the model indicated that school and educational center closures reduced the number of infected people by 4.96% each week, on average, and 49.61% in total in Urmia city from February 21 until May 10. Heeding social distancing strategy by 30% and 70% of people of Urmia city from March 27, led to decrease the number of infected people by 5.24% and 10.07% each week, on average and 31.46% and 60.44% in total, respectively, and when 30% and 70% of civil servants of Urmia city did not go to work, from February 21 until May 10, the number of infected people was decreased by 3.30% and 5.25% each week, on average and 32.98% and 52.48% in total, respectively. As a result of this research, regarding the current situation of Urmia city, in order to slow down the speed of the COVID-19 outbreak, heeding social distancing by the majority of people is recommended. The results of this research can be helpful to health policymakers in selecting appropriate strategies to decrease the outbreak of the COVID-19 in Urmia city.

The outbreak of a disease is a highly complex natural phenomenon, and a specific model cannot be utilized for all regions of the world since not only diverse parameters affect the spread of the disease but also these parameters vary from one place to another. People cultures, level of literacy and awareness of people, the way people interact with each other, available public transportations, urban context, population density, job diversity, variety in factors of age, gender, number of people employed, number of students, number of people having personal vehicles, number of people using public transportations, and etc. are among the parameters that make differences in the way COVID-19 spreads in different places. Therefore, it is suggested for future research that the outbreak of COVID-19 will be simulated for other regions of the world by taking into account various parameters as well as applying diverse control strategies.

Funding information

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.