Infectious disease pandemic and permanent volatility of international stock markets: A long-term perspective

Abstract

Understanding the impact of infectious disease pandemic on stock market volatility is of great concerns for investors and policy makers, especially during recent new coronavirus spreading period. Using an extended GARCH-MIDAS model and a newly developed Infectious Disease Equity Market Volatility Tracker (EMV-ID), we investigate the effects of infectious disease pandemic on volatility of US, China, UK and Japan stock markets through January 2005 to April 2020. The empirical results show that, up to 24-month lag, infectious disease pandemic has significant positive impacts on the permanent volatility of international stock markets, even after controlling the influences of past realized volatility, global economic policy uncertainty and the volatility leverage effect. At different lags of eruptions in infectious disease pandemic, EMV-ID has distinct effects on various stock markets while it has the smallest impact on permanent volatility of China's stock market.

1. Introduction

Understanding the drivers of stock market volatility is crucial for risk management, portfolio allocation and regulatory decisions (Basta and Molnar, 2018; Caporale et al., 2020; Lei et al., 2019; Wei et al., 2019, 2020a, 2020b). Many empirical studies have identified that various direct and indirect factors, such as macroeconomic fundamental, investor attention, technical indicator and price volatility in commodity, interest and FX markets, play important roles in motivating stock market volatilities (Mittnik et al., 2015; Wei et al., 2017). Notably, the Coronavirus (COVID-19) outbreak in December 2019 has brought great pains to global macroeconomy and financial markets. Intuitively, stock market reacts to this pandemic more promptly and directly than other sectors in economic and financial system. Indeed, several recent studies confirm that the eruption of COVID-19 causes greater fluctuations in stock, gold and cryptocurrency markets than in days before that (Corbet et al., 2020; Haroon and Rizvi, 2020; Zhang et al., 2020). For example, Ali et al. (2020) find that China's stock market presents a relatively smaller decrease in returns in both COVID-19 epidemic and pandemic periods while for the bigger economies such as the US, UK, Germany and South Korea the overall average volatility increases tremendously from epidemic to pandemic period.1 Zaremba et al. (2020) investigate the stringency of policy responses to the novel coronavirus pandemic in 67 countries and prove that non-pharmaceutical interventions significantly increase equity market volatility.

However, we find that all these latest researches focus only on the short-term reactions of global stock markets to the COVID-19 pandemic by using data from the December 2019 to now. No studies pay attention to the long-term impacts of infectious disease pandemic on the volatility of international stock markets, especially its effect on permanent volatility of stock market. The motivation of paper, therefore, is to investigate whether and how infectious disease pandemic can affect the stock market volatility from a long-term outlook instead of just focusing on one single public health emergency. To fulfill this task, we employ two novel methods: one the one hand, a mixed data sampling approach, GARCH-MIDAS model, is utilized to identify the impact of infectious disease pandemic on permanent volatility of international stock market. The advantage of the GARCH-MIDAS approach over other volatility models is that it can not only distinguish short-term and permanent volatilities from the total ones, but is capable of investigating the impacts of exogenous variables on permanent volatility across different time horizons. On the other hand, we adopt a new index developed by Baker et al. (2020), Infectious Disease Equity Market Volatility Tracker (EMV-ID), to quantitatively measure the magnitude of infectious disease pandemic, which is available from January 1985 to the present. This data enables us to get an overall picture of global infectious disease pandemic in a long period instead of just focusing on the shock of isolated public health incident.

We offer clear evidence that infectious disease pandemic has significant positive impact on permanent volatility of international stock markets even after controlling the effects of past realized volatility (RV) lagged through 3 months to 2 years in these markets. The remainder of the article proceeds as follows. Section 2 describes the econometric model of GARCH-MIDAS and Section 3 discusses the data used in this paper. Section 4 presents our empirical findings and finally Section 5 concludes the study.

2. Empirical methodology

The GARCH-MIDAS model introduced by Engle and Rangel (2008) and Engle et al. (2013) is utilized in this paper to determine the predictive ability of the monthly sampled predictors for daily volatility. The conditional volatility obtained by the GARCH-MIDAS model is construct by a short-term volatility component and a long-term volatility component. The short-term volatility component is driven by a GARCH process of high-frequency data while the long-term volatility component is given by the MIDAS regression of low-frequency data. Using this model, the out-of-sample predictive ability of monthly predictors for daily volatility can be explored.

For the GARCH-MIDAS model, the logarithmic return on day i in month t, r _i,t, follows:

$$r_{i,t}-\omega =\sqrt{g_{i,t}{\tau }_t}{z}_{i,t},\forall i=1,\dots ,N_t,$$ (1)

$$z_{i,t}|I_{i-1,t}\sim N(0,1),$$

where ω = E _{i − 1, t}(r _i,t) is the conditional expectation of r _i,t given the information set, I _{i − 1, t}, available at the (i-1)th day of month t, N_t is the total number of trading days in month t, z _i,t is the i.i.d. random variable. g _i,t in Eq. (1) is the short-term volatility component which follows the GARCH (1,1) process:

$$g_{i,t}=(1-\alpha -\beta )+\alpha \frac{{(r_{i-1,t}-\omega )}^2}{{\tau }_t}+\beta g_{i-1,t},$$ (2)

where α > 0, β > 0 and 1 − α − β > 0. τ_t in Eq. (1) is the permanent (long-term) volatility component, and the logarithmic τ_t is captured by the MIDAS regression:

$$\log \left({\tau }_t\right)=m+{\theta }_1\sum _{k=1}^K{\phi }_k(w_{1,1},w_{1,2})R{V}_{t-k},$$ (3)

where K is the number of periods (time lags) for smoothing the permanent volatility, $R{V}_{t-k}={\sum }_{i=1}^{N_t}{r}_{i,t-k}^2$ is the realized volatility (RV) in month t-k, ϕ_k(w _1,1, w _1,2) is the weighting scheme and is calculated by a Beta polynomial:

$${\phi }_k(w_{1,1},w_{1,2})=\frac{{(k/K)}^{w_{1,1}-1}{(1-k/K)}^{w_{1,2}-1}}{\sum _{j=1}^K{(j/K)}^{w_{1,1}-1}{(1-j/K)}^{w_{1,2}-1}},$$ (4)

where w _1,1 ≥ 1 and w _1,2 ≥ 1. In this paper, we set w _1,1 to be one, and rewrite Eq. (4) as:

$${\phi }_k\left(w_1\right)=\frac{{(1-k/K)}^{w_1-1}}{\sum _{j=1}^K{(1-j/K)}^{w_1-1}},$$ (5)

where w ₁ in Eq. (5) corresponds to w _1,2 in Eq. (4). Then, the total conditional volatility is measured by ${\sigma }_{i,t}^2={\tau }_t·g_{i,t}$. The model specification described above is the standard GARCH-MIDAS model. To further explore the explanatory ability of other monthly exogenous variables on daily volatility, e.g. EMV-ID in this paper, we extend Eq. (3) by involving another monthly exogenous variable, X, along with RV as:

$$\log \left({\tau }_t\right)=m+{\theta }_1\sum _{k=1}^K{\phi }_k\left(w_1\right)R{V}_{t-k}+{\theta }_2\sum _{k=1}^K{\phi }_k\left(w_2\right)X_{t-k},$$ (6)

where ϕ(w ₂) is calculated by replacing w ₁ in Eq. (5) with w ₂. In the following applications, we use a rolling-window method in determining the monthly variables in each step of estimation, that is, the long-run component varies every period.

3. Data

In this paper, there are two categories of data sampling at daily and monthly frequencies, respectively. The daily data consists of four price quotations of S&P 500, CSI 300, FESE 100 and NIKKEI 225 indices, which present the stock market performances of US, China, UK and Japan. The reason of choosing these four markets are twofold: on the one hand, these markets are the largest stock markets in the world, usually being regarded as leading indicators for international stock markets. On the other hand, recent COVID-19 pandemic broke out firstly in China and then spreads to US, UK and Japan eventually. More importantly, these four countries are reported to have taken different responses in this pandemic and experience different stock market performances in recent time. The monthly data is the Infectious Disease Equity Market Volatility Tracker (EMV-ID) constructed by Baker et al. (2020). This EMV-ID index is developed in the following steps: first, they specify terms in four sets, as follows (term variants also included): 1) E: {economic, economy, financial}; 2) M: {stock market, equity, equities, Standard and Poors}; 3) V: {volatility, volatile, uncertain, uncertainty, risk, risky} and 4) ID: {epidemic, pandemic, virus, flu, disease, coronavirus, MERS, SARS, EBOLA, H5N1, H1N1}. Second, they obtain daily counts of newspaper articles that contain at least one term in each of E, M, V, and ID across approximately 3000 US Newspapers. Third, they scale the raw EMV-ID counts by the count of all articles in the same day. In a final step, they multiplicatively rescale the resulting series mirroring our approach to scale a Categorical EMV series in the overall EMV tracker. That is, they match the level of the VIX between 1990 and 2016 using the overall EMV index and then scale this ID-EMV index to reflect the ratio of the ID-EMV articles to total EMV articles. The original time frequency for EMV-ID is daily while we covert it to monthly frequency for the reason that there are many EMV-ID records with zero values in daily frequency. To be specific, there are 8240 zero values out of 12,904 total daily records of EMV-ID from January 1, 1985 to April 30, 2020. Thus, it is hard to track the change rate of it in daily frequency. In addition, we are more interested in the long-term impacts of infectious disease pandemic on stock market volatility. So, we sum the daily EMV-ID records within month t to get the monthly EMV-ID_t index in this paper. Finally, till January 2005, China has launched its first integrated stock price index, CSI 300, to account for the overall performance of Shanghai and Shenzhen Stock Exchanges. Therefore, the data used in this paper covers the time horizon through January 4, 2005 to April 30, 2020. The stock indices are available at Datastream and EMV-ID data is collected from http://www.policyuncertainty.com/infectious_EMV.html.

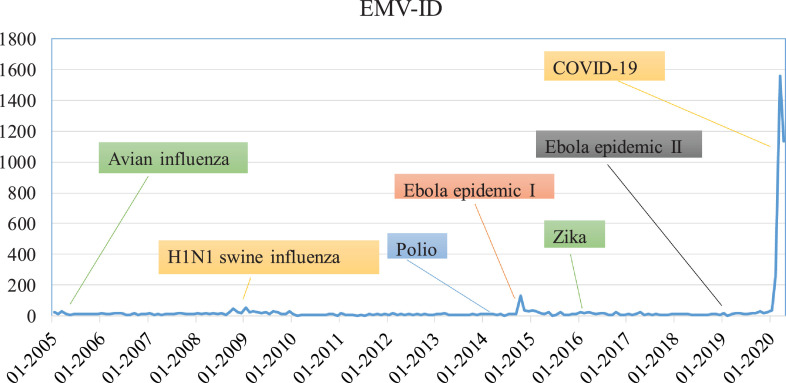
Fig. 1 reveals the time evaluations of EMV-ID during the data sample. Since 2005, WHO has declared several "public health emergencies of international concern". For example, in April 2009, Mexico, the United States and other countries successively outbroke of influenza A H1N1 (also known as H1N1 swine influenza) epidemic. In August 2014, the Ebola epidemic in West Africa was spiraling out of control. In 2019, another Ebola burst in the Democratic Republic of the Congo. The latest incident occurred in January 2020, when a novel coronavirus (COVID-19) broke out in China. Obviously, the recent COVID-19 pandemic gets much more news reports than other public health emergencies with its unprecedented shocks to the whole world.

Fig. 1.

Time evolution of EMV-ID index.

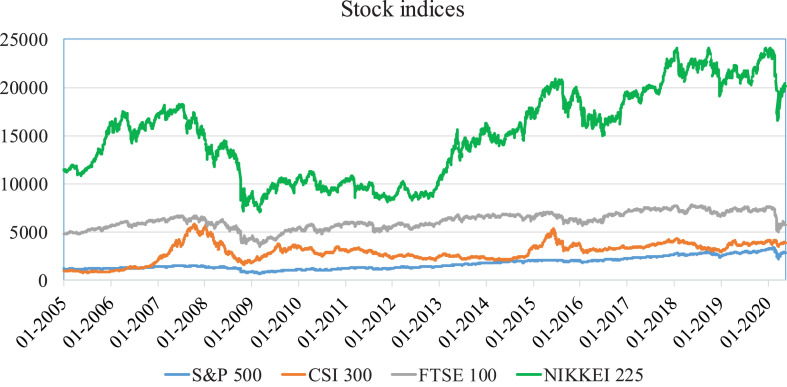
Fig. 2 shows the time evolutions of S&P 500, CSI 300, FESE 100 and NIKKEI 225 indices. We can find similar price movements across the four indices for most of the time, indicating high integration of international stock markets. And during the period of COVID-19 pandemic, huge price volatilities are observed in all the four stock indices. In the following empirical analysis, EMV-ID and stock indices are transferred to logarithm returns. Table 1 reports the descriptive of these time series. We observe that EMV-ID have much larger standard deviation than those of stock indices. All the series have significant auto-correlation up to 10th lag. In addition, all the stock indices show significant negative skewness and positive excess kurtosis, indicating that they are not normally distributed. Finally and most importantly, the ADF and P-P tests reject the null hypotheses of one unit root, proving that they are all stationary.

Fig. 2.

Time evolutions of four major stock indices.

Table 1.

Descriptive statistics for EMV-ID and stock indices.

	EMV-ID	S&P 500	CSI 300	FTSE 100	NIKKEI 225
Frequency	Monthly	Daily	Daily	Daily	Daily
Mean (%)	1.9332	0.0237	0.0370	0.0064	0.0150
Standard deviation (%)	69.2293	1.2704	1.7274	1.1832	1.5006
Skewness	0.1137	−0.7163***	−0.5250***	−0.5034***	−0.5762***
Excess kurtosis	0.5611	16.9998***	3.8935***	11.9707***	9.3731***
Jarque–Bera	2.8109	45,160.6847***	2523.3587***	22,392.4308***	13,838.2657***
Q (5)	45.3251***	62.5455***	18.5580***	39.5701***	4.2850
Q (10)	53.5262***	85.9171***	38.0772***	65.3942***	17.505*
ADF	−22.5643***	−69.2395***	−59.5424***	−26.7805***	−61.9367***
P-P	−23.5473***	−69.2653***	−59.5511***	−62.3814***	−61.9731***

Notes: The Jarque–Bera statistic tests for the null hypothesis of normality in sample returns distribution. Q(n) is the Ljung-Box statistics of the return series for up to nth order serial correlation. ADF and P-P are statistics of Augmented Dickey-Fuller and Phillips-Perron unit root test based on least AIC criterion respectively. ***, ** and * indicate rejection at the 1%, 5% and 10% significance level, respectively.

4. Empirical results

In this section, we employ GARCH-MIDAS model to quantitatively capture the impacts of EMV-ID on volatilities of four major international stock markets. Table 2 shows the estimation results of the GARCH-MIDAS model with both lagged realized volatility (RV) and EMV-ID as exogenous explanatory variables. To ensure robust results, this model is estimated with four different time lags in RV and EMV-ID, i.e. 3, 6, 12 and 24 months.

Table 2.

Estimation results of GARCH-MIDAS+RV+EMV-ID model.

Stock index	ω	α	β	m	θ1	θ2	w1	w2	BIC
Panel A: lag K = 3 months
S&P 500	0.0678***	0.1254***	0.8588***	0.4291**	−0.0045**	0.0078***	1.7390**	1.5683***	9814.57
	(0.0128)	(0.0083)	(0.0086)	(0.2110)	(0.0019)	(0.0022)	(0.8591)	(0.4051)
CSI 300	0.0495***	0.0628***	0.9353***	1.8367***	−0.0062***	0.0021**	1.0010***	3.8105*	13,370.90
	(0.0190)	(0.0035)	(0.0034)	(0.2821)	(0.0011)	(0.0010)	(0.1459)	(2.1773)
FTSE 100	0.0397***	0.1166***	0.8629***	0.3162**	−0.0024*	0.0061***	7.5366	1.3510***	10,127.60
	(0.0127)	(0.0091)	(0.0102)	(0.1510)	(0.0014)	(0.0021)	(7.1834)	(0.4060)
NIKKEI 225	0.0632***	0.1027***	0.8839***	1.0761***	−0.0032**	0.0106***	2.5909**	1.4990***	12,290.10
	(0.0186)	(0.0064)	(0.0073)	(0.1837)	(0.0013)	(0.0023)	(1.1527)	(0.2534)
Panel B: lag K = 6 months
S&P 500	0.0679***	0.1240***	0.8574***	0.3165*	−0.0045*	0.0148***	3.8744	1.4503***	9685.68
	(0.0130)	(0.0083)	(0.0090)	(0.1826)	(0.0027)	(0.0033)	(2.5416)	(0.3106)
CSI 300	0.0491**	0.0640***	0.9335***	1.5921***	−0.0073***	0.0028**	2.3788***	7.2521*	13,115.00
	(0.0192)	(0.0037)	(0.0035)	(0.4309)	(0.0019)	(0.0014)	(0.6923)	(4.2782)
FTSE 100	0.0375***	0.1305***	0.8174***	−0.2271***	0.0106***	0.0123***	1.0058***	1.0349***	9984.41
	(0.0133)	(0.0106)	(0.0146)	(0.0836)	(0.0014)	(0.0032)	(0.1939)	(0.1849)
NIKKEI 225	0.0606***	0.1021***	0.8801***	0.9427***	−0.0029*	0.0090**	5.4749	3.3293**	12,147.50
	(0.0192)	(0.0066)	(0.0078)	(0.1606)	(0.0017)	(0.0036)	(3.5115)	(1.3636)
Panel C: lag K = 12 months
S&P 500	0.0708***	0.1301***	0.8515***	0.3418*	−0.0040	0.0223***	8.7063	1.7036***	9400.41
	(0.0134)	(0.0088)	(0.0094)	(0.1993)	(0.0031)	(0.0062)	(7.6282)	(0.4907)
CSI 300	0.0447**	0.0630***	0.9337***	1.2773***	−0.0061**	0.0029**	5.5741**	14.5700	12,735.10
	(0.0195)	(0.0038)	(0.0036)	(0.3361)	(0.0023)	(0.0015)	(2.6346)	(9.1368)
FTSE 100	0.0341**	0.1328***	0.8121***	−0.2543***	0.0124***	0.0130**	2.0656***	1.7320**	9733.75
	(0.0139)	(0.0111)	(0.0153)	(0.0873)	(0.0017)	(0.0052)	(0.5824)	(0.8542)
NIKKEI 225	0.0501**	0.1011***	0.885***	1.1579***	−0.0039*	0.0082**	8.6552	7.3802*	11,732.50
	(0.0198)	(0.0065)	(0.0076)	(0.2389)	(0.0023)	(0.0041)	(5.3192)	(3.8643)
Panel D: lag K = 24 months
S&P 500	0.0734***	0.1449***	0.8260***	−0.0569	0.0086***	0.0659***	1.7018***	1.0011***	8852.62
	(0.0140)	(0.0104)	(0.0115)	(0.1571)	(0.0022)	(0.0107)	(0.6161)	(0.0642)
CSI 300	0.0335	0.0582***	0.9398***	2.5874***	−0.0204***	0.0018	1.1093***	36.6950	11,715.00
	(0.0208)	(0.0035)	(0.0033)	(0.5369)	(0.0058)	(0.0012)	(0.2240)	(32.7200)
FTSE 100	−0.1126***	0.1191***	0.8808***	−11.753	−0.0530***	0.1584***	4.2737***	1.0113***	9416.54
	(0.0099)	(0.0055)	(0.0039)	(10.8020)	(0.0108)	(0.01654)	(0.8794)	(0.0322)
NIKKEI 225	0.0496**	0.1032***	0.8805***	1.0262***	−0.0028	0.0074**	24.0030	18.2600*	10,914.60
	(0.0207)	(0.0069)	(0.0082)	(0.1927)	(0.0019)	(0.0036)	(18.5720)	(9.5953)

Note: θ₁ and θ₂ indicate the impacts of lagged RV and EMV-ID on the permanent volatility of the four stock markets, respectively. The bracketed numbers are the standard errors of the estimations. *, **, and *** denote significance at the 10%, 5%, and 1% levels, respectively.

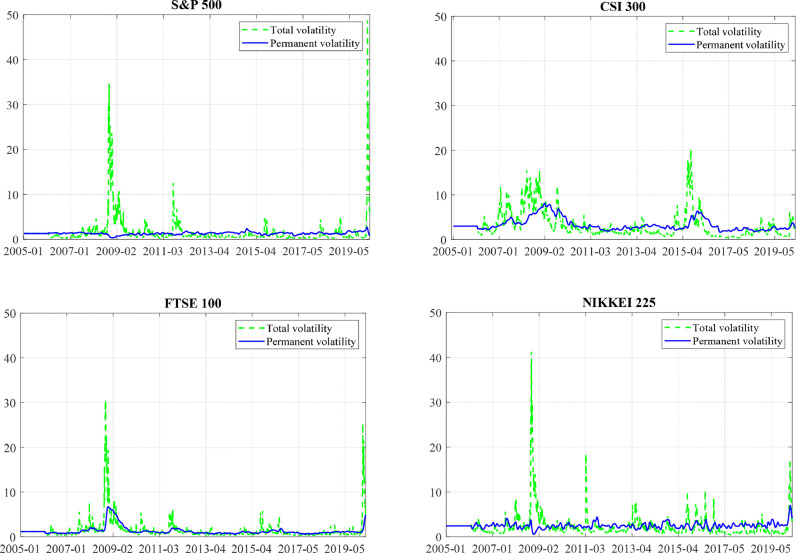
Firstly, Table 2 shows that almost all the estimated coefficients are significant, indicating that this GARCH-MIDAS model incorporating monthly RV and EMV-ID fits the volatility of four stock markets very well. Secondly, β coefficients are all significant at 1% level, which vary from about 0.81 to 0.93, confirming high degree of volatility persistence in the four stock markets. Thirdly, most of the θ ₁ parameters, which indicate the impact of lagged RV on permanent volatility of stock market, are significant except for the ones of S&P 500 and NIKKEI 225 indices at 12- and 24-month lags, respectively. This result indicates that past RV in stock market, especially in short terms (3- and 6-month lags shown in this table) has noticeable influence on permanent volatility component at the present time. Finally and most importantly, we can see that all the θ ₂ coefficients, quantifying the effects of EMV-ID on permanent volatility of stock markets are all positive significant at least at 5% level, with only one exception of CSI 300 index at 24-month lag. These findings present strong evidence that infectious disease pandemic has affirmative influence on the price fluctuations in international stock markets. In addition, we find that at different lags EMV-ID have distinct effects on various markets. For instance, at 3-month lag EMV-ID has much larger shock on Japan's stock market than on others. The UK's stock market, however, responses more violently to EMV-ID at the 24-month lag than others do. Moreover, we observe that, unanimously, EMV-ID has the smallest impacts on permanent volatility of CSI 300 index, implying that China's stock market is more stable during international public health emergencies. This outcome is qualitatively in line with the study of Ali et al. (2020), where they find that Chinese markets displayed relative calm with lower volatility during both epidemic and pandemic periods in recent COVID-19 spread. Fig. 3 reveals the estimated total and permanent volatilities of the four stock markets at time lag of 12 months for RV and EMV-ID. In this figure, we do find that lagged monthly RV and EMV-ID have different effects on permanent volatility of the stock markets. In addition, the US, UK and Japan's stock markets have experienced a wave of huge volatilities since January 2020, however, the Chinese stock market has been fairly stable during this COVID-19 epidemic.

Fig. 3.

Estimated total and permanent volatility of four stock markets at the lag of 12 months for RV and EMV-ID.

5. Robustness checks

5.1. Empirical results based on gjr-garch-midas model

Leverage effect is a well-known stylized fact in stock market volatility, which describes the phenomenon of potential larger impact of negative shocks on stock volatility than that of positive shocks. To capture this leverage effect, Glosten et al. (1993) propose a widely used model named as GJR-GARCH as follows:

$${\sigma }_t^2=\omega +\left[\alpha +\lambda I({\epsilon }_{t-1}<0)\right]{\epsilon }_{t-1}^2+\beta {\sigma }_{t-1}^2,$$ (7)

where ${\sigma }_t^2$ and ${\epsilon }_t$ is the conditional volatility and residual (shock) of stock returns at time t, respectively. I(.) is an indicator function, i.e., when the condition in () is met, I(.) = 1, and 0 otherwise. λ is the coefficient to quantify the volatility leverage effect. In this subsection, we use this GJR-GARCH model to substitute the simple GARCH (1,1) specification of short-term volatility in stock market indicated in Eq. (2) and estimate this GJR-GARCH-MIDAS model incorporating monthly RV and EMV-ID to further examine the robustness of the findings in Section 4. Table 3 reports the estimation results.

Table 3.

Estimation results of GJR-GARCH-MIDAS+RV+EMV-ID model.

Stock index	ω	α	β	λ	m	θ1	θ2	w1	w2	BIC
Panel A: lag K = 3 months
S&P 500	0.0281**	1.437e-09	0.8675***	0.2213***	0.1538	−0.0020**	0.0039*	8.2411	1.8210**	9608.66
	(0.0129)	(0.0086)	(0.0089)	(0.0160)	(0.1691)	(0.0010)	(0.0020)	(8.7749)	(0.8480)
CSI 300	0.0478**	0.0599***	0.9358***	0.0046	1.8045***	−0.0060***	0.0019*	1.0010***	3.5829	13,358.80
	(0.0200)	(0.0052)	(0.0036)	(0.0056)	(0.2907)	(0.0011)	(0.0011)	(0.1495)	(2.2578)
FTSE 100	0.0034	7.0088e-09	0.8939***	0.1679***	0.1210	−0.0024**	−1.2083e-05	10.8450	6.0241	9944.88
	(0.0138)	(0.0072)	(0.0082)	(0.0125)	(0.1286)	(0.0009)	(0.0009)	(11.7470)	(635.6400)
NIKKEI 225	0.0292	0.0339***	0.8741***	0.1347***	0.7848***	−0.0017*	0.0080***	5.8402	1.4257***	12,179.30
	(0.0192)	(0.0051)	(0.0080)	(0.0104)	(0.1172)	(0.0010)	(0.0021)	(5.0035)	(0.2959)
Panel A: lag K = 6 months
S&P 500	0.0306**	2.9086e-08	0.8673***	0.2179***	0.0896	−0.0020*	0.0068**	15.1260	1.7108**	9480.93
	(0.0130)	(0.0087)	(0.0089)	(0.0156)	(0.1514)	(0.0010)	(0.0032)	(16.6070)	(0.7591)
CSI 300	0.0484**	0.0621***	0.9343***	0.0021	1.5726***	−0.0069***	0.0028*	2.4344***	6.6077	13,103.00
	(0.0202)	(0.0054)	(0.0036)	(0.0057)	(0.4269)	(0.0019)	(0.0015)	(0.7381)	(4.2943)
FTSE 100	0.0038	8.2399e-09	0.8938***	0.1644***	0.0720	−0.0028***	0.0113***	18.7030	1.0010***	9823.46
	(0.0138)	(0.0070)	(0.0085)	(0.0125)	(0.1165)	(0.0010)	(0.0029)	(16.4300)	(0.1169)
NIKKEI 225	0.0289	0.0299***	0.8713***	0.1381***	0.7078***	−0.0012	0.0092**	15.4690	2.0924**	12,032.20
	(0.0197)	(0.0054)	(0.0083)	(0.0110)	(0.1034)	(0.0010)	(0.0038)	(19.4170)	(0.9201)
Panel C: lag K = 12 months
S&P 500	0.0328**	3.2348e-08	0.8643***	0.2250***	0.1157	−0.0019*	0.0094*	34.047	1.8915*	9197.42
	(0.0133)	(0.0090)	(0.0093)	(0.0160)	(0.1627)	(0.0010)	(0.0055)	(40.4390)	(1.1306)
CSI 300	0.0438**	0.0605***	0.9342***	0.0037	1.2703***	−0.0058**	0.0029*	5.7976**	12.8240	12,722.70
	(0.0206)	(0.0055)	(0.0037)	(0.0056)	(0.3328)	(0.0022)	(0.0017)	(2.7957)	(9.0169)
FTSE 100	−0.0009	5.0996e-09	0.8343***	0.2114***	−0.3729***	0.0131***	0.0086**	2.0324***	1.7397	9545.87
	(0.0146)	(0.0093)	(0.0140)	(0.0185)	(0.0794)	(0.0014)	(0.0040)	(0.4227)	(1.1550)
NIKKEI 225	0.0146	0.0306***	0.8778***	0.1344***	0.7908***	−0.0016	0.0170**	20.2320	1.5909**	11,622.60
	(0.0202)	(0.0051)	(0.0083)	(0.0102)	(0.1313)	(0.0013)	(0.0073)	(21.7010)	(0.6556)
Panel D: lag K = 24 months
S&P 500	0.0309**	5.0533e-09	0.8411***	0.2480***	−0.2861**	0.0106***	0.0479***	1.6094***	1.0010***	8649.12
	(0.0140)	(0.0110)	(0.0113)	(0.0188)	(0.1341)	(0.0016)	(0.0099)	(0.3122)	(0.0797)
CSI 300	0.0775***	0.1160***	0.8212***	0.1253***	−8.2023	−0.2617***	0.0997***	3.1162***	1.0620***	12,255.70
	(0.0147)	(0.0059)	(0.0046)	(0.0098)	(1.1905e+11)	(0.0111)	(0.0227)	(0.1106)	(0.1025)
FTSE 100	−0.0022	2.6215e-10	0.8364***	0.2082***	−0.3652***	0.0131***	0.0293***	4.1055***	1.2041***	8944.87
	(0.0155)	(0.0095)	(0.0147)	(0.0192)	(0.0877)	(0.0016)	(0.0073)	(0.9355)	(0.3193)
NIKKEI 225	0.0315**	0.0695***	0.9013***	0.0582***	0.0002	−0.0640***	0.0656***	4.9933***	4.9990***	11,059.10
	(0.0157)	(0.0050)	(0.0041)	(0.0060)	(0.5191)	(0.0059)	(0.0209)	(0.4640)	(1.5622)

Note: λ is the volatility leverage coefficient in the GJR-GARCH model of Eq. (7). θ₁ and θ₂ indicate the impacts of lagged RV and EMV-ID on the permanent volatility of the four stock markets, respectively. The bracketed numbers are the standard errors of the estimations. *, **, and *** denote significance at the 10%, 5%, and 1% levels, respectively.

We can see in Table 3 that, firstly, most of the leverage coefficients λ are significant except for several cases of CSI 300 index at short- and medium-term lags. More importantly, all these λ coefficient estimates are positive, revealing larger impact of negative shocks on stock volatility than that of positive shocks. Secondly, all the θ ₂ coefficients measuring the impact of EMV-ID on permanent volatility of stock market are significantly positive with only one exception of FTSE 100 at 3-month lag. Furthermore, through lags of 3 to 12 months, EMV-ID has the smallest impacts on permanent volatility of CSI 300 index, which is in high degree of consistency with the previous finding in Table 2. Finally, we can conclude that, even after considering the leverage effect in volatility, infectious disease pandemic has strong positive impacts on the permanent volatility of the four international stock markets.

5.2. Empirical results by controlling effects of economic policy uncertainty

Many researches prove that economic policy uncertainty (Baker et al., 2016) is an extremely important factor driving volatilities of financial markets (see Fang et al., 2019; Wang et al., 2019, 2020 for example). In this sub-section, therefore, we intend to have a further look at the role of EMV-ID on permanent volatility of stock markets by controlling the effects of both RV and global economic policy uncertainty. This task is fulfilled through adding past monthly global economic policy uncertainty index (GEPU) into the left side of Eq. (6) as:

$$\log \left({\tau }_t\right)=m+{\theta }_1\sum _{k=1}^K{\phi }_k\left(w_1\right)R{V}_{t-k}+{\theta }_2\sum _{k=1}^K{\phi }_k\left(w_2\right)X_{t-k}+{\theta }_3\sum _{k=1}^K{\phi }_k\left(w_3\right)GEP{U}_{t-k},$$ (8)

where parameter θ ₃ reveals the impact of global economic policy uncertainty (GEPU) on permanent volatility of the four stock markets.

Table 4 shows the estimation results of GARCH-MIDAS model incorporating three monthly exogenous explanatory variables: RV, EMV-ID and GEPU index. It also offers very similar empirical findings to those reported in Table 2. First, most coefficients in Table 4 are significant, suggesting the good fitness of the model for the stock market volatility. Second, after controlling the effects of both RV and global economic policy uncertainty, most θ ₂ parameters indicating the impact of EMV-ID on permanent volatility of stock market are significantly positive with few exceptions in FTSE 100 and CSI 300 indices. In particular, the θ ₂ parameters for CSI 300 index with 12- and 24-month lags of exogenous explanatory variables are not significant while the corresponding θ ₁ and θ ₃ parameters are significant, further confirming that China's stock market are less affected by infectious disease pandemic through more timely and effective medical and economic responses to epidemic infections. In addition, very close to the results in Table 2, all the significant θ ₂ coefficients are positive, clearly indicating that infectious disease pandemic has affirmative impacts on the long-term price fluctuations in international stock markets. Finally, in line with the findings in Fang et al. (2019), Wang et al. (2019) and Wang et al. (2020), most θ ₃ coefficients are significantly positive across the four stock indices, implying that global economic policy uncertainty has long-term and comprehensive impacts on the volatilities of international stock markets.

Table 4.

Estimation results of GARCH-MIDAS+RV+EMV-ID+GEPU model.

Stock index	ω	α	β	m	θ1	θ2	θ3	w1	w2	w3	BIC
Panel A: lag K = 3 months
S&P 500	0.0666***	0.1197***	0.8623***	0.3016	−0.0035*	0.0072***	0.0088***	2.0400	1.5977***	49.9790	9822.01
	(0.0129)	(0.0082)	(0.0087)	(0.1891)	(0.0018)	(0.0022)	(0.0016)	(1.2700)	(0.4389)	(80.8860)
CSI 300	0.0494***	0.0628***	0.9353***	1.8339***	−0.0062***	0.0021*	0.0004	1.0010***	3.8055*	49.8950	13,387.40
	(0.0190)	(0.0035)	(0.0034)	(0.2853)	(0.0011)	(0.0010)	(0.0018)	(0.1464)	(2.2468)	(1742.7000)
FTSE 100	0.0382***	0.1162***	0.8620***	0.2776*	−0.0020*	−0.0004	0.0092***	15.3520	17.4630	49.9640	10,138.80
	(0.0128)	(0.0091)	(0.0103)	(0.1459)	(0.0011)	(0.0007)	(0.0022)	(25.4380)	(90.8760)	(86.3370)
NIKKEI 225	0.0614***	0.0967***	0.8868***	0.8589***	−0.0018**	0.0084***	0.0148***	7.4657	1.6877 ***	49.9850	12,279.20
	(0.0183)	(0.0066)	(0.0078)	(0.1555)	(0.0009)	(0.002)	(0.0019)	(5.6611)	(0.3800)	(63.5050)
Panel B: lag K = 6 months
S&P 500	0.0670***	0.1198***	0.8600***	0.2425	−0.0037	0.0141***	0.0079***	4.5075	1.4430***	49.9970	9695.05
	(0.0131)	(0.0083)	(0.0091)	(0.1771)	(0.0024)	(0.0036)	(0.0015)	(3.4414)	(0.3295)	(51.7650)
CSI 300	0.0481**	0.0637***	0.9339***	1.5797***	−0.0068***	0.0032**	−0.0135	2.3319***	6.7988*	1.9273	13,129.70
	(0.0192)	(0.0039)	(0.0036)	(0.4320)	(0.0020)	(0.0015)	(0.0122)	(0.7594)	(3.7842)	(1.5323)
FTSE 100	0.0362***	0.1126***	0.8623***	0.1916	−0.0026**	0.0172***	0.0090***	24.0920	1.0041***	49.9800	10,010.90
	(0.0130)	(0.0092)	(0.0106)	(0.1263)	(0.0012)	(0.0035)	(0.0023)	(26.6790)	(0.0981)	(47.8310)
NIKKEI 225	0.0589***	0.0988***	0.8807***	0.8044***	−0.0017*	0.0088**	0.0149***	17.4320	2.7745**	49.9910	12,138.40
	(0.0189)	(0.0069)	(0.0083)	(0.1348)	(0.0009)	(0.0037)	(0.0022)	(14.8810)	(1.2535)	(34.6840)
Panel C: lag K = 12 months
S&P 500	0.0712***	0.1311***	0.8511***	0.3595	−0.0039	0.0231***	−0.0078	8.1755	1.6723***	8.4993	9415.88
	(0.0134)	(0.0089)	(0.0094)	(0.2308)	(0.0035)	(0.0063)	(0.0103)	(8.1375)	(0.4904)	(11.4070)
CSI 300	0.0455**	0.0670***	0.9252***	0.6578**	0.0078***	0.0025	−0.0529**	1.2771*	14.9080	1.4018***	12,752.50
	(0.0206)	(0.0043)	(0.0055)	(0.3325)	(0.0029)	(0.0016)	(0.0218)	(0.7130)	(11.8160)	(0.4758)
FTSE 100	0.0326**	0.1331***	0.8054***	−0.3362***	0.0125***	0.0123**	0.0478***	1.6093***	1.8825*	1.9645***	9744.65
	(0.0143)	(0.0115)	(0.0162)	(0.0900)	(0.0017)	(0.0053)	(0.0169)	(0.4345)	(0.9965)	(0.6909)
NIKKEI 225	0.0480**	0.1009***	0.8818***	0.9464***	−0.0021*	0.0074*	0.0125***	26.0080	7.1162*	49.9920*	11,735.50
	(0.0195)	(0.0070)	(0.0081)	(0.1756)	(0.0011)	(0.0041)	(0.0029)	(19.4430)	(4.1976)	(28.6100)
Panel D: lag K = 24 months
S&P 500	0.0733***	0.1451***	0.8259***	−0.0793	0.0084***	0.0660***	0.0252	1.5646***	1.0010***	1.1054	8868.76
	(0.0140)	(0.0105)	(0.0116)	(0.1730)	(0.0023)	(0.0108)	(0.0331)	(0.5836)	(0.0694)	(1.0436)
CSI 300	0.0277*	0.1030***	0.8970***	−0.1701	−0.0158***	0.0246	−0.1134*	4.9618***	4.9529	4.9499 *	11,823.70
	(0.0157)	(0.0043)	(0.0040)	(1.0955)	(0.0054)	(0.0240)	(0.0655)	(1.8295)	(4.8771)	(2.9231)
FTSE 100	0.0298**	0.1286***	0.8100***	−0.3992***	0.0130***	0.0549***	0.0709***	2.1055***	1.0573***	2.8333**	9130.60
	(0.0149)	(0.0119)	(0.0178)	(0.1000)	(0.0020)	(0.0098)	(0.0273)	(0.5560)	(0.1527)	(1.3014)
NIKKEI 225	0.0468**	0.1105***	0.8485***	0.3876***	0.0063***	0.0057*	0.0117***	4.3919**	19.5390*	49.9980*	10,923.30
	(0.0209)	(0.0080)	(0.0124)	(0.1122)	(0.0015)	(0.0030)	(0.0041)	(1.8483)	(11.5740)	(28.4080)

Note: θ₁, θ₂ and θ₃ indicate the impacts of lagged RV, EMV-ID and GEPU on the permanent volatility of the four stock markets, respectively. The bracketed numbers are the standard errors of the estimations. *, **, and *** denote significance at the 10%, 5%, and 1% levels, respectively.

In summary, according to the results reported in Sections 4 and 5, we confirm the robustness of our conclusions that infectious disease pandemic can really drive the permanent volatility in international stock markets even after controlling the volatility leverage effect, the influences of lagged realized volatility and global economic policy uncertainty.

6. Conclusions

The COVID-19 outbroken in December 2019 brings unprecedented impacts on global economy in various ways. Significant economic recession, surge in unemployment, sharp decline in international trade and huge rising in fiscal deficit are already serious challenges that every government must face now. Stock market is a barometer of the macroeconomy, and thus the impacts of infectious disease pandemic on economy are directly reflected in the price volatilities of stock markets. In this paper, we use a newly established EMV-ID tracker to measure the magnitude of infectious disease pandemic and an extended GARCH-MIDAS model to quantify its shocks on volatilities of four major international stock markets. We find that infectious disease pandemic occurring within the last 24 months can impose significant positive impact on present permanent volatility of international stock markets. Moreover, due to the distinctive actions in response to infectious disease pandemic by governments, different stock markets have different reactions to the pandemic. Timely actions taken by one authority, e.g., China, can reduce the volatility of its stock market volatility as shown in this paper based on data sample through 2005 to now, which is also verified by Ali et al. (2020) in recent COVID-19 pandemic.

Declaration of Competing Interest

The authors declare no conflict of interest.