Abstract
Background: Intrinsically disordered proteins or regions (IDPs or IDRs) lack stable structures in solution, yet often fold upon binding with partners. IDPs or IDRs are highly abundant in all proteomes and represent a significant modification of sequence → structure → function paradigm. The Protein Data Bank (PDB) includes complexes containing disordered segments bound to globular proteins, but the molecular mechanisms of such binding interactions remain largely unknown. Results: In this study, we present the results of various disorder predictions on a nonredundant set of PDB complexes. In contrast to their structural appearances, many PDB proteins were predicted to be disordered when separated from their binding partners. These predicted-to-be-disordered proteins were observed to form structures depending upon various factors, including heterogroup binding, protein/DNA/RNA binding, disulfide bonds, and ion binding. Conclusions: This study collects many examples of disorder-to-order transition in IDP complex formation, thus revealing the unusual structure–function relationships of IDPs and providing an additional support for the newly proposed paradigm of the sequence → IDP/IDR ensemble → function.
Introduction
Intrinsically disordered proteins or regions (IDPs or IDRs) lack rigid 3D folded structures in the native state yet often form stable conformations when bound with partners,1−8 or in some cases, called fuzzy complexes, the IDPs or IDRs remain partially or completely unstable and dynamic even in the bound form.9−11 IDPs and IDRs are both very common in all three domains of life.12−15 Even enzymes, almost all of which are structured, often use IDRs to assist with the function.16 Unlike ordered globular proteins, which typically function as enzymes or transporters, IDPs or IDRs are involved in more diverse biological processes, such as gene regulation, signal transduction, and cell-cycle control.17−19 For these and many other important biological processes, molecular recognition by IDPs, IDRs, and structured domains almost always plays important roles in key steps of such processes. IDP- or IDR-mediated molecular recognition is proposed to enable binding to diverse partners with high specificity and low affinity and in many cases with relatively large interface areas.18 These features provide great advantages in molecular interactions involving IDPs or IDRs and thereby enable their use in a wide variety of biological processes.
The Protein Data Bank (PDB) is a database of 3D structures of proteins and nucleic acids, the structure of which are typically obtained by X-ray crystallography, nuclear magnetic resonance spectroscopy and, increasingly, cryoelectron microscopy. Proteins in the PDB are generally considered to be ordered or structured. However, in contrast to appearances, many of the structures in the PDB contain one or more IDPs. Molecular recognition by IDPs is often accompanied by a disorder-to-order transition, and the structures of many resulting folded complexes have been determined.
At least two distinct methods have been developed to distinguish ordered components from disordered components of protein complexes. One method examines the radius of gyration per residue (Rg/N), an approach that is based on the idea that disordered proteins tend to take on extended conformations when complexed with their partners; this extended shape is in contrast to the collapsed and generally more globular conformations of ordered proteins.20 The other method examines the surface area and the interface area of components in a complex. IDPs tend to have a greater exposed surface area and create larger interfaces, per residue, than ordered proteins.21 In other words, for dimers formed from structured proteins, both the monomeric and interfacial surface areas are relatively small (think of two globular objects in contact with each other). On the other hand, dimers formed from IDPs are intertwined, so both the monomeric and the interfacial surface areas are much larger. Thus, on plots of normalized monomer surface area (NMA) versus normalized interfacial surface area (NIA), structured monomers are closer to the origin than intrinsically disordered monomers.21 We have previously applied this NMA–NIA analysis to a variety of protein complexes.22−24
Here, we compare estimates of disorder by performing NMA–NIA analysis with the Rg/N classifier and with various other predictions of disorder. This work aims to identify complexes containing IDPs or IDRs in the PDB and to suggest possible mechanisms for structure formation by the predicted-to-be-disordered proteins. A large number of potential IDPs or IDRs were indeed found, but many discrepancies were observed among the disorder predictions using different methods. Thus, an additional aim is to determine the underlying causes for the observed discrepancies among various predictors.
Materials and Methods
Dataset
Test Set
The initial data was a nonredundant set of PDB files with more than one chain derived from the NCBI nonredundant table (ftp:/ftp.ncbi.nlm.nih.gov/mmdb/nrtable/). Monomers including more than one chain were removed by the biological unit annotation from the PDB files. Biological units are functional forms of the molecules, and monomers are identified using the keyword ‘biological unit: MONOMERIC’ in the PDB files. To be consistent with the earlier study,20 we used their same criteria to exclude short peptides (≤20 residues), coiled coils, and transmembrane proteins. All the protein chains with more than two nonstandard residues (any residues that are not included in the 22 standard residues, annotated as X in PDB sequence files) in the protein sequences were also discarded. This set includes 6141 chains and is called the test set.
Positive Validation Set
To test prediction accuracy, two positive sets of complexes containing verified IDPs binding to ordered or disordered partners were used from two previously published papers.25,26 These sets were from the DIsordered Binding Sites (DIBS) database and the Mutual Folding Induced by Binding (MFIB) database. They were selected not only because IDPs in both databases were experimentally confirmed or inferred from the homology or motifs but also because the biological contacts among the partners were checked to exclude artificial crystal-packing interactions. IDP sequences containing nonstandard residues were not included. To ensure the independence of these positive validation sets, the complexes that are included in the test set mentioned in the last paragraph were removed. As a result, 698 complexes from DIBS and 157 complexes from MFIB were collected. All DIBS complexes contained IDP binding to one or more ordered protein partners, and all MFIB complexes included two or more IDP partners.
Negative Validation Set
In addition, a negative set of complexes containing fully ordered proteins binding to one or more proteins were obtained from the PDB as of October 2, 2018. This set included X-ray- and NMR-determined structures of complexes containing the target chains that were mapped from a set of stable single-chain monomers without missing densities, ligands, and disulfide bonds. Such fully ordered monomers were collected using the same methods proposed in the reference.27 Monomers with ligands or disulfide bonds were removed to exclude the induced folding structures of IDPs undergoing disorder-to-order transition upon binding to ligands or upon formation of disulfide bonds. Monomer coiled-coil structures were also removed because they are known to be unstable in isolation (such as PDB id 1L2P). Structures predicted to be disordered but to form folded structures stabilized by interdomain interfaces were also removed (such as PDB id 3TIP). A total of 693 such monomers were collected. Then, the PDB entries of these stable monomers were mapped to their parent UniProt proteins using the mapping provided by SIFTS.28 PDB complexes containing the same regions of matched UniProt protein names were considered to be in the bound state of those monomers. Each of these bound-state chains mapped from the fully ordered monomers should be predicted to be ordered in the complexes. This set included 543 complexes.
Disorder Prediction Based on Protein Structures
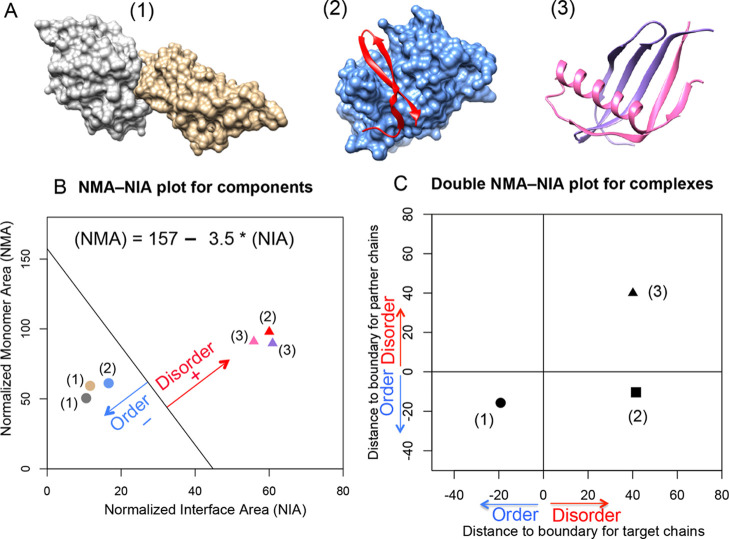
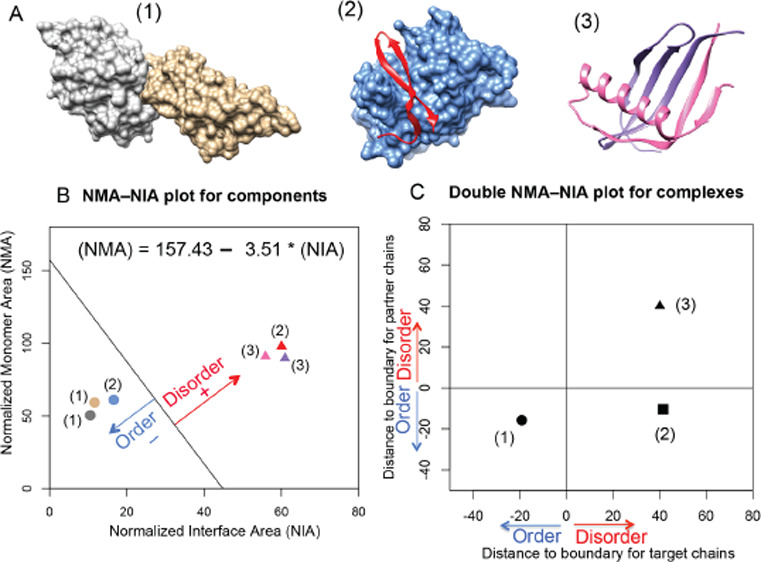
To predict the disorder or order status of each partner in a protein complex (see three different examples in Figure 1A), we applied the analysis of the NMA and the NIA based on PDB structures.22−24 The NMA is calculated as the surface area of a chain without considering other complex components, and the NIA is calculated as the difference between the surface area of individual components and the surface area of the complex. An optimized boundary between the ordered and the disordered partners in the NMA–NIA plot23 was determined using an expanded dataset relative to the original reported boundary.21 The NMA–NIA boundary separates IDPs (with relatively high monomer and interaction surface areas per residue) from the ordered proteins (with relatively low monomer and interaction surface areas per residue). The set of disordered proteins in the expanded dataset was constructed by combining two previously reported datasets21,29 with selected PDB chains found in DisProt.30 This selection took only chains from the PDB that were entirely disordered according to the corresponding DisProt annotations. The set of ordered proteins in the expanded dataset was constructed by mapping monomeric structures to complex structures, requiring at least 30% sequence identity. Both ordered and disordered protein sets were filtered for a maximum of 30% identity, giving datasets with 2542 and 145 structured chains, respectively. A linear boundary between ordered and disordered protein components in the NMA–NIA plot as defined by the following equation, (NMA) = 157 – 3.5 × (NIA) in Figure 1B, was determined with a Support Vector Machine, with the algorithm weighted to find the optimum separation of ordered and disordered proteins. The distance of a NMA and NIA point to the boundary is used to classify partners, where a positive value indicates a disordered partner, and a negative value indicates an ordered partner (Figure 1B).
Figure 1.
Disorder and order prediction based on complex structures using NMA–NIA analysis. (A) Three different types of complexes containing (1) two ordered proteins, (2) one disordered protein and one ordered protein, and (3) two disordered proteins. Their PDB ids are: 2I26, 3IXS, and 1KRL, respectively. (B) Normalized monomer area and interface area (NMA–NIA) of components in each complex. Disordered and ordered components are represented using triangles and circles, respectively. The components are colored as same as the structures presented in (A). The distance of each component to the linear boundary was calculated. The equation for the boundary ((NMA) = 157 – 3.5 × (NIA)) was determined in the reference23 as mentioned in the Methods section. Disordered components were defined as having positive distances, and ordered components were defined as having negative distances. (C) Double NMA–NIA plot is generated by plotting the distances for each member of an interacting pair. The values for chains of interest (target chains) are designated as x-axis, and the values for binding partners as designated as y-axis. The combination of positive or negative values for components will lead to distinct locations of different complexes in the plot.
The NMA–NIA boundary distances of both partners in a dimeric complex can be plotted against each other so that the binding interactions can be divided into groups (Figure 1C): (a) both are ordered (boundary distances both <0, such as complex(1)); (b) one is ordered and the other is disordered (NMA–NIA boundary distances are <0 and >0 in either order, such as complex(2)); and (c) both partners are disordered (NMA–NIA boundary distances both >0, such as complex(3)). See ref (22) for further details.
PDB files often contain heterogroups (designated as HETATM. These can be substrates, ligands, solvent, or metal ions). Such heteroatoms often contribute to protein conformational changes. Herein, we calculated the surface/interface area for the target chains in three different kinds of situations: (1) only included proteins or nucleic acids for both target and partner chains (polymers_only); (2) included heterogroups with their parent target chains (hetero_as_target); (3) included heterogroups with the partner chains (hetero_as_partner). This was done to identify the NMA–NIA boundary differences between (1) and (3), which is interesting because such differences could potentially classify two types of disorder-to-order transition: protein/DNA/RNA binding and heterogroup binding.
For comparison with NMA–NIA, the other structure-based classifier, Rg/N, was used as described in previous work.20Rg/N was defined as radius of gyration (Rg) divided by the protein length (N). It was calculated using the Perl script rgyr.pl from the Multiscale Modeling Tools for Structural Biology tool sets.31 The Rg/N classifier was developed to identify 330 IDP complexes using an optimized threshold, with values larger than 0.26 being predicted to be disordered.20
Disorder Prediction Based on Amino Acid Sequences
To contrast the structure-based disorder prediction, the sequence-based disorder predictors, VSL2b and VLXT, from the metapredictor PONDR-FIT were also used.32 These two predictors were chosen because of the results of a previous predictor analysis39 and because VSL2b ranked highest among 19 commonly used predictors for long disordered regions,33 and VLXT is useful for predicting potential binding regions.27 These two per-residue predictors assign each residue a disorder score ranging from 0 to 1, with scores ≥0.5 indicating likely disorder and scores <0.5 indicating likely order. Per-residue predictions of VLXT were used to make whole-protein disorder classifications if the percent predicted disorder residues exceeded a threshold of 35%.27
Additionally, two sequence-based whole protein predictors, charge–hydropathy value (CH_value) and PONDR VLXT cumulative distribution function (CDF) analysis, were also used to avoid the arbitrary selection of cutoff for per-residue predictors to determine the disorder or order for a whole protein. CH values were calculated by the distances from a linear boundary line on the mean net charge and the mean hydropathy plot. The boundary was determined,27 positive CH values were indicators of the predicted disorder, and negative values were indicators of the predicted order. The PONDR CDF analysis was from an empirical cumulative distribution of VLXT scores. A boundary of seven points were determined to separate the CDF curves of disordered and ordered proteins.27,34 The CDF curves of disordered proteins generally fall below this seven-point boundary and those from ordered proteins usually fall above this boundary. Thus, a protein CDF curve that falls below a majority of seven points (≥4 and ≤7) is classified as disordered; otherwise, it is defined as ordered, and the numbers of points that an ordered protein CDF curve fall below can be ≤3 and ≥0.
Structural Exmination of Predicted-to-be-Disordered Proteins
Several mechanisms have been proposed whereby predicted-to-be-disordered domains are induced to form a structure.35 Here, we also partitioned the structures into similar groups: (1) heterogroup binding, such as co-factors, ligands, or substrates; (2) protein binding; (3) DNA or RNA binding; (4) disulfide bond formation; and (5) ion binding. The first three groups were identified by NMA–NIA boundary distances. The disulfide bonds and ion-binding structures were identified from the “SSBOND” and “LINK” record in the PDB entry files.
Analysis of Trimer Structures
Complexes having three different partners (with three different UniProt IDs) were decomposed by taking one partner as the target chain and the other two chains together as a single unit; the NMA–NIA boundary distances for the one-component target and the two-component unit were then calculated and plotted versus each other. This was repeated with each chain as the target, giving three pairs of distances in the NMA–NIA boundary analysis and three points on the double NMA–NIA plot. The three points from the same complex were then connected as a triangle using R package ggplot2.
Results and Discussion
Comparison of Disorder Predictions by Different Methods
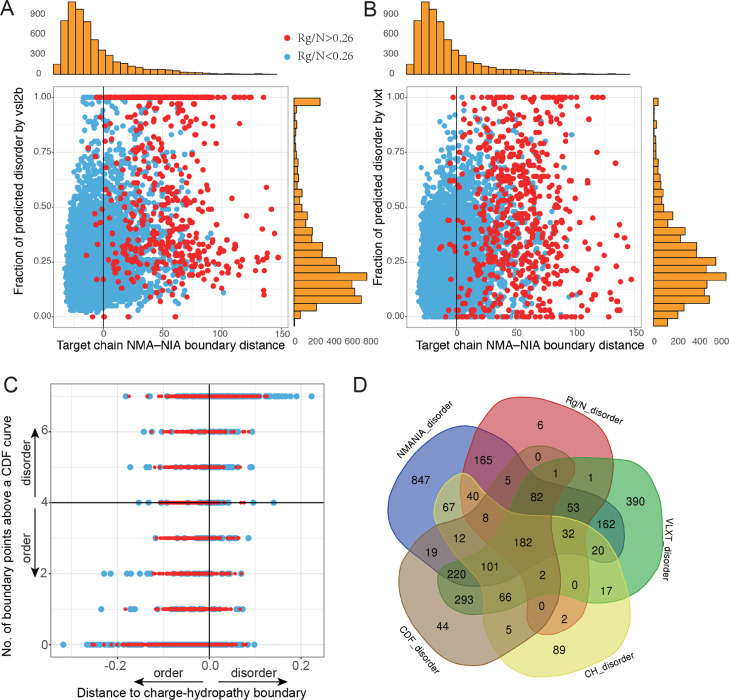
Six methods of structural and sequence disorder predictions were applied on the set of PDB complexes. The initial data included a nonredundant set of 6907 PDB chains. After filtering the monomers, short peptides, and nonstandard-residue-containing chains, the remaining 6141 chains were used to identify potential IDP- or IDR-containing complexes. Comparison of disorder predictions by different methods was presented in Figure 2. We first compared the results of Rg/N (see the raw data in the Supporting Information, column C in sheet 2) with structure-based NMA–NIA boundary distances (see the raw data in the Supporting Information, column M in sheet 2) and sequence-based VSL2b and VLXT (Figure 2A,B). Each point represented one protein chain (target chain) and red indicated proteins that were predicted to be disordered by Rg/N (>0.26), and blue were those predicted to be ordered by Rg/N (<0.26). The orange marginal histograms above and on the right represent the distribution of NMA–NIA boundary distances and fractions of disorder by VSL2b (Figure 2A) or VLXT (Figure 2B), respectively. The comparison between Rg/N and the CH_value and CDF_count was given in Figure 2C. The common and divergent results by five different methods with the cutoff values are presented in Figure 2D. While the variously predicted disorder chains showed significant overlap with each other, in addition, each method predicted an exclusive set of disordered chains.
Figure 2.
Comparison of disorder/order predictions by six different methods. (A) Comparison of NMA–NIA boundary distances, Rg/N, and VSL2b. (B) Comparison of NMA–NIA boundary distances, Rg/N, and VLXT. Red points: proteins with Rg/N higher than 0.26 (prediction of disorder). Blue points: proteins with Rg/N lower than 0.26 (prediction of order). Vertical marginal histograms (orange) are the distribution of the disorder prediction by VSL2b (A) and by VLXT (B), respectively. Horizontal marginal histograms shown in the figure are the distribution of NMA–NIA boundary distances for the target chains. (C) Comparison of two binary classification of disorder and order with Rg/N. The indications of colored points are the same as (A,B). (D) Numbers of the predicted disordered chains by different approaches. The cutoffs for each method are: NMANIA_disorder: NMA–NIA boundary distance >0; Rg/N_disorder: Rg/N > 0.26; VLXT_disorder: fraction of predicted disordered residues >0.35 (this threshold was proposed in ref (27) but needs further investigation). CH_disorder: distance to the charge-hydropathy boundary >0; CDF_disorder: numbers of CDF points ≥4.
Next, we examined the prediction differences between NMA–NIA and Rg/N because these two predictions were both based on structures. Predictions of disorder by NMA–NIA were the proteins on the right side of the vertical zero line, where the predictions of disorder by Rg/N were mainly localized (Figure 2A,B). This suggested that our disordered prediction covered most of the disordered proteins identified by Rg/N. However, many blue points that were predicted to be ordered by Rg/N were predicted to be disordered by NMA–NIA (a total of 1448 chains).
In addition, there were a few red points (12 chains) localized on the left of the zero vertical line, where the predicted disorder was only identified by Rg/N. Among these examples, six of them (including: 1B35:D, 1LU0:A, 2GYP:A, 2PNV:A, 2QIH:B, and 3CI9:B) contained biological units, which were believed to be the functional forms of proteins. We used asymmetric units (which may be either a part of the biological units or include several biological units) for the calculations. To examine whether the inconsistence was caused by the difference of biological units and asymmetric units, we recalculated these examples using their biological unit files, and the result showed that they were indeed predicted to be disordered by NMA–NIA boundary distances (data not shown). For the other six examples, five of them (1E52:A, 1WDG:A, 2PM5:A, 1I8G:B, and 2JUP:W) were very close to the threshold of Rg/N, and the remaining one protein (1M8O:B) could be a prediction error by NMA–NIA because NMR has shown that it contains a C-terminal disordered segment (A737–T762).36 However, this protein was predicted to be disordered by the CH_value. Thus, except for the 12 inconsistent examples, our structure-based disorder prediction covered nearly all disordered chains found by Rg/N and additionally identified 1448 chains likely to be disordered.
In summary, the numbers of predicted-to-be-disordered chains by four whole protein prediction methods and by any two or more of them are given in Table 1. Only these four methods were listed here because VSL2b and VLXT were per-residue predictions, and their threshold for whole protein disorder is currently not well-defined. By these estimates, about 10–33% of the chains in the PDB are likely to be disordered when isolated from their binding partners.
Table 1. Numbers of Chains Predicted to be Disordered by Different Methods.
| methods | cut-off for predicted disorder | numbers of chains (fraction of whole set) |
|---|---|---|
| NMA–NIA | >0 | 2015 (32.8%) |
| Rg/N | >0.26 | 579 (9.4%) |
| CH_value | >0 | 643 (10.5%) |
| CDF_count | ≥4 and ≤7 | 1040 (16.9%) |
| anytwo or more methods | as indicated above | 1011 (16.5%) |
Some of these predictions are likely in error. Where multiple methods agree, those predictions are more likely to be correct. If so, errors are likely concentrated in idiosyncratic predictions. The relatively low numbers of idiosyncratic predictions from CDF and CH prediction methods are comparable to their characterized error rates.27 One certain source of error is in proteins that have a mix of ordered and disordered regions, where regions may be interspersed—in the case of structured domains with disordered loops—and/or segregated into ordered and disordered domains. These types of proteins are not directly considered by the methods compared in this work (Table 1); they are considered as only completely ordered proteins and disordered proteins in training. Methods will classify mixed proteins as ordered or disordered based on their predominant characteristic, with a metric specific to each method. However, we cannot address these classifications quantitatively because none of these methods has been calibrated on mixed ordered and disordered proteins. Qualitatively, many partial disordered proteins are likely present in the idiosyncratic predictions of disorder because of the diverse metrics of each method. For example, VLXT has the second largest proportion of idiosyncratic predictions, which is likely due to its threshold of 35% of the predicted disordered residues that makes it oversensitive to partially disordered proteins. Similarly, perhaps, a large number of NMA–NIA idiosyncratic predictions are due in part to the use of a relatively low threshold.
The validation datasets indicate fairly accurate predictions for all of the methods with generally better predictions on the ordered partners (Table 2). The Rg/N method does very well for the ordered protein prediction for complexes with structured proteins and for complexes with an ordered protein and an IDP. It also does well for IDP prediction for complexes involving one IDP and one ordered protein. However, NMA–NIA performs much better than Rg/N for complexes formed from two IDPs (Table 2). Examination of several complexes for which Rg/N gives errors shows that such errors occur when the chains are relatively compact but without making large numbers of intramolecular contacts, which leads to low Rg/N values indicating order.
Table 2. Comparison of Different Methods on Validation Datasets.
| accuracy
for DIBS dataset (698 complexes of IDP
binding to ordered proteins) |
accuracy
for MFIB dataset (157 complexes of IDP
binding to IDPs) |
accuracy for fully ordered dataset (543 complexes) | |||||
|---|---|---|---|---|---|---|---|
| methods | disorder prediction on IDPs (%) | order prediction on IDP partners (%) | complex predictionc (%) | disorder prediction on IDPs (%) | disorder prediction on IDP partners (%) | complex prediction (%) | order prediction (%) |
| NMA–NIA | 99.7 | 92.1 | 91.8 | 84.1 | 77.7 | 77.1 | 91.6 |
| Rg/N | 99.1 | 96.8 | 93.7 | 34.4 | 46.6 | 29.3 | 98.8 |
| CDFb | 70.1 | 83.4 | 58.1 | 42.9 | 41.1 | 35.3 | 89.2 |
| CH_value | 67.5 | 84.8 | 57.3 | 34.0 | 37.4 | 28.2 | 95.6 |
Bold and underline highlights indicate the best prediction accuracy by different methods for different datasets in the columns.
CDF predictor does not have results for short chains (<30 amino acids). The percentage showing here only includes chains that are longer than 30 amino acids.
Complex prediction means that both components in the protein complexes are correctly predicted.
Overall, NMA–NIA is much more sensitive to the disordered monomers than Rg/N. This is due to the extended structure being sufficient but not necessary for monomer disorder; as observed, both extended and relatively compact proteins that lack intramolecular contacts are both manifestations of disordered monomers.
Additionally, the data in Table 1 have important implications for building datasets for assessing per residue predictions of disorder.33 The large fraction of chains in PDB complexes that show significant disorder emphasizes that the PDB, on the whole, cannot be viewed as a gold standard for ordered proteins. Many assessments of disorder predictions recognize this and consider only single-chain monomer structures from the PDB as fully ordered protein datasets.27,32,34 The structure-based analysis, such as NMA–NIA, could be used to include many disordered proteins from complex structures, which would increase the coverage of IDPs in prediction assessments. Hopefully, thus would increase the robustness of such assessments.
Predicted-to-be-Disordered Proteins Likely Form Structures Stablized by Various Facors
For the 1448 chains predicted to be disordered by NMA–NIA and ordered by Rg/N, we first defined two groups of disorder-to-order transitions, namely protein/DNA/RNA binding and heterogroup binding. These were identified by comparing the boundary distances of the polymer_only (see the raw data in the Supporting Information, column E in sheet 3) with those of the heterogroups as partners (see the raw data in the Supporting Information, column E in sheet 4). A plot of NMA–NIA boundary distances for target chains including protein/DNA/RNA only (polymer_only) and target chains including heterogroups as partners (hetero_as_partner) was generated (Figure 3). Over a third of proteins showed a shift toward larger boundary distance (points above the diagonal) when considering small molecules as binding partners, suggesting small molecules can contribute strongly to protein stability. Interestingly, 145 chains (points in the upper left quadrant) were observed to change from the predicted order (NMA–NIA boundary distance < 0, when calculations were based on polymer_only without heterogroups) to predicted disorder (NMA–NIA boundary distance > 0 when considering heterogroups as partners). These boundary distance differences suggested two possible situations: (1) heterogroup binding is the major factor of disorder/order transition, and (2) heterogroup binding is just a contributing factor. This result is consistent with the fact that conformational changes are often observed when proteins are associated with small-molecule (a common heterogroup) binding.37
Figure 3.
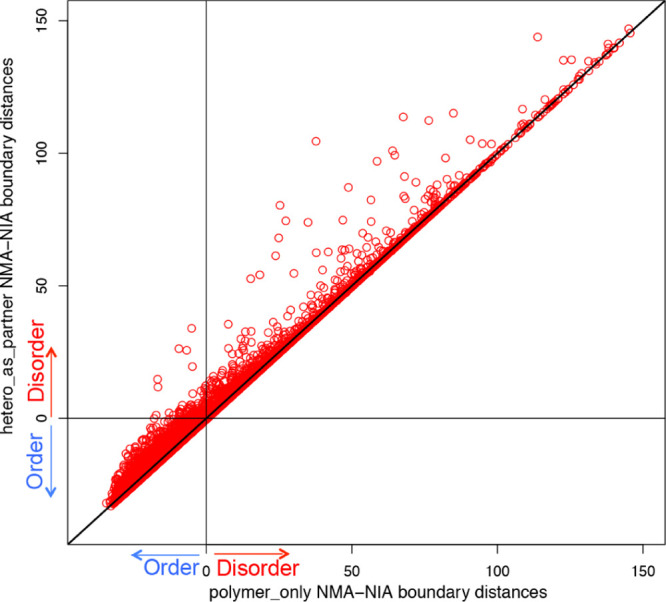
Changes of NMA–NIA boundary distances between polymer_only and hetero_as_partner. Each point represents a PDB chain. The x-axis indicates the NMA–NIA boundary distances for target chains considering protein/DNA/RNA only (polymer_only). The y-axis indicates the NMA–NIA boundary distances for target chains considering hetero groups as partner (hetero_as_partner). The chains located on the diagonal line are those without distance changes, which means their heterogroup binding does not induce the disorder/order transition of these protein chains. All the other points (>1/3) showed distance changes, suggesting that the heterogroup binding contributes to the disorder/order transition. Particularly, the points in the upper left quadrant changed from prediction of order (x-axis < 0) to prediction of disorder (y-axis > 0), when considering heterogroups as binding partners. This means that for these (totally 145 chains), heterogroup binding is likely to induce them undergo order-to-disorder transition.
Further, structural formation of the predicted-to-be-disordered proteins was proposed to be associated with several other factors (Table 3). Ion binding and DNA/RNA/protein binding are listed because these factors were proposed to induce disordered domains to undergo disorder-to-order transition.35 The disulfide-bond group was excluded in the previous study, considering them to be false positives.20 In contrast, we included them in our current study because they were likely IDPs or IDRs that are stabilized by disulfide bonds. The investigation of experimental evidences (mainly by literature searching) for disorder-to-order transition induced by these various factors is still ongoing.
Table 3. Groups of Predicted-to-be-Disordered Structures Likely Stabilized by Various Factors.
| groups | numbers of PDB chains |
|---|---|
| hetero group bindinga | 145 |
| DNA/RNA binding | 88 |
| protein binding | 863 |
| disulfide bonds | 147 |
| ion bindingb | 290 |
Group a and b were identified by different methods. Group a was identified by the NMA–NIA boundary distances, while group b was identified by “LINK” annotation in PDB files. These two groups had 14 identical chains.
Analysis of Trimer Structures
NMA–NIA boundary distances have been mainly used for dimer structures. We extended this to the analysis of trimers, by breaking interactions into three sets of interfaces, with one chain interaction surface with the other two chains. In total, 58 trimers consisting of three different chains were collected, and binding of each target chain with the remaining two partner chains was represented in the triangle plot in Figure 4. As can be seen, the shapes of these triangles are diverse, and their area had a wide range (from 0.06 to 2086.94). The partners involved in a single triangle span multiple quadrants, suggesting diversity in the order/disorder composition of complexes.
Figure 4.
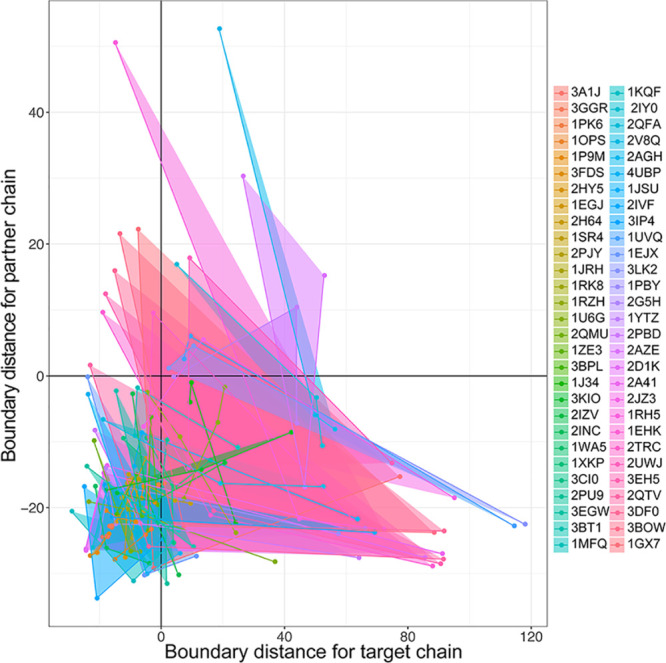
Converting triad binding into binary interactions by NMA–NIA boundary distances. These three different chain complexes are represented as triangles in the plot because each chain in these complexes is alternatively taken as the one-component target and the remaining two chains are taken as partners. The x-axis and y-axis are the NMA–NIA boundary distances for the one-component target chains and two-component partner chains, respectively. The figure legend on the right indicates the PDB ids of these complexes.
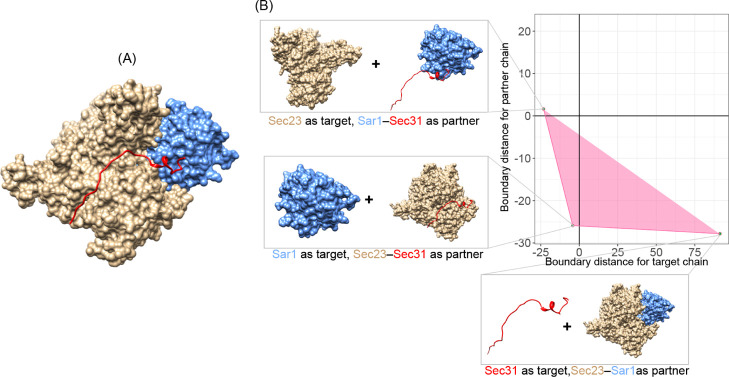
To elaborate how the triangle can be used to interpret trimer-binding interactions, we have shown the Sec23–Sar1–Sec31 complex as an example in Figure 5. Figure 5A shows the crystal structure of the whole complex. Figure 5B shows the shape of the triangle, and each individual chain was separated from its two-component partners. The positions of each point in the triangle indicated three types of binary binding interactions:
-
1
upper left: order binds to disorder. While considering Sec23 (tan in Figure 5) as the target chain and Sar1–Sec31 as its partner, our approach predicted Sar1–Sec31 to be “disordered”. With only the N terminal of Sec31 (residues 907–919) binding to Sar1, it looks like Sar1–Sec31 interacting with Sec23 with a long “disordered tail”.
-
2
bottom left: order binds to order. While taking Sar1 (blue in Figure 5) as the target chain and Sec23–Sec31 as its partner, both components are predicted to be ordered. Indeed, most part of Sec31 (20 out of 36 residues) forms intimate contact to Sec23.38 This makes Sec23–Sec31 look just similar to the one globular protein.
-
3
bottom right: disorder binds to order. That is, Sec31 (red in Figure 5) is predicted to be disordered, and its partner Sar1–Sec23 is predicted to be ordered. This is in agreement with the fact that isolated Sec31 is likely to be disordered in solution.38
Figure 5.
Decomposition of binding interactions by NMA–NIA boundary distances. (A) Whole complex structure of Sec23–Sar1–Sec31. PDB id: 2QTV. Tan: protein Sec23. Blue: small COPII coat GTPase Sar1. Red: protein Sec31. (B) Interpretation of the binding interactions by alternatively dividing the three-partner-containing complex into one-component chain and two-component partner.
This investigation of the binding manners for triad complexes extended the application of NMA–NIA boundary distances, which is used only to present two partners of a complex in the plot. Now, we can use it to examine complexes containing more than two partners. Further work may make an effort to examine the binding in complexes having even more components.
Conclusions
The current work provides a survey of intrinsic disorder in the PDB complexes based on both structure-based and sequence-based disorder predictions. Also included are suggestions for the molecular mechanisms of structural formation. Our recent work35 investigated the intrinsic disorder in conserved Pfam domains starting from predictions of the sequences and then investigation of the predictions of disorder based on the domain structures. Both of these studies identified many IDP structures that undergo disorder-to-order transitions that depend on a variety of factors. Our results emphasize the importance of intrinsic disorder in complex formation. The induced folding mechanisms identified so far suggest unusual structure–function relationships for IDPs or IDRs.
Acknowledgments
We thank Dr. Eric T. C. Wong from the University of British Columbia (Canada) for providing the original data with calculation of radius of gyration for the nonredundant set PDB files.
Glossary
Abbreviations
- IDPs or IDRs
intrinsically disordered proteins or regions
- PDB
Protein Data Bank
- Rg/N
radius of gyration (Rg) divided by protein length (N)
- NMA–NIA
normalized monomer area and normalized interface area
- CDF
cumulative distribution function
- CH
charge–hydropathy
- PONDR
prediction of naturally disordered regions
- Vsl2b
predictor for various short and long regions, version 2b
- VLXT
PONDR predictors trained on variously characterized long disordered regions and X-ray characterized terminal disordered regions
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.9b03927.
Raw prediction data. Results of Rg/N (Distance_RgN) and NMA-NIA boundary distances. Calculations of the surface/interface area for the target chains in three different kinds of situations: (1) only included proteins or nucleic acids for both target and partner chains (polymer_only); (2) included heterogroups with the partner chains (hetero_as_partner); and (3) included heterogroups with their parent target chains (hetero_as_target).(XLSX)
Author Present Address
⊥ PLOS, 1160 Battery street, San Francisco, CA, 94111 US.
Author Contributions
C.J.O. provided the methods (NMA–NIA, and the sequence-based predictors) and performed the disorder predictions. J.Z. did the remaining data analysis and wrote the major sections of the manuscript. All authors helped with the editing and improved the manuscript significantly; especially, C.J.O. and A.K.D. helped the Background and Discussion sections. B.S. and A.K.D. supervised the project together. All authors approved the final version of the manuscript.
This work is supported by the joint PhD program of the China Scholarship Council (no. 201306920022) and Professor A. Keith Dunker during Jianhong Zhou’s visit to Indiana University and the National Natural Science Foundation of China (grant no. 31670851).
The authors declare no competing financial interest.
Supplementary Material
References
- Dunker A. K.; Lawson J. D.; Brown C. J.; Williams R. M.; Romero P.; Oh J. S.; Oldfield C. J.; Campen A. M.; Ratliff C. M.; Hipps K. W.; Ausio J.; Nissen M. S.; Reeves R.; Kang C.; Kissinger C. R.; Bailey R. W.; Griswold M. D.; Chiu W.; Garner E. C.; Obradovic Z. Intrinsically disordered protein. J. Mol. Graphics Modell. 2001, 19, 26–59. 10.1016/s1093-3263(00)00138-8. [DOI] [PubMed] [Google Scholar]
- Tompa P. Intrinsically unstructured proteins. Trends Biochem. Sci. 2002, 27, 527–533. 10.1016/s0968-0004(02)02169-2. [DOI] [PubMed] [Google Scholar]
- Uversky V. N. Intrinsically disordered proteins from A to Z. Int. J. Biochem. Cell Biol. 2011, 43, 1090–1103. 10.1016/j.biocel.2011.04.001. [DOI] [PubMed] [Google Scholar]
- Babu M. M. Intrinsically disordered proteins. Mol. BioSyst. 2012, 8, 21. 10.1039/c1mb90045e. [DOI] [PubMed] [Google Scholar]
- Tompa P. Intrinsically disordered proteins: a 10-year recap. Trends Biochem. Sci. 2012, 37, 509–516. 10.1016/j.tibs.2012.08.004. [DOI] [PubMed] [Google Scholar]
- Oldfield C. J.; Dunker A. K. Intrinsically disordered proteins and intrinsically disordered protein regions. Annu. Rev. Biochem. 2014, 83, 553–584. 10.1146/annurev-biochem-072711-164947. [DOI] [PubMed] [Google Scholar]
- Tompa P.; Schad E.; Tantos A.; Kalmar L. Intrinsically disordered proteins: emerging interaction specialists. Curr. Opin. Struct. Biol. 2015, 35, 49–59. 10.1016/j.sbi.2015.08.009. [DOI] [PubMed] [Google Scholar]
- Dunker A. K.; Bondos S. E.; Huang F.; Oldfield C. J. Intrinsically disordered proteins and multicellular organisms. Semin. Cell Dev. Biol. 2015, 37, 44–55. 10.1016/j.semcdb.2014.09.025. [DOI] [PubMed] [Google Scholar]
- Sharma R.; Raduly Z.; Miskei M.; Fuxreiter M. Fuzzy complexes: Specific binding without complete folding. FEBS Lett. 2015, 589, 2533–2542. 10.1016/j.febslet.2015.07.022. [DOI] [PubMed] [Google Scholar]
- Borgia A.; Borgia M. B.; Bugge K.; Kissling V. M.; Heidarsson P. O.; Fernandes C. B.; Sottini A.; Soranno A.; Buholzer K. J.; Nettels D.; Kragelund B. B.; Best R. B.; Schuler B. Extreme disorder in an ultrahigh-affinity protein complex. Nature 2018, 555, 61–66. 10.1038/nature25762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mittag T.; Orlicky S.; Choy W. Y.; Tang X.; Lin H.; Sicheri F.; Kay L. E.; Tyers M.; Forman-Kay J. D. Dynamic equilibrium engagement of a polyvalent ligand with a single-site receptor. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 17772–17777. 10.1073/pnas.0809222105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunker A. K.; Obradovic Z.; Romero P.; Garner E. C.; Brown C. J. Intrinsic protein disorder in complete genomes. Genome Inf. Ser. Proc. Workshop Genome Inf. 2000, 11, 161–171. [PubMed] [Google Scholar]
- Ward J. J.; Sodhi J. S.; McGuffin L. J.; Buxton B. F.; Jones D. T. Prediction and functional analysis of native disorder in proteins from the three kingdoms of life. J. Mol. Biol. 2004, 337, 635–645. 10.1016/j.jmb.2004.02.002. [DOI] [PubMed] [Google Scholar]
- Peng Z.; Mizianty M. J.; Xue B.; Kurgan L.; Uversky V. N. More than just tails: intrinsic disorder in histone proteins. Mol. BioSyst. 2012, 8, 1886–1901. 10.1039/c2mb25102g. [DOI] [PubMed] [Google Scholar]
- Peng Z.; Yan J.; Fan X.; Mizianty M. J.; Xue B.; Wang K.; Hu G.; Uversky V. N.; Kurgan L. Exceptionally abundant exceptions: comprehensive characterization of intrinsic disorder in all domains of life. Cell. Mol. Life Sci. 2015, 72, 137–151. 10.1007/s00018-014-1661-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeForte S.; Uversky V. N. Not an exception to the rule: the functional significance of intrinsically disordered protein regions in enzymes. Mol. BioSyst. 2017, 13, 463–469. 10.1039/c6mb00741d. [DOI] [PubMed] [Google Scholar]
- Uversky V. N.; Oldfield C. J.; Dunker A. K. Showing your ID: intrinsic disorder as an ID for recognition, regulation and cell signaling. J. Mol. Recognit. 2005, 18, 343–384. 10.1002/jmr.747. [DOI] [PubMed] [Google Scholar]
- Iakoucheva L. M.; Brown C. J.; Lawson J. D.; Obradović Z.; Dunker A. K. Intrinsic disorder in cell-signaling and cancer-associated proteins. J. Mol. Biol. 2002, 323, 573–584. 10.1016/s0022-2836(02)00969-5. [DOI] [PubMed] [Google Scholar]
- Wright P. E.; Dyson H. J. Intrinsically disordered proteins in cellular signalling and regulation. Nat. Rev. Mol. Cell Biol. 2014, 16, 18–29. 10.1038/nrm3920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong E. T. C.; Na D.; Gsponer J. On the importance of polar interactions for complexes containing intrinsically disordered proteins. PLoS Comput. Biol. 2013, 9, e1003192 10.1371/journal.pcbi.1003192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gunasekaran K.; Tsai C.-J.; Nussinov R. Analysis of ordered and disordered protein complexes reveals structural features discriminating between stable and unstable monomers. J. Mol. Biol. 2004, 341, 1327–1341. 10.1016/j.jmb.2004.07.002. [DOI] [PubMed] [Google Scholar]
- Mohan A.; Oldfield C. J.; Radivojac P.; Vacic V.; Cortese M. S.; Dunker A. K.; Uversky V. N. Analysis of molecular recognition features (MoRFs). J. Mol. Biol. 2006, 362, 1043–1059. 10.1016/j.jmb.2006.07.087. [DOI] [PubMed] [Google Scholar]
- Oldfield C. J.; Meng J.; Yang J. Y.; Yang M. Q.; Uversky V. N.; Dunker A. K., Flexible nets: disorder and induced fit in the associations of p53 and 14-3-3 with their partners. BMC Genomics 2008,9 Suppl 1, S1. 10.1186/1471-2164-9-s1-s1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng Z.; Oldfield C. J.; Xue B.; Mizianty M. J.; Dunker A. K.; Kurgan L.; Uversky V. N. A creature with a hundred waggly tails: intrinsically disordered proteins in the ribosome. Cell. Mol. Life Sci. 2014, 71, 1477–1504. 10.1007/s00018-013-1446-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fichó E.; Reményi I.; Simon I.; Mészáros B. MFIB: a repository of protein complexes with mutual folding induced by binding. Bioinformatics 2017, 33, 3682–3684. 10.1093/bioinformatics/btx486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schad E.; Fichó E.; Pancsa R.; Simon I.; Dosztányi Z.; Mészáros B. DIBS: a repository of disordered binding sites mediating interactions with ordered proteins. Bioinformatics 2018, 34, 535–537. 10.1093/bioinformatics/btx640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oldfield C. J.; Cheng Y.; Cortese M. S.; Brown C. J.; Uversky V. N.; Dunker A. K. Comparing and combining predictors of mostly disordered proteins. Biochemistry 2005, 44, 1989–2000. 10.1021/bi047993o. [DOI] [PubMed] [Google Scholar]
- Velankar S.; Dana J. M.; Jacobsen J.; van Ginkel G.; Gane P. J.; Luo J.; Oldfield T. J.; O’Donovan C.; Martin M. J.; Kleywegt G. J. SIFTS: Structure Integration with Function, Taxonomy and Sequences resource. Nucleic Acids Res. 2013, 41, D483–D489. 10.1093/nar/gks1258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mészáros B.; Simon I.; Dosztányi Z. Prediction of protein binding regions in disordered proteins. PLoS Comput. Biol. 2009, 5, e1000376 10.1371/journal.pcbi.1000376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sickmeier M.; Hamilton J. A.; LeGall T.; Vacic V.; Cortese M. S.; Tantos A.; Szabo B.; Tompa P.; Chen J.; Uversky V. N.; Obradovic Z.; Dunker A. K. DisProt: the Database of Disordered Proteins. Nucleic Acids Res. 2007, 35, D786–D793. 10.1093/nar/gkl893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feig M.; Karanicolas J.; Brooks C. L. 3rd MMTSB Tool Set: enhanced sampling and multiscale modeling methods for applications in structural biology. J. Mol. Graphics Modell. 2004, 22, 377–395. 10.1016/j.jmgm.2003.12.005. [DOI] [PubMed] [Google Scholar]
- Xue B.; Dunbrack R. L.; Williams R. W.; Dunker A. K.; Uversky V. N. PONDR-FIT: a meta-predictor of intrinsically disordered amino acids. Biochim. Biophys. Acta 2010, 1804, 996–1010. 10.1016/j.bbapap.2010.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oldfield C. J.; Ulrich E. L.; Cheng Y.; Dunker A. K.; Markley J. L. Addressing the intrinsic disorder bottleneck in structural proteomics. Proteins: Struct., Funct., Genet. 2005, 59 (3), 444–453. 10.1002/prot.20446. [DOI] [PubMed] [Google Scholar]
- Peng Z.-L.; Kurgan L. Comprehensive comparative assessment of in-silico predictors of disordered regions. Curr. Protein Pept. Sci. 2012, 13, 6–18. 10.2174/138920312799277938. [DOI] [PubMed] [Google Scholar]
- Xue B.; Oldfield C. J.; Dunker A. K.; Uversky V. N. CDF it all: consensus prediction of intrinsically disordered proteins based on various cumulative distribution functions. FEBS Lett. 2009, 583, 1469–1474. 10.1016/j.febslet.2009.03.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou J.; Oldfield C. J.; Huang F.; Yan W.; Shen B.; Dunker A. K. In Intrinsic disorder in conserved Pfam domains, In International Conference on Bioinformatics & Computational Biology, Las Vegas, Hamid R., Arabnia F. G. T., Quoc-Nam T., Yang M., Eds.; CSREA: Las Vegas, 2018; pp 3–9.
- Vinogradova O.; Velyvis A.; Velyviene A.; Hu B.; Haas T. A.; Plow E. F.; Qin J. A structural mechanism of integrin alpha(IIb)beta(3) ″inside-out″ activation as regulated by its cytoplasmic face. Cell 2002, 110, 587–597. 10.1016/s0092-8674(02)00906-6. [DOI] [PubMed] [Google Scholar]
- Nicklaus M. C.; Wang S.; Driscoll J. S.; Milne G. W. A. Conformational changes of small molecules binding to proteins. Bioorg. Med. Chem. 1995, 3, 411–428. 10.1016/0968-0896(95)00031-b. [DOI] [PubMed] [Google Scholar]
- Bi X.; Mancias J. D.; Goldberg J. Insights into COPII coat nucleation from the structure of Sec23.Sar1 complexed with the active fragment of Sec31. Dev. Cell 2007, 13, 635–645. 10.1016/j.devcel.2007.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.