Towards Predicting the Evolution of Lung Tumors During Radiotherapy Observed on a Longitudinal MR Imaging Study Via a Deep Learning Algorithm

Abstract

Purpose:

To predict the spatial and temporal trajectories of lung tumor during radiotherapy monitored under a longitudinal MRI study via a deep learning algorithm for facilitating adaptive radiotherapy (ART).

Methods:

We monitored ten lung cancer patients by acquiring weekly MRI-T2w scans over a course of radiotherapy. Under an ART workflow, we developed a predictive neural network (P-net) to predict the spatial distributions of tumors in the coming weeks utilizing images acquired earlier in the course. The 3-step P-net consisted of a convolutional neural network to extract relevant features of the tumor and its environment, followed by a recurrence neural network constructed with gated recurrent units to analyze trajectories of tumor evolution in response to radiotherapy, and finally an attention model to weight the importance of weekly observations and produce the predictions. The performance of P-net was measured with Dice and root mean square surface distance (RMSSD) between the algorithm-predicted and experts-contoured tumors under a leave-one-out scheme.

Results:

Tumor shrinkage was 60% ± 27% (mean ± standard deviation) by the end of radiotherapy across nine patients. Using images from the first three weeks, P-net predicted tumors on future weeks (4, 5, 6) with a Dice and RMSSD of (0.78±0.22, 0.69±0.24, 0.69±0.26), and (2.1±1.1mm, 2.3± 0.8mm, 2.6± 1.4mm), respectively.

Conclusion:

The proposed deep learning algorithm can capture and predict spatial and temporal patterns of tumor regression in a longitudinal imaging study. It closely follows the clinical workflow, and could facilitate the decision making of ART. A prospective study including more patients is warranted.

I. INTRODUCTION

Radiotherapy is advancing towards incorporating longitudinal image studies into its effort to consistently deliver tumoricidal dose to the tumor while sparing the adjacent organs at risk (OAR). A snapshot of the tumor/OAR at the simulation phase still serves a fundamental role as defining a target in an initial treatment plan, but loses its dominance because morphological changes observed on daily/weekly surveillance scans can also trigger a replanning process to ensure appropriate dosage. Furthermore, as we accumulate multiple snapshots of the tumor/OAR in a longitudinal study, we hypothesize that the underlying spatial and temporal patterns of evolution can be extracted on the basis of both patient population and the particular patient of interest, eventually extrapolated to a patient-specific spatial distribution of tumor at a later time point in the treatment course. Adaptive radiotherapy (ART) may potentially benefit from the timely predictions because the earlier the changes can be determined, the sooner the action such as replanning can be taken, and the better the therapeutic ratio can be achieved. We have reported a patient population-based atlas model to predict residual tumor after radiotherapy via principal component analysis of tumor geometry at simulation, and its potential clinical usage to benefit patients with significant dose escalations to the residual tumor.^1–3 In this paper, we investigate the feasibility of expanding the prediction model to incorporate all available image scans in the longitudinal study and make a series of weekly predictions along the remaining treatment course.

Prediction of a time series using recurrence neural networks (RNN) has been primarily investigated in the context of natural language processing,^4–8 financial stock market prediction,^9–10 and computer vision problems including object recognition,^11,12 tracking,^13,14 and image caption.¹⁵ Recently RNN has been rapidly extended to healthcare applications and achieved a great success in electronic health records analysis,^16,17 disease progression analysis,^18,19 and analysis of tumor cell growth.²⁰ RNN constructs a series of sequentially-connected nodes to store the time-dependent status of an object, and explicitly forms a dynamic representation of the studied object in the deep learning algorithm. In the supervised learning process, because the future states of the object are calculated as a nonlinear function of the weighted sum of the past, the embedded history information is well preserved and ready for relevant predictions. Meanwhile, convolutional neural network (CNN) is best-suited for extracting both global and fine features of an object. Frameworks that combined CNN (encoding spatial information) and RNN (encoding temporal information) have achieved significant success in video prediction.^21–23 Inspired by these studies, we developed a customized deep learning algorithm that integrated both CNN and RNN units to predict the spatial tumor distribution in a longitudinal imaging study, and evaluated the impact of the structural design on the predictive accuracy. Furthermore, we assessed the characteristics of the prediction including its timing, frequency, and spatial accuracy to prepare for its integration into the clinical workflow of ART.

II. METHOD AND MATERIALS

2.1. Weekly MRI study

The prediction algorithm was based on weekly magnetic resonance imaging (MRI) data acquired via a retrospective IRB approved longitudinal study that monitors geometrical changes of tumor for patients with locally advanced non-small cell lung cancer. MRI was selected to help the visualization and segmentation of mediastinal tumors because of its superior soft tissue contrast compared to CT or CBCT. Patients received 2Gy/fraction in a 30-fraction radiotherapy course of 6–7 weeks with concurrent chemotherapy. A respiratory triggered (at exhalation) T2-weighted MRI scan (TR/TE=3000–6000/120ms, 43 slices, NSA=2, FOV=300×222×150mm³) was acquired weekly with a resolution of 1.1×1.0×2.5mm³ on a Philips Ingenia 3 Tesla MRI scanner. All weekly MRI images were rigidly registered to the first weekly scan with respect to the tumor to minimize the motion effect.²⁴ Tumors were segmented by radiation oncologists, serving as ground truth. Subsequently an ROI around the tumor was cropped and standarized to prepare for studying the regression patterns of the primary tumors.

The primary tumors of all ten patients exhibited shrinkage ranging from 15% to 92% with a median of 55% at the end relative to the start of the treatment. However, on a weekly basis, the patterns of tumor evolution were neither unidirectional (three patients, #5, #6, and #9 showed noticeable early tumor expansion) nor homogeneous as illustrated in Figure 1. The weekly shrinkage did not correlate with tumor volume or the number of weeks into radiotherapy. Most of the weekly shrinkages occurred between weeks 2 and 4.

Figure 1.

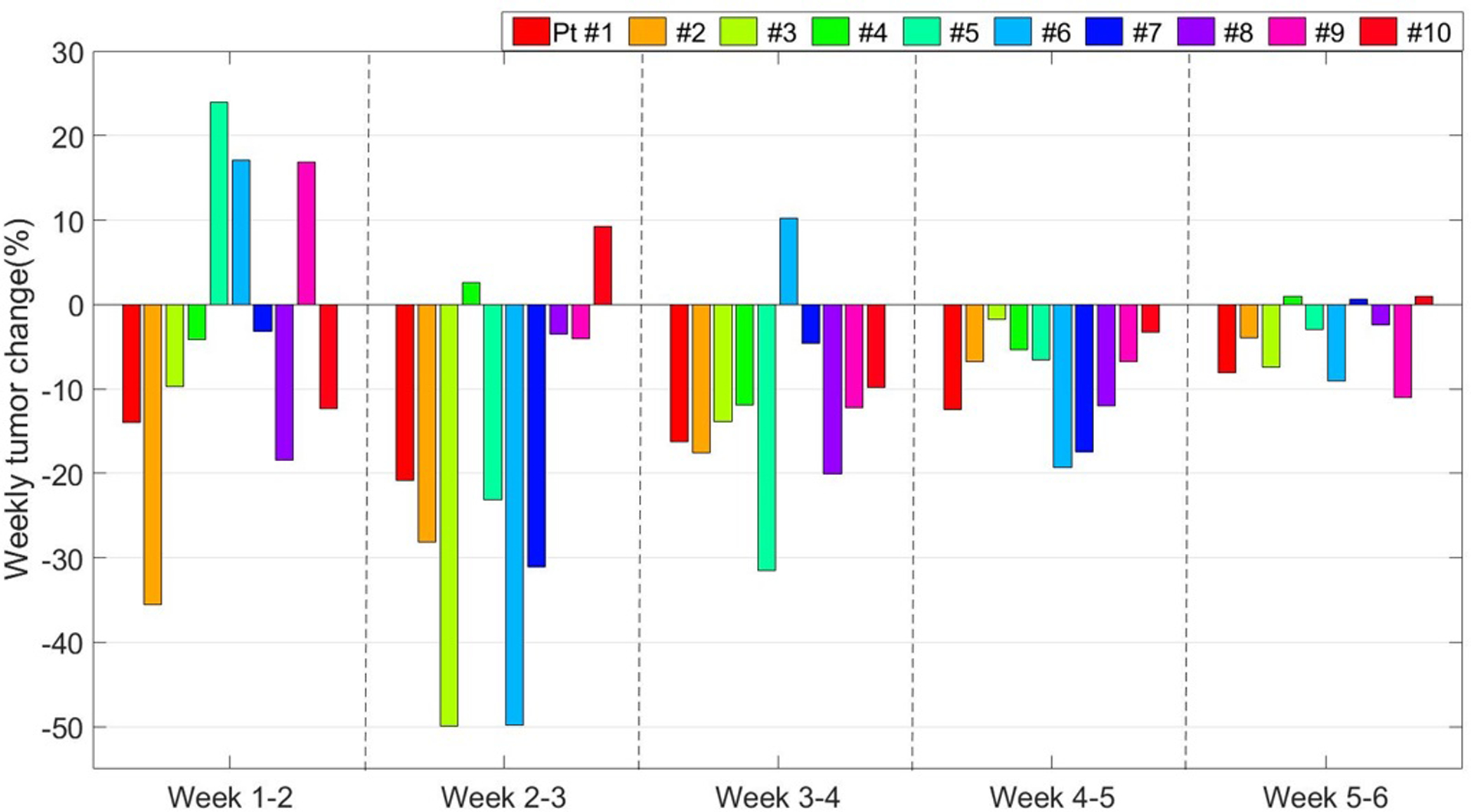
The patient specific weekly tumor volume changes during lung radiotherapy. The weekly changes are calculated with respect to the first week.

2.2. Prediction via P-net

2.2.1. P-net structure

We developed a deep learning algorithm called P-net as illustrated in Figure 2 to make a series of predictions of spatial tumor distributions in the later part of the radiotherapy course. P-net was specifically designed to match the clinical workflow and facilitate the decision making of ART. We implemented P-Net using the open-source neural-machine translation toolbox²⁵ on the python platform. P-net consisted of three major components: (1) a six-layer CNN to extract relevant features on the weekly MRI scans; (2) a RNN constructed with gated recurrent unit (GRU²⁶) to store and process the trajectories of tumor evolution in response to radiotherapy; and (3) an attention model to weight the importance of weekly observations and produce the final predictions.

Figure 2.

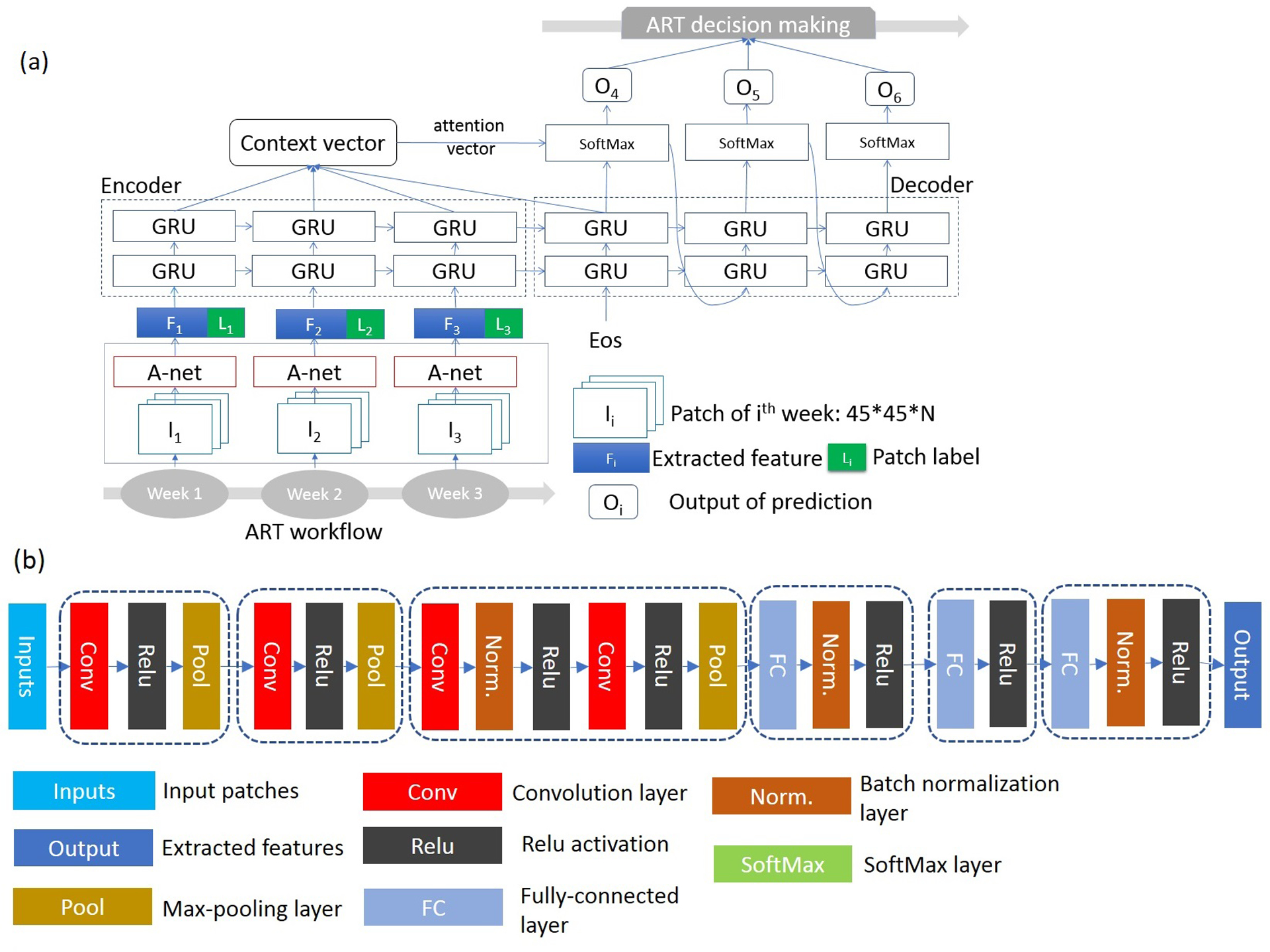
(a) Design of a patient-specific deep learning algorithm (P-Net) for predicting tumor in future weeks of radiotherapy. (b) Block diagram of a 6-level deep CNN for extracting image feature in a longitudinal study.

Many pilot investigations in medical imaging that utilize deep learning algorithms suffer from the restrictions of the small number of patients recruited in the study. To overcome the limitation of a small dataset, methodologies that utilize finer patches rather than whole images have been developed and tested in a variety of applications including neuroanatomy segmentation,²⁷ cartilage voxel classification,²⁸ image template matching,²⁹ and assessing image deformations.³⁰ Although patches are likely highly correlated, they contain sufficient features as a diversified group and provide enough data for training the neural networks and achieve reasonable accuracies.^31,32 Similarly we adapted a 3D patches-based approach for prediction. We first constructed a volume of interest (VOI) as a union of the gross tumor volume (GTV) observed on the first three weekly scans and expanded with margins proportional to the dimension of the tumor.³² The number of voxels inside the VOI from each individual patient ranged from 8K to 80K. Centered around each voxel inside the VOI, a 3D patch was formed by cropping out three consecutive 2D slices: the 45×45 pixels transverse image, and the two-immediate above and below neighbor images, to incorporate all the intensity and environmental information useful for prediction. A patch was classified either as tumor or background according to the label of its center. We generated image patches from the same location on the first three weekly MRI scans as inputs to P-net. The number of patches created from all ten patients were approximately 440K, which covers a wide variety of shrinkage patterns and is well-suited for the task of training the deep learning algorithm. The output of P-net was the patch’s classification predicted for weeks 4, 5 and 6, which was successively assembled into a full spatial tumor distribution for each future week.

2.2.2. Six-layer CNN

To extract all the pertinent features of a patch, we modified a neural network originally designed for segmenting tumors in the same longitudinal study³² as shown in Figure 2b. The covariate shift is a common challenge for a prediction problem because the distribution of the underlying data may vary between the training and testing set, especially due to inter-patient or inter-fractional acquisition uncertainties. To mitigate the effect of the internal covariate shift, we added a process of batch normalization to equalize the intensity distribution.³³ The first four convolutional layers were configured with a standard 3×3 filter, and two pixels convolutional stride. Max pooling was performed over a 2×2 kernel with one-pixel stride. All convolutional and fully connected layers were followed by a nonlinearity rectification layer. The number of convolutional channels began with 64 in the first level, increased 2-fold in each subsequent level until finally reaching 512. The last three fully connected layers sequentially processed and produced high-level features, representing the temporal and spatial pattens for prediction.

2.2.3. Recurrent Neural Network

The extracted high-level features along with the binary labels were subsequently fed into RNN. The sequential labels were critical priors and explicitly included to reinforce the ability of prediction. The hierarchical structure of RNN includes two layers of GRU with 512 hidden units per layer to strengthen the processing power. The inputs from individual weeks passed through GRUs in a recursive route. GRU modulates the information flow via two gates: a reset to determine the portion of the previous memory to forgo, and an update gate to decide the portion of the history information to pass through. GRUs are trained to remove the irrelevant information for prediction, formulate a useful representation vector over time, and leverage the prediction. In a mathematical form, at a given time t, a hidden state h_t, was a direct output of each individual GRU, and expressed as a combination of its precursor and current input:

$$h_t=GRU\left(h_{t-1},I_t;\theta \right)$$ (1)

with h₀ as the initial state.

2.2.4. Attention model

Not all inputs from the time series contributed equally to the prediction results. An attention model parsed the weights of the inputs which were used to calculate the prediction. We applied a global attention³⁴ to approximate the attention distribution of all hidden states (h₁, …, h_T) from the encoder, and generated a context vector $c_t= \sum _{i=1}^T{a}_{t,i}{h}_{i }$, where the attention distribution weights a_t,I of each hidden state h_i is calculated by:

$$a_{t,i}=\frac{\mathit{\text{exp}}\left(\mathit{\text{score}}\right(h_t,h_i\left)\right)}{\sum _{i=1}^T\mathit{\text{exp}}\left(\mathit{\text{score}}\right(h_t,h_i\left)\right)}$$ (2)

where the score (·) is an alignment model, formulated as:

$$\mathit{\text{score}}\left(h_t, h_i\right)={\beta }^T\mathit{\text{tanh}}\left(w_1{h}_t+w_2{h}_i\right)$$ (3)

The application of the attention model relieved the burden of encoding all the information into a fixed length vector, and spread out the burden through all the encoder hidden layers. Subsequently, a decoder calculated the probability of there being tumor in a future output according to the previous outputs and hidden states via a SoftMax layer as:

$$p(o_{t+1}|y_1,\dots ,y_t,V)=\mathit{\text{softmax}}(W^{out}{o}_t)$$ (4)

where o_t = tanh(W^c[h_t;c_t]), and W^out, W^c are weighting parameters.

The direct output of P-net was mapped back to the original MRI scan and formed a binary mask of predicted tumors. Morphological filters such as imfill and bwareopen²⁵ were applied to fill the holes, and remove the background noise and small isolated islands.

2.2.4. Training and testing

P-net was trained and cross validated by using the leave-one-out strategy. A cross entropy loss function was selected for training, which was optimized with an ADAM algorithm³⁵ for both CNN and RNN. The initial and consistent learning rate and maximal number of epochs were set to 10⁻⁴, and 15, respectively. Training and testing were completed on an institutional Lilac GPU cluster equipped with 72 Ge-force GTX1080 GPUs, each GPU installed with 8GB memory.

2.2.5. Exploring variations of P-net structures

Variations to the architecture of P-net can substantially influence the behavior of the prediction algorithm. We explored some competitive alternatives to search for optimal settings and justify the selection of our design. These investigations include: (1) searching the optimal size of the input patch among 35×35×3, 35×35×5, 45×45×3, 45×45×5, and 55×55×3; (2) substituting GRU with Long-Short Term Memory (LSTM),³¹ another popular yet slightly complicated design for RNN; (3) revealing the functionality of the attention model via comparisons with skipping it in the design; (4) shortening the number of fully convolutional layers in CNN from 3 to 2; and (5) changing the timing of the prediction by utilizing two rather than three weekly scans to predict the rest of the radiotherapy course. We evaluated the impact of these changes in terms of the balance between calculation efficiency and predictive effectiveness of the deep learning algorithm.

2.3. Evaluation

To verify the prediction against expert-contoured tumor on the weekly MRI scans, we evaluated the performance of P-net by tabulating precision, Dice coefficient, and sensitivity to assess the predictive power, calculating root-mean-square surface distance (RMSSD) to measure the spatial uncertainty, and analyzed computational costs and speed of convergence to estimate the burden on the clinical workflow.

Because our purpose was to monitor and predict the spatial distribution of tumor, we aligned the weekly scans by rigidly registering the images according to the lung outer surface and spine, rather than the tumor itself. Even in a gated image acquisition protocol, residual interfractional uncertainties in the respiratory patterns can cause misalignments of the tumor. These registration errors contribute to uncertainties in calculating all the evaluation indices. We shifted the predictions of P-net with fixed steps in the lateral, anterior-posterior, and superior-inferior directions, re-calculated RMSSD, and analyzed the changes of RMSSD with respect to potential spatial errors as a measure to evaluate the impact of registration. Similarly, inter-observer contour variations also influence the predictive accuracy. We produced predictions using one observer’s contour, verified against a second observer’s segmentation, and calculated the spatial deviations to investigate this impact.

2.4. Prediction via deformable registration

Deformable registration is a popular clinical tool to fuse longitudinal imaging studies and analyze the geometric changes. As a control to P-net, we implemented a prediction method based on the deformable vector field (DVF). We first registered the 2^nd and 3^rd to the 1^st weekly MRI via Plastimatch (www.plastimatch.org) and obtained the corresponding DVF^1→2 and DVF^1→3. On a voxel basis, we extrapolated DVF using a linear-log model, derived predictions of DVF on the 4^th, 5^th, and 6^th week, shifted the tumor voxels according to the predicted DVFs, and eventually formed predictions of weekly tumor distributions. The results were compared to the actual weekly tumor distributions, and its predictive accuracy was compared to that of P-net.

III. RESULTS

The number of samples utilized for training and validating P-net averaged 315k and 84k, respectively. The training process converged at an accuracy of 97%. The accuracy of validation was 95%. The training and validation of P-net took around 11 hours on the high-performance computer cluster, while the testing on one patient (averaged 42K patches) only took 2 minutes, which is well-tolerated by the ART workflow with a weekly surveillance frequency. Predictions made via P-net with five choices of patch sizes are shown in Figure 3. Measured by the dice and RMSSD, a patch size of 45×45×3 results in the best predictive performance across the remaining weeks of the radiotherapy course.

Figure 3.

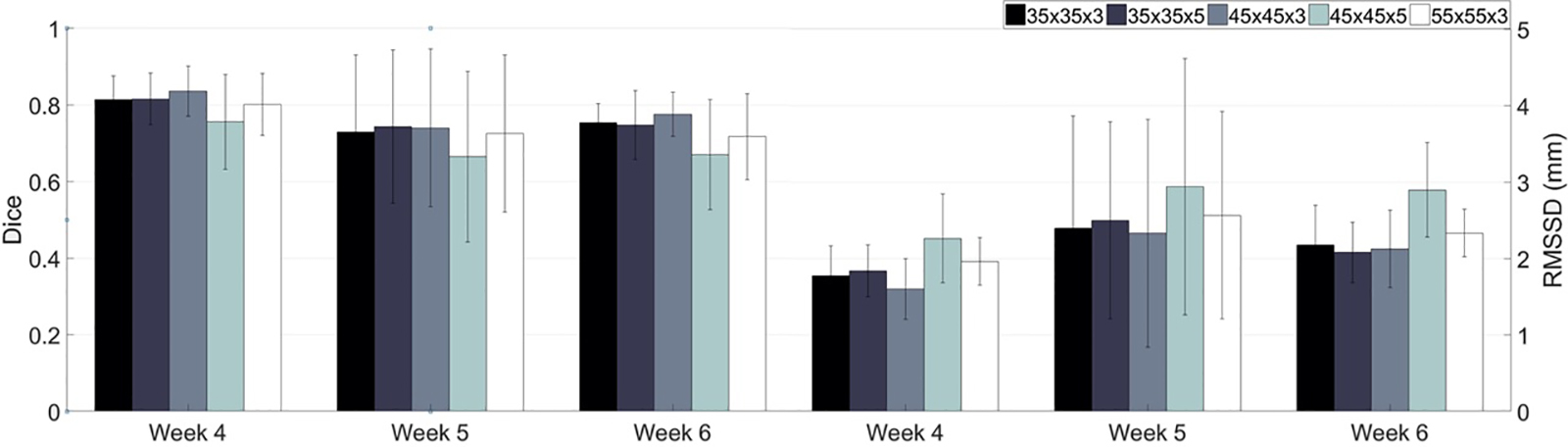
Performance of P-net peaks with a patch size of 45×45×3 measured by dice and RMSSD.

The detailed characteristics of predictions made with different timing schedules are listed in Table 1. When P-net was fed with the first three weekly MRI scans, the predictive performance scored the largest Dice and lowest RMSSD. The precision of the prediction and its robustness declined along weeks, evidenced by the moderate correlation between tumor shrinkage and RMSSD (0.54), despite no correlations between tumor volume and RMSSD (−0.12). Compared to predictions made from the first three weeks of images, predictions at an earlier time point in the treatment course and using only the first two weeks were more challenging, less accurate and less robust (as indicated by the larger standard deviations). There was a noticeable drop in performance when forecasting weeks 5 and 6 compared to weeks 3 and 4.

Table 1:

Characteristics of predictions made via P-net.

Predicting 3 future weeks based on first 3 weeks
	Dice	RMSSD (mm)	Precision	Sensitivity
Week 4	0.84±0.07	1.6±0.4	0.83±0.10	0.84±0.04
Week 5	0.74±0.21	2.3±1.5	0.74±0.22	0.76±0.20
Week 6	0.78±0.06	2.1±0.5	0.73±0.21	0.81±0.08
Predicting 4 future weeks based on first 2 weeks
	Dice	RMSSD (mm)	Precision	Sensitivity
Week3	0.76±0.11	2.4±0.5	0.77±0.14	0.75±0.08
Week 4	0.73±0.13	2.5±0.7	0.75±0.14	0.71±0.12
Week 5	0.67±0.19	3.3±1.5	0.66±0.20	0.68±0.18
Week 6	0.65±0.08	3.3±1.0	0.64±0.13	0.66±0.06

Replacing GRU with LSTM in the design of RNN had little impact on the predictive performance, but prolonged the training time by 25%. The attention model does provide a boost to the performance. If the attention model is removed from the P-net structure, the predictive accuracy suffers a loss of 0.07±0.02 in Dice, and a deterioration of 0.7±0.1mm in RMSSD, respectively. Installing three fully convolutional layers moderately outperformed two layers, which lifted Dice by 0.04±0.01, and lowered RMSSD by 0.4±0.3mm.

Examples of predictions made with an initial timing at week 4 (top row) for a typical case (patient #1) are shown in Figure 4 at the tumor center cut. When compared to the predictions made via the deformable registration approach (center row), P-net is more accurate and reliable, evidenced by the improvements of 0.10, 0.19, and 0.31 in Dice, and reductions of 0.4mm, 0.9mm, and 1.7mm in RMSSD, for week 4, 5, and 6, respectively. Predictions made with an initial timing at week 3 (bottom row) is also inferior to the timing of week 4.

Figure 4.

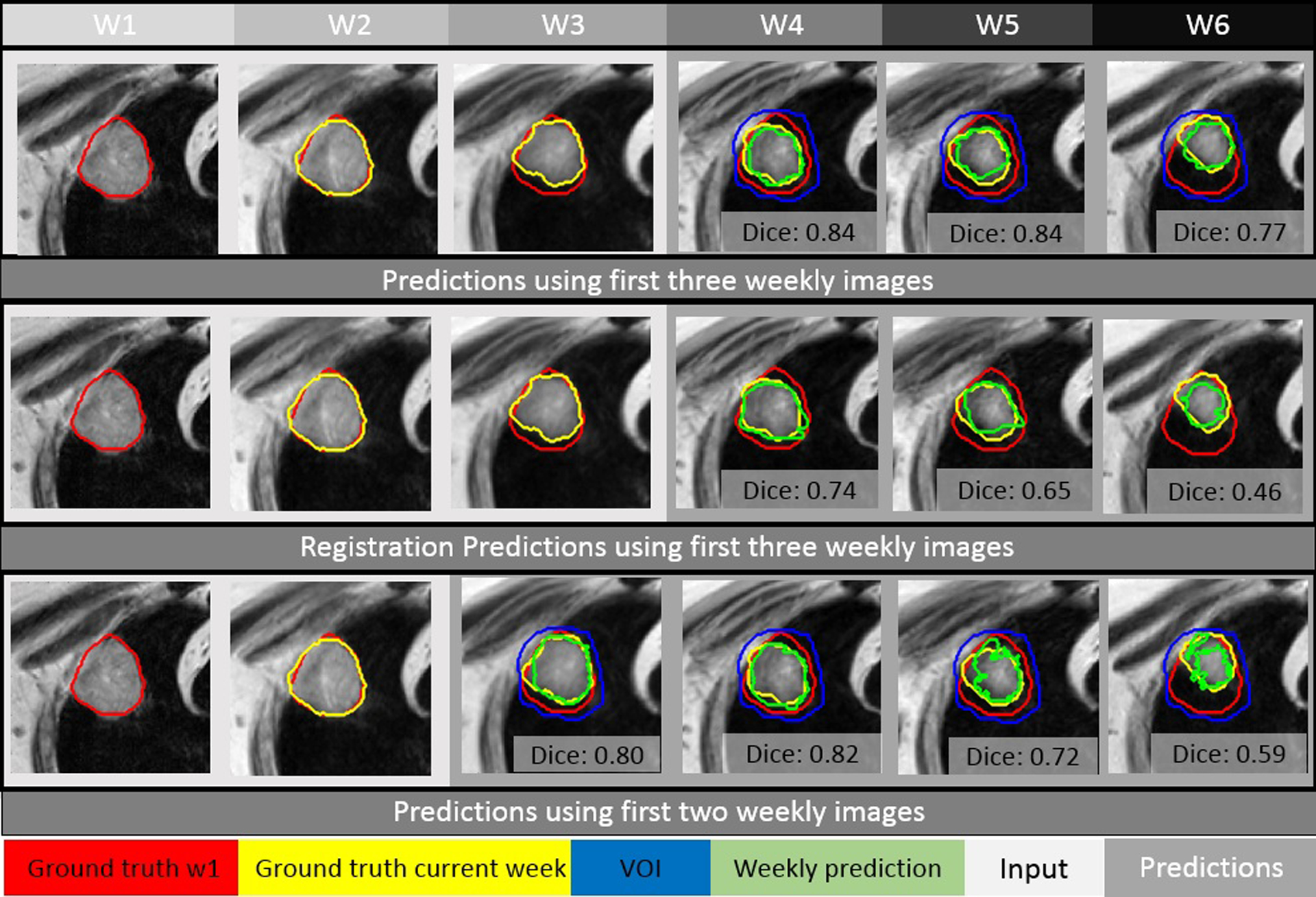
Using the first two or three weekly MRI images as input (in the light gray box), predictions (images in the dark gray box) of tumor are made with P-net and deformable registration for patient #1. The initial week 1 contour, the actual tumor at a specific week, and the corresponding weekly prediction (via P-net or registration) are shown in red, yellow, and green, respectively.

In the analysis of predictions for each individual patient as shown in Figure 5, we discovered that P-net failed to make a reasonable prediction for patient #2, week 5: Dice fell to 0.16, which was 2 standard deviation (2×0.21) below the group mean. The low Dice could be caused by a combination of its small volume of 5cc, and extreme shrinkages of 92% at the end of chemoradiation. In this scenario, its RMSSD of 6.4mm would be a more applicable evaluation metrics. Nevertheless, this outlier out of the 30 incidences (3 weeks × 10 patients) does reveal the limitations of P-net.

Figure 5.

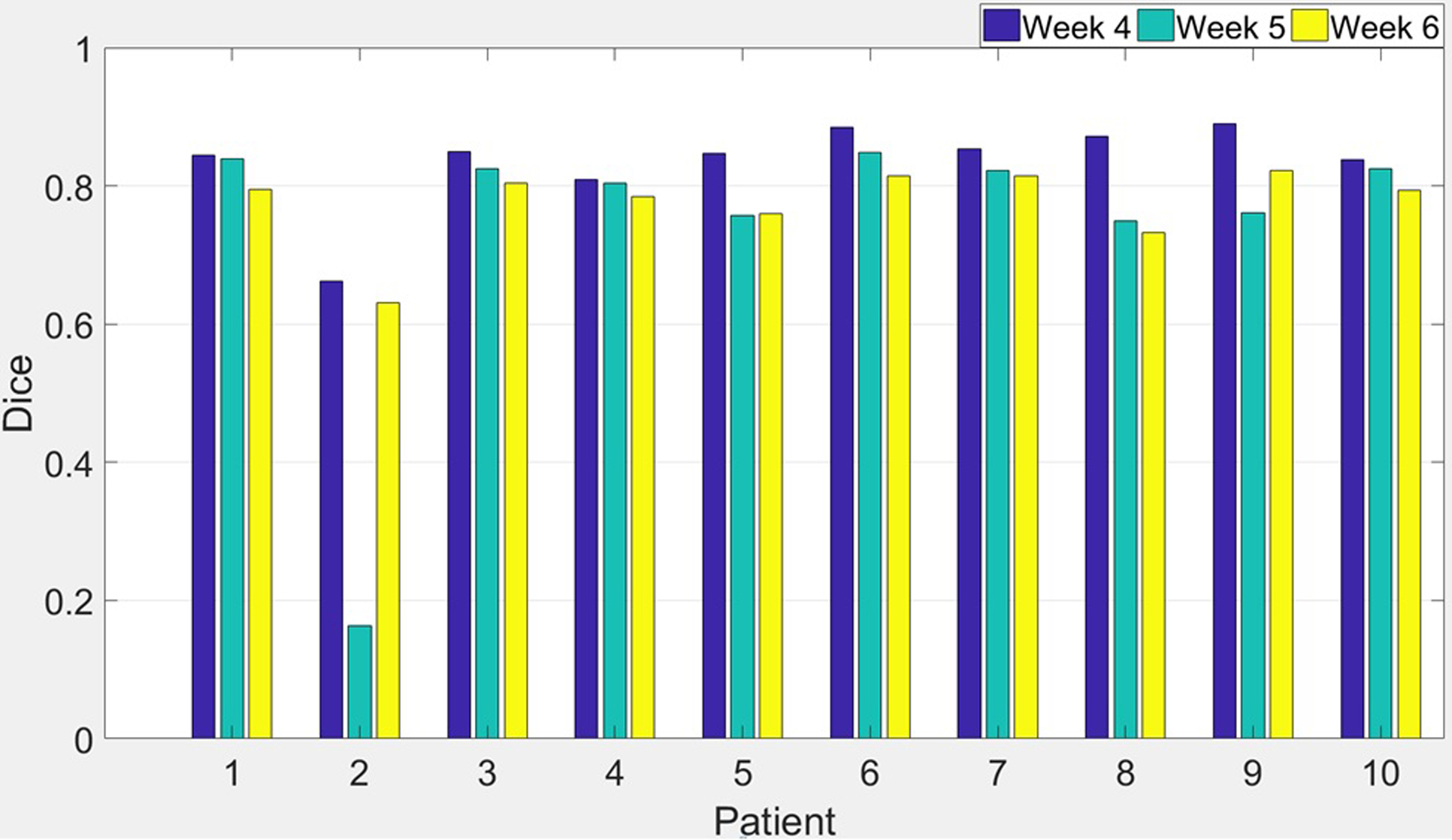
Dice coefficient of predictions made by P-net using first three weeks image data under the leave-one-out testing scheme.

Even under a gated MR acquisition protocol, noticeable residual motions of tumor often occur with irregular respiratory patterns. If such movements are not fully compensated in the registration process, the accuracy of prediction may suffer. In fact, there was a large positional difference of 8mm along the anterior-posterior direction for the 5^th weekly scan of patient #4, which could cause a drop of 0.36 (from 0.81 to 0.45) in Dice if uncorrected. In a further investigation, we specifically examined the effect of uncorrected tumor motion on the predictive performance. By artificially shifting tumor positions on the weekly images (both input and output) to simulate alignment errors of 1mm, 3mm and 5mm, we found that RMSSD of the prediction increased an averaged 0.2mm, 0.9mm, and 2.7mm, respectively.

The RMSSD between the segmentations derived from two observers averaged 2.0mm. When predictions were produced using one observer’s contour, but verified against the second observer’s segmentation, or vice versa, the RMSSD averaged 1.4mm. While P-net seems to be robust to certain registration and contouring errors, these uncertainties need to be accounted for when the prediction is used in radiotherapy, most probably by incorporating them into the margin of the planning target volume.

IV. DISCUSSION

Our study’s findings show that P-net can predict changes in lung tumor location and spatial extent from weekly imaging over a course of radiotherapy. P-net exploits the information in the weekly images themselves rather than simplified countours or binary masks of the tumor. Preprocessing steps such as labeling the tumor as parenchymal or mediastinal, located in left/right/upper/lower lung, and grouping based on similarities, can be eliminated because the CNN components inside P-net automatically extract and process the information. Furthermore, the RNN components in P-net determine the weighting of the time series coming from previous weeks in producing the predictions via non-linear functions, thereby expanding the capacity of P-net compared to using linear combinations such as a Kalman filter.³⁶ Although the training of P-net is based on a population of patients, predictions are patient-specific because the input data rely on the patient’s own weekly images. In addition, patterns of apparent tumor expansion due to inflammation are included in the training patient cohort. Therefore a well-trained P-net can make predictions of local tumor shrinkage as well as expansion, and become a reliable tool to monitor and understand tumor response at any time point along the treatment course. Meanwhile, predictive power of P-net could be enhanced by explicitly integrating the planning FDG-PET image (reflecting metabolic activities) as well as the accumulated dose distributions into the input. After we collect more clinical data, we will investigate such capabilities in our future studies.

It is a big leap for the P-net to make a wealth of predictions covering multiple time points along the course of radiotherapy. Pairing such timely predictions with the design of ART is critical to maximize the benefit of radiotherapy. A credible patient-specific prediction can be made as early as the second week (1/3 of the course). This valuable prediction can be used as an early signal as whether the treated tumor has responded to radiotherapy, subsequently applied to estimate the optimal dosing scheme such as number of fractions and fraction size, and eventually adjust the treatment plan to achieve a better therapeutic ratio. Three weeks into the middle of the treatment, the prediction reveals the spatial distribution of the tumor with high fidelity. A fine tuning of the existing plan, aiming at reshaping the local dose distribution according to the dynamic interplays between tumor shrinkage and surrounding OAR, can be closely investigated. The initial plan can be reoptimized to escalate dose to the predicted residual tumors, maintaining a therapeutic dose even to the regions where tumors are predicted to disappear, but does not compromise the sparing of the surrounding healthy tissues. Under this design, a poor prediction only translates to a random dose escalation to portions of the PTV, and would not cause unnecessary damages to normal tissues. Therefore, even though the predictive power of PNet is limited by the small number of patients in its current form, the impact of integrating such predictions, small or large, is always positive. A series of comprehensive planning studies will be performed to evaluate the actual dosimetric impacts of the ART strategies, and explore remedies to deal with uncertainties of the prediction.

In our previous study, we built a geometric atlas based on 12 lung patients from our institution to predict the distribution of residual tumors after radiotherapy using initial tumors observed on the planning CTs.² When this atlas was tested using a similarly structured external dataset from another institution including 22 lung patients, the predictive accuracy only dropped a little, from 0.74 to 0.71 measured in DICE.³ Furthermore, when combining patients from two institutions, the rebuilt atlas has recovered its predictive accuracy to a DICE of 0.74. Therefore, even though the atlas was built with a small number of patients, it still can catch the patterns of how lung tumors respond to radiotherapy, and its application can be extended to a larger patient cohort. Since the patients in our current study are similar to those in the previous studies in terms of disease stage, tumor location, and prescription dose, we expect that P-net is also applicable and expandable to a larger patient cohort in a similar way as the geometric atlas. As we accumulate more patients through the ongoing clinical protocol or collaborations with external institutions, we will update the P-net, and further improve its accuracy and robustness.

V. CONCLUSION

The proposed deep learning algorithm can capture and predict the spatial and temporal patterns of tumor regression in a longitudinal imaging study. It closely follows the clinical workflow, and could facilitate the decision making of ART. A prospective study including more patients is warranted.