Benchmarking the performance of time-dependent density functional theory methods on biochromophores

Abstract

Quantum chemical calculations are important for elucidating light-capturing mechanisms in photobiological systems. The time-dependent density functional theory (TDDFT) has become a popular methodology due to its balance between accuracy and computational scaling, despite its problems in describing, e.g., charge transfer states. As a step towards systematically understanding the performance of TDDFT calculations on biomolecular systems, we here study 17 commonly used density functionals, including 7 long-range separated functionals, and compare the obtained results with excitation energies calculated at the approximate second order coupled-cluster theory level (CC2). The benchmarking set includes the first five singlet excited states of 11 chemical analogs of biochromophores from the green fluorescent protein (GFP), rhodopsin/bacteriorhodopsin (Rh/bR), and the photoactive yellow protein (PYP). We find that commonly used pure density functionals such as BP86, PBE, M11-L and hybrid functionals with 20%-25% of Hartree-Fock (HF) exchange (B3LYP, PBE0) have a tendency to consistently underestimating vertical excitation energies (VEE) relative to the CC2 values, whereas hybrid density functionals with around 50% HF exchange such as BHLYP, PBE50 and M06-2X as well as long-range corrected functionals such as CAM-B3LYP, ωPBE, ωPBEh, ωB97X, ωB97XD, BNL, and M11 overestimate the VEEs. We observe that calculations using the CAM-B3LYP and ωPBEh functionals with 65% and 100% long-range HF exchange, respectively, lead to an overestimation of the VEEs by 0.2-0.3 eV for the benchmarking set. To reduce the systematic error, we introduce here two new empirical functionals: CAMh-B3LYP and ωhPBE0, for which we adjusted the long-range HF exchange to 50%. The introduced parameterization reduces the mean signed average (MSA) deviation to 0.07 eV and the root mean square (RMS) deviation to 0.17 eV as compared to the CC2 values. In the present TDDFT calculations using the aug-def2-TZVP basis sets, the best performing functionals relative to CC2 are: ωhPBE0 (RMS=0.17, MSA=0.06 eV); CAMh-B3LYP (RMS=0.16, MSA=0.07 eV); and PBE0 (RMS=0.23, MSA=−0.14 eV). For the the popular range-separated CAM-B3LYP functional, we obtain a RMS value of 0.31 eV and a MSA value of 0.25 eV, which can be compared with the RMS and MSA values of 0.37 eV and −0.31 eV as obtained at the B3LYP level.

Graphical Abstract

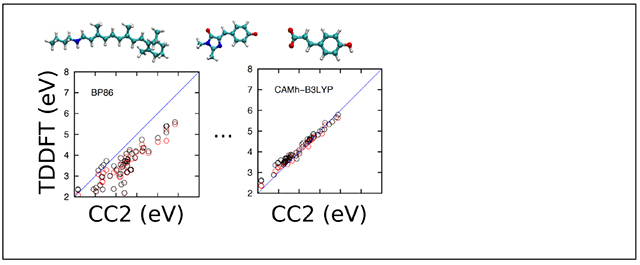
1. Introduction

The development of accurate electronic structure theory methods for studies of electronic excited states has opened new possibilities for elucidating molecular mechanisms of photobiological processes.^1–24 In photobiological studies, the employed computational method should be able to predict optical transitions within chemical accuracy and have a favorable computational scaling that allows modeling of large extended systems of biochromophores embedded by nearby protein residues. Linear-response time-dependent density functional theory (TDDFT) calculations^25–32 provide excitation energies at relatively low computational costs and have therefore become a popular approach for investigating excited states of large molecules. A large number of density functionals have been developed,^33–36 which can be divided into different categories, such as functionals at the local density approximation (LDA), functionals at the generalized gradient approximation (GGA), meta-GGA functionals, hybrid functionals, range-separated functionals, as well as double-hybrid functionals. However, many functionals are known to provide an inadequate description for charge-transfer and Rydberg excitations,^37,38 affecting the accuracy of calculated excitation energies for biomolecules and large molecules.

Correlated ab initio methods are generally more accurate. However, the computational scaling renders photobiological applications difficult at correlated ab initio levels, because the chromophore and its nearest environment have to be considered at the quantum mechanical (QM) level when aiming at accurate results. Even low-order correlated ab initio methods, such as approximate second-order coupled cluster (CC2)^39,40 calculations are computationally expensive for large biochromophores. The computational cost can, however, be enhanced by using the reduced virtual space (RVS) approach^{10,14,22,41,42} and algorithms based on Laplace transformations.^43,44 Nevertheless, low-order ab initio methods fail to describe excited states when the ground state has a significant multiconfiguration character or double excitations are needed to accurately describe the excited state. The molecular structure and the potential energy surface of the excited states may in such cases be less accurate at the low-order ab initio levels than obtained in TDDFT calculations.^45,46

A number of benchmark studies have reported comparisons of excitation energies calculated using various TDDFT functionals with experimental data and with values obtained at correlated ab initio levels.^47–67 Leang et al.,⁶² studied the performance of 24 density functionals, including 14 meta-GGA functionals and one range-separated functional on excitation energies for 14 small organic molecules. They found that the M06-2X⁶⁸ and PBE0⁶⁹ functionals have the smallest mean absolute errors (MAE) of 0.26 eV and 0.28 eV as compared with experimental values, respectively. The CAM-B3LYP range-separated functional⁷⁰ was found to have an MAE of about 0.3 eV for singlet excited states, whereas a large MAE of about 1.1 eV was obtained for the excitation energies of excited triplet states.

Isegawa et al.⁶⁴ reported excitation energies calculated at the TDDFT level using 30 density functionals including many commonly-used meta-GGAs and range-separated functionals. They also reported excitation energies for 69 valence and Rydberg states of 11 small organic molecules. They found that the M06-2X⁶⁸ and the ωB97X-D⁷¹ functionals yield the smallest MAE error of 0.30 eV. The use of the CAM-B3LYP functional resulted in a slightly larger MAE error of 0.32 eV.

Charaf-Eddin et al.⁶⁵ calculated the absorption and emission spectra of 20 conjugated molecules in solvents with six hybrid functionals (B3LYP,^72–74 PBE0,⁶⁹ M06,⁶⁸ M06-2X,⁶⁸ CAM-B3LYP⁷⁰ and LC-PBE^75,76) and found that the B3LYP functional provides the smallest MAE errors for the absorption and emission maxima. They also noticed that the M06-2X functional provides accurate excitation energies for problematic molecules.

Fang et al.⁶⁶ calculated vertical, adiabatic and 0-0 excitation energies for 96 excited states of 79 organic and inorganic molecules using low-order correlated ab initio methods such as configuration interaction singles (CIS) and CC2. They compared the obtained values with excitation energies calculated at the TDDFT level using six functionals (BP86,^77–79 B3LYP, PBE0, M06-2X, M06-HF,⁸⁰ CAM-B3LYP, and ωB97X-D). The 0-0 excitation energies obtained at the CC2 level were found to be in the best agreement with experimental values. The B3LYP, PBE0, M06-2X, CAM-B3LYP, and ωB97X-D functionals also yield values that largely agree with experimental data, whereas larger MAE errors were obtained with BP86, M06-HF and CIS.

Here, we employ the biomolecular benchmarking set of Send et al.,⁵⁷ who performed CC2 calculations and TDDFT calculations using the B3LYP functional on excited states of biochromophore models from retinal proteins, green fluorescent protein (GFP) and the photoactive yellow protein (PYP). They compared the obtained vertical excitation energies (VEE) with benchmarking data calculated at the many-body Green’s function theory level by Ma et al.⁵⁴ Send et al. found that the VEEs calculated at the CC2 level for the lowest excited states of GFP and retinal chromophores agreed within 0.15 eV with experimental values, whereas the B3LYP calculations yielded VEEs that had a somewhat larger deviation of 0.1-0.3 eV from the experimental values. For the PYP chromophore models, larger deviations of 0.3-0.4 eV and 0.1-0.5 eV were obtained at the CC2 and B3LYP levels, respectively.

Since these chromophores are particularly relevant for photobiological applications, we extend the TDDFT calculations from B3LYP to 14 other density functionals and to two new empirical functionals. We compare the obtained TDDFT results with previously calculated VEEs at the CC2 level and with experimental data. We address: (I) how range-separated functionals such as CAM-B3LYP,⁷⁰ ωB97X,⁸¹ ωB97X-D,⁷¹ ωPBEh⁸² perform relatively to the CC2 method, (II) we investigate the extent of previously reported overestimation of VEEs when using range-separated functionals and address ways to reduce this systematic error, (III) we investigate the performance of the PBE0 and M06-2X functionals on biochromophores, (IV) we estimate errors introduced by the Tamm-Dancoff approximation, and (V) we study ways to accelerate the convergence of the VEEs calculated at the TDDFT level towards the basis set limit.

This article is structured as follows. In Section 2, we briefly review the theory of linear-response time-dependent density functional theory (TDDFT) and introduce the employed functionals. In Section 3, we discuss the overall performance of different TDDFT functionals, and in Section 4 we summarize the obtained results.

2. Computational details

2.1. TDDFT and the Tamm-Dancoff approximation (TDA)

Time-dependent density functional theory can to first order be formulated as linear response to the density functional theory (DFT) calculation on the ground state,

$$\left(\begin{array}{cc}\hfill A\hfill & \hfill B\hfill \\ \hfill B\hfill & \hfill A\hfill \end{array}\right)\left(\begin{array}{c}\hfill X\hfill \\ \hfill Y\hfill \end{array}\right)=\Delta E\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1\hfill \end{array}\right)\left(\begin{array}{c}\hfill X\hfill \\ \hfill Y\hfill \end{array}\right).$$ (1)

where X and Y are the first-order orbital response and ΔE is the corresponding excitation energy. For the general case of range-separated functionals, the A and B matrices are given by

$$\begin{gathered} A_{\mathit{ia},\mathit{jb}}={\delta }_{\mathit{ij}}{\delta }_{\mathit{ab}}({ϵ}_a-{ϵ}_i)+(\mathit{ia}\mid \mathit{jb})-C_{\mathrm{HF}}^{\mathrm{sr}}{(\mathit{ij}\mid \mathit{ab})}_{\mathit{sr}}-C_{\mathrm{HF}}^{\mathrm{lr}}{(\mathit{ij}\mid \mathit{ab})}_{\mathrm{lr}}+(\mathit{ia}\mid \varpi \mid \mathit{jb}) \\ {B}_{\mathit{ia},\mathit{jb}}=(\mathit{ia}\mid \mathit{bj})-C_{\mathrm{HF}}^{\mathrm{sr}}{(\mathit{ib}\mid \mathit{aj})}_{\mathrm{sr}}-C_{\mathrm{HF}}^{\mathrm{lr}}{(\mathit{ib}\mid \mathit{aj})}_{\mathrm{lr}}+(\mathit{ia}\mid \varpi \mid \mathit{bj}), \end{gathered}$$ (2)

where i, j are indices for occupied Kohn-Sham molecular orbitals (ψ_i, ψ_j), and a, b denotes the unoccupied Kohn-Sham orbitals (ψ_a, ψ_b), which are obtained from the ground-state DFT calculation. ϵ_i and ϵ_a are the energies of occupied and virtual orbitals, respectively. The rest of the terms in Eq. 2 considers two-electron Coulomb interactions, short-range HF exchange, long-range HF exchange, and exchange-correlation term (f_xc) of the employed density functional. The integrals in Eq. 2 are given by

$$\begin{gathered} (\mathit{ia}\mid \mathit{jb})=\int \int {\psi }_i({\mathbf{r}}_1){\psi }_a({\mathbf{r}}_1)\frac{1}{r_{12}}{\psi }_j({\mathbf{r}}_2)d{\mathbf{r}}_{1}d{\mathbf{r}}_2 \\ {(\mathit{ij}\mid \mathit{ab})}_{\mathrm{sr}}=\int \int {\psi }_i({\mathbf{r}}_1){\psi }_j({\mathbf{r}}_1)\frac{\mathrm{erfc}(\omega r_{12})}{r_{12}}{\psi }_a({\mathbf{r}}_2){\psi }_b({\mathbf{r}}_2)d{\mathbf{r}}_{1}d{\mathbf{r}}_2 \\ {(\mathit{ij}\mid \mathit{ab})}_{\mathrm{lr}}=\int \int {\psi }_i({\mathbf{r}}_1){\psi }_j({\mathbf{r}}_1)\frac{\mathrm{erf}(\omega r_{12})}{r_{12}}{\psi }_a({\mathbf{r}}_2){\psi }_b({\mathbf{r}}_2)d{\mathbf{r}}_{1}d{\mathbf{r}}_2 \\ (\mathit{ia}\mid \varpi \mid \mathit{jb})=\int {\psi }_i(\mathbf{r}){\psi }_a(\mathbf{r})\frac{{\partial }^2{f}_{\mathrm{xc}}}{\partial {\rho }^2}{\psi }_j(\mathbf{r}){\psi }_b(\mathbf{r})d\mathbf{r}, \end{gathered}$$ (3)

where erf(ωr₁₂) and erfc(ωr₁₂) are the error function and complementary error function, respectively. At the Tamm-Dancoff approximation (TDA), the B matrix is set to zero yielding

$$\mathit{AX}=\Delta \mathit{EX}.$$ (4)

At the HF level, i.e., with 100% short-range and long-range HF exchange and 0% exchange-correlation contribution, Eq. 1 is the HF linear response equation also known as the random-phase approximation (RPA).^83,84 Eq. 4 corresponds to the configuration interaction singles (CIS) level.^85,86 The TDA (CIS) and TDDFT (RPA) equations are usually solved using direct diagonalization methods.^47,48,87

2.2. Considered DFT functionals

In the present study, vertical excitation energies (VEE) have been calculated at the following levels:

• CIS and RPA levels using HF orbitals and orbital energies.

• TDDFT level using the BP86^77–79 and PBE^88,89 GGA functionals without HF exchange as well as the M11-L⁹⁰ range-separated meta-GGA functional that does not contain any HF exchange term.

• TDDFT level using the B3LYP^72–74 and PBE0⁹¹ hybrid functionals with 20% and 25% HF exchange, respectively.

• TDDFT level using the BHLYP⁹² functional with 50% HF exchange and the PBE50 functional with 50% PBE exchange, 50% HF exchange and 100%PBE correlation as well as the M06-2X functional, which is a meta-GGA hybrid functional with 54% HF exchange.⁹³

• TDDFT level using range-separated functionals. The amount of short-range and long-range HF exchange is given in Table 1. The employed range-separated functionals are: CAM-B3LYP,⁷⁰ ωPBE,^82,94 ωPBEh,⁸² ωB97X,⁸¹ ωB97X-D,⁷¹ BNL^95,96 and M11.⁹⁷

• TDDFT level using our empirical parameterization of the CAM-B3LYP and ωPBE0 functionals with 50% long-range HF exchange. The amount of HF exchange in our CAMh-B3LYP and ωhPBE0 functionals are given in Table 1.

Table 1:

The amount of short-range and long-range HF exchange in the 17 studied DFT functionals. $C_{\mathrm{HF}}^{\mathrm{sr}}$ and $C_{\mathrm{HF}}^{\mathrm{sr}}$ is the amount of HF exchange in the short-range (sr) and long-range (lr) regime, respectively. The ω values of the error function of the range-separated functionals are also given.

Functional	Reference	$C_{\mathrm{HF}}^{\mathrm{sr}}$	$C_{\mathrm{HF}}^{\mathrm{lr}}$	ω
CIS/RPA	84–86	1.0	1.0	-
B3LYP	72–74	0.2	-	-
BHLYP	92	0.5	-	-
CAM-B3LYP	70	0.19	0.65	0.33
CAMh-B3LYP	this work	0.19	0.50	0.33
BP86	77–79	0	-	-
PBE	88,89	0	-	-
PBE0	91	0.25	-	-
PBE50	88,89,91	0.5	-	-
ωPBE	82,94	0	1.0	x.z
ωhPBE0	this work	0.25	0.50	x.s
ωPBEh	82	0.20	1.0	x.d
ωB97X	81	0.157706	1.0	x.d
ωB97X-D	71	0.222036	1.0	x.d
BNL	95,96	0	1.0	-
M06-2X	93	0.54	-	-
M11	97	0.428	1.0	-
M11-L	90	0	-	-

The exact shape of the long-range exchange-correlation potential corresponds to 100% Hartree-Fock exchange. However, functionals whose exchange-correlation potential corresponds to a smaller amount of Hartree-Fock exchange, such as CAM-B3LYP (65%) or here CAMh-B3LYP (50%) may suffer from charge transfer problems. However, studies have shown that around 50% Hartree-Fock exchange in the functional is in general enough to avoid spurious charge-transfer states to enter among the lowest excited states.^{31,37,38,63,65,82,98,99}

2.3. Benchmark Set

The investigated molecules comprise analogs of the biochromophores from the photoactive yellow protein (PYP), the green fluorescent protein (GFP), rhodopsin/bacteriorhodopsin (Rh/bR), which have been thoroughly studied in previous works.^54,57 The molecular structures are shown in Figure 1 and the Cartesian coordinates are given as supporting information (SI). The investigated molecules are:

• PYP chromophore models: p-vinyl phenol (pVP), trans-p-coumaric acid (pCA), deprotonated trans-p-coumaric acid (pCA′⁻), trans-p-coumarate (pCA″⁻), thiomethyl-p-coumarate (TMpCA⁻), and thiophenyl p-coumarate (pCT⁻). The doubly ionic (pCA²⁻) chromophore of the benchmarking set by Send et al.⁵⁷ was not included in our current data set, because doubly charge anions not generally bound without counter anions.

• GFP chromophore models: the anionic, neutral, and cationic models of p-hydroxy-benzyledene imidazolinone models pHBDI⁻, pHBDI, pHBDI⁺.

• Rh/bR chromophore models: the protonated Schiff base retinal model PSBT⁺ (all-trans) with a butyl group that mimics the lysine residue of the retinal protein, and ${\mathrm{PSB}11\mathrm{Me}}_2^{+}$ (11-cis retinal), with two methyl groups connected to the Schiff base nitrogen.

Figure 1:

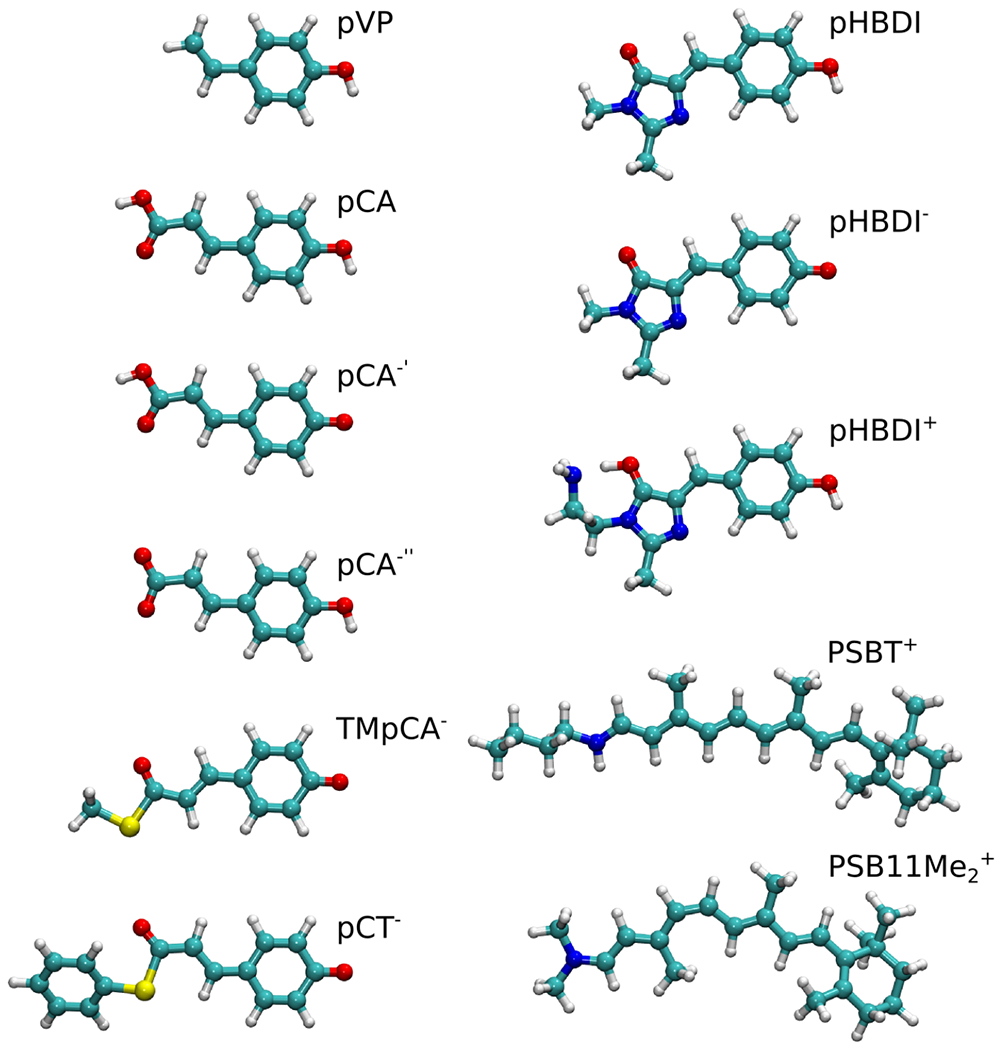
The molecular structures of the studied biochromophores optimized at the B3LYP/def2-SVP level of theory. The figure was prepared using VMD.¹⁰⁸

The molecular structures were optimized at the B3LYP/def2-SVP level^72–74,100 using TURBOMOLE v6.3.^101,102 The same molecular structures were used at all employed levels of theory, which is may introduce some uncertainties in the calculated VEEs.³¹ However, optimizing the molecular structures at each theory level would also introduces uncertainties, as all functionals do not yield accurate molecular structures.

The VEEs calculated using the B3LYP structures differ by less than 0.05 eV from those obtained at the same level of theory using the molecular structures optimized at the second-order Møller-Plesset level.⁵⁷ (See Table S1 in the SI). Excitation energies were calculated using the Q-Chem v4.1^103,104 using the DFT functionals presented in Section 2.2. The def2-TZVP¹⁰⁵ and aug-def2-TZVP¹⁰⁶ Karlsruhe basis sets were used, where aug denotes that the basis sets were augmented with diffuse functions from Dunning’s aug-cc-pVTZ basis set.¹⁰⁷ The root mean square (RMS) deviation and the mean signed average (MSA) deviation relative to the excitation energies calculated at the CC2 level were obtained as

$$\begin{gathered} \mathrm{RMS}=\sqrt{\frac{{\sum }_{i=1}^N{({\mathrm{VEE}}_{\mathrm{TDDFT},i}-{\mathrm{VEE}}_{\mathrm{CC}2,i})}^2}{N}} \\ \mathrm{MSA}=\frac{{\sum }_{i=1}^N({\mathrm{VEE}}_{\mathrm{TDDFT},i}-{\mathrm{VEE}}_{\mathrm{CC}2,i})}{N}. \end{gathered}$$ (5)

2.4. Protein models

The performance of the functionals on large protein models were investigated by calculating VEEs at the B3LYP, CAM-B3LYP, CAMh-B3LYP level using the def2-TZVP basis sets.¹⁰⁵ The obtained results are compared to experimental data and to VEEs calculated at the CC2 level on DFT-optimized protein models of the green fluorescent protein (GFP) and the retinoid-binding protein II (hCRBPII) shown in Figure 2.

Figure 2:

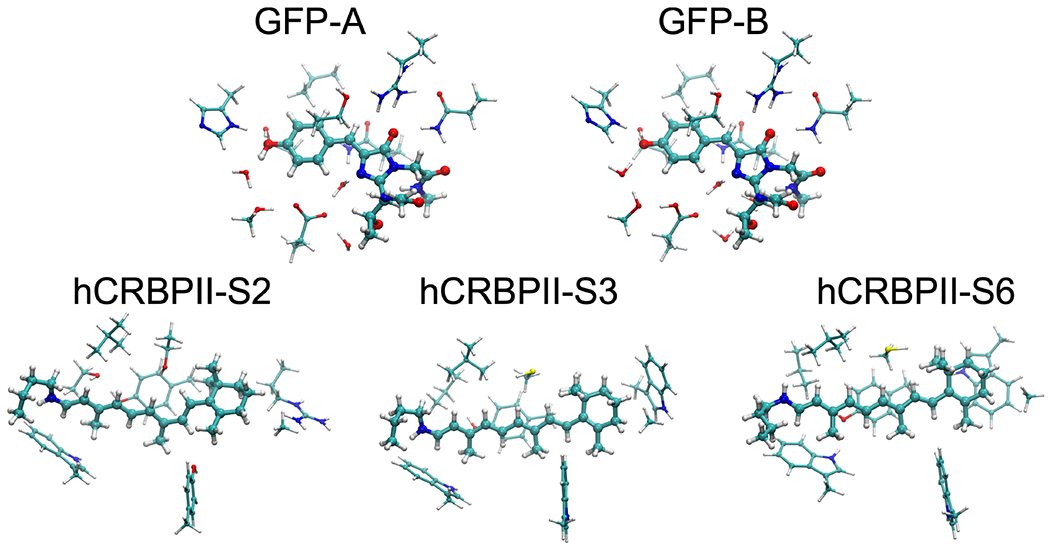
The molecular structures of the studied protein models. The figure was prepared using VMD.¹⁰⁸

The hCRBPII models were constructed as described in Ref. 109. They are based on the X-ray structures whose PDB IDs are 4EXZ (model S2), 4EFG (model S3), and 4EEJ (model S6).¹¹⁰ The protein models comprise the retinal chromophore, and the first/second sphere of amino acid residues, as well as Lys-108, which is covalently linked to the retinyl moiety by a protonated Schiff base. To simulate the rigidity of the protein backbone, the amino acids were cut at the C_β-positions and saturated with hydrogen atoms. The protein models consist of 170-190 atoms. All proteins models were optimized at the B3LYP-D3/def2-SVP level using COSMO with relative dielectric constant (ϵ) of 4.^{72–74,100,111,112} The references VEE values were calculated at the CC2/def2-TZVP level with virtual orbitals higher than 70 eV above the highest occupied molecular orbital (HOMO) frozen.

The protein models for GFP were constructed based on the X-ray structure of the protein from Aequorea victoria (PDB ID:1EMB), as described in Refs 10 and 11. The protein models comprise the pHBDI chromophore, and first sphere amino acid residues and five surrounding water molecules. The protein residues were cut at the C_β-positions, which were saturated with hydrogen atoms and fixed during structure optimization at the B3LYP/def2-SVP/ϵ = 4 level. The GFP models, comprising 161 atoms, were optimized in the A and B forms of the GFP photocycle, with the phenol group of pHBDI protonated/Glu-222 deprotonated and pHBDI deprotonated/Glu-222 protonated, respectively. The VEE references values were calculated at the CC2/def2-TZVP level with virtual orbitals higher than 60 eV above the HOMO frozen.

3. Results and discussion

3.1. Analysis of the five lowest excitations

The five lowest VEEs of the 11 biochromophore analogs were computed at the CIS, RPA, TDA and TDDFT levels using def2-TZVP and aug-def2-TZVP basis sets. The TDA and TDDFT excitation energies calculated using the def2-TZVP and aug-def2-TZVP basis sets are plotted against the corresponding CC2 values in Figures 3 and 4, respectively. The lowest VEEs obtained at each level are summarized in Table S1. All calculated VEEs and oscillator strengths are compared in Tables S2–S12 with reference CC2 values calculated by Send et al.⁵⁷ Figures 3 and 4 show that calculations with 100% HF exchange, i.e., CIS/RPA severely overestimates the excitation energies, while pure functionals (BP86, PBE, and M11-L) with 0% HF exchange, tend to underestimate the excitation energies, which is consistent with several previous studies (See Ref. 37). One can also see in the figures that functionals with intermediate amount of short-range and long-range HF exchange yield excitation energies in better agreement with the CC2 values. The RMS and MSA deviations of the excitation energies relatively to the CC2 values are shown in Figure 5, whose raw data are given in Tables S13 and S14.

Figure 3:

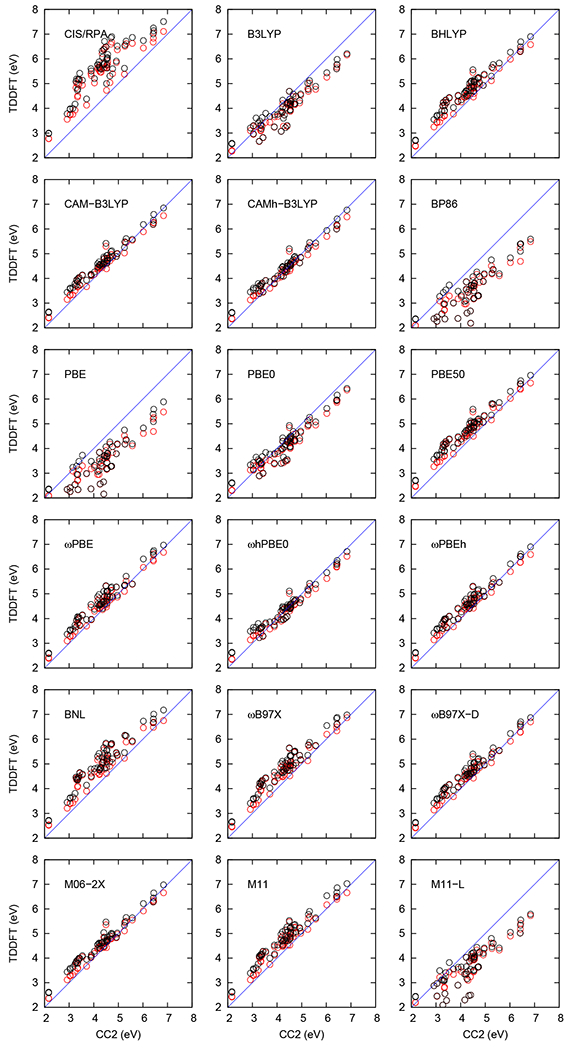
The performance of TDDFT functionals as compared with CC2 excitation energies calculated using def2-TZVP basis sets. The VEEs (in eV) calculated using TDDFT and TDA method are shown in red and black, respectively.

Figure 4:

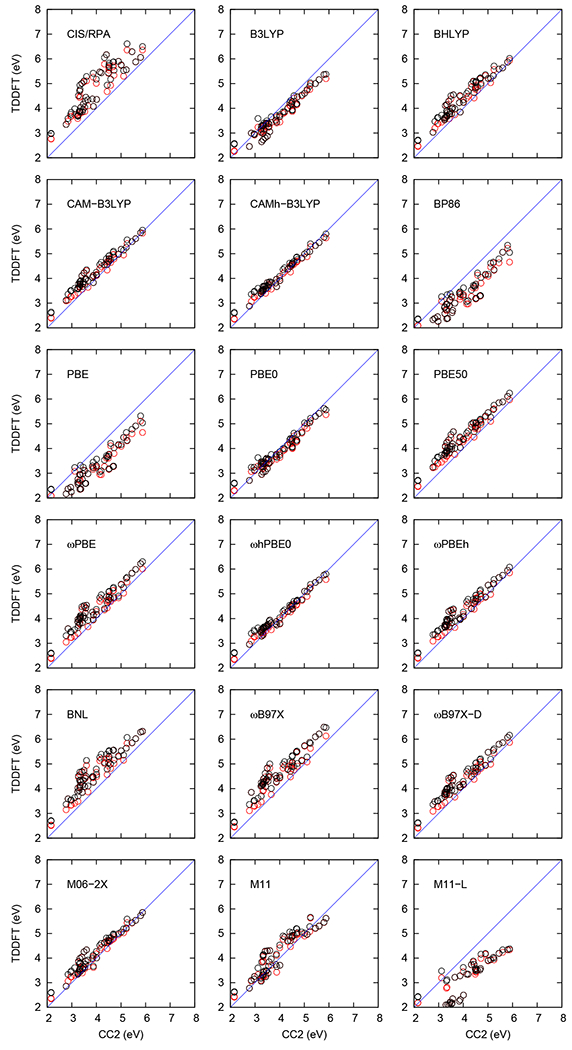
The performance of TDDFT functionals as compared with CC2 excitation energies calculated using aug-def2-TZVP basis sets. The VEEs (in eV) calculated using TDDFT and TDA method are shown in red and black, respectively.

Figure 5:

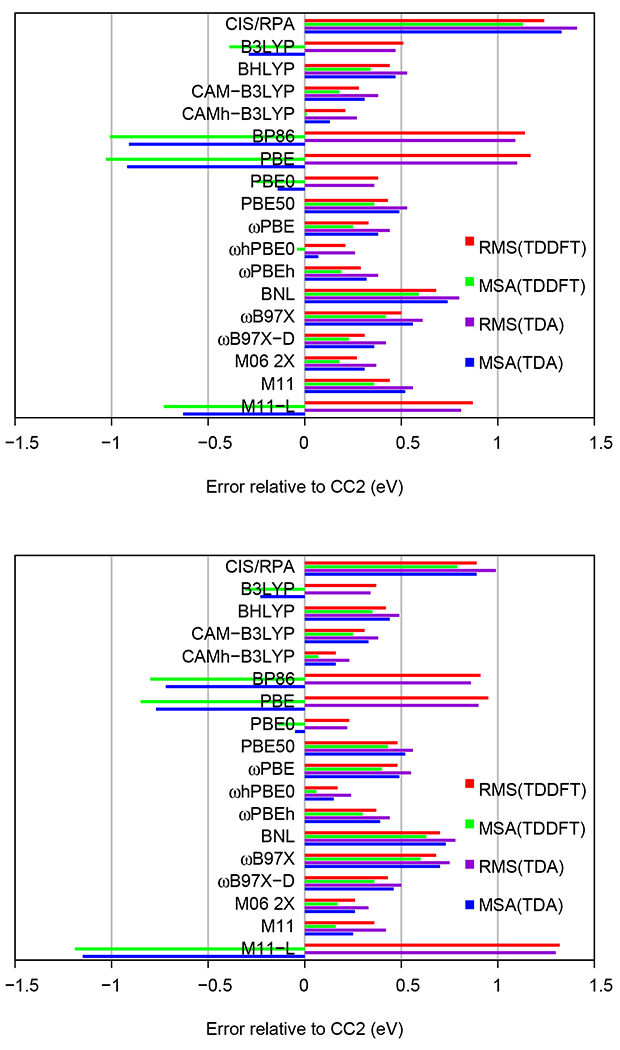
The root-mean-square (RMS) and mean signed average (MSA) differences (in eV) between VEEs calculated at the TDDFT, TDA and CC2 levels using the def2-TZVP basis sets (top panel) and aug-def2-TZVP basis sets (bottom panel). The excitation energies of the five lowest excited state of the 11 chromophores are included.

Note that both the oscillator strengths and the orbital character have to be considered in order to confirm that the VEEs of the same states are compared. It is a very comprehensive task that would most like to lead to a general improvment of the performance of the hybrid functionals, because charge transfer effects and spurious dark low-lying states are more common for pure density functionals.

3.1.1. B3LYP, BHLYP, CAM-B3LYP and CAMh-B3LYP

The amount of HF exchange in the three hybrid functionals B3LYP (20%), BHLYP (50%), and CAM-B3LYP (19% short-range, 65% long-range) strongly affects the calculated excitation energies as shown in Figures 3 and 4, as well as in Figure 5, whose raw data are given in Tables S13 and S14. The B3LYP functional with a def2-TZVP (aug-def2-TZVP) basis underestimates the VEEs by a MSA of −0.39 eV (−0.31 eV) relative to CC2, whereas BHLYP overestimates the respective VEEs by 0.34 eV (0.35 eV). For the CAM-B3LYP functional we obtain a MSA of 0.18 eV (0.25 eV). The CAM-B3LYP functional performs on average somewhat better than the B3LYP and BHLYP functionals.

The sign of the MSA deviations indicates that the increased long-range HF exchange of the CAM-B3LYP functional overcorrects the underestimated VEEs obtained at the B3LYP level relative to the CC2 reference values. The B3LYP and CAM-B3LYP functionals contain nearly the same amount of short-range HF exchange (20% versus 19%, Table 1), suggesting that the 65% long-range HF exchange is responsible for the systematic blueshift of the VEEs in the CAM-B3LYP calculations.

Mixing the B3LYP and CAM-B3LYP functionals with a ratio of 1:2 roughly cancels the MSA values suggesting a new empirical functional with 19% short-range HF exchange and 50% long-range HF exchange, which we denote as CAMh-B3LYP, where h indicates the 50% HF exchange in the long-range part. CAMh-B3LYP calculations reproduce the CC2 results rather well as seen in Figures 3 and 4. The MSA values are 0.01 eV and 0.07 eV for the def2-TZVP and aug-def2-TZVP basis sets, respectively. The calculations also show that the CAMh-B3LYP functional not only reduces the systematic errors of the B3LYP and CAM-B3LYP, but it also improves the RMS deviations of the benchmarking set, which are 0.51 eV (B3LYP) > 0.28 eV (CAM-B3LYP) > 0.21 eV (CAMh-B3LYP) with the def2-TZVP basis sets and 0.37 eV (B3LYP) > 0.31 eV (CAM-B3LYP) > 0.16 eV (CAMh-B3LYP) with the aug-def2-TZVP basis sets. The MSA and RSM values are compared in Figure 5.

3.1.2. PBE, PBE0, PBE50, ωPBE, ωPBEh, and ωhPBE0

The VEEs obtained using the PBE-type functionals are shown in Figures 3 and 4, whose raw data are given in Tables S2–S12. The PBE functional using the def2-TZVP (aug–def2-TZVP) basis sets significantly underestimates the VEEs with an MSA value of −1.03 eV (−0.85 eV), while the PBE50 functional with 50% exchange overestimates the VEEs by 0.36 eV (0.43 eV, Figure 5).

The hybrid functional PBE0 (25% short-range, 25% long-range) and the range-separated ωPBE (100% long-range) and ωPBEh (20% short-range, 100 % long-range) functionals yield excitation energies in better agreement with the CC2 reference data. The obtained MSA values are −0.25 eV (−0.14 eV), 0.25 eV (0.40 eV), and 0.19 eV (0.30 eV) for PBE0, ωPBE, and ωPBEh, respectively.

By using the same mixing procedure as for the CAMh-B3LYP functional, we propose a functional with more long-range HF exchange relative to PBE0 (25%), but less than for ωPBEh (100%). The empirical ωhPBE0 functional has 25% short-range HF exchange and 50% long-range HF exchange. The obtained RMS values for the PBE-type functionals are 1.17 eV (PBE) > 0.43 eV (PBE50) > 0.38 eV (PBE0) > 0.33 eV (ωPBE) > 0.29 eV (ωPBEh) > 0.21 eV (ωhPBE0) with the def2-TZVP basis sets, and 0.95 eV (PBE) > 0.48 eV (PBE50, ωPBE) > 0.37 eV (ωPBEh) > 0.23 eV (PBE0) > 0.17 eV (ωhPBE0) with the aug-def2-TZVP basis sets (Figure 5). By further augmenting the basis set with diffuse functions could improve the performance of the PBE0 functional. However, it could also introduce charge-transfer problems, because PBE0 has only 25% HF exchange.

3.1.3. ωB97X and ωB97X-D

Although, the ωB97X-D functional was initially designed for studies of electronic ground states,⁷¹ it was suggested that it could also be used in studies of electronic excited states.⁶⁴ The calculations yielded even better excitation energies that those obtained with the ωB97X functional.⁸¹ Both functionals have a tendency to overestimate the VEEs of the biochromophores relative to the CC2 values as seen in Figures 3 and 4. The ωB97X-D functional has MSA values of 0.23 eV (0.36 eV) with the def2-TZVP (aug-def2-TZVP), which about half the MSA values of 0.42 eV (0.60 eV) obtained with the ωB97X functional. The RMS deviations follow the same trend with 0.31 eV (0.43 eV) and 0.50 eV (0.68 eV) at the ωB97X-D and ωB97X levels, respectively (Figure 5).

3.1.4. M06-2X, M11, and M11-L

The M06-2X, M11, and M11-L functionals are meta-GGAs that also depend on the kinetic energy density. Wheeler and Houk¹¹³ reported that very fine numerical integration grids might be required when studying chemical reactions using meta-GGA functionals. We therefore employed two atomic grids in the numerical integration.¹¹⁴ The SG-1 grid,¹¹⁵ which is a pruned (50, 194) grid and an unpruned (99, 590) grid were used. We did not find any significant grid dependence, since the obtained excitation energies differ by less than 0.014 eV when using these grids.

The M06-2X functionals perform well, which is also consistent with the findings of Isegawa et al.⁶⁴ (Figures 3 and 4). The obtained MSA values for the M06-2X functional are 0.17-0.18 eV and the RMS values are 0.26-0.27 eV for the two basis sets. M11 also performs well with the aug-def2-TZVP basis sets (MSA=0.16, RMS=0.36 eV), whereas it has a larger error with def2-TZVP basis sets (MSA=0.36, RMS=0.44 eV). The excitation energies calculated with the M11-L functional are underestimated. The MSA values are −0.73 eV and −1.19 eV when using the def2-TZVP and aug-def2-TZVP basis sets, respectively, which agrees with the MSA values obtained with the other GGA functionals. The MSA and RMS values are shown in Figure 5.

3.1.5. Other functionals

BP86 is an old GGA functional that also underestimates the VEEs. The MSA and RMS values are −1.01 eV (−0.80 eV) and 1.14 eV (0.91 eV) with the def2-TZVP (aug-def2-TZVP) basis sets, respectively. BNL is a range-separated functional whose ω parameter one should adjust for each molecule.¹¹⁶ However, here we have used the generic value of ω=0.5 for all molecules. The VEEs obtained with the BNL functional deviate significantly from the CC2 reference values. The obtained MSA and RMS values are 0.59 eV (0.63 eV) and 0.68 eV (0.70 eV), respectively, when using the def2-TZVP (aug-def2-TZVP) basis sets. The VEEs are compared with the CC2 data in Figures 3 and 4. The MSA and RMS values are given in Figure 5.

3.1.6. TDDFT vs. TDA

The computational costs for TDA calculations of the VEEs are somewhat smaller than for TDDFT calculations, because the size of the TDA matrices is a factor of two smaller. It is also of interest to investigate the performance of the TDA method, since a number of TDA studies has recently been reported.^117–120 The VEEs calculated at the TDA and TDDFT levels are compared with the CC2 reference values in Figures 3 and 4, whose raw data are listed in Tables S2–S12 and S15–S25. The corresponding MSA and RSM values are compared in Figure 5. The VEEs calculated at the TDDFT and TDA levels deviate in a similar manner from the CC2 values. However, the VEEs calculated using the TDA method are in general less accurate than the ones obtained in TDDFT calculations. The VEEs calculated using TDA and TDDFT methods are compared in Figures S1 and S2.

The TDDFT calculations often yield smaller excitation energies than obtained with the TDA method implying that for functional that underestimate the VEEs, the MSA values of the TDA calculations are smaller due to cancellation of errors. Larger VEEs are generally obtained with the TDA method when using GGA functionals and many hybrid functionals such as B3LYP and PBE0. However, no significant changes in the RMS values between the TDA and TDDFT calculations are obtained at the B3LYP and PBE0 levels (Figure 5). For cases where the TDA and the TDDFT calculations overestimate the VEEs, such as with the range-corrected CAM-B3LYP, CAMh-B3LYP, ωhPBE0, ωPBEh, ωB97X-D, M06-2X and M11 functionals, the TDDFT calculations yield VEEs in closer agreement with the CC2 results than with TDA. The TDA excitation energies are for some molecules more accurate than the VEEs calculated at the corresponding TDDFT level, which is most likely due to error cancellations, because TDA is an approximation to TDDFT.

3.1.7. Similarities among different functionals

Cross RMS values, shown in Figure 6 can be used to detect similarities in performance of the studied functionals. The following similarities were identified:

• The GGA functionals BP86 and PBE have generally too small VEEs and a similar cross-RMS of 0.07 eV, suggesting that VEEs are underestimated similarly by both methods.

• The two new empirically parameterized functionals CAMh-B3LYP and ωhPBE0 have a cross-RMS of 0.08 eV. Similar cross-RMS values are also obtained for the ωB97X-D, ωPBE and ωB97X-D, ωPBEh pair of functionals with 100% long-range HF exchange.

• The long-range corrected functional CAM-B3LYP has a cross-RMS of 0.10 eV with ωPBEh and 0.13 eV with M06-2X.

• BHLYP and PBE50 with 50% HF exchange have a cross-RMS of 0.13 eV.

Figure 6:

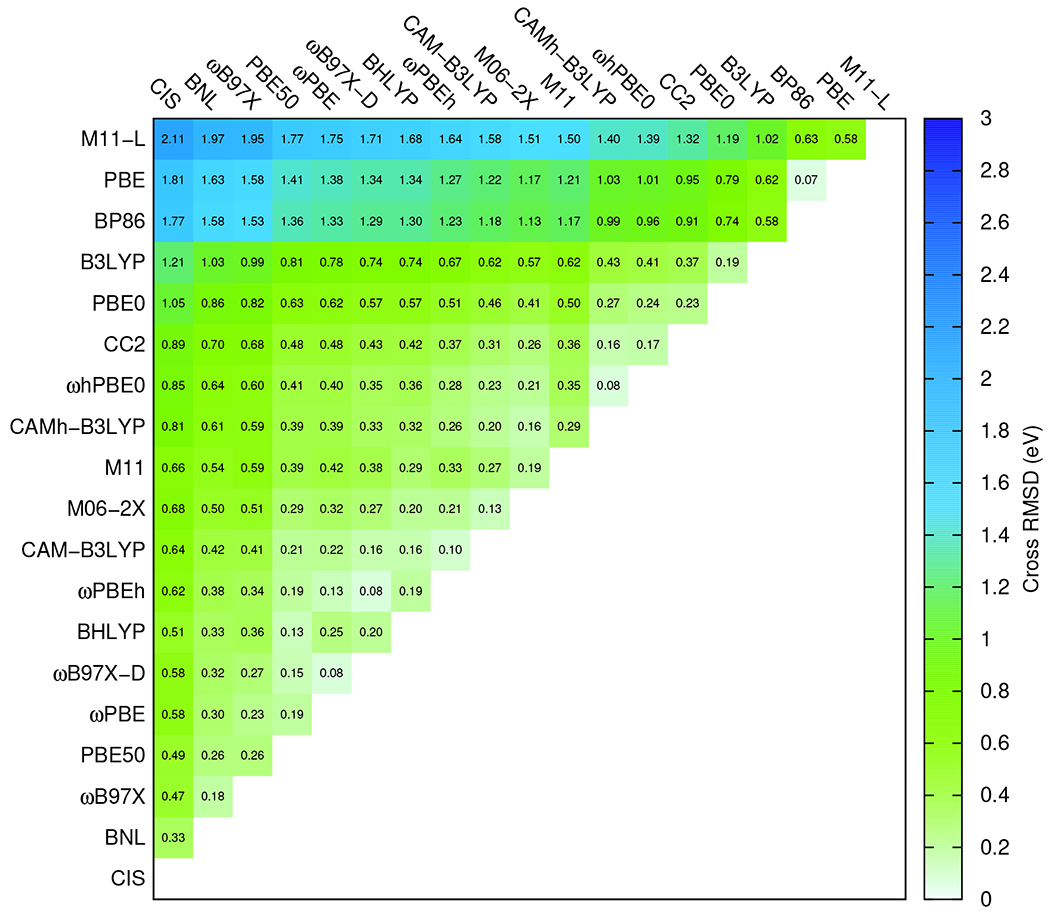
Cross-RMS values calculated for VEEs at the TDDFT level using different functionals obtained and the aug-def2-TZVP basis sets.

3.2. Analysis of the lowest excited state and relative VEEs

3.2.1. Lowest excited state

The lowest excited state is often the most photobiologically relevant state for biomolecules. From a computational perspective, the lowest excited state is less prone to charge-transfer problems and does usually not have a significant Rydberg character, implying that range-separated functionals are not generally needed when studying them.

The RMS of the B3LYP functional diminishes from 0.37 eV to 0.26 eV, when considering only the lowest excited state instead of the five lowest states using the aug-def2-TZVP basis sets. For the range-separated CAM-B3LYP functional, the RMS values obtained for the lowest state and for the five lowest states are 0.31 eV and 0.26 eV, respectively. The RMS values for the two new functionals (CAMh-B3LYP and ωhPBE0) are almost the same for the first excited state (0.16-0.17 eV) and the five lowest excited states (0.18-0.19 eV), respectively. In contrast to the CAM-B3LYP functionals and the ωhPBE0 functional, the RMS value of the first state is significantly better than for the five lowest states for the other range-separated functionals: ωPBE (0.48 eV → 0.23 eV), ωPBEh (0.37 eV → 0.24 eV), ωB97X-D (0.68 → 0.26 eV). The M11 functional has a better RMS value of 0.25 eV for the first excited state as compared to 0.36 eV for the five lowest states, while the RMS values for the M06-2X and M11-L are almost the same for the first and the five first excited states. Similar trends are obtained with the def2-TZVP level basis set. All RMS values are reported in Tables S13 and S14 and summarized in Figures S3 and S4.

A complication that appears when comparing VEEs calculated using different functionals is that the photochemically relevant bright state may not always be the lowest excited state.⁵⁷ Thus, oscillator strengths and orbital character have to be considered in order to assess whether the VEEs of the same states are compared. Such an analysis is more comprehensive and outside the scope of this work. However, it would most like to lead to a general improved performance of the hybrid functionals, because charge transfer effects and spurious dark low-lying states are more common for pure density functionals.

3.2.2. Relative excitation energies

In calculations of surface crossings or spectral overlap in fluorescence resonance energy transfer (FRET), the optical gaps between different excited states is more important than the absolute VEEs. The deviations of the TDDFT and TDA excitation energies with respect to the CC2 values are shown in Tables S2–S12 and Tables S15–S25 and summarized in Figure 5. For many of the functionals, the RMS values for the relative VEEs are much smaller than for vertical transition energy from the ground state. The RMS values obtained using the aug-def2-TZVP basis sets are CAM-B3LYP (0.12 eV), M06-2X (0.13 eV), CAMh-B3LYP (0.15 eV), BHLYP (0.17 eV), ωhPBE0 (0.19 eV), and ωPBEh (0.20 eV), all of which reproduce best the CC2 results for the current data set.

3.3. Mixed basis sets

For the 11 molecules studied here, the number of basis functions is 327-1003 with the def2-TZVP basis sets and 573-1745 with the aug-def2-TZVP basis sets. Adding diffuse functions to the def2-TZVP basis sets improves the accuracy of the VEEs of states with performance for with significant Rydberg character. However, the computational costs are 3-5 times higher. In order to avoid the significant increase in computational efforts, we employed a mixed basis set, where the diffuse functions are placed only on the hydrogen atoms, which lie mainly at the outer edge of the chromophore. Diffuse molecular centered basis functions has also been used for reducing the computational costs when studying excited states with significant Rydberg character.¹²¹ The use of the mixed basis set leads to a small increase of about 25% in the computational time as compared to the calculations with the def2-TZVP basis sets.

We studied eight of the molecules with the mixed basis sets, listed in Figure 1. We omitted pHBDI⁺, PSBT⁺, ${\mathrm{PSB}11\mathrm{Me}}_2^{+}$, which are cations with a very small basis-set dependence of the calculated VEEs. The largest difference between the VEEs obtained with the def2-TZVP and aug-def2-TZVP basis sets is 0.07 eV. We calculated VEEs using eight functionals and the mixed basis sets. The obtained results for each of the molecules are reported in Tables S26–S33 and summarized in Table S34.

For def2-TZVP basis sets, the VEEs deviate from aug-def2-TZVP values with MSA values of 0.32-0.51 eV and RMS values of 0.47-0.69 eV. With the mixed basis sets, the MSA and RMS values relatively to the aug-def2-TZVP data are only 0.05-0.09 eV and 0.09-0.13 eV, respectively.

The mixed basis sets better reproduce not only the VEEs, but also the character of the wave functions of the excited states, which was assessed by calculating the overlap attachment $S_{12}^A$ and detachment $S_{12}^D$ integrals for the five excited states, defined as

$$\begin{gathered} S_{12}^A=\int {({\rho }_1^A(\mathbf{r}))}^{\frac{1}{2}}{({\rho }_2^A(\mathbf{r}))}^{\frac{1}{2}}d\mathbf{r}, \\ {S}_{12}^D=\int {({\rho }_1^D(\mathbf{r}))}^{\frac{1}{2}}{({\rho }_2^D(\mathbf{r}))}^{\frac{1}{2}}d\mathbf{r} \end{gathered}$$ (6)

where ${\rho }_1^A$ and ${\rho }_2^A$ are attachment densities with basis sets 1 and 2, and ${\rho }_1^D$ and ${\rho }_2^D$ are the corresponding detachment densities.¹²² For identical basis sets 1 and 2, the overlap integrals are equal to 1, reflecting that one electron is excited from the occupied space into the virtual space.

The overlap integrals computed from TDA calculations for the pVP molecule are given in Table S35 for the B3LYP and CAM-B3LYP functionals. At the B3LYP level using the def2-TZVP and aug-def2-TZVP basis sets, the wave functions of the five lowest excited states have $S_{12}^D$ values of 0.99, 0.97, 0.97, 0.82, and 0.94, indicating that all states except the fourth one have nearly identical detachment densities. The corresponding overlap integrals of attachment densities ($S_{12}^A$) are 0.99, 0.24, 0.24, 0.37, and 0.28, suggesting that the second to fifth excited states have significant Rydberg characters. The mixed basis-set calculations yield attachment and detachment densities that are very similar to the ones obtained with the aug-def2-TZVP basis sets, since the $S_{12}^A$ and $S_{12}^D$ overlaps are all larger than 0.98. The same behavior was obtained at the CAM-B3LYP level as shown in Table S35.

3.4. Comparison to experimental values

CC2 calculations generally reproduce experimental excitation energies within 0.2 eV, if the ground state of the molecule does not have a significant multireference character or the double excitations from the ground state are needed for an accurate description of the excited state.^38,123–126

Direct comparison of calculated VEEs to the experimental spectrum is difficult as the peaks of the spectrum are broadened by e.g., vibrational and dynamical effects as well as due to intensity borrowing for weak transitions. We follow here the common convention to compare calculation VEEs with the experimental peak maximum.^127–129 The lowest VEEs are compared with the experimental absorption maxima in Table S36. However, some of the experimental values have been measured in solvents, in the protein or extrapolated towards to the expected vacuum absorption maxima (pHBDI chromophores) rendering it difficult to accurately determine the deviations of the calculated VEEs from experimental values. Nevertheless, when neglecting this source of uncertainty, 11 of 15 VEEs calculated at the CC2 level agree within 0.25 eV from the experimental values. The VEEs deviating less than 0. 25 eV from the experimental values are marked in bold font in Table S36. The functionals that best reproduce the available experimental data are: B3LYP (12 out of 15 values within 0.25 eV deviation), PBE0 (7 out of 15 values), and ωhPBE0 (6 out of 15 values). However, B3LYP and PBE0 tend to underestimate the VEEs for higher excited states that might have significant Rydberg state characters. Interestingly, all TDDFT functionals predict blueshifted VEEs for the first excited state of the retinal models.

3.5. Performance on protein models

The VEEs computed at the B3LYP, CAM-B3LYP, and CAMh-B3LYP levels for the protein models described in Section 2.4 and shown in Figure 2 are reported in Table 2, where the obtained energies are compared to VEEs calculated at the CC2 level and to experimental data. The VEEs calculated at the CC2 level agree within 0.1 eV with the absorption maximum in the experimental spectra. For the A and B forms of the GFP models, the B3LYP functional yields almost the same VEEs, whereas the CAM-B3LYP functional overestimates the VEE of the A form. The proposed CAMh-B3LYP functional yields VEEs in good agreement with CC2 values and with experimental data.

Table 2:

Excitation energies (in eV) for DFT-optimized protein models of the green fluorescent protein (GFP) and the retinoid-binding protein II (hCRBPII) calculated at the CC2 and TDDFT levels using a few selected functionals. The calculations were performed with def2-TZVP basis sets.

Model/Method	CC2	B3LYP	CAM-B3LYP	CAMh-B3LYP	Exp.
GFP-Aa	3.13	2.98	3.70	3.14	3.12
GFP-Ba	2.72	2.91	2.79	2.76	2.61
hCRBPII-S2b	2.37	1.78	2.60	2.51	2.44
hCRBPII-S3b	2.13	1.45	2.42	2.39	2.10
hCRBPII-S6b	2.03	1.26	2.34	2.31	1.99

^aCC2 data and protein model from Refs 10 and 11.

^bCC2 data and protein model from Ref. 109.

Calculations of VEEs of retinal proteins are also challenging at the TDDFT level using commonly used functionals, because the photoexcitation leads to a transfer of positive charge from the protonated Schiff base to the β-ionine unit. The B3LYP functional severely underestimates the VEEs by about 0.7 eV, whereas CAM-B3LYP overestimates them with a mean error of 0.27 eV. The proposed CAMh-B3LYP functional also overestimates the VEEs with a slightly improved mean error of 0.22 eV. The TDDFT calculations suggest that not only charge transfer but also correlation effects are important for accurate modelling of excited states of retinal proteins. Multiconfiguration effects are not significant, because the mean error of the VEEs calculated at the CC2 level is less than 0.05 eV. The calculations on the protein models suggest that the new CAMh-B3LYP functional may be useful for studies of excited states of large photobiological protein models.

4. Conclusions

We have computationally studied the excitation energies of the five lowest excited singlet states of 11 chemical analogs of PYP, GFP, and Rh/bR chromophores at the CIS, RPA, TDA and TDDFT levels using the def2-TZVP and aug-def2-TZVP basis sets. In the TDA and TDDFT calculations, 17 density functionals were employed including 7 existing range-separated functionals and two new empirical range-separated functionals that have 50% long-range HF exchange. The VEEs are compared with previously reported benchmark data calculated at the CC2 level. The main conclusions are:

1. Pure density functionals (BP86, PBE, M11-L) and hybrid functionals with 20% or 25% of HF exchange (B3LYP, PBE0) have a tendency of consistently underestimating VEEs. Hybrid density functionals with 50% or 54% HF exchange (BHLYP, PBE50 and M06-2X) and long-range corrected functionals (CAM-B3LYP, ωPBE, ωPBEh, ωB97XD, and M11) yield results in closer agreement with CC2 values. However, they overestimate the VEEs of excitation the present benchmarking set. The two new empirical functionals (CAMh-B3LYP and ωhPBE0) have smaller deviations from the CC2 data than the other employed functionals.

2. For the five lowest VEEs, the best performance is obtained with the CAMh-B3LYP (RMS=0.16, MSA=0.07 eV); ωhPBE0 (RMS=0.17, MSA = 0.06 eV); PBE0 (RMS=0.23, MSA=−0.14 eV); M06-2X (RMS=0.26, MSA=0.17 eV); CAM-B3LYP (RMS=0.31, MSA=0.25 eV); M11 (RMS=0.36, MSA = 0.16 eV) and ωPBEh (RMS=0.37, MSA=0.30 eV) when using the aug-def2-TZVP basis sets.

3. TDA calculations can yield smaller MSA errors that TDDFT calculations due to cancellation of errors, when using density functionals that underestimate the VEEs, while for range-separated functionals (CAM-B3LYP, CAMh-B3LYP, ωhPBE0, ωPBEh, ωB97X-D) and for functionals with more HF exchange (M06-2X and M11), the VEEs calculated at the TDDFT level are in better agreement with CC2 data.

4. For the lowest excited singlet state (S₁), the B3LYP, PBE0 and M06-2X functionals yield similar results as obtained with the range-separated functionals (CAM-B3LYP, CAMh-B3LYP, ωPBE, ωhPBE0, ωPBEh, ωB97X-D) when using the aug-def2-TZVP basis sets.

5. The most accurate transition energies between excited states for the current photobiological data set are obtained with the M06-2X, CAM-B3LYP, CAMh-B3LYP, BHLYP, ωhPBE0, and ωPBEh functionals.

6. When using aug-def2-TZVP basis functions on only the hydrogen atoms, the computational costs increase by about 25% as compared to calculations using the def2-TZVP basis sets, while the MSA deviates by less than 0.1 eV from the values obtained with the aug-def2-TZVP basis sets.

7. The proposed CAMh-B3LYP functional improves the accuracy of calculated VEEs for large protein models.