Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Jul 17;5(29):18403–18410. doi: 10.1021/acsomega.0c02215

Strain-Induced Band Modulation, Work Function, and QTAIM Analysis of Surface O-Functionalized Ti2C MXene

Xiao-Hong Li †,‡,*, Rui-Zhou Zhang †, Hong-Ling Cui †
PMCID: PMC7391937  PMID: 32743217

Abstract

graphic file with name ao0c02215_0011.jpg

Functionalized MXenes have wide applications in the fields of gas sensors, thermoelectric materials, and hydrogen storage. Strain-induced band engineering and the work function (WF) of Ti2CO2 MXene are investigated theoretically. The calculations reveal that Ti2CO2 MXenes are stable because of the negative Ecoh, and all the strains considered are within the elastic limit. For Ti2CO2 MXene, strain-induced blue shift of the Ti d state results in the transformation from a semiconductor to a metal. At about 4%, Ti2CO2 MXene transforms from an indirect band gap to a direct band gap. The decreased WF induced by the strain improves the power efficiency of Ti2CO2 MXene.

1. Introduction

Lithium-ion batteries (LIBs) have been the most important and efficient energy storage devices because of their commercialization and are widely applied to smart grids.1 However, the applications of LIBs have been hindered by safety issues such as overcharge, thermal runaway, lithium dendrites, and so on. In addition, the high cost of LIBs is another factor that hinders their application. Two-dimensional (2D) materials such as layered materials, graphene, and so on2−5 have been explored in detail because of their potential application in LIBs. Because of the unique structure, these layered materials have excellent properties such as thermal properties, variable band gap, and so forth.6−9 For graphene, the limited range of the band gap hinders its application in the field of nanoelectronics, etc. In addition, the carbon network and the high cost of graphene further impeded its application. Therefore, extensive works are continued to design photodetectors and search for new layered materials with a wide band gap and good thermal stability.

2D materials with a general formula of MnXn–1 (MXenes), where n = 1–4, have outstanding properties and are extensively used in battery electrode materials.10,11 MXene nanosheets can be obtained from MAX materials, which we have discussed before.12 In this process, some functionalized groups such as F, O, and/or OH are on the surface of the monolayer, which results in the formation of functionalized MXenes (denoted Mn+1XnTx). Here, T represents the functionalized groups F, O, and/or OH and x is the termination number.13

To date, more than 70 of the MAX compounds are synthesized,14 while the synthesized MXenes are severely scarce. Among all potential MXene phases, Ti2C has the biggest superficial area per weight and is one of the most potential electrode materials. Guo et al.15 investigated the stress–strain curves of Ti2C and the deformation mechanism theoretically. They thought that 2D Ti2C is less stiff than graphene but stiffer than MoS2. In addition, they also thought that the terminating O-functional groups on the 2D Ti2C surface can improve the mechanical properties.15 Gao et al.16 theoretically explored the adsorption behavior of mercury on Ti2CO2. Ti2CO2 is a semiconducting feature with superhigh carrier mobility17−20 and thermal stability.21 It has the band gap of 0.26 eV based on density functional theory (DFT).22 The hole mobility of Ti2CO2 is the highest among the semiconducting MXenes23 and its thermal conductivity is 21.9 W m–1 K–1 at room temperature, so Ti2CO2 MXene can be considered as a thermoelectric material or gas sensor. In addition, Ti2CO2 is also widely applied in energy storage24 and wastewater treatment.25

Work function (WF) has an important role in field-effect transistors.26,27 Materials with low WFs can improve the power efficiency. The strain or electric field can modulate the WFs, which is important to maximize the performances of the device.28,29 Until now, the modulation of Ti2CO2 under strain is not available.

Structural variation can affect the properties of 2D materials.30,31 Applying strain or vacancy defect can tune the band gap of MXenes,12,32−34 which is desired in technological applications. In this paper, the band gap and WF are modulated by biaxial strain which is desired in industrial applications, and the electronic structure and the migrant mechanism of Ti2CO2 are investigated further. The comparison of the related properties between Ti2CO2 and similar 2D materials and the analysis of Bader’s quantum theory of atoms in molecules (QTAIM) for Ti2CO2 are performed in our paper, which is not available in previous works. Our investigation will provide useful information to modulate the physical and chemical properties of MXenes.

2. Results and Discussion

2.1. Structural Properties

Figure 1a presents the structures of the Ti2AlC MAX phase and Ti2CO2 MXene. Previous research studies indicate that the energetically most stable structure is that the O atom is at the position of etched away Al atoms.35,36 Mechanical strain is an effective approach to modulate the electronic structure.37 The schematic illustration of the biaxial strain is shown in Figure 1b. In our paper, the strain is set as ε = [(a – a0)/a0] × 100%, where a0 is the lattice parameter without strain and a is the lattice parameter with strain. Figure 1b also denotes the supercell by a dashed line frame, and the supercell size is 6.0596 Å. Figure 1c presents the Ti2CO2 monolayer from the side view.

Figure 1.

Figure 1

Open in a new tab

Atomic structure as ball-and-stick models. (a) Ti2AlC MAX phase; (b) Ti2CO2 monolayer top view; and (c) Ti2CO2 monolayer side view.

Cohesive energy (Ecoh) can be used to understand the phase stability. For Ti2CO2, Ecoh is generated by eq 1.

2.1. 1

where Etot is the total energy of Ti2CO2 with strain and Eatm represents the energies of three single atoms. Negative Etot indicates the stable crystal structure.

Table 1 lists the Ecoh for Ti2CO2 with strain from −5 to +5%. In Table 1, negative Ecoh indicates the stable structure of Ti2CO2 under strain.

Table 1. Cohesive Energy Ecoh of the Ti2CO2 Monolayer.

strain (%) Ecoh (eV/atom) strain (%) Ecoh (eV/atom)
0 –3.573 +1 –3.569
–1 –3.569 +2 –3.559
–2 –3.558 +3 –3.543
–3 –3.539 +4 –3.521
–4 –3.512 +5 –3.494
–5 –3.477    
Open in a new tab

2.2. Band Gap Modulation by Strain

Ti2CO2 MXene without strain is a semiconductor with an indirect band gap, which interrupts efficient light emission and hinders its application in optical devices. No magnetism is found for Ti2CO2 under strain in our computation. The band gap of Ti2CO2 without strain is 0.256 eV, which is smaller than those of Sc2CF2 (1.023 eV)38 and MoS2 (1.76 eV).39

Figure 2 presents the band structure of Ti2CO2 under strain. The indirect band gap for Ti2CO2 MXene is the valence band maximum (VBM) at the Γ point and the conduction band minimum (CBM) at the M point. From Figure 2, the indirect band gap from M to Γ point decreases with strain from −1 to −3%. Moreover, Ti2CO2 undergoes semiconductor-to-metal transformation with the strain larger than −3%. The band gap increases with the strain from 0 to 5%. There is an M → Γ indirect band gap with the strain from 1 to 3% and a Γ → Γ direct band gap with the strain larger than 3%. From Figure 2, the Γ to Γ direct band gap is not so sensitive to the strain. The band gap of Ti2CO2 changes from 0.256 to 0.449 eV with the strain from 0 to 5%. Therefore, the transformation from an indirect to a direct band gap for Ti2CO2 enables it to have potential applications in fields such as thermoelectric materials and so on.

Figure 2.

Figure 2

Open in a new tab

(a–f) Band gap of Ti2CO2 under biaxial strain.

The strain energy is explored to check whether the strain considered is within the elastic limit. Strain energy Es = (Estrained – Eunstrained)/n, with n being the number of atoms in the unit cell. Figure 3 presents the Es and the band gap under strain. The characteristic of the quadratic function of the strain–energy curve indicates that all the strains considered are within the elastic range of Ti2CO2 and are fully reversible. From Figure 3, the band gap is maximum (∼0.449 eV) under 4% strain. At about −3% strain, Ti2CO2 goes from a semiconductor to a metal.

Figure 3.

Figure 3

Open in a new tab

Band gap and strain energy of Ti2CO2 MXene under strain.

Figure 4 presents the direct and indirect band gaps between Γ and M points for Ti2CO2 under strain. The energy difference between Γ → Γ and Γ → M band gaps is 0.006 eV at 4% strain. Therefore, 4% strain is the critical point at which Ti2CO2 transforms from an indirect to a direct band gap.

Figure 4.

Figure 4

Open in a new tab

Direct and indirect band gaps between Γ and M points under strain.

The contribution of each atom to the energy level (EL) is investigated in order to confirm which factor mainly affects the band gap and plotted in Figure 5. We consider two Ti (Ti1 and Ti2) atoms, two O (O1 and O2) atoms, and a C atom. For Ti2CO2 without strain, C, 2Ti, and 2O atoms contribute 39.58, 28.7, and 31.7% to the EL at the VBM, respectively. 2Ti and 2O atoms contribute 48.7% and 33.7% to the EL at the CBM, respectively. Ti2CO2 with +5% strain has a Γ → Γ direct band gap. The C, 2Ti, and 2O atoms contribute 38.9% (28.6%), 30.6% (37.7%), and 30.5% (33.6) to the EL at the VBM (CBM), respectively.

Figure 5.

Figure 5

Open in a new tab

Contribution of each atom in monolayer Ti2CO2 to the energy level at the (a) strain-free and (b) 5% tensile states. The contribution of each atom is marked by different colors. The blue arrows represent the VBM and CBM states at the band structure of the dominant atoms.

Figure 6 presents the partial density of states (PDOS) under strain. The dotted vertical lines in Figure 6 indicate the Fermi level. Ti d and O p have the strong hybridization in the energy range of −6 to −4 eV for Ti2CO2 without strain. The peaks around −2 eV mainly originate from the Ti d, O p, and C p states. The Ti d state provides the main contribution for the peak at 2.5 eV. Ti2CO2 without strain is a semiconductor. The Ti d state undergoes a red shift with the increase in the compression strain and across the Fermi level at −3% strain. The Ti d state undergoes a blue shift with the increase of tensile strain, resulting in the increase of the band gap.

Figure 6.

Figure 6

Open in a new tab

(a–f) PDOS of Ti2CO2 under strain.

Figure 7 plots the PDOS of each atom of Ti2CO2 with strain. From Figure 7, it can be observed that for Ti2CO2 without strain, Ti dz2 mainly contribute to the CBM state (M point), while C px and O pz to the VBM (Γ point). For Ti2CO2 with +5% strain, C pz and O pz provide the main contribution to VBM (Γ point), while Ti dz2, Ti dxz, and O pz mainly contribute to the CBM state (M point).

Figure 7.

Figure 7

Open in a new tab

PDOS of Ti2CO2 without strain (a) and with +5% biaxial strain (b).

2.3. WF Engineering by Strain

WF is an important physical parameter of materials and plays a significant role in light-emitting diodes and field effect transistors. WF, ϕ, is defined as the energy required to promote an electron from the Fermi EL to vacuum: ϕ = E0 – EF, where E0 and EF are the potential in the vacuum and the Fermi level, respectively.

Figure 8 presents the WFs of Ti2CO2 under strain. The WF of Ti2CO2 without strain is 5.90 eV, which is close to the results of Khazaei et al.40 but larger than that of Sc2CF2 (4.803 eV)39 and the graphene/black phosphorene bilayer (5.38 eV).41 The WF decreases gradually with the increase of tensile strain and is 5.72 eV at +5% strain. This indicates that strain can modulate the WF effectively. For Ti2CO2 MXene, increasing tensile strain can improve the catalytic activity of materials.

Figure 8.

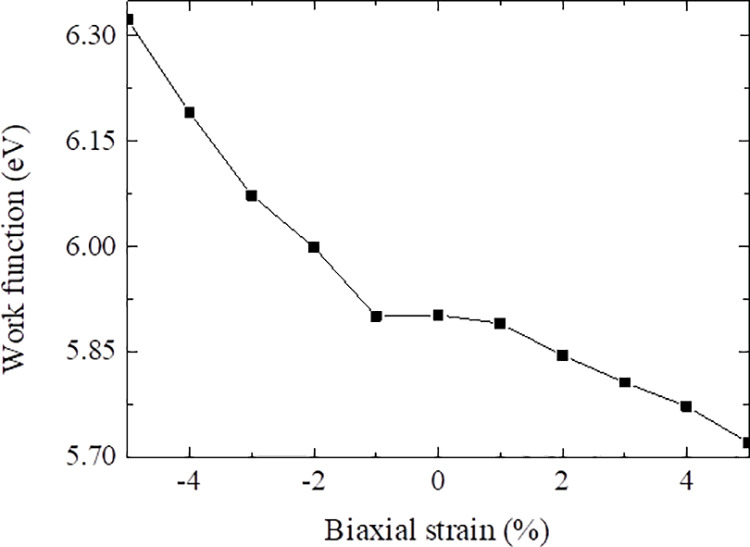
Figure 8

Open in a new tab

Variation of the WF of Ti2CO2 MXene as a function of biaxial strain.

According to the report of Ma et al.,42 Ti2CO2 under compressive strain has a higher WF, which can reduce the Schottky barrier and decrease the field emission performance. Ti2CO2 under tensile strain has a lower WF, which can improve the field emission performance. Ti2CO2 under +5% strain has a better field emission performance, while Ti2CO2 under −5% strain has a poor field emission performance. On the other hand, Ti2CO2 under tensile strain can be treated as a cathode because of the lower WF, while Ti2CO2 under compressive strain can be considered as an anode because of the higher WF.

2.4. Migration Mechanism of the Carrier

In order to get a deep insight into the electronic distribution, the electron localization function (ELF) for the Ti2CO2 monolayer is investigated. The ELF can measure the probability of finding an electron with the same spin. The ELF ranges from 0 to 1. ELF = 1 indicates perfect localization, ELF = 0.5 indicates the metallic bond, while ELF = 0 indicates delocalization. Here, we only list the ELF without strain and with +5 and −5% strain along the y-direction (shown in Figure 1), in Figure 9.

Figure 9.

Figure 9

Open in a new tab

ELF of Ti2CO2 without strain (a), with +5% strain (b), and with −5% strain (c).

From Figure 9, it can be observed that there exist strong Ti–O and Ti–C interactions under 0, +5, and −5% strain. The ELF values around the O and C sites are larger than the EFL value around the Ti site. Therefore, there exist partially covalent bonds between Ti and O and Ti and C atoms.

Spatial charge distributions are also explored in our study. Figure 10 exhibits the partial charge distribution of the CBM and the VBM of Ti2CO2 without strain and with +5% strain. The VBMs are located around C and O atoms, whereas most of the charge shifts to the Ti atom in the CBM state for Ti2CO2 without strain. For Ti2CO2 with +5% strain, the distribution of the VBM is same as that without strain. In the CBM state, most of the charge shifts to the Ti atom and a little shifts to the O atom. This analysis is in accordance with the result of PDOS of Ti2CO2. The different CBM and VBM distributions can inhibit the recombination of electron–hole pairs.

Figure 10.

Figure 10

Open in a new tab

Spatial charge distributions of the VBM (a) and the CBM (b) without strain and the VBM (c) and the CBM (d) with +5% strain.

From Bader analysis, the charges of each of the O, Ti, and C atoms without strain are −1.2518, +2.2504, and −1.9944 e–, respectively. (The numbers of valence electrons employed in the calculations for O, Ti, and C atoms are 6, 4, and 4, respectively.) The charges of each of the O, Ti, and C atoms with +5% strain are −1.3201, +2.3668, and −2.0935 e–, respectively. For O, Ti, and C atoms with −5% strain, the charges are −1.3087, 2.4188, and −2.2211 e–, respectively. Each of the O and C atoms gains more electrons from the Ti atom with the increase of the strain, which indicates that there exists enhanced bonding.

2.5. Quantum Theory of Atoms in Molecules

Bader’s QTAIM can confirm the chemical bonding in a molecule. Li et al.43 described the QTAIM analysis in detail. ρ(r) > 0 and ∇2ρ < 0 indicate the predominant covalent interaction, while small ρ(r) and ∇2ρ > 0 indicate the ionic interaction. The total energy density component at a bond critical point (BCP), H(r), is equal to the sum of the local electron potential energy density V(r) and the electron kinetic energy density G(r).

2.5. 2

The ratio ξ can also be used to reveal the nature of atomic interactions. From Table 2, it can be seen that ξ under stain is larger than 1 and less than 2 for the listed bonds, which indicates that all listed bonds (Ti–O and Ti–C) have the intermediate character. Table 2 also lists the other parameters such as the three curvatures (λ1, λ2, and λ3) of the electronic density and so forth

Table 2. Position and Properties of Ti2CO2 Electron Density BCP.

strain (%) Bonds position ρ(rc)/e·Å–3 ∇2ρ(rc)/e·Å–5 H(rc)/hartree·Å–3 G(rc)/hartree·Å–3 V(rc)/hartree·Å–3 ξ λ1a/e·Å–5 λ2a/e·Å–5 λ3a/e·Å–5 d1b/Å d2b/Å Dc/Å
0 Ti(1)–O(1) (0.4959 0.5041 0.5902) 0.1043 0.3736 0.0271 0.0663 –0.0392 1.69 –0.196 –0.174 0.744 1.918 1.819 1.055
  O(2)–Ti(2) (0.5040 0.4960 0.4412) 0.1039 0.3731 0.0273 0.0659 –0.0386 1.71 –0.195 –0.174 0.742 1.820 1.920 0.948
  Ti(2)–C(1) (0.1632 0.8368 0.4885) 0.0742 0.1927 0.0106 0.0376 –0.0270 1.39 –0.082 –0.081 0.356 2.097 2.033 1.031
5 Ti(1)–O(1) (0.4971 0.5031 0.5879) 0.0951 0.3192 0.0229 0.0569 –0.0340 1.67 –0.1825 –0.1572 0.6588 1.949 1.865 1.045
  O(2)–Ti(2) (0.5026 0.4975 0.4435) 0.0923 0.3130 0.0241 0.0541 –0.0300 1.80 –0.1765 –0.1510 0.6404 1.877 1.959 0.958
  Ti(2)–C(1) (0.1661 0.8338 0.4893) 0.0672 0.1594 0.0080 0.0319 –0.0239 1.33 –0.0798 –0.0739 0.3132 2.133 2.100 1.016
–5 Ti(1)–O(1) (0.5054 0.4945 0.4385) 0.1144 0.4372 0.0319 0.0774 –0.0454 1.70 –0.2068 –0.1909 0.8349 1.777 1.888 0.941
  O(2)–Ti(2) (0.4945 0.5053 0.5929) 0.1141 0.4395 0.0328 0.0771 –0.0442 1.74 –0.2065 –0.1870 0.8330 1.889 1.778 1.063
  Ti(2)–C(1) (0.1595 0.3185 0.4875) 0.0818 0.2132 0.0090 0.0443 –0.0353 1.25 –0.0950 –0.0917 0.3999 1.969 2.061 0.956
Open in a new tab
a

λ1, λ2, λ3: eigenvalues.

b

d1, d2: the distance between the bcp and each bonded atom.

c

D: total bond path length.

3. Conclusions

In this paper, the electronic properties and WF of monolayered Ti2CO2 under strain are investigated based on first-principles calculations. The negative Ecoh indicates the stability of Ti2CO2 under strain. Ti2CO2 undergoes the semiconductor-to-metal transformation under −3% strain, which results from the red shift of the Ti d state. Ti2CO2 undergoes an indirect–direct transformation of the band gap under strain larger than +3% because of the blue shift of the Ti d state. The band gap of Ti2CO2 increases from 0.256 to 0.449 eV in the strain range of 0 to 5%. The critical point with an indirect-to-direct gap is 4%. Increasing the tensile strain can improve the power efficiency of materials for Ti2CO2 MXene. The charge analysis indicates that each of the O and C atoms gains more electrons from the Ti atom with increasing strain, which indicates that there exists a strong intermediate bonding and is further confirmed by the analysis of QTAIM.

4. Computational Details

First-principles calculations were performed by DFT implemented in the Vienna ab initio simulation package (VASP).44 The projector-augmented wave (PAW) method45 was used to describe the interactions between the valence electrons and ionic cores. The exchange–correlation energy was treated within the generalized gradient approximation using the Perdew–Burke–Ernzerhof functional.22 The pseudopotentials utilized the valence state of 3d34s1, 2s22p2, and 2s22p4 for Ti, C, and O, respectively. A vacuum space of 25 Å was used in the z-direction to avoid the interaction. The Brillouin zone was sampled by using a 12 × 12 × 1 k-mesh according to the Monkhorst–Pack method.46 The spin polarization is considered. The van der Waals (vdW) interaction is taken into consideration by using the semiempirical correction of Grimme (DFT-D3).47 The energy cutoff of the plane waves was set to 700 eV. The positions of atoms were fully optimized, and the energy converged threshold was 10–6 eV per atom, and 0.05 eV/Å in force. A denser 25 × 25 × 1 mesh is used to calculate the electronic density of states.

Acknowledgments

This work was supported by the Program for Science&Technology Innovation Talents in Universities of Henan Province (No 14HASTIT039) and the Innovation Team of Henan University of Science and Technology (2015XTD001).

The authors declare no competing financial interest.

References

  1. Wen J.; Yu Y.; Chen C. A Review on lithium-ion batteries safety issues: existing problems and possible solutions. Mater. Express 2012, 2, 197–212. 10.1166/mex.2012.1075. [DOI] [Google Scholar]
  2. Novoselov K. S.; Fal’ko V. I.; Colombo L.; Gellert P. R.; Schwab M. G.; Kim K. A roadmap for graphene. Nature 2012, 490, 192–200. 10.1038/nature11458. [DOI] [PubMed] [Google Scholar]
  3. Li Y.; Wu D.; Zhou Z.; Cabrera C. R.; Chen Z. Enhanced Li adsorption and diffusion on MoSL2 zigzag nanoribbons by edge effects: a computational study. J. Phys. Chem. Lett. 2012, 3, 2221–2227. 10.1021/jz300792n. [DOI] [PubMed] [Google Scholar]
  4. Putungan D. B.; Lin S.-H.; Kuo J.-L. Metallic VS2 monolayer polytypes as potential sodium-ion Battery anode via ab initio random structure searching. ACS Appl. Mater. Interfaces 2016, 8, 18754–18762. 10.1021/acsami.6b03499. [DOI] [PubMed] [Google Scholar]
  5. Ren X.; Lian P.; Xie D.; Yang Y.; Mei Y.; Huang X.; Wang Z.; Yin X. Properties, preparation and application of black phosphorus/phosphorene for energy storage: a review. J. Mater. Sci. 2017, 52, 10364–10386. 10.1007/s10853-017-1194-3. [DOI] [Google Scholar]
  6. Koppens F. H. L.; Mueller T.; Avouris P.; Ferrari A. C.; Vitiello M. S.; Polini M. Photodetectors based on graphene, other two-dimensional materials and hybrid systems. Mat. Nanotechnol. 2014, 9, 780–793. 10.1038/nnano.2014.215. [DOI] [PubMed] [Google Scholar]
  7. Naguib M.; Mochalin V. N.; Barsoum M. W.; Gogotsi Y. 25th Anniversary Article: MXenes: A new family of two-dimensional materials. Adv. Mater. 2014, 26, 992–1005. 10.1002/adma.201304138. [DOI] [PubMed] [Google Scholar]
  8. Hu J. K.; Zhang Z. H.; Fan Z. Q.; Zhou R. L. Electronic and transport properties and physical field coupling effects for net-Y nanoribbons. Nanotechnology 2019, 30, 485703. 10.1088/1361-6528/ab3c8d. [DOI] [PubMed] [Google Scholar]
  9. Kuang W.; Hu R.; Fan Z. Q.; Zhang Z. H. Spin-dependent carrier mobility and its gate- voltage modifying effects for functionalized single walled black phosphorus tubes. Nanotechnology 2019, 30, 145201. 10.1088/1361-6528/aafb29. [DOI] [PubMed] [Google Scholar]
  10. Hu M.; Li Z.; Zhang H.; Hu T.; Zhang C.; Wu Z.; Wang X. Self-assembled Ti3C2Tx MXene film with high gravimetric capacitance. Chem. Commun. 2015, 51, 13531–13533. 10.1039/c5cc04722f. [DOI] [PubMed] [Google Scholar]
  11. Dall’Agnese Y.; Taberna P. L.; Gototsi Y.; Simon P. Two-dimensional vanadium carbide (MXene) as positive electrode for sodium-ion capacitors. J. Phys. Chem. Lett. 2015, 6, 2305–2309. 10.1021/acs.jpclett.5b00868. [DOI] [PubMed] [Google Scholar]
  12. Li X.-H.; Su X.-Y.; Zhang R.-Z. Strain-induced band modulation of surface F-functionalized two dimensional Sc2C. Appl. Surf. Sci. 2019, 491, 276–285. 10.1016/j.apsusc.2019.06.139. [DOI] [Google Scholar]
  13. Magne D.; Mauchamp V.; Celerier S.; Chartier P.; Cabioch T. Spectroscopic evidence in the visible-ultraviolet energy range of surface functionalization sites in the multilayer Ti3C2 MXene. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91, 201409. 10.1103/physrevb.91.201409. [DOI] [Google Scholar]
  14. Hu C.; Zhang H.; Li F.; Huang Q.; Bao Y. New phases’ discovery in MAX family. Int. J. Refract. Met. Hard Mater. 2016, 36, 300–312. 10.1016/j.ijrmhm.2012.10.011. [DOI] [Google Scholar]
  15. Guo Z.; Zhou J.; Si C.; Sun Z. Flexible two-dimensional Tin+1Cn (n = 1, 2 and 3) and their functionalized MXenes predicted by density functional theories. Phys. Chem. Chem. Phys. 2015, 17, 15348–15354. 10.1039/c5cp00775e. [DOI] [PubMed] [Google Scholar]
  16. Gao X.; Zhou Y.; Tan Y.; Cheng Z.; Yang B.; Ma Y.; Shen Z.; Jia J. Exploring adsorption behavior and oxidation mechanism of mercury on monolayer Ti2CO2 (MXenes) from first principles. Appl. Surf. Sci. 2019, 464, 53–60. 10.1016/j.apsusc.2018.09.071. [DOI] [Google Scholar]
  17. Lai S.; Jeon J.; Jang S. K.; Xu J.; Choi Y. J.; Park J.-H.; Hwang E.; Lee S. Surface group modification and carrier transport properties of layered transition metal carbides (Ti2CTx, T: −OH, −F and −O). Nanoscale 2015, 7, 19390–19396. 10.1039/c5nr06513e. [DOI] [PubMed] [Google Scholar]
  18. Zha X.-H.; Huang Q.; He J.; He H.; Zhai J.; Francisco J. S.; Du S. The thermal and electrical properties of the promising semiconductor MXene Hf2CO2. Sci. Rep. 2016, 6, 27971. 10.1038/srep27971. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Khazaei M.; Arai M.; Sasaki T.; Chung C.-Y.; Venkataramanan N. S.; Estili M.; Sakka Y.; Kawazoe Y. Novel electronic and magnetic properties of two-dimensional transition metal carbides and nitrides. Adv. Funct. Mater. 2013, 23, 2185–2192. 10.1002/adfm.201202502. [DOI] [Google Scholar]
  20. Zha X.-H.; Luo K.; Li Q.; Huang Q.; He J.; Wen X.; Du S. Role of the surface effect on the structural, electronic and mechanical properties of the carbide MXenes. Europhys. Lett. 2015, 111, 26007. 10.1209/0295-5075/111/26007. [DOI] [Google Scholar]
  21. Gan L.-Y.; Huang D.; Schwingenschlögl U. Oxygen adsorption and dissociation during the oxidation of monolayer Ti2C. J. Mater. Chem. A 2013, 1, 13672–13678. 10.1039/c3ta12032e. [DOI] [Google Scholar]
  22. Perdew J. P.; Burke K.; Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/physrevlett.77.3865. [DOI] [PubMed] [Google Scholar]
  23. Zha X.-H.; Zhou J.; Zhou Y.; Huang Q.; He J.; Francisco J. S.; Luo K.; Du S. Promising electron mobility and high thermal conductivity in Sc2CT2 (T = F, OH) MXenes. Nanoscale 2016, 8, 6110–6117. 10.1039/c5nr08639f. [DOI] [PubMed] [Google Scholar]
  24. Liang X.; Garsuch A.; Nazar L. F. Sulfur cathodes based on conductive MXene nanosheets for high-performance lithium–sulfur natteries. Angew. Chem., Int. Ed. 2015, 54, 3907–3911. 10.1002/anie.201410174. [DOI] [PubMed] [Google Scholar]
  25. Gao X.; Zhang X.; Zhao S.; Huang Q.; Xue J. High adsorption capacity of heavy metals on two-dimensional MXenes: an ab initio study with molecular dynamics simulation. Phys. Chem. Chem. Phys. 2016, 18, 228–233. 10.1039/c5cp06078h. [DOI] [PubMed] [Google Scholar]
  26. Ando Y.; Gohda Y.; Tsuneyuki S. Dependence of the Schottky barrier on the work function at Metal/SiON/SiC(0001) interfaces identified by first-principles calculations. Surf. Sci. 2012, 606, 1501–1506. 10.1016/j.susc.2012.05.023. [DOI] [Google Scholar]
  27. Freeouf J. L.; Woodall J. M. Schottky barriers: An effective work function model. Appl. Phys. Lett. 1981, 39, 727–729. 10.1063/1.92863. [DOI] [Google Scholar]
  28. Yu Y.-J.; Zhao Y.; Ryu S.; Brus L. E.; Kim K. S.; Kim P. Tuning the graphene work function by electric field effect. Nano Lett. 2009, 9, 3430–3434. 10.1021/nl901572a. [DOI] [PubMed] [Google Scholar]
  29. Wang Y.; Tong S. W.; Xu X. F.; Özyilmaz B.; Loh K. P. Interface engineering of layer-by-layer stacked graphene anodes for high-performance organic solar cells. Adv. Mater. 2011, 23, 1514–1518. 10.1002/adma.201003673. [DOI] [PubMed] [Google Scholar]
  30. Lee Y.; Cho S. B.; Chung Y.-C. Tunable indirect to direct band gap transition of monolayer Sc2CO2 by the strain effect. ACS Appl. Mater. Interfaces 2014, 6, 14724–14728. 10.1021/am504233d. [DOI] [PubMed] [Google Scholar]
  31. Peng X.; Wei Q.; Copple A. Strain-engineered direct-indirect band gap transition and its mechanism in two-dimensional phosphorene. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 085402. 10.1103/physrevb.90.085402. [DOI] [Google Scholar]
  32. Xiao-Hong L.; Su X. Y.; Zhang R. Z. Effect of vacancies on the structural and electronic properties of Ti2CO2. RSC Adv. 2019, 9, 27646. 10.1039/c9ra04393d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Hu R.; Li Y. H.; Zhang Z. H.; Fan Z. Q.; Sun L. O-Vacancy-line defective Ti2CO2 nanoribbons: novel magnetism, tunable carrier mobility, and magnetic device behaviors. J. Mater. Chem. C 2019, 7, 7745–7759. 10.1039/c9tc01807g. [DOI] [Google Scholar]
  34. Zhao T.; Fan Z. Q.; Zhang Z. H.; Zhou R. L. Electronic structure, strain effects and transport property of armchair graphene nanoribbon with variously possible edge oxidation. J. Phys. D: Appl. Phys. 2019, 52, 475301. 10.1088/1361-6463/ab3888. [DOI] [Google Scholar]
  35. Balci E.; Ozden U.; Berber S. Band gap modification in doped MXene: Sc2CF2. J. Mater. Chem. C 2017, 5, 5956–5961. 10.1039/c7tc01765k. [DOI] [Google Scholar]
  36. Tang Q.; Zhou Z.; Shen P. Are MXenes promising anode materials for Li ion batteries? Computational studies on electronic properties and Li storage capability of Ti3C2 and Ti3C2X2(X= F, OH) monolayer. J. Am. Chem. Soc. 2012, 134, 16909–16916. 10.1021/ja308463r. [DOI] [PubMed] [Google Scholar]
  37. Yu X.-f.; Cheng J.-b.; Liu Z.-b.; Li Q.-z.; Li W.-z.; Yang X.; Xiao B. The band gap modulation of monolayer Ti2CO2 by strain. RSC Adv. 2015, 5, 30438–30444. 10.1039/c5ra01586c. [DOI] [Google Scholar]
  38. Li X.-H.; Su X.-Y.; Zhang R.-Z.; Xing C.-H.; Zhu Z.-L. Pressure-induced band engineering, work function and optical properties of surface F-functionalized Sc2C MXene. J. Phys. Chem. Solids 2020, 137, 109218. 10.1016/j.jpcs.2019.109218. [DOI] [Google Scholar]
  39. Qi J.; Li X.; Qian X.; Feng J. Bandgap engineering of rippled MoS2 monolayer under external electric field. Appl. Phys. Lett. 2013, 102, 173112. 10.1063/1.4803803. [DOI] [Google Scholar]
  40. Khazaei M.; Arai M.; Sasaki T.; Ranjbar A.; Liang Y.; Yunoki S. OH-terminated two-dimensional transition metal carbides and nitrides as ultralow work function materials. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 92, 075411. 10.1103/physrevb.92.075411. [DOI] [Google Scholar]
  41. Cai Y.; Zhang G.; Zhang Y.-W. Electronic properties of phosphorene/graphene and phosphorene/hexagonal boron nitride heterostructures. J. Phys. Chem. C 2015, 119, 13929–13936. 10.1021/acs.jpcc.5b02634. [DOI] [Google Scholar]
  42. Ma Y.; Shen C.; Zhang A.; Chen L.; Liu Y.; Chen J.; Liu Q.; Li Z.; Amer M. R.; Nilges T.; Ahmad A.; Abbas A. N.; Zhou C. Black phosphorus field-effect transistors with work function tunable contacts. ACS Nano 2017, 11, 7126–7133. 10.1021/acsnano.7b02858. [DOI] [PubMed] [Google Scholar]
  43. Li X.-H.; Cui H.-L.; Yong Y.-L.; Zhang R.-Z. Elastic, electronic properties and QTAIM of new H-enriched hydrogen storage material Mg(BH4)2·(NH3)2(NH3BH3). Int. J. Hydrogen Energy 2019, 44, 7414–7421. 10.1016/j.ijhydene.2018.09.209. [DOI] [Google Scholar]
  44. Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
  45. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953–17979. 10.1103/physrevb.50.17953. [DOI] [PubMed] [Google Scholar]
  46. Monkhorst H. J.; Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B: Solid State 1976, 13, 5188–5192. 10.1103/physrevb.13.5188. [DOI] [Google Scholar]
  47. Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES