Identification and estimation of the SEIRD epidemic model for COVID-19

Abstract

This paper studies the SEIRD epidemic model for COVID-19. First, I show that the model is poorly identified from the observed number of deaths and confirmed cases. There are many sets of parameters that are observationally equivalent in the short run but lead to markedly different long run forecasts. Second, I show that the basic reproduction number $R_0$ can be identified from the data, conditional on epidemiologic parameters, and propose several nonlinear SUR approaches to estimate $R_0$. I examine the performance of these methods using Monte Carlo studies and demonstrate that they yield fairly accurate estimates of $R_0$. Next, I apply these methods to estimate $R_0$ for the US, California, and Japan, and document heterogeneity in the value of $R_0$ across regions. My estimation approach accounts for possible underreporting of the number of cases. I demonstrate that if one fails to take underreporting into account and estimates $R_0$ from the reported cases data, the resulting estimate of $R_0$ may be biased downward and the resulting forecasts may exaggerate the long run number of deaths. Finally, I discuss how auxiliary information from random tests can be used to calibrate the initial parameters of the model and narrow down the range of possible forecasts of the future number of deaths.

1. Introduction

The SIR (Susceptible, Infectious, Recovered) model and its variations are widely used in epidemiology to model the spread of epidemics. Since the outbreak of COVID-19, it has seen increased popularity among economists who are trying to assess the economic consequences of the coronavirus and various mitigation policies, such as Acemoglu et al. (2020), Atkeson, 2020b, Atkeson, 2020c, Avery et al. (2020), Berger et al. (2020), Eichenbaum et al. (2020), Ellison (2020), Fernandez-Villaverde and Jones (2020), Piguillem and Shi (2020), Toda (2020), and others. In this paper, I study identification and estimation of the modification of the SIR model called SEIRD (Susceptible, Exposed, Infectious, Recovered, and Dead) and present several findings.

First, I show that the SEIRD model has too many degrees of freedom and is poorly identified from the short run data on the number of deaths and confirmed cases. Conditional on the values of epidemiologic parameters, i.e. parameters that reflect the clinical progression of the disease, the only model parameter that is identified is the basic reproduction number $R_0$. While $R_0$ governs the speed of spread of the virus, the key driver of the long run number of deaths in the model is the infection fatality rate (IFR), which is not identified separately from initial values. As a result, models that are observationally equivalent in the short run can produce markedly different long run forecasts of the number of deaths.

Second, I propose several nonlinear seemingly unrelated regressions (SUR) approaches to estimate $R_0$ based on the deaths and confirmed cases data. The approaches I consider differ in whether they use cumulative or daily data and how they introduce errors in the model. I study the performance of different approaches in simulations and find that the methods based on cumulative data typically outperform those based on daily data in terms of the mean squared error (MSE) of the estimate of $R_0$. While there is no clear ranking of the approaches based on the data in levels or logarithms, the former do not involve trimming and thus may be more convenient in practice.

Next, I estimate the basic reproduction number $R_0$ for the US, California, and Japan for different values of epidemiologic parameters. I show that there is substantial heterogeneity in the values of $R_0$: for the same values of epidemiologic parameters, the estimates of $R_0$ for the US and California are about 2–4 times higher than for Japan. Moreover, the estimates of $R_0$ are highly sensitive to the values of epidemiologic parameters. There is no agreement in the medical literature on the length of the incubation and infectious period for COVID-19, and different values of these parameters result in the estimates of $R_0$ for the US that range from under 5 to around 17. Despite these large differences in the estimates of $R_0$, the resulting models lead to virtually identical fit of the observed data. These findings highlight that there is no single value of $R_0$ that is consistent with the data, at least in the short run. The appropriate value of $R_0$ depends both on the region and on the model.

My model and estimation strategy take into account possible underreporting of the number of COVID-19 cases. Even though the fraction of all cases that is reported is not identified, I show that it is important to allow it to differ from one. I demonstrate that if one does not take underreporting into account and estimates $R_0$ from the confirmed cases data, assuming that all cases are reported, the estimate of $R_0$ may be biased downward and the long run number of deaths may be overestimated.

Finally, I use the example of Iceland to show how auxiliary data can be used to narrow down the range of possible forecasts of the long run number of deaths from the epidemic. I use the results of presumably random testing conducted in Iceland to calibrate the initial conditions of the model and show that doing so results in a more than 4-fold reduction in the range of possible forecasts. This finding highlights the importance of random testing. Once more countries conduct tests of random samples of population for having COVID-19 as well as for having antibodies to it, it may become possible to calibrate the initial values better and obtain more precise forecasts about the future.

The remainder of the paper is organized as follows. Section 2 presents the SEIRD model. Section 3 describes the data I use. Section 4 discusses identification of the model. Section 5 outlines the estimation procedure. Section 6 contains Monte Carlo evidence. Section 7 presents the empirical results. Section 8 concludes. Appendix A presents additional results.

2. Model

In this paper I study a version of the SEIR model that includes dead among its compartments. Similar models have been used in epidemiology by Chowell et al. (2007), Lin et al. (2020), Wang et al. (2020), and others. More advanced versions of the model with more compartments are considered in Chowell et al., 2003, Chowell et al., 2006. I consider a model with five groups of people: susceptible (S), exposed (E), infectious (I), recovered (R), and dead (D). Susceptible are those who have not gotten the virus yet and can become infected. Exposed are those who have gotten the virus but cannot transmit it to others yet. This corresponds to the so called incubation period. Infectious are those who have the virus and are contagious. Recovered are those who were sick in the past but have recovered from the virus. Dead are those who have died because of the virus.

Including the exposed compartment in the model is important because, according to the CDC, COVID-19 involves an incubation period of up to 14 days.1 As a result, the SEIRD model should reflect the progression of the epidemic more accurately than a simpler SIRD model that does not include an incubation period.

The number of people in different groups evolves over time as follows:

$$\frac{dS\left(t\right)}{dt}=-\beta \frac{S\left(t\right)}{N}I\left(t\right)$$ (2.1)

$$\frac{dE\left(t\right)}{dt}=\beta \frac{S\left(t\right)}{N}I\left(t\right)-\sigma E\left(t\right)$$ (2.2)

$$\frac{dI\left(t\right)}{dt}=\sigma E\left(t\right)-\gamma I\left(t\right)$$ (2.3)

$$\frac{dR\left(t\right)}{dt}=(1-\alpha )\gamma I\left(t\right)$$ (2.4)

$$\frac{dD\left(t\right)}{dt}=\alpha \gamma I\left(t\right)$$ (2.5)

$$\frac{dC\left(t\right)}{dt}=\lambda \gamma I\left(t\right)$$ (2.6)

$N$ is the population size of a given country or region. I assume that it is fixed and does not vary over time. I could model the dynamics of the population size to account for the fact that some people die from the disease, but then I would also need to model births and deaths due to other causes. In order to avoid these complications, I simply fix $N$, as is commonly done in the literature. $C\left(t\right)$ is the cumulative number of cases confirmed. It does not affect the model dynamics but is used to match the model to the confirmed cases data. In my main analysis, I assume that it is the people who are infectious, rather than exposed, who are tested for the virus. In my robustness checks, I replace $I\left(t\right)$ in Eq. (2.6) with $E\left(t\right)$ and find that the results remain virtually unchanged.

The evolution of the SEIRD model depends on several parameters. I will refer to $\gamma$ and $\sigma$ as epidemiologic parameters. The parameter $\gamma$ reflects the estimated duration of illness. Its estimates in the literature vary from $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$18$}\right.$ (e.g. Wang et al. (2020)) to $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$ (e.g. Lin et al. (2020)). The parameter $\sigma$ reflects the estimated incubation period of the disease. Its estimates in the literature vary from $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$ (e.g. Wang et al. (2020), Lauer et al. (2020)) to $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$ (Lin et al. (2020)).

The parameter $\beta$ reflects the rate at which infectious people interact with others. It is often written as $\beta =R_0\gamma$, where $R_0$, called the basic reproduction number, measures the transmission of the disease with no mitigation efforts. Liu et al. (2020) review the literature on the estimation of $R_0$ for COVID-19 and conclude that the average and median estimates in the literature are around 3. However, Sanche et al. (2020) estimate that $R_0$ in China was equal to 5.7, much higher than found in the previous literature.

The parameter $\alpha$ is the infection fatality rate (IFR). As discussed in Korolev (2020), the IFR has serious limitations and heavily depends on the composition of people who get sick. The IFR may also not be constant over time and can substantially increase if the health care system becomes overwhelmed. However, for simplicity, I assume that $\alpha$ is fixed and try to estimate it. Finally, $\lambda$ is the proportion of all COVID-19 cases that is reported. It is also estimated.

The initial conditions for the number of recovered and dead are $R\left(0\right)=0$ and $D\left(0\right)=0$. Because the evolution of the model does not depend on initial number of confirmed cases $C\left(0\right)$, its choice does not affect my identification results. For simplicity, I set $C\left(0\right)=0$. Any other fixed value could be used, or $C\left(0\right)$ could be estimated. Next, I need to pick the initial number of infectious $I\left(0\right)$ and exposed $E\left(0\right)$. I discuss their choice later in the paper. Finally, the initial number of susceptible people is $S\left(0\right)=N-I\left(0\right)-E\left(0\right)-R\left(0\right)-D\left(0\right)=N-I\left(0\right)-E\left(0\right)$.

3. Data

In my estimation, I use the deaths and confirmed cases data for COVID-19. The country level data is collected by the Center for Systems Science and Engineering at Johns Hopkins University and is available online.2 The state level data for the US is collected by the New York Times and is also available online.3 The population of different countries and regions is taken from World Population Prospects 2019 by United Nations4 and from the US Census Bureau.5

I use $T=60$ observations in my sample, with the first observation being January 22, 2020 (for the US and Japan) or January 25, 2020 (for California). Around that time, cases of coronavirus were widely registered outside China, e.g. in the US (January 21),6 Germany (January 27),7 and the UK (January 31).8 However, as I show below, the initial conditions and the epidemic start date are not identified separately from the IFR and the fraction of cases reported. I discuss the identification challenges in more detail below.

I limit the sample to the first 60 observations because several states in the US issued stay home orders in March, e.g. California on March 19 and New York on March 22.9 One may be worried that these measures affected the value of the basic reproduction number $R_0$. By considering the first 60 observations, i.e. the data up to March 21 (for the US and Japan) or March 24 (for California), I should be able to address this concern. I consider alternative sample sizes in the robustness checks.

One may be concerned that the number of deaths because of the virus is misreported. It could be underreported because some people who die from the virus are not tested or overreported because some people who test positive for the virus actually die from other causes. If misreporting is constant over time, then the esimate of $R_0$ will be correct but the estimate of $\alpha$ will be biased. If the degree of deaths misreporting varies over time, then the estimate of $R_0$ may be biased. Similarly, if the fraction of cases that is reported changes over time, this may result in biased estimates of $R_0$.

4. Identification

In this section, I study identification of the model parameters based on the deaths and confirmed cases data. There are several earlier papers on identification of the parameters of the SIR and related models, e.g. Marinov et al. (2014), Magal and Webb (2018), and Ducrot et al. (2019), but they are not directly applicable in the current setting. In particular, they do not study whether the parameters are identified based on the short run data only. Atkeson (2020a), written concurrently and independently of this paper, attempts to answer the question similar to mine in the context of the usual SIR model. Manski and Molinari (2020) discuss identification problems in estimating the COVID-19 infection rate, but they do not consider SIR type models studied in this paper.

In the econometrics literature, identification studies whether the parameters of the model would be known if the researcher knew the population that data is drawn from (see, e.g., Lewbel (2019)). In the context of this paper, the question is somewhat different: if we observed the evolution of deaths $D\left(t\right)$ and confirmed cases $C\left(t\right)$ in the short run without any noise, would we then know the parameters of the model? Or, in other words, do different parameter values lead to different realizations of the observable data in the short run? Because the SEIRD model is difficult to solve in closed form, I simulate the deaths and reported cases paths from models with different parameter values and investigate whether these paths are identical instead of studying identification theoretically. I present a more rigorous treatment of identification in the simplified SIRD, rather than SEIRD, model in Supplementary Appendix A.1 and obtain similar results.

First, I assume that epidemiologic parameters $\gamma$ and $\sigma$ are known constants and study identification of the remaining parameters. The parameters of the model then include the basic reproduction number $R_0$, the infection fatality rate $\alpha$, the fraction $\lambda$ of all cases that is reported, and the initial conditions: the number of infectious people $I\left(0\right)=I_0$, the number of exposed people $E\left(0\right)=E_0$, and the time $T_0$ that has passed since the epidemic started. For instance, $T_0=1$ means that the epidemic just started and the initial values $(E_0,I_0)$ correspond to the first period we observe. $T_0=2$ means that the epidemic started last period and the current period corresponds to $(E\left(1\right),I\left(1\right))$. $T_0=10$ means that the epidemic started 9 periods ago from values $(E_0,I_0)$ and the current values are $(E\left(9\right),I\left(9\right))$. I denote the vector of parameters $\theta =(R_0,\alpha ,\lambda ,E_0,I_0,T_0)$ and study whether these parameters can be identified based on the short run (say, 60 days) data.

The upper panel of Fig. 1 plots the simulated paths of deaths and confirmed cases for three sets of parameters: ${\theta }^1=(5,0.01,0.2,2,2,2)$, ${\theta }^2=(5,0.005,0.1,4,4,2)$, and ${\theta }^3=(5,0.004,0.08,2,2,10)$. The first two sets of parameters share the same start date and reproduction number, but differ in the initial values and the values of $\alpha$ and $\lambda$. Essentially, the epidemic that corresponds to the second set of parameters just scales the first epidemic up by a factor of two, but cuts the fatality rate and the reported fraction of cases in half. As a result, these two epidemics are indistinguishable in the short run. In other words, we cannot tell from the short run data whether we observe a large epidemic with a low fatality rate and large number of unreported cases, or a small epidemic with a high fatality rate and small number of unreported cases.

Fig. 1.

Parameter identification. The upper panel shows the short run number of deaths and reported cases for three sets of parameters ${\theta }^1=(5,0.01,0.2,2,2,2)$, ${\theta }^2=(5,0.005,0.1,4,4,2)$, and ${\theta }^3=(5,0.004,0.08,2,2,10)$, where $\theta =(R_0,\alpha ,\lambda ,E_0,I_0,T_0)$. The middle panel shows the long run forecasts from these models. The lower panel fixes the initial conditions and shows the short run number of deaths and reported cases for $(R_0,\alpha ,\lambda )=(5,0.01,0.2)$, $(3,0.01,0.2)$, and $(3,0.05,0.8)$.

The third epidemic starts from the same values of $(E_0,I_0)$ as the first one, but nine periods ago instead of last period. At the same time it reduces the fatality rate and the observable fraction by a factor of 2.5. It produces more cases in the current period than the first epidemic, but a smaller fraction of them is reported and a smaller fraction leads to death. As a result, the third epidemic is indistinguishable from the first one.

While the three sets of parameters are indistinguishable in the short run, the middle panel of Fig. 1 shows that the resulting epidemics lead to very different long run deaths forecasts. The epidemic with the highest fatality rate $\alpha$ will result in about twice as many deaths as any of the other two epidemics.

Next, I study identification of $R_0$. The bottom panel of Fig. 1 shows that $R_0$ affects the curvature of the deaths and reported cases curves, while other parameters only tilt it around the origin. As a result, $R_0$ can be uniquely identified from the curvature of deaths and confirmed cases.

Fig. 2 parallels Fig. 1, but plots the logarithms of deaths and reported cases rather than their levels. It starts from day 30 rather than day 1, because logarithms are very sensitive to small values of different variables that are observed in the very beginning of the epidemic. The figure shows that changes in the initial conditions, the fatality rate $\alpha$, or the observable fraction of cases $\lambda$ shift the lines up or down without affecting their slope, while changes in the reproduction number $R_0$ change the slope of the lines. Thus, $R_0$ can be identified from the slope of the log series, but the remaining parameters cannot be separately identified.

Fig. 2.

Parameter identification in logarithms. The upper panel shows the logarithms of the short run number of deaths and reported cases for three sets of parameters ${\theta }^1=(5,0.01,0.2,2,2,2)$, ${\theta }^2=(5,0.005,0.1,4,4,2)$, and ${\theta }^3=(5,0.004,0.08,2,2,10)$, where $\theta =(R_0,\alpha ,\lambda ,E_0,I_0,T_0)$. The lower panel fixes the initial conditions and shows the logarithms of the short run number of deaths and reported cases for $(R_0,\alpha ,\lambda )=(5,0.01,0.2)$, $(3,0.01,0.2)$, and $(3,0.05,0.8)$.

Because one cannot separately identify $\alpha$, $\lambda$, $E_0$, $I_0$, and $T_0$, I set $T_0=1$ and $I_0=0$. In my empirical analysis, I will generally set $E_0=1$, unless it leads to computational issues. The model with the lowest possible value of $E_0$ corresponds to the highest possible value of the IFR and yields the upper bound on the long run number of deaths. I consider alternative choices of $E_0$ in the robustness checks.

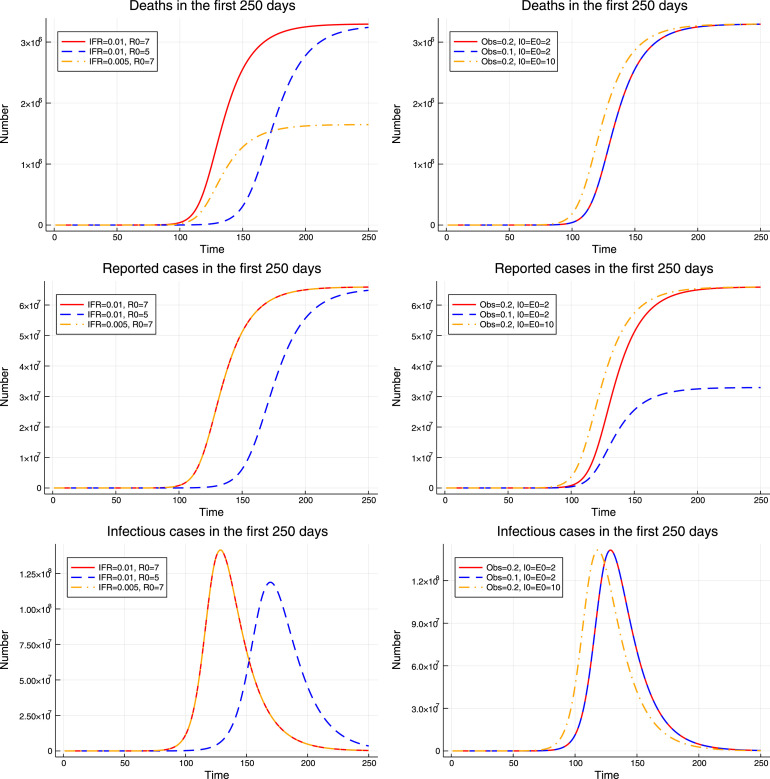
Next, Fig. 3 explores the role of different parameters in the evolution of the model. It demonstrates that changes in the value of $R_0$ primarily affect the timing of the epidemic but have little effect on the total death toll. The values of $\alpha$ and $\lambda$ affect the number of deaths and reported cases respectively, but they have no effect on the model dynamics. Finally, the initial values $E_0$ and $I_0$ affect the timing of the model, but to a much smaller extent than the value of $R_0$. Thus, if we are interested in modeling the evolution of the epidemic and its burden in terms of the number of deaths, the primary parameters of interest are $R_0$ and $\alpha$, while the remaining model parameters can be viewed as nuisance parameters.

Fig. 3.

Role of different parameters. The upper panel shows the evolution of the number of deaths. The middle panel shows the evolution of the number of reported cases. The lower panel shows the evolution of the (unobserved) number of infectious cases. Left: $(R_0,\alpha )=(7,0.01)$, $(5,0.01)$, and $(7,0.005)$. Right: $(\lambda ,E_0)=(0.2,2)$, $(0.1,2)$, and $(0.2,10)$.

5. Estimation

In this section, I turn to estimation of the SEIRD model. In order to rationalize the model with the observed data, one needs to introduce errors in the model. There are several possible ways to introduce errors, and they can lead to different estimation approaches. First, one could introduce errors directly in the cumulative numbers. They would be given by

$$D^{obs}\left(t\right)=D(t,R_0,\alpha )+{\epsilon }_D\left(t\right),$$ (5.1)

$$C^{obs}\left(t\right)=C(t,R_0,\lambda )+{\epsilon }_C\left(t\right),$$ (5.2)

where $E\left[({\epsilon }_D\left(t\right),{\epsilon }_C\left(t\right))\right]=0$. $D(t,R_0,\alpha )$ and $C(t,R_0,\lambda )$ denote the cumulative number of deaths and reported cases in the model,10 while $D^{obs}\left(t\right)$ and $C^{obs}\left(t\right)$ denote the cumulative number of deaths and reported cases observed in the data. Because the errors ${\epsilon }_D\left(t\right)$ and ${\epsilon }_C\left(t\right)$ enter the cumulative equations, they would likely exhibit strong autocorrelation.

One could introduce errors that are possibly independent over time by modeling the daily numbers of deaths and reported cases. Denote by $\Delta A\left(t\right)$ the first differences in the series $A\left(t\right)$. Then $\Delta D^{obs}\left(t\right)$ and $\Delta C^{obs}\left(t\right)$ would correspond to the observed daily number of deaths and reported cases. One could model them as

$$\Delta D^{obs}\left(t\right)=\Delta D(t,R_0,\alpha )+{\eta }_D\left(t\right),$$ (5.3)

$$\Delta C^{obs}\left(t\right)=\Delta C(t,R_0,\lambda )+{\eta }_C\left(t\right),$$ (5.4)

where $E\left[({\eta }_D\left(t\right),{\eta }_C\left(t\right))\right]=0$. In fact, the model in Eqs. (5.1), (5.2) can be viewed as the model in Eqs. (5.3), (5.4) if ${\epsilon }_D\left(t\right)={\sum }_{s=1}^t{\eta }_D\left(s\right)$ and ${\epsilon }_C\left(t\right)={\sum }_{s=1}^t{\eta }_C\left(s\right)$.

Alternatively, one could assume that additive errors enter the equations for the logarithms of the daily numbers of deaths and reported cases rather than their levels:

$$log\left(\Delta D^{obs}\left(t\right)\right)=log\left(\Delta D(t,R_0,\alpha )\right)+{\nu }_D\left(t\right),$$ (5.5)

$$log\left(\Delta C^{obs}\left(t\right)\right)=log\left(\Delta C(t,R_0,\lambda )\right)+{\nu }_C\left(t\right),$$ (5.6)

where $E\left[({\nu }_D\left(t\right),{\nu }_C\left(t\right))\right]=0$. This model implies that

$$\Delta D^{obs}\left(t\right)=\Delta D(t,R_0,\alpha )exp\left({\nu }_D\left(t\right)\right),$$ (5.7)

$$\Delta C^{obs}\left(t\right)=\Delta C(t,R_0,\lambda )exp\left({\nu }_C\left(t\right)\right),$$ (5.8)

i.e. the errors in the daily numbers are multiplicative.

Yet another estimation approach introduces errors in the logarithms of the cumulative number of deaths and reported cases:

$$log\left(D^{obs}\left(t\right)\right)=log\left(D(t,R_0,\alpha )\right)+{\zeta }_D\left(t\right),$$ (5.9)

$$log\left(C^{obs}\left(t\right)\right)=log\left(C(t,R_0,\lambda )\right)+{\zeta }_C\left(t\right),$$ (5.10)

with where $E\left[({\zeta }_D\left(t\right),{\zeta }_C\left(t\right))\right]=0$.

There is no agreement on the choice of the model and estimation method in the literature. Chowell et al. (2007) estimate the model using the cumulative number of cases, i.e. Eq. (5.2). In turn, Toda (2020) uses the natural logarithm of the cumulative number of cases, i.e. Eq. (5.10). Finally, Fernandez-Villaverde and Jones (2020) estimate the model using the daily number of deaths, i.e. Eq. (5.3).

All these papers use data either on the number of reported cases or on the number of deaths, but not both. In contrast, I estimate the model using both series simultaneously. All four models (5.1)–(5.2), (5.3)–(5.4), (5.5)–(5.6), and (5.9)–(5.10) can be viewed as versions of the nonlinear SUR model (see, e.g., Gallant (1975) and Chapter 9 in Davidson and MacKinnon (1993)). This model has the following form:

$$y_j\left(t\right)=f_j(t,\theta )+u_j\left(t\right),E\left[u_j\left(t\right)\right]=0,j=1,2,$$

where $j=1$ corresponds to the deaths equation and $j=2$ corresponds to the reported cases equation. The parameters are $\theta =(R_0,\alpha ,\lambda )$. $R_0$ enters both equations, $\alpha$ only enters the deaths equation, and $\lambda$ only the cases equation. While it is possible to estimate the model equation by equation, this would result in two different estimates of $R_0$ and could lead to efficiency loss. Instead, as is usually done in the SUR literature, I estimate both equations jointly. Let $Y\left(t\right)={(y_1\left(t\right),y_2\left(t\right))}^{\prime }$, $F(t,\theta )={(f_1(t,\theta ),f_2(t,\theta ))}^{\prime }$, $U\left(t\right)={(u_1\left(t\right),u_2\left(t\right))}^{\prime }$. Then the objective function is given by

$$Q_T\left(\theta \right)=\frac{1}{T}\sum _{t=1}^T{(Y\left(t\right)-F(t,\theta ))}^{\prime }{W}^{-1}(Y\left(t\right)-F(t,\theta )),$$

where $W$ is a 2 × 2 weighing matrix. Several choices of $W$ are possible. The simplest possible choice is $W=I$, a 2 × 2 identity matrix, which assigns the same weight to both equations. Another possibility is

$$W=\left(\begin{array}{cc}\hfill {\hat{\sigma }}_1^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\hat{\sigma }}_2^2\hfill \end{array}\right),$$

where ${\hat{\sigma }}_j^2=\frac{1}{T}{\sum }_{t=1}^t{\tilde{u}}_j{\left(t\right)}^2$ is the estimate of the variance of the error terms equation by equation, ${\tilde{u}}_j\left(t\right)=y_j\left(t\right)-f_j(t,\tilde{\theta })$ are the residuals based on some preliminary estimates $\tilde{\theta }$ of $\theta$. These preliminary estimates could be the equation by equation estimates (with different values of $R_0$ for the two equations) or the estimates based on the known weighting matrix $W=I$. This choice of $W$ accounts for possibly different variances of the error terms in two equations but discards possible correlation between them.

Yet another choice is given by

$$W=\frac{1}{T}\sum _{t=1}^T\tilde{U}\left(t\right)\tilde{U}{\left(t\right)}^{\prime },$$

where $\tilde{U}\left(t\right)={({\tilde{u}}_1\left(t\right),{\tilde{u}}_2\left(t\right))}^{\prime }$, and ${\tilde{u}}_j\left(t\right)$ are the same as above. This choice of the weighting matrix accounts not only for possibly different variances of the error terms, but also for the correlation between them.

Finally, if one suspects heteroskedasticity, one could use the objective function

$$Q_T\left(\theta \right)=\frac{1}{T}\sum _{t=1}^T{(Y\left(t\right)-F(t,\theta ))}^{\prime }W{\left(t\right)}^{-1}(Y\left(t\right)-F(t,\theta )),$$

where $W\left(t\right)$ is an estimate of the variance of $U\left(t\right)$ that is allowed to vary over $t$. Because estimating $W\left(t\right)$ may be somewhat tricky, I do not consider this class of estimators in this paper.

While inference is also beyond the scope of this paper, I note that there are several interesting directions for future research. First, one could study how to conduct inference on the model parameters, e.g. the basic reproduction number $R_0$. While there are certain methods that would seem reasonable, such as the asymptotic SUR standard errors or the bootstrap (as in Chowell et al. (2007)), one would need to carefully account for partial identification of model parameters, possible heteroskedasticity and autocorrelation in the errors, and for the fact that the estimates of $\alpha$ and $\lambda$ may be close to the boundary of the parameter space (0 or 1). Second, one could be able to develop specification tests based on the difference between different estimates, e.g. with different weighting matrices, along the lines of Hausman (1978) and White (1981).

6. Simulations

In this section I investigate the performance of different estimation methods described above in a number of Monte Carlo studies. I consider several data generating processes (DGPs). In the first DGP, the deterministic part of the model is exactly as in Eqs. (2.1)–(2.6), while the errors are introduced as in Eqs. (5.3)–(5.4). I generate the simulated data as follows. First, I simulate the model from Eqs. (2.1)–(2.6) for the parameter values $R_0=5.75$, $\alpha =0.0067$, $\lambda =0.12$. Second, I construct the daily values of deaths and reported cases from the simulated model. Next, I draw the realizations of deaths and reported cases at time $t$ from the Poisson distributions with means $\Delta D(t,R_0,\alpha )$ and $\Delta C(t,R_0,\lambda )$ respectively. In other words,

$$\Delta D^{\ast }(t,R_0,\alpha )\sim \text{Poisson}\left(\Delta D(t,R_0,\alpha )\right),\Delta C^{\ast }(t,R_0,\lambda )\sim \text{Poisson}\left(\Delta C(t,R_0,\lambda )\right),$$

where the star superscript denotes simulated values. Thus, $E\left[\Delta D^{\ast }(t,R_0,\alpha )\right]=\Delta D(t,R_0,\alpha )$ and $E\left[\Delta C^{\ast }(t,R_0,\lambda )\right]=\Delta C(t,R_0,\lambda )$, so the errors in the simulated daily deaths and reported cases have mean zero by construction. Finally, I reconstruct the cumulative series $D^{\ast }(t,R_0,\alpha )$ and $C^{\ast }(t,R_0,\lambda )$ and estimate the parameters using all of the methods discussed above. In the DGP, the initial values are $E_0=2$, $I_0=0$. In the estimation, I try several fixed choices of $E_0$ as well as attempt to estimate $E_0$ and $I_0$. When I estimate $E_0$ and $I_0$, I restrict my attention to the approaches based on cumulative numbers, because the approaches based on daily numbers turn out to be prone to numerical issues.11

Table 1, Table 2, Table 3, Table 4 report the mean, bias, standard deviation, and MSE of the estimates of $R_0$ across 500 simulation draws. I consider two estimation approaches when logarithms are used: one trims all observations with $D^{obs}\left(t\right)\le 25$ or $C^{obs}\left(t\right)\le 75$, another one uses all observations with $D^{obs}\left(t\right)>0$ and $C^{obs}\left(t\right)>0$. I refer to the former approach as “Trim” and to the latter as “No Trim” in the tables.

Table 1.

Mean of estimates of $R_0$ for DGP (5.3)–(5.4).

	Deaths	Cases	SUR, Efficient $W$	SUR, Diagonal $W$	SUR, Identity $W$
Panel A: True $E_0=2$ and $I_0=0$, Assumed $E_0=2$ and $I_0=0$
Levels, Cumulative	5.774	5.754	5.757	5.754	5.754
Levels, Daily	5.781	5.755	5.759	5.756	5.756
Logs, Cumulative, Trim	5.771	5.755	5.753	5.751	5.761
Logs, Daily, Trim	5.799	5.763	5.757	5.758	5.776
Logs, Cumulative, No Trim	5.613	5.786	5.728	5.727	5.691
Logs, Daily, No Trim	4.725	5.786	5.664	5.640	5.239
Panel B: True $E_0=2$ and $I_0=0$, Assumed $E_0=1$ and $I_0=0$
Levels, Cumulative	5.773	5.754	5.757	5.754	5.754
Levels, Daily	5.780	5.755	5.759	5.755	5.755
Logs, Cumulative, Trim	5.770	5.755	5.753	5.750	5.761
Logs, Daily, Trim	5.796	5.763	5.757	5.758	5.775
Logs, Cumulative, No Trim	5.613	5.786	5.728	5.727	5.690
Logs, Daily, No Trim	4.725	5.786	5.662	5.638	5.246
Panel C: True $E_0=2$ and $I_0=0$, Assumed $E_0=16$ and $I_0=0$
Levels, Cumulative	5.788	5.765	5.769	5.765	5.765
Levels, Daily	5.801	5.781	5.789	5.797	5.781
Logs, Cumulative, Trim	5.782	5.762	5.761	5.758	5.769
Logs, Daily, Trim	5.857	5.777	5.770	5.771	5.792
Logs, Cumulative, No Trim	5.623	5.789	5.731	5.730	5.694
Logs, Daily, No Trim	4.725	5.793	5.669	5.644	5.241
Panel D: True $E_0=2$ and $I_0=0$, Estimated $E_0$ and $I_0$
Levels, Cumulative	5.774	5.755	5.763	5.764	5.769
Logs, Cumulative, Trim	5.772	5.756	5.755	5.754	5.762
Logs, Cumulative, No Trim	5.617	5.788	5.732	5.731	5.693

The table presents the mean of the estimates of $R_0$ across 500 simulation draws. The true value is $R_0=5.755$. The estimates in the first column are based on the deaths data only. The estimates in the second column are based on the reported cases data only. The estimates in the remaining three columns combine the deaths and reported cases data and use different weighting matrices.

Table 2.

Bias of estimates of $R_0$ for DGP (5.3)–(5.4).

	Deaths	Cases	SUR, Efficient $W$	SUR, Diagonal $W$	SUR, Identity $W$
Panel A: True $E_0=2$ and $I_0=0$, Assumed $E_0=2$ and $I_0=0$
Levels, Cumulative	0.019	−0.001	0.002	−0.001	−0.001
Levels, Daily	0.026	0.000	0.005	0.001	0.002
Logs, Cumulative, Trim	0.016	0.001	−0.001	−0.004	0.006
Logs, Daily, Trim	0.045	0.009	0.003	0.003	0.022
Logs, Cumulative, No Trim	−0.141	0.032	−0.026	−0.028	−0.064
Logs, Daily, No Trim	−1.030	0.032	−0.091	−0.115	−0.515
Panel B: True $E_0=2$ and $I_0=0$, Assumed $E_0=1$ and $I_0=0$
Levels, Cumulative	0.018	−0.001	0.002	−0.001	−0.001
Levels, Daily	0.025	0.000	0.004	0.000	0.000
Logs, Cumulative, Trim	0.016	0.000	−0.001	−0.004	0.006
Logs, Daily, Trim	0.042	0.009	0.003	0.003	0.021
Logs, Cumulative, No Trim	−0.142	0.031	−0.026	−0.028	−0.064
Logs, Daily, No Trim	−1.030	0.031	−0.092	−0.117	−0.508
Panel Dc: True $E_0=2$ and $I_0=0$, Assumed $E_0=16$ and $I_0=0$
Levels, Cumulative	0.034	0.011	0.014	0.011	0.011
Levels, Daily	0.046	0.026	0.034	0.043	0.026
Logs, Cumulative, Trim	0.027	0.007	0.007	0.003	0.014
Logs, Daily, Trim	0.102	0.022	0.016	0.016	0.037
Logs, Cumulative, No Trim	−0.132	0.035	−0.023	−0.025	−0.060
Logs, Daily, No Trim	−1.029	0.038	−0.085	−0.110	−0.514
Panel D: True $E_0=2$ and $I_0=0$, Estimated $E_0$ and $I_0$
Levels, Cumulative	0.020	0.000	0.009	0.009	0.014
Logs, Cumulative, Trim	0.017	0.001	0.001	0.000	0.007
Logs, Cumulative, No Trim	−0.137	0.033	−0.023	−0.023	−0.062

The table presents the average bias of the estimates of $R_0$ across 500 simulation draws. The estimates in the first column are based on the deaths data only. The estimates in the second column are based on the reported cases data only. The estimates in the remaining three columns combine the deaths and reported cases data and use different weighting matrices.

Table 3.

Standard deviation of estimates of $R_0$ for DGP (5.3)–(5.4).

	Deaths	Cases	SUR, Efficient $W$	SUR, Diagonal $W$	SUR, Identity $W$
Panel A: True $E_0=2$ and $I_0=0$, Assumed $E_0=2$ and $I_0=0$
Levels, Cumulative	0.317	0.072	0.076	0.072	0.071
Levels, Daily	0.512	0.117	0.118	0.118	0.119
Logs, Cumulative, Trim	0.424	0.089	0.092	0.091	0.219
Logs, Daily, Trim	0.570	0.123	0.119	0.117	0.281
Logs, Cumulative, No Trim	0.826	0.251	0.206	0.224	0.430
Logs, Daily, No Trim	0.470	0.230	0.166	0.217	0.286
Panel B: True $E_0=2$ and $I_0=0$, Assumed $E_0=1$ and $I_0=0$
Levels, Cumulative	0.316	0.071	0.075	0.072	0.071
Levels, Daily	0.511	0.116	0.114	0.114	0.116
Logs, Cumulative, Trim	0.423	0.089	0.092	0.091	0.218
Logs, Daily, Trim	0.567	0.123	0.118	0.117	0.280
Logs, Cumulative, No Trim	0.825	0.251	0.206	0.224	0.431
Logs, Daily, No Trim	0.470	0.230	0.170	0.220	0.270
Panel C: True $E_0=2$ and $I_0=0$, Assumed $E_0=16$ and $I_0=0$
Levels, Cumulative	0.328	0.073	0.078	0.074	0.073
Levels, Daily	0.500	0.122	0.175	0.255	0.123
Logs, Cumulative, Trim	0.435	0.091	0.093	0.093	0.223
Logs, Daily, Trim	0.719	0.127	0.123	0.121	0.293
Logs, Cumulative, No Trim	0.844	0.253	0.208	0.226	0.434
Logs, Daily, No Trim	0.471	0.235	0.168	0.220	0.287
Panel D: True $E_0=2$ and $I_0=0$, Estimated $E_0$ and $I_0$
Levels, Cumulative	0.318	0.072	0.083	0.087	0.089
Logs, Cumulative, Trim	0.424	0.090	0.095	0.098	0.219
Logs, Cumulative, No Trim	0.831	0.251	0.212	0.229	0.429

The table presents the standard deviation of the estimates of $R_0$ across 500 simulation draws. The estimates in the first column are based on the deaths data only. The estimates in the second column are based on the reported cases data only. The estimates in the remaining three columns combine the deaths and reported cases data and use different weighting matrices.

Table 4.

MSE of estimates of $R_0$ for DGP (5.3)–(5.4).

	Deaths	Cases	SUR, Efficient $W$	SUR, Diagonal $W$	SUR, Identity $W$
Panel A: True $E_0=2$ and $I_0=0$, Assumed $E_0=2$ and $I_0=0$
Levels, Cumulative	0.101	0.005	0.006	0.005	0.005
Levels, Daily	0.263	0.014	0.014	0.014	0.014
Logs, Cumulative, Trim	0.180	0.008	0.008	0.008	0.048
Logs, Daily, Trim	0.327	0.015	0.014	0.014	0.079
Logs, Cumulative, No Trim	0.702	0.064	0.043	0.051	0.189
Logs, Daily, No Trim	1.282	0.054	0.036	0.060	0.347
Panel B: True $E_0=2$ and $I_0=0$, Assumed $E_0=1$ and $I_0=0$
Levels, Cumulative	0.100	0.005	0.006	0.005	0.005
Levels, Daily	0.262	0.013	0.013	0.013	0.013
Logs, Cumulative, Trim	0.179	0.008	0.008	0.008	0.048
Logs, Daily, Trim	0.323	0.015	0.014	0.014	0.079
Logs, Cumulative, No Trim	0.701	0.064	0.043	0.051	0.190
Logs, Daily, No Trim	1.281	0.054	0.037	0.062	0.331
Panel C: True $E_0=2$ and $I_0=0$, Assumed $E_0=16$ and $I_0=0$
Levels, Cumulative	0.109	0.005	0.006	0.006	0.005
Levels, Daily	0.253	0.016	0.032	0.067	0.016
Logs, Cumulative, Trim	0.190	0.008	0.009	0.009	0.050
Logs, Daily, Trim	0.528	0.017	0.015	0.015	0.087
Logs, Cumulative, No Trim	0.729	0.065	0.044	0.052	0.192
Logs, Daily, No Trim	1.281	0.057	0.036	0.060	0.346
Panel D: True $E_0=2$ and $I_0=0$, Estimated $E_0$ and $I_0$
Levels, Cumulative	0.101	0.005	0.007	0.008	0.008
Logs, Cumulative, Trim	0.180	0.008	0.009	0.010	0.048
Logs, Cumulative, No Trim	0.709	0.064	0.045	0.053	0.188

The table presents the MSE of the estimates of $R_0$ across 500 simulation draws. The estimates in the first column are based on the deaths data only. The estimates in the second column are based on the reported cases data only. The estimates in the remaining three columns combine the deaths and reported cases data and use different weighting matrices.

As we can see, the estimation methods based on taking the logarithms without trimming have the largest bias and standard deviation, and as a result the worst MSE. Among the remaining four approaches, the ones based on cumulative numbers (or their logarithms) tend to outperform the ones based on the daily numbers (or their logarithms). Overall, it appears that estimation based on the cumulative numbers, done in levels rather than logarithms, leads to the lowest MSE of the estimates of $R_0$, and the estimation results are pretty insensitive to the choice of the weighting matrix $W$.

Using incorrect initial conditions (e.g. $E_0=16$ instead of $E_0=2$) has almost no effect on the quality of resulting estimates. It introduces small bias but does not affect the standard deviation of the estimates. Because in most cases the variance term dominates the squared bias term, the MSE remains almost unchanged. Moreover, in terms of the MSE, it is actually better to use an incorrect fixed initial condition rather than to estimate it from the data. Estimating $E_0$ and $I_0$ may reduce bias, but increases variance and hence leads to slightly worse MSE.

Table 5 presents the mean of the estimates of the fatality rate $\alpha$ for different initial conditions. In line with the identification results, when $E_0$ increases (decreases), the estimates of $\alpha$ decrease (increase) proportionally. For instance, the mean of the estimates of $\alpha$ for $E_0=2$ is eight times as large as for $E_0=16$, but is smaller by a factor of two than for $E_0=1$.

Table 5.

Mean of estimates of $\alpha$ for DGP (5.3)–(5.4).

	SUR, Efficient $W$	SUR, Diagonal $W$	SUR, Identity $W$
Panel A: True $E_0=2$ and $I_0=0$, Assumed $E_0=2$ and $I_0=0$
Levels, Cumulative	0.0067	0.0068	0.0067
Levels, Daily	0.0068	0.0068	0.0068
Logs, Cumulative, Trim	0.0068	0.0068	0.0071
Logs, Daily, Trim	0.0067	0.0067	0.0071
Logs, Cumulative, No Trim	0.0080	0.0081	0.0098
Logs, Daily, No Trim	0.0091	0.0097	0.0181
Panel B: True $E_0=2$ and $I_0=0$, Assumed $E_0=1$ and $I_0=0$
Levels, Cumulative	0.0134	0.0135	0.0135
Levels, Daily	0.0135	0.0136	0.0136
Logs, Cumulative, Trim	0.0136	0.0137	0.0143
Logs, Daily, Trim	0.0134	0.0134	0.0143
Logs, Cumulative, No Trim	0.0160	0.0162	0.0198
Logs, Daily, No Trim	0.0182	0.0194	0.0352
Panel C: True $E_0=2$ and $I_0=0$, Assumed $E_0=16$ and $I_0=0$
Levels, Cumulative	0.0008	0.0008	0.0008
Levels, Daily	0.0008	0.0008	0.0008
Logs, Cumulative, Trim	0.0008	0.0008	0.0009
Logs, Daily, Trim	0.0008	0.0008	0.0009
Logs, Cumulative, No Trim	0.0010	0.0010	0.0012
Logs, Daily, No Trim	0.0011	0.0012	0.0023

The table presents the mean of the estimates of ${\alpha }_0$ across 500 simulation draws. The true value is $\alpha =0.0067$. The estimates in different columns combine the deaths and reported cases data and use different weighting matrices.

Next, I study the robustness of the estimate of $R_0$ to a particular form of model misspecification. In the true DGP, I replace Eq. (2.6) with $\frac{dC\left(t\right)}{dt}=\lambda \sigma E\left(t\right)$, so that the reported cases are based on the number of exposed rather than infectious. However, I estimate the model as if it was generated by Eqs. (2.1)–(2.6). Table 6 reports the results. As we can see, this form of misspecification has no noticeable effect on the estimates of $R_0$.

Table 6.

Robustness of Estimates of $R_0$.

	Deaths	Cases	SUR, Efficient $W$	SUR, Diagonal $W$	SUR, Identity $W$
Panel A: Mean
Levels, Cumulative	5.775	5.753	5.753	5.753	5.753
Levels, Daily	5.814	5.756	5.756	5.757	5.756
Logs, Cumulative, Trim	5.750	5.751	5.752	5.750	5.749
Logs, Daily, Trim	5.832	5.755	5.755	5.755	5.789
Logs, Cumulative, No Trim	5.528	5.764	5.739	5.735	5.642
Logs, Daily, No Trim	4.590	5.777	5.720	5.719	5.225
Panel B: Bias
Levels, Cumulative	0.021	−0.002	−0.001	−0.001	−0.002
Levels, Daily	0.060	0.002	0.002	0.003	0.002
Logs, Cumulative, Trim	−0.004	−0.003	−0.003	−0.005	−0.006
Logs, Daily, Trim	0.077	0.001	0.001	0.000	0.034
Logs, Cumulative, No Trim	−0.226	0.009	−0.015	−0.019	−0.113
Logs, Daily, No Trim	−1.165	0.023	−0.035	−0.036	−0.530
Panel C: Standard Deviation
Levels, Cumulative	0.316	0.041	0.044	0.042	0.041
Levels, Daily	0.508	0.069	0.070	0.069	0.070
Logs, Cumulative, Trim	0.423	0.055	0.057	0.055	0.214
Logs, Daily, Trim	0.567	0.071	0.072	0.071	0.282
Logs, Cumulative, No Trim	0.876	0.153	0.112	0.144	0.433
Logs, Daily, No Trim	0.512	0.165	0.104	0.154	0.199
Panel D: MSE
Levels, Cumulative	0.100	0.002	0.002	0.002	0.002
Levels, Daily	0.262	0.005	0.005	0.005	0.005
Logs, Cumulative, Trim	0.179	0.003	0.003	0.003	0.046
Logs, Daily, Trim	0.327	0.005	0.005	0.005	0.081
Logs, Cumulative, No Trim	0.818	0.023	0.013	0.021	0.201
Logs, Daily, No Trim	1.618	0.028	0.012	0.025	0.320

The table presents the mean, bias, standard deviation, and MSE of the estimates of $R_0$ across 500 simulation draws when $\lambda \gamma I\left(t\right)$ in Eq. (2.6) is replaced with $\lambda \sigma E\left(t\right)$. The true value is $R_0=5.755$. Initial conditions: $E_0=2$, $I_0=0$. The estimates in the first column are based on the deaths data only. The estimates in the second column are based on the reported cases data only. The estimates in the remaining three columns combine the deaths and reported cases data and use different weighting matrices.

Another DGP I consider is based on the model in Eqs. (2.1)–(2.6) but involves a different way of introducing errors. I focus on the model in logarithms of the daily numbers and simulate the data as in Eqs. (5.5)–(5.6), where ${\nu }_D\left(t\right)$ and ${\nu }_C\left(t\right)$ are both $N(0,0.025^2)$. I then compute $\Delta D^{\ast }(t,R_0,\alpha )$ and $\Delta C^{\ast }(t,R_0,\lambda )$ by taking exponents and construct the cumulative series accordingly. Unlike the previous DGPs, which produced integer values as a result, this DGP will generally produce the number of deaths and reported cases that are not integers. In addition to this DGP I also consider its modified version that rounds the number of daily deaths and reported cases to the nearest integer. The true initial values are $E_0=2$, $I_0=0$. In estimation, I use these fixed values as well as attempt to estimate the initial values.

Table 7, Table 8, Table 9, Table 10 report the mean, bias, standard deviation, and mean squared error of the estimates of $R_0$ across 500 simulation draws. The upper two panels of each table correspond to the DGP without rounding, while the bottom two panels correspond to the DGP with rounding. For the DGP without rounding, the estimation approaches based on logarithms (either cumulative or daily) without trimming dominate all other approaches in terms of the MSE, and their performance is insensitive to the choice of the weighting matrix. This is perhaps not surprising, because the model in logarithms is indeed the true model. However, for the DGP with rounding, this is no longer true: different approaches yield pretty similar values of MSE.

Table 7.

Mean of Estimates of $R_0$ for DGP (5.5)–(5.6).

	Deaths	Cases	SUR, Efficient $W$	SUR, Diagonal $W$	SUR, Identity $W$
Panel A: No Rounding, True $E_0=2$ and $I_0=0$, Assumed $E_0=2$ and $I_0=0$
Levels, Cumulative	5.755	5.755	5.755	5.755	5.755
Levels, Daily	5.762	5.752	5.757	5.758	5.753
Logs, Cumulative, Trim	5.755	5.753	5.754	5.754	5.754
Logs, Daily, Trim	5.756	5.755	5.756	5.756	5.755
Logs, Cumulative, No Trim	5.755	5.755	5.755	5.755	5.755
Logs, Daily, No Trim	5.755	5.755	5.755	5.755	5.755
Panel B: No Rounding, True $E_0=2$ and $I_0=0$, Estimated $E_0$ and $I_0$
Levels, Cumulative	5.757	5.756	5.759	5.760	5.766
Logs, Cumulative, Trim	5.756	5.754	5.757	5.759	5.755
Logs, Cumulative, No Trim	5.757	5.759	5.757	5.757	5.757
Panel C: Rounding, True $E_0=2$ and $I_0=0$, Assumed $E_0=2$ and $I_0=0$
Levels, Cumulative	5.836	5.760	5.771	5.776	5.760
Levels, Daily	5.772	5.752	5.762	5.762	5.753
Logs, Cumulative, Trim	5.878	5.761	5.783	5.789	5.819
Logs, Daily, Trim	5.777	5.755	5.764	5.764	5.766
Logs, Cumulative, No Trim	6.424	5.793	5.772	5.795	6.104
Logs, Daily, No Trim	5.483	5.759	5.750	5.752	5.620
Panel D: Rounding, True $E_0=2$ and $I_0=0$, Estimated $E_0$ and $I_0$
Levels, Cumulative	5.837	5.761	5.777	5.788	5.770
Logs, Cumulative, Trim	5.879	5.761	5.785	5.792	5.820
Logs, Cumulative, No Trim	6.425	5.793	5.772	5.795	6.105

The table presents the mean of the estimates of $R_0$ across 500 simulation draws for different estimation methods. The true value is $R_0=5.755$. The estimates in the first column are based on the deaths data only. The estimates in the second column are based on the reported cases data only. The estimates in the remaining three columns combine the deaths and reported cases data and use different weighting matrices.

Table 8.

Bias of estimates of $R_0$ for DGP (5.5)–(5.6).

	Deaths	Cases	SUR, Efficient $W$	SUR, Diagonal $W$	SUR, Identity $W$
Panel A: No Rounding, True $E_0=2$ and $I_0=0$, Assumed $E_0=2$ and $I_0=0$
Levels, Cumulative	0.0007	0.0004	0.0009	0.0005	0.0002
Levels, Daily	0.0078	−0.0027	0.0026	0.0031	−0.0013
Logs, Cumulative, Trim	0.0003	−0.0013	−0.0007	−0.0009	−0.0005
Logs, Daily, Trim	0.0011	−0.0001	0.0012	0.0011	0.0004
Logs, Cumulative, No Trim	0.0002	0.0003	0.0002	0.0002	0.0002
Logs, Daily, No Trim	0.0001	0.0002	0.0002	0.0002	0.0002
Panel B: No Rounding, True $E_0=2$ and $I_0=0$, Estimated $E_0$ and $I_0$
Levels, Cumulative	0.0020	0.0014	0.0040	0.0054	0.0110
Logs, Cumulative, Trim	0.0010	−0.0006	0.0025	0.0040	0.0001
Logs, Cumulative, No Trim	0.0029	0.0047	0.0022	0.0022	0.0025
Panel C: Rounding, True $E_0=2$ and $I_0=0$, Assumed $E_0=2$ and $I_0=0$
Levels, Cumulative	0.081	0.005	0.016	0.021	0.005
Levels, Daily	0.017	−0.003	0.007	0.008	−0.001
Logs, Cumulative, Trim	0.124	0.006	0.029	0.034	0.065
Logs, Daily, Trim	0.023	0.001	0.010	0.010	0.012
Logs, Cumulative, No Trim	0.669	0.038	0.017	0.040	0.349
Logs, Daily, No Trim	−0.271	0.005	−0.005	−0.002	−0.134
Panel D: Rounding, True $E_0=2$ and $I_0=0$, Estimated $E_0$ and $I_0$
Levels, Cumulative	0.082	0.006	0.022	0.033	0.015
Logs, Cumulative, Trim	0.125	0.007	0.030	0.038	0.066
Logs, Cumulative, No Trim	0.671	0.038	0.018	0.041	0.350

The table presents the average bias of the estimates of $R_0$ across 500 simulation draws for different estimation methods. The estimates in the first column are based on the deaths data only. The estimates in the second column are based on the reported cases data only. The estimates in the remaining three columns combine the deaths and reported cases data and use different weighting matrices.

Table 9.

Standard deviation of estimates of $R_0$ for DGP (5.5)–(5.6).

	Deaths	Cases	SUR, Efficient $W$	SUR, Diagonal $W$	SUR, Identity $W$
Panel A: No Rounding, True $E_0=2$ and $I_0=0$, Assumed $E_0=2$ and $I_0=0$
Levels, Cumulative	0.0364	0.0352	0.0258	0.0255	0.0351
Levels, Daily	0.1110	0.1010	0.0706	0.0693	0.1026
Logs, Cumulative, Trim	0.0260	0.0261	0.0195	0.0188	0.0176
Logs, Daily, Trim	0.0464	0.0451	0.0343	0.0340	0.0325
Logs, Cumulative, No Trim	0.0065	0.0069	0.0049	0.0049	0.0048
Logs, Daily, No Trim	0.0061	0.0064	0.0044	0.0044	0.0044
Panel B: No Rounding, True $E_0=2$ and $I_0=0$, Estimated $E_0$ and $I_0$
Levels, Cumulative	0.0366	0.0351	0.0270	0.0275	0.0396
Logs, Cumulative, Trim	0.0261	0.0261	0.0227	0.0239	0.0177
Logs, Cumulative, No Trim	0.0075	0.0079	0.0056	0.0056	0.0053
Panel C: Rounding, True $E_0=2$ and $I_0=0$, Assumed $E_0=2$ and $I_0=0$
Levels, Cumulative	0.050	0.035	0.037	0.032	0.035
Levels, Daily	0.112	0.101	0.070	0.070	0.103
Logs, Cumulative, Trim	0.060	0.027	0.038	0.031	0.033
Logs, Daily, Trim	0.082	0.046	0.045	0.044	0.047
Logs, Cumulative, No Trim	0.097	0.021	0.022	0.021	0.048
Logs, Daily, No Trim	0.073	0.024	0.023	0.024	0.038
Panel D: Rounding, True $E_0=2$ and $I_0=0$, Estimated $E_0$ and $I_0$
Levels, Cumulative	0.050	0.035	0.043	0.043	0.040
Logs, Cumulative, Trim	0.060	0.027	0.038	0.034	0.033
Logs, Cumulative, No Trim	0.097	0.021	0.022	0.021	0.048

The table presents the standard deviation of the estimates of $R_0$ across 500 simulation draws for different estimation methods. The estimates in the first column are based on the deaths data only. The estimates in the second column are based on the reported cases data only. The estimates in the remaining three columns combine the deaths and reported cases data and use different weighting matrices.

Table 10.

MSE of estimates of $R_0$ for DGP (5.5)–(5.6).

	Deaths	Cases	SUR, Efficient $W$	SUR, Diagonal $W$	SUR, Identity $W$
Panel A: No Rounding, True $E_0=2$ and $I_0=0$, Assumed $E_0=2$ and $I_0=0$
Levels, Cumulative	0.0013	0.0012	0.0007	0.0006	0.0012
Levels, Daily	0.0124	0.0102	0.0050	0.0048	0.0105
Logs, Cumulative, Trim	0.0007	0.0007	0.0004	0.0004	0.0003
Logs, Daily, Trim	0.0022	0.0020	0.0012	0.0012	0.0011
Logs, Cumulative, No Trim	0.00004	0.00005	0.00002	0.00002	0.00002
Logs, Daily, No Trim	0.00004	0.00004	0.00002	0.00002	0.00002
Panel B: No Rounding, True $E_0=2$ and $I_0=0$, Estimated $E_0$ and $I_0$
Levels, Cumulative	0.0013	0.0012	0.0007	0.0008	0.0017
Logs, Cumulative, Trim	0.0007	0.0007	0.0005	0.0006	0.0003
Logs, Cumulative, No Trim	0.00007	0.00008	0.00004	0.00004	0.00003
Panel C: Rounding, True $E_0=2$ and $I_0=0$, Assumed $E_0=2$ and $I_0=0$
Levels, Cumulative	0.009	0.001	0.002	0.001	0.001
Levels, Daily	0.013	0.010	0.005	0.005	0.011
Logs, Cumulative, Trim	0.019	0.001	0.002	0.002	0.005
Logs, Daily, Trim	0.007	0.002	0.002	0.002	0.002
Logs, Cumulative, No Trim	0.457	0.002	0.001	0.002	0.124
Logs, Daily, No Trim	0.079	0.001	0.001	0.001	0.020
Panel D: Rounding, True $E_0=2$ and $I_0=0$, Estimated $E_0$ and $I_0$
Levels, Cumulative	0.009	0.001	0.002	0.003	0.002
Logs, Cumulative, Trim	0.019	0.001	0.002	0.003	0.005
Logs, Cumulative, No Trim	0.459	0.002	0.001	0.002	0.125

The table presents the MSE of the estimates of $R_0$ across 500 simulation draws for different estimation methods. The estimates in the first column are based on the deaths data only. The estimates in the second column are based on the reported cases data only. The estimates in the remaining three columns combine the deaths and reported cases data and use different weighting matrices.

Overall, based on the simulation results, methods based on the cumulative numbers seem to outperform methods based on daily values. Relative performance of different estimation approaches (e.g. based on levels versus logarithms) depends on the true DGP. One advantage of the approach based on levels is that it does not involve trimming.

The use of the SUR approach to estimation with the efficient weighting matrix may be motivated by the desire to obtain more efficient parameter estimates. Interestingly, this is not always the case in my simulations. While joint estimation of the model based on the deaths and reported cases data yields better (in terms of the MSE) estimates than estimation based on the deaths data alone, the MSE of the SUR estimates is often very similar to the MSE of the estimates based on the reported cases data alone. Moreover, the choice of the weighting matrix does not always affect the MSE of the resulting estimates: the estimates based on the naive weighting matrix $W=I$ are often as good as the estimates based on the efficient choice of $W$.

7. Empirical results

This section presents the empirical results. Before I move on to the main results, I discuss computational issues associated with estimation of the model. Based on the arguments from the previous sections, when initial parameters change, the estimate of $R_0$ should remain virtually unchanged, while the estimates of $\alpha$ and $\lambda$ should change proportionally to the changes in initial parameters. In practice, however, this is not always the case. Both $\alpha$ and $\lambda$ are constrained to lie between 0 and 1, and when these constraints are binding or close to binding, changes in the initial values can have a substantial effect on the estimate of $R_0$.

Table 11, Table 12 compare the estimation results for USA and California for the values of epidemiologic parameters $\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$ and $\gamma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$ when the initial conditions change from $E_0=1$, $I_0=0$ to $E_0=2$, $I_0=0$. The parameter estimates for California behave as expected: the estimate of $R_0$ remains virtually unchanged, while the estimates of $\alpha$ and $\lambda$ are cut in half. However, for the US as a whole the picture is different. The estimates of $R_0$ change substantially as the initial conditions change, while the changes in the estimates of $\alpha$ and $\lambda$ do not follow the expected pattern. For instance, when the model is estimated in levels, the estimates of $\alpha$ and $\lambda$ remain virtually unchanged as the initial condition changes. This example illustrates that when the parameter estimates are close to the boundary, changes in initial conditions may lead to somewhat unexpected estimation results.

Table 11.

Estimates of $R_0$, $\alpha$, and $\lambda$ for USA.

	$E_0=1,I_0=0$			$E_0=2,I_0=0$
	SUR, Efficient $W$	SUR, Diagonal $W$	SUR, Identity $W$	SUR, Efficient $W$	SUR, Diagonal $W$	SUR, Identity $W$
Panel A: Levels, Cumulative
$R_0$	9.265	9.519	9.743	8.806	9.144	9.291
$\alpha$	0.00006	0.00004	0.00003	0.00006	0.00004	0.00003
$\lambda$	0.0033	0.0024	0.0018	0.0031	0.0020	0.0017
Panel B: Logs, Cumulative, Trim
$R_0$	8.599	8.443	8.368	8.343	8.371	8.386
$\alpha$	0.00016	0.00019	0.00021	0.00011	0.00011	0.00010
$\lambda$	0.0068	0.0083	0.0091	0.0047	0.0046	0.0045
Panel C: Logs, Cumulative, No Trim
$R_0$	10.595	9.584	8.311	10.415	9.673	8.331
$\alpha$	0.00003	0.00007	0.00030	0.00002	0.00003	0.00014
$\lambda$	0.0007	0.0020	0.0082	0.0004	0.0009	0.0040

The table presents the estimates of $R_0$, $\alpha$, and $\lambda$ for $\gamma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$, $\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$, and different initial values.

Table 12.

Estimates of $R_0$, $\alpha$, and $\lambda$ for California.

	$E_0=1,I_0=0$			$E_0=2,I_0=0$
	SUR, Efficient $W$	SUR, Diagonal $W$	SUR, Identity $W$	SUR, Efficient $W$	SUR, Diagonal $W$	SUR, Identity $W$
Panel A: Levels, Cumulative
$R_0$	5.062	5.094	5.058	5.064	5.097	5.060
$\alpha$	0.0040	0.0038	0.0041	0.0020	0.0019	0.0020
$\lambda$	0.217	0.206	0.219	0.108	0.103	0.109
Panel B: Logs, Cumulative, Trim
$R_0$	4.890	4.842	5.060	4.888	4.840	5.064
$\alpha$	0.0054	0.0059	0.0040	0.0027	0.0029	0.0020
$\lambda$	0.292	0.318	0.218	0.147	0.159	0.109
Panel C: Logs, Cumulative, No Trim
$R_0$	5.277	5.308	5.601	5.279	5.309	5.602
$\alpha$	0.0024	0.0023	0.0015	0.0012	0.0012	0.0008
$\lambda$	0.154	0.148	0.099	0.077	0.074	0.049

The table presents the estimates of $R_0$, $\alpha$, and $\lambda$ for $\gamma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$, $\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$, and different initial values.

Table 13 presents the estimates of $R_0$ for the US, California, and Japan. All three panels of the table use cumulative data to estimate the model. The upper panel uses levels, the middle panel uses logarithms with trimming, and the lower panel uses logarithms without trimming. Different rows within a panel correspond to different choices of the weighting matrix $W$.

Table 13.

Estimates of $R_0$.

		$\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$, $\gamma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$	$\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$, $\gamma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$	$\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$, $\gamma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$18$}\right.$	$\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$, $\gamma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$, $q=0.5$
Panel A: Levels
USA	SUR, Efficient $W$	4.834	9.265	16.698	5.947
	SUR, Diagonal $W$	4.963	9.519	17.399	6.089
	SUR, Identity $W$	5.053	9.743	18.249	6.167
California	SUR, Efficient $W$	3.043	5.062	8.536	3.852
	SUR, Diagonal $W$	3.058	5.094	8.599	3.872
	SUR, Identity $W$	3.041	5.058	8.528	3.850
Japan	SUR, Efficient $W$	1.716	2.685	4.566	2.249
	SUR, Diagonal $W$	1.717	2.684	4.559	2.248
	SUR, Identity $W$	1.714	2.681	4.587	2.245
Panel B: Logs, Trim
USA	SUR, Efficient $W$	4.501	8.599	15.175	5.571
	SUR, Diagonal $W$	4.552	8.443	15.190	5.640
	SUR, Identity $W$	4.581	8.368	15.198	5.679
California	SUR, Efficient $W$	2.960	4.890	8.199	3.748
	SUR, Diagonal $W$	2.937	4.842	8.105	3.719
	SUR, Identity $W$	3.043	5.060	8.536	3.855
Japan	SUR, Efficient $W$	1.688	2.569	4.215	2.179
	SUR, Diagonal $W$	1.689	2.570	4.217	2.180
	SUR, Identity $W$	1.700	2.642	4.502	2.219
Panel C: Logs, No Trim
USA	SUR, Efficient $W$	5.504	10.595	19.545	6.682
	SUR, Diagonal $W$	5.124	9.584	17.543	6.285
	SUR, Identity $W$	4.544	8.311	15.038	5.638
California	SUR, Efficient $W$	3.143	5.277	8.958	3.979
	SUR, Diagonal $W$	3.157	5.308	9.018	3.997
	SUR, Identity $W$	3.294	5.601	9.595	4.167
Japan	SUR, Efficient $W$	1.862	2.816	4.710	2.328
	SUR, Diagonal $W$	1.859	2.823	4.731	2.329
	SUR, Identity $W$	1.879	2.821	4.991	2.329

The table presents the estimates of $R_0$ for different countries and different values of epidemiologic parameters $\sigma$ and $\gamma$. Initial conditions: $E_0=1,I_0=0$ for USA and California, $E_0=10$ for Japan. The middle panel trims all observations with $D^{obs}\left(t\right)\le 25$ or $C^{obs}\left(t\right)\le 75$. The lower panel uses all observations with $D^{obs}\left(t\right)>0$ and $C^{obs}\left(t\right)>0$.

Because there is no agreement in the medical literature on the appropriate values of epidemiologic parameters $\gamma$ and $\sigma$, I consider several scenarios in the table: “fast” with $\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$, $\gamma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$, “medium” with $\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$, $\gamma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$, and “slow” with $\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$, $\gamma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$18$}\right.$. I also consider a modified version of the SEIRD model that replaces $\beta \frac{S\left(t\right)}{N}I\left(t\right)$ in Eqs. (2.1), (2.2) with $\beta \frac{S\left(t\right)}{N}(I\left(t\right)+qE\left(t\right))$ for $q=0.5$. This version of the model assumes that people in the exposed compartment can be contagious, but to a lesser extent that people in the infectious compartment. While these exact choices are somewhat arbitrary, considering several values of epidemiologic parameters instead of just one allows me to better understand their effect on the estimation results and forecasts.

The initial conditions are $E_0=1$, $I_0=0$ for the US and California and $E_0=10$, $I_0=0$ for Japan. The choice of the initial conditions for Japan is tricky because the estimate of $\lambda$ is at the upper bound of 1, and the choice of initial conditions affects the estimate of $R_0$. Given that Bommer and Vollmer (2020) estimate that the detection rate in Japan in March was around 20%–25%, even the initial condition $E_0=10$ may be too low.

As we can see from the table, the estimates of $R_0$ for a given country or region change a lot as epidemiologic parameters change. For example, the estimate of $R_0$ for the US ranges from under 5 in the “fast” scenario to around 15–18 in the “slow” one. Moreover, for the fixed values of epidemiologic parameters $\gamma$ and $\sigma$, the estimates of $R_0$ differ a lot between regions. For instance, in the “medium” scenario with $\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$ and $\gamma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$, the estimates of $R_0$ vary from 2.6 for Japan to around 9.5 for the US. While the magnitude of these differences might be surprising, heterogeneity itself is not. If various mitigation or suppression policies can reduce $R_0$, then one could expect that different countries have different values of $R_0$ due to the differences in their approaches to dealing with COVID-19, as well as differences in social norms, population density, etc.

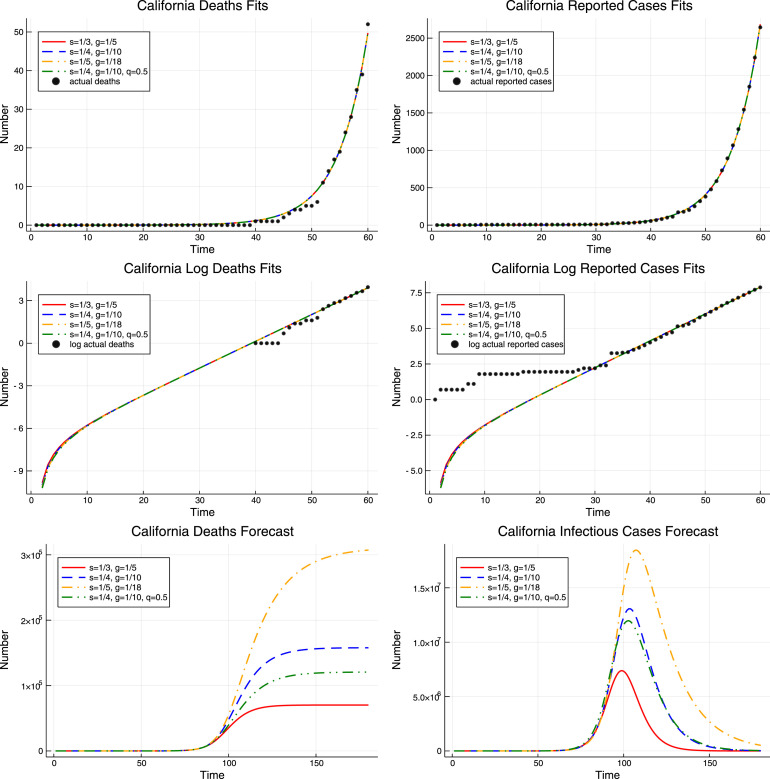
Next, I present my results graphically. I focus on the results for California because they are least prone to numerical issues, as discussed above. For the sake of space I only present the results from the model estimated in levels. Additional results are presented in the online supplement.

The upper panel of Fig. 4 plots the fitted values of deaths and reported cases for California from the models with different values of epidemiologic parameters. The estimates of $R_0$ are based on the efficient weighting matrix $W$. As we can see, even though the four models have different values of epidemiologic parameters and different estimates of $R_0$, they appear to be indistinguishable in the short run: the resulting paths of deaths and reported cases are identical. However, in the long run the story is different. The lower panel of Fig. 4 demonstrates that the predicted total number of deaths from the COVID-19 epidemic in the four models ranges from around 70 thousand to more than 300 thousand.

Fig. 4.

Results for California. The upper panel shows the fit of the actual cumulative deaths and reported cases by models with four different values of epidemiologic parameters $\sigma$ and $\gamma$. The middle panel shows the fit of the logarithms of the actual cumulative deaths and reported cases for the same four models. The lower panel shows the forecasts from the same four models.

Next, Fig. 5 fixes the values of epidemiologic parameters $\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$ and $\gamma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$ and considers the pessimistic and optimistic scenarios, given by different initial conditions, for which the resulting models are observationally equivalent. The pessimistic scenario corresponds to the initial condition $E_0=1$, $I_0=0$, while the optimistic scenario corresponds to $E_0=30$, $I_0=0$. Intuitively, the lower the initial values, the lower the cumulative number of people who have had the virus, the higher the estimated fatality rate, and the higher the forecasted death toll.

Fig. 5.

Pessimistic and optimistic scenarios for California. The upper panel shows the fit of the actual cumulative deaths and reported cases by models with different initial conditions. The middle panel shows the fit of the logarithms of the actual cumulative deaths and reported cases by these models. The lower panel shows the forecasts from these models. The values of epidemiologic parameters are $\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$, $\gamma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$.

We can see that different initial conditions lead to observationally equivalent models in the short run. However, there are large differences in estimates of unobserved variables and in long run forecasts. For instance, the model with $E_0=1,I_0=0$ estimates that the number of people with COVID-19 (here I count people both in the exposed and infectious compartments) in California on March 22 was around 50 thousand and predicts over 150 thousand deaths in the long run. In contrast, the model with $E_0=30,I_0=0$ estimates that there were around 1.6 million people with COVID-19 and predicts less than 5 thousand deaths in the long run, a 32-fold difference.

Next, I demonstrate empirically why it is important to allow the fraction of all cases that is reported to differ from one. Fig. 6 presents the results for different estimates of $R_0$ in the “medium” scenario with $\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$ and $\gamma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$. One model corresponds to the pessimistic case scenario from Fig. 5 with ${\hat{R}}_0=5.06$ and $E_0=1$. The forecasted long run number of deaths for that model is around 150 thousand. The remaining two models estimate $R_0$ from the confirmed cases data assuming that all cases are reported, i.e. $\lambda =1$, and then recover $\alpha$ from the deaths data. The resulting estimates of $R_0$ are lower, 4.18 when the initial condition is $I_0=0$, $E_0=1$, and 2.90 when the initial condition is $I_0=10$, $E_0=10$. The estimates of $R_0$, $\alpha$, and $\lambda$ for these models are reported in Table 14. As we can see from the upper panel of the figure, the resulting models, especially the latter one, provide a poorer fit of the observed data: they cannot generate enough curvature because of the low $R_0$.

Fig. 6.

Results for California for different values of $R_0$. The upper panel shows the fit of the actual cumulative deaths and reported cases by models with and without underreporting and different initial conditions. The middle panel shows the fit of the logarithms of the actual cumulative deaths and reported cases by these models. The lower panel shows the forecasts from these models. The values of epidemiologic parameters are $\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$, $\gamma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$.

Table 14.

Estimates of $R_0$ for California, with and without Underreporting.

	Possible Underreporting, $E_0=1$	No Underreporting, $E_0=1$	No Underreporting, $E_0=10$
$R_0$	5.062	4.176	2.908
$\alpha$	0.004	0.018	0.018
$\lambda$	0.217	1	1

The table presents the estimates of $R_0$, $\alpha$, and $\lambda$ for California for $\gamma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$, $\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$. The left panel allows for underreporting of the number of cases and estimates all parameters from the data on deaths and reported cases jointly. The right two panels assume that all cases are reported, estimate $R_0$ from the reported cases data, and then recover $\alpha$, conditional on the estimated value of $R_0$, from the deaths data.

The bottom panel of Fig. 6 shows that the forecasted long run number of deaths from both these models is over 600 thousand, a lot higher than in the pessimistic model with higher $R_0$ that fits the data well. Thus, estimating $R_0$ based on the confirmed cases data under the assumption that all cases are reported leads to the downward bias in the estimate of $R_0$, poor fit of the observed data, and severe overestimation of the long run number of deaths.

Finally, I study whether additional information can help calibrate the initial conditions using Iceland as an example. Iceland is an interesting country to study because it was among the first countries to launch wide-scale random, or nearly random, testing of its population.12 While it is debatable whether testing in Iceland is completely random, my goal here is to demonstrate how information from these tests could in principle be used to calibrate the initial values. I fix the epidemiologic parameter values at $\sigma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$ and $\gamma =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$. Because the number of deaths in the data is very low, I use the first 70, rather than 60, observations to estimate the model.

The tests done in Iceland by deCode Genetics between March 13 and March 21 found 48 positives among 5,571 people who were tested for COVID-19, for the positive test rate of 0.86%. The 95% Wilson score confidence interval for the positive test rate is $[0.65\text{\%},1.14\text{\%}]$.13 I assume that the fraction of Iceland’s population who had COVID-19 on March 21, when the results were published, was the same as in the test. I then use the test results to calibrate the initial values in the model such that the fraction of Iceland’s population with COVID-19 on March 21 in the model is the same as in the test.

Given the population of 341,250, the positive test rate of 0.86% translates into 2,940 cases, with the 95% Wilson score confidence interval of $[2,220,3,891]$. I hold $I_0=0$ and calibrate $E_0$ so that the sum of exposed and infectious people on March 21 matches the these numbers. $E_0=4.25$ yields 2,939 cases, $E_0=3.26$ yields 2,217 cases, and $E_0=5.51$ yields 3,892 cases on March 21. For simplicity, I do not require that $E_0$ be an integer.

The results are presented in the right panel of Fig. 7. For comparison, the left panel of Fig. 7 plots the results for $E_0=1.5$ and $E_0=10$. As we can see, both in the left and right panel all models are indistinguishable on the available data. However, in the left panel, the forecasted death toll varies from under 77 for $E_0=10$ to 592 for $E_0=1.5$; in the right panel, it varies from 152 for $E_0=5.51$ to 264 for $E_0=3.26$. Thus, the use of additional information leads to a more than 4-fold reduction in the range of forecasted deaths for observationally equivalent models. This result demonstrates the value of auxiliary information that becomes available due to random testing.

Fig. 7.

Results for Iceland. The figure presents the results for Iceland. The left panel does not use any additional information. The right panel matches the number of active COVID-19 cases on March 21 to the one estimated based on testing a random sample of population. The upper panel shows the cumulative deaths fit by models with different initial values $E_0$. The middle panel shows the cumulative reported cases fit by these models. The lower panel shows the deaths forecasts from these models.

8. Conclusion

In this paper, I show that the SEIRD model for COVID-19 is poorly identified from the short run data on deaths and reported cases. There can be many different models that are indistinguishable in the short run but result in markedly different long run forecasts. For instance, the forecasted number of deaths in California in observationally equivalent models ranges from under 5 thousand to over 150 thousand. Thus, this paper highlights that long run forecasts for COVID-19 heavily depend on arbitrary choices made by the researcher. Available data cannot be used to determine which model is correct because there are many models that look identical in the short run.

Next, I propose several nonlinear SUR approaches to estimate the basic reproduction number $R_0$, which is identified conditional on the values of epidemiologic parameters. Unlike most papers in the literature, which use data either on deaths or on reported cases, the proposed estimation methods combine these two series. Simulations suggest that the proposed methods lead to precise estimates of $R_0$.

I then estimate $R_0$ for the US, California, and Japan for different values of epidemiologic parameters. The resulting estimates of $R_0$ heavily depend on the epidemiologic parameters and are heterogeneous across regions: they are 2–4 times higher in the US and California than in Japan.

My model takes into account possible underreporting of the number of cases. I demonstrate that the estimates of $R_0$ based on the confirmed cases data under the assumption that all cases are reported may be biased downward. The resulting models may be inconsistent with the observed data and may dramatically overestimate the long run number of deaths.

Finally, I demonstrate that auxiliary information from random tests for COVID-19 can help calibrate the initial values of the model and reduce the range of possible forecasts that are consistent with the observed data. Random, or nearly random, tests were conducted in Iceland, and utilizing the information from these tests leads to a more than 4-fold reduction in the range of the forecasted number of deaths.

The model I consider is fairly simplistic and does not take into account important factors such as possible overloading of the health care system, mitigation efforts, behavioral responses to the epidemic, etc. There are more sophisticated and realistic epidemic models that may be able to predict the spread of COVID-19 and the long run number of deaths better than the model studied here. However, those models usually have even more parameters, so one may worry that their identification would be even more troublesome.

Appendix A. Additional results

A.1. Lack of identification in SIRD models

In this section, I study an approximate solution of the simplified SIRD model to illustrate which model parameters can be identified from the data. The model is:

$$\frac{dS\left(t\right)}{dt}=-\beta \frac{S\left(t\right)}{N}I\left(t\right)$$ (A.1)

$$\frac{dI\left(t\right)}{dt}=\beta \frac{S\left(t\right)}{N}I\left(t\right)-\gamma I\left(t\right)$$ (A.2)

$$\frac{dR\left(t\right)}{dt}=(1-\alpha )\gamma I\left(t\right)$$ (A.3)

$$\frac{dD\left(t\right)}{dt}=\alpha \gamma I\left(t\right)$$ (A.4)

$$\frac{dC\left(t\right)}{dt}=\lambda \gamma I\left(t\right)$$ (A.5)

During the early stages of the epidemic, $S\left(t\right)∕N\approx 1$, so that the equation for the evolution $I\left(t\right)$ is, approximately,

$$\frac{dI\left(t\right)}{dt}\approx (\beta -\gamma )I\left(t\right)=\gamma (R_0-1)I\left(t\right)$$

The solution is given by $I\left(t\right)=I\left(0\right)exp\left(\gamma (R_0-1)t\right)$. It is possible to show then that the approximate solutions for $D\left(t\right)$ and $C\left(t\right)$ are given by

$$D\left(t\right)\approx \frac{\alpha }{R_0-1}I\left(0\right)(exp\left(\gamma (R_0-1)t\right)-1)$$ (A.6)

$$C\left(t\right)\approx \frac{\lambda }{R_0-1}I\left(0\right)(exp\left(\gamma (R_0-1)t\right)-1),$$ (A.7)

Because $D\left(t\right)$ and $C\left(t\right)$ depend on $\alpha$, $\lambda$, and $I\left(0\right)$ through the products $\alpha I\left(0\right)$ and $\lambda I\left(0\right)$, $\alpha$ and $\lambda$ cannot be identified separately from $I\left(0\right)$. $R_0$ can be identified for a fixed value of $\gamma$, but it cannot be identified separately from $\gamma$ in general: one can increase $R_0$ and decrease $\gamma$, so that $\gamma (R_0-1)$ remains unchanged, and adjust $\alpha$ and $\lambda$ accordingly so that $\frac{\alpha }{R_0-1}I\left(0\right)$ and $\frac{\lambda }{R_0-1}I\left(0\right)$ remain unchanged.

Finally, note that for a large enough $t$, $exp\left(\gamma (R_0-1)t\right)\gg 1$, so that $log(exp\left(\gamma (R_0-1)t\right)-1)\approx logexp\left(\gamma (R_0-1)t\right)=\gamma (R_0-1)t$. Thus, for a large enough $t$,

$$logD\left(t\right)\approx \gamma (R_0-1)t+log\alpha +logI\left(0\right)-log(R_0-1)$$ (A.8)

$$logC\left(t\right)\approx \gamma (R_0-1)t+log\lambda +logI\left(0\right)-log(R_0-1)$$ (A.9)

These equations demonstrate that the log series are approximately linear in $t$ and that $R_0$ and $\gamma$ affect the slope of the log series, while $\alpha$, $\lambda$, and $I\left(0\right)$ only affect the level.

A.2. Computational challenges

In this section, I describe some of the computational challenges associated with estimating the SEIRD model. Estimation consists of two steps. First, I simulate the model for a given choice of $R_0$, $\alpha$, and $\lambda$ using the DifferentialEquations package in Julia, developed by Rackauckas and Nie (2017). More specifically, the routine takes the model (2.1)–(2.6) and simulates the paths of $S\left(t\right)$, $E\left(t\right)$, $I\left(t\right)$, $R\left(t\right)$, $D\left(t\right)$, and $C\left(t\right)$ for the given values of $R_0$, $\alpha$, and $\lambda$. Next, I compute the difference between the modeled and observed quantities (cumulative or daily, in levels or logarithms) and minimize the appropriate nonlinear objective function using the Optim package.14 I use the Nelder–Mead algorithm to find the solution, as I found that it outperforms other algorithms available in Optim, such as simulated annealing or particle swarm.

The Nelder–Mead algorithm in Optim does not allow for bounds on the parameters. Because $R_0$ is constrained to be nonnegative and $\alpha$ and $\lambda$ are constrained to lie between 0 and 1, I use a reparametrization to ensure that all parameter estimates satisfy the constraints. Namely, I write $R_0=exp\left(x_1\right)$, $\alpha =exp\left(x_2\right)∕(1+exp\left(x_2\right))$, $\lambda =exp\left(x_3\right)∕(1+exp\left(x_3\right))$, where $(x_1,x_2,x_3)$ are the parameters of the routine. The choice of the parameters $R_0=5.75$, $\alpha =0.0067$, $\lambda =0.12$, used in simulations, corresponds to $(x_1,x_2,x_3)=(1.75,-5,-2)$.

Appendix B. Supplementary material

The following is the Supplementary material related to this article.

MMC S1

Additional results.