Abstract
Virus proliferation involves gene replication inside infected cells and transmission to new target cells. Once positive-strand RNA virus has infected a cell, the viral genome serves as a template for copying (“stay-strategy”) or is packaged into a progeny virion that will be released extracellularly (“leave-strategy”). The balance between genome replication and virion release determines virus production and transmission efficacy. The ensuing trade-off has not yet been well characterized. In this study, we use hepatitis C virus (HCV) as a model system to study the balance of the two strategies. Combining viral infection cell culture assays with mathematical modeling, we characterize the dynamics of two different HCV strains (JFH-1, a clinical isolate, and Jc1-n, a laboratory strain), which have different viral release characteristics. We found that 0.63% and 1.70% of JFH-1 and Jc1-n intracellular viral RNAs, respectively, are used for producing and releasing progeny virions. Analysis of the Malthusian parameter of the HCV genome (i.e., initial proliferation rate) and the number of de novo infections (i.e., initial transmissibility) suggests that the leave-strategy provides a higher level of initial transmission for Jc1-n, whereas, in contrast, the stay-strategy provides a higher initial proliferation rate for JFH-1. Thus, theoretical-experimental analysis of viral dynamics enables us to better understand the proliferation strategies of viruses, which contributes to the efficient control of virus transmission. Ours is the first study to analyze the stay-leave trade-off during the viral life cycle and the significance of the replication-release switching mechanism for viral proliferation.
A theoretical-experimental analysis of viral dynamics reveals a stay/leave trade-off during the viral life cycle and demonstrates the significance for viral proliferation of a replication-release switching mechanism.
Introduction
Hepatitis C virus (HCV) is an RNA virus specifically infecting liver cells. HCV produces progeny viruses rapidly, with approximately 1012 copies sometimes observed in patients [1]. Following virus entry into target cells, viral genomic RNA produces structural proteins (S proteins) and nonstructural proteins (NS proteins) (Fig 1A). Using the genomic RNA as a template, the viral NS proteins amplify HCV RNA (“RNA replication”). Genomic RNA can also be assembled with viral S proteins into progeny virions to be egressed outside of cells, creating the opportunity for transmission (in this study, we call the process including particle assembly and egress “release”). Thus, a single HCV genomic RNA molecule can be used either for RNA replication or for release, and the balance between these processes governs viral proliferation. The molecular mechanisms underlying each event in the viral life cycle have been extensively investigated [2,3], yet the replication-release trade-off and its significance for viral proliferation remain poorly understood.
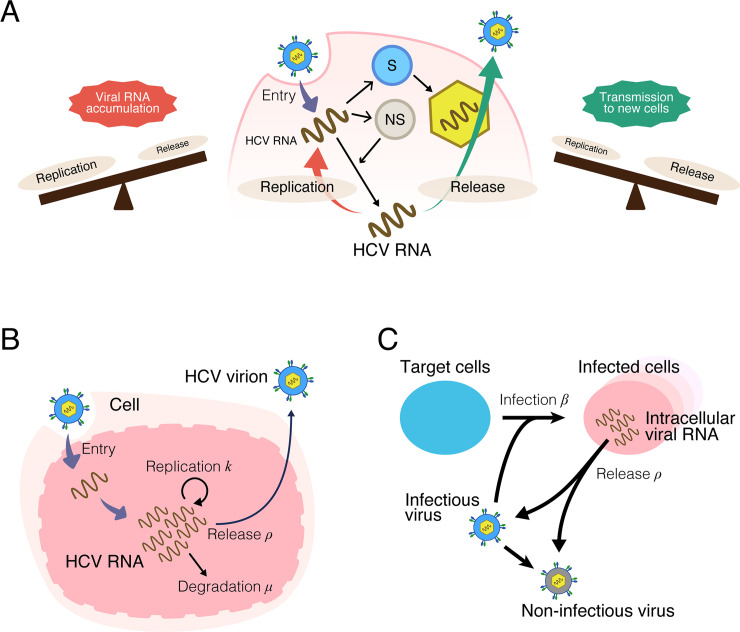
Fig 1. Schematic representation of multiscale HCV infection and mathematical model.
(A) Schematic representation of intracellular HCV life cycle and trade-off between viral replication and release of intracellular viral RNA. Viral RNA in cells is translated to produce S and NS proteins. Viral RNA is either amplified through the functions of NS proteins through replication or is assembled with S proteins and released as a progeny virus. If the balance between viral replication and release leans toward replication, intracellular viral RNAs will accumulate. In contrast, high rates of intracellular RNA release will create opportunities for transmission to new cells but will deplete viral RNA in the cell. (B) Modeling the intracellular virus life cycle. Intracellular viral RNA either replicates inside the cell at rate k, is degraded at rate μ, or assembles with viral proteins to be released within HCV virions at rate ρ. (C) Multiscale modeling of intracellular replication and intercellular infection. Target cells are infected by infectious viruses at rate β. HCV, hepatitis C virus; NS protein, nonstructural protein; S protein, structural protein.
HCV JFH-1 is a genotype 2a strain isolated by our group from a patient with fulminant hepatitis [4]. JFH-1 has been a standard strain used for experiments to characterize HCV infection, virus-host interactions, and immune responses against HCV [4]. In addition, Jc1 or J6/JFH (a chimeric strain in which a region of the JFH-1 genome from the core to NS2 was replaced by sequences from another genotype 2a virus, the J6 strain) was developed as a laboratory strain to improve virus production. Jc1 is used for development of antiviral agents and vaccines, which requires large amounts of virus [5,6]. In spite of their high sequence similarity (97% identity over the whole genome), these two viruses have different virological characteristics especially in terms of the release process: whereas JFH-1 particles assemble on lipid droplet membranes, particle assembly of J6/JFH-1-chimeric laboratory strains is associated with endoplasmic reticulum–derived membranes [2,3]. Thus, these two related strains are a useful reference set to compare the dynamics of release and RNA replication.
In this study, we used a cell culture model of infection with these two HCV reference strains and measured the time course of viral production (including HCV RNA inside cells and virions produced outside of the cells), infectivity of progeny HCV, and infected cell numbers. We also developed a multiscale mathematical model to describe intra- and intercellular HCV dynamics. This interdisciplinary approach suggests that different strategies exist for viral proliferation: the stay-at-home strategy (JFH-1) and the leaving-home strategy (Jc1-n, a J6/JFH-1-chimeric strain). We discuss the relevance of these strategies for viral proliferation, while referring to [7] for wider evolutionary context.
Results
Age-structured multiscale modeling of HCV infection
To describe the intracellular replication dynamics of HCV viral RNA, we used the following mathematical model:
| (1) |
where R(a) is the amount of intracellular viral RNA in cells that have been infected for time a. The intracellular viral RNA replicates at rate k per day, degrades at rate μ per day, and is released to extracellular space at rate ρ per day (Fig 1B). Note that if viruses have small or large ρ, then they tend to stay inside or leave the cell, respectively (see later). In our virus experiments (see Methods), the released viruses could infect other target cells. To describe multiround virus transmission (i.e., de novo infection), we needed to couple intracellular viral replication with a standard mathematical model for intercellular virus infection in cell culture [8,9] (Fig 1C). In S1 Text, we derived the following multiscale ordinary differential equation (ODE) model for HCV infection from the corresponding age-structured partial differential equation (PDE) model [10,11]:
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
Here, the intercellular variables T(t) and I(t) represent the numbers of uninfected and infected target cells (cells/well), respectively, and V(t) and Vθ(t) represent the total amount of extracellular viral RNA (copies/well) and the extracellular viral infectious titer expressed (focus formation unit [ffu]/well), respectively. The intracellular variable A(t) represents the total amount of intracellular viral RNA. The parameters g and K represent the growth rate (per day) and the carrying capacity of target cells, respectively, and βθ and fθ are the converted infection rate constant ([ffu/well・day]-1) and the fraction of infectious virus (RNA copies・ffu-1), respectively. Note that we assume no cellular loss induced by infection because HCV is a noncytopathic virus [4]. We assumed that progeny viruses were cleared at rate c per day via degradation at rate cRNA per day and washing at rate cw per day (i.e., c = cRNA+cw), and that infectious virions lose infectivity at rate r. Because of the different RNA sequence and the resulting different RNA modification status as well as the different physical property of virions, specific stability/degradation rate of each virus strain is expected. Separately, we directly estimated g, K, c, μ, and r for both HCV JFH-1 and Jc1-n in S1 Fig. Detailed explanations of Eqs 2–6 are given in S1 Text.
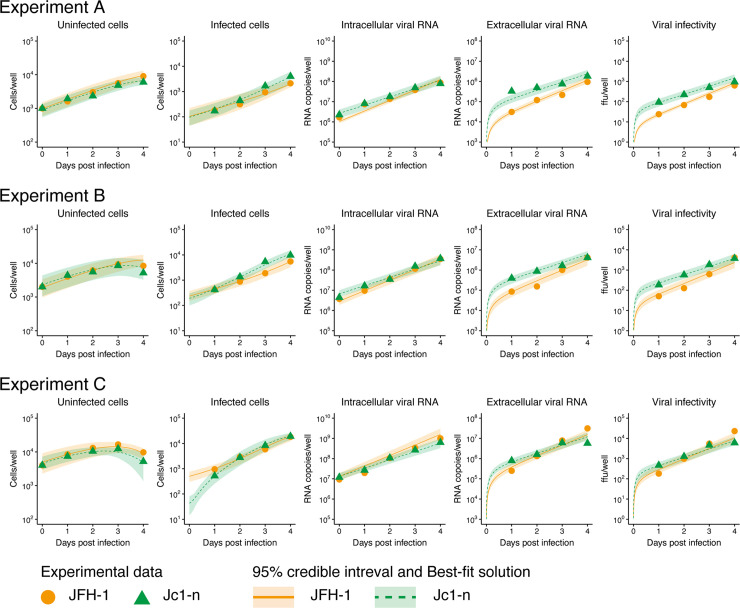
To assess the variability of kinetic parameters and model predictions, we performed Bayesian estimation for the whole dataset using Markov chain Monte Carlo (MCMC) sampling (see Methods). Simultaneously, we fitted Eqs 2–6 to the experimentally determined numbers of uninfected and infected cells (cells/well), extracellular viral RNA (copies/well) and infectious titer (ffu/well), and intracellular viral RNA (copies/well). These figures were derived from infection experiments using different numbers of plated cells for either HCV JFH-1 or Jc1-n as described previously [8,9,12,13]. The remaining free model parameters (i.e., βθ, k, ρ, fθ) along with initial values for variables (i.e., T(0), I(0), A(0), Vθ(t), V(0)) were estimated from the MCMC sampling. Experimental measurements below the detection limit were excluded in the fitting. The estimated parameters and initial values are listed in Table 1 and S1 Table. The typical behavior of the model using these best-fit parameter estimates is shown together with the data in Fig 2 for HCV JFH-1 (orange) and Jc1-n (green) (see Methods for HCV strains) and indicated that Eqs 2–6 described the in vitro data very well. The shadowed regions corresponded to 95% posterior predictive intervals, the solid and dashed lines gave the best-fit solution (mean) for Eqs 2–6, and the orange circles and green triangles showed the experimental datasets.
Table 1. Parameter values estimated from the cell culture infection experiment.
| Parameter Name | Symbol | Unit | HCV JFH-1 | HCV Jc1 | ||
|---|---|---|---|---|---|---|
| Value | 95% CI | Value | 95% CI | |||
| Fitted parameters from separate experiments | ||||||
| Rate of virion infectivity loss | r | day-1 | 1.52 | ― | 2.16 | ― |
| Degradation rate of extracellular viral RNA | cRNA | day-1 | 7.55×10−2 | (0.238–1.99)×10−1 | 0.240 | 0.238–0.469 |
| Clearance rate of extracellular viral RNA due to washing | cw | day-1 | 1.18 | ― | 1.82 | ― |
| Degradation rate of intracellular viral RNA | μ | day-1 | 2.54 | 2.14–3.01 | 2.75 | 2.21–3.43 |
| Estimated parameters from in vitro total cell growth data | ||||||
| Proliferation rate of Huh-7 cells | g | day-1 | 0.670 | ― | 0.665 | ― |
| Carrying capacity of Huh-7 cells | K | cells | 4.12×104 | ― | 3.75×104 | ― |
| Parameters obtained from simultaneous fitting of full in vitro dataset | ||||||
| Rate constant for infections | βθ | (ffu/well・day)-1 | 1.26×10−4 | (0.788–1.89)×10−4 | 2.29×10−4 | (1.32–3.64)×10−4 |
| Replication rate of intracellular viral RNA | k | day-1 | 3.75 | 3.64–3.86 | 3.75 | 3.64–3.86 |
| Release rate of intracellular viral RNA | ρ | day-1 | 2.36×10−2 | (1.73–3.15)×10−2 | 6.38×10−2 | (4.20–9.34)×10−2 |
| Converted fraction of infectious viral RNA | fθ | RNA copies・ffu-1 | 1.19×10−3 | (0.970–1.44)×10−3 | 1.08×10−3 | (0.773–1.48)×10−3 |
Abbreviations: ffu, focus formation unit; HCV, hepatitis C virus
Fig 2. Dynamics of HCV JFH-1 and Jc1-n infection in cell culture.
Fitting of the mathematical model to the experimental data of HCV JFH-1 and Jc1-n infection in cell culture. Three different numbers of Huh-7 cells infected with either HCV JFH-1 or Jc1-n 1 day after inoculation were seeded (experiment A: 1,000, experiment B: 2,000, and experiment C: 4,000 cells per well) and chased to detect the following values at days 0, 1, 2, 3, and 4 post seeding (log10 scale): numbers of uninfected and infected cells, amount of intracellular and extracellular viral RNA (copies/well), and extracellular viral infectivity (ffu/well) (orange circle: JFH-1, green triangle: Jc1-n). The shadowed regions correspond to 95% posterior intervals and the solid curves give the best-fit solution (mean) for Eqs 2–6 to the time-course dataset. All data for each strain were fitted simultaneously. The underlying data for this figure can be found in S1 Data. ffu, focus formation unit.
Using the estimated parameters shared between the original PDE model in S1 Text and the transformed ODE model (i.e., Eqs 2–6), we successfully reconstructed age information for intracellular viral RNA in infected cells of infection age a, which cannot be obtained through conventional experiments alone (S2A Fig). S2B Fig shows the differences in intracellular JFH-1 and Jc1-n viral RNA levels in cells of infection age a. At the beginning of the experiment, intracellular viral RNA increased faster under Jc1-n infection than under JFH-1 infection (shown in green). However, intracellular JFH-1 viral RNA gradually accumulated to higher levels than Jc1-n at later time points after infection (shown in yellow to brown). These data illustrated the different dynamics of these two strains and the impact of these dynamics on intracellular viral RNA production, all resulting from different strategies to transmit the viral genome (see below).
Dynamics of HCV JFH-1 and Jc1-n strain replication
Our model (Eqs 2–6) applied to time-course experimental data allowed us to extract the following kinetic parameters: the distribution of the rate constant for infection, βθ; the release rate of intracellular viral RNA, ρ; the converted fraction of infectious viral RNA, fθ; and the replication rate of intracellular viral RNA, k (Fig 3 and Table 1). Comparing these parameters for JFH-1 and Jc1-n showed a significant difference between the rate constant for infections, βθ, of JFH-1 (1.26×10−4 [ffu/well・day]-1, 95% CI 0.788–1.89×10−4 [ffu/well・day]-1) and Jc1-n (2.29×10−4 [ffu/well・day]-1, 95% CI 1.32–3.64×10−4 [ffu/well・day]-1) (p = 1.48×10−4 by repeated bootstrap t test) (Fig 3A). In addition, the release rates of intracellular viral RNA, ρ, for JFH-1 and Jc1-n were 2.36×10−2 per day (95% CI 1.73–3.15×10−2) and 6.38×10−2 per day (95% CI 4.20–9.34×10−2), respectively (p<0.01 by repeated bootstrap t test) (Fig 3B). These estimates indicated that Jc1-n infects cells 1.82 times faster and produces progeny viruses from infected cells 2.70 times faster than JFH-1. The estimate was further validated by independent experiments, in which Jc1-n entry and virus production were indeed significantly higher than those of JFH-1, although early replication was similar for the two strains (S2 Text and S3A–S3C Fig). The cell line used in our in vitro model was deficient in interferon induction by HCV infection (S3D Fig), as reported previously [14]. No significant difference was apparent in the converted fraction of infectious virus, fθ (Fig 3C). Because JFH-1 and Jc1-n have identical nonstructural regions essential for RNA replication (NS3–NS5B), we estimated the same viral RNA replication rate, k, for these two viruses (Fig 3D). Hence, our parameter estimation captured the characteristics of the two strains well and was able to quantitatively describe viral infection dynamics.
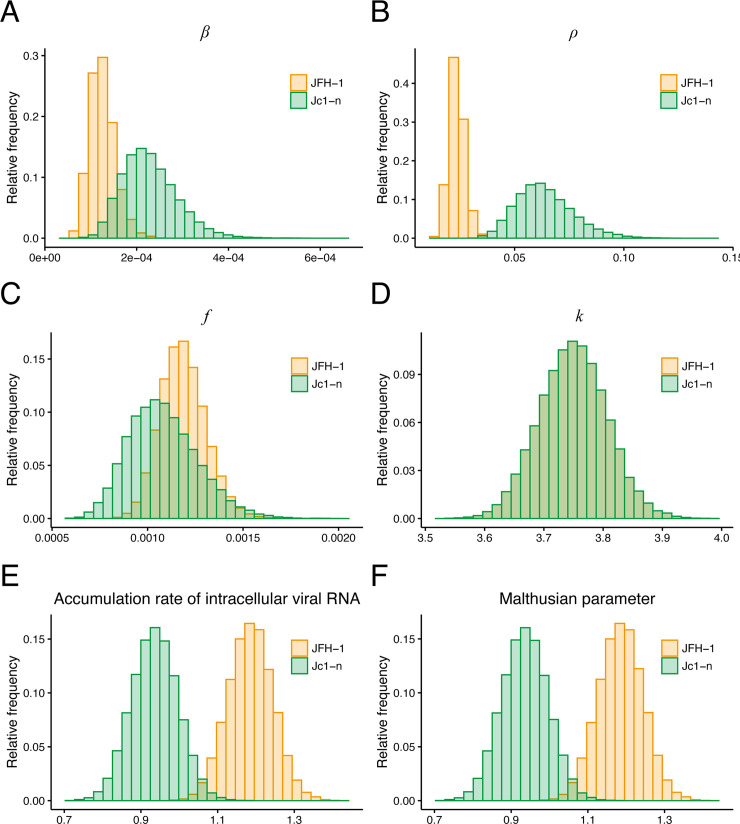
Fig 3. Characterization of viral dynamics of HCV JFH-1 and Jc1-n.
The distributions of the rate constant for infection, βθ; the release rate of intracellular viral RNA, ρ; the converted fraction of infectious viral RNA, fθ; and the replication rate of intracellular viral RNA, k, inferred by MCMC computations are shown in (A), (B), (C) and (D), respectively, for HCV JFH-1 (orange) and Jc1-n (green). Parameters βθ and ρ for Jc1-n were significantly larger than for JFH-1, whereas there was no significant difference in fθ between the two strains as assessed by repeated bootstrap t test. JFH-1 and Jc1-n stains had identical viral RNA replication rates. The distributions of accumulation rates of intracellular viral RNA, k−μ−ρ, and the Malthusian parameter, M, calculated from all accepted MCMC parameter estimates are shown in (E) and (F), respectively, for HCV JFH-1 (orange) and Jc1-n (green). These indices were significantly larger for JFH-1 than for Jc1-n as assessed by the repeated bootstrap t test. The underlying data for this Figure can be found in S2 Data. HCV, hepatitis C virus; MCMC, Markov chain Monte Carlo.
In our multiscale model (Eqs 2–6), the accumulation rate of intracellular viral RNA was defined as the difference between the replication rate and the sum of the degradation rate and the release rate (i.e., k−μ−ρ). The distributions of calculated intracellular RNA accumulation rates for JFH-1 (1.19 per day, 95% CI 1.07–1.30) and Jc1-n (0.936 per day, 95% CI 0.819–1.05) are shown in Fig 3E (p = 8×10−6 by bootstrap t test) (Table 1). The preferential accumulation of JFH-1 RNA inside cells was consistent with its tendency toward gradual increased levels of intracellular RNA at later time points (S2B Fig). The difference in the site of virion assembly and the trafficking pathway as well as in the viral genome RNA stability may explain the higher accumulation of JFH-1 RNA in the cells. To further evaluate the total viral RNA level considering multiround virus transmission, the Malthusian parameter, M, was used as an indicator of the initial growth rate of intracellular viral RNA for each HCV strain [8,12,15]. Here, the Malthusian parameter was given by
| (7) |
(see S3 Text for derivation of the Malthusian parameter). The Malthusian parameters for JFH-1 and Jc1-n were calculated as 1.19 (95% CI 1.07–1.30) and 0.936 (95% CI 0.819–1.05), respectively, and were significantly different from one another (p = 8×10−6 by bootstrap t test) (Fig 3F and Table 1). Interestingly, even if Jc1-n had a larger infection rate, βθ, and release rate, ρ, compared with JFH-1, the initial growth rate of total JFH-1 RNA was higher than that of Jc1-n. This result demonstrated that the capacity to accumulate viral RNA inside cells predominantly determines the initial growth rate rather than release of progeny viruses.
Stay-at-home strategy or leaving-home strategy for “optimizing” HCV proliferation
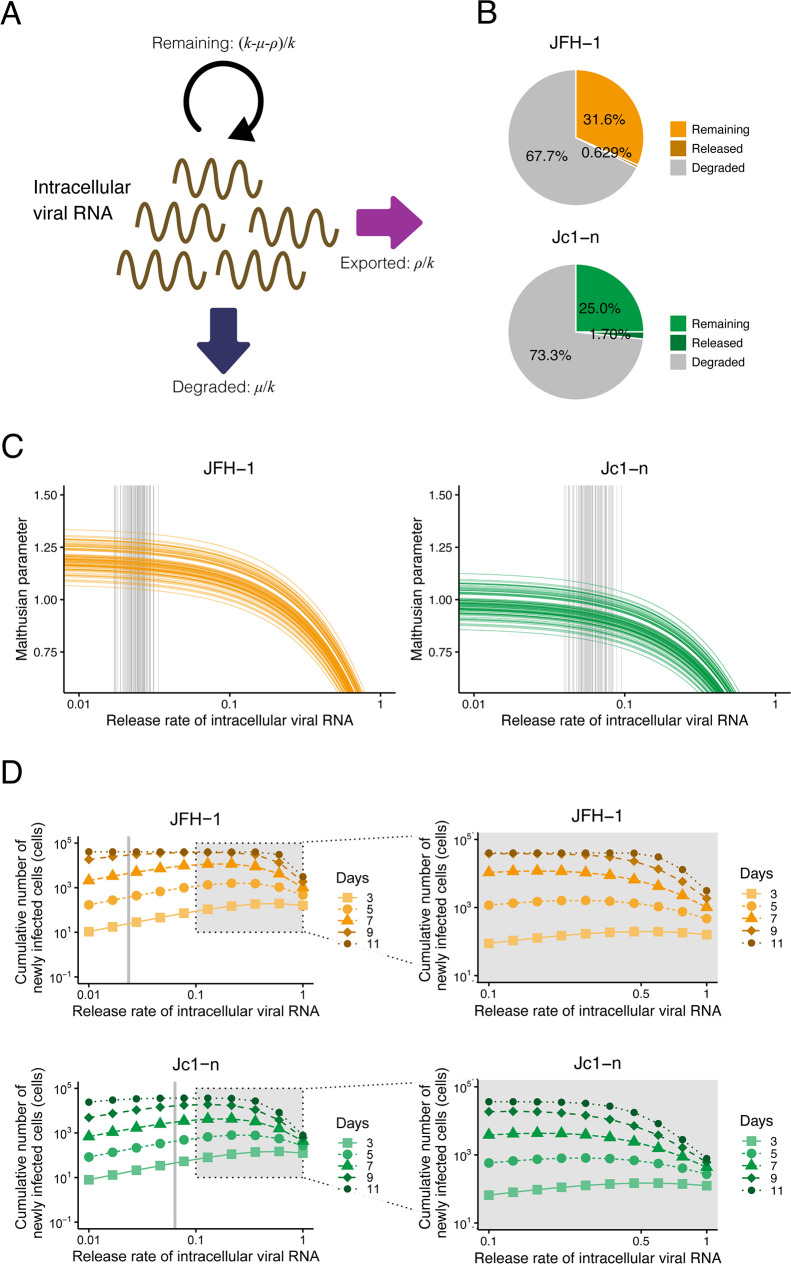
We investigated how differences between the two strains, JFH-1 and Jc1-n, might be interpreted in an evolutionary perspective. As mentioned above, we considered two opposing strategies: the “stay-at-home strategy” and the “leaving-home strategy”: if viruses have smaller ρ, they preferentially stay inside the cell, but if they have larger ρ, they leave the cell. To quantitatively characterize these different strategies, we defined the fraction of viral RNA remaining in the cells ((k−μ−ρ)/k), released from the cells (ρ/k), and degraded in the cells (μ/k) within the total intracellular viral RNA produced (Fig 4A). Using all accepted MCMC parameter estimates from the time-course experimental datasets, we calculated that the fractions of viral RNA remaining were 31.6% and 25.0%, the fractions of viral RNA degraded were 67.7% and 73.3%, and the fractions of viral RNA released were 0.629% and 1.70% for JFH-1 and Jc1-n, respectively (Fig 4B). Comparing the lattermost fractions, Jc1-n used intracellular viral RNA 2.70 times more for virus release than JFH-1, explaining the rapid transmission of Jc1-n (S2B Fig). These results indicate the preferential “leaving-home” strategy of Jc1-n as compared with JFH-1, which adopts a “stay-at-home” strategy.
Fig 4. Different strategies adopted by JFH-1 and Jc1-n for viral proliferation.
(A) Schematic representation of the fate of replicated intracellular viral RNA. Viral RNA is used either for driving RNA replication in cells or for producing progeny viruses for release outside cells or is degraded. (B) Percentage of replicated intracellular HCV JFH-1 and Jc1-n viral RNA that remains inside cells, is released outside cells, and is degraded. (C) Change in the Malthusian parameter (Eq 7) with various release rates of intracellular viral RNA. The orange and green curves show Malthusian parameters calculated using 100 parameter sets sampled from MCMC parameter estimates as functions of ρ for JFH-1 and Jc1-n, respectively. The gray vertical lines are the corresponding release rates estimated from the actual experimental data. (D) Change in the cumulative number of newly infected cells with the various release rates (Eq 8). (Left panels) The orange and green curves represent the cumulative numbers of newly infected cells until 3, 5, 7, 9, and 11 days post infection calculated using the means of estimated parameters as a function of ρ for JFH-1 and Jc1-n, respectively. The gray vertical line represents the mean release rate estimated from the experimental data. (Right panels) Enlarged views of the gray zones in left panels. Finely calculated cumulative numbers of newly infected cells are shown. The underlying data for this figure can be found in S3 Data. HCV, hepatitis C virus; MCMC, Markov chain Monte Carlo.
To further investigate these two opposing strategies, we addressed the relevance of viral RNA release rates for viral proliferation using in silico analysis. With various values of the release rate of intracellular viral RNA, ρ, we calculated the Malthusian parameter (Eq 7) for each strain as an indicator of viral fitness (Fig 4C). Each curve shows Malthusian parameters calculated using 100 parameter sets sampled from MCMC parameter estimates as functions of ρ, and each gray vertical line is the corresponding estimated release rate. Interestingly, the smaller the release rate, the larger the Malthusian parameter HCV achieves. This is because intracellular viral RNAs can be amplified faster compared with viral RNAs outside of cells that are degraded or enter new cells. This result showed that the JFH-1 strain is more optimized in terms of its Malthusian parameter compared with Jc1-n because of the smaller estimated values of ρ. That is, HCV JFH-1 adopts the stay-at-home strategy for acquiring a higher initial growth rate.
Next, we defined the cumulative number of newly infected cells at time t to evaluate viral transmissibility:
| (8) |
We also calculated the cumulative number of newly infected cells for each strain using the means of the estimated parameters as functions of ρ (Fig 4D). Each curve shows the calculated cumulative numbers of infected cells until 3, 5, 7, 9, and 11 days post infection, and the gray vertical line represents the mean release rate estimated from the infection experiment. The value of the release rate, which maximized the cumulative number of newly infected cells, was between 0.1 and 0.5. This is because an intermediate release rate effectively increases extracellular viral RNA for new infection: lower release rates do not effectively produce new infections, whereas higher release rates decrease intracellular viral RNA levels and thus diminish future new infections. Thus, it appears that Jc1-n is more optimized for producing newly infected cells. This implies that HCV Jc1-n adopts the leaving-home strategy to acquire an advantage in producing newly infected cells.
Taken together, our theoretical investigation based on viral infection experiments revealed that the JFH-1 strain optimizes its initial growth rate, but the Jc1-n strain optimizes de novo infection. Ours is the first report to quantitatively evaluate these opposing evolutionary strategies and to show their significance for virus proliferation at the intracellular and intercellular levels.
Discussion
To understand the replication mechanisms of HCV and to develop effective drugs for the treatment of HCV, many mathematical modeling studies have been conducted. A mathematical model describing the intracellular dynamics of HCV replication in detail provided a framework to investigate HCV replication dynamics using the well-established HCV replicon system [16]. Another study combined data obtained from the HCV replicon system with an expanded mathematical model and revealed that the replication compartment and unknown host factors played important roles in the maintenance and control of viral RNAs in cells [17]. Another expanded and modified model using data from an HCV cell culture system enabled predictions of the dynamics of HCV infection and viral protein mechanisms [18]. A multiscale model was applied to data from patients treated with several drugs, based on a basic mathematical model of viral dynamics with age structures of HCV replication; this work provided new insights into viral decay dynamics and the mechanisms of action of anti-HCV drugs [19,20]. Other multiscale models, combining the detailed intracellular replication dynamics and basic infection dynamics, also explained the dynamics of viral loads in vivo [21].
In this study, through a combined experimental-theoretical approach, we analyzed the dynamics of the HCV life cycle using two related HCV strains, JFH-1 and Jc1-n, employing different particle assembly/release strategies. We quantified the intra- and intercellular viral dynamics of these strains by applying an age-structured multiscale model to time-course experimental data from an HCV infection cell culture assay (Fig 2 and Table 1): as in [10,11], we transformed the multiscale model formulated by PDEs to an identical multiscale ODE model (i.e., Eqs 2–6), and we estimated parameters shared between the PDE and ODE models. It is technically challenging to obtain experimental measurements with age information, but thanks to the estimated values of these common parameters, we managed to reconstruct age information for intracellular viral RNA (S2 Fig). We also derived values for standard parameters as previously reported. For example, the numbers of viruses produced per cell per day in our multiscale model, which correspond to ρA(t)/I(t) in Eqs 2–6, were 102–103 and 103–104 for JFH-1 and Jc1-n, respectively. These values are relatively high compared with previously estimated values [1], potentially because of the high efficiency of viral replication in our Huh7.5.1 cell culture system. Note that values of ρ for JFH-1 and Jc1-n were both estimated as small compared with previous estimates [19], although we confirmed these estimated viral release rates using independent single-cycle infection experiments. This discrepancy is likely due to differences among experimental systems or mathematical models of intracellular viral replication dynamics. Interestingly, comparing the calculated Malthusian parameters (i.e., Eq 7) and the cumulative number of newly infected cells (i.e., Eq 8) between the two strains (Fig 3E and 3F), we found that the JFH-1 strain had a higher initial growth rate but that Jc1 produced more de novo infections.
Based on our results, we propose two opposing strategies for viral proliferation: the “stay-at-home strategy” and the “leaving-home strategy.” From an evolutionary perspective, JFH-1 adopts a stay-at-home strategy and preferentially uses viral genomic RNA for increasing intracellular replication. In contrast, adopting a leaving-home strategy, Jc1-n uses more viral genomic RNA for producing progeny virions capable of new transmission events to increase the number of infected cells (Fig 4). Thus, Jc1-n infects cells 1.82 times faster and produces viral RNA from infected cells 2.70 times faster than JFH-1. In the context of the replication-release trade-off, a previous theoretical study indicated that allocation and reallocation of intracellular viral RNA toward translation and replication rather than virus release induced higher viral production [22]. Although our model did not describe intracellular dynamics in detail, the “stay-at-home strategy” of JFH-1, resulting in more efficient accumulation of viruses by remaining in cells, was partially consistent with the results of previous work. Our group and others reported that JFH-1 assembled progeny virions on the membranes of hepatic lipid droplets, whereas J6/JFH-1 chimeric strains mainly used endoplasmic reticulum–derived membranes for particle production [2,3]. Although the molecular aspects of this difference have been analyzed, its significance for viral proliferation and dynamics is not completely understood. Our results raise the possibility that different subcellular locations for particle assembly and subsequent differential intracellular trafficking impact the rates of particle assembly and release, which in turn determine virus proliferation. Further analysis might shed light on why one HCV strain has to be assembled on the lipid droplet membrane whereas another assembles in association with the endoplasmic reticulum.
We confirmed that the replication rate and release rate can be approximated as constant regardless of infection age using independent single-cycle experiments. Thus, we assumed the kinetic parameters of intracellular replication were constant, which is a potential limitation of our study. To further validate this assumption, we confirmed that the numerical solution of the multiscale model with time-dependent intracellular kinetic parameters coincided well with that of our multiscale model (i.e., constant kinetic parameters). In addition, by comparison with previous models describing the HCV replicon, HCV cell culture systems, or in vivo data [16–18,21], we excluded the detailed biological processes of HCV replication to enable simple and robust parameter estimation. Thus, our tightly designed multicycle infection experiments and multiscale mathematical model enabled us to evaluate intracellular strategies of HCV strains on the basis of various aspects such as viral fitness and transmissibility, which together reflected the entire infection process.
The choice of replication strategy not only determines virus proliferation but also affects the pathogenic features of the virus: JFH-1, which preferentially amplifies intracellular RNA, caused fulminant hepatitis with rapid viral replication and severe inflammation. By contrast, J6, the original strain encoding the Jc1-n structural region, was isolated from a patient with chronic hepatitis and generally replicates more moderately, with robust spread of infected cells used as a longer-term strategy to establish persistent infection. Characterization of the proliferation strategies of viruses is of significant importance when trying to understand their clinical as well as evolutionary properties.
Methods
Cell culture and HCV infection
Huh-7.5.1 (kindly provided by Dr. Francis Chisari, The Scripps Research Institute) and Huh7-25 cells were cultured in Dulbecco’s Modified Eagle’s Medium (Invitrogen) supplemented with 10% fetal bovine serum (Sigma), 10 units/mL penicillin, 10 mg/mL streptomycin, 0.1 mM nonessential amino acids (Invitrogen), 1 mM sodium pyruvate, and 10 mM HEPES (pH 7.4) at 37°C under a humidified atmosphere containing 5% CO2. We used HCV strains JFH-1, a genotype 2a clinical isolate from a patient with fulminant hepatitis [4], and Jc1-n, a J6/JFH-1 chimeric laboratory strain [13]. JFH-1 and Jc1-n have 96.7% amino acid identity over the whole genome. HCV inoculum for infection experiments was recovered from the culture supernatants of Huh-7.5.1 cells transfected with the corresponding HCV RNA as described [4]. Huh-7.5.1 cells were inoculated with JFH-1 or Jc1-n at a multiplicity of infection (MOI) of 0.05 for 4 hours and then passaged to seed a new 96-well plate at different cell densities (1,000, 2,000, or 4,000 cells/well). Under these conditions, the starting number of HCV-infected cells varied. At days 0, 1, 2, 3, and 4 post seeding, culture supernatants and cell lysates were recovered to quantify HCV RNA by real-time RT-PCR as previously described [13]. The infectivity of HCV in culture supernatants was measured using a focus-forming assay as described [13]. To quantify the number of uninfected and infected cells, cells were fixed and stained with anti-HCV core antibody by immunofluorescence assay as described [13]. We prepared three replicate samples for these experiments and used the average values of replicates for analysis.
Data fitting and parameter estimation
The parameters g and K were separately estimated (see S4 Text) and fixed at 0.670 per day and 4.12×104 cells, respectively, for the JFH-1 strain and 0.665 per day and 3.75×104 cells, respectively, for the Jc1-n strain. A statistical model adopted from Bayesian inference assumed that measurement error followed a normal distribution with mean zero and constant variance (error variance). The noninformative prior distributions with upper and lower limits were used as the prior distributions of parameters. The posterior predictive parameter distribution as an output of MCMC computation represented parameter variability. Distributions of model parameters (i.e., βθ, k, ρ, fθ) and initial values (i.e., T(0), I(0), A(0), Vθ(t), V(0)) in Eqs 2–6 were inferred directly by MCMC computations. We also tested structural identifiability for all parameter estimates by calculating profile likelihood [23,24] using package dMod [25] in R Statistical Software [26]. All parameter estimates were confirmed to be structural identifiable (see S4 Fig). Distributions of derived quantities were calculated from the inferred parameter sets (Fig 3E and 3F for graphical representation). A set of computations for Eqs 2–6 with estimated parameter sets gives a distribution of outputs (the number of cells and the intra- and extracellular viral loads) as model predictions. To investigate variation in model predictions, global sensitivity analyses were performed. The ranges of possible variation are shown in Fig 2 as 95% posterior predictive intervals. Technical details of MCMC computations are summarized below.
Statistical analysis
Package FME [27] in R Statistical Software [26] was used to infer posterior predictive parameter distributions. The delayed rejection and Metropolis method [28] was used as a default computation scheme for FME to perform MCMC computations. MCMC computations for parameter inference were implemented using the predefined function modMCMC() in package FME as introduced in Methods. Convergence of Markov chains to a stationary distribution was required to ensure parameter sets were sampled from a posterior distribution. Only the last 90,000 of 100,000 chains were used as burn-in. The convergence of the last 90,000 chains was manually checked with figures produced by package coda [29], a collection of diagnostic tools for MCMC computation. The 95% posterior predictive intervals shown as a shadowed region in each panel of Fig 2 were produced from 100 randomly chosen inferred parameter sets and corresponding model predictions. We employed a bootstrap t test [30] to quantitatively characterize differences in parameters and derived quantities between HCV JFH-1 and Jc1-n. In total, 100,000 parameter sets were sampled with replacement from the posterior predictive distributions to calculate the bootstrap t-statistics. To avoid potential sampling bias, the bootstrap t test was performed 100 times repeatedly. The averages of the computed p-values were used as indicators of differences.
Supporting information
(A) Decay of extracellular HCV was estimated. HCV JFH-1 and Jc1-n were incubated in medium without cells and recovered at days 0, 1, 2, 3, 4, and 5 to quantify viral RNA and infectivity. Linear regressions yielded a rate of RNA degradation and a loss of virion infectivity per day. (B) Effect of changing medium on the clearance of extracellular viral RNA was estimated. Changing medium reduced viral RNA by 69.1% and 83.7% for JFH-1 and Jc1-n, respectively, and these losses were modeled by approximating the sampling of virus as a continuous exponential decay (S1 Protocol and S5 Text). (C) Decay kinetics of intracellular viral RNA was investigated upon complete inhibition of RNA replication/release by antiviral treatment with 2 μM SOF + 1 μM LDV. By applying linear regressions, the degradation rates of intracellular viral RNA for JFH-1 and Jc1-n were estimated. (D) By counting total Huh7.5.1 cells on days 0, 1, 2, 3, 4 in experiments A, B, and C, the growth kinetics of the cells were estimated. The underlying data for this figure can be found in S4 Data. HCV, hepatitis C virus; LDV, ledipasvir; SOF, sofosbuvir.
(DOCX)
(A) Dynamics of the distributions of intracellular viral RNA according to infection age, a. The distributions were calculated using the original multiscale PDE model (Eq S2–6 in S1 Text) using the means of parameter estimates for HCV JFH-1 and Jc1-n. The colored bars represent amounts of intracellular viral RNA. (B) Differences in the distribution of intracellular viral RNA in total infected cells of infection age, a, between HCV JFH-1 and Jc1-n. The colored bar shows the difference in the amount of intracellular viral RNA (green: intracellular viral RNA during Jc1-n infection is more abundant than during JFH-1 infection; yellow-red-brown: intracellular viral RNA is more abundant for JFH-1 than for Jc1-n; gray: no new infection occurs owing to depletion of target cells). The underlying data for this figure can be found in S5 Data. HCV, hepatitis C virus; PDE, partial differential equation.
(DOCX)
(A) Difference in viral entry mediated by the envelopes of JFH-1 and J6 (structural region of Jc1-n). HCVtcp prepared with an HCV E1/E2 derived from JFH-1 and J6 were used to inoculate Huh7.5.1 cells. At 72 hours post inoculation, luciferase activity was measured to evaluate differences in viral entry between JFH-1 and Jc1-n according to previous work [31]. (B) A single-cycle virus production assay was performed by transfecting Huh7-25 cells with JFH-1 or Jc1-n RNA. Huh7-25 cells are deficient for an HCV receptor, CD81, and do not support reinfection [32]. HCV RNA produced in the culture supernatant at 72 hours post transfection was quantified by real-time RT-PCR to evaluate viral production. (C) Single-cycle virus production assay for examining early HCV replication. Production of HCV core and NS5A proteins acted as an internal control and was detected by immunoblotting of Huh7-25 cells transfected with RNA derived from either JFH-1 or Jc1-n at early time points (16, 20, 25, and 30 hours post transfection). (D) Host IFN response against infection by JFH-1 and Jc1-n. Huh7.5.1 cells were infected with either JFH-1 or Jc1-n, and induction of IFN-stimulated genes (MxA, and ISG56) and expression of HCV core, NS5A, and actin proteins were assessed by immunoblotting. Exogenous IFN-α was used as a positive control for ISG induction. (E) Expression of host factors regulating HCV particle assembly switching in JFH-1- and Jc1-n-infected cells at different infection ages. YTHDF1, 2, 3, and METTL14 as well as actin were detected in JFH-1- and Jc1-n-infected cells at infection ages of 3, 5, and 7 days by immunoblotting. The underlying data for this figure can be found in S6 Data. E, envelope; HCV, hepatitis C virus; HCVtcp, trans-complemented HCV particles; IFN, interferon; ISG, interferon stimulated genes; METTL14, methyltransferase Like 14; RT-PCR, reverse transcription PCR.
(DOCX)
All estimated parameters were confirmed to be structurally identifiable by calculation of profile likelihood [23–25].
(DOCX)
(DOCX)
(XLSX)
(XLSX)
(XLSX)
(XLSX)
(XLSX)
(XLSX)
(ZIP)
(DOCX)
(DOCX)
HCV, hepatitis C virus.
(DOCX)
ODE, ordinary differential equation; PDE, partial differential equation.
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
Acknowledgments
Huh7.5.1 cells were kindly provided by Dr. Francis Chisari at The Scripps Research Institute.
Abbreviations
- ffu
focus formation unit
- HCV
hepatitis C virus
- MCMC
Markov chain Monte Carlo
- NS protein
nonstructural protein
- ODE
ordinary differential equation
- PDE
partial differential equation
- S protein
structural protein
Data Availability
All data are available as part of this manuscript and provided in the S1 Data supplemental Excel sheets.
Funding Statement
This study was supported by funding from the following sources: a Grant-in-Aid for JSPS Research Fellows 19J12319 (to S. Iwanami), 19J21395 (to KK), Scientific Research (KAKENHI) B 18KT0018 (to S. Iwami), 18H01139 (to S. Iwami), 16H04845 (to S. Iwami), 17H04085 (to KW), Scientific Research in Innovative Areas 20H05042 (to S. Iwami), 19H04839 (to S. Iwami), 18H05103 (to S. Iwami); AMED CREST 19gm1310002 (to S. Iwami); AMED J-PRIDE 19fm0208006s0103 (to S. Iwami), 19fm0208014h0003 (to S. Iwami), 19fm0208019h0103 (to S. Iwami), 19fm0208019j0003 (to KW); AMED Research Program on HIV/AIDS 19fk0410023s0101 (to S. Iwami); Research Program on Emerging and Re-emerging Infectious Diseases 19fk0108050h0003 (to S. Iwami); Program for Basic and Clinical Research on Hepatitis 19fk0210036h0502 (to S. Iwami), 19fk0210036j0002 (to KW); Program on the Innovative Development and the Application of New Drugs for Hepatitis B 19fk0310114h0103 (to S. Iwami), 19fk0310114j0003 (to KW), 19fk0310101j1003 (to KW), 19fk0310103j0203 (to KW); JST MIRAI 18077147 (to S. Iwami and KW); Mitsui Life Social Welfare Foundation (to S. Iwami and KW); Shin-Nihon of Advanced Medical Research (to S. Iwami); Suzuken Memorial Foundation (to S. Iwami); Life Science Foundation of Japan (to S. Iwami); SECOM Science and Technology Foundation (to S. Iwami); The Japan Prize Foundation (to S. Iwami); Toyota Physical and Chemical Research Institute (to S. Iwami); The Yasuda Medical Foundation (to KW); Smoking Research Foundation (to KW); and The Takeda Science Foundation (to KW). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Neumann AU, Lam NP, Dahari H, Gretch DR, Wiley TE, Layden TJ, et al. Hepatitis C viral dynamics in vivo and the antiviral efficacy of interferon-alpha therapy. Science. 1998;282(5386):103–7. Epub 1998/10/02. 10.1126/science.282.5386.103 . [DOI] [PubMed] [Google Scholar]
- 2.Miyanari Y, Atsuzawa K, Usuda N, Watashi K, Hishiki T, Zayas M, et al. The lipid droplet is an important organelle for hepatitis C virus production. Nat Cell Biol. 2007;9(9):1089–97. Epub 2007/08/28. 10.1038/ncb1631 . [DOI] [PubMed] [Google Scholar]
- 3.Boson B, Granio O, Bartenschlager R, Cosset FL. A concerted action of hepatitis C virus p7 and nonstructural protein 2 regulates core localization at the endoplasmic reticulum and virus assembly. PLoS Pathog. 2011;7(7):e1002144 Epub 2011/08/05. 10.1371/journal.ppat.1002144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wakita T, Pietschmann T, Kato T, Date T, Miyamoto M, Zhao Z, et al. Production of infectious hepatitis C virus in tissue culture from a cloned viral genome. Nat Med. 2005;11(7):791–6. Epub 2005/06/14. 10.1038/nm1268 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lindenbach BD, Evans MJ, Syder AJ, Wolk B, Tellinghuisen TL, Liu CC, et al. Complete replication of hepatitis C virus in cell culture. Science. 2005;309(5734):623–6. Epub 2005/06/11. 10.1126/science.1114016 . [DOI] [PubMed] [Google Scholar]
- 6.Pietschmann T, Kaul A, Koutsoudakis G, Shavinskaya A, Kallis S, Steinmann E, et al. Construction and characterization of infectious intragenotypic and intergenotypic hepatitis C virus chimeras. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(19):7408–13. Epub 2006/05/03. 10.1073/pnas.0504877103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dieckmann U, Metz JA, Sabelis MW. Adaptive dynamics of infectious diseases: in pursuit of virulence management. Cambridge University Press; 2005. [Google Scholar]
- 8.Iwanami S, Kakizoe Y, Morita S, Miura T, Nakaoka S, Iwami S. A highly pathogenic simian/human immunodeficiency virus effectively produces infectious virions compared with a less pathogenic virus in cell culture. Theor Biol Med Model. 2017;14(1):9 10.1186/s12976-017-0055-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Iwami S, Holder BP, Beauchemin CA, Morita S, Tada T, Sato K, et al. Quantification system for the viral dynamics of a highly pathogenic simian/human immunodeficiency virus based on an in vitro experiment and a mathematical model. Retrovirology. 2012;9(1):18 Epub 2012/03/01. 10.1186/1742-4690-9-18 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kitagawa K, Nakaoka S, Asai Y, Watashi K, Iwami S. A PDE multiscale model of hepatitis C virus infection can be transformed to a system of ODEs. J Theor Biol. 2018;448:80–5. Epub 2018/04/11. 10.1016/j.jtbi.2018.04.006 . [DOI] [PubMed] [Google Scholar]
- 11.Kitagawa K, Kuniya T, Nakaoka S, Asai Y, Watashi K, Iwami S. Mathematical Analysis of a Transformed ODE from a PDE Multiscale Model of Hepatitis C Virus Infection. Bull Math Biol. 2019;81(5):1427–41. Epub 2019/01/16. 10.1007/s11538-018-00564-y . [DOI] [PubMed] [Google Scholar]
- 12.Iwami S, Takeuchi JS, Nakaoka S, Mammano F, Clavel F, Inaba H, et al. Cell-to-cell infection by HIV contributes over half of virus infection. Elife. 2015;4:e08150 Epub 2015/10/07. 10.7554/eLife.08150 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ohashi H, Nishioka K, Nakajima S, Kim S, Suzuki R, Aizaki H, et al. The aryl hydrocarbon receptor-cytochrome P450 1A1 pathway controls lipid accumulation and enhances the permissiveness for hepatitis C virus assembly. J Biol Chem. 2018;293(51):19559–71. Epub 2018/11/02. 10.1074/jbc.RA118.005033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sumpter R Jr, Loo YM, Foy E, Li K, Yoneyama M, Fujita T, et al. Regulating intracellular antiviral defense and permissiveness to hepatitis C virus RNA replication through a cellular RNA helicase, RIG-I. J Virol. 2005;79(5):2689–99. Epub 2005/02/15. 10.1128/JVI.79.5.2689-2699.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nowak M, May RM. Virus dynamics: mathematical principles of immunology and virology: mathematical principles of immunology and virology. Oxford University Press; 2000. [Google Scholar]
- 16.Dahari H, Ribeiro RM, Rice CM, Perelson AS. Mathematical modeling of subgenomic hepatitis C virus replication in Huh-7 cells. J Virol. 2007;81(2):750–60. Epub 2006/10/13. 10.1128/JVI.01304-06 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Binder M, Sulaimanov N, Clausznitzer D, Schulze M, Huber CM, Lenz SM, et al. Replication vesicles are load- and choke-points in the hepatitis C virus lifecycle. PLoS Pathog. 2013;9(8):e1003561 Epub 2013/08/31. 10.1371/journal.ppat.1003561 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Aunins TR, Marsh KA, Subramanya G, Uprichard SL, Perelson AS, Chatterjee A. Intracellular Hepatitis C Virus Modeling Predicts Infection Dynamics and Viral Protein Mechanisms. J Virol. 2018;92(11). Epub 2018/03/23. 10.1128/JVI.02098-17 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Guedj J, Dahari H, Rong L, Sansone ND, Nettles RE, Cotler SJ, et al. Modeling shows that the NS5A inhibitor daclatasvir has two modes of action and yields a shorter estimate of the hepatitis C virus half-life. Proc Natl Acad Sci U S A. 2013;110(10):3991–6. Epub 2013/02/23. 10.1073/pnas.1203110110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rong L, Guedj J, Dahari H, Coffield DJ Jr., Levi M, Smith P, et al. Analysis of hepatitis C virus decline during treatment with the protease inhibitor danoprevir using a multiscale model. PLoS Comput Biol. 2013;9(3):e1002959 Epub 2013/03/22. 10.1371/journal.pcbi.1002959 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Clausznitzer D, Harnisch J, Kaderali L. Multi-scale model for hepatitis C viral load kinetics under treatment with direct acting antivirals. Virus Res. 2016;218:96–101. Epub 2015/09/27. 10.1016/j.virusres.2015.09.011 . [DOI] [PubMed] [Google Scholar]
- 22.McLean AK, Luciani F, Tanaka MM. Trade-offs in resource allocation in the intracellular life-cycle of hepatitis C virus. J Theor Biol. 2010;267(4):565–72. Epub 2010/10/05. 10.1016/j.jtbi.2010.09.031 . [DOI] [PubMed] [Google Scholar]
- 23.Maiwald T, Hass H, Steiert B, Vanlier J, Engesser R, Raue A, et al. Driving the Model to Its Limit: Profile Likelihood Based Model Reduction. PLoS ONE. 2016;11(9):e0162366 Epub 2016/09/03. 10.1371/journal.pone.0162366 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Raue A, Kreutz C, Maiwald T, Bachmann J, Schilling M, Klingmuller U, et al. Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics. 2009;25(15):1923–9. Epub 2009/06/10. 10.1093/bioinformatics/btp358 . [DOI] [PubMed] [Google Scholar]
- 25.Kaschek D, Mader W, Fehling-Kaschek M, Rosenblatt M, Timmer J. Dynamic Modeling, Parameter Estimation, and Uncertainty Analysis in R. Journal of Statistical Software. 2019;88(10):1–32. 10.18637/jss.v088.i10 WOS:000467010500001. [DOI] [Google Scholar]
- 26.R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; 2019. [Google Scholar]
- 27.Soetaert K, Petzoldt T. Inverse Modelling, Sensitivity and Monte Carlo Analysis in R Using Package FME. J Stat Softw. 2010;33(3):1–28. 10.18637/jss.v033.i03 WOS:000275203400001.20808728 [DOI] [Google Scholar]
- 28.Haario H, Laine M, Mira A, Saksman E. DRAM: Efficient adaptive MCMC. Stat Comput. 2006;16(4):339–54. 10.1007/s11222-006-9438-0 WOS:000241260600002. [DOI] [Google Scholar]
- 29.Plummer M, Best N, Cowles K, Vines K. CODA: convergence diagnosis and output analysis for MCMC. R news. 2006;6(1):7–11. [Google Scholar]
- 30.Efron B, Tibshirani RJ. An introduction to the bootstrap. CRC; 1994. [Google Scholar]
- 31.Suzuki R, Saito K, Kato T, Shirakura M, Akazawa D, Ishii K, et al. Trans-complemented hepatitis C virus particles as a versatile tool for study of virus assembly and infection. Virology. 2012;432(1):29–38. Epub 2012/06/26. 10.1016/j.virol.2012.05.033 . [DOI] [PubMed] [Google Scholar]
- 32.Kato T, Choi Y, Elmowalid G, Sapp RK, Barth H, Furusaka A, et al. Hepatitis C virus JFH-1 strain infection in chimpanzees is associated with low pathogenicity and emergence of an adaptive mutation. Hepatology. 2008;48(3):732–40. Epub 2008/08/21. 10.1002/hep.22422 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(A) Decay of extracellular HCV was estimated. HCV JFH-1 and Jc1-n were incubated in medium without cells and recovered at days 0, 1, 2, 3, 4, and 5 to quantify viral RNA and infectivity. Linear regressions yielded a rate of RNA degradation and a loss of virion infectivity per day. (B) Effect of changing medium on the clearance of extracellular viral RNA was estimated. Changing medium reduced viral RNA by 69.1% and 83.7% for JFH-1 and Jc1-n, respectively, and these losses were modeled by approximating the sampling of virus as a continuous exponential decay (S1 Protocol and S5 Text). (C) Decay kinetics of intracellular viral RNA was investigated upon complete inhibition of RNA replication/release by antiviral treatment with 2 μM SOF + 1 μM LDV. By applying linear regressions, the degradation rates of intracellular viral RNA for JFH-1 and Jc1-n were estimated. (D) By counting total Huh7.5.1 cells on days 0, 1, 2, 3, 4 in experiments A, B, and C, the growth kinetics of the cells were estimated. The underlying data for this figure can be found in S4 Data. HCV, hepatitis C virus; LDV, ledipasvir; SOF, sofosbuvir.
(DOCX)
(A) Dynamics of the distributions of intracellular viral RNA according to infection age, a. The distributions were calculated using the original multiscale PDE model (Eq S2–6 in S1 Text) using the means of parameter estimates for HCV JFH-1 and Jc1-n. The colored bars represent amounts of intracellular viral RNA. (B) Differences in the distribution of intracellular viral RNA in total infected cells of infection age, a, between HCV JFH-1 and Jc1-n. The colored bar shows the difference in the amount of intracellular viral RNA (green: intracellular viral RNA during Jc1-n infection is more abundant than during JFH-1 infection; yellow-red-brown: intracellular viral RNA is more abundant for JFH-1 than for Jc1-n; gray: no new infection occurs owing to depletion of target cells). The underlying data for this figure can be found in S5 Data. HCV, hepatitis C virus; PDE, partial differential equation.
(DOCX)
(A) Difference in viral entry mediated by the envelopes of JFH-1 and J6 (structural region of Jc1-n). HCVtcp prepared with an HCV E1/E2 derived from JFH-1 and J6 were used to inoculate Huh7.5.1 cells. At 72 hours post inoculation, luciferase activity was measured to evaluate differences in viral entry between JFH-1 and Jc1-n according to previous work [31]. (B) A single-cycle virus production assay was performed by transfecting Huh7-25 cells with JFH-1 or Jc1-n RNA. Huh7-25 cells are deficient for an HCV receptor, CD81, and do not support reinfection [32]. HCV RNA produced in the culture supernatant at 72 hours post transfection was quantified by real-time RT-PCR to evaluate viral production. (C) Single-cycle virus production assay for examining early HCV replication. Production of HCV core and NS5A proteins acted as an internal control and was detected by immunoblotting of Huh7-25 cells transfected with RNA derived from either JFH-1 or Jc1-n at early time points (16, 20, 25, and 30 hours post transfection). (D) Host IFN response against infection by JFH-1 and Jc1-n. Huh7.5.1 cells were infected with either JFH-1 or Jc1-n, and induction of IFN-stimulated genes (MxA, and ISG56) and expression of HCV core, NS5A, and actin proteins were assessed by immunoblotting. Exogenous IFN-α was used as a positive control for ISG induction. (E) Expression of host factors regulating HCV particle assembly switching in JFH-1- and Jc1-n-infected cells at different infection ages. YTHDF1, 2, 3, and METTL14 as well as actin were detected in JFH-1- and Jc1-n-infected cells at infection ages of 3, 5, and 7 days by immunoblotting. The underlying data for this figure can be found in S6 Data. E, envelope; HCV, hepatitis C virus; HCVtcp, trans-complemented HCV particles; IFN, interferon; ISG, interferon stimulated genes; METTL14, methyltransferase Like 14; RT-PCR, reverse transcription PCR.
(DOCX)
All estimated parameters were confirmed to be structurally identifiable by calculation of profile likelihood [23–25].
(DOCX)
(DOCX)
(XLSX)
(XLSX)
(XLSX)
(XLSX)
(XLSX)
(XLSX)
(ZIP)
(DOCX)
(DOCX)
HCV, hepatitis C virus.
(DOCX)
ODE, ordinary differential equation; PDE, partial differential equation.
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
Data Availability Statement
All data are available as part of this manuscript and provided in the S1 Data supplemental Excel sheets.