Abstract
Self-mixed optical feedback interferometry based laser sensors show promising results in the measurement of the vibration frequency. To date several measurement methods have been developed to extract the vibration information from the self-mixed (SM) signal; however, the complexity and accuracy of the methods still need improvement. The presented work tries to fulfill the gap by realizing a novel method using maximal overlap discrete wavelet transformation (MODWT) and multi-resolution analysis (MRA). The proposed method can reconstruct the micro-harmonic (<) vibration up to 1 kHz even under weak feedback conditions. The mean squared error and the maximum relative error of the proposed method for this range remained below 1.89& 8.79%, respectively. Although, above 1 kHz, the proposed method turns out to be futile to reconstruct the vibration signal but still capable to measure vibration frequency up to 10 kHz with an accuracy of 0.0001. The method also found suitable to measure non-sinusoidal vibration frequency with reasonable accuracy even for the moderate feedback conditions. The authors envision that the proposed method will provide a compact, non-contact, and low-cost alternative for the vibration frequency measurement hence useful in early fault detection schemes and lung abnormality diagnosis.
Keywords: Self-mixing interferometry, Maximal overlap discrete wavelet transformation, Vibration measurement, Trend analysis, Optical sensor
Highlights
-
•
The paper presents micro-harmonic vibration measurement method based on wavelet trend analysis using Self-mixing interferometry.
-
•
The proposed method can reconstruct the micro-harmonic vibration (<) upto 1 kHz under weak feedback condition.
-
•
The inherent filtering of wavelet transformation and the trend extraction technique used in the proposed method suppresses the undesired artefacts and produce a smooth output signal.
-
•
The uniqueness of the method is that it does not require any additional optical components, like photodiode, beam-splitters, and EOM for measurement.
-
•
The compact, self-aligned and low-cost hardware structure with non-contact measurement principle make the interferometry suitable for various applications.
1. Introduction
Vibration is one of the critical parameters of modern non-contact metrological and medical analysis. Vibrations contain various information about the subject and offer analytical support for the process advancement. For example, vibration in the mechanical system indicates mechanical faults [1], whereas the abnormality in chest vibrations indicates poor functioning of the lungs [2], [3], [4]. Thus, the analysis of the vibrations offers various advantages to improve the functional quality of the measurement system, whether it is a machine or human body. To date, various optical interferometry’s such as Mach–Zehnder [5], fiber-optic [6], heterodyne [7], speckle pattern [8] and self-mixing [9] has been developed to measure vibration’s frequency. However, in recent years, self-mixing interferometry (SMI) has been widely explored due to its compact, low-cost, and self-aligned structure [10]. SMI is a kind of optical modulator that alters the laser properties such as emission intensity, polarization states, and phase behavior [11] according to the characteristics of coherent reflections. Typically, the interference between the coherent reflections and the resonant light is measured by the integrated photodiode placed inside the laser cavity; thus, the induction of interference does not require any external components. Till date various methodologies have been developed to extract the vibration information from the self-mixing interferometric (SMI) signal such as fringes detection [12], Hilbert transforms [10], [13], pre-feedback mirror [14], digital closed-loop [15], wavelet transform [16], phase unwrapping [17], Genetic algorithm method [18], envelope extraction using Fourier transform [19], local maximum detection method [20] and quadrature demodulation [21]. These methodologies provide robust vibration measurement schemes with nanometric resolution up to 40 nm. However, each method has its demerits. For example, either they need additional components such as beam splitter and electro-optic modulator or follow a complicated computational process.
A typical SMI signal has four characteristics points, i.e., peak (P), jump (J), valley (V), and reverse (R), referring to the different transitions of vibrations [22] as illustrated in Fig. 1. The location of these points is dynamic and shifts according to the vibration. The P & V points indicate the maximum & the minimum value of the SMI waveform, respectively, whereas the J point specifies the sudden change in the waveform. Apart from the waveform characterization, point R indicates the maximum reach of the vibrating amplitude, i.e., change in the direction of the movement. The dynamicity of characteristics points according to the variation in the vibration frequency, concludes that the SMI signal follows the vibration frequency. Therefore, the authors envisioned that the vibration information can be demodulated from the SMI signal by extracting the trend of the SMI signal. To validate this hypothesis, the authors propose a trend analysis method based on maximal overlap discrete wavelet transformation (MODWT) and multi-resolution analysis (MRA) to obtain the vibration information. The main motivation behind the use of MODWT is that it does not require any starting point in the time series data because it essentially includes all the possible placement of averaging interval. Whereas, MRA is used to decompose the signal into components of the same time scale as the original data signal. So that an accurate and precise measurement of the vibration information is possible even when the data was recorded for a random position of the vibration. The presented method has inherent structural advantages of SMI, i.e., compactness, self-alignment, and low-cost optical components with the low computational complexity of wavelet transformation. The authors foresee that the presented method provides a simple, compact, and self-alignment optical arrangement without any external component for the rapid assessment of the vibration.
Fig. 1.
An SMI signal waveform obtained at a wavelength of 850 nm from a target vibrating at a frequency of 100 Hz with a amplitude and placed at a distance of 20 cm. The characteristic points are also marked in the waveform.
2. Background
2.1. Self-mixing interferometry
The self-mixing phenomena describe the interaction between the emitted field and the fraction of the field reflected or scattered from the subject and re-enter the laser cavity. The interference between the two fields alters/modulates the carrier density inside the laser cavity depending upon the characteristics of the re-entered field. During the flight time, the laser beam encounters various optical events that alter the beam characteristics. Hence, the re-entered field contains the modulated information about the external cavity and the subject. The modulated signal is typically detected either by measuring the variation in the junction voltage or through the integrated monitor photodiode of the laser diode. In literature, the Lang–Kobayashi equations and three mirror approaches are prominently used for the analysis of the SMI [23], [24]. The Lang–Kobayashi equations describe the dynamic behavior of the laser through multi-stable and hysteresis phenomena while the three-mirror model is based on the static analysis. Irrespective of the method of modeling and complexity, both the approach accurately describes the self-mixing process under different feedback levels. Based on these models, various mathematical models have been deduced to explain the self-mixing process more precisely [25]. A prominently accepted mathematical model is given as:
| (1) |
| (2) |
| (3) |
| (4) |
The model describes the SMI signal as a ratio of the emitted power to the free-running power that required to generate a wavelength of . The output of the model is a time-varying power ratio govern by the interference function . These equations also provide relationship among the different characteristical parameters such as (length of the external cavity), (free-running phase of the laser beam), (phase of the laser beam after feedback), (linewidth enhancement factor), C (Acket’s parameter or feedback level), and m (modulation index). Eqs. (1)–(4) are widely solved numerically to produce the synthetic SMI signals for the analysis of distance and vibration measurement schemes [26], [27].
The set of equations described above explains the self-mixing effect through the change in the effective-phase of the laser beam due to the optical events occurred in the optical path. Typically, the power variations are observed through the integrated photodiode of the laser package. The power variation can also be detected by measuring the voltage fluctuation across the laser terminal. The phase of the feedback signal is related to the threshold gain of the laser and any variation in the threshold gain is proportionally correlated to optical power as follows:
| (5) |
| (6) |
where denotes the coupling coefficient and typically depends on the reflectivity of the subject (r3) and the front facet of the laser (r2). While the modulation index prominently depends on the feedback level and the length of the external cavity. The feedback level defines the quality of the reflection and typically distributed into three categories: low feedback (C 1), moderate feedback (C 1), and high feedback (C 1). At a low feedback level, the laser is considered in a stable condition. In contrast, at the moderate level, the operation becomes conditionally stable, and at a higher level, the laser operations vary according to the strength of the feedback. Mathematically the Acket’s parameter is a dimensionless quantity and given as:
| (7) |
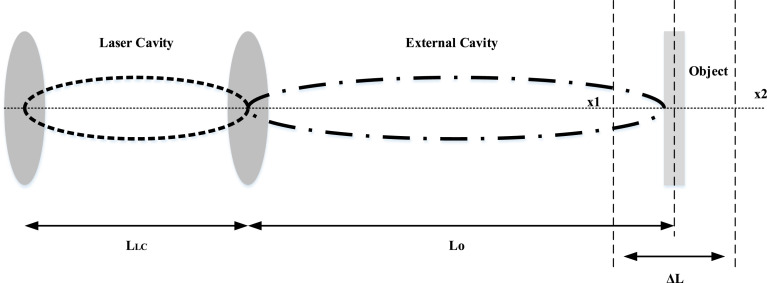
The vibrations in a subject can also be defined as a continuous physical variation in the effective distance between the subject and the point of observation. In context to the SMI, the point of the observation is the front facet of the laser diode, while the distance considers as the length of the external cavity, as illustrated in Fig. 2. Thus, the effective length of the external cavity is defined as:
| (8) |
where, denotes the equilibrium or nominal length of the external cavity; denotes the amplitude of the vibration and represents the frequency of the vibration. Therefore, systematic variations in the power ratio of the laser diode are observed, and the SMI signal produces.
Fig. 2.
Schematic of Self-mixing interferometry targeting a vibration subject placed at a distance of Lo and vibrating with an amplitude of L.
The mathematical & theoretical relationship discussed above concludes that the harmonic vibrations in the subject create a systematic variation in the SMI signal. As the variations in the SMI signal are systematic and govern by a mathematical model, the trend of the SMI signal can be demodulated to extract the vibration information as hypothesized. In the next section, a basic understanding of the MODWT is discussed with the required mathematical equations.
2.2. Maximal overlap discrete wavelet transformation
The MODWT is developed by Walden and Cristan [28] as an alternative to cosine packet transform, and the short-time Fourier transform to interpret the time-series signal. The MODWT perform linear filtering to transform a series of data into scaled coefficients. Similar to the DWT method, the MODWT decomposes the analyte signal into time-dependent data sets called wavelet and scaling coefficients.
The decomposition process involves circularly high-pass filtering to yield wavelet coefficients and low pass filtering to obtain scaling coefficients to a level j as follows:
| (9) |
| (10) |
where are the transfer function of the high pass filter and low pass filter, respectively that circularly filter the signal X= {X, t=0, 1… n-1}. Fig. 3 illustrates a MODWT operation perform on signal X to decompose the signal into three levels of detail and approximation. Here it is worth noting that the MODWT does not require the down-sampling as both the coefficients are of the same length ‘N’.
Fig. 3.
Illustration of three-level MODWT of signal X.
The obtained coefficients are further processed for signal characterization using a multi-resolution analysis (MRA). In the MRA, the multiscale correlation between the signals is estimated by convolving the dilated and translated wavelet with the signal. The multiscale variance process detects the patterns and provides in-depth signal characterization. Mathematical, MRA signal is represented with the help of two components called detail (D) and approximation (A) as follows:
| (11) |
| (12) |
| (13) |
Although both the DWT and MODWT perform basic similar linear filtering operations to generate a set of time-dependent wavelet and scaling coefficients. But MODWT has several merits in comparison to DWT, such as highly redundancy, non-orthogonal transform, and arbitrary signal length. The major demerit of the MODWT as compared to the DWT is its requirement of more computational power because the MODWT needs O(Nlog2N) multiplication compared to the O(N) multiplication to compute DWT. However, the required computational power is equal to the power required to execute the fast Fourier transformation (FFT) algorithm. Hence, compared to the FFT, the MODWT is preferable for an arbitrary length of the signal at a cost of the same computational power. A further detailed mathematical modeling and comparison are extensively reported in several works of literature [29], [30], [31], [32], [33], [34], [35] and discussing that is out of the scope of presented work.
3. Method
The theoretical analysis presented in the previous section concludes that the SMI waveform obtained from the vibrating subjects has four characteristics points i.e., P, J, V, and R. The locations of characteristics points are varied corresponding to the amplitude and frequency of the vibration. Therefore, vibration information can be estimated by extracting the trend of the SMI signal. In the proposed method the trend of the SMI signal is extracted using the wavelet transformation method. The wavelet transform is a widely used method for the trend analysis and successfully implemented in various fields such as environmental science, biomedical, and cybersecurity [36], [37], [38], [39]. Broadly the proposed method follows four basic steps. In the first step, the trend of the SMI signal obtained from the vibrating object is extracted using the MODWT method.
In the second step, a local signal is generated having the same frequency and amplitude as of the extracted trend signal. In the third step, a cross-correlation between the trend and the local signal is evaluated to determine the similarity index and phase difference between them. In the last step, a time scale shifting in the locally generated signal is performed based on the cross-correlation analysis. The time-shifted or reconstructed signal is a processed copy of the trend signal, hence contains the same characteristical nature as followed by the vibration signal as per the hypothesis. Fig. 4 illustrates the flowchart of the methodology. To validate the hypothesis/proposed method, self-mixing interferometry was designed. The arbitrary vibration signals were produced on a loudspeaker membrane through a signal generator. A total number of fifty different vibration signals were generated for validation purposes. The signal set includes sinusoidal and saw-tooth types waveforms having a different combination of frequencies and amplitudes. The details of the experimental setup and signal processing are discussed in the subsequent sections.
Fig. 4.
Flowchart of the proposed method.
3.1. Experimental setup
Fig. 5 illustrates the SMI design to obtain the signal generated by a vibrating subject. The vertical-cavity surface-emitting laser (OPV314) emitting a wavelength of 850 nm was used as a source while the integrated monitor photodiode was used as a detector. The laser beam was collimated using an aspheric lens with a focal length of 200 mm and a numerical aperture of 0.23. The laser beam impinges on a loudspeaker placed at an arbitrary location (), hence forming an external cavity. A rough paper sheet & retro-reflector tape was pasted on the central-membrane of the loudspeaker to produce a weak and moderate level of feedback. The loudspeaker was driven by a signal generator to generate the vibration of absolute amplitudes i.e. 50 mV peak to peak in the frequency range of 0 to 10 kHz. The laser diode was operated above the threshold condition at a constant voltage & current of 2.6 V and 26 mA, respectively. The monitor photodiode was connected to a customized trans-impedance amplifier (TIA). The TIA was designed using OPA857IRGTT to convert the photodiode current to an appropriate voltage level (peak to peak 3V). The output of the TIA was fed to a bandpass filter (BPF) having a lower and upper cutoff frequency of 8 Hz and 20 kHz, respectively for first-level electronic filtering. The filtered SMI signal was acquired using a data acquisition system (DAQ, Rigol-M300).
Fig. 5.
Schematic of the setup used to obtain the SMI signal.
3.2. Signal processing
The acquired signal was digitally preprocessed through Matlab to improve the quality of the signal. The preprocessing included smoothing of signal followed by noise removal steps such as median filtering and moving average filtering. The preprocessing step removes the common noise from the SMI signal and provides a smooth signal for further analysis. In the next step, the MODWT was performed on the preprocessed signal to an appropriate decomposition level. The evaluated coefficients were then analyzed using MRA. The post-processing involves the signal characterization, i.e., estimation of the amplitude and frequency of the decomposed signal using Z-transformation followed by the normalization process. A local signal was generated based on the post-processing result as a pure sinusoid. In the next step, a cross-correlation was performed between the decomposed signal and the locally generated signal. The cross-correlation process evaluates the similarity index between the decomposed & locally generates signals. Lastly, by analyzing the decomposed or reconstructed signal (locally generated), the vibration information such as frequency and amplitude were evaluated. Except for the measurement, a statistical operation was also performed to evaluate the relative and mean squared error.
4. Results & discussions
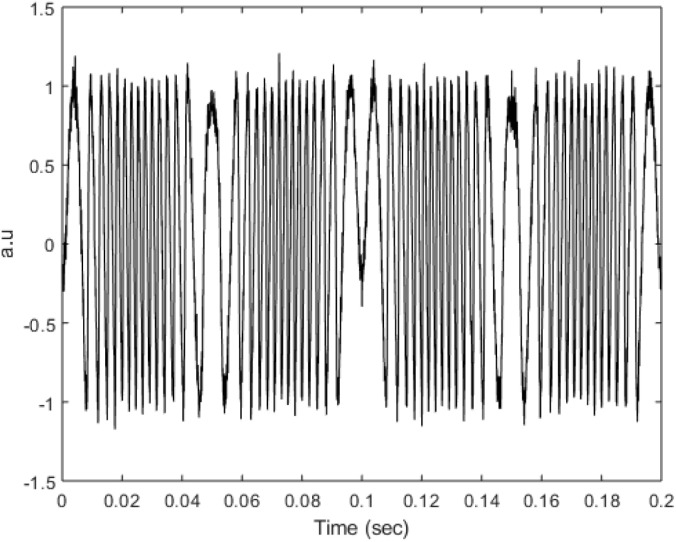
Fig. 6 illustrates the normalized SMI signal and corresponding harmonically vibration of 100 Hz frequency with a peak to peak amplitude of 2.. The SMI signal is plotted in continuous line; while the dashed-dot line represents the vibration signal. The SMI signal was obtained at moderate feedback conditions from a distance of 10 cm. The lines xa1 and xa2 marked the minimum and maximum amplitude of the vibration signal. The graph depicts more details about the nature of the vibration. For example, (a) The spikes patterns in the waveform indicates the transition of the subject between two extreme points, i.e., xa1 and xa2. (b) The lower positioned fringes (between zero axes and xa1) represents the movement of the subject away from the interferometry. (c) The upper positioned fringes (between xa1 and xa2) specify the motion of the subject towards the interferometry. The variation in the SMI signal shows that the interference patterns replicate the trend of the vibration signal. The vibration information can be demodulated by trend-characterization of the SMI signal.
Fig. 6.
Illustration of the normalized graph plotted to indicate the harmonic-vibration signal (dashed dot line) and the corresponding SMI signal (continuous line).
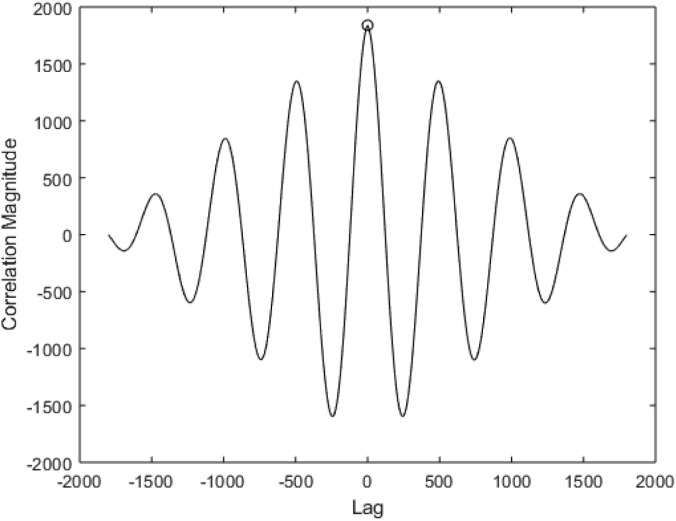
The extraction of the vibration information from the SMI signal was performed through the step by step process as per the flowchart illustrated in Fig. 4 using Matlab. In the first step, an SMI setup was employed to obtain the signal, as discussed in the previous section and illustrated in Fig. 5. In the next step, median and moving average filtering were performed on the experimentally obtained SMI signal to obtain a smooth signal. Fig. 7 shows a pre-processed SMI signal obtained at a distance of 20 cm from a source vibrating at a 10 Hz frequency with a peak to peak amplitude of . The pre-processed signal was decomposed to n levels using MODWT. The MODWT operation was performed using Symlet wavelets with four vanishing moments. The output of this step is an MRA of the transformation matrix. Fig. 8 shows the MRA of the nine levels MODWT based on the sym4 wavelet. For ease of representation, only odd levels of decomposition i.e. j 3, 5, 7 & 9 are represented in the figure. The parameters of the resultant signal were evaluated in the fourth step to generate a local vibration signal. The evaluation process includes the measurement of frequency, amplitude, and phase of the decomposed signal. The locally generated signal has the same peak to peak amplitude and the frequency as of the decomposed signal. In the proceeded step, a cross-correlation between the locally generated signal and the vibration signal was evaluated. The cross-correlation examines the similarity between the two signals and provides information about the time-shift between the two signals. Fig. 9 shows the result of the cross-correlation between the locally generated signal and the decomposed signal. Based on the cross-correlation, the locally generated signal was shifted to produce a local signal having the same phase as of the decomposed signal.
Fig. 7.
SMI signal obtained at a distance of 20 cm from a source vibrating at a 10 Hz frequency with a peak to peak amplitude of .
Fig. 8.
Different levels of SMI signal decomposition.
Fig. 9.
Cross-correlation between the locally generated signal and the decomposed signal.
The comprehensive study concludes that the phase-shift between the decomposed signal and the locally generated signal is equal to the feedback phase () of the SMI. Therefore, as per Eq. (2), under the weak-feedback conditions [40] the feedback phase is equal to the resonant phase, i.e., ), hence the length of the external cavity is given as [10]:
| (14) |
The length of the external cavity evaluated from the feedback phase is a combination of the nominal distance () and the vibration amplitude (), as defined in Eq. (8). Thus, based on the knowledge of the feedback phase and the nominal distance (equilibrium length of the external cavity), the vibration amplitude is estimated. While the frequency of the decomposed signal or locally generated signal is the frequency of the vibration. Fig. 10 illustrates the original vibration signal with a continuous line and the reconstructed signal with the dashed line. The error signal between the two signals is also depicted in a dashed-dot line. A relative error of 4.4% and the mean-squared error of 1.910−3 was recorded for the above-discussed scenario.
Fig. 10.
Representation of vibration signal (continuous line), reconstructed signal (dashed line), and the error signal (dashed-dot line).
The more detailed experimental study was performed on the fifty different combinations of frequency and amplitude. The study concludes that the method can reconstruct the vibration signals up to 1 kHz frequency with a maximum amplitude of under the weak feedback conditions. The mean squared, and the relative errors did not exceed beyond 1.8910& 8.79%, respectively. However, above 1 kHz vibration frequency, a sudden jump in the relative error is recorded, and the method becomes ineffective to reconstruct the vibration signal due to the ambiguity in amplitude measurement. However, the vibration frequency can be recorded with an accuracy of 0.0001 up to 10 kHz. For non-sinusoidal vibrations such as saw-tooth, the method is not able to reconstruct the vibration signal even for the low-frequency range. But still, the frequency of vibration is measured with an accuracy of 0.12 up to 1 kHz. In the case of a moderate feedback condition, the method again becomes futile to reconstruct the vibration signal even for the low-frequency range. The reason for futility is the mismatch in the feedback and the resonant phase, which negates Eq. (14). Even in this instance, the frequency of vibration is measured with high precision.
The study also concludes that the decomposition level needs to be supervised based on the SNR/ shape of the decomposed signal and should be processed for more than three cycles of the SMI signals. The inherent advantage of the method is that it does not require a complex filtering process for de-noising as the wavelet transform inherently filters the signal. The second significant advantage of the proposed method is logged for the peak deteriorated SMI signals. It is often observed that the peaks of the SMI signal are distorted during the electronic translation such as the conversion of current to voltage. In such a case, the proposed method remains intact during the measurement of vibration frequency with reasonable accuracy due to the use of trend analysis approach. The third advantage of the method is reported in the structural domain. The optical arrangement does not require any external components such as beam-splitter or EOM in the optical path due to efficiently processing of the integrated monitor photo-diode signal by the proposed method. Thus, the method does not increase the structural complexity and cost of the setup. The fourth advantage of the proposed method is the requirement of moderate computational power. As discussed in the earlier section, the MODWT requires the same computational power i.e. O(Nlog2N) as consumed by the FFT. Thus, during the execution of the algorithm, there is no need for extraordinary computational power. The last noticeable advantage of the algorithm is that it does not have a constraint in terms of signal length and applies to any arbitrary length of the signal compared to the equivalent FFT algorithm.
Conclusion
In this paper, a compact and low-cost vibration measurementscheme is proposed to extract vibration information from the SM signal. After analyzing the complexity of existing SM based vibration measurement methods, a dire need was felt to develop a simple and convenient method with significant accuracy. The paper presents the analysis of the self-mixing interferometric (SMI) signal using maximal overlap discrete wavelet transformation (MODWT). The proposed method has the ability to reconstruct the signal of harmonic vibration efficiently with the mean squared error of 1.8910 and the maximum relative error of 8.79%. The uniqueness of the method is that it does not require any additional optical components, like photodiode, beam-splitters, and EOM for measurement, making it more compact, handy and ready to use in remote locations as well as in biomedical applications. The proposed technique proves its efficiency in vibration frequency measurement in various conditions even when the peak of the SMI signal was deteriorated, or subject is vibrating at a higher frequency, i.e., greater than 1 kHz. One of the possible applications of the proposed method can be found in the lung abnormality diagnosis through the local chest vibration measurement method. Typically, the multipath-scattering from the skin and respiratory maneuvers of the sensors produces the artifacts, which overshadow the desired information in the conventional measurement methods. However, the inherent filtering of wavelet transformation and the trend extraction technique used in the proposed method suppresses the undesired artifacts and produce a smooth output signal. Therefore, the authors envision that the technique can be useful for the measurement of chest vibrations into a non-contact chest vibration measurement. The non-contact procedure of measurement will also provide a safe and hygiene mode of diagnosis under COVID-19 scenario. Similarly, it will be useful in measuring the mechanical vibrations of machines, providing a non-contact and compact source of information to foresee the performance of a particular machine/plant The major limitations of the proposed method are that it needs a supervision to decide the level of decomposition and for the reconstruction of the vibration signal the feedback phase must be equal to the resonant phase, i.e., . Hence, these limitations are considered as a motivating challenge for future research.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Dyer D., Stewart R.M. Detection of rolling element bearing damage by statistical vibration analysis. Amer. Soc. Mech. Eng. 1977;100(77-DET-83):229–235. [Google Scholar]
- 2.Mohsenifar Z., Rosenberg N., Goldberg H.S., Koerner S.K. Mechanical vibration and conventional chest physiotherapy in outpatients with stable chronic obstructive lung disease. Chest. 1985;87(4):483–485. doi: 10.1378/chest.87.4.483. [DOI] [PubMed] [Google Scholar]
- 3.Binks A.P., Bloch-Salisbury E., Banzett R.B., Schwartzstein R.M. Oscillation of the lung by chest-wall vibration. Respir. Physiol. 2001;126(3):245–249. doi: 10.1016/S0034-5687(01)00223-7. [DOI] [PubMed] [Google Scholar]
- 4.Milesi I., Norgia M., Pompilio P.P., Svelto C., Dellaca R.L. Measurement of local chest wall displacement by a custom self-mixing laser interferometer. IEEE Trans. Instrum. Meas. 2011;60(8):2894–2901. doi: 10.1109/TIM.2011.2118830. [DOI] [Google Scholar]
- 5.Sun Q., Liu D., Wang J., Liu H. Distributed fiber-optic vibration sensor using a ring Mach–Zehnder interferometer. Opt. Commun. 2008;281(6):1538–1544. doi: 10.1016/j.optcom.2007.11.055. [DOI] [Google Scholar]
- 6.Drake A.D., Leiner D.C. Fiber-optic interferometer for remote subangstrom vibration measurement. Rev. Sci. Instrum. 1984;55(2):162–165. doi: 10.1063/1.1137721. [DOI] [Google Scholar]
- 7.Willemin J.F., Khanna S.M., Dandliker R. Heterodyne interferometer for cellular vibration measurement. Acta Otolaryngol. 1989;108(s467):35–42. doi: 10.3109/00016488909138319. [DOI] [PubMed] [Google Scholar]
- 8.Wang W.-C., Hwang C.-H., Lin S.-Y. Vibration measurement by the time-averaged electronic speckle pattern interferometry methods. Appl. Opt. 1996;35(22):4502. doi: 10.1364/ao.35.004502. [DOI] [PubMed] [Google Scholar]
- 9.Huang Y., Du Z., Deng J., Cai X., Yu B., Lu L. A study of vibration system characteristics based on laser self-mixing interference effect. J. Appl. Phys. 2012;112(2) doi: 10.1063/1.4739293. [DOI] [Google Scholar]
- 10.Zhang Z., Li C., Huang Z. Vibration measurement based on multiple Hilbert transform for self-mixing interferometry. Opt. Commun. 2019;436(2018):192–196. doi: 10.1016/j.optcom.2018.12.032. [DOI] [Google Scholar]
- 11.Kane D.M., Shore K.A. Wiley; 2005. Unlocking Dynamical Diversity: Optical Feedback Effects on Semiconductor Lasers. [Google Scholar]
- 12.Usman M., Zabit U., Bernal O.D., Raja G., Bosch T. Detection of multimodal fringes for self-mixing-based vibration measurement. IEEE Trans. Instrum. Meas. 2019:1–10. doi: 10.1109/tim.2019.2895928. [DOI] [Google Scholar]
- 13.Tao Y., Wang M., Xia W. Semiconductor laser self-mixing micro-vibration measuring technology based on Hilbert transform. Opt. Commun. 2016;368:12–19. doi: 10.1016/j.optcom.2015.12.061. [DOI] [Google Scholar]
- 14.Zhu W., Chen Q., Wang Y., Luo H., Wu H., Ma B. Improvement on vibration measurement performance of laser self-mixing interference by using a pre-feedback mirror. Opt. Lasers Eng. 2018;105(2017):150–158. doi: 10.1016/j.optlaseng.2018.01.022. [DOI] [Google Scholar]
- 15.Magnani A., Melchionni D., Pesatori A., Norgia M. Self-mixing digital closed-loop vibrometer for high accuracy vibration measurements. Opt. Commun. 2016;365:133–139. doi: 10.1016/j.optcom.2015.12.002. [DOI] [Google Scholar]
- 16.Jha A., Azcona F.J., Yañez C., Royo S. Extraction of vibration parameters from optical feedback interferometry signals using wavelets. Appl. Opt. 2015;54(34):10106. doi: 10.1364/ao.54.010106. [DOI] [PubMed] [Google Scholar]
- 17.Bernal O.D., Zabit U., Bosch T. Study of laser feedback phase under self-mixing leading to improved phase unwrapping for vibration sensing. IEEE Sens. J. 2013;13(12):4962–4971. doi: 10.1109/JSEN.2013.2276106. [DOI] [Google Scholar]
- 18.Bhardwaj V.K., Maini S. Estimation of absolute distance and high-frequency vibration from the modulated SM-OFI signal using compound mutated genetic algorithm. Opt. Lasers Eng. 2020;134 [Google Scholar]
- 19.Li D., Huang Z., Mo W., Ling Y., Zhang Z., Huang Z. Equivalent wavelength self-mixing interference vibration measurements based on envelope extraction fourier transform algorithm. Appl. Opt. 2017;56(31):8584. doi: 10.1364/ao.56.008584. [DOI] [PubMed] [Google Scholar]
- 20.Zhang Z., Jiang C., Shen L., Li C., Huang Z. Vibration measurement based on the local maximum detection algorithm for laser self-mixing interferometry. IEEE Access. 2020;8:63462–63469. doi: 10.1109/ACCESS.2020.2984282. [DOI] [Google Scholar]
- 21.Guo D. Quadrature demodulation technique for self-mixing interferometry displacement sensor. Opt. Commun. 2011;284(24):5766–5769. doi: 10.1016/j.optcom.2011.08.027. [DOI] [Google Scholar]
- 22.Fan Y., Yu Y., Xi J., Chicharo J.F. Improving the measurement performance for a self-mixing interferometry-based displacement sensing system. Appl. Opt. 2011;50(26):5064. doi: 10.1364/AO.50.005064. [DOI] [PubMed] [Google Scholar]
- 23.Lang R., Kobayashi K. External optical feedback effects on semiconductor injection laser properties. IEEE J. Quantum Electron. 1980;16(3):347–355. doi: 10.1109/JQE.1980.1070479. [DOI] [Google Scholar]
- 24.Schunk N., Petermann K. Numerical analysis of the feedback regimes for a singlemode semiconductor laser with external feedback. IEEE J. Quantum Electron. 1988;24(7):1242–1247. doi: 10.1109/3.960. [DOI] [Google Scholar]
- 25.Taimre T., Nikolić M., Bertling K., Lim Y.L., Bosch T., Rakić A.D. Laser feedback interferometry: a tutorial on the self-mixing effect for coherent sensing. Adv. Opt. Photonics. 2015;7(3):570. doi: 10.1364/AOP.7.000570. [DOI] [Google Scholar]
- 26.Kliese R. Solving self-mixing equations for arbitrary feedback levels: a concise algorithm. Appl. Opt. 2014;53(17):3723. doi: 10.1364/AO.53.003723. [DOI] [PubMed] [Google Scholar]
- 27.Ramírez-Miquet E.E. Optical feedback interferometry: From basics to applications of laser flowmetry. Rev. Cuba. Fis. 2017;34(1):48–57. [Google Scholar]
- 28.Walden A.T., Cristan A.C. The phase–corrected undecimated discrete wavelet packet transform and its application to interpreting the timing of events. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998;454(1976):2243–2266. doi: 10.1098/rspa.1998.0257. [DOI] [Google Scholar]
- 29.Cornish C.R., Bretherton C.S., Percival D.B. Maximal overlap wavelet statistical analysis with application to atmospheric turbulence. Boundary-Layer Meteorol. 2006;119(2):339–374. doi: 10.1007/s10546-005-9011-y. [DOI] [Google Scholar]
- 30.Percival D.B., Walden A.T. Wavelet Methods for Time SeriesAnalysis, no. May. Cambridge University Press; Cambridge: 2017. The maximal overlap discrete wavelettransform; pp. 159–205. [Google Scholar]
- 31.Percival D.B. Analysis of geophysical time series using discrete wavelet transforms: An overview. Lect. Notes Earth Sci. 2008;112:61–79. doi: 10.1007/978-3-540-78938-3_4. [DOI] [Google Scholar]
- 32.Walden A.T. European Congress of Mathematics. Birkhäuser Basel; Basel: 2001. Wavelet analysis of discrete time series; pp. 627–641. [Google Scholar]
- 33.Vetterli M., Herley C. Wavelets and filter banks: theory and design. IEEE Trans. Signal Process. 1992;40(9):2207–2232. doi: 10.1109/78.157221. [DOI] [Google Scholar]
- 34.Seo Y., Choi Y., Choi J. River stage modeling by combining maximal overlap discrete wavelet transform, support vector machines and genetic algorithm. Water (Switzerland) 2017;9(7) doi: 10.3390/w9070525. [DOI] [Google Scholar]
- 35.Percival D.B., Walden A.T. Cambridge University Press; Cambridge: 2000. Wavelet Methods for Time SeriesAnalysis. [Google Scholar]
- 36.Oh Y.Y., Yun S.T., Yu S., Kim H.J., Jun S.C. Characterization of environmental drivers controlling the baseline of soil surface co2 flux using wavelet-based multiresolution state-space model and wavelet denoising. Energy Procedia. 2018;154:157–162. doi: 10.1016/j.egypro.2018.11.026. [DOI] [Google Scholar]
- 37.Partal T., Küçük M. Long-term trend analysis using discrete wavelet components of annual precipitations measurements in Marmara region (Turkey) Phys. Chem. Earth. 2006;31(18):1189–1200. doi: 10.1016/j.pce.2006.04.043. [DOI] [Google Scholar]
- 38.Gurumoorthy S., Muppalaneni N.B., Chandra Sekhar G., Sandhya Kumari G. Springer, Vol. 1054. Springer Singapore; 2020. Implementation of signal processing algorithms on epileptic EEG signals; pp. 367–376. [Google Scholar]
- 39.He F., Zhang Y., Liu D., Dong Y., Liu C., Wu C. In: Mixed Wavelet-Based Neural Network Model for Cyber Security Situation Prediction using MODWT and Hurst Exponent Analysis, Vol. 10394. Yan Z., Molva R., Mazurczyk W., Kantola R., editors. Springer International Publishing; Cham: 2017. pp. 99–111. [Google Scholar]
- 40.Kane D., Shore A. John Wiley & Sons Ltd; Chichester: 2005. Unlocking Dynamical Diversity, Vol. 1. [Google Scholar]