Translation and Eccentric Rotation In Ocular Motor Modeling

Abstract

Current models of ocular mechanics do not fully account for potentially large globe translations associated with eye rotation. Such combined motion can be measured using magnetic resonance imaging in axial planes. We imaged orbits of normal volunteers fixating horizontally eccentric targets. These data indicate that the human eye acts as if it rotates eccentrically about a varying point typically anterior to the geometric globe center, but significantly lateral in abduction and medial in adduction. Assumed eccentricity of the ocular rotational center would vary the torque lever arms for the horizontal rectus muscles, with an appreciably smaller relative lever arm for the medial rectus muscle in adduction than would be the case for oculocentric rotation. Such variation in ocular rotational center might alter muscle torque without commensurate change in muscle tension, as appears to happen in convergence.

In 1975, David A. Robinson published a computational model of the rotational mechanics of an eye that predicted eye orientation for a given set of extraocular muscle (EOM) innervations (Robinson, 1975). The algorithm worked by finding the eye orientation for which passive and active torques on the globe are balanced. Muscle torques were determined by multiplying, for each EOM, its tension by its unit axis of action (m), which depended on the EOM’s origin, its effective insertion, and the ocular rotational center. All forces were assumed to act on the surface of a rigid, spherical globe, so the common moment arm for EOM torques could be neglected. Possible ocular translation was also neglected.

Joel M. Miller collaborated with Robinson to publish in 1984 an improved model of ocular statics (Miller and Robinson, 1984). This extended model was binocular and, among its numerous enhanced features, incorporated the possibility of globe translation. At the time, there was a paucity of data available on globe translation during ocular rotation, so the model included a stiffness term for orbital fat of 27 gm/mm anteroposteriorly along the orbital axis and twice this value for superior and lateral translations (Miller and Robinson, 1984). Miller and Robinson noted that “Translation also alters the position of the globe relative to the muscle origins and, so, alters the axes of rotation m.” The authors went on to simulate the errors they believed would result from ignoring translation in a normal eye and reported these errors to be so small as to be virtually invisible in their Fig. 7. Through the commercial entity Eidactics, Miller and other collaborators continued to improve the computational simulation as a program ultimately known as Orbit 1.8 (Miller et al., 1999). Orbit 1.8 also includes passive connective tissue pulleys for the EOMs (Miller, 2007) and, to date, remains the most comprehensive model of binocular mechanics.

Since the development of the foregoing models, advances in the imaging of the ocular motor plant have revealed that it harbors additional complexities. For example, each EOM contains an orbital layer that is not directly oculorotary, but instead inserts on the connective tissue of the pulley system to control the unit vector m of one or more EOMs (Demer et al., 2000, Demer, 2004). The oculorotary parts of each EOM are also generally compartmentalized into separately-controlled regions that can contract differently during some physiological (da Silva Costa et al., 2011, Demer, 2014, Le et al., 2015, Demer and Clark, 2014) and occasionally pathological situations (Suh et al., 2016, Clark and Demer, 2014). Finally, the pulley system contains substantial deposits of smooth muscle (Kono et al., 2002, Demer et al., 1997), particularly in the inferomedial region between the inferior and medial rectus (MR) pulleys extending towards the superior rectus pulley (Miller et al., 2003).

Magnetic resonance imaging (MRI) has been particularly valuable in uncovering new aspects of ocular motor behavior. In particular, we have used MRI to document globe translation during horizontal eye rotation. For example, Fig. 1 superimposes, at partial opacity, axial MRI of a normal subject fixating in right gaze with the same image plane in left gaze. The large gaze shift can be appreciated by the shift in positions of the cornea and lens of each eye. Most striking, however, is the shift of each eye’s sclera, temporally in abduction and nasally in adduction, indicating that the globes did not rotate about their centers., which are marked in the two gaze positions by crosses.

Fig. 1.

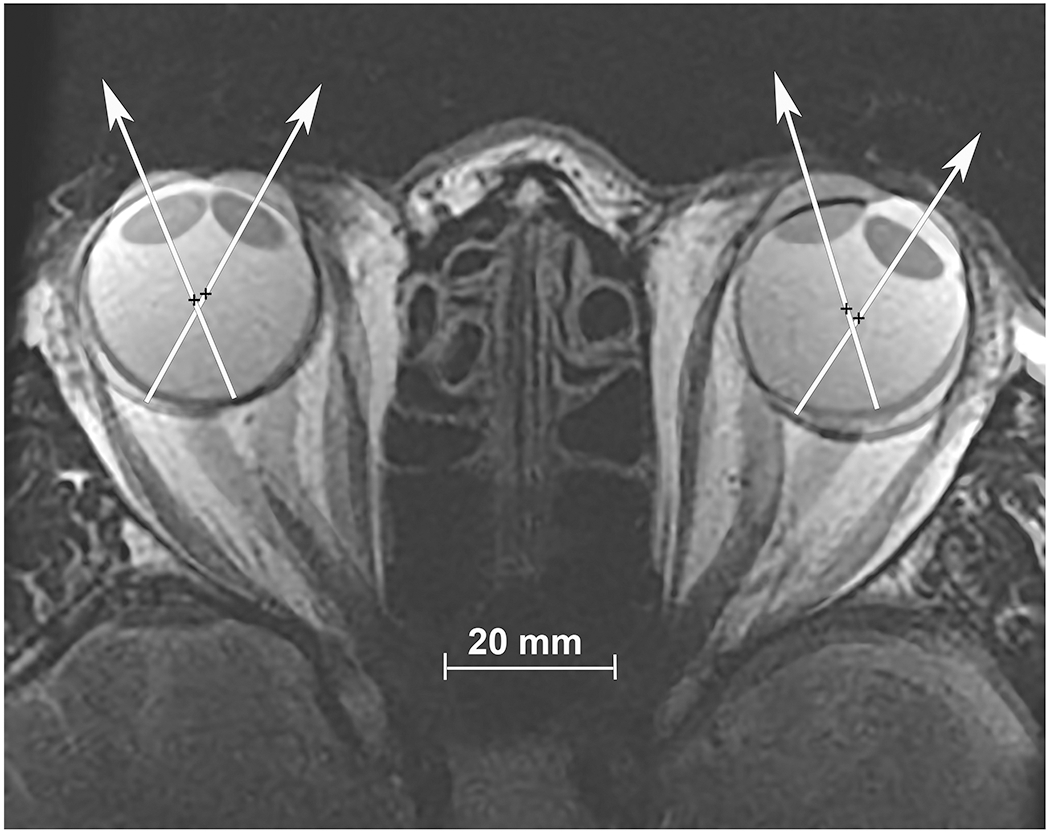
Axial, T2-weighted MRI obtained using surface coils in a normal subject fixating in right gaze, and superimposed at partial opacity on the image separately obtained in left gaze. Visual axes are depicted by superimposed white arrows, and rotational center by black crosses. Note the globe translation during this large horizontal rotation of each eye.

The foregoing globe translation can also be determined from contiguous sets of quasi-coronal image planes perpendicular to the long axis of the orbit. Horizontal and vertical components of the translation are directly measurable at subpixel resolution from shifts of the area centroids of the globe’s cross sections in contiguous image planes spaced across the globe’s diameter. Anteroposterior globe shifts in the orbit can also be determined because of the locally linear variation in the cross-sectional area of the bony orbit. While we have earlier measured horizontal and vertical ocular rotations based upon shifts in the coronal plane location of the globe-optic nerve junction, such analysis assumes globe rotation about its geometric center, an assumption we now recognize to be seriously erroneous at times. Therefore, while globe translations reported below were determined from quasi-coronal MRI, the horizontal duction angles were determined from axial images such as in Fig. 1 while subjects fixated the same targets.

Figure 2 illustrates with the dark black triangles the globe translation observed in 38 orbits of 19 normal adult volunteers as they monocularly fixated the ends of fine optical fibers that served as afocal, illuminated targets placed at approximately 29±1° ab- and 34±1° adduction. Imaging was performed using T2-weighted MRI in 2 mm thick planes at 312 m pixel resolution, as published elsewhere (Demer and Dusyanth, 2011). Also plotted in Fig. 2 are the lateral and anterior globe translations predicted by Orbit 1.8. Measured posterior translation of 0.4 mm in abduction is not significantly different from the 0.1 mm predicted value of Orbit 1.8, but the 0.14 mm anterior translation in adduction does differ significantly from the Orbit prediction of 0.2 mm posterior shift (P<0.05, Fig. 2). The globe centroid shifted an average of about 0.77 mm laterally in abduction, much more than the 0.1 mm predicted by Orbit 1.8 (P<10⁻⁶). The small medial globe translation in adduction did not differ significantly from the Orbit 1.8 prediction.

Fig. 2.

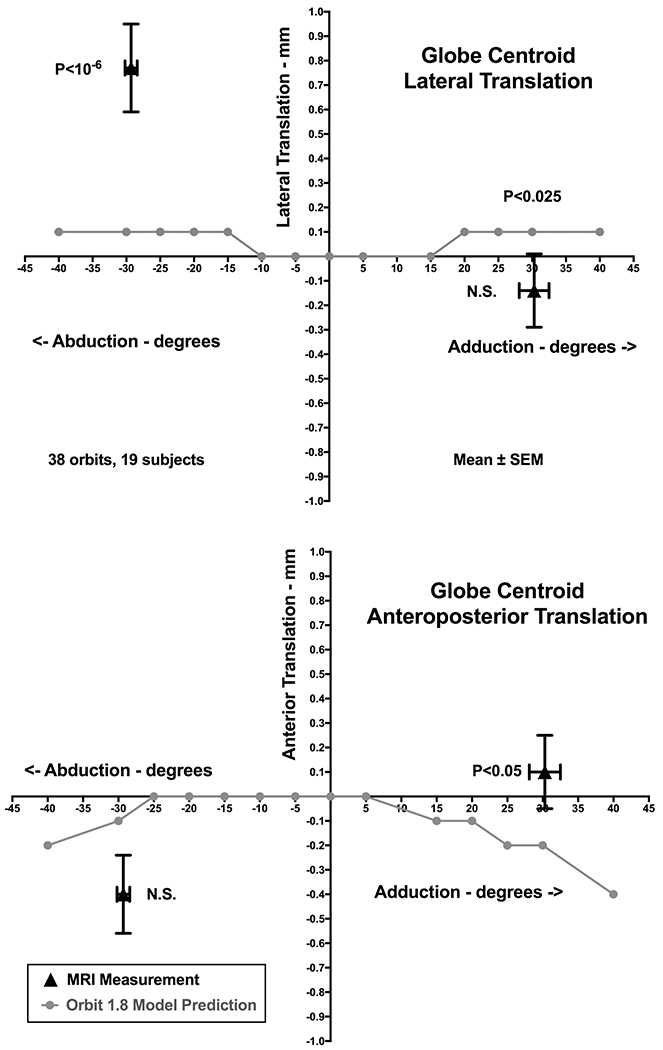
Globe translation during large horizontal eye rotations in 38 orbits of 19 normal adult volunteers. The globe translates an average of 0.77 mm laterally in abduction but 0.14 mm medially in adduction. Lateral translation in abduction was much more than the predicted in gray symbols by the Orbit 1.8 model, but translation in adduction was not significantly different. Globe retraction of about 0.4 mm in abduction was not significantly greater than predicted by Orbit 1.8, but the 0.14 mm mean anterior translation in adduction was significantly greater than the Orbit 1.8 prediction. SEM -standard error of the mean.

The centroid of a rigid body rotating about a fixed eccentric point must translate as it rotates, and we consider initially how this could be applied to the eye. Linear algebra permits computation of the location of the fixed eccentric rotation axis of a rigid body. For any point (x,y) on a rigid body rotating in a plane about an axis point $\left(\genfrac{}{}{0pt}{}{x_c}{y_c}\right)$, it is possible to find the coordinates of $\left(\genfrac{}{}{0pt}{}{x_c}{y_c}\right)$ following a rotation through known angle α given the initial $\left(\genfrac{}{}{0pt}{}{x_1}{y_1}\right)$ and final $\left(\genfrac{}{}{0pt}{}{x_2}{y_2}\right)$ coordinates of the point.

$$\left(\begin{array}{c}{x}_c\\ y_c\end{array}\right)=\frac{1}{2(1-\cos (\alpha ))}\left[\begin{array}{cc}\cos (\alpha )-1& \sin (\alpha )\\ -\sin (\alpha )& \cos (\alpha )-1\end{array}\right]\left(\left[\begin{array}{cc}\cos (\alpha )& -\sin (\alpha )\\ \sin (\alpha )& \cos (\alpha )\end{array}\right]\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right)-\left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)\right)$$ Eq. 1

Expanding and simplifying:

$$x_c=\frac{(x_1+x_2+\sin (\alpha )(y_1-y_2)-\cos (\alpha )(x_1+x_2))}{2(1-\cos (\alpha ))}$$ Eq. 2

$$y_c=\frac{(y_1+y_2+\sin (\alpha )(x_2-x_1)-\cos (\alpha )(y_1+y_2))}{2(1-\cos (\alpha ))}$$ Eq. 3

If we have the coordinates of any other point on the rigid body that moves during rotation from initial $\left(\genfrac{}{}{0pt}{}{x_3}{y_3}\right)$ to final $\left(\genfrac{}{}{0pt}{}{x_4}{y_4}\right)$, angle α can be obtained from:

$$\cos (\alpha )=\frac{(x_3+x_1)(x_4+x_2)+(y_3-y_1)(y_4-y_2)}{\sqrt{[{(x_3+x_1)}^2+{(y_3-y_1)}^2][{(x_4+x_2)}^2+{(y_4-y_2)}^2]}}$$ Eq. 4

$$\sin (\alpha )=\frac{(x_3+x_1)(y_4-y_2)-(y_3-y_1)(x_4-x_2)}{\sqrt{[{(x_3+x_1)}^2+{(y_3-y_1)}^2][{(x_4+x_2)}^2+{(y_4-y_2)}^2]}}$$ Eq. 5

We apply this approach to MRI by computing (x_c, y_c) from two different points readily identifiable from axial images: the lens centroid and the center of the optic nerve head. Of course, the MRI planes must first be translated and rotated as necessary until bony cranial landmarks such as the orbital walls are in exact correspondence before computing coordinates. This approach also assumes that the globe is indeed rigid, so that the relationship between the lens and optic nerve remains geometrically constant. Furthermore, the globe is assumed not to translate or rotate perpendicular to the axial imaging plane, which would alter the apparent distances between the lens centroid and optic nerve center. In practice, the registration of digital images can be challenging and the measurements are subject to resolution uncertainty of the image both before and after rotations. Calculated rotational centers are therefore most reliable for larger ocular rotations.

We computed the ocular rotational centers using the foregoing methods in 38 orbits of 19 normal subjects monocularly fixating targets in ab- and ad-duction from central starting gaze. The rotational center was analyzed in an orbitally-fixed coordinate system that corresponded at the initiation of the eye movement to the ocular centroid, but of course did not remain at the ocular center during eccentric rotation. It is evident from the data in Fig. 3 that the ocular rotational center was eccentric relative to the geometric globe center. For both ab- and adduction, mean rotational center was located more than 1 mm anterior to the globe centroid. As may be seen from Fig. 3, however, the computed horizontal center is about 1.0 mm lateral in abduction, and about 0.8 mm medial in adduction. Both these eccentricities differ significantly from zero (P<0.02). The observation that the computed rotational center differs with the direction of rotation complicates the analysis because the rotational axis is not fixed in position relative to the orbit. Further consideration of this concept therefore makes the hazardous assumption that the rotational center remains constant at least for the same direction of rotation, ab- or adduction.

Fig. 3.

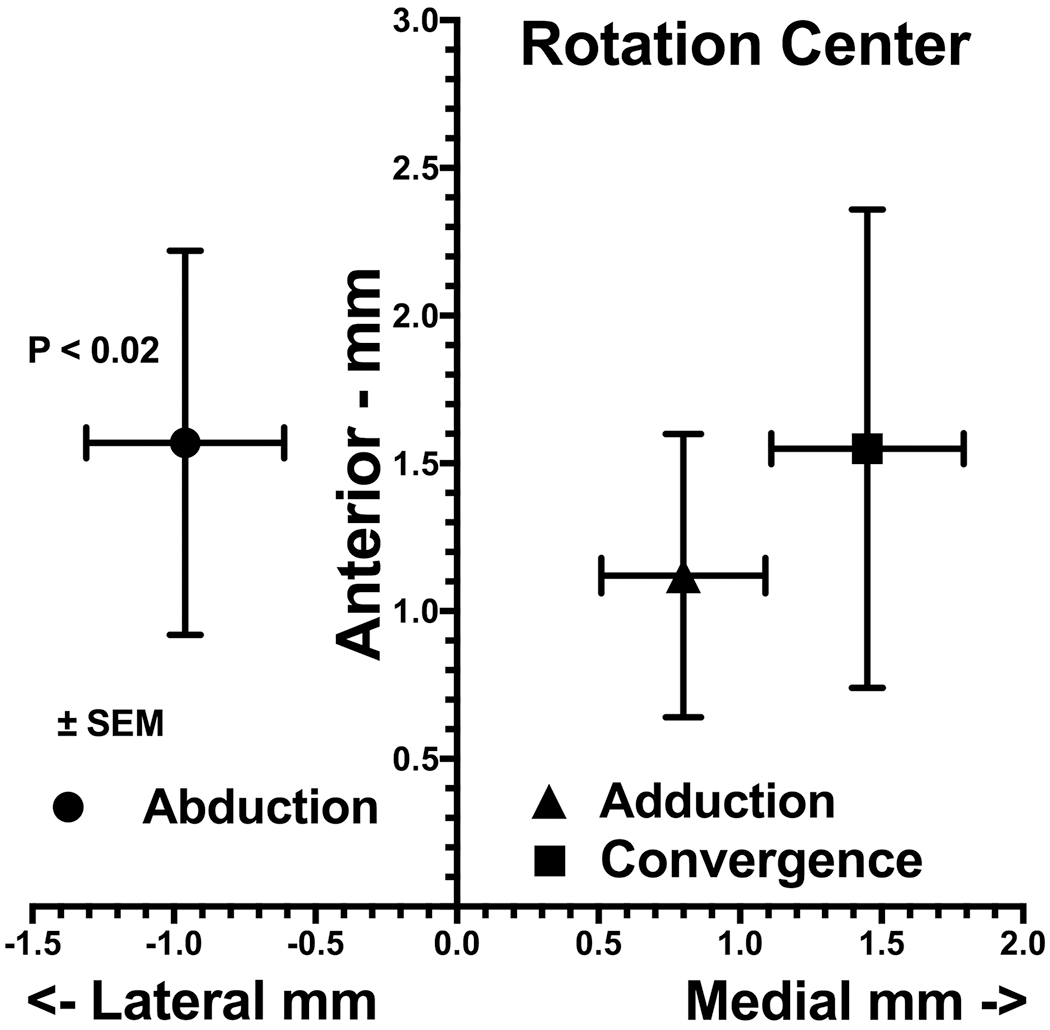
Mean ocular rotational center of 38 orbits of 19 normal subjects monocularly fixating targets in 29° ab- and 34° adduction, and 8 orbits of 7 subjects in 21° convergence. The horizontal center was significantly lateral to globe center in abduction but significantly medial in adduction (P < 0.02, 2-tail t-test), while its significantly (P < 0.02) anterior location did not vary appreciably with rotation direction. The rotation center in convergence was farther medial than in adduction.

In a different group of 8 orbits of 7 normal subjects, we performed MRI during asymmetrical convergence with the target aligned to one eye, as previously described (Demer and Clark, 2014, Demer et al., 2003). Because the adducting eye achieved 21° convergence, it was possible to determine its rotational center. While also about 1.5 mm anterior to globe center as for conjugate adduction, the rotational center for the eye during convergence was almost twice as far medial at 1.5 mm as it was during conjugate adduction. Because the globe only shifted by about 0.1 mm medially and 0.5 mm anteriorly to achieve this convergence angle, a change in globe position alone cannot account for the change in position of a fixed rotational center.

Assuming provisionally that the ocular rotational center remains fixed for each direction of eye rotation, we can compute the lever arms for the LR and MR in abduction, adduction, and convergence as the distances between the ocular rotational center and the positions of the muscle insertions , corrected for non-tangential force application at the insertions. As positions for the insertions we used normative averages, but verified that our results are insensitive to physiological deviations from those. Figure 4 illustrates the result of this analysis to the foregoing data set. While the LR lever arm was computed to be similar to the MR lever arm in abduction, the relative advantage shifted markedly in favor of the LR in adduction, where the approximately one-third shortening of the MR lever arm gives the LR a nearly 60% advantage. Although this comparison should be interpreted cautiously because it was measured in a different group of subjects, the data also suggest that the MR lever arm in convergence may be about a third greater than in adduction. Since the LR lever arm is similar in convergence and adduction, this implies that in convergence the LR would not need to relax as much it does in conjugate adduction. Another way to interpret the finding is that the LR would need to increase its tension by about 33% to balance maintained MR force to achieve the same eye position in convergence as in conjugate gaze. This phenomenon may provide a solution to the long-mysterious “convergence force paradox,” as stated by Miller et al. in 2011: “For a given eye position, firing rates of abducens neurons generally (Mays and Porter, 1984), and LR motoneurons in particular (Gamlin et al., 1989), are higher in converged gaze than when convergence is relaxed, whereas LR and MR muscle forces are slightly lower (Miller et al., 2002).” The present data suggest that higher LR motoneuron firing rate is required in convergence to maintain its torque to balance the increased MR torque arising from its increased lever arm. This balance might even occur with a slightly lower total of LR and MR forces, since MR tension could decrease modestly even as MR torque increased by virtue of its greater lever arm, thus explaining observed co-relaxation in the horizontal rectus muscles of the aligned eye during asymmetrical convergence (Miller et al., 2011).

Fig. 4.

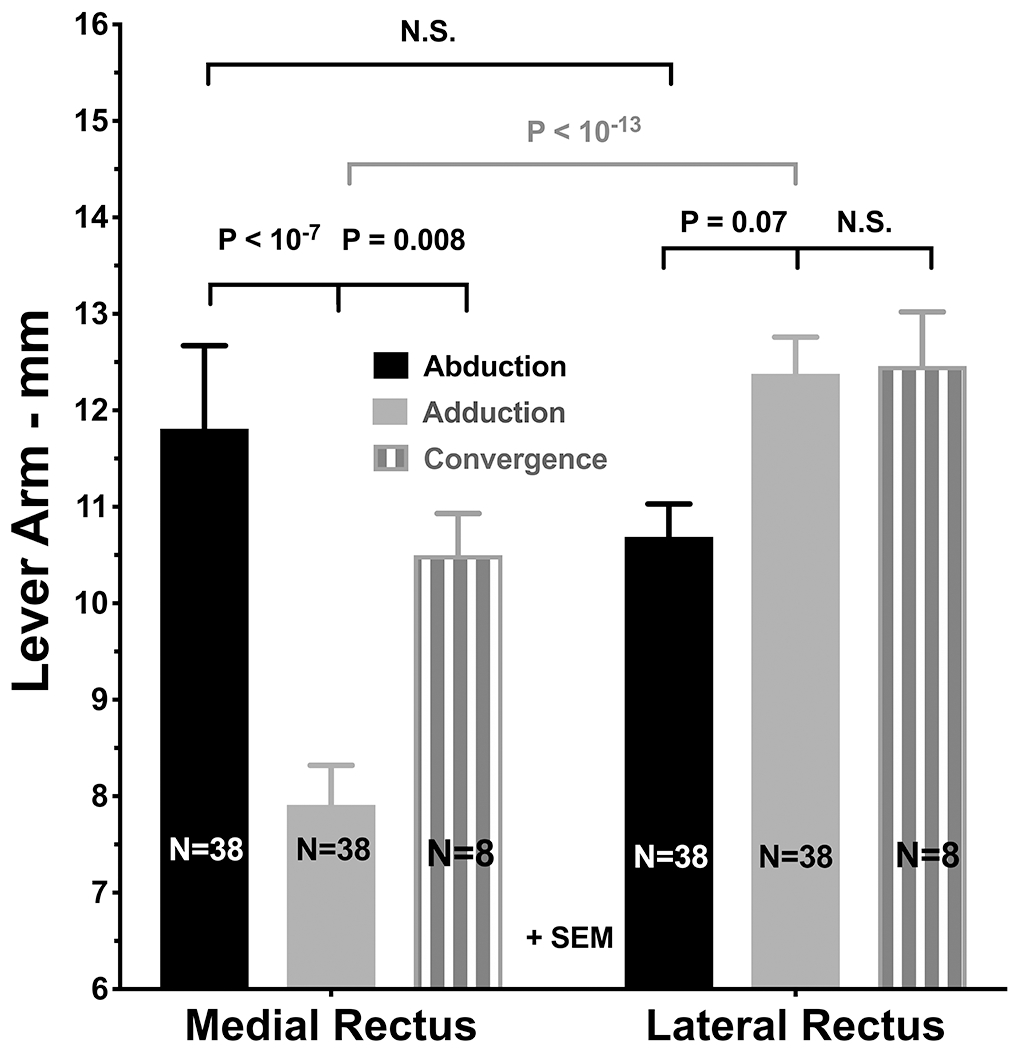
Mean lever arms of the medial (MR) and lateral rectus (LR) muscles of 38 orbits of 19 normal subjects monocularly fixating targets in 29° ab- and 34° adduction, and of 8 orbits of 7 subjects in 21° aligned convergence. Computations assume that the rotational center is constant for each direction of rotation, and that each muscle departs the globe at its scleral insertion. Note that the MR lever arm is much shorter than the LR lever arm in adduction, but increases by about 33% in convergence.

We have shown that translation of the normal eye in abduction is appreciably larger than predicted by the best currently available biomechanical model, Orbit 1.8. Anteroposterior translation is also modestly larger than predicted in adduction. It is clear from the observation of large globe translation during rotation that the eye does not rotate about its geometric center. Translation of a rigid body during rotation about a fixed center is mathematically equivalent to rotation about an eccentric point, enabling computation of the center using Eqns. 1 and 2. Even were it fixed, precise empirical determination of the ocular rotational axis by MRI would be technically challenging due to several practical factors. These include large artifacts of even small head translations and rotations, as well as possible local globe deformations that may occur during ocular rotation. A more significant empirical conundrum is that the computed ocular rotational center differs markedly when measured in large angle abduction from that measured in large angle adduction. While for both directions that rotational center is typically anterior to the globe’s geometric center (Fig. 3), it is likely that the horizontal location of the ocular rotational center varies continuously with the direction and probably the size of each horizontal eye movement. While this assumption could in theory be tested by imaging incremental ocular rotations, measurements of rotational center for small rotations tend to be unreliable because the effects are small relative to measurement errors.

A more complex model will be needed to predict these translations. This model must consider that ocular translation during horizontal eye rotation is anisotropic, being much larger laterally than anteroposteriorly in normal subjects. In part, this is likely to be due to globe tethering by the taut optic nerve when its length redundancy in exhausted in large angle adduction (Demer, 2016). Optical coherence tomographic imaging of the optic nerve head suggests that such tethering occurs at adduction angles exceeding 26° (Suh et al., 2017), considerably less than the adduction studied here. Anisotropic translation during rotation must also be related to properties of the orbital connective tissue system, including smooth muscle in the pulley suspensions. This leaves open the possibility that translational behavior might, to some extent, be subject to neural control during different types of eye movements. These structures and potential mechanisms will have to be incorporated in any model that aims to have predictive power, but orbital biomechanical properties will require further study to permit such modeling.