Subsurface Imaging of Cell Organelles by Force Microscopy

Abstract

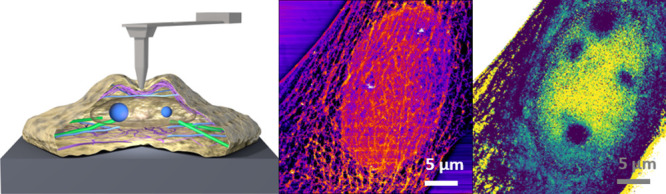
The development of high-resolution, label-free, noninvasive, and subsurface microscopy methods of living cells remains a formidable problem. Force-microscopy-based stiffness measurements contribute to our understanding of single-cell nanomechanics. The elastic properties of the cell’s outer structures, such as the plasma membrane and actin cytoskeleton, dominate stiffness measurements, which in turns prevents the imaging of intracellular structures. We propose that the above limitation could be overcome by combining 2D sections of the cell’s viscoelastic properties. We show the simultaneous imaging of the outer cell’s cytoskeleton and the organelles inside the nucleus. The elastic component of interaction force carries information on the cell’s outer elements as the cortex and the actin cytoskeleton. The inelastic component is sensitive to the hydrodynamic drag of the inner structures such the nucleoli.

Atomic force microscopy (AFM) generates images and stiffness maps of cells in near physiological conditions.¹⁻³ Stiffness measurements have dominated AFM experiments performed on cells for two main reasons. First, the stiffness is a useful mechanical marker to track the physiology of a single cell.⁴⁻⁶ Second, the existence of well-established contact mechanical models provide analytical relationships between the force and the elastic parameters.⁷⁻¹⁰ Stiffness maps deduced from force–distance curves (FDC) provide a direct measurement of the elastic response of the actin cytoskeleton components which lie within 500 nm from the cell’s plasma membrane (cell surface).¹¹⁻¹⁸ Thus, AFM-based stiffness measurements are unsuitable to image intracellular structures.

Energy dissipation processes have been widely used to enhance the compositional contrast obtained from AFM images on a heterogeneous sample.¹⁹⁻²² For example, AFM phase imaging²⁰ relies on detecting the amount of the energy transferred (dissipated) from the tip to the sample as a function of the lateral position. A key feature of a viscoelastic material is that a deformation is associated with the dissipation of energy. We hypothesize that the viscoelastic interactions experienced by an AFM tip while imaging a cell in liquid could be exploited to generate subsurface images of a cell.

The AFM has been used to measure rheological properties of cells.²³⁻³³ These measurements were not based on the recording of FDCs. It is not straightforward to compare AFM-based rheology data with stiffness maps derived from FDCs. Recently, viscoelastic models have been applied to interpret FDCs in terms of linear viscoelastic models.³¹⁻³⁴ Some of these models provide analytical solutions to relate the forces measured by the AFM and the viscoelastic properties of the cell.³²

Several AFM-based methods have been proposed to image nanostructures embedded on gels or soft polymeric films.³⁵⁻⁴¹ Acoustic waves detected by an AFM tip have been applied to image fixed cells.^40,41 However, those methods seem unsuitable to image intracellular structures of adherent cells immersed in a physiological buffer. Kasas et al. proposed a stiffness tomography approach to image animal, bacterial, and plant cells.^42,43 This method has been applied by Lafont and co-workers to image a cell infected by a bacteria.⁴⁴

Here, we develop a force-microscopy-based method to generate three-dimensional maps of eukaryotic cells immersed in a cell culture medium. The method enables imaging of the nucleoli inside the nucleus. In fact, these organelles lie 1–4 μm from the cell’s outer surface. At the same time, it provides very high resolution maps (∼50 nm) of the actin cytoskeleton structure near the plasma membrane. The method involves the acquisition of FDCs (retraction and approaching sections) on each point of the cell surface. The FDC is divided in different indentation (depth) sections. Each FDC section is processed by using a linear viscoelastic model which gives a 2D representation of the variations of either the Young’s modulus or the viscosity coefficient. The 2D maps are organized to provide a 3D representation of the cell’s structure and mechanical response.

Results and Discussion

Theory of Viscoelastic Response

Figure 1a shows the structure of a cell in the z-axis. The cell is shown in layers from the plasma membrane to the nucleus. Figure 1b shows a scheme of the tip–cell interface. A complete FDC is acquired on each point of the cell surface (Figure 1c). The force is recorded as a function of the tip–cell distance when the tip is approached and retracted from the surface. The maximum value of the indentation is chosen to enable the detection of subsurface structures. The FDCs are divided into several indentation sections (Figure 1c).

Figure 1.

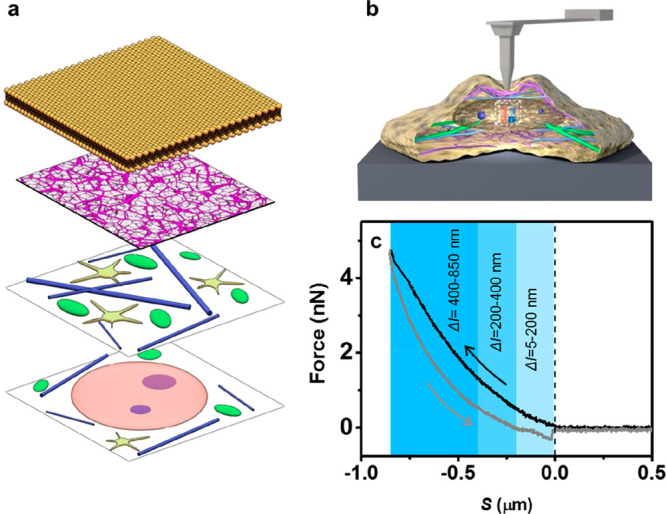
(a) Schematic layered structure of a eukaryotic cell. From top to bottom layer, plasma membrane, actin cortex, organelles, and cytoskeleton, nucleolus within nucleosol. (b) Scheme of a force microscope–cell interface. (c) FDC acquired on a fibroblast cell immersed in buffer (see Materials and Methods). The arrows indicate the direction of the tip motion with respect to the cell.

We have used a 3D Kelvin–Voigt model to simulate the cell viscoelastic response (see Materials and Methods). This model parametrizes the viscoelastic response in terms of the cell’s Young’s modulus E and shear viscous coefficient η. The force F exerted by a conical tip of half-angle θ on the cell is given by

1

I is the indentation and v is the velocity of indentation. The sample’s thickness h is included in the model, so the effects of the finite dimensions of the cell are taken into account.³² For a triangular indentation (v = constant), it is possible express the viscoelastic parameters in terms of force values:

2

3

where F_a and F_r are, respectively, the forces measured in the approach and in the retraction part of the curve for a given indentation. The indentation I is related to the instantaneous tip–sample distance d(t) by

4

The above expressions enable the determination of the Young’s modulus E(x, y, ΔI) and the viscosity coefficient η (x, y, ΔI) as a function of the spatial coordinates. ΔI represents the indentation range of the section of the FDC used to determine E and η.

The details of the linear viscoelastic model^24,28,31,33 used to fit the data are critical to determine with accuracy the rheological properties; however, for the purpose of observing intracellular and subsurface features, they are not relevant. For this reason, we omit a discussion on the linear viscoelastic model features used to describe the cell’s viscoelastic properties.^31,32

Nanomechanical Maps of Fibroblasts at Different Depths

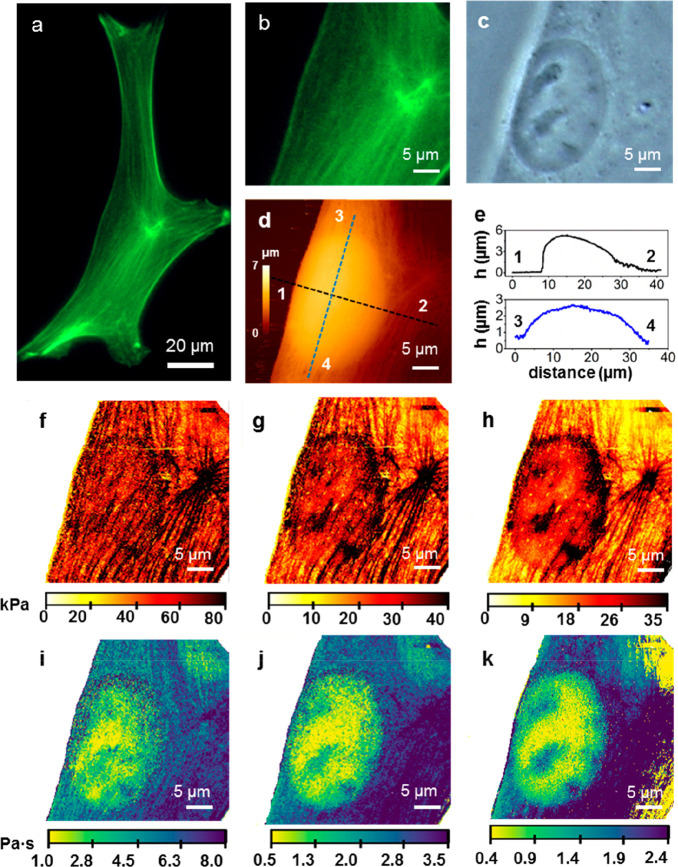
Figure 2 shows optical and AFM images of a fibroblast cell in buffer. A fluorescent image of the actin cytoskeleton is shown in Figure 2a. Figure 2b shows a region of the same cell that includes a section with a high density of actin fibers. An optical image (phase contrast) of a region of the cell that includes the nucleus shows the presence of several organelles (Figure 2c). The AFM topographic imaged of the middle region of the cell (Figure 2d) shows the overall 3D shape. The height cross sections (Figure 2e) show the highest point (5.5 μm) very close to the cell’s left edge. The local height features of the cytoskeleton architecture (in the 10–50 nm range) are masked by the overall topography (Figure 2e).

Figure 2.

(a) Fluorescence microscope image of the actin cytoskeleton of a NIH-3T3 fibroblast. (b) Zoomed-in image from (a) according to the AFM scan area. (c) Optical phase contrast image of the region shown in (b). (d) AFM image of the region shown in panels (b,c). (e) Height cross sections along the dashed line marked in (d). (f–h) Stiffness panels extracted at different indentation ranges. (i–k) Nucleus and some organelles are visualized. To record the AFM images, a triangular waveform movement was applied to the cantilever. Each FDC was characterized by a constant tip velocity of 250 μm/s and maximum force of 4 nN (see more details in Materials and Methods).

The FDCs have been divided in three indentation sections, ΔI = 5–200 nm, ΔI = 201–400 nm, and ΔI = 401–800 nm. In each section, we plot the values of E (x, y) and η (x, y) obtained by averaging the values measured in the section. The 2D Young’s modulus map of the first section (Figure 2f) shows some of the elements of the cortex and the actin cytoskeleton. An actin star site⁴⁵ marking the confluence of several actin bundles appears on the right of the image. The actin star site has the highest value of the Young’s modulus and correlates with the strong green fluorescence signal (Figure 2b) associated with a high concentration of actin bundles. The edges of the nucleus are barely indicated in this section. In the second section (Figure 2g), the contrast of the actin cytoskeleton architecture and the edges of the cell nucleus are enhanced. The last section (Figure 2h) shows a decrease in the contrast of the actin bundles in the cytoplasm, around and above the nucleus. The image shows that the average value of the stiffness over the nuclear region is higher than that in the rest of the cytoplasm.^11,46

Figure 2i–k shows the 2D viscosity coefficient maps of the different sections. In the first section (Figure 2i), there is a large oval region characterized by a viscosity coefficient smaller than the one measured on the cytoplasm (1 Pa·s vs 4–7 Pa·s). The oval region matches the shape and size of the nucleus. The actin star site shows the largest viscosity coefficient value (8 Pa·s). On the top right corner, we observe a region characterized by low viscosity coefficient (2–3 Pa·s). That region is not observed in the corresponding elastic modulus maps. The image of the middle section (Figure 2j) has a better signal-to-noise ratio. The improvement in the contrast reveals the existence of local variations of the viscosity within the nucleus. These variations are enhanced in the image of the last section (Figure 2k). There are five spots where the viscosity coefficient is larger than that in the surrounding nuclear regions. The position of these spots coincides with the position of the nucleoli indicated in the optical image (Figure 2c).

The comparison between the 2D stiffness and viscosity coefficient maps reveals some differences in the capability of detecting subsurface components. The Young’s modulus maps provide high spatial resolution images of the outer cell structures such as the actin cross-linked networks (cortex) and the stress fibers. These maps indicate that, on average, higher Young’s modulus values are obtained when the tip is placed over the nucleus than when it is placed over a region of the cytoplasm far from the nucleus. Topographic images do not show significant differences between the actin cytoskeleton structure over the nucleus with respect to that of the cytoplasm. This observation suggests that, in part, the elastic response associated with the nucleus has a nonlocal character. Hence, this global response together with the variations associated with the actin cytoskeleton structure above it and the response of the nuclear organelles appear mixed in the elastic component of the force. In contrast, a viscosity coefficient map detects the presence of intracellular and subsurface structures with none or little interference from the outer actin cytoskeleton structures or from nonlocal effects.

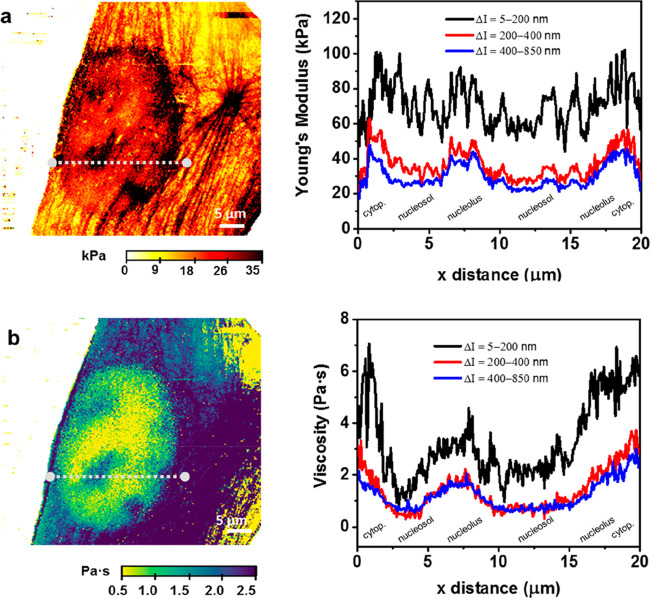
An analysis of the cross sections extracted from the above 2D maps illustrates the interplay among topographic features, physical interactions, and imaging contrast. The stiffness cross sections show a jagged profile associated with the actin cytoskeleton structure (Figure 3a). These variations make it hard to identify the cell’s inner structures. The roughness of the Young’s modulus profile decreases as well as its value for each xy position by increasing the indentation depth. The viscosity coefficient cross sections inside the nucleus show some local variations (Figure 3b). The local hydrodynamic force associated with the displacement of the nucleolus enables its detection. The viscosity of the cytoplasm is also higher than that of the nucleosol.

Figure 3.

(a) Young’s modulus cross sections across the line marked on the stiffness map (left panel). The cross sections have been extracted from Figure 2f–h. (b) Viscosity coefficient map along the line marked on the viscosity coefficient map (left panel). The cross sections have been extracted from Figure 2i–k.

Finite Element Simulations

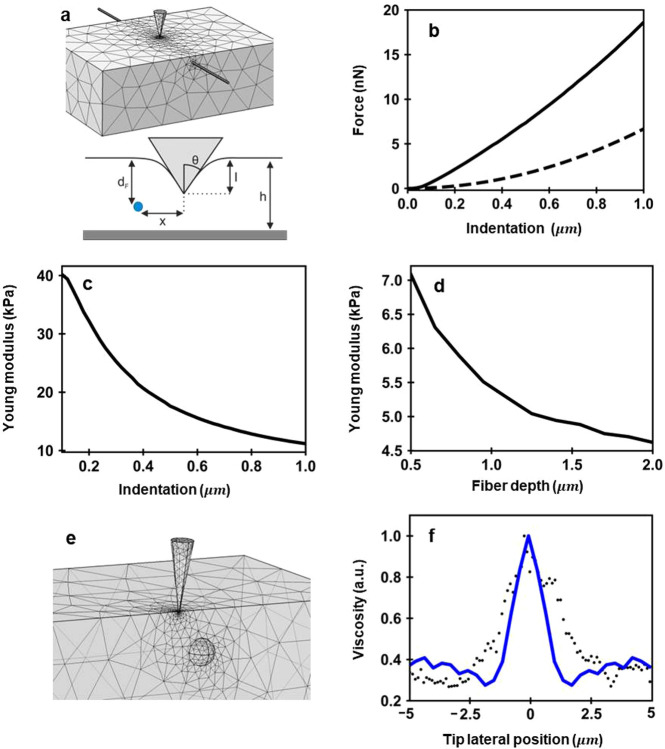
To understand these observations, we have performed finite element (FEM) simulations. To estimate the influence of the actin bundles on the stiffness measurements, we simulate the deformation of a system composed of a fiber embedded in a soft matrix (Figure 4a). This system simulates the elastic response of an actin bundle within the cytoplasm under the force exerted by a tip. The bundle is made of a fiber of 200 nm diameter and a cross-sectional Young’s modulus of 1 GPa. The fiber is embedded in a 5 μm thick layer characterized by E = 4 kPa and ν = 0.5 (Poisson coefficient). The FEM simulations provide the FDCs. These curves are then fitted to the Sneddon model to get the Young’s modulus.

Figure 4.

(a) FEM scheme used to simulate the elastic response of an actin bundle within the cytoplasm. A fiber (r = 100 nm, E = 1 GPa) is embedded in a finite thickness material (E = 4 kPa). The fiber is placed at a depth d from the matrix surface; x is the lateral displacement of the tip with respect to the fiber’s axis. (b) FDC (solid line) for a fiber placed 100 nm from the surface. The discontinuous line shows the FDC when the tip is very far to the left of the fiber. (c) E as a function of the indentation. The values of E are determined from the solid curve shown in (b). (d) Measured Young’s modulus as a function of the distance of the fiber to the surface of the layer. The FEM simulation has been performed for an I_max = 500 nm. (e) FEM scheme used to simulate the viscoelastic response of an organelle (r = 300 nm, E = 1 GPa) inside the nucleous (E = 4 kPa, η = 5 Pa s). (f) Cross section of the viscosity coefficient along the x axis. Further details about FEM simulations can be found in Materials and Methods.

Figure 4b shows the FDC for a fiber embedded in a soft matrix system. The simulations consider a fiber (diameter = 200 nm) whose main axis lies 100 nm from the surface while the tip indents up to 1000 nm. The stiffening effect of the fiber is illustrated by comparing the FDC with the one obtained by removing the fiber from the matrix. The forces exerted on the heterogeneous system are larger than those measured on the homogeneous material.

Figure 4c shows that the effective Young’s modulus of the heterogeneous system decreases by increasing the indentation range at which the modulus is calculated. The highest value (40 kPa) is obtained for small indentations (I = 100 nm). At I = 1 μm, the Young’s modulus of the heterogeneous system is about 11 kPa.

The trend given by the FEM simulations coincides with the dependence observed experimentally (Figure 2f–h and Figure 3a). This result facilitates the interpretation of the experimental data. By increasing the tip’s penetration, the tip pushes the actin bundles toward the inner regions of the cytoplasm. At the same time, a larger region of the cytoplasm (which has a smaller Young’s modulus) contributes to the net force value. Although the fiber and the matrix are deformed by the tip, the contact area is dominated by the matrix, and as a consequence, the measured Young’s modulus is reduced from 40 to 11 kPa. The measured Young’s modulus will converge to the one of the matrix (4 kPa) by applying larger indentations.

To get a better estimation of the E of the fiber will require the deformation to the fiber to be confined. This would imply the use of very small indentations, say below 10 nm. The experimental incertitude in the determination of the contact point between the tip and the cell might prevent these deformations from being applied. That explains the difference between the value measured at I = 100 nm (40 KPa) and the fiber’s nominal value (1 GPa).

A complementary estimation of the influence of a fiber is obtained by placing the fiber at different distances from the matrix surface. The effective Young’s modulus decreases as the fiber is located deeper inside the cell (Figure 4d). In fact, when the fiber is located more than 2.5 μm underneath the surface of the matrix and the tip’s penetration is smaller than the fiber depth, the effective Young’s modulus converges toward the value of the matrix (4 kPa). In this case, the tip does reach the fiber and its stiffness does not affect the measurement. The above simulation was performed by assuming an indentation (maximum value) of 500 nm.

Figure 4e shows the scheme to simulate the local variations of the viscoelastic response inside the nucleus. In the model, a nucleolus is considered as a rigid elastic sphere immersed in a viscoelastic medium (nucleosol). The force exerted by the tip on nucleolus will cause its motion in the nucleosol, and this, in turn, will give rise to some hydrodynamic drag forces. The viscosity coefficient across the nucleus shows a 3-fold increase with respect to the one of the nucleosol. This result agrees with the experimental observation (Figure 3b). The agreement between simulations and experiments indicates that the variations of the viscosity within the nucleus are associated with hydrodynamic friction forces that originate from the displacement of solid elements across the nucleosol. This dissipation mechanism is different from the one dominating the viscosity in the cytoplasm. Experiments performed with the exposure of cells to antiactin cytoskeleton drugs³¹ have supported a poroelastic model for the cytoplasm.²⁶

The actin bundles closer to the plasma membrane surface will always appear in a stiffness map with independence of the indentation range. This effect will mask subsurface and intracellular structures in stiffness maps. The influence of the actin cytoskeleton in a viscosity coefficient map is more indirect. The viscosity coefficient maps can be summarized as follows. First, the viscosity coefficient of the cytoplasm is larger than the one of the nucleus. Second, the viscosity coefficient inside the nucleus shows local variations that enable the localization of the nucleoli. Within the cytoplasm, the viscosity arises from the hydrodynamic friction associated with squeezing the cytosol through the reticular voids of the branched cytoskeleton structure. The capability to observed nuclear organelles is associated with the hydrodynamic resistance that the nucleosol offers to the displacement of an organelle.

3D Tomographic View

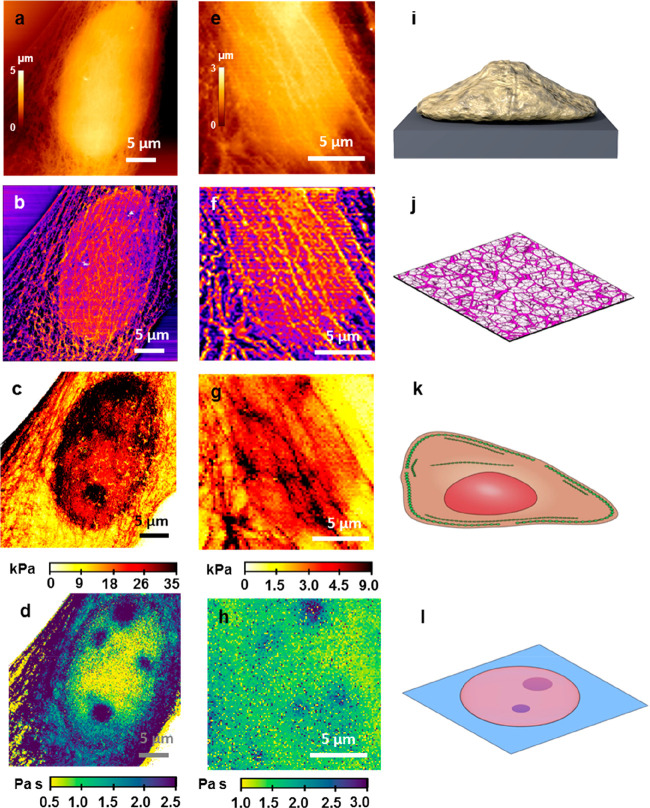
The topography, the elastic modulus, and the viscosity coefficient images are organized to provide a 3D tomographic view of the cell’s static and dynamic mechanical response. Figure 5 shows the 3D images of two fibroblast cells, one fixed (Figure 5a–d) and the other live (Figure 5e–h). The top image shows the cell’s surface topography. This image has been filtered^47,48 (Figure 5b) to reveal the actin cytoskeleton structure including long filaments and branched networks. Figure 5c shows the elastic response of the cell under a compressive stress. In general, the actin cytoskeleton structure provides the stiffer sections of the cell. The nucleus is an additional stiffening factor. The lower image provides a subsurface image of the nucleoli inside the nucleus. The hydrodynamic drag associated with the tip compression is increased in the vicinity of a nucleolus. This effect enables one to resolve the nucleoli in the nucleosol. Similar results are obtained for live cells (Figure 5e–h). Currently, the time to generate a 3D tomographic image is considerable (30 min). This factor contributes to the increase of noise in the images of live cells. The schemes depicted in Figure 5i–l illustrate the different cell properties imaged by the AFM method.

Figure 5.

AFM tomographic sections of live and fixed NIH-3T3 fibroblast cells. (a) Topography of the cell surface (fixed); cell depth = 0 nm. (b) Topography of the actin cytoskeleton; cell depth = 0–100 nm. (c) Young’s modulus image; cell depth z = 500 nm. (d) Viscous coefficient map; cell depth = 1000 nm. (e) Surface topography of a live cell; cell depth = 0 nm. (f) Topography of the actin cytoskeleton; cell depth = 0–100 nm.(g) Young’s modulus image; cell depth = 500 nm. (h) Viscous coefficient map; cell depth = 1000 nm.  (i) Scheme of an AFM topography image taken on a single cell. (j) Scheme of the actin based cell cortex. (k) Scheme of some of the cell elements that dominate the cell stiffness. (l) Scheme of some cell organelles immersed in the nucleosol.

Conclusions

We have developed a force microscopy method that enables the imaging of cellular organelles inside the nucleus. Viscoelastic maps provide unobstructed images of intracellular structures. The method combines the imaging at very high spatial resolution of the actin cytoskeleton (∼50 nm) with the imaging of nuclear organelles that lie about 1 μm from the plasma membrane. The method has been demonstrated on both live and fixed cells. This method provides a label-free and noninvasive approach to study with high spatial resolution the interplay between mechanics and biology within a single cell.

The stiffness of an actin bundle depends on the indentation used for its determination. This result reflects the interplay between the intrinsic stiffness of the bundle and the softer response of the cytoplasm. Lower values of Young’s modulus are obtained by increasing the indentation. We identify two different viscoelastic mechanisms in a cell. Within the cytoplasm, the variations observed in the viscoelastic response are associated with poroelasticity. In the nucleus, the hydrodynamic drag associated with the displacement of a nucleolus in the nucleosol dominates the viscous response.

Materials and Methods

AFM-Based Viscoelastic Theory

The model used for describing the cell was an incompressible Kelvin–Voigt material. This material is described by its elasticity E and its shear viscosity η, whereas the Poisson ratio is fixed (ν = 0.5). Full details about the deduction of eq 1 are found in Garcia et al.(32) The expression of the Young’s modulus and viscosity coefficient as a function of the force values during approach and retraction is described in Guerrero et al.(31)

Cell Culture

NIH-3T3 fibroblasts (Sigma-Aldrich, UK) were cultured in Dulbecco’s modified Eagle medium (Gibco Life Technologies, UK) supplemented with 10% fetal bovine serum (Gibco Life Technologies, UK) and 1% penicillin/streptomycin (Gibco Life Technologies, UK). Cell were maintained at 37 °C in an atmosphere of controlled humidity (90%) and CO₂ (5%) during culturing, and handling was performed in a microbiological safety cabinet. For AFM measurements in physiological conditions, the culture medium was changed for Leibovitz’s L-15 (Gibco Life Technologies, UK) supplemented with 10% fetal bovine serum (Gibco Life Technologies, UK). The fixation of the fibroblast was performed with a solution of 4% of formaldehyde (ThermoFisher Scientific, USA) in phosphate-buffered saline (Sigma-Aldrich, UK). The exposure time was 15 min.

Optical and Fluorescence Microscopy

The phase contrast and the immunofluorescence images were performed on an AXIO Observer D1 (Carl Zeiss, Oberkochen, Germany). The microscope was equipped with a mercury lamp HBO 100 (Carl Zeiss, Oberkochen, Germany) for the dye excitation. The immunofluorescence microscopy was exclusively performed on fixed cells. The F-actin was stained with an AlexaFluor 488 phalloidin (Invitrogen, ThermoFisher Scientific). On the other hand, tubulin was stained with an indirect immunofluorescence protocol using two antibodies: anti-α-tubulin (bovine), mouse IgG1, monoclonal 236-10501 (Invitrogen, ThermoFisher Scientific), and Alexa Fluor 594 F(ab’)2 fragment of rabbit anti-mouse IgG (H+L) (Invitrogen, ThermoFisher Scientific).

Atomic Force Microscopy

AFM experiments were performed with a JPK Nanowizard III (JPK Instruments, Germany) mounted on an inverted optical microscope (AXIO Observer D1; Carl Zeiss, Germany). We used BL-AC40TS cantilevers (Oxford Instruments, UK) with a nominal spring constant of 0.09 N/m and a conical tip shape (cone half angle θ = 18°). The geometry of the above cantilever minimizes the hydrodynamic drag during the acquisition of FDCs. The actual spring constant of the cantilever was determined using the thermal noise method.

FDCs were acquired by following a force volume methodology. Indeed, these FDCs were obtained with a triangular waveform movement of the tip. A modulation frequency of 50 Hz was used. The imaging region was divided in a grid of 512 × 512 pixels trying to cover all of the area enclosing a single cell. The maximum force exerted on a cell during a single FDC was 4 nN on fixed cells and 3 nN on live cells. To determine the contact point, we used a ratio of variance protocols and a homemade code written in python.

Live cell experiments were performed at 37 ± 0.1 °C (BioCell system, JPK Instruments, Germany). Experiments on fixed cells were carried out with the samples immersed in a phosphate-buffered saline.

Nanomechanical Spectroscopy

By using eqs 2 and 3, we have transformed every FDC into equivalent viscosity–distance curves (VDC) and elasticity–distance curves (EDC). Each pixel of an elasticity map has been obtained by averaging the EDC values included in the indentation range of that map. A similar procedure has been applied to the VDC to determine the pixels of a viscosity coefficient map.

The instantaneous tip–cell distance is calculated by

5

where z(t) is the z-piezo displacement, Δz is the cantilever deflection, and z₀ marks the z-piezo displacement at which the tip establishes mechanical contact with the cell surface (approach).

Topography Filters

From each FDC, a value of the maximum indentation was calculated. With these values, we compiled a maximum indentation map. Subsequently, a spatial high-pass filter^47,48 was applied on these maps, showing a high definition image of the cell cytoskeleton.

Finite Element Simulations

The numerical simulations of the indentation were performed with commercial FEM software (COMSOL Multiphysics, COMSOL AB, Stockholm, Sweden). The indenter was a rigid cone (θ = 70°), and the material model used for it was a linear elastic material (isotropic and homogeneous, E = 20 GPa). The sample was simulated as a homogeneous cylinder with a 50 μm radius and 5 μm thickness. We have simulated two heterogeneous systems, a fiber embedded in an elastic matrix and a rigid sphere embedded in a viscoelastic matrix. In the first case, the fiber is a cylinder with a radius of 100 nm and a Young’s modulus of 1 GPa. Its length coincides with the lateral size of the matrix, and it is clamped at both ends without being prestressed. The tip–fiber contact point is far from these fiber ends (Figure 4a). The matrix representing the sample was also elastic (linear, isotropic, E = 1 GPa). The indentation has a triangular waveform (v = 2 um/s) and the maximum indentation (I_max = 500 nm). For the second case, the hydrodynamic drag associated with the displacement of a nucleolus was simulated by an elastic sphere with a radius of 300 nm and a Young’s modulus of 1 GPa. The sphere is immersed in a viscoelastic matrix of E = 4 kPa, η = 5 Pa·s.

The bottom of the sample (matrix) was fixed to a rigid substrate. The mesh parameters were refined until a convergence in the solutions was obtained. This final converged mesh was graded to be more refined close to the indenter and in the surroundings of the fiber (0.01 μm) and coarser at the edges of the sample (up to 0.1 μm). The simulations were performed assuming a frictionless contact. The tip was moved perpendicular to the sample surface. COMSOL solved the full 3D differential equations of viscoelasticity, although currently, the AFM measurements provide 1D vertical data.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.9b04808.

• Experimental methodology details, FDCs taken on different locations of the cells, proof of the method reproducibility, nanomechanical and optical images of nuclear organelles, FEM simulations of different fiber density, and a FEM study of FDC sensitivity to the fiber-bundle radius (PDF)

Author Contributions

^† C.R.G. and P.D.G contributed equally to this work.

The authors declare no competing financial interest.