Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Jul 15;5(29):18527–18534. doi: 10.1021/acsomega.0c02623

Ga2Se3 Defect Semiconductors: The Study of Direct Band Edge and Optical Properties

Ching-Hwa Ho 1,*
PMCID: PMC7392520  PMID: 32743231

Abstract

graphic file with name ao0c02623_0005.jpg

Direct band edge is a crucial factor for a functional chalcogenide to be applied in luminescence devices, photodetectors, and solar-energy devices. In this work, the room-temperature band-edge emission of III–VI Ga2Se3 has been first observed by micro-photoluminescence (μPL) measurement. The emission peak is at 1.85 eV, which matches well with the band-edge transition that is measured by micro-thermoreflectance (μTR) and micro-transmittance (μTransmittance) for verification of the direct band edge of Ga2Se3. The temperature-dependent μTR spectra of Ga2Se3 show a general semiconductor behavior with its temperature-energy shift following Varshni-type variation. With the well-evident direct band edge, the peak responsivities of photovoltaic response (∼6.2 mV/μW) and photocurrent (∼2.25 μA/μW at f = 30 Hz) of defect zincblende Ga2Se3 can be, respectively, detected at ∼2.22 and ∼1.92 eV from a Cu/Ga2Se3 Schottky solar cell and a Ga2Se3 photoconductor. On the basis of experimental analysis, the optical band edge and photoresponsivity properties of a III–VI Ga2Se3 defect semiconductor are thus realized.

Introduction

Recently, owing to the invention of graphene,1 two-dimensional (2D) semiconductors such as transition-metal dichalcogenides (TMDCs) MX2 (M = W, Mo, Re and X = S, Se)2−6 and layered III–VI compounds such as NX (N = Ga, In, and X = S, Se)7−10 have been enthusiastically studied due to their scientific merits of smooth surface,11 flexibility,12−14 ultrathinness, larger area, high carrier mobility,15−17 in-plane optical anisotropy,18,19 and thickness-tunable band gap modulation.20,21 From the research works on TMDCs and III–VI compounds, band-edge characteristics turn out to be a key reason for further application of these layered semiconductors in optoelectronics, electronics, or photocatalysis devices. Based on the characteristics, it is interesting that bulk TMDCs (e.g., MoS2) are usually indirect semiconductors, but they would become direct band-gap compounds by thinning their thicknesses close to a monolayer limit.20 On the other hand, for the III–VI layered chalcogenides, the band-edge property is opposed to the other TMDCs because most of the bulk and multilayer III–VI compounds are direct semiconductors. However, they would gradually become indirect materials (like InSe) if their thicknesses are approaching the monolayer or very thin scale.22 Therefore, bulk and multilayer TMDCs such as MoS2 and WSe2 are not suited for luminescence-device application because of their indirect band gap. On the other hand, III–VI layer compounds such as GaSe and InSe are generally direct semiconductors. They can easily produce luminescence emission23 from bulk to multilayer even without any intentional exfoliation to get a monolayer. The highly spherical symmetry of the s-like conduction band derived from Ga and In ions may play an important role in achieving the direct band edge of the GaSe and InSe layer compounds.13,24 Because of these native advantages of high luminescence efficiency and direct band edge in the III–VI GaSe, it is important for further studying the structure, band edge, and optical properties of Ga2Se3, a rarely studied III–VI defect semiconductor.

Ga2Se3 is one of the important members of III–VI compounds, which crystallizes in a defect zincblende structure as the natural sphalerites.25,26 Unlike the III–V semiconductors such as GaAs and InP owning a stronger covalent bond, the misvalency of the III and VI elements usually makes a III–VI compound, possessing different stoichiometries, diversified crystal phases, and also changing lattice forms. Thus, GaSe and Ga2Se3 are the general constituents of stoichiometry existing in the gallium selenides. There are three crystalline phases of α,27 β,28 and γ29 structures that can be found in the Ga2Se3 crystals obtained by different growth temperatures. Sphalerite α-Ga2Se3 usually crystallizes in a defect zincblende structure possessing a cubic unit cell, which may be the most stable phase in the defective Ga2Se3 crystal owing to its higher growth temperature.27 The cubic α-Ga2Se3 may also be a fundamental unit for building β (monoclinic)28 and γ (orthorhombic)29 phases in a Ga2Se3 lattice. This result implies that the three phases of α-, β-, and γ-Ga2Se3 are essentially comparable structures with equivalent axes marked as [100]β = [11̅2̅]α, [010]β = [110]α, and [001]β = [11̅2]α, as displayed in Figure 1d.30 For a perfect zincblende structure of a III–V compound like GaAs, the stoichiometric content ratio of Ga/As should be 1:1. Nevertheless, for a defect zincblende structure of α-Ga2Se3, the stoichiometry ratio of Ga/Se is only 2:3. Consequently, one-third of the cations (Ga) would be vacant with respect to that of the anions (Se) in all of the phases of Ga2Se3. The crystalline condition and lattice form are similar to its Ga2S3 counterpart.31,32 Thus, the structural vacancies of Ga (VGa) in a defect zincblende Ga2Se3 would be ordered in the lattice and they might be an important factor for determination of the crystal structure and band structure of the Ga2Se3 defect semiconductor. Some experimental and theoretical works on the determination of band gap using optical absorption,25 DC photoconductivity,26 UV–visible diffuse reflectance,33 and density-function calculations34 had been done; however, multidisciplinary gaps ranging from 1.79 to 2.4 eV were obtained. There is still lack of evidence on the photoluminescence emission of Ga2Se3 at room temperature for verification of its direct band edge in the defect semiconductor.

Figure 1.

Figure 1

Open in a new tab

(a) X-ray diffraction pattern of Ga2Se3 from 2θ = 20 to 90°. The peak indices of the diffraction planes are indicated. (b) Representative scheme of the defect zincblende structure of cubic α-Ga2Se3. (c) Atomic arrangement of the {111} plane (preferred orientation) in the defect zincblende structure. (d) Comparison of cubic α-Ga2Se3 and monoclinic β-Ga2Se3 defect semiconductors. They are approximately equivalent with the unit-cell volume of β-Ga2Se3 being about 3 times as large as that of α-Ga2Se3 along the β-[010] (i.e., α-[110]) direction.

Results and Discussion

Figure 1a shows the powdered X-ray diffraction (XRD) pattern of Ga2Se3 grown by the chemical vapor transport (CVT) method. A Cu Kα radiation (containing Kα1 = 1.5406 and Kα2 = 1.5444 Å) was used as the X-ray source. Several sharp peaks of (111), (200), (220), (311), (222), (400), (331), (420), and (422) are found, which index to a cubic α-Ga2Se3 phase of zincblende structure [JCPDS card no. 05-0724].27 The crystal structure of the α-Ga2Se3 phase is the defect zincblende structure, as shown in the representative scheme in Figure 1b, where 1/3 cation (Ga) atoms are vacant with respect to the anionic (Se) sites, owing to a perfect zincblende structure of 1:1 cation to anion ratio (e.g., GaAs). Thus, Ga vacancy (VGa) can be ordered in the zincblende lattice, and it would also contribute to the crystal and band structures of Ga2Se3. From Figure 1a, the interplanar spacings measured from XRD are d(111) = 3.145, d(200) = 2.726, d(220) = 1.927, d(311) = 1.645, d(222) = 1.574, d(400) = 1.364, d(331) = 1.254, d(420) = 1.220, and d(422) = 1.114 Å. The values of interplanar spacing render an averaged cubic lattice constant of a = 5.45 Å for α-Ga2Se3. As shown in Figure 1a, the strongest XRD peak is the (111) plane. The {111} plane has the most close-packing facet and is one of the frequently occurring orientations inside a cube-like structure of diamond, zincblende, pyrite,35 or chalcopyrite [denoted as (112)] compounds.36 The representative scheme of the atomic arrangement of the {111} plane in the defective zincblende Ga2Se3 is shown in Figure 1c. Essentially, it is a honeycomb structure, which would frequently build a trigonal-shaped facet occurring in the crystals with a cubic phase. Figure 1d shows a contrast of an atomic scheme between cubic α-Ga2Se3 and monoclinic β-Ga2Se3.28 In general, the unit-cell volume of β-Ga2Se3 is 3 times as large as that of α-Ga2Se3, formed along the [010]β ([110]α) direction. The crystal axes of [001]β and [100]β (β phase) are also equivalent to those of [11̅2]α and [11̅2̅]α (α phase) in the Ga2Se3 defect semiconductor.

Figure 2a displays the micro-photoluminescence (μPL) spectrum of a Ga2Se3 microcrystal (∼80 μm in size) on the {111} plane in the energy range of 1.5–2.2 eV at room temperature. The right inset shows the crystal image of the Ga2Se3 sample under excitation with a 532 nm laser using a 50× objective lens. A clear PL peak at ∼1.85 eV is observed owing to the band-edge free exciton (BEFX) combined with the bound exciton (BX) and defect emissions occurring in the α-Ga2Se3 sample (i.e., sample S1). The inference of the free-exciton (FX), BX, and defect emission in Ga2Se3 can be verified by the temperature-dependent μPL spectra obtained from the other sample (i.e., sample S2), as displayed in the left inset of Figure 2a. At a low temperature of ∼160 K, both free-exciton (FX ∼ 1.945 eV) and bound-exciton (BX ∼ 1.822 eV) peaks are simultaneously detected in the μPL spectrum similar to the other direct chalcogenide semiconductor such as GaTe.37 As the temperature increases, the PL intensity of the BX feature decreases faster than that of the FX emission due to the debound effect from the impurity or defect state inside the Ga2Se3 microcrystal caused by the increasing temperature. Because of the free to bound behavior, the BX emission would decrease promptly and the FX emission can finally dominate the main PL emission peak at 300–320 K, as shown in the left inset of Figure 2a. At 320 K, the emission peak of Ga2Se3 is at about 1.835 eV. The thermal-ionization temperature of the BX emission is about 300 K (i.e., k·T ∼ 26 meV) for Ga2Se3. The BX feature is inferred to be an acceptor-bound exciton in α-Ga2Se3. As shown in Figure 2a, the PL line widths (i.e., 1.85 eV peak) of the samples S1 and S2 at 300 K range from ∼0.1 to ∼0.4 eV. The values are larger than those of the general direct semiconductors like GaAs. The emission peak of PL may also contain the contribution of defects inside Ga2Se3. Moreover, in comparison with its GaSe counterpart, the PL quantum efficiency of Ga2Se3 in Figure 2a is approximately 25% lower than that of the GaSe at room temperature.13,23

Figure 2.

Figure 2

Open in a new tab

(a) Room-temperature μPL spectrum of Ga2Se3. The left inset shows temperature-dependent bound-exciton (BX) and free-exciton (FX) emissions of an additional Ga2Se3 sample for verification of the direct band edge. The right inset displays the microscopic image of the Ga2Se3 microcrystal. (b) μRaman spectrum of Ga2Se3. The inset shows some of the vibrational atomic movements in the fundamental GaSe4 sp3 unit.

Figure 2b shows the μRaman spectrum of the Ga2Se3 microcrystal from 100 to 500 cm–1. There are about five Raman peak features, at A′ ∼ 119 cm–1, A1 ∼ 156 cm–1, A1 ∼ 190 cm–1, A′ ∼ 240 cm–1, and F2 ∼ 289 cm–1, that can be detected in the α-Ga2Se3 microcrystal, similar to previous ordered Ga2Se3.38 Most of the mode frequencies are indexed to the internal and external vibrations of the tetrahedral GaSe4 groups39 in the zincblende Ga2Se3. In the defect semiconductors of Ga2X3 (X = S, Se), even Ga2S3 is crystallized in a defect wurtzite structure (β),27 and 1/3 Ga vacancies are still ordered in the Ga2X3 lattice similar to that of α-Ga2Se3. The atomic arrangement of the wurtzite {0001} plane also resembles that of zincblende {111} on the top layer surface of Ga2X3 (see Figure 1c). Thus, the measured Raman frequencies of Ga2S3 are observed to shift to higher frequencies (i.e., A′ ∼ 147 cm–1, A1 ∼ 233 cm–1, A1 ∼ 280 cm–1, A′ ∼ 307 cm–1, and F2 ∼ 386 cm–1)31,40 as compared to those of Ga2Se3 in Figure 2b due the shrinkage of the Ga–X bond length inside the GaX4 tetrahedra.27 The symmetric GaSe4 sp3 unit inside the zincblende structure has vibration modes at the Γ center represented by Γ = A1 + E + F1 + F2.39,41 Four standard vibrations of atomic movement, ν1(A1), ν2(E), ν3(F2), and ν3(F2), in the GaSe4 molecule are depicted in the inset of Figure 2b for contrast. All of the full-width at half-maximum (FWHM) values of the Raman peaks (A′ – F2) in Figure 2b range from 15 to 38 cm–1 by Raman fits. The FWHM values are higher than those of the Raman peak observations in GaAs and Si with a zincblende and diamond structure for identification of the defect zincblende character of Ga2Se3.

To further identify the direct band edge of Ga2Se3, μTransmittance and μTR measurements of the Ga2Se3 microcrystals are, respectively, carried out. The experimental results of μTransmittance and μTR spectra at 300 and 20 K are shown in Figure 3a,b, respectively. Modulation spectroscopy of a semiconductor, like TR measurement,42,43 has been proven to be a very powerful technique for the characterization of excitons, direct band edge, and interband transitions in the semiconductor’s band structure.44 The derivative spectral line features suppress unintentional spectral background and emphasize the direct critical-point transitions in the band structure. As shown in Figure 3a, the direct band-edge transition of μTR feature matches well with the center-edge position of the μTransmittance spectrum at Egd = 1.85 eV. In comparison with the μPL peak in Figure 2a, the Eg μTR feature is in agreement with the PL emission of Ga2Se3 to verify its direct band edge. The agreement of the Egd position in the μTR and μTransmittance spectra can also be found in Figure 3b, where the value of the band-edge transition blue shifts to Eg ≈ 2.0 eV at 20 K. Figure 3c shows the temperature-dependent μTR spectra of α-Ga2Se3 between 20 and 320 K. For comparison purpose, the 2D contour plot of μTR spectra is also depicted in Figure 3d for contrast. The direct band-edge feature (Egd) shows enhanced amplitude at 20 K, while it demonstrates an energy red shift and line-shape broadened character when the temperature increased to 320 K, such as the general semiconductor behavior. The broadened Eg μTR feature is likely owing to the intrinsic defect (like VGa) and alloy scattering effect existing inside the Ga2Se3 crystal at higher temperature. There is a small μTR feature D present in the lower-energy side (i.e., T > 260 K) in Figure 3c. It is likely caused by a defect transition in Ga2Se3.

Figure 3.

Figure 3

Open in a new tab

μTR and μTransmittance spectra of Ga2Se3 at (a) 300 K and (b) 20 K. (c) Temperature-dependent μTR spectra from 20 to 320 K near band edge. (d) 2D contour plot of the temperature-dependent μTR spectra of α-Ga2Se3. (e) Temperature dependence of band-edge transition energies of α-Ga2Se3 as a function of temperature.

The occurrence of the direct band edge of Ga2Se3 can be attributed to the spherical-like Ga 4s orbital constituting the lowest conduction band, while the Se 4p state hybrid with Ga 4p + 4s electrons constructs the top of the valence band,34 similar to the defect semiconductor counterpart Ga2S3.45Figure 3e shows the temperature dependence of band-edge transition energies (with representative error bars) from 20 to 320 K for the Egd transition in Ga2Se3. The solid squares are the experimental data obtained from μTR measurement and the solid line is the least-square fit to a Varshni-type formula expressed as Eg(T) = Eg(0) – α·T2/(β + T),46 where Eg(0) is the energy at 0 K, the Varshni constant α is related to the strength of an electron (exciton)–phonon interaction, and β is closely related to the Debye temperature of the material. The obtained values of the fitting parameters for the direct band edge of Ga2Se3 are Eg(0) = 2.005 ± 0.002 eV, α = (7.1 ± 0.7) × 10–4 eV/K, and β = 120 ± 40 K. The values are similar to those obtained by its III–VI defect semiconductor counterparts such as In2S3 in cubic phase (or a tetragonal phase),47 wherein the defect crystal still owns one-third of the cation vacancy’s ordered arrangement in the crystal.

To evaluate the functional performance of Ga2Se3 for further solar-energy and optoelectronic device applications, the photoelectric conversion and photodetection behavior of as-grown Ga2Se3 crystals were also investigated. A larger as-grown Ga2Se3 crystal was cut and polished into a size of 0.3 × 0.2 × 0.04 cm3. The crystal was selected for fabrication in a Cu/Ga2Se3 Schottky solar cell (SSC), as shown in the representative scheme in the inset of Figure 4a. A mica-clamped copper mesh contacting the Ga2Se3 surface acts as the top electrode of the SSC. The Ga2Se3 crystal was mounted on a copper sample holder using a silver paste for the bottom electrode. Figure 4a shows the surface photovoltaic (SPV) response spectrum of the Cu/Ga2Se3 SSC structure in the energy range between 1.5 and 5 eV. The spectrum was normalized to the spectral light intensity. Figure 4b depicts the representative energy-band diagram of the Cu/Ga2Se3 SSC structure. Essentially, the as-grown Ga2Se3 is a p-type semiconductor as confirmed by our Hall measurement. The dark resistivity of Ga2Se3 is about 145 Ω·cm and Hall mobility is ∼11 cm2/V·s at 300 K. The p-type behavior of Ga2Se3 would make the SSC structure with downward band bending near the Cu/Ga2Se3 rectified junction, as displayed in Figure 4b. When the photon is incident (hν ≥ Egd), the electron–hole pair is generated and then the electron–hole pair is separated by a built-in electric field of the Schottky junction. Thus, the SPV response voltage for different wavelengths in the SSC can be measured. As shown in Figure 4a, with E > 1.85 eV (Eg), the SPV response spectrum starts to increase, and the responsivity reaches a maximum intensity of ∼6.2 mV/μW at 2.25 eV. Then, the SPV responsivity is gradually decreased with the incident photon energy increasing up to 5 eV. The decrease of SPV is dominated by the surface-recombination effect of the Ga2Se3 sample, which reduces the net excess carriers and forms a photoresponse peak near the band gap.48 The SPV spectrum in Figure 4a still reveals a good responsivity of Ga2Se3 in the visible range from 1.9 to 3.1 eV.

Figure 4.

Figure 4

Open in a new tab

(a) Surface photovoltaic response spectrum of the Cu/Ga2Se3 Schottky solar cell measured from 1.5 to 5 eV. The inset depicts the representative scheme of SPV response measurement. (b) Representative band scheme of the Cu/p-Ga2Se3 Schottky junction with a built-in electric field under light illumination. (c) Photocurrent responsivity spectrum of the Ga2Se3 photoconductor with chopped frequency f = 30 Hz and applied bias V = 30 V. The inset depicts the measurement configuration of photoconductivity (PC) measurement. (d) Frequency dependence of the peak responsivity (A/W) at 1.93 eV from 30 to 1000 Hz for the Ga2Se3 photoconductor in (c). The inset shows the representative PC band scheme of Ga2Se3 with a defect level (Et) inside the band gap to prolong the photocurrent lifetime.

Figure 4c shows the photocurrent photoresponsivity spectrum in a Ga2Se3 photoconductor at room temperature. The size of the Ga2Se3 crystal is similar to that for the SPV measurement. The photoconductivity (PC) value is measured by applying 30 V to the Ga2Se3 photoconductor, and the chopped frequency (f) is set at 30 Hz. The inset of Figure 4c depicts the experimental setup for the PC measurement, where the photocurrent is derived from a load resistor and the incident light is chopped with different frequencies to evaluate the PC responsivity of the Ga2Se3 photoconductor. In Figure 4c, the photocurrent responsivity spectrum of Ga2Se3 clearly shows a photocurrent peak of ∼2.25 μA/μW occurring at 1.93 eV near and above the band edge (Egd). The residual absorption below Eg (i.e., 1.65–1.85 eV) is detected, which may be caused by imperfect states (defect and impurity) inside the Ga2Se3 defect semiconductor. The inset in Figure 4d shows the band scheme of the Ga2Se3 photoconductor operating under the application of an external electrical field. Unlike the SSC structure in Figure 4b, the separation of the photogenerated electron and the hole might depend on applying the external field, and the path of carrier transport should be much longer (distance) than that in the Schottky junction in Figure 4b. If there is a trap state or trap level (Et) in the band gap of the defect semiconductor (e.g., VGa), the thermal bounce of electrons and holes between EV and Et would prolong the PC lifetime of the Ga2Se3 photoconductor. Thus, when the chopped frequency of the incident light is increased, the peak photocurrent value decreases, owing to a longer lifetime τ in the Ga2Se3 defect semiconductor. The peak photocurrent versus chopped frequency f at 1.93 eV (operation see Figure 4c) is shown in Figure 4d. The frequency range is set from 30 to 1000 Hz and the maximum photocurrent responsivity decreases exponentially with f. The hollow triangles in Figure 4d are the experimental data and the solid line is fitted to the expression

graphic file with name ao0c02623_m001.jpg 1

where I0 is the DC photocurrent responsivity (f = 0 Hz) and τ is the lifetime of the photoconductor. The obtained values of the fitting parameters in Figure 4d are I0 = 3.24 A/W and τ = 12.5 ms. The efficiency for generation of photocurrent in a photoconductor is known as the responsivity (R). The DC responsivity is R = 3.24 A/W and R = 2.25 A/W at 30 Hz for the Ga2Se3 photoconductor (under bias = 30 V at E = 1.93 eV, λ = 642 nm). The lifetime τ is closely related to photoconductive gain Γ, defined as Γ = τ/τtran = τ·μ·V2/l, where τtran is the transit time of electron across the photoconductor, V is the bias, μ is the mobility, and l is the transit distance. When photons with power P are incident on a photoconductor, the photocurrent is defined by ip = (q/E)·P·η·Γ, where E is the photon energy (in eV) and η is the quantum efficiency (#electrons/#photons). Because the photoconductive gain Γ is dependent on the bias (V) and geometry (l) we can further use a normalized gain, which is expressed by the product of lifetime, mobility, and quantum efficiency as49

graphic file with name ao0c02623_m002.jpg 2

where R is the responsivity given by R = ip/P, and q is the charge. The DC responsivity of Ga2Se3 is R = 3.24 A/W. Substituting the channel length l = 0.2 cm and bias V = 30 V at E = 1.93 eV in eq 2, the normalized gain of the Ga2Se3 photoconductor can be determined to be Γn = 8.34 × 10–3 cm2/V. The responsivity R of a photoconductor depends on the photocurrent but is independent of the dark current idark. In the real case of a photodetector′s application, the dark current and noise current are the drawbacks of the detector while they should be taken into account for the evaluation of the photodetector performance. Thus, detectivity (D*) is defined as the figure-of-merit of a photodetector and is given by50

graphic file with name ao0c02623_m003.jpg 3

assuming unit bandwidth (i.e., Δf = 1 Hz) and A being the lateral area of the photoconductor. Jdark is the dark current density of the photodetector. If the bandwidth Δf of the Ga2Se3 photoconductor is ∼30 Hz, as seen from Figure 4d, the detectivity is calculated to be D*·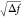Inline graphic = 2.5 × 1010 Jones (cm·Hz1/2·W–1). Table 1 lists the values of responsivity (R), normalized gain (Γn), and detectivity (D*) of Ga2Se3 together with those of III–VI compounds and transition-metal dichalcogenides (TMDCs) are also included for comparison. For the Ga2Se3 defective-type photoconductor operated at 642 nm, the value of detectivity D* is close to those of the other III–VI GaSe field-effect phototransistors measured at 532 51 and 254 nm52 of the visible and ultraviolet region, while the responsivity R of Ga2Se3 is slightly larger than that of the layered GaSe, which is not defective type. The high detectivity of the Ga2Se3 implies lower dark current Jdark of the photodetector and the value of D* is comparable to its defect semiconductor counterpart, cubic γ-Ga2S3, operated at 350 nm owing to the larger direct band gap of Ga2S3.53 For a In2Se3/MoS2 heterostructure (HS) field-effect transistor (FET) at λ = 450 nm,54 the R value is similar to that of Ga2Se3 at 642 nm, while the detectivity of Ga2Se3 is greater than that of the HS FET, likely owing to the lower dark current in the Ga2Se3 photoconductor. In comparison with the GaSe photo-FET51 and WSe2 FET,55 the normalized gain Γn of Ga2Se3 is larger than those of GaSe and WSe2. The higher normalized gain of Ga2Se3 is likely due to the longer lifetime τ of the photoconductor caused by its native defect character.

Table 1. Comparison of Values of Responsivity (R), Normalized Gain (Γn), and Detectivity (D*) of Ga2Se3, Layered III–VI Chalcogenides, and TMDCs.

chalcogenides and detector type λa (nm) Va la (μm) R (A·W–1) Γn (cm2·V–1) D* (Jones) refs
Ga2Se3 photoconductor 642 Vbias = 30 V 2000 3.24 8.34 × 10–3 2.5 × 1010 this work
GaSe FET 532 Vgs = −18 V, Vds = 10 V 47 0.9   8.08 × 1011 (51)
GaSe photo-FET 254 Vgs = 1 V, Vds = 5 V 20 2.8 1.1 × 10–5 2.36 × 1011 (52)
γ-Ga2S3 FET 350 Vgs = −40 V, Vds = 1 V 15 61.3   1.52 × 1010 (53)
In2Se3/MoS2 HS FET 450 Vgs = 60 V, Vds = 1 V 15 4.47   1.07 × 109 (54)
WSe2 FET 655 Vgs = 5 V, Vds = −5 V 5 5750 ∼1 × 10–3 5.3 × 1010 (55)
Open in a new tab
a

λ is the excitation wavelength, V is the applied bias, and l is the channel length of the photodetector.

Conclusions

In conclusion, the structure, band edge, and photodetection properties of Ga2Se3 have been studied. High-quality Ga2Se3 bulk and microcrystals were grown by the chemical vapor transport method using ICl3 as the transport agent. The as-grown Ga2Se3 crystals are crystallized in the α-phase defect zincblende structure with a lattice constant of 5.45 Å. A direct band-edge emission caused by free exciton, bound exciton, and defect was observed at ∼1.85 eV in α-Ga2Se3. Temperature-dependent μPL spectra of the α-Ga2Se3 microcrystal reveal that the BX-emission peak gradually decreases and merges with the FX emission finally similar to the luminescence behavior of a general direct semiconductor. The μTR and μTransmittance results of the α-Ga2Se3 microcrystals also verify that the direct band edge of Ga2Se3 is observed at 1.85 eV and 300 K. The μRaman spectrum of Ga2Se3 reveals similar vibration group of Raman modes (but lower frequency) as compared to its defect semiconductor counterpart Ga2S3. The μTR feature of the band-edge transition reveals energy reduction and a line-shaped broadened character with respect to the temperature increasing from 20 to 320 K. The energies of μTR and μPL measurements are comparable for verification of the direct band edge of Ga2Se3. With the optimal direct band edge, a peak SPV responsivity of ∼6.2 mV/μW can be detected in a Cu/Ga2Se3 SSC structure at 2.25 eV, while a maximum photoresponsivity of R ∼ 2.25 A/W of the Ga2Se3 photoconductor (at f = 30 Hz) can be measured at 642 nm. The normalized gain and detectivity of the Ga2Se3 photoconductor are estimated to be Γn = 8.34 × 10–3 cm–2·V–1 and D* = 2.5 × 1010 Jones. The value of normalized gain is higher than that for previous GaSe and WSe2 photo-FETs owing to the defect nature of Ga2Se3, which can extend the carrier lifetime of the photoconductor.

Experimental Section

Crystal Growth

Ga2Se3 single crystals were grown by the chemical vapor transport method using ICl3 as the transport agent. The starting-material powders with a stoichiometric composition of Ga (99.99% pure) and Se (99.999% pure) were first prepared. The starting materials together with appropriate amount of the transport agent ICl3 (10 mg/cm3) were cooled with liquid nitrogen and were then sealed in a vacuum of ∼10–6 Torr inside a quartz ampoule. The growth temperature was set as 850 → 780 °C with a gradient of −3.5 °C/cm for simultaneously growing two ampoules of Ga2Se3. The reaction was kept for 280 h for growing large single crystals. After the growth, several bulk crystals and microcrystals with a size ranging from hundred cubic micrometers to hundred cubic millimeters and showing a dark red color were obtained. Powder XRD measurement was implemented using the Cu Kα line as the X-ray source. The result showed a zincblende phase of the as-grown Ga2Se3 crystals.

Micro-Raman and Micro-Photoluminescence Experiments

The μRaman and μPL measurements were carried out in an integrated RAMaker microscope spectrometer with a 532 nm solid-state diode-pump laser as the excitation source. A light-guiding microscope (LGM) equipped with an Olympus objective lens (50×, working distance ∼8 mm) acted as the interconnection-coupled medium between the microcrystal sample, incident and reflected lights, and the charge-coupled device (CCD) spectrometer. A Janis liquid helium open-circled cryostat equipped with a Lakeshore 335 digital thermometer controller facilitated low-temperature and temperature-dependent measurements.

Micro-Thermal-Modulated Reflectance and Micro-Transmission

Samples for μTR and μTransmittance measurements were prepared in sheet-plate Ga2Se3 of dimensions ∼0.8 × 0.8 × 0.06 mm3 and a polished surface. For μTR measurement, a 150 W tungsten halogen lamp acted as the white light source. The sheet-plate Ga2Se3 was closely attached to an Au-evaporated quartz plate. A 4 Hz heating current (∼0.5 A) was supplied to the Au heater periodically for thermal modulation of the lattice constant and band edge of the sample. The Janis liquid helium cryostat was also used to facilitate the temperature-dependent measurement from low to room temperature. The white light source was dispersed by a monochromator equipped with a 1200 grooves/mm grating for providing the monochromatic light. The monochromatic light source was coupled to the sheet-plate Ga2Se3 sample using silica fiber and passed through the LGM. The reflected light from the layered sample was collected by the LGM and coupled to an EG&G HUV200B Si detector using silica fiber. The optical alignment of the nanoflake sample was facilitated by the adjustment of a CCD imaging camera equipped in the LGM. For micro-transmission measurement, the LGM was used for guiding the incident white light of a tungsten halogen lamp onto the sheet-plate Ga2Se3 sample using silica fiber. The sample was closely mounted on the cryostat with a center hole of size ∼80 μm for light transmission. The transmission light of the sample was collected by the fiber and then coupled to a CCD spectrometer.

Surface Photovoltaic Response and Photoconductivity Measurements

For SPV response measurement, a Ga2Se3 crystal of size 0.3 × 0.2 × 0.04 cm3 was attached to a copper sample holder using a silver paste; the holder acted as the bottom electrode of the measurement. The top sample surface was contacted with a copper mesh for acting as the top electrode. The incident monochromatic light source of SPV response measurement is similar to μTR. The photoexcited electron–hole pairs from the surface band-bending region were extracted from the top and bottom electrodes of the capacitor-like configuration and sent to an EG&G model 7265 lock-in amplifier. The incident light of SPV response measurement was chopped at 200 Hz. For PC measurement, the size of the Ga2Se3 crystal was made similar to that for the SPV response measurement. The two ends of the photoconductor sample were coated with indium for acting as the ohmic contact electrodes. A 1 MΩ load resistor was connected in series to the sample and a bias of 30 V was applied. The chopped frequencies of incident monochromatic light were set from 30 to 1000 Hz for evaluation of frequency-dependent PC responses. All of the SPV response and PC spectra were normalized to the optical power measured using an Ophir optical power meter at each wavelength.

Acknowledgments

This work was sponsored by funding from the Ministry of Science and Technology, Taiwan, under grant numbers MOST107-2112-M-011-001-MY3 and MOST108-2221-E-011-138-MY2.

The author declares no competing financial interest.

References

  1. Novoselov K. S.; Geim A. K.; Morozov S. V.; Jiang D.; Zhang Y.; Dubonos S. V.; Grigorieva I. V.; Firsov A. A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
  2. Yin Z.; Li H.; Li H.; Jiang L.; Shi Y.; Sun Y.; Lu G.; Zhang Q.; Chen X.; Zhang H. Single-Layer MoS2 Phototransistors. ACS Nano 2012, 6, 74–80. 10.1021/nn2024557. [DOI] [PubMed] [Google Scholar]
  3. Ovchinnikov D.; Gargiulo F.; Allain A.; Pasquier D. J.; Dumcenco D.; Ho C. H.; Yazyev O. V.; Kis A. Disorder Engineering and Conductivity Dome in ReS2 with Electrolyte Gating. Nat. Commun. 2016, 7, 12391 10.1038/ncomms12391. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Ho C. H.; Huang C. E. Optical Property of the Near Band-Edge Transitions in Rhenium Disulfide and Diselenide. J. Alloys Compd. 2004, 383, 74–79. 10.1016/j.jallcom.2004.04.011. [DOI] [Google Scholar]
  5. Zhou X.; Tian Z.; Kim H. J.; Wang Y.; Xu B.; Pan R.; Chang Y. J.; Di Z.; Zhou P.; Mei Y. Rolling up MoSe2 Nanomembranes as a Sensitive Tubular Photodetector. Small 2019, 15, 1902528 10.1002/smll.201902528. [DOI] [PubMed] [Google Scholar]
  6. Sun J.; Wang Y.; Guo S.; Wan B.; Dong L.; Gu Y.; Song C.; Pan C.; Zhang Q.; Gu L.; Pan F.; Zhang J. Lateral 2D WSe2 p–n Homojunction Formed by Efficient Charge-Carrier-Type Modulation for High-Performance Optoelectronics. Adv. Mater. 2020, 32, 1906499 10.1002/adma.201906499. [DOI] [PubMed] [Google Scholar]
  7. Ho C. H.; Wu C. C.; Cheng Z. H. Crystal Structure and Electronic Structure of GaSe1–xSx Series Layered Solids. J. Cryst. Growth 2005, 279, 321–328. 10.1016/j.jcrysgro.2005.02.042. [DOI] [Google Scholar]
  8. Jung C. S.; Shojaei F.; Park K.; Oh J. Y.; Im H. S.; Jang D. M.; Park J.; Kang H. S. Red-to-Ultraviolet Emission Tuning of Two-Dimensional Gallium Sulfide/Selenide. ACS Nano 2015, 9, 9585–9593. 10.1021/acsnano.5b04876. [DOI] [PubMed] [Google Scholar]
  9. Wu C. C.; Ho C. H.; Shen W. T.; Cheng Z. H.; Huang Y. S.; Tiong K. K. Optical Properties of GaSe1–xSx Series Layered Semiconductors Grown by Vertical Bridgman Method. Mater. Chem. Phys. 2004, 88, 313–317. 10.1016/j.matchemphys.2004.07.011. [DOI] [Google Scholar]
  10. Ho C. H. Thickness-dependent Carrier Transport and Optically Enhanced Transconductance Gain in III-VI Multilayer InSe. 2D Mater. 2016, 3, 025019 10.1088/2053-1583/3/2/025019. [DOI] [Google Scholar]
  11. Lin Z.; Liu Y.; Halim U.; Ding M.; Liu Y.; Wang Y.; Jia C.; Chen P.; Duan X.; Wang C.; Song F.; Li M.; Wan C.; Huang Y.; Duan X. Solution-processable 2D Semiconductors for High-performance Large-area Electronics. Nature 2018, 562, 254–258. 10.1038/s41586-018-0574-4. [DOI] [PubMed] [Google Scholar]
  12. Akinwande D.; Petrone N.; Hone J. Two-dimensional Flexible Nanoelectronics. Nat. Commun. 2014, 5, 5678 10.1038/ncomms6678. [DOI] [PubMed] [Google Scholar]
  13. Chuang C. A.; Lin M. H.; Yeh B. X.; Ho C. H. Curvature-dependent Flexible Light Emission from Layered Gallium Selenide Crystals. RSC Adv. 2018, 8, 2733–2739. 10.1039/C7RA11600D. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gao L. Flexible Device Applications of 2D Semiconductors. Small 2017, 13, 1603994 10.1002/smll.201603994. [DOI] [PubMed] [Google Scholar]
  15. Li H.; Huang J. K.; Shi Y.; Li L. J. Toward the Growth of High Mobility 2D Transition Metal Dichalcogenide Semiconductors. Adv. Mater. Interfaces 2019, 6, 1900220 10.1002/admi.201900220. [DOI] [Google Scholar]
  16. Ho P. H.; Chang Y. R.; Chu Y. C.; Li M. K.; Tsai C. A.; Wang W. H.; Ho C. H.; Chen C. W.; Chiu P. W. High-Mobility InSe Transistors: The Role of Surface Oxides. ACS Nano 2017, 11, 7362–7370. 10.1021/acsnano.7b03531. [DOI] [PubMed] [Google Scholar]
  17. Li M.; Lin C. Y.; Yang S. H.; Chang Y. M.; Chang J. K.; Yang F. S.; Zhong C.; Jian W. B.; Lien C. H.; Ho C. H.; Liu H. J.; Huang R.; Li W.; Lin Y. F.; Chu J. High Mobilities in Layered InSe Transistors with Indium-Encapsulation-Induced Surface Charge Doping. Adv. Mater. 2018, 30, 1803690 10.1002/adma.201803690. [DOI] [PubMed] [Google Scholar]
  18. Ho C. H.; Liu Z. Z. Complete-series Excitonic Dipole Emissions in Few Layer ReS2 and ReSe2 Observed by Polarized Photoluminescence Spectroscopy. Nano Energy 2019, 56, 641–650. 10.1016/j.nanoen.2018.12.014. [DOI] [Google Scholar]
  19. Ho C. H.; Yen P. C.; Huang Y. S.; Tiong K. K. Photoreflectance Study of the Excitonic Transitions of Rhenium Disulphide Layer Compounds. Phys. Rev. B 2002, 66, 245207 10.1103/PhysRevB.66.245207. [DOI] [Google Scholar]
  20. Mak K. F.; Lee C.; Hone J.; Shan J.; Heinz T. F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805 10.1103/PhysRevLett.105.136805. [DOI] [PubMed] [Google Scholar]
  21. Kang J.; Zhang L.; Wei S. H. A Unified Understanding of the Thickness-Dependent Bandgap Transition in Hexagonal Two-Dimensional Semiconductors. J. Phys. Chem. Lett. 2016, 7, 597–602. 10.1021/acs.jpclett.5b02687. [DOI] [PubMed] [Google Scholar]
  22. Mudd G. W.; Svatek S.; Ren T.; Patane A.; Makarovski O.; Eaves L.; Beton P. H.; Kovalyuk Z. D.; Lashkarev G. V.; Kudrynskyi Z. R.; Dmitriev A. I. Tuning the Bandgap of Exfoliated InSe Nanosheets by Quantum Confinement. Adv. Mater. 2013, 25, 5714–5718. 10.1002/adma.201302616. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Ho C. H.; Huang K. W. Visible Luminescence and Structural Property of GaSe1–xSx (0≤x≤1) Series Layered Crystals. Solid State Commun. 2005, 136, 591–594. 10.1016/j.ssc.2005.09.029. [DOI] [Google Scholar]
  24. Ho C. H.; Chu Y. J. Bending Photoluminescence and Surface Photovoltaic Effect on Multilayer InSe 2D Microplate Crystals. Adv. Opt. Mater. 2015, 3, 1750–1758. 10.1002/adom.201500390. [DOI] [Google Scholar]
  25. Park K. H.; Kim H. G.; Kim W. T.; Kim C. D.; Jeong H. M.; Lee K. J.; Lee B. H. Optical Properties of Ga2Se3:Co2+ Single Crystals. Solid State Commun. 1989, 70, 971–974. 10.1016/0038-1098(89)90639-X. [DOI] [Google Scholar]
  26. Abdal-Rahman M.; Shaikh H. A. E. Photoelectric Properties of Ga2Se3 Single Crystals. J. Phys. D: Appl. Phys. 1996, 29, 889–892. 10.1088/0022-3727/29/3/057. [DOI] [Google Scholar]
  27. Hahn H.; Klingler W. Über die Kristallstrukturen von Ga2S3, Ga2Se3 und Ga2Te3. Z. Anorg. Chem. 1949, 259, 135–142. 10.1002/zaac.19492590111. [DOI] [Google Scholar]
  28. Lübbers D.; Leute V. The Crystal Structure of β-Ga2Se3. J. Solid State Chem. 1982, 43, 339–345. 10.1016/0022-4596(82)90250-X. [DOI] [Google Scholar]
  29. Palatnik L. S.; Belova E. K. Investigation of the Polymorphism of Ga2Se3 Selenide of Variable Composition. Inorg. Mater. 1965, 1, 1703. [Google Scholar]
  30. Ueno K.; Kawayama M.; Dai Z. R.; Koma A.; Ohuchi F. S. Growth and Characterization of Ga2Se3/GaAs(100) Epitaxial Thin Films. J. Cryst. Growth 1999, 207, 69–76. 10.1016/S0022-0248(99)00359-0. [DOI] [Google Scholar]
  31. Ho C. H.; Chen H. H. Optically Decomposed Near-band-edge Structure and Excitonic transitions in Ga2S3. Sci. Rep. 2015, 4, 6143 10.1038/srep06143. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Liu H. F.; Ansah Antwi K. K.; Yakovlev N. L.; Tan H. R.; Ong L. T.; Chua S. J.; Chi D. Z. Synthesis and Phase Evolutions in Layered Structure of Ga2S3 Semiconductor Thin Films on Epiready GaAs (111) Substrates. ACS Appl. Mater. Interfaces 2014, 6, 3501–3507. 10.1021/am4056535. [DOI] [PubMed] [Google Scholar]
  33. Park K.; Lee J.; Kim D.; Seo J.; Lee J. A.; Kwak I. H.; Kwon I. S.; Ahn J. P.; Park J. GaAsSe Ternary Alloy Nanowires for Enhanced Photoconductivity. J. Phys. Chem. C 2019, 123, 3908–3915. 10.1021/acs.jpcc.8b11652. [DOI] [Google Scholar]
  34. Peressi M.; Baldereschi A. Structural and Electronic Properties of Ga2Se3. J. Appl. Phys. 1998, 83, 3092–3095. 10.1063/1.367066. [DOI] [Google Scholar]
  35. Ho C. H.; Huang C. E.; Wu C. C. Preparation and Characterization of Ni-incorporated FeS2 Single Crystals. J. Cryst. Growth 2004, 270, 535–541. 10.1016/j.jcrysgro.2004.07.017. [DOI] [Google Scholar]
  36. Ho C. H.; Lo S. F.; Chi P. C. Electronic Structure and E1 Excitons of CuInS2 Energy-Related Crystals Studied by Temperature-Dependent Thermoreflectance Spectroscopy. J. Electrochem. Soc. 2010, 157, H219–H226. 10.1149/1.3270434. [DOI] [Google Scholar]
  37. Ho C. H.; Chiou M. C.; Herninda T. M. Nanowire Grid Polarization and Polarized Excitonic Emission Observed in Multilayer GaTe. J. Phys. Chem. Lett. 2020, 11, 608–617. 10.1021/acs.jpclett.9b03569. [DOI] [PubMed] [Google Scholar]
  38. Finkman E.; Tauc J.; Kershaw R.; Wold A. Lattice dynamics of tetrahedrally bonded semiconductors containing ordered vacant sites. Phys. Rev. B 1975, 11, 3785 10.1103/PhysRevB.11.3785. [DOI] [Google Scholar]
  39. Julien C.; Barnier S.; Ivanov I.; Guittard M.; Pardo M. P.; Chilouet A. Vibrational Studies of Copper Thiogallate Solid Solutions. Mater. Sci. Eng., B 1999, 57, 102–109. 10.1016/S0921-5107(98)00418-8. [DOI] [Google Scholar]
  40. Lucazeau G.; Leory J. Etude Vibrationnelle de α-Ga2S3. Spectrochim. Acta, Part A 1978, 34, 29–32. 10.1016/0584-8539(78)80181-0. [DOI] [Google Scholar]
  41. Heo J.; Yoon J. M.; Ryou S.-Y. Raman Spectroscopic Analysis on the Solubility Mechanism of La3+ in GeS2–Ga2S3 Glasses. J. Non-Cryst. Solids 1998, 238, 115–123. 10.1016/S0022-3093(98)00577-8. [DOI] [Google Scholar]
  42. Ho C. H.; Tseng C. Y.; Tien L. C. Thermoreflectance Characterization of β-Ga2O3 Thin-film Nanostrips. Opt. Express 2010, 18, 16360–16369. 10.1364/OE.18.016360. [DOI] [PubMed] [Google Scholar]
  43. Ho C. H.; Tsai M. C.; Wong M. S. Characterization of Indirect and Direct Interband Transitions of Anatase TiO2 by Thermoreflectance Spectroscopy. Appl. Phys. Lett. 2008, 93, 081904 10.1063/1.2975846. [DOI] [Google Scholar]
  44. Aspnes D. E.Modulation Spectroscopy/Electric Field Effects on the Dielectric Fuction of Semiconductors. In Handbook on Semiconductors 2; Balkanski M., Ed.; North Holland: Amsterdam, 1980; Chapter 4A, pp 109–154. [Google Scholar]
  45. Zhang M. J.; Jiang X. M.; Zhou L. J.; Guo G. C. Two Phases of Ga2S3: Promising Infrared Second-order Nonlinear Optical Materials with Very High Laser Induced Damage Thresholds. J. Mater. Chem. C 2013, 1, 4754–4760. 10.1039/c3tc30808a. [DOI] [Google Scholar]
  46. Varshni Y. P. Temperature Dependence of the Energy Gap in Semiconductors. Physica 1967, 34, 149–154. 10.1016/0031-8914(67)90062-6. [DOI] [Google Scholar]
  47. Ho C. H.; Wang Y. P.; Chan C. H.; Huang Y. S.; Li C. H. Temperature-dependent Photoconductivity in β-In2S3 Single Crystals. J. Appl. Phys. 2010, 108, 043518 10.1063/1.3478719. [DOI] [Google Scholar]
  48. Ho C. H.; Wang Y. P.; Huang Y. S. Optical Characterization of Band-Edge Property of In6S7 Compound. Appl. Phys. Lett. 2012, 100, 131905 10.1063/1.3698334. [DOI] [Google Scholar]
  49. Yang H. W.; Hsieh H. F.; Chen R. S.; Ho C. H.; Lee K. Y.; Chao L. C. Ultraefficient Ultraviolet and Visible Light Sensing and Ohmic Contacts in High-Mobility InSe Nanoflake Photodetectors Fabricated by the Focused Ion Beam Technique. ACS Appl. Mater. Interfaces 2018, 10, 5740–5749. 10.1021/acsami.7b15106. [DOI] [PubMed] [Google Scholar]
  50. Alam M. J.; Murkute P.; Ghadi H.; Sushama S.; Dwivedi S. M. M. D.; Ghosh A.; Ghosh C.; Mondal A.; Paul S.; Mondal S.; Chakrabarti S. Enhancing Responsivity and Detectivity in Broadband UV–VIS Photodetector by Ex-situ UV–ozone Annealing Technique. Superlattices Microstruct. 2020, 137, 106333 10.1016/j.spmi.2019.106333. [DOI] [Google Scholar]
  51. Abderrahmane A.; Jung P. G.; Kim N. H.; Ko P. J.; Sandhu A. Gate-tunable Optoelectronic Properties of a Nano-layered GaSe Photodetector. Opt. Mater. Express 2017, 7, 587–592. 10.1364/OME.7.000587. [DOI] [Google Scholar]
  52. Hu P.; Wen Z.; Wang L.; Tan P.; Xiao K. Synthesis of Few-Layer GaSe Nanosheets for High Performance Photodetectors. ACS Nano 2012, 6, 5988–5994. 10.1021/nn300889c. [DOI] [PubMed] [Google Scholar]
  53. Zhou N.; Gan L.; Yang R.; Wang F.; Li L.; Chen Y.; Li D.; Zhai T. Nonlayered Two-Dimensional Defective Semiconductor γ-Ga2S3 toward Broadband Photodetection. ACS Nano 2019, 13, 6297–6307. 10.1021/acsnano.9b00276. [DOI] [PubMed] [Google Scholar]
  54. Zou Z.; Li D.; Liang J.; Zhang X.; Liu H.; Zhu C.; Yang X.; Li L.; Zheng B.; Sun X.; Zeng Z.; Yi J.; Zhuang X.; Wang X.; Pan A. Epitaxial Synthesis of Ultrathin β-In2Se3/MoS2 Heterostructures with High Visible/Near-infrared Photoresponse. Nanoscale 2020, 12, 6480–6488. 10.1039/C9NR10387B. [DOI] [PubMed] [Google Scholar]
  55. Kang D. H.; Kim M. S.; Shim J.; Jeon J.; Park H. Y.; Jung W. S.; Yu H. Y.; Pang C. H.; Lee S.; Park J. H. High-Performance Transition Metal Dichalcogenide Photodetectors Enhanced by Self-assembled Monolayer Doping. Adv. Funct. Mater. 2015, 25, 4219–4227. 10.1002/adfm.201501170. [DOI] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES