Extraction technique of trap states based on transient photo-voltage measurement

Abstract

This article puts forward a technique for extracting the density of trap states (DOS_T) distribution based on the transient photo-voltage (TPV) measurement result. We prove that when the TPV result is linear, the DOS_T distribution is exponential type and vice versa. Compared to the approach based on the space charge limited current measurement, the method given in this paper has the advantage of requiring less calculation. The results obtained by our method provides a guidance for preparing less trap states solar cells.

Introduction

In order to improve the photo-voltaic performance of perovskite solar cells (PSCs), we need to further explore the mechanism such as carrier mobility^1–3, ion migration^4–8, density of trap states (DOS_T) distribution^9–13, carrier recombination^14–18 and so on. The DOS_T distribution is a crucial factor that determines the photovoltaic performance of PSCs^19–33. According to the literatures in recent years^19–23, current density–voltage (J–V) hysteresis is caused by the ion migration and trap assisted carrier recombination. The DOS_T distribution affects the carrier recombination^24–27, influences the open circuit voltage^28–30, and hinders the enhancement of power conversion efficiency (PCE)^31–34. The DOS_T distribution cannot be obtained by experimental measurement directly. There are only few methods for the extraction of DOS_T distribution. The space charge limited current (SCLC) method uses the deconvolution to extract the DOS_T distribution^35–40, based on the measured J–V data at different temperatures. Walter et al.^41–45 put forward the impedance spectroscopy (IS) method to extract the DOS_T distribution. They extract the DOS_T distribution based on the plot of equivalent chemical capacitance versus frequency given by IS measurement^41–45. They regard the capture and de-capture of carrier by the trap states in the PSCs as charging and discharging of the equivalent chemical capacitance⁴¹. They put forward the formula DOS_T (E_ω) = (V_bi/eW)(dC/dω)(ω/k_B) to extract the DOS_T distribution^41–45. Here, C is the equivalent chemical capacitance. ω is the angular frequency of the ac signal. V_bi is the built-in electric voltage. W is the depletion width. k_B is the Boltzmann constant. e is the elementary charge. The corresponding energy level is calculated by the formula E_ω = k_BTln(ω₀/ω), where T is the ambient temperature and ω₀ is the attempt-to-escape frequency^41–45. Wang et al.⁴⁶ proposed a transient photo-voltage (TPV) method for DOS_T distribution extraction. Based on the hypothesis of exponential type DOS_T distribution^46–49, multiple-trapping model^46,50–52, and the zero-temperature approximation^46,52, they find that when the DOS_T distribution is exponential type, the logarithm of carrier lifetime and the photo-voltage satisfy linear relation. They use this relation to extract the DOS_T distribution based on the TPV result^46–48. Because of the hypothesis of exponential type distribution^46–49, their method is effective only when the TPV result is linear. The DOS_T distribution extracted by their method is an exponential type distribution^46–48.

However, according to the TPV experiments reported in recent years^46–48, the majority of TPV results are non-linear. In these cases, the method of Wang et al. is not effective to extract the DOS_T distribution. In this article, we put forward a new technique for extraction of DOS_T distribution based on the TPV measurement result. We give up the hypothesis of exponential type DOS_T distribution^46–49 and zero-temperature approximation^46,52. The method given in our work is based on the single hypothesis of multiple-trapping model^46,50–52. Our method is effective for arbitrary TPV results and can be used to extract general type DOS_T distribution.

Results and discussion

Establishment of theory and method

In this section, we establish the equation for the extraction of DOS_T distribution based on the TPV result.

Because of the trap states in the perovskite absorber layer, the behavior of trapping and de-trapping of carrier by the trap states determines the recombination rate, which can be described by the multiple-trapping model^46,50–52. According to the multiple-trapping model, the relation of carrier lifetime τ_n and the free carrier lifetime τ_f satisfies^46,50–52

$${\tau }_{\text{n}}=(\partial n/\partial n_{\text{c}}){\tau }_{\text{f}}.$$ 1

Here n = n_t + n_c denotes the sum of electron density in trap states n_t and electron density in conduct band n_c.

Therefore, we have

$${\tau }_{\text{n}}=(1+\partial n_{\text{t}}/\partial n_{\text{c}}){\tau }_{\text{f}},$$ 2

which can be rewritten as

$${\tau }_{\text{n}}=\left(1+\frac{\partial n_{\text{t}}/\partial E_{\text{Fn}}}{\partial n_{\text{c}}/\partial E_{\text{Fn}}}\right){\tau }_{\text{f}}.$$ 3

The density of electron in trap states satisfies^46,52

$$n_{\text{t}}=\int {\rho }_{\text{t}}\left(E\right)f\left(E\right)dE.$$ 4

Here ${\rho }_{\text{t}}\left(E\right)$ denotes the DOS_T distribution. $f\left(E\right)=\frac{1}{exp\left(\frac{E-E_{\text{Fn}}}{k_{B}T}\right)+1}$ denotes the Fermi–Dirac distribution⁵³.

Therefore, we have

$$\frac{\partial n_{\text{t}}}{\partial \left(\frac{E_{\text{Fn}}}{k_{\text{B}}T}\right)}=\frac{\partial }{\partial \left(\frac{E_{\text{Fn}}}{k_{\text{B}}T}\right)}\left(\int {\rho }_{\text{t}}\left(E\right)f\left(E\right)dE\right).$$ 5

According to the Fermi–Dirac distribution⁵³, we have

$$\frac{\partial n_{\text{t}}}{\partial \left(\frac{E_{\text{Fn}}}{k_{\text{B}}T}\right)}=\int {\rho }_{\text{t}}\left(E\right)f\left(E\right)\left(1-f\left(E\right)\right)dE.$$ 6

We rewrite Eq. (6) as

$$\frac{\partial n_t}{\partial E_{\mathit{Fn}}}=\frac{1}{k_{B}T}\int {\rho }_{\text{t}}\left(E\right)f\left(E\right)\left(1-f\left(E\right)\right)dE.$$ 7

The carrier density in conductor band satisfies^46,52,53

$$n_{\text{c}}=N_{\text{c}}exp\left(\frac{E_{\text{Fn}}-E_{\text{c}}}{k_{\text{B}}T}\right).$$ 8

Here N_c is the density of effective states in conduction band. E_c is the conduction band energy level position⁵³.

Therefore, we have

$$\partial n_{\text{c}}/\partial E_{\text{Fn}}=n_{\text{c}}/k_{\text{B}}T.$$ 9

According to Eqs. (3), (7), and (9), we have

$${\tau }_{\text{n}}=\left(1+\frac{\int {\rho }_{\text{t}}\left(E\right)f\left(E\right)\left(1-f\left(E\right)\right)dE}{n_{\text{c}}}\right){\tau }_{\text{f}}.$$ 10

We rewrite Eq. (10) as

$$\int {\rho }_{\text{t}}\left(E\right)f\left(E\right)\left(1-f\left(E\right)\right)dE=\left(\frac{{\tau }_{\text{n}}}{{\tau }_{\text{f}}}-1\right)n_{\text{c}}.$$ 11

Substituting the Fermi–Dirac distribution into Eq. (11), we have

$$\int {\rho }_{\text{t}}\left(E\right)\frac{1}{exp\left(\frac{E-E_{\text{Fn}}}{k_{B}T}\right)+1}\left(1-\frac{1}{exp\left(\frac{E-E_{\text{Fn}}}{k_{B}T}\right)+1}\right)dE=\left(\frac{{\tau }_{\text{n}}}{{\tau }_{\text{f}}}-1\right)n_{\text{c}}.$$ 12

We rewrite Eq. (12) as

$$\int {\rho }_{\text{t}}\left(E\right)\frac{1}{exp\left(\frac{-\left(E_{\text{Fn}}-E\right)}{k_{B}T}\right)+1}\left(1-\frac{1}{exp\left(\frac{-\left(E_{\text{Fn}}-E\right)}{k_{B}T}\right)+1}\right)dE=\left(\frac{{\tau }_{\text{n}}}{{\tau }_{\text{f}}}-1\right)n_{\text{c}}.$$ 13

We define a derivation factor

$$g\left(E_{\text{Fn}}-E\right)=\frac{1}{exp\left(\frac{-\left(E_{\text{Fn}}-E\right)}{k_{B}T}\right)+1}\left(1-\frac{1}{exp\left(\frac{-\left(E_{\text{Fn}}-E\right)}{k_{B}T}\right)+1}\right).$$ 14

and rewrite Eq. (13) as

$$\int {\rho }_{\text{t}}\left(E\right)g\left(E_{\text{Fn}}-E\right)dE=\left(\frac{{\tau }_{\text{n}}}{{\tau }_{\text{f}}}-1\right)n_{\text{c}}.$$ 15

According to the TPV result, the carrier lifetime is a function of photo-voltage^46–49. Therefore, we rewrite Eq. (15) as

$$\int {\rho }_{\text{t}}\left(E\right)g\left(E_{\text{Fn}}-E\right)dE=\left(\frac{{\tau }_{\text{n}}\left(V_{\text{ph}}\right)}{{\tau }_{\text{f}}}-1\right)n_{\text{c}}.$$ 16

Equation (16) is the fundamental equation of our method. The right-hand side of Eq. (16) can be obtained from experimental measurement. τ_n(V_ph) can be measured from TPV experiment. n_c can be obtained from differential charging method⁵ or from SCLC under different intensity of illumination³⁹. We can use absorbance spectrum, Kelvin probe (KP), ultraviolet photoemission spectroscopy (UPS), and X-ray photoelectron spectroscopy (XPS) to get conduction band energy level position E_c, valence band energy level position E_v, Fermi energy level position E_F0 and band gap E_g³⁵, respectively. After getting the conductor band electron density in dark n₀ and in different intensity of illumination n_c, according to the relation E_Fn = E_F0 + k_BTln(n_c/n₀)⁵³, we obtain the electron quasi Fermi energy level E_Fn corresponding to the photo-voltage V_ph in the different intensity of illumination. The free carrier lifetime τ_f can be measured or can be calculated according to the equationτ_f = 1/C_nN_t⁵⁴. Here, N_t is the electron trap concentration. C_n denotes the capture coefficients for electrons. Since the left-hand side of Eq. (16) is the convolution integral of the DOS_T distribution and the derivative factor, we can get the DOS_T distribution by deconvolution. We use the numerical deconvolution function ([q,r] = deconv(u,v)) of MATLAB to solve the equation for DOS_T distribution.

For intrinsic perovskite, the electron density in conductor band satisfies⁵³

$$n_{\text{c}}=N_{\text{c}}exp\left(\frac{E_{\text{Fn}}-E_{\text{cb}}}{k_{\text{B}}T}\right)=n_{0}exp\left(\frac{V_{\text{ph}}e}{2k_{\text{B}}T}\right).$$ 17

Here $n_0=N_{\text{c}}exp\left(\frac{E_{\text{F}0}-E_{\text{cb}}}{k_{\text{B}}T}\right)$ is the electron density in conductor band at dark state⁵³.

Substituting Eq. (17) into Eq. (16), we have

$$\int {\rho }_{\text{t}}\left(E\right)g\left(E_{\text{Fn}}-E\right)dE=\left(\frac{{\tau }_{\text{n}}\left(V_{\text{ph}}\right)}{{\tau }_{\text{f}}}-1\right)n_{0}exp\left(\frac{V_{\text{ph}}e}{2k_{\text{B}}T}\right).$$ 18

Equation (18) is the fundamental equation for DOS_T distribution extraction of intrinsic perovskite. Similarly, we obtain the DOS_T distribution using numerical deconvolution function in MATLAB. The parameters used for calculation are list in Table 1^27,35.

Table 1.

Parameters used for DOS_T distribution calculation^27,35.

Sym	Description	Value
e	Elementary charge	1.60 × 10–19 C
kB	Boltzmann constant	1.38 × 10–23 JK−1
Ec	Conduction band minimum	− 4.18 eV
Eg	Band gap	1.52 eV
EF0	Fermi energy level	− 4.3 eV
T	Ambient temperature	300 K
Nc	Conduction band DoS	1 × 1024 m−3
Cn	Electron trap coefficients	1 × 10–15 m3 s−1
Nt	Electron trap concentration	1 × 1019 m−3

Exponential type DOS_T distribution

In this section, we explore the exponential type DOS_T distribution. Wang et al.⁴⁶ find that for the exponential type DOS_T distribution, the logarithm of carrier lifetime is proportional to the photo-voltage (TPV result). The proof of this relation is shown as follows.

The exponential type DOS_T distribution satisfies^46–49

$${\rho }_{\text{t}}\left(E\right)=\frac{N_T}{E_{\text{B}}}exp\left(\frac{E-E_{\text{c}}}{E_{\text{B}}}\right).$$ 19

Here, E_B is the characteristic energy and N_T is the total density of the trapped state. Substituting formula (19) into formula (4), and taking zero-temperature approximation^46,52, we have

$$n_{\text{T}}=N_{\text{T}}\left(exp\left(\frac{E_{\text{Fn}}-E_{\text{c}}}{E_{\text{B}}}\right)-exp\left(\frac{E_{\text{v}}-E_{\text{c}}}{E_{\text{B}}}\right)\right).$$ 20

Making the approximation of n ≈ n_T⁵⁰, we rewrite the multiple-trapping model^46,50–52 as

$${\tau }_{\text{n}}=(\partial n_{\text{T}}/\partial n_{\text{c}}){\tau }_{\text{f}},$$ 21

which is equivalent to

$${\tau }_{\text{n}}=\frac{\partial n_{\text{T}}/\partial V_{\text{ph}}}{\partial n_{\text{c}}/\partial V_{\text{ph}}}{\tau }_{\text{f}}.$$ 22

The electron density in conductor band satisfies⁵³

$$n_{\text{c}}=N_{\text{c}}exp\left(\frac{E_{\text{Fn}}-E_{\text{c}}}{k_{\text{B}}T}\right).$$ 23

According to Eqs. (20), (22), and (23) and from the relation of E_Fn = E_Fp + eV_ph, we have

$$ln{\tau }_{\text{n}}=\left(e/E_{\text{B}}-e/k_{\text{B}}T\right)V_{\text{ph}}+lnA.$$ 24

Here $A=\frac{N_{\text{T}}{k}_{\text{B}}T}{N_{\text{c}}{E}_{\text{B}}}exp\left(\frac{E_{\text{Fp}}-E_{\text{c}}}{E_{\text{B}}}-\frac{E_{\text{Fp}}-E_{\text{c}}}{k_{\text{B}}T}\right){\tau }_{\text{f}}$.

We write Eq. (24) as linear mathematical form lnτ_n = aV_ph + b.

Here, a = e/E_B − e/k_BT, b = lnA.

Therefore, we finish the proof of this relation. Note that for the intrinsic perovskite, Eq. (24) can be written as

$$ln{\tau }_{\text{n}}=\left(e/2E_{\text{B}}-e/2k_{\text{B}}T\right)V_{\text{ph}}+lnA.$$ 25

Here $A=\frac{N_{\text{T}}{k}_{\text{B}}T}{N_{\text{c}}{E}_{\text{B}}}exp\left(\frac{E_{\text{F}0}-E_{\text{c}}}{E_{\text{B}}}-\frac{E_{\text{F}0}-E_{\text{c}}}{k_{\text{B}}T}\right){\tau }_{\text{f}}$. We write Eq. (25) as linear form lnτ_n = aV_ph + b. Here, a = e/2 E_B− e/2k_BT, b = lnA.

Similarly, we can also prove that when TPV result is linear, the extracted DOS_T distribution is exponential type. Details of the proof are given in the supporting information. We can use this relation to extract the DOS_T distribution when the TPV result is linear. Below, this method is called analytic method.

We can use the analytic method to verify the validity of our numerical method. We use both our numerical method and the analytic method to extract the DOS_T distribution and make a comparison. In Fig. 1a–c, we set the b = − 5 and the slope parameter a as − 1.5, − 2 and − 2.5, respectively. Using the analytic method, we derive E_B and N_T (see Table 2). Figure 1d–f shows the extracted DOS_T distributions from Fig. 1a–c using our numerical method. As expected by the analytic method, the DOS_T distribution is exponential type. In order to compare with the DOS_T distribution extracted by analytic method, we use the exponential fitting (f(E) = cexp(dE)) to calculate the E_B and N_T (see Table 2). As shown in Table 2, the E_B and N_T calculated by our numerical method are consistent with the E_B and N_T calculated by the analytic method, indicating that the numerical algorithm to do the deconvolution in our calculation is reliable. We explain the slight deviation of E_B and N_T extracted by the two methods as follows. The analytic method is established based on the three hypothesis of multiple-trapping model^46,50–52, zero-temperature approximation^46,52, and exponential type DOS_T distribution^46–49. Our numerical method is established based on the unique hypothesis of multiple-trapping model^46,50–52. Therefore, the slight deviation of E_B and N_T extracted by the two methods is attributed to the zero-temperature approximation and the fitting error.

Figure 1.

(a)–(c) Plots of carrier lifetime versus photo-voltage. We set b =  − 5 and a as − 1.5, − 2 and − 2.5, respectively. (d)–(f) DOS_T distributions extracted from (a)–(c), respectively. The blue dots represent the extracted DOS_T distributions, the red lines represent the exponential fitting of extracted DOS_T distributions.

Table 2.

Exponential fitting coefficients, distribution coefficients calculated from Fig. 2.

Coefficients	Example 1	Example 2	Example 3
Chosen parameters
a	− 1.5	− 2.0	− 2.5
b	− 5	− 5	− 5
Exponential fitting
c (exponential fitting)	1.525 × 1034	7.536 × 1033	3.666 × 1033
d (exponential fitting)	− 2.542 × 1020	− 2.466 × 1020	− 2.388 × 1020
R-square	1	1	1
Calculation result
EB(analytic method)	28.0 meV	28.8 meV	29.7 meV
EB(our method)	24.6 meV	25.3 meV	26.1 meV
NT(analytic method)	7.3050 × 1013 cm−3	7.5158 × 1013 cm−3	7.7392 × 1013 cm−3
NT(our method)	5.9992 × 1013 cm−3	3.0560 × 1013 cm−3	1.5352 × 1013 cm−3

Non-exponential type DOS_T distribution

In this section, we investigate the non-exponential type DOS_T distribution. We take the TPV data in Ref.⁴⁷ as an example. As shown in Fig. 2a,b, the TPV result is non-linear. Hence, we cannot use the analytic method to extract the DOS_T distribution.

Figure 2.

Plots of carrier lifetime versus photo-voltage given by TPV measurement⁴⁷. The black lines represent the result of TPV measurement. The red lines represent linear fitting in the subintervals. (a) shows the linear fittings of TPV in two subintervals, respectively. (b) shows the linear fittings of TPV in three subintervals, respectively.

To overcome this difficulty, Wang et al.⁴⁷ made a linear fitting in the subintervals of 0.05–0.6 V and 0.6–0.91 V (see Fig. 2a). They used formula (24) to get two values of E_B in these two subintervals, respectively⁴⁷. They explained these two E_B as two types of exponential type DOS_T distribution (They called them as deep trap type and shallow trap type)⁴⁷. However, there are some difficulties in their method. (1) Equation (24) is derived from one exponential type DOS_T distribution, not the two types of DOS_T distribution (deep trap state type DOS_T distribution and shallow trap state type DOS_T distribution). We cannot derive Eq. (24) based on these two types of distribution. (2) There is no clear boundary for deep and shallow trap. So the definition of deep and shallow trap is ambiguous. (3) It is more accurate to take linear fittings in three subintervals, respectively (see Fig. 2b). According to the differential theory, we can divide the photo-voltage interval into infinite differential subintervals and use Eq. (24) to calculate the E_B in these differential subintervals, respectively. These E_B cannot be explained by the concept of deep and shallow trap.

Our method is effective for arbitrary TPV results, which can be used to extract general type DOS_T distribution. Using our method, we extract the DOS_T distribution (as illustrated in Fig. 3). It can be seen that the extracted DOS_T distribution is not an exponential type distribution. Compared to the method given by Wang et al., our method is more accurate and it can give the fine structure of DOS_T distribution.

Figure 3.

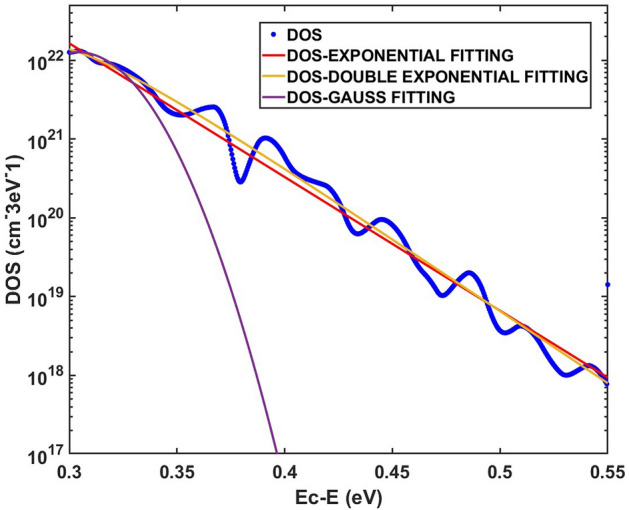
DOS_T distribution calculated by our method given in this article. The blue dots represent the extracted DOS_T distribution. The red, yellow and purple lines represent the exponential, double exponential and Gauss fittings for the extracted DOS_T distribution, respectively.

We make the exponential, double exponential and Gauss fittings for the extracted DOS_T distribution, respectively (see Fig. 3). The R-square (Coefficient of determination) of these fittings are given in Table 3. It can be see that the R-square of double exponential fitting is larger than the exponential fitting and Gauss fitting, indicating that the DOS_T distribution is more consistent with the double exponential type distribution than with the exponential type distribution. Therefore, when the TPV result is non-linear, the extracted DOS_T distribution is non-exponential type.

Table 3.

Different type fitting for extracted DOS_T distribution.

Fitting type	Exponential	Double exponential	Gauss
R-square	0.9679	0.9864	0.9331

Calculation example

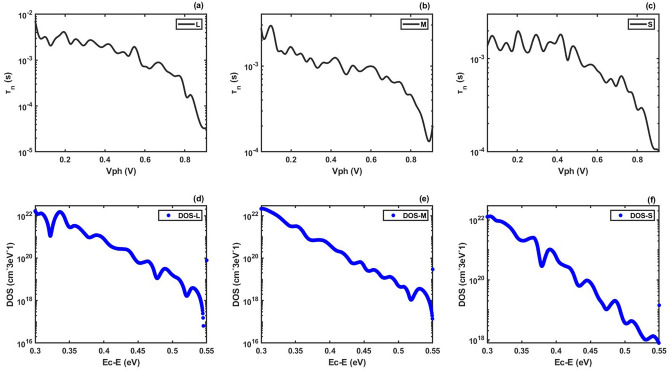
In this section, we give some examples of DOS_T distribution extraction using our method. We take the TPV data in Ref.⁴⁷ as an example. Figure 4a–c shows the TPV results for meso-structured perovskite solar cells with large, middle and small size of perovskite grain, respectively. Using our method, we extract the DOS_T distributions from Fig. 4a–c, respectively, (as shown in Fig. 4d–f).

Figure 4.

(a)–(c) TPV results for meso-structured perovskite solar cells with large, middle and small size of perovskite grain⁴⁷. (d)–(f) DOS_T distributions extracted by our method from (a)–(c), respectively.

For comparing, we plot the extracted DOS_T distributions in Fig. 5. Using the formula $T_{\mathrm{total}}=\int {\rho }_{\mathrm{t}}\left(E\right)dE$, we calculate the total amount of trap states for three solar cells. We derived T_total = 5.4431 × 10²⁰ cm⁻³ (large size), T_total = 5.9096 × 10²⁰ cm⁻³ (middle size) and T_total = 4.5628 × 10²⁰ cm⁻³ (small size). It can be seen that the solar cell with small size of perovskite grain has the least amount of trap states. This result could give a guidance for preparing perovskite solar cells with less trap states.

Figure 5.

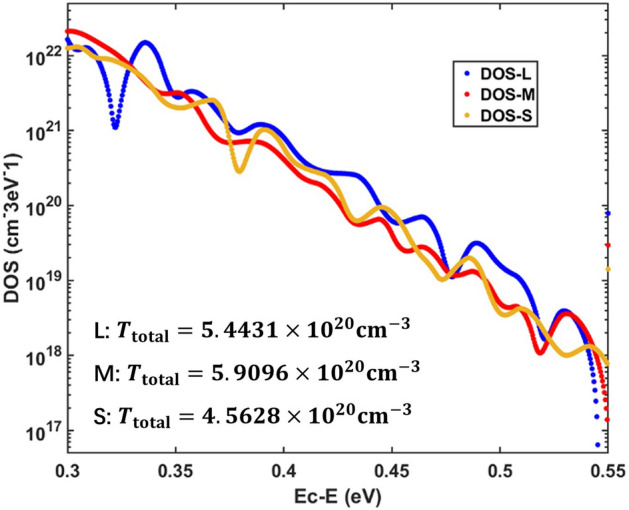
DOS_T distributions for meso-structured perovskite solar cells with large, middle and small size of perovskite grain extracted by our method given in this paper.

Comparison to SCLC method

SCLC measurement gives the relation of current density and voltage at different temperatures (j = j (U, T)). For SCLC method, we extract the DOS_T distribution adopting the equations listed as follows^35–40

$$E_{\text{a}}=-dlnj/d{\left(k_{\text{B}}T\right)}^{-1},$$ 26

$$m=d\left(\mathit{lnj}\right)/d\left(\mathit{lnU}\right),$$ 27

$$B=-\left[dm/d\left(\mathit{lnU}\right)\right]/\left[m\left(m-1\right)\left(2m-1\right)\right],$$ 28

$$C=\left(B\left(2m-1\right)+B^2\left(3m-2\right)+d\left(ln\left(1+B\right)\right)/d\left(\mathit{lnU}\right)\right)/\left(1+B\left(m-1\right)\right),$$ 29

$$\int {\rho }_{\text{t}}\left(E\right)f\left(E\right)\left(1-f\left(E\right)\right)dE=\frac{1}{k_{\text{B}}T}\frac{\epsilon U}{e{L}^2}\frac{2m-1}{m^2}\left(1+C\right).$$ 30

Here j denotes the current density. U denotes the voltage. E_a is the activation energy. m, B, C are the parameters for calculation. L is the thickness of perovskite absorber layer. e is the elementary charge. ε is the dielectric constant of perovskite absorber layer. Based on the SCLC measurement result, we need to calculate E_a, m, B, C and finally use Eq. (30) to extract the DOS_T by deconvolution^35–40. The calculations of E_a, m, B, C are complicated. For our method, we only need to use formula (18) to extract the DOS_T distribution by deconvolution. Therefore, our method takes less computation.

Conclusion

In conclusion, this article presents a new technique for DOS_T distribution extraction based on the TPV measurement result. The approach given in this paper is effective for extraction of general type DOS_T distribution. We prove that when the TPV result is linear, the DOS_T distribution is exponential type and vice versa. Our method needs less computation than the SCLC method. The obtained results provide a guidance for preparing perovskite solar cells with less trap states.

Methods

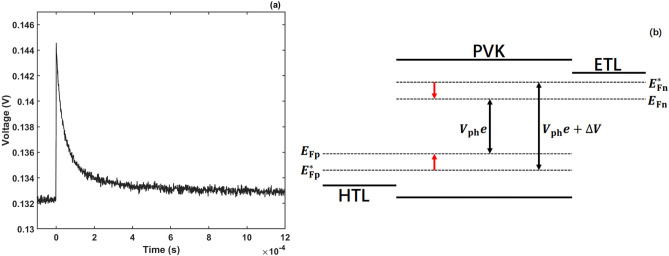
The transient photo-voltage measurement is an effective technique for the study of carrier recombination^3,46–49. Figure 6a shows the typical TPV measurement result. Figure 6b shows the mechanism of TPV experiment. Photo-voltaic device is held under open circuit. At the start of the TPV experiment, we use a steady-state bias light to illuminate the device until the equilibrium between generation and recombination is established. The steady-state bias light produces a bias photo-voltage V_ph. As a result, the Fermi energy level E_F0 changes to electron quasi Fermi energy level E_Fn and hole quasi Fermi energy level E_Fp. Thereafter, we apply an additional small light pulse to the device. With the perturbation of small light pulse, the photo-voltage increases to V_ph + ΔV. The electron quasi Fermi energy level E_Fn shifts to $E_{\mathrm{Fn}}^{\ast }$, and the hole quasi Fermi energy level E_Fp to $E_{\mathrm{Fp}}^{\ast }$. After switching off the small light pulse source, due to carrier recombination, the photo-voltage decays exponentially until it reaches the bias value V_ph. The electron quasi Fermi energy level comes back to E_Fn from $E_{\mathrm{Fn}}^{\ast }$ and the hole quasi Fermi energy level comes back to E_Fp from $E_{\mathrm{Fp}}^{\ast }$.The carrier lifetime τ_n is defined as the time taken for the photo-voltage to decay from V_ph + ΔV to V_ph + ΔV/e. Here, e is the natural constant. By tuning the intensity of steady-state bias light I, we get the relation between the photo-voltage V_ph and carrier lifetime τ_n, which is written as τ_n = τ_n(V_ph) (TPV result)^46–49.

Figure 6.

(a) Result of TPV measurement. (b) Mechanism of TPV experiment.

Author contributions

The whole work of this article is finished by Z.L.

Competing interests

The author declares no competing interests.

Supplementary information

is available for this paper at 10.1038/s41598-020-69914-y.