Abstract
While p–n homojunctions in two-dimensional transition metal dichalcogenide materials have been widely reported, few show an ideality factor that is constant over more than a decade in current. In this paper, electric double layer p–i–n junctions in WSe2 are shown with substantially constant ideality factors (2–3) over more than 3 orders of magnitude in current. These lateral junctions use the solid polymer, polyethylene oxide: cesium perchlorate (PEO:CsClO4), to induce degenerate electron and hole carrier densities at the device contacts to form the junction. These high carrier densities aid in reducing the contact resistance and enable the exponential current dependence on voltage to be measured at higher currents than prior reports. Transport measurements of these WSe2 p–i–n homojunctions in combination with COMSOL multiphysics simulations are used to quantify the ion distributions, the semiconductor charge distributions, and the simulated band diagram of these junctions, to allow applications to be more clearly considered.
Subject terms: Electrical and electronic engineering, Electronic devices
Introduction
Methods for forming p–n junctions in two-dimensional (2D) transition metal dichalcogenide (TMD) channels have been widely sought to enable electronic and optoelectronic applications1. Lateral TMD p–n junctions have been induced using a wide variety of approaches including buried gates (in WSe2 by Pospischil2, Baugher3, and Ross4, and in MoS2 by Sutar5), using combinations of buried gates and surface charge layers (in MoTe2 by Lim6), by ion gating using solid polymers (in MoTe2 by Xu7 and in WSe2 by Fathipour8), using ionic liquids (in WSe2 by Kozawa9 and Zhang10,11), by chemical doping (in MoS2 by Choi12 and Li13), and by thickness-dependent work-function engineering (in WSe2 by Xu14). A vertical p–n homojunction was demonstrated by Jin15 by transfer of Nb-doped, p-type MoSe2 onto transferred, undoped, n-type MoSe2 on SiO2 and an ideality approaching unity was achieved. In addition to these homojunction demonstrations, many 2D p–n heterojunctions have been demonstrated, as reviewed in Frisenda16, but few of these reports are ideal in the sense that the forward current increases exponentially with voltage for decades in current. The most ideal heterojunction reported is obtained in a transferred, vertical p-WSe2/n-InAs stack, by Chuang17, showing an ideality factor of 1.1 over approximately 4 orders of magnitude in current.
In homojunction TMD p–n junctions, the most ideal junctions have been achieved using buried gates5, or an ion-containing (solid polymers or ionic liquid) electrolytes biased to create an electric double layer (EDL) at the semiconductor surface. The double layer consists of a cation-electron or an anion-hole layer with a high capacitance density (e.g. 4 μF/cm2 as measured by Xu7). Once the double layers are formed, the ions are locked in place by cooling below a critical temperature. This method of doping in WSe2 has produced contact resistances as low as 3.4 and 1 kΩ μm (n and p respectively) and currents as high as 58 and 50 μA/μm at |VDS| = 2 V (n and p respectively)18. The method of forming p-n junctions by application of EDLs has its roots in the light emitting electrochemical cell as discussed by Pei19, Gao20, and Edman21. Our aim in this paper is to analyze the current–voltage (I–V) characteristics of the WSe2 p–i–n junction7 using the solid polymer, PEO:CsClO4. Through COMSOL multiphysics modeling we provide a quantitative physical understanding of the ion and carrier distributions in the electrolyte and channel. Simulation of EDL properties is of recent interest, as demonstrated by Ueda’s22 work using a drift–diffusion formalism. The doping method described in this paper has allowed demonstration of a homojunction WSe2 Esaki tunnel diode23.
Results and discussion
Schematic cross sections for two p–i–n junctions are shown in Fig. 1a,b, respectively, in two different channel structures. Following the benchmarking of Sylvia24 for ultrascaled field-effect transistors (FETs), we focus on WSe2 as the channel material. Device D1 has a centered top gate with an Al2O3 thickness of 5.3 nm and device D2 has an open channel. Fabrication details are provided in the Methods section. The upper layer is the solid polymer electrolyte, PEO:CsClO4. The CsClO4 dissociates into cations, Cs+, and anions, ClO4−, as indicated by the circled + and − symbols in Fig. 1a,b. The metal contact to WSe2 consists of an electron beam deposition of Ti to partially cover the exfoliated WSe2 surface followed by Pd deposition. This leads to a dual work-function contact providing low Schottky barriers to both valence and conduction bands18. With a positive bias applied to the right contact with respect to the left contact, ions accumulate at the contacts as indicated in the schematic with the bulk of the PEO:CsClO4 remaining charge neutral. An EDL forms where the ions accumulate. Shown in Fig. 1c,d are transmission electron microscope (TEM) images of the contact region made after electrical measurements were completed. An interfacial layer at the scale of approximately 1 nm can be seen at the metal contact/WSe2 interface. This contact is formed by partially covering the WSe2 with Ti and then completing the metallization with Pd. For this reason, some transition layer can be expected. This dual work-function contact yielded contact resistances as low as 1 and 3.4 kΩ μm for n and p type contacts, respectively, comparable to the best reports for WSe218. The physical attributes of the two devices are summarized in Table 1.
Figure 1.
Schematic cross sections of two lateral WSe2 p–i–n junctions: (a) with top gate (5.3 nm Al2O3), (b) without top gate. (c) TEM image of contact region (Pd/Ti/WSe2) of device D1 and (d) device D2. The TEMs correspond to the same devices for which electrical measurements are reported.
Table 1.
Device structure parameters. The cool-down bias lists the drain and source biases, which are fixed during cooling to immobilize the ions.
| Device D1 | Device D2 | ||
|---|---|---|---|
| Top gate length | 1.5 | No top gate | μm |
| WSe2 thickness | 6.8 | 6.5 | nm |
| Channel length | 1.7 | 3.5 | μm |
| Channel width | 2 | 4 | μm |
| Ti/Pd contacts | 0.8/90 | 0.8/90 | nm |
| Cool-down bias | VD = − VS = 1.5 | VD = − VS = 2 | V |
To form the p–i–n junction, a positive bias is applied to the drain contact and a negative bias of the same magnitude is applied to the source contact, at room temperature. This accumulates negative ions at the drain contact and positive ions at the source contact, Fig. 1a,b. The ions then induce free carriers in the WSe2 of opposite sign, i.e. electrons at the source and holes at the drain. The structure D1 enforces an undoped region in the center of the channel because the top gate keeps ions out of the central channel region, while the open structure D2 has a central undoped channel due to the charge neutral electrolyte in the region between the electrodes. Once the ions are positioned along the channel, they are locked into place by cooling the device below the glass transition temperature of the PEO:CsClO4 (measured by Xu7 to be 240 K) while maintaining the biases on the contacts. Below the glass transition temperature, the ions are immobilized and do not respond to external biases and the device can be tested without ion reconfiguration.
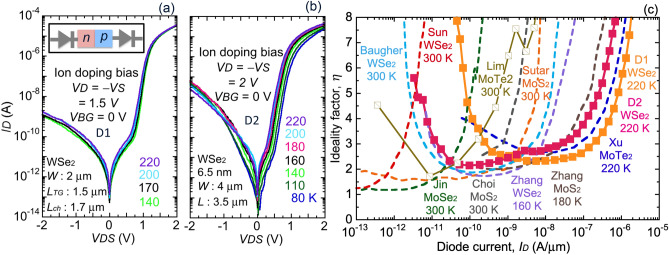
The transfer characteristic of the p–i–n diodes, D1 and D2, are shown in Fig. 2a,b, respectively. The I–V characteristics show a clear rectifying behavior with a forward to reverse current ratio of ~ 28,000 for D1 and ~ 2,000 for D2. More notable is the exponential dependence of the current on voltage over more than 4 orders of magnitude in both device geometries. The p–i–n junction is in series with metal/WSe2 Schottky contacts with an n-Schottky barrier on the left contact and a p-Schottky barrier on the right, Fig. 2a inset. Under forward bias, the two Schottky contacts are reverse-biased tunnel contacts resulting from the degenerate n and p carrier densities of the EDLs near the contact/channel edges. This series arrangement of Schottky barrier contacts means that the voltage across the junction will be somewhat less than the applied voltage.
Figure 2.
Temperature dependence of the I–V characteristics of WSe2 p–i–n junctions exhibiting exponential turn-on and clear rectification: (a) device D1 and (b) device D2. The inset in (a) is a reminder that the p–i–n junction is in series with an n-Schottky (left source contact) and a p-Schottky (right drain contact). (c) Comparison of ideality factor vs current per width for D1 and D2 vs. published TMD homojunction p–n diodes.
The current in the forward-biased p–n junction, I = IO exp[V/ηVT], is predominantly controlled by the exponential factor V/ηVT where V is the voltage across the p–n junction, VT is the thermal voltage, VT = kT/q, η is ideality factor, IO is reverse saturation current, k is Boltzmann’s constant, T is temperature, and q is fundamental charge. The ideality factor of D1 and D2 can be extracted from the forward biased I–V characteristic using η = [(kT/q)ln(10)(dlog(I)/dV)]−1, which is valid when the applied voltage is predominantly dropped across the p–n junction. Figure 2c compares the ideality factor vs. current in D1 and D2 vs. published TMD p–n homojunctions. In Zhang10 and Sutar5 the width of the MoS2 junction was not specified and 4 μm is used. Choi’s12 report, on MoS2 using chemical doping, is an example where the ideality factor varies strongly with current, which is likely due to a series resistance. Sutar5 formed the p–i–n junction in MoS2 electrostatically by applying asymmetric biases to buried gates. The ideality factor in Sutar’s report is constant over 4 orders of magnitude in current with ideality less than approximately 2. The p–i–n junctions that extend to the highest currents in Fig. 2c were created by the formation of EDLs. Among these reports, Zhang10,11 used ionic liquids, while in the junctions of Xu7 and this work, PEO:CsClO4 was used. The WSe2 p–i–n junctions of this work exhibit substantially constant ideality factor vs. current, over 3 orders of magnitude; these lateral junctions show ideality factors ranging from 2 to 3. In contrast, the transferred MoSe2 homojunction of Jin15 exhibited nearly unity ideality, suggesting that trap-mediated generation/recombination25 is playing a role in lateral junctions. In the lateral p–i–n junction, the reverse leakage is also higher than the reverse saturation current, consistent with traps playing a significant role.
While it may appear that the D2 junction has a larger temperature dependence than D1, this is only because the measured temperature range is larger for D2. The temperature coefficient, ΔI/ΔT of the forward current is similar in the two junctions 1.4 (nA/μm)/K in D1 and 1.1 (nA/μm)/K in D2 (at 10 nA, normalized by the junction width W). The positive temperature coefficient in forward bias is opposite to what is expected from the exp(qV/kT) factor at fixed voltage. This is because the prefactor, IO, depends on the energy band gap, EG, making the full forward current proportional to exp[− (EG − qV)/kT] as outlined by Sze26, and giving a positive temperature coefficient.
The temperature coefficient of the Schottky contacts and access region can be separated out in the same device. To facilitate this, device D2 was cooled to below the glass transition temperature of PEO, with a 2.5 V side gate bias and 0 V on the source and drain contacts. Thus, positive Cs+ ions are driven onto the WSe2 surface, as indicated in Fig. 3a, to induce electrons in the channel, as described in the band diagram in Fig. 3b. Nonrectifying I–V characteristic were obtained as a result of this unipolar doping, Fig. 3c, and the temperature coefficient of the current is weakly negative.
Figure 3.
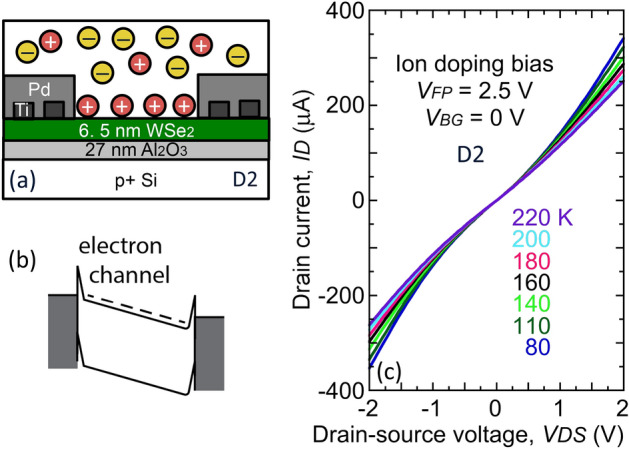
Unipolar doping of the WSe2 channel in device D2, used to measure Schottky contact temperature dependence. (a) Schematic cross section under side gate bias to accumulate positive ions on the channel, doping the channel n-type. (b) Corresponding band diagram for unipolar n-doping. (c) Symmetric, nonrectifying characteristics are obtained. To support the highest current measured in Fig. 2 requires less than ~ 0.4 V drop across the two contacts and access region.
A negative temperature coefficient is not readily explained from Schottky barrier transport, considering Schottky barrier lowering27 and thermionic field-emission28. A negative temperature coefficient is instead an indication of mobility degradation with temperature due to phonon scattering, as is also observed in Si metal–oxide–semiconductor FET inversion layers29. A negative temperature coefficient of the conductance has also been observed in WSe2 FETs using PEO:CsClO48. The measured series resistance can be directly measured from Fig. 3c in the linear region below 1 V, where 8.7 kΩ is obtained, corresponding to a channel resistivity of 6.5 mΩ cm, which is reasonable for WSe2 mobility and sheet carrier density (100 cm2/Vs and 6 × 1012/cm2). Because both the p–i–n junction current and the series resistance increase with temperature, the voltage drop across the p–i–n junction decreases with temperature.
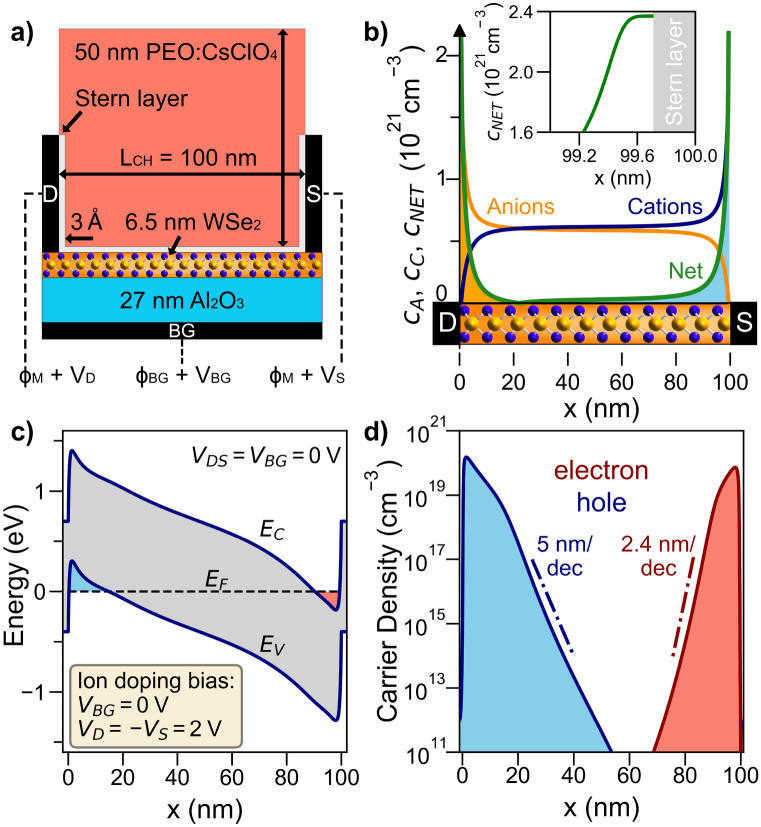
COMSOL multiphysics simulations were performed to better understand the EDL junction formation. Given that this junction formation method is yielding the most ideal and high current homojunctions it is of interest to quantify the expected carrier densities and profiles. Figure 4a represents the simulated device structure for device D2, consisting of a 100 nm-long, 6.5 nm-thick WSe2 channel (EG = 1.2 eV, χ = 3.9 eV) on 27 nm Al2O3. A shorter channel was used than in the experiments to reduce the simulation time while being sufficiently long to capture the electrostatic lengths of the ion distributions. On top of the semiconductor channel, there is a 50 nm layer of PEO electrolyte at a concentration of 1,000 mol/L of monovalent anions and cations. The presence of a Stern layer defining the separation between the ions in the solid polymer and the carriers in the semiconductor channel, is taken into account by inserting a 0.3 nm vacuum layer.
Figure 4.
COMSOL simulations of the EDL p–i–n junction in WSe2. (a) Simulated device structure, representing a scaled-version of the fabricated device consisting of a 100 nm WSe2 channel and including source, drain, and backgate metal contacts, with PEO:CsClO4 on the surface. PEO:CsClO4 is modeled as a dielectric with εPEO = 7 and a concentration of 1,000 mol/L of monovalent ions. A thin, 0.3 nm vacuum layer at the metal/semiconductor interfaces with PEO:CsClO4 represents the effect of the Helmholtz layer. (b) Computed steady-state ion profile after a bias of VD = − VS = 2 V is applied at the drain/source metal contacts. (c) Simulated band diagram along the channel length after the ion locking step at 220 K. (d) Charge density profile along the same cut showing an accumulation of image charges at the two ends of the channel, several orders of magnitude higher than that concentration in the middle of the channel.
A modified Poisson–Nernst–Planck (MPNP) theory of electrodiffusion accounting for steric effects at large applied biases is applied to calculate the dynamics of ions within the electrolyte23,30. The system of equations consists of the Poisson's equation for the electrostatics and the modified Nernst–Planck equation for ion transport. The semi-classical transport of electrons and holes in the semiconductor is described by a drift-diffusion model. The drift-diffusion equations consist of the Poisson's equation for electrostatics, and the continuity equation for electrons and holes. Dirichlet boundary conditions are applied at the metal contacts (φM = 4.8 eV, φBG = 5.0 eV), while Neumann boundary conditions are used at the remaining boundaries. The semiconductor and the solid electrolyte domains are connected via an insulating interface so no charge transfer is enabled. Therefore, the two domains are coupled only electrostatically by means of the Poisson's equation.
The simulations follow the p–i–n junction formation protocol for device D2. First, at room temperature, the ion and semiconductor transport are solved self consistently, under an applied voltage of VD = − VS = 2 V (VBG = 0 V) to build-up the desired ion distribution in the electrolyte. The in-line electric field splits the positive and negative ions and as Fig. 4b suggests, ions accumulate at the two contacts and decay exponentially towards the middle of the channel. The high bulk ion concentrations resulting in a Debye screening length of order ~ 1 nm. To highlight the impact of the adopted MPNP, the inset of Fig. 4b shows the net ion concentration at the source extremity of the channel reaching a saturation value of cMAX = 1/(NA a3) ≈ 3.94 mol/L (≈ 2.37 × 1021 cm−3), where NA is Avogadro’s constant. The heuristic parameter, a = 0.75 nm, returns sheet charge density ~ 1014 cm−2 in accordance with experimental results31. This simple assessment reveals that the portion of the channel strongly affected by the presence of ions is mainly in close proximity to the source and drain contacts, hence it justifies our choice to simulate a scaled version of the fabricated device. The Al2O3 central gate in device D1 plays an insignificant role in the transport as the p–i–n junction is controlled by the high carrier density regions located within ~ 20 nm of the contacts. This is why devices D1 and D2 produce similar characteristics. The stabilized ion doping profile forms a p–i–n junction in the polymer, and the resulting net ion distribution mirrors the same junction at the surface of the underlying semiconductor channel.
With the computed steady-state room-temperature ion distribution, Poisson’s equation is then solved at 220 K under zero bias conditions using the net ion concentration as a fixed charge input. The accumulated anions (cations) near the drain (source) contact induce holes (electrons) in the underlying semiconductor layer. The equilibrium band diagram (VDS = VBG = 0 V) in Fig. 4c clearly shows that a barrier is formed due to the ion-separation, which is confirmed by the free carrier accumulation near the two ends of the semiconductor up to degenerate levels as shown in Fig. 4d. The band diagram also shows a graded profile due to the exponential decay in free carrier density. The graded profile reduces the abruptness of the junction profile, which is limited by the channel length linking the two highly-doped regions. The asymmetry in the hole and electron profiles is a consequence of the Schottky barriers at the metal contacts and the metal–oxide–semiconductor structure leading to a slight background accumulation of holes in the channel (~ 1013 cm−3). The carrier density slopes, 2.4 nm/decade for electrons and 4.1 nm/decade for holes, are highly abrupt relative to impurity dopant slopes, which are larger by a factor of two or more32.
Conclusions
Lateral EDL WSe2 p–i–n junctions are demonstrated with substantially constant ideality factors over nearly 4 orders of magnitude using PEO:CsClO4 to accumulate electrons and holes at the channel contacts. The high carrier densities at the contacts lead to a low resistance of the Schottky barriers and a series resistance which is dominated by the channel access resistance. The lower series resistance of these structures enables observation of the exponential dependence of the forward current over a wider range than previous studies. COMSOL simulations reveal that degenerate carrier densities are induced with abrupt carrier profiles in the vicinity of the contacts. The junction formation method of this paper using PEO:CsClO4 and without a side gate achieves the highest currents with most ideal rectification properties reported to date in doping homojunctions in 2D materials.
In considering applications of this junction formation method, the requirement that the ions need to be positioned under bias and cooled to freeze them in place is undesirable and likely impractical. This freezing requirement can be lifted if a polymer with a higher glass transition temperature is used, as discussed by Kinder33, or if the EDL-induced junction can be frozen in place at room temperature via crosslinking using a thermally triggered polymerization, as demonstrated by Liang34. Another way to eliminate the need to freeze the ions in place is to make the ion positioning bias and the operating bias the same; in this case cooling is not required as the fixed forward bias holds the ions in place. This is used, for example, in p–i–n junctions formed by this technique and used as light-emitters19,20. However, if the terminal biases change, the ions will re-equilibrate and the emission characteristics can be expected to change accordingly.
Another question for this technology is scalability. There exist reports of carbon nanotubes (CNTs) with diameter of 2 nm coated and controllably electrolytically gated with PEO:LiClO435, showing that there is no intrinsic limit to coating cylindrical structures at the 2 nm scale. InAs nanowires with 50 nm diameter have also been successfully coated and gated with PEO:LiClO436. The electrolyte itself can also be scaled; ultrathin films of PEO have been spin coated down to 8 nm thickness, and exhibit well-behaved electrical properties37. However, to our knowledge there is no investigation of the viability of this doping method in highly-scaled VLSI (very large scale integration) geometries. Regarding the scaling of the TMD thickness, there are no fundamental impediments to the junction formation approach at the single monolayer thickness.
Methods
Devices D1 and D2 were fabricated in separate process runs. The fabrication began with backside evaporation of Ti/Au (5/100 nm) on the unpolished side of a p+ Si wafer. Next, 27 nm of Al2O3 was deposited on the Si top surface by atomic layer deposition (ALD). Synthesized WSe2 flakes (from 2D Semiconductors Co. with 99.9995% purity) were exfoliated on the oxide using dicing tape (Semiconductor Equipment Corp. P/N 18074). The flakes were patterned for source and drain using electron beam lithography (EBL) followed by metal deposition of Ti/Pd (0.8 nm/90 nm) and lift off. Device D1 omitted the gate process. Device D2 used a TiOPc adhesion layer following by the ALD process of Park and Fathipour38. Finally, the top gate contacts were patterned using EBL, followed by thermal metal deposition of 90 nm Pd and lift off. The oxide was then etched from the access regions of the FET in buffered HF, using the top gate as an etch mask. The device structures of this paper were fabricated in the same process run reported in reference18; in that paper the transistor and contact properties were analyzed using side-gates to position the ions. In this paper we focus on the formation of p–i–n junctions in transistor geometries without the use of auxiliary gates.
The solid-polymer electrolyte preparation and materials have been previously detailed18. In short, PEO (95,000 g/mol) and CsClO4 were dissolved in anhydrous acetonitrile at a concentration of 1 wt%, and an ether oxygen to Cs+ molar ratio of 168:1. The solution was drop-cast in an Ar-filled glove box, < 0.1 ppm O2 and H2O, and then annealed for 3 min at 90 °C. Current–voltage measurements were made in a Cascade Microtech PLC50 vacuum probe station at 1.2 × 10–6 Torr. Devices that employ PEO:CsClO4 are stable and give reproducible electrical characteristics under testing over months, as long as the applied voltages are kept within the electrochemical window of the electrolyte (± 4 V) and wafers are stored between testing in an Ar or vacuum ambient to prevent water absorption of the PEO.
Acknowledgements
This work was supported in part by the Center for Low Energy Systems Technology (LEAST), a STARnet Semiconductor Research Corporation program sponsored by MARCO and DARPA.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Fiori G, Bonaccorso F, Iannacone G, Palacios T, Neumaier D, Seabaugh A, Banerjee SK, Colombo L. Electronics based on two-dimensional materials. Nat. Nanotechnol. 2014;9:768–779. doi: 10.1038/nnano.2014.207. [DOI] [PubMed] [Google Scholar]
- 2.Pospischil A, Furchi MM, Mueller T. Solar-energy conversion and light emission in an atomic monolayer p–n diode. Nat. Nanotechnol. 2014;9:257–261. doi: 10.1038/nnano.2014.14. [DOI] [PubMed] [Google Scholar]
- 3.Baugher BWH, Churchill HOH, Yang Y, Jarillo-Herrero P. Optoelectronic devices based on electrically tunable p–n diodes in a monolayer dichalcogenide. Nat. Nanotechnol. 2014;9:262–267. doi: 10.1038/nnano.2014.25. [DOI] [PubMed] [Google Scholar]
- 4.Ross JS, Klement P, Jones AM, Ghimire NJ, Yan J, Mandrus DG, Taniguchi T, Watanabe K, Kitamura K, Yao W, Cobden DH. Electrically tunable excitonic light-emitting diodes based on monolayer WSe2p–n junctions. Nat. Nanotechnol. 2014;9:268–272. doi: 10.1038/nnano.2014.26. [DOI] [PubMed] [Google Scholar]
- 5.Sutar S, Agnihotri P, Comfort E, Taniguchi T, Watanabe K, Ung Lee J. Reconfigurable p-n junction diodes and the photovoltaic effect in exfoliated MoS2 films. Appl. Phys. Lett. 2014;104:122104. [Google Scholar]
- 6.Lim JY, et al. Homogeneous 2D MoTe2p–n junctions and CMOS inverters formed by atomic-layer-deposition-induced doping. Adv. Mater. 2017;29:1701798. doi: 10.1002/adma.201701798. [DOI] [PubMed] [Google Scholar]
- 7.Xu H, Fathipour S, Kinder EW, Seabaugh AC, Fullerton-Shirey SK. Reconfigurable ion gating of 2H-MoTe2 field-effect transistors using poly(ethylene oxide)-CsClO4 solid polymer electrolyte. ACS Nano. 2015;9:4900–4910. doi: 10.1021/nn506521p. [DOI] [PubMed] [Google Scholar]
- 8.Fathipour, S., Paletti, P., Fullerton-Shirey, S. & Seabaugh, A. C. Demonstration of electric double layer p–i–n junction in WSe2. 2016 Dev. Res. Conf. (DRC), 1–2. [DOI] [PMC free article] [PubMed]
- 9.Kozawa D, Pu J, Shimizu R, Kimura S, Chiu M-H, Matsuki K, Wada Y, Sakanoue T, Iwasa Y, Li L-J, Takenobu T. Photodetection in p–n junctions formed by electrolyte-gated transistors of two-dimensional crystals. Appl. Phys. Lett. 2016;109:201107. [Google Scholar]
- 10.Zhang YJ, Ye JT, Yomogida Y, Takenobu T, Iwasa Y. Formation of a stable p–n junction in a liquid-gated MoS2 ambipolar transistor. Nano Lett. 2013;13:3023–3028. doi: 10.1021/nl400902v. [DOI] [PubMed] [Google Scholar]
- 11.Zhang YJ, Oka T, Suzuki R, Ye JT, Iwasa Y. Electrically switchable chiral light-emitting transistor. Science. 2014;344:725–728. doi: 10.1126/science.1251329. [DOI] [PubMed] [Google Scholar]
- 12.Choi MS, Qu D, Lee D, Liu X, Watanabe K, Taniguchi T, Yoo WJ. Lateral MoS2p–n junction formed by chemical doping for use in high-performance optoelectronics. ACS Nano. 2014;8:9332–9340. doi: 10.1021/nn503284n. [DOI] [PubMed] [Google Scholar]
- 13.Li HM, Lee D, Qu D, Liu X, Ryu J, Seabaugh AC, Yoo WJ. Ultimate thin vertical p–n junction composed of two-dimensional layered molybdenum disulfide. Nat. Commun. 2015;6:6564. doi: 10.1038/ncomms7564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Xu Z-Q, Zhang Y, Wang Z, Shen Y, Huang W, Xia X, Yu W, Xu Y, Sun L, Zheng C, Lu Y, Liao L, Bao Q. Atomically thin lateral p-n junction photodetector with large effective detection area. 2D Mater. 2016;3:041001. [Google Scholar]
- 15.Jin Y, Keum DH, An S-J, Kim J, Lee HS, Lee YH. A Van der Waals homojunction: ideal p–n diode behavior in MoSe2. Adv. Mater. 2015;27:5534–5540. doi: 10.1002/adma.201502278. [DOI] [PubMed] [Google Scholar]
- 16.Frisenda R, Molina-Mendoza AJ, Mueller T, Castellanos-Gomez A, van der Zant HSJ. Atomically thin p-n junctions based on two-dimensional materials. Chem. Soc. Rev. 2018;47:3339–3358. doi: 10.1039/c7cs00880e. [DOI] [PubMed] [Google Scholar]
- 17.Chuang S, Kapadia R, Fang H, Chang TC, Yen W-C, Chueh YL, Javey A. Near-ideal electrical properties of InAs/WSe2 van der Waals heterojunction diodes. Appl. Phys. Lett. 2013;102:242101. [Google Scholar]
- 18.Fathipour S, Pandey P, Fullerton-Shirey S, Seabaugh AC. Electric-double-layer doping of WSe2 field-effect transistors using polyethylene-oxide cesium perchlorate. J. Appl. Phys. 2016;120:234902. [Google Scholar]
- 19.Pei Q, Yu G, Zhang C, Yang Y, Heeger AJ. Polymer light-emitting electrochemical cells. Science. 1995;269:1086–1088. doi: 10.1126/science.269.5227.1086. [DOI] [PubMed] [Google Scholar]
- 20.Gao J, Li Y, Yu G, Heeger AJ. Polymer light-emitting electrochemical cells with frozen junctions. J. Appl. Phys. 1999;86:4594. [Google Scholar]
- 21.Edman L, Summers MA, Buratto SK, Heeger AJ. Polymer light-emitting electrochemical cells: doping, luminescence, and mobility. Phys. Rev. B. 2004;70:115212. [Google Scholar]
- 22.Ueda A, Zhang Y, Sano N, Imamura H, Iwasa Y. Ambipolar device simulation based on the drift-diffusion model in ion-gated transition metal dichalcogenide transistors. npj Comput. Mater. 2020;6:144. [Google Scholar]
- 23.Paletti P, Yue R, Hinkle C, Fullerton-Shirey SK, Seabaugh A. Two-dimensional electric-double-layer Esaki diode. npj 2D Mater. Appl. 2019;3:603–607. [Google Scholar]
- 24.Sylvia SS, Alam K, Lake RK. Uniform benchmarking of low-voltage van der Waals FETs. IEEE J. Explor. Solid State Comput. Devices Circuits. 2016;2:28–35. [Google Scholar]
- 25.Sze SM. Physics of Semiconductor Devices. 2. New York: Wiley; 1981. pp. 89–92. [Google Scholar]
- 26.Ibid. pp. 88-89.
- 27.Ibid. p. 281, Eq. (82).
- 28.Padovani FA, Stratton R. Field and thermionic-field emission in Schottky barriers. Solid State Electron. 1966;9:695–707. [Google Scholar]
- 29.Takagi S, Toriumi A, Iwase M, Tango H. On the universality of inversion layer mobility in Si MOSFET's: part I—effects of substrate impurity concentration. IEEE Trans. Electron Devices. 1994;41:2357–2362. [Google Scholar]
- 30.Kilic MS, Bazant MZ, Ajiri A. Steric effects in the dynamics of electrolytes at large applied voltages. II. Modified Poisson–Nernst–Planck equations. Phys. Rev. E. 2007;75:021503. doi: 10.1103/PhysRevE.75.021503. [DOI] [PubMed] [Google Scholar]
- 31.Ueno K, Shimotani H, Yuan H, Ye J, Kawasaki M, Iwasa Y. Field-induced superconductivity in electric double layer transistors. J. Phys. Soc. Jpn. 2014;83:032001. [Google Scholar]
- 32.Kujirai H, Murakami E, Kimura S. Ultra-shallow and abrupt boron profiles in Si by δ-doping technique. Jpn. J. Appl. Phys. 1995;34:782–786. [Google Scholar]
- 33.Kinder EW, Fuller A, Lin Y-C, Robinson JA, Fullerton-Shirey SK. Increasing the room-temperature electric double layer retention time in two-dimensional crystal FETs. ACS Appl. Mater. Interfaces. 2017;9:25006–25013. doi: 10.1021/acsami.7b03776. [DOI] [PubMed] [Google Scholar]
- 34.Liang J, Xu K, Arora S, Laaser JE, Fullerton-Shirey SK. Ion-locking in solid polymer electrolytes for reconfigurable gateless lateral graphene p–n junctions. Materials. 2020;13:1089. doi: 10.3390/ma13051089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lu C, Fu Q, Huang S, Liu J. Polymer electrolyte-gated carbon nanotube field-effect transistor. Nano Lett. 2004;4:623–627. [Google Scholar]
- 36.Carrad DJ, et al. Electron-beam patterning of polymer electrolyte films to make multiple nanoscale gates for nanowire transistors. Nano Lett. 2014;14:94–100. doi: 10.1021/nl403299u. [DOI] [PubMed] [Google Scholar]
- 37.Gonzalez-Serrano, K. A. & Seabaugh, A. C. Electrical properties of spin-coated polyethylene oxide capacitors as thin as 8 nm. 2020 Electronic Materials Conf (2020).
- 38.Park JH, Fathipour S, Kwak I, Sardashti K, Ahles CF, Wolf SF, Edmonds M, Vishwanath S, Xing HG, Fullerton-Shirey SK, Seabaugh A, Kummel AC. Atomic layer deposition of Al2O3 on WSe2 functionalized by titanyl phthalocyanine. ACS Nano. 2016;10:6888–6896. doi: 10.1021/acsnano.6b02648. [DOI] [PubMed] [Google Scholar]