Abstract
The extrusion process is a very complex process due to the number of process parameters that are associated with it which are prone to high fluctuations. The main purpose of this work is to determine the realistic extrusion process parameters in the thermoplastic extrusion process in Nigeria cable manufacturing industries with the use of an artificial neural network. Conventionally, the use of trial and error technique which involves full-size experiments is generally used to determine the process parameters in the thermoplastic extrusion process. This conventional technique is expensive and it is also time-consuming. The use of an artificial neural network to predict extrusion process parameters before plant execution will make extrusion process operations more efficient. This technique also bridges the gap that exists between theoretical analysis and real manufacturing system because real manufacturers' data was used. The neural network was developed in a MATLAB environment and was trained with a supervised learning method based on Levenberg Marquardt Algorithm and the developed ANN model is capable of predicting manufacturing process parameters for different grades of PVC thermoplastic material.
Keywords: Electrical engineering, Industrial engineering, Mechanical engineering, Computer-aided engineering, Electrical cable, Ann, Extrusion, Extruder
Electrical engineering; Industrial engineering; Mechanical engineering; Computer-aided engineering; Electrical cable; Ann; Extrusion; Extruder
1. Introduction
The extrusion process is a manufacturing technique in which materials are moved along a screw and are pushed out through a die at a certain temperature and pressure. One of the most common places the extrusion process is utilized is in the cable manufacturing industries. It is very useful in the extrusion of thermoplastic material (PVC, PE, or XLPE) in electrical cable insulation [1, 2]. One of the most common thermoplastic PVC [3]. Cable manufacturing in Nigeria today is faced with some challenges which can affect the quality of the cables [4]. The challenges are often associated with the complex processes that are involved in the manufacturing process of the cables. In cable manufacturing industries, there are a vast amount of parameters (known as process parameters) that affect the output product obtained after the extrusion process [4, 5]. The process parameters include the melt temperature, speed, pressure settings, screw speed, type of die used and cooling medium in an extrusion machine. The melt temperature and pressure are some of the most important parameters in an extrusion process. These parameters indicate the performance quality of an extruder [6]. The melt temperature variations in an extruder are also important to determine the stability of the extrusion process [7]. Krzysztof stated that the temperature, pressure, and the fluctuations in the process parameters in an extruder are essential to determine the quality of an extrusion output. Other properties include the degree at which the polymer compositions are well mixed and the rheological properties of the polymer [8]. These process parameters are very prone to fluctuations, therefore cause issues in cable manufacturing industries [9]. Some of these issues include the production of poor quality cables, an increase in the manufacturing cost and time and as well as the waste of materials in manufacturing industries [10].
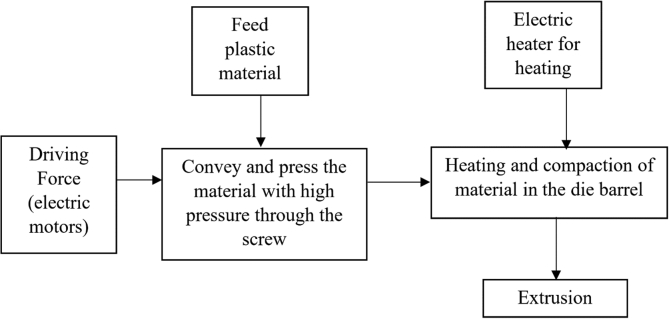
The complexity and the high number of process parameters that are involved in the manufacturing of these cables make the entire process difficult to control and monitor [11]. Improper operations in the manufacturing process often cause defects in the cables manufactured [4]. These defects can be in the form of pimples, cracking, air cavity, and porosity in cable insulations [4]. Figure 1 shows the diagrammatic representation of an electrical cable with defects. Electrical cable insulation defects can lead to insulation breakdown that can lead to the loss of life and properties. The improper operations in electrical cable manufacturing industries can also lead to an increase in manufacturing cost, downtime, and waste of material [12]. Furthermore, it can also cause a reduction in economic benefits while increasing energy and labor [12, 13]. Therefore, discovering ways to improve the manufacturing process of electrical cables to provide quality outputs is very important. Figure 2 shows the block diagram of a typical extrusion process technique and Figure 3 shows the schematic diagram of an extruder.
Figure 1.
Electrical cable insulation with defects.
Figure 2.
Block diagram of Extrusion process.
Figure 3.
Schematic diagram of a single screw extruder.
Over the years, many methods have been developed to optimize the extrusion process in the industry. These techniques are developed to ensure that the production of high-quality extrusion output is achieved while reducing manufacturing cost, downtime, waste of material, energy, labor, and increasing economic benefits [9, 13]. Some researchers investigated how the thermoplastic extrusion process can be improved in the industry. They asserted that the quality of the PVC which is used in the cable industry can impact the output quality from an extruder [4]. Jing and colleagues proposed a low-cost real-time energy monitoring method which is used to study the effect of process settings on efficiency and melt quality [14, 15]. Chamil and colleagues also established that energy efficiency is a concern and they identified ways to optimize energy efficiency [16]. Zinnatullin and colleagues investigated the use of an automatic control system in the extrusion of polymer cable insulation [17]. Abeykoon proposed a model-based controller that can be utilized in a polymer extrusion process. In this work, the author stated that since the melt temperature is a major process parameter that can impact the output of an extruder, there is a need for accurate thermal monitoring and control [18]. The proposed system was capable of achieving the melt temperature that was desired and it also reduces the temperature variance in the extrusion line. Pathak and colleagues investigated the effects of the process parameters in the extrusion process by utilizing the finite element method [19]. The best process parameters for hot extrusion was also studied by Sivaprasad and colleagues by using finite element simulation [20, 21]. Dharmendra and Sunil proposed a method of optimizing the process parameters of high-density polyethylene (HDPE) material using the Taguchi approach [22, 23]. Many other researchers have utilized the Taguchi approach to obtain great results in extrusion processes [22, 23, 24]. Vicente and colleagues proposed the use of regression models to predict the quality in a tubing extrusion process. They discussed how quality cannot be overemphasized in the manufacturing process [25, 26]. Chamil and colleagues developed an extruder melt temperature control with fuzzy logic [27]. Nastaj and Wilczynski in their work were able to optimize the single screw extrusion process using process simulations [28]. The process simulation technique was based on Genetic Algorithms Screw Extrusion Optimization procedures which have been developed using the Genetic Algorithm. This technique was used to optimize both the starve and flood fed screw extrusion. The authors were able to conclude that the starving fed extrusion is optimal with a high extrusion output and low energy consumption [28]. Bingol and some of his colleagues developed an ANN model to predict the load for lateral extrusion. In their study, the authors used the billet diameters, height, and teeth for input parameters and the results shows that the ANN model developed was capable of estimating the required load for lateral extrusion [29]. Furthermore, Carmine and colleagues also developed an ANN model to optimize the extrusion of aluminum alloy [30]. In their study, they postulated that the extrusion of aluminum alloy is complex which is due to the materials and process parameters used in the extrusion process. The authors used Levenberg Marquardt algorithm to train an ANN model using experimental data from an industrial process. In their study, they predicted the temperature profile of an extruder machine using ANN and they were able to agree that the predicted values are very close to the experimental values [30]. Other researchers such as Su-Hai Hsiang et al. [31] and Mekras [32] have also utilized ANN in the extrusion process and the results were satisfactory. These have shown that the use of ANN in the extrusion process is not entirely new and the results that have been obtained in these processes are relevant to the reasons why the use of ANN has been utilized in the study. This study focuses on the use of artificial neural networks to predict extrusion process parameters in cable manufacturing industries. The method provides a better way of selecting process parameters that can be used in cable manufacturing industries. The prospects of using artificial neural network controllers in the PVC thermoplastic extrusion process were also discussed.
2. Methods and materials
2.1. Dataset material
In this study, the Polyvinyl Chloride (PVC) thermoplastic material was considered. The relevant data of the appropriate process parameters settings as well as the datasheet of different grades of PVC thermoplastic material was obtained from two cable manufacturing industries. The two cable manufacturing industry were selected based on their capability to produce high-quality cables and easy accessibility. Forty-two (42) different PVC grade material was utilized in this study. The datasheet of the PVC grade materials was obtained from two cable manufacturing industries. The datasheet information was used as the input parameters in the model. Furthermore, the industrial process parameters settings which are used in the extrusion process of these materials were also obtained from the cable manufacturing industries. These process parameters settings were used as the output parameters of the developed ANN model. The artificial neural network model was developed in a MATLAB environment. The datasheet that was obtained for the PVC thermoplastic extrusion can be seen in Tables 1, 2 and 3. The process parameters that were considered include the zone temperatures, clamp temperature, neck temperature, crosshead temperature, and the die temperature. Tables 1, 2, and 3 shows the training datasets while Table 4 shows the testing dataset that was utilized in this study.
Table 1.
Dataset for different grades of PVC thermoplastic material (1).
| Grade Name (input) | KI-041S | KI-09 | KI-11 | KI-12 | KI-13K | KI-14 | KI-15SC | KI-21 | KI-22 | KI-25J | KI-06S | KI-06 | KI-05 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Maximum Operating temperature (°C) | 70 | 70 | 70 | 70 | 70 | 70 | 80 | 85 | 85 | 85 | 70 | 70 | 70 |
| Specific Gravity (G/CC) | 1.46 | 1.47 | 1.46 | 1.38 | 1.38 | 1.4 | 1.35 | 1.38 | 1.38 | 1.38 | 1.56 | 1.47 | 1.47 |
| Hardness, (Shore A) | 90 | 91 | 90 | 88 | 87 | 90 | 93 | 88 | 90 | 90 | 90 | 86 | 86 |
| Thermal Stability (°C) | 110 | 90 | 100 | 80 | 120 | 120 | 120 | 150 | 200 | 200 | 60 | 60 | 60 |
| Tensile Strength, TS (MPa) | 16 | 15 | 15 | 17 | 17 | 17 | 20 | 16 | 16 | 16 | 15 | 15 | 15 |
| Elongation at break, EB (%) | 250 | 250 | 250 | 300 | 275 | 250 | 280 | 250 | 250 | 250 | 200 | 250 | 250 |
| Ageing Temperature (°C) | 80 | 80 | 80 | 80 | 80 | 80 | 100 | 135 | 135 | 135 | 90 | 80 | 80 |
| Variations of TS (%) | 20 | 20 | 20 | 20 | 20 | 20 | 25 | 25 | 25 | 25 | 20 | 20 | 20 |
| Variations of EB (%) | 20 | 20 | 20 | 20 | 20 | 20 | 25 | 25 | 25 | 25 | 20 | 20 | 20 |
| Profile Settings (target) | |||||||||||||
| 1st Zone (°C) | 130 | 131 | 130 | 129 | 129 | 132 | 125 | 130 | 132 | 132 | 160 | 131 | 131 |
| 2nd Zone (°C) | 150 | 155 | 150 | 153 | 153 | 153 | 150 | 153 | 154 | 154 | 180 | 157 | 157 |
| 3rd Zone (°C) | 160 | 165 | 160 | 160 | 160 | 162 | 163 | 160 | 160 | 160 | 185 | 160 | 160 |
| 4th Zone (°C) | 160 | 160 | 165 | 159 | 159 | 160 | 164 | 160 | 160 | 160 | 185 | 160 | 160 |
| 5th Zone (°C) | 165 | 160 | 165 | 161 | 161 | 162 | 165 | 160 | 160 | 160 | 185 | 160 | 160 |
| 6th Zone (°C) | 160 | 162 | 160 | 161 | 160 | 161 | 160 | 160 | 160 | 160 | 185 | 162 | 162 |
| 7th Zone (°C) | 160 | 165 | 160 | 160 | 171 | 160 | 160 | 160 | 160 | 160 | 185 | 165 | 165 |
| Clamp (°C) | 170 | 170 | 172 | 170 | 155 | 171 | 175 | 171 | 175 | 175 | 190 | 170 | 170 |
| Neck (°C) | 155 | 155 | 155 | 156 | 170 | 155 | 150 | 155 | 150 | 150 | 160 | 154 | 154 |
| Crosshead (°C) | 175 | 170 | 170 | 170 | 169 | 170 | 170 | 170 | 170 | 170 | 170 | 170 | 170 |
| Die (°C) | 180 | 170 | 180 | 175 | 175 | 175 | 175 | 175 | 175 | 175 | 165 | 170 | 170 |
Table 2.
Dataset for different grades of PVC thermoplastic material (2).
| Grade Name (input) | KI-75 | KI-02 | KI-26 | KI-42 | KI-31 | KI-04FR | KI-33B | KI-26 | KI-05 | KI-25JW | KI-23 | KI-05 | KI-15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Maximum Operating temperature (°C) | 90 | 90 | 90 | 90 | 90 | 70 | 90 | 90 | 86 | 95 | 93 | 86 | 93 |
| Specific Gravity (G/CC) | 1.44 | 1.48 | 1.47 | 1.47 | 1.5 | 1.5 | 1.57 | 1.48 | 1.47 | 1.33 | 1.38 | 1.47 | 1.38 |
| Hardness, (Shore A) | 80 | 90 | 90 | 88 | 90 | 90 | 92 | 90 | 86 | 95 | 93 | 86 | 93 |
| Thermal Stability (°C) | 80 | 120 | 120 | 100 | 120 | 90 | 150 | 60 | 60 | 240 | 100 | 60 | 100 |
| Tensile Strength, TS (MPa) | 16 | 15 | 15 | 15 | 15 | 15 | 14 | 14 | 13 | 16 | 17 | 13 | 17 |
| Elongation at break, EB (%) | 300 | 275 | 250 | 250 | 250 | 250 | 200 | 250 | 250 | 250 | 250 | 250 | 250 |
| Ageing Temperature (°C) | 80 | 100 | 100 | 100 | 100 | 90 | 100 | 80 | 80 | 135 | 80 | 80 | 80 |
| Variations of TS (%) | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 25 | 25 | 20 | 25 |
| Variations of EB (%) | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 25 | 25 | 20 | 25 |
| Profile Settings (target) | |||||||||||||
| 1st Zone (°C) | 135 | 130 | 130 | 130 | 158 | 158 | 160 | 130 | 130 | 120 | 130 | 130 | 130 |
| 2nd Zone (°C) | 155 | 150 | 150 | 150 | 180 | 180 | 180 | 145 | 150 | 135 | 155 | 150 | 155 |
| 3rd Zone (°C) | 160 | 165 | 165 | 165 | 180 | 180 | 185 | 150 | 165 | 140 | 160 | 165 | 160 |
| 4th Zone (°C) | 160 | 160 | 160 | 160 | 180 | 180 | 185 | 160 | 160 | 150 | 160 | 160 | 160 |
| 5th Zone (°C) | 162 | 160 | 160 | 160 | 180 | 180 | 185 | 160 | 160 | 150 | 160 | 160 | 160 |
| 6th Zone (°C) | 165 | 162 | 160 | 160 | 180 | 180 | 185 | 165 | 160 | 155 | 160 | 160 | 160 |
| 7th Zone (°C) | 165 | 165 | 165 | 170 | 180 | 180 | 185 | 165 | 175 | 155 | 165 | 175 | 165 |
| Clamp (°C) | 170 | 170 | 170 | 170 | 185 | 185 | 190 | 170 | 175 | 160 | 175 | 175 | 175 |
| Neck (°C) | 155 | 155 | 155 | 155 | 160 | 160 | 160 | 155 | 155 | 160 | 150 | 155 | 150 |
| Crosshead (°C) | 170 | 170 | 170 | 170 | 165 | 165 | 170 | 170 | 170 | 160 | 170 | 170 | 170 |
| Die (°C) | 170 | 170 | 170 | 170 | 150 | 150 | 165 | 170 | 170 | 155 | 175 | 170 | 175 |
Table 3.
Dataset for different grades of PVC thermoplastic material (3).
| Grade Name (input) | KI-06 | ASTM 668-96 | ASTM A975-97 | KI-06H | KI-10H | KI-26H | KI-AVSS | KI-10 | KI-09H | KI-AV |
|---|---|---|---|---|---|---|---|---|---|---|
| Maximum Operating temperature (°C) | 92 | 93 | 96 | 70 | 70 | 90 | 70 | 70 | 105 | 70 |
| Specific Gravity (G/CC) | 1.45 | 1.4 | 1.34 | 1.47 | 1.38 | 1.47 | 1.34 | 1.36 | 1.35 | 1.37 |
| Hardness, (Shore A) | 92 | 93 | 96 | 86 | 88 | 88 | 90 | 90 | 92 | 90 |
| Thermal Stability (°C) | 80 | 100 | 100 | 60 | 80 | 100 | 100 | 100 | 110 | 90 |
| Tensile Strength, TS (MPa) | 15 | 15 | 15 | 15 | 17 | 15 | 15 | 15 | 17 | 15 |
| Elongation at break, EB (%) | 250 | 250 | 250 | 250 | 300 | 250 | 180 | 180 | 250 | 180 |
| Ageing Temperature (°C) | 80 | 63 | 63 | 80 | 80 | 100 | 100 | 100 | 135 | 100 |
| Variations of TS (%) | 20 | 20 | 25 | 20 | 20 | 20 | 90 | 90 | 25 | 90 |
| Variations of EB (%) | 20 | 20 | 25 | 20 | 20 | 20 | 70 | 70 | 25 | 70 |
| Profile Settings (target) | ||||||||||
| 1st Zone (°C) | 128 | 132 | 131 | 131 | 129 | 130 | 120 | 130 | 130 | 130 |
| 2nd Zone (°C) | 145 | 155 | 155 | 157 | 153 | 150 | 140 | 154 | 154 | 153 |
| 3rd Zone (°C) | 155 | 161 | 162 | 160 | 160 | 165 | 140 | 160 | 160 | 160 |
| 4th Zone (°C) | 160 | 159 | 161 | 160 | 159 | 160 | 150 | 160 | 160 | 159 |
| 5th Zone (°C) | 160 | 161 | 160 | 160 | 161 | 160 | 150 | 160 | 165 | 161 |
| 6th Zone (°C) | 160 | 160 | 161 | 162 | 161 | 160 | 155 | 160 | 165 | 160 |
| 7th Zone (°C) | 175 | 161 | 160 | 165 | 160 | 170 | 155 | 165 | 165 | 171 |
| Clamp (°C) | 175 | 171 | 171 | 170 | 170 | 170 | 165 | 175 | 175 | 155 |
| Neck (°C) | 155 | 154 | 155 | 154 | 156 | 155 | 165 | 150 | 150 | 170 |
| Crosshead (°C) | 165 | 171 | 170 | 170 | 170 | 170 | 160 | 170 | 170 | 169 |
| Die (°C) | 170 | 169 | 169 | 170 | 175 | 170 | 155 | 175 | 175 | 175 |
Table 4.
Testing Dataset for different grades of PVC thermoplastic material.
| Grade Name (predict) | KI-16H | KI-AV10 | KI-26H | KI-AV2 | ASTM 667-98 | ASTM 668-98 |
|---|---|---|---|---|---|---|
| Maximum Operating temperature (°C) | 70 | 90 | 70 | 70 | 80 | 85 |
| Specific Gravity (G/CC) | 1.38 | 1.47 | 1.4 | 1.38 | 1.35 | 1.38 |
| Hardness, (Shore A) | 88 | 88 | 90 | 87 | 93 | 90 |
| Thermal Stability (°C) | 80 | 100 | 120 | 120 | 120 | 200 |
| Tensile Strength, TS (MPa) | 17 | 15 | 17 | 17 | 20 | 16 |
| Elongation at break, EB (%) | 300 | 250 | 250 | 275 | 280 | 250 |
| Ageing Temperature (°C) | 80 | 100 | 80 | 80 | 100 | 135 |
| Variations of TS (%) | 20 | 20 | 20 | 20 | 25 | 25 |
| Variations of EB (%) | 20 | 20 | 20 | 20 | 25 | 25 |
| Profile Settings (Expected Values) | ||||||
| 1st Zone (°C) | 129 | 130 | 132 | 129 | 125 | 132 |
| 2nd Zone (°C) | 153 | 150 | 153 | 153 | 150 | 154 |
| 3rd Zone (°C) | 160 | 165 | 162 | 160 | 163 | 160 |
| 4th Zone (°C) | 159 | 160 | 160 | 159 | 164 | 160 |
| 5th Zone (°C) | 161 | 160 | 162 | 161 | 165 | 160 |
| 6th Zone (°C) | 161 | 160 | 161 | 160 | 160 | 160 |
| 7th Zone (°C) | 160 | 170 | 160 | 171 | 160 | 160 |
| Clamp (°C) | 170 | 170 | 171 | 155 | 175 | 175 |
| Neck (°C) | 156 | 155 | 155 | 170 | 150 | 150 |
| Crosshead (°C) | 170 | 170 | 170 | 169 | 170 | 170 |
| Die (°C) | 175 | 170 | 175 | 175 | 175 | 175 |
2.2. Artificial neural network
Artificial Neural Network, popularly known as ANN is a machine learning technique/algorithm which is inspired by the biological nervous system. ANN is a machine learning technique that is capable of exploring the relationships between different variables with very high accuracy. Artificial neural network emulates the human neurological system to be able to analyze and discover patterns from historical data. ANN models the way a brain performs a particular task or function. ANN due to its computing power can learn and generalize. Generalization is the ability of neural networks to produce reasonable outputs for inputs that are not used during training. ANN is composed of processing units known as neurons which is an information processing unit that is fundamental to the operation of a neural network. Figure 4 shows the model of a neuron.
Figure 4.
Diagrammatic representation of a neuron.
A neuron consists of connecting links with weights, an adder, and an activation function for limiting the output of a neuron (squashes the amplitude range of the output signal to a finite value).
Mathematically, a neuron can be described by the following equations:
| (1) |
| (2) |
are the input signals; are the synaptic weights of neuron . is the linear combiner output due to the input signal; is the bias; is the activation function; and is the output signal. Different types of activation functions can be used in an ANN model. Some common types include the sigmoid, linear, Gaussian, and gaussian complement functions. However, the most commonly used type is the sigmoid function which was also used in this study. The sigmoid function can be expressed mathematically in Eq. (3). Artificial neural networks also consist of different types of models which include the multilayer perceptron (MLP), wavelet neural network, Elman neural network, radial basis, etc. In this work, the multilayer perceptron model was utilized in predicting the insulation thickness in the thermoplastic extrusion process.
| (3) |
The use of ANN has been studied intensively since the 1990s. An ANN is capable of performing non-linear curve fitting and it is very suitable to predict the performance of the extrusion process as it is a non-linear process. The artificial neural network is inspired by the biological system of the human brain in the way it processes information. There are neurons in the human brain which are interconnected and are vital for receiving information through the connections. The ANN simply attempts to simulate the way the real neurons in the human brain behaves. The ANN is capable of learning by example the same way the human brain learns in real life. Depending on the type of problem, ANN can be applied in numerous ways. Figure 5 shows the interconnections that can be seen in an ANN.
Figure 5.
Architecture of an artificial neural network.
Figure 5 shows an example of a feed-forward topology. The feed-forward topology is simply an architecture in which the signals at the input are moved in one way from the input to the output via the hidden layer. This can kind of topology can easily map an input to the output in a very quick and easy way. The feedback topology is another type of artificial neural network architecture. They differ from the feedforward topology because they can send signals in both directions in a network. These kinds of network topologies are very dynamic and they always change up until when equilibrium is accomplished. They are also quite complicated but are also very powerful. Other types of learning methods include the semi-supervised and the reinforcement learning algorithm.
2.3. Artificial neural network learning regime
In artificial neural networks, there are two distinct types of learning regimes. These are supervised and unsupervised learning. Supervised learning is a learning technique in which the output units are given the expected results to an input signal. The major problem with this type of learning regime are issues associated with convergence errors. The goal of the supervised learning regime is to reduce the error between a desired and computed value. Hence, appropriate weighting functions are developed to minimize these errors. A particular type of training known as backpropagation is a type of supervised learning regime and it is most commonly used during the training of an artificial neural network. In the backpropagation technique, a training sample is fed into the network and the appropriate output values are obtained based on the provided inputs in the forward direction. The errors obtained at the output neurons are then propagated back to the input layer where the weights are adjusted for each of the neurons and an appropriate algorithm is implemented to determine the weighting function that can reduce the error. The unsupervised learning regime, however, is when information is provided to the neural network with no desired target. The weight of the neurons is generally altered based on the type of response that is gotten from the input signals. When a set of information is provided, the artificial neural network randomly treats the information, and uses this information to obtain certain properties and produce the expected result. The supervised learning algorithm that was utilized in this study is the Levenberg Marquardt algorithm. The algorithm was able to appropriately produce accurate results with very high speed.
2.4. Multilayer perceptron
The multilayer perceptron is the building block for all neural network models. It consists of one input layer, one output layer, and one or more hidden layers. The input layer is responsible for receiving input data from an external source while the hidden layer receives inputs and sends the appropriate output in the network. The neurons of each of the layers are connected to the neurons of the following layer however, neurons on the same layer are not connected. The multilayer perceptron neural network developed in this work consists of one (1) input layer, two (2) hidden layers, and one (1) output layer.
2.5. Structure of the artificial neural network
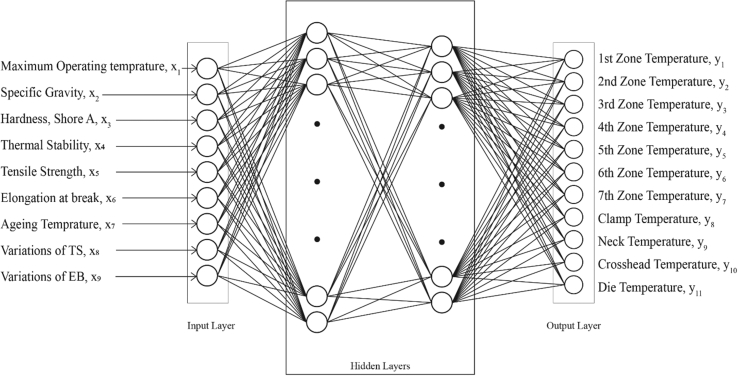
In this study, the ANN model was developed in MATLAB environment. Figure 6 shows the schematic diagram of the neural network model. The neural network consists of one input layer with nine (9) input neurons, two hidden layers with fifty (50), and forty (40) hidden neurons respectively, one output layer with eleven (11) neurons. The input parameters consist of the physical properties as obtained from the PVC material datasheet. These parameters are the maximum operation temperature, specific gravity, shore hardness, thermal stability, tensile strength, elongation at break, aging temperature, variations of the tensile strength (TS), and the variation of elongation break (EB). The output parameters of the model consist of the zonal temperature of the extruder machine from the first zone to the seventh zone, clamp, neck, crosshead, and die temperatures. The training algorithm that was utilized in this study was the Levenberg Marquardt algorithm and it provides the best result for the prediction of extrusion process parameters in PVC thermoplastic extrusion. Figures 7 and 8 shows the network diagram and the function fitting neural network for the proposed ANN model.
Figure 6.
Schematic diagram of the neural network model.
Figure 7.
Network diagram for the neural network model for PVC extrusion process parameters prediction.
Figure 8.
Function fitting neural network.
The activation function between the input and hidden layer is the Tansig function while the activation function between the hidden layer and the output layer is the Purelin function. Figures 9 and 10 represents the block representations of the Tansig and Purelin functions respectively.
Figure 9.
Tansig activation function Simulink diagram.
Figure 10.
Purelin function Simulink diagram.
Based on the network architecture utilized in this study, the mapping has two forms between the output and the input (independent) variables. The mapping is expressed in the equations below:
| (4) |
| (5) |
| (6) |
| (7) |
where are the weights of the links between the input layer and the hidden layer which are specific to independent variable and neuron , are the biases, are the input dataset, is the activation function and is the output. After successive iterations, the output equation can be generalized as follows [15]:
| (8) |
2.6. The Levenberg Marquardt Algorithm
One of the most efficient training algorithm used in ANN is the Levenberg Marquardt Algorithm. When we consider a neuron with input of a network with a number of neurons, and weights , the output is [33]:
| (9) |
| (10) |
where , , , and are the index, bias, activation function, and the sum of weighted input respectively. is a damping factor often used in the Levenberg Marquardt algorithm. The damping factor is often adjusted at every iteration until when the sum of the squared errors decreases. Eq. (11) shows the equation for the learning process.
| (11) |
where are the weights, is the Jacobian matrix, and is the error gradient. To summarize, the Levenberg Marquardt algorithm can be summarized thus; the network weights are initialized and the sum square error () is calculated and evaluated. The Jacobian matrix is also computed and the error gradient is computed as well. The cross-product is calculated and the equation is evaluated to find . The network parameters are adjusted using and the sum square errors are recalculated using the updated network's parameters. When the mean square error increase, the weights are changed to a former value and the damping factor is stepped up and the algorithm is done again. When the mean square error value decreases, the damping factor is reduced. The whole process is repeated with new weights value until the mean square error gets to the desired value.
2.7. Performance evaluation criteria
To be able to validate and evaluate the performance of the neural network developed, the mean square error (MSE) technique was utilized in this study. The values of the performance criteria must be as close to zero (0) as possible to indicate the high quality of the neural network developed. The performance criteria are described with the equations below:
| (12) |
where is the number of observations, is the desired values and is the predicted value.
3. Results and discussions
3.1. Prediction extrusion process parameters
The results that were obtained from the prediction of the extrusion process parameters for PVC thermoplastic are discussed in this section. Each of the results for different grades of PVC thermoplastic material is presented with accompanying figures, tables, and graphical representations. The discussions and the relevance of the work were also clearly highlighted.
3.2. Prediction extrusion process parameters for PVC thermoplastic materials
A multilayer perceptron model (MLP) was developed to predict the extrusion process parameters for PVC thermoplastic material. The MLP developed consists of four layers. The number of layers and the accompanying number of neurons were determined by using a heuristic approach until the best result was obtained. The dataset consists of forty-two (42) different grades of PVC thermoplastic material. Each of these grades was accompanied by their corresponding properties and the appropriate profile settings from cable manufacturing industries. The input layer consists of nine (9) neurons with each neuron representing the property of the PVC material. These represent the input variables in the artificial neural network system. The two hidden layers consist of fifty (50) and forty (40) neurons respectively while the output layer consists of eleven (11) neurons which are the melt temperature profile settings. The melt temperature profile settings are the process parameters that represent the output variables. About fifteen percent (15%) of the entire dataset was used to test and validate the result of the neural network that was developed. This invariably means that bout six (6) different grades of PVC thermoplastic material which were not used in the training process were used to test the model to determine the accuracy of the system. Table 5 shows a summary of the MLP neural network design approach.
Table 5.
Summary of the MLP neural network design approach.
| Thermoplastic Material | PVC |
|---|---|
| Number of datasets | 42 |
| Training dataset | 36 |
| Validation dataset | 6 |
| Training Algorithm | Levenberg Marquardt |
| Activation Function | Tansig and Purelin |
| Training Time | 5 s |
| Number of Iterations | 6 iterations |
| Performance Evaluation | Mean Square Error |
| Number of Inputs Layers | 1 |
| Number of Input Neurons | 9 (represents the properties for different grades of PVC thermoplastic) |
| Number of Hidden Layers | 2 |
| Number of Hidden Neurons (1st layer) | 50 |
| Number of Hidden Neurons (2nd layer) | 40 |
| Number of Output Layer | 1 |
| Number of Output Neuron | 11 (represents output variable, i.e. profile settings) |
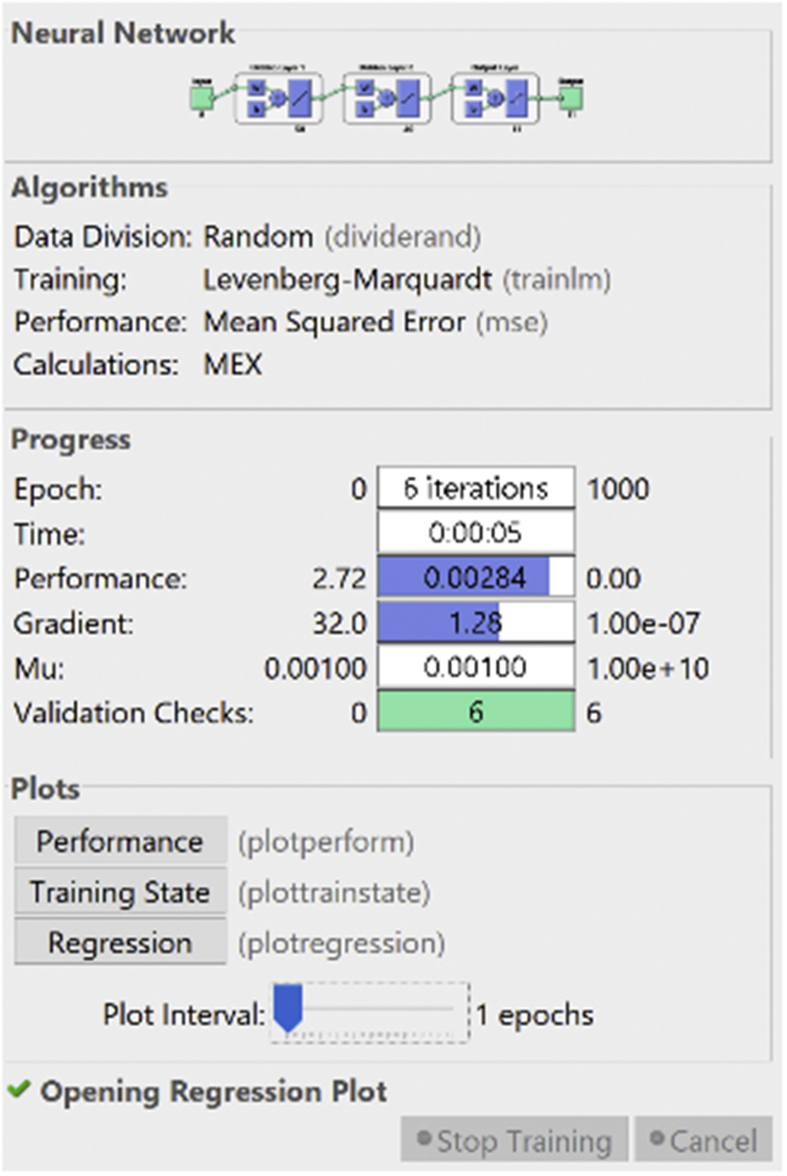
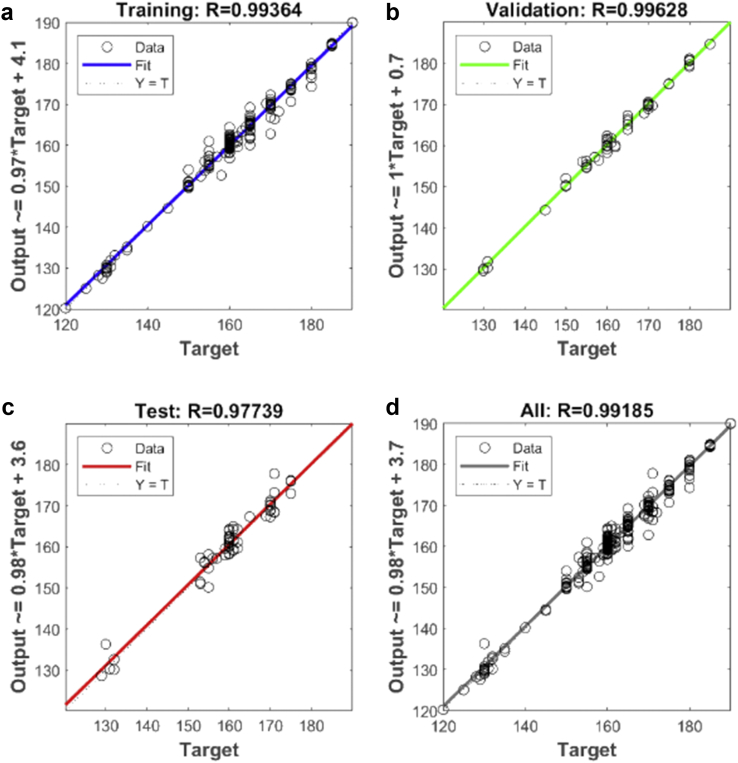
The output results from the simulation in MATLAB can be seen in Figure 11. The performance, gradient as well as the training time of the developed neural network model can be observed from Figure 11. The regression plot for the Levenberg Marquardt neural network developed for the prediction of extrusion process parameters is shown in Figure 12. Table 6 shows the MSE and R values for the training, testing, and validation of the neural network.
Figure 11.
Training process result from the simulation in MATLAB environment (PVC process parameters).
Figure 12.
Regression analysis plot for Levenberg Marquardt algorithm (PVC process parameters). (a) – Training plot, (b) – Validation plot, (c) – Test plot, (d) – All plot.
Table 6.
MSE and Regression values for the training, validation, and testing.
| MSE | R | |
|---|---|---|
| Training | 0.99364 | |
| Validation | 0.99628 | |
| Test | 0.97739 | |
| All | - | 0.99185 |
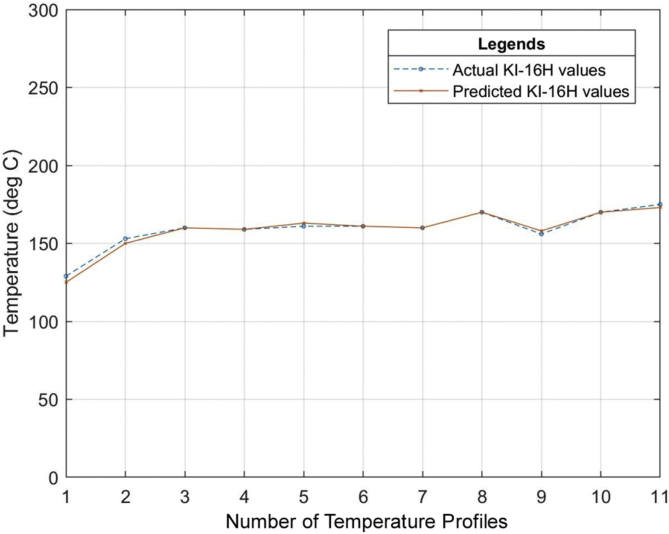
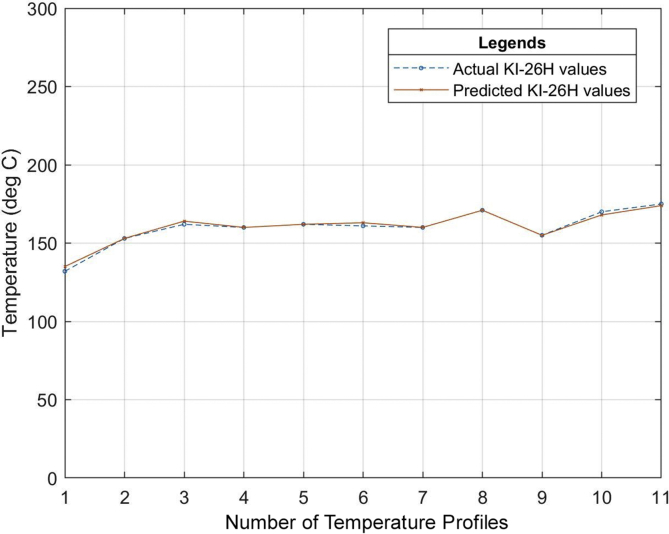
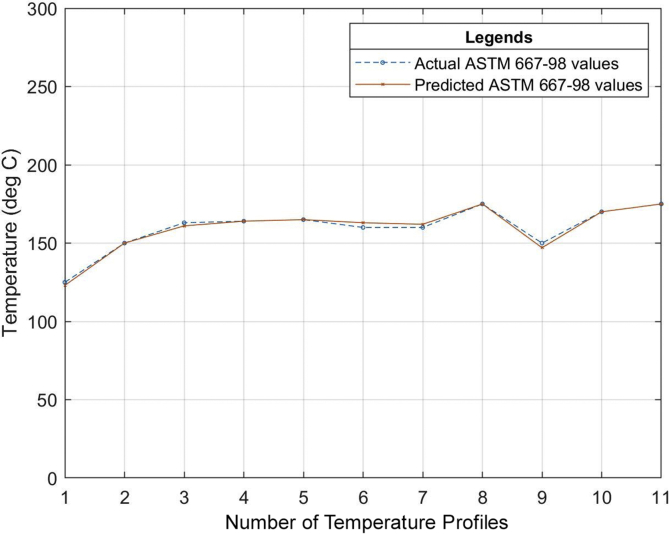
Six (6) different grades of PVC material were used to test the developed neural network system. The different properties of the PVC materials such as the specific gravity, hardness, thermal stability, tensile strength, etc. all obtained from the datasheet of the PVC material as specified by the manufacturer were used as the input of the neural network that was developed. The relationship between the actual values for the process parameters settings (existing industrial values of the temperature profile) and the predicted values (temperature profile output of the ANN model) for the different grades of PVC are outlined in Tables 7, 8 and 9. The graphical representations of these relationships can also be seen in Figures 13, 14, 15, 16, 17, 18, and 19.
Table 10.
Mean Square Error obtained from the prediction of the extrusion process parameters of different PVC materials grades.
| PVC Grade Material | Mean Square Error (MSE) |
|---|---|
| KI-16H | 2.705474 |
| KI-AV10 | 1.484374 |
| KI-26H | 2.037342 |
| KI-AV2 | 0.855364 |
| ASTM 667-98 | 2.705474 |
| ASTM 668-98 | 1.278916 |
Table 7.
Relationship between actual and predicted values for KI-16H and KI-AV10.
| Name |
KI-16H |
KI-AV10 |
||||
|---|---|---|---|---|---|---|
| Settings (°C) | Actual Value (°C) | Predicted Value (°C) | Error | Actual Value (°C) | Predicted Value (°C) | Error |
| 1st Zone | 129 | 125.0032 | 3.9968 | 130 | 132.0817 | -2.0817 |
| 2nd Zone | 153 | 150.0025 | 2.9975 | 150 | 150.0300 | -0.03 |
| 3rd Zone | 160 | 159.9970 | 0.003 | 165 | 167.0148 | -2.0148 |
| 4th Zone | 159 | 158.9953 | 0.0047 | 160 | 159.9504 | 0.0496 |
| 5th Zone | 161 | 162.9919 | -1.9919 | 160 | 161.9800 | -1.98 |
| 6th Zone | 161 | 161.0064 | -0.0064 | 160 | 159.9505 | 0.0495 |
| 7th Zone | 160 | 159.9877 | 0.0123 | 170 | 169.9878 | 0.0122 |
| Clamp | 170 | 170.0038 | -0.0038 | 170 | 168.0015 | 1.9985 |
| Neck | 156 | 157.9894 | -1.9894 | 155 | 154.9835 | 0.0165 |
| Crosshead | 170 | 169.9988 | 0.0012 | 170 | 170.1180 | -0.118 |
| Die | 175 | 173.0034 | 1.9966 | 170 | 169.9742 | 0.0258 |
Table 8.
Relationship between actual and predicted values for KI-26H and KI-AV2.
| Name |
KI-26H |
KI-AV2 |
||||
|---|---|---|---|---|---|---|
| Settings (°C) | Actual Value (°C) | Predicted Value (°C) | Error | Actual Value (°C) | Predicted Value (°C) | Error |
| 1st Zone | 132 | 135.0287 | -3.0287 | 129 | 129.4109 | -0.4109 |
| 2nd Zone | 153 | 153.0101 | -0.0101 | 153 | 152.9500 | 0.05 |
| 3rd Zone | 162 | 164.0193 | -2.0193 | 160 | 159.6972 | 0.3028 |
| 4th Zone | 160 | 160.0020 | -0.002 | 159 | 158.8450 | 0.155 |
| 5th Zone | 162 | 162.0000 | 0 | 161 | 162.4825 | -1.4825 |
| 6th Zone | 161 | 162.9937 | -1.9937 | 160 | 160.1620 | -0.162 |
| 7th Zone | 160 | 160.0191 | -0.0191 | 171 | 170.5228 | 0.4772 |
| Clamp | 171 | 170.9839 | 0.0161 | 155 | 154.6700 | 0.33 |
| Neck | 155 | 155.0033 | -0.0033 | 170 | 168.4966 | 1.5034 |
| Crosshead | 170 | 167.9737 | 2.0263 | 169 | 170.2469 | -1.2469 |
| Die | 175 | 173.9614 | 1.0386 | 175 | 173.3428 | 1.6572 |
Table 9.
Relationship between actual and predicted values for ASTM 667-98 and ASTM 668-98.
| Name |
ASTM 667-98 |
ASTM 668-98 |
||||
|---|---|---|---|---|---|---|
| Settings (°C) | Actual Value (°C) | Predicted Value (°C) | Error | Actual Value (°C) | Predicted Value (°C) | Error |
| 1st Zone | 125 | 123.0092 | 1.9908 | 132 | 130.9756 | 1.0244 |
| 2nd Zone | 150 | 150.0148 | -0.0148 | 154 | 156.9521 | -2.9521 |
| 3rd Zone | 163 | 160.9945 | 2.0055 | 160 | 159.9292 | 0.0708 |
| 4th Zone | 164 | 164.0042 | -0.0042 | 160 | 159.9243 | 0.0757 |
| 5th Zone | 165 | 164.9903 | 0.0097 | 160 | 159.9500 | 0.05 |
| 6th Zone | 160 | 163.0020 | -3.002 | 160 | 159.9783 | 0.0217 |
| 7th Zone | 160 | 162.0140 | -2.014 | 160 | 159.9548 | 0.0452 |
| Clamp | 175 | 174.9839 | 0.0161 | 175 | 175.9558 | -0.9558 |
| Neck | 150 | 147.0494 | 2.9506 | 150 | 148.1633 | 1.8367 |
| Crosshead | 170 | 169.9934 | 0.0066 | 170 | 169.9781 | 0.0219 |
| Die | 175 | 175.0047 | -0.0047 | 175 | 174.9769 | 0.0231 |
The mean square error (MSE) for the PVC grades to determine the accuracy of the proposed model is as shown in Table 10.
Figure 13.
Relationship between actual values and production values (KI–16H).
Figure 14.
Relationship between actual values and production values (KI-AV10).
Figure 15.
Relationship between actual values and production values (KI–26H).
Figure 16.
Relationship between actual values and production values (KI-AV2).
Figure 17.
Relationship between actual values and production values (ASTM 667-98).
Figure 18.
Relationship between actual values and production values (ASTM 668-98).
Figure 19.
Block diagram of a proposed neural network controller in extrusion process.
From the results, it can be seen that the artificial neural network is capable of predicting the extrusion process parameters for any grade of PVC thermoplastic that is used in cable manufacturing industries. Only PVC thermoplastic material was considered in this thesis due to the unavailability of real manufacturing data for different grades of PE thermoplastic materials. The training, validation, and testing MSE recorded in this study are , and respectively. The regression values were observed to be 0.99364, 0.99628, and 0.99185 for the training, validation, and testing dataset respectively. Six (6) different grades of PVC were used with the developed model to attempt to predict the process parameters and the results were satisfactory. The results of this work, when compared with the best work in literature so far, have proven to be better by providing a reduced MSE value [25]. reported eight different methods of predicting product quality with the best method having an MSE value of which is still higher than the MSE recorded in this thesis. The use of ANN in predicting extrusion process parameters can improve the thermoplastic extrusion process experience in cable manufacturing industries.
3.3. Prospects of using artificial neural network in the extrusion process
It can be observed from this study that the use of an artificial neural network can accurately predict the extrusion process parameters in thermoplastic extrusion. This can significantly improve the output quality and increase the production rate of electrical cables. Production managers in industries can be equipped with the appropriate tools which can enable them to produce quality cable insulation while eradicating the need to perform long experiments which can lead to waste of materials and increase the cost of production. The prospects of utilizing the artificial neural network in the extrusion process are endless as it can also be used for the control of the entire system. The neural network controller coupled with an extruder (which enables it to be able to predict future plant behaviors and select appropriate control input) which can optimize future performance. Figure 19 shows the block diagram of the proposed prediction neural network controller which can be utilized to predict future extruder plant behavior.
4. Conclusion
This study has examined the extrusion process in cable manufacturing industries and developed an artificial neural network model to predict extrusion process parameters. A multilayer perceptron neural network trained with backpropagation using the Levenberg Marquardt algorithm was developed for predicting extrusion process parameters. The artificial neural network model developed in this study was able to accurately predict the extrusion process parameters for different grades of PVC cable in the thermoplastic extrusion used cable manufacturing industries. The use of artificial neural networks can eradicate the need for trial and error techniques which can improve the output quality in the thermoplastic extrusion process, and it will also reduce production time and cost. An artificial neural network is best suited to solve an industrial problem because it can be applied to real manufacturing execution systems.
Declarations
Author contribution statement
Ayokunle Adesanya: Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Ademola Abdulkareem: Conceived and designed the experiments; Wrote the paper.
Lambe Mutalub Adesina: Contributed reagents, materials, analysis tools or data.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- 1.Shrivastava A. Introduction to plastics engineering. In: A. B. T.-I., Shrivastava P.E., editors. Plastics Design Library. William Andrew Publishing; 2018. pp. 1–16. [Google Scholar]
- 2.Biron M. Chapter 5 - thermoplastic processing. In: M. B. T.-T., Biron T.C.E., editors. Plastics Design Library. third ed. William Andrew Publishing; 2018. pp. 767–820. [Google Scholar]
- 3.Akovali G. Plastic materials: polyvinyl chloride (PVC) In: Pacheco-Torgal F., Jalali S., A. B. T.-T, Fucic B.M., editors. Woodhead Publishing Series in Civil and Structural Engineering. Woodhead Publishing; 2012. pp. 23–53. [Google Scholar]
- 4.Abdulkareem A., Agbetuyi A.F., Akinbulire T. Improving the thermoplastic extrusion process in cable manufacturing. IMPACT Int. J. Res. Appl. Nat. Soc. Sci. (IMPACT IJRANSS) 2014;2(4):193–202. [Google Scholar]
- 5.Rosato D.V. 1998. Extruding Plastics. [Google Scholar]
- 6.Chris Rauwendaal, Understanding extrusion, Hanser.
- 7.Plochocki A.P., Dey S.K., Wilczynski K. Evaluating screw performance: extrusion process stability and the degree of mixing from melt rheology data and from measurement on an instrumented extruder. Polym. Eng. Sci. 1986;26(14):1007–1011. [Google Scholar]
- 8.Wilczyński K. Evaluating screw performance in a single-screw extrusion process. Polym. Plast. Technol. Eng. 1989;28(7–8):671–690. [Google Scholar]
- 9.Abeykoon C. Single screw extrusion control: a comprehensive review and directions for improvements. Control Eng. Pract. 2016;51:69–80. [Google Scholar]
- 10.Manley T.R. Polymer extrusion: C. Rauwendaal Carl Hanser Verlag, Munich. 1986;28(1):560. £29.65, 1987. [Google Scholar]
- 11.Abeykoon C. A novel soft sensor for real-time monitoring of the die melt temperature profile in polymer extrusion. IEEE Trans. Ind. Electron. 2014;61(12):7113–7123. [Google Scholar]
- 12.Biron M. In: Thermoplastics: Economic Overview. M. B. T.-M. S., Biron T.P., editors. William Andrew Publishing; Oxford: 2016. pp. 77–111. [Google Scholar]
- 13.Campbell G., Spalding M. 2013. Single-Screw Extrusion: Introduction and Troubleshooting; pp. 1–22. [Google Scholar]
- 14.Deng J. Energy monitoring and quality control of a single screw extruder. Appl. Energy. 2014;113:1775–1785. [Google Scholar]
- 15.Njobet N. 2012. Energy Analysis in the Extrusion of Plastics. [Google Scholar]
- 16.Abeykoon C. Investigation of the process energy demand in polymer extrusion: a brief review and an experimental study. Appl. Energy. 2014;136:726–737. [Google Scholar]
- 17.Zinnatullin R.R., Kazakov A.V., Trufanova N.M. Automatic control system of extrusion of polymer cable insulation. Russ. Electr. Eng. 2011;82(11):596–599. [Google Scholar]
- 18.Abeykoon C. A novel model-based controller for polymer extrusion. IEEE Trans. Fuzzy Syst. 2014;22(6):1413–1430. [Google Scholar]
- 19.Ramya K., Sreedevi K. Modeling and optimization of extrusion process parameters of AA6061 using Taguchi method. Eng. Mech. 2016:1753–1756. [Google Scholar]
- 20.Sivaprasad P.V., Venugopal S., Davies C.H.J., Prasad Y.V.R.K. Identification of optimum process parameters for hot extrusion using finite element simulation and processing maps. Model. Simul. Mater. Sci. Eng. 2004;12(2):285–291. [Google Scholar]
- 21.Alatawneh N. “Effects of cable insulations’ physical and geometrical parameters on sheath transients and insulation losses. Int. J. Electr. Power Energy Syst. 2019;110:95–106. [Google Scholar]
- 22.Patil P.M., Sadaphale D.B. A review on optimization of extrusion process parameters to reduce uneven wall thickness in HDPE pipes. 2018;6(Xi):136–140. [Google Scholar]
- 23.Kumar D., Kumar S. Process parameters optimization for HDPE material in extrusion blown film machinery using Taguchi method. IOSR J. Mech. Civ. Eng. 2015;12(4) 2278–1684. [Google Scholar]
- 24.Solomon Kerealme, Srirangarajalu N., Assefa Asmare. Parameter optimization of extrusion machine producing UPVC pipes using Taguchi method: a case of Amhara pipe factory. Int. J. Eng. Res. 2016;V5(1) [Google Scholar]
- 25.García V., Sánchez J., Rodríguez-Picón L., Mendez L., Ochoa H. Using regression models for predicting the product quality in a tubing extrusion process. J. Intell. Manuf. Aug. 2019;30:2535–2544. [Google Scholar]
- 26.Montaño J., Palmer A., Sesé A., Cajal B. Using the R-MAPE index as a resistant measure of forecast accuracy. Psicothema. Nov. 2013;25:500–506. doi: 10.7334/psicothema2013.23. [DOI] [PubMed] [Google Scholar]
- 27.Abeykoon C., Li K., McAfee M., Martin P.J., Irwin G.W. Extruder melt temperature control with fuzzy logic. IFAC. 2011;44(1 PART 1) [Google Scholar]
- 28.Nastaj A., Wilczyński K. Optimization for starve fed/flood fed single screw extrusion of polymeric materials. Polymers (Basel) 2020;12(1):149. doi: 10.3390/polym12010149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bingol S., Altinbalik T., Kilicgedik H Y. 56th Int. Conf. Mach. Des. Dep. ICMD. 2015. Artificial neural network modeling for the application of lateral extrusion process; p. 2015. September. [Google Scholar]
- 30.Lucignano C., Montanari R., Tagliaferri V., Ucciardello N. Artificial neural networks to optimize the extrusion of an aluminium alloy. J. Intell. Manuf. 2010;21(4):569–574. [Google Scholar]
- 31.Hsiang S.H., Kuo J.L., Yang F.Y. Using artificial neural networks to investigate the influence of temperature on hot extrusion of AZ61 magnesium alloy. J. Intell. Manuf. 2006;17(2):191–201. [Google Scholar]
- 32.Mekras N., Artemakis I. Using artificial neural networks to model extrusion processes for the manufacturing of polymeric micro-tubes. IOP Conf. Ser. Mater. Sci. Eng. 2012;40(1) [Google Scholar]
- 33.Models N., Breakwaters S. 2016. Numerical Methods and Procedures; pp. 93–108. [Google Scholar]