Abstract
The inter-comparison of MODIS reflective solar bands onboard Aqua and Terra is very important for assessment of each instrument’s calibration. One of the limitations is the lack of simultaneous nadir overpasses. Their measurements over a selected Earth view target have significant differences in solar and view angles, which magnify the effects of atmospheric scattering and Bidirectional Reflectance Distribution Function (BRDF). In this work, an inter-comparison technique is formulated after correction for site’s BRDF and atmospheric effects. The reflectance measurements over Libya desert sites 1, 2, and 4 from both the Aqua and Terra MODIS are regressed to a BRDF model with an adjustable coefficient accounting for calibration difference. The ratio between Aqua and Terra reflectance measurements are derived for bands 1 to 9 and the results from different sites show good agreement. For year 2003, the ratios are in the range of 0.985 to 1.010 for band 1 to 9. Band 3 shows the lowest ratio 0.985 and band 1shows the highest ratio 1.010. For the year 2014, the ratio ranges from approximately 0.983 for bands 2 and 1.012 for band 8. The BRDF corrected reflectance for the two instruments are also derived for every year from 2003 to 2014 for stability assessment. Bands 1 and 2 show greater than 1% differences between the two instruments. Aqua bands 1 and 2 show downward trends while Terra bands 1 and 2 show upward trends. Bands 8 and 9 of both Aqua and Terra show large variations of reflectance measurement over time.
Index Terms –: Inter-comparison, MODIS, Radiometric calibration, BRDF, Atmospheric correction
1. INTRODUCTION
The Moderate Resolution Imaging Spectroradiometer (MODIS) onboard the Terra and Aqua satellites have successfully operated since their launch in 1999 and in 2002, providing more than 16 and 14 years of continuous global observations for science research and applications [1–4]. Due to limitations of the instrument’s on-board calibrators and large changes in sensor responses over time, vicarious calibration and instrument inter-comparison approaches have been developed as alternative calibration methods to maintain sensor calibration accuracy [5–8]. In Collection (or version) 6 of the MODIS calibration algorithm, the time-dependent response versus scan-angle (RVS) for the reflective solar bands (RSB) is characterized using measurements over select Earth view sites, combining with the on-board calibrators and lunar observations [9, 10]. The long-term trending over select Earth view sites and the inter-comparison between the instruments has also been used for MODIS calibration assessment. Aqua and Terra MODIS have almost identical relative spectral response, spatial resolution, and dynamic range for each RSB. The site dependent correction for a sensor spectral band pair is not necessary for Terra and Aqua MODIS comparison. The inter-comparison between Aqua and Terra MODIS over vicarious calibration sites can be very supportive for the instrument calibration and uncertainty assessment. However, for RSB, a major challenge in cross-sensor comparison of instruments on different satellites are their measurement differences in solar angle and view angle over selected pseudo-invariant sites.
Observations from simultaneous nadir overpasses (SNO) between two polar orbiting satellites have been used to reduce these effects [11–17]. However, Terra is in the morning orbit with an equator crossing time of 10:30 am, and Aqua is in the afternoon orbit with equator crossing time of 1:30 pm. Consequently, there is a dearth of SNOs between the two instruments. As a result, an inter-comparison effort between the two MODIS instruments is a challenging effort. Due to the sun-synchronous orbit and a 16-day repeat orbit, both the solar angle variation and view angle coverage are limited for a given Earth view site. The insufficient samples and limited coverage for BRDF modeling lead to a greater uncertainty in the regression and therefore a reduced quality for the inter-comparison. In this study, a regression method is developed and applied for the inter-comparison between Aqua and Terra MODIS RSB. The satellite sensor measures the top of the atmosphere (TOA) reflectance. For the short-wavelength bands, the atmospheric scattering (primarily Rayleigh) bears a significant impact on the retrieved TOA reflectance. In this paper a correction for these atmospheric scattering effects is performed using a vector version of the Second Simulation of a Satellite Signal in the Solar Spectrum - Vector (6SV) model [18–22]. After the correction for the atmosphere scattering and transmittance, the surface reflectance is retrieved and modeled using BRDF function for each selected reflectance band. The surface reflectance from both instruments over a select Earth view site is regressed to a BRDF model. The difference in the reflectance measurement between the two instruments can be caused by the calibration. An adjustable ratio is used for each band to compensate the difference between Terra and Aqua. Either one of them can be used as reference in the comparison while Aqua is chosen in this paper. The least-square method is applied to derive the ratio and the BRDF coefficients. In this approach, the BRDF regression is performed using significant amount of samples with extended coverage of solar angle and view angle, thus improving the modeling accuracy. Various BRDF models, including several semi-empirical and empirical models, have been developed and applied to account for the effects of different illumination and view geometry [23–29]. The BRDF is surface type dependent and a spatially and spectrally homogeneous scene is desirable to have a uniform BRDF effect over a selected site. Desert sites 1, 2, and 4 are known to be pseudo-invariant, meaning they are spatially, spectrally and temporally uniform. Thus, they are frequently used for vicarious calibration, and are among the sites used for developing MODIS collection 6 RSB calibration [30–33]. Terra and Aqua are calibrated independently and the inter-comparison using these sites is very supportive for calibration improvement. In this paper, a formulation of the inter-comparison methodology is presented. Using this method, the comparison between Terra MODIS and Aqua MODIS is performed for bands 1 to 9 from year 2003 to 2014. The atmospheric scattering in the TOA reflectance is corrected using 6SV model. The regression of the reflectance of the Earth view pixels with the BRDF model is performed for each site, and a per-band ratio between the two instruments is derived. To have sufficient solar angle coverage, the ratio is derived for each year and the temporal stability of the derived ratios is assessed. The focus of this paper is to assess the calibration difference between two instruments and their stability. The BRDF corrected reflectance from each instrument is normalized to the Aqua MODIS result from 2003 and the long-term trending of the normalized reflectance is evaluated. The per-band BRDF coefficients of three Libya Desert sites are also derived and these parameters are useful for instrument vicarious calibration, assessment, and inter-comparison.
2. BACKGROUND
2.1. MODIS calibration overview
MODIS has 36 spectral bands and among them, bands 1–19 and 26 are the RSB that provide images from daytime reflected solar radiation with spectral coverage from 0.4 to 2.2 μm [1–4]. MODIS RSB calibration is reflectance-based, and the on-board solar diffuser (SD) is used to establish the reflectance factor with the solar diffuser stability monitor (SDSM) used to track changes in the SD reflectance. The calibration parameter from the solar diffuser and RVS are determined for every RSB detector and each scan mirror side [5–7]. After 16 and 14 years on-orbit operation on Terra and Aqua respectively, the SD and scan mirror have exhibited significant degradation and changes. The accuracy of on-orbit calibration is inadequate for characterizing the sensor response and it results in long-term reflectance drifts while observing the time-invariant targets. C6 Level 1B (L1B) incorporated several algorithm enhancements over its predecessor Collection 5 (C5) [9, 10]. For Terra bands 1–4, 8–9 and Aqua bands 8 and 9, the on-board SD and lunar measurements have been supplemented with observations from pseudo-invariant sites from the Libya Desert. Since then, the EV-based approach has been extended to apply to Terra band 10 and Aqua bands 1–4.
2.2. 6SV model
6SV uses basic radiative transfer model to calculate atmospheric correction. It facilitates accurate simulations of satellite and airplane observations, including MODIS [18–21]. It is widely used, rigorously validated, and well-documented radiative transfer models known in the scientific remote-sensing community. The characterization of the atmospheric scattering effects, especially Rayleigh scattering at short wavelengths, is the model application in this work. For satellite sensor over uniform targets, such as MODIS observation over the Libyan sites, the TOA reflectance from the simplified model can be expressed as [22]
| (1) |
where θs(v) are solar zenith or view zenith angle, ϕ is the relative difference of solar and view azimuth angles, Rscattering (θs, θv, ϕ) is scattering with solar and view angle dependencies, S is the spherical albedo of the atmosphere, T (θs) and T(θv) are downward and upward transmittances. Rt in Eq. (1) is the input target reflectance. However, the retrieved measurement from satellite sensor is TOA reflectance and the 6SV model is used to derive the corrected target reflectance. The 6SV manual describes a scheme for the atmospheric correction using the above model [18–21]. The use of this scheme and a correction look-up-table (LUT) method for the atmospheric correction in this work are presented in section 3.2.
2.3. BRDF model
As the two instruments view a ground target at different solar and view angles, a BRDF model should be applied for the correction of bidirectional effects. A physical BRDF model is the ideal option to reduce the solar and view angle dependency. Semi-empirical models and empirical model have also been developed for BRDF correction [23–29]. In this work, the measurements are over pseudo-invariant desert sites. Considering the computation time, two BRDF models are applied for surface reflectance correction. These two models, one semi-empirical model and one empirical model, are very different. The comparison between the results from these two model can be used as a verification.
2.3.1. Semi-empirical model (Roujean)
A semi-empirical model developed by Roujean is widely used to correct for bidirectional effect on the reflectance and its model coefficients are adjustable to account for the variations in surface type [27]. In this model, the surface reflectance is expressed as
| (2) |
where
And
with cosξ = cosθs cosθv + sinθs sinθv cosϕ. k0 represents the surface reflectance with zero solar zenith angle and view zenith angle, k1 f1(θs, θv, ϕ) is the contribution from volume scattering, and k2 f2(θs, θv, ϕ) accounts for the surface scattering and geometric shadow casting. The model coefficients k0 , k1 , and k2 are surface type dependent. Although Libya 1, 2, and 4 have a similar surface type, they are expected to have small differences and the measurements over these sites cannot be regressed with the same coefficients. The coverages of solar angle range and view angle range, the sample amount, reflectance retrieval condition variation, and sensor reflectance measurement bias may affect the precision of these coefficients.
2.3.2. Empirical model (modified Walthall)
To verify the impact of different BRDF models on the comparison, an empirical BRDF model is also evaluated. A sophisticated empirical model proposed by Walthall and modified by Nilson and Kuusk has been demonstrated for its feasibility for accounting for the bidirectional reflectance effect [23–26]. With this model, the principle of reciprocity and the angle dependent reflectance are expressed as,
| (3) |
a0–3 are the model coefficients. a3 is the BRDF corrected reflectance, same as k0 in Eq (2). The first three terms are used to account for the BRDF effects and the coefficients are derived empirically from the regression with the measurement data. For the case of limited data amount and angular coverage, the correlation between these BRDF effect terms can be higher. The individual term of the model does not relate to a physical meaning and the sum of these three terms should be used to account for the overall BRDF effects.
2.4. Reflectance Data and Science Products
The TOA reflectance measurements can be retrieved for MODIS RSB from L1B data. Levels 2 and 3 products provide surface reflectance and BRDF adjusted albedo by combining the measurements from both Terra and Aqua MODIS. The MODIS surface reflectance product (MOD09) is a seven-band surface reflectance product computed from MODIS L1B bands 1–7. Vermote et.al reported that the accuracy of MOD09 is primarily limited by the accuracy of the sensor calibration, atmospheric parameter inputs, and the radiative transfer code in forward simulation [34]. Starting Collection 6 (C6), NASA’s Land Data Operational Products Evaluation (LDOPE) restructured the processing for the level 2 products used to generate various land products such as surface reflectance [8]. The polarization sensitivity of MODIS was measured during the prelaunch characterization by the instrument vendor. In the case of the short-wavelength VIS bands, especially for Terra MODIS, the polarization sensitivity has exhibited changes on-orbit. The MODIS Ocean Biology Processing Group (OBPG) developed corrections for the changing polarization sensitivity based on Aqua MODIS and SeaWifs [35–37]. These corrections have been implemented in the level 2 product generation process to generate a polarization corrected L1B. Additionally, a de-trending correction, as developed by Lyapustin et.al, is applied during this process to remove the long-term residual impacts due to calibration inadequacies [38]. A kernel-driven linear model relying on the weighted sum of an isotropic parameter and two kernels for viewing and illumination geometry is used to estimate the BRDF is the operational MODIS albedo and reflectance anisotropy algorithm. One kernel is derived from radiative transfer models and the other is based on surface scattering and geometric shadow casting theory. The kernel weights are derived by performing a best fit to cloud-clear atmospherically corrected surface reflectance measurements. MODIS level 3 product (MCD43 BRDF/Albedo) are generated by combining Terra and Aqua MODIS using a kernel-driven semi-empirical BRDF model and using the RossThick-LiSparse kernel functions for characterizing isotropic, volume and surface scattering [28, 29]. The MCD43 level 3 products also cover MODIS bands 1 to 7. Due to lack of simultaneous overpasses, atmospheric correction is vital in the evaluation of the calibration consistency between Terra and Aqua MODIS. A comparison of the downstream Terra and Aqua MODIS science products (BRDF or surface reflectance) will facilitate a comparison after atmospheric corrections. However, a drawback of this approach is the fact that an additional de-trending correction has been incorporated in these products to ensure a long-term calibration consistency. It is therefore essential to perform this comparison at the L1B, with correction for atmospheric scattering and BRDF effect as presented in this work.
3. METHODOLOGY
3.1. Site selection and data processing
The L1B data with geolocation information are processed to retrieve the reflectance for bands 1 through 9 for each instrument at a 1-km pixel resolution. Since the BRDF effect is wavelength dependent, table 1 lists the center wavelength of the bands for reference. To account for the variation of the solar and view angles, the reflectance, solar zenith angle, solar azimuth angle, sensor zenith angle, and sensor azimuth angle of all the pixels over selected sites in a one-year period of time are analyzed. Each selected desert site is 20 km X 20 km at nadir with 400 1-km pixels. Terra and Aqua overpass the site once a day. In most days, the data acquired while overpassing a site are in one 5-minute granule in L1B data covering 1354 X 2030 pixels. The 1354 pixels in the cross-track direction represent the scan angle range of ±55°. Occasionally, the measurements over one site are split into two granules. In the plots in section 4.1, the measurements over a site are averaged over the pixels in one granule.
Table. 1.
The center wavelength for MODIS bands 1 to 9.
| Band | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Wavelength (nm) | 646.3 | 856.5 | 465.7 | 553.7 | 1242.3 | 1629.4 | 2114.2 | 411.8 | 442.1 |
The selected pseudo-invariant desert sites are Libya Desert sites 1, 2, and 4 which provide good coverage of view angle and mirror scan angle. The corner coordinates of the chosen region from these sites are listed in table 2. The data from the 2003 to 2014 period are processed and the reflectance atmospheric correction is performed as described in section 3.2. The Aqua/Terra ratio and BRDF characterization for each year is derived using the steps described in section 3.3. The data process, regression using BRDF model, and the comparison are performed for each site and for each year.
Table. 2.
The latitude and Longitude ranges of three Libya Desert sites
| Site | Lat_min | Lat_max | Lon_min | Lon_max |
|---|---|---|---|---|
| Libya 1 | 24.95 | 25.15 | 20.38 | 20.58 |
| Libya 2 | 24.32 | 24.52 | 13.25 | 13.45 |
| Libya 4 | 28.45 | 28.65 | 23.29 | 23.49 |
3.2. Atmospheric correction
The atmospheric correction scheme presented in 6SV manual is used for this work [22]. With this scheme, the TOA reflectance is an input and the corrected reflectance can be retrieved as
| (4) |
with
| (5) |
where S is spherical albedo and Ra is the atmospheric scattering, which are derived from the model. However, executing this correction for every single MODIS measurement is computationally expensive. In this work, a correction LUT is prepared for different input TOA reflectance, solar zenith angle, view zenith angle, and relative azimuth angle. For a reflectance measurement, the correction is determined using the LUT for each band with inputs of TOA reflectance, solar zenith angle, view zenith angle, and relative azimuth angle. The interpolation method is applied across four dimensions. Although it is time-consuming to derive a LUT with finer resolution in four dimensions, it can be used to correct for all the measurements.
3.3. Regression
The BRDF models presented in section 2.3 are applied for BRDF correction in this work. Since these models are for surface reflectance, the target reflectance of the three sites after atmospheric correction will be analyzed. An empirical BRDF model presented in section 2.3.2 is used to verify the comparison between Aqua and Terra. With the consideration of BRDF effect, the “true” reflectance for one band can be expressed as
| (6) |
The first term R0 represents the at-nadir reflectance with zero solar zenith angle. The second term ΔR(θs, θv, ϕ) represents the BRDF correction for off-nadir solar and view angles. Assuming both Terra and Aqua MODIS have biases in their measurements due to the calibration inadequacies and the biases being proportional to the reflectance measurement, the retrieved reflectance can be express as
| (7) |
where the superscript T or A stands for Terra or Aqua MODIS. Without knowing the “truth”, the ratio between the two instruments can be used
| (8) |
where is the ratio between the measurements from same band of the two instruments. For a given calibration site, the reflectance measurements from Aqua and Terra both have different solar and view angles, appending the two sets of data and the ensemble still follow the BRDF model
| (9) |
The ⊕ operation is to ensemble the two sets of data, instead of mathematical summation. This operation on the left of Eq (9) is to append adjusted Terra measurements to Aqua measurements and on the right side, the BRDF corrections are appended accordingly. The BRDF models used in this analysis are the semi-empirical model and empirical model in section 2.3. As an example, applying this method to the semi-empirical BRDF model in section 2.3.1, Eq (2) becomes
| (10) |
where RA⊕αT (θsA⊕T, θvA⊕T, ϕA⊕T) stand for RA(θsA, θvA, ϕA) ⊕ αRT(θsT, θvT, ϕT), θ(ϕ) A⊕T stands for θ(ϕ)A ⊕θ(ϕ)T, and ki′ = αAki for i=0,1,2 are the Aqua BRDF coefficients. For simplification, ki is used in rest of the paper to represent the BRDF coefficients for Aqua reflectance measurements. A similar methodology is also applied to evaluate the empirical model.
The regression of the model with Aqua and Terra measurements is to determine the Aqua/Terra ratio and to derive the BRDF coefficients using least-square method. The least-square method is to minimize the difference between the model and measurements by adjusting the ratio and BRDF coefficients. For the semi-empirical model in Eq (2), applying the least-square method, we can have,
| (11) |
Where N A(T) are the sample numbers from Aqua and Terra measurements, RA⊕αT = RA⊕αT (θs A⊕T , θvA⊕T ), and f1(2)A⊕T = f1(2) (θsA⊕T, θvA⊕T, ϕA⊕T). To balance the contributions from the two instruments, measurement data over the same period of time is used in the regression. In this work, the reflectance measurements over the entire year are processed to derive the ratio and BRDF coefficients. The same method can be applied to the regression using the empirical BRDF model presented in section 2.3.2.
4. RESULTS
4.1. Regression results
The accuracy of the regression results using the model depends on the sample amount and the data coverage in the measurement, including the coverage of solar zenith angle, view zenith angle, and relative azimuth angle. A broad coverage of solar and view angles combined with even distribution between Aqua and Terra can lead to a higher accuracy of the modeling results. The measurement data coverage is analyzed using the measurements from the year 2003 for both instruments. Figures 1 and 2 shows the coverage of solar zenith angle, sensor zenith angle, and relative azimuth angle difference. Both Terra and Aqua orbits are sun-synchronous and have 16-day repeat period. These orbit features can cause correlation between sensor view angle and solar angle. The plots in Figure 1 are solar zenith angle and relative azimuth angle against sensor view zenith angle. The sensor view zenith angle is set to negative for the left side of nadir to distinguish the direction relative to nadir. The relative azimuth angle is less than 90° on one side, while it is greater than 90° on the other side. The plots in Figure 2 shows the variations of relative azimuth angle difference and solar zenith angle with day of year. As expected, the solar zenith angle and relative azimuth angle difference vary seasonally. During the middle of the calendar year, solar zenith angle is lower. In addition, the sun illumination and reflectance path are close to the principle plane. There are no measurements with relative azimuth angles close to 90°. For solar angles and sensor view angles, Terra and Aqua have symmetric distributions, which reduce the impact of the angle dependency on the model uncertainty.
Figure 1.
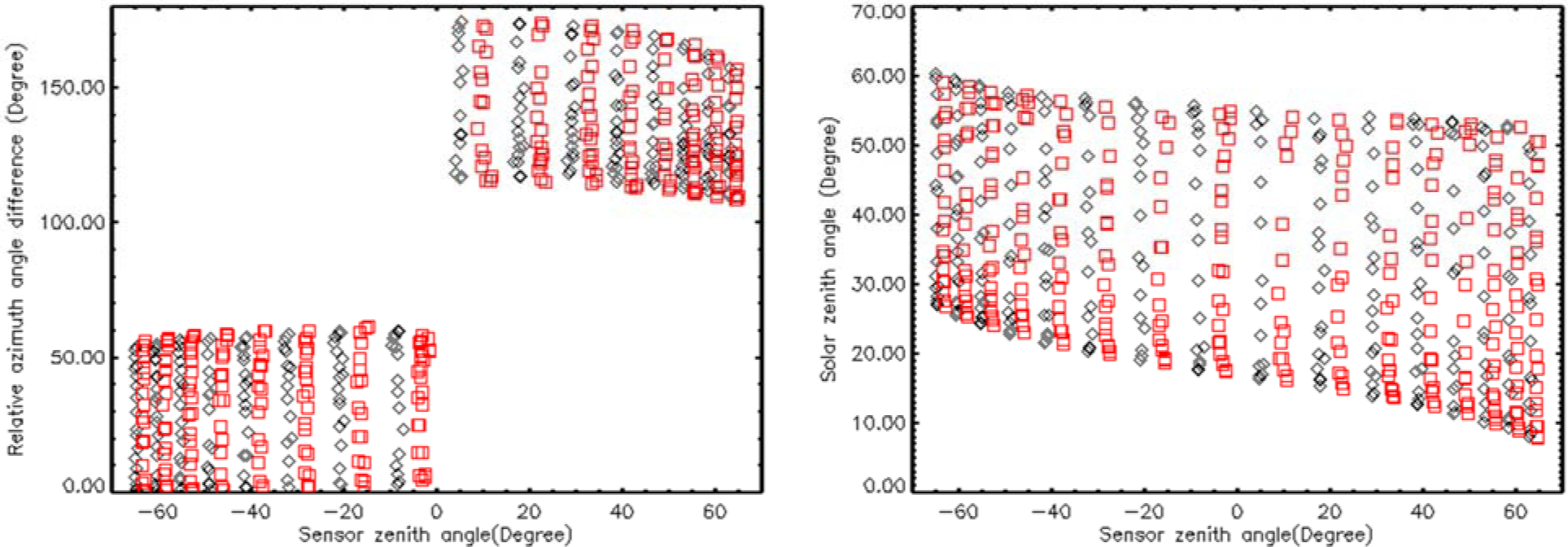
The correlation of the relative azimuth angle with sensor zenith angle (left), solar zenith angle with sensor zenith angle (right), for Libya Desert 4 in year 2003. Each symbol presents the average of reflectance measurement of the pixels in one granule. The black diamonds are for Aqua and the red squares are for Terra.
Figure 2.
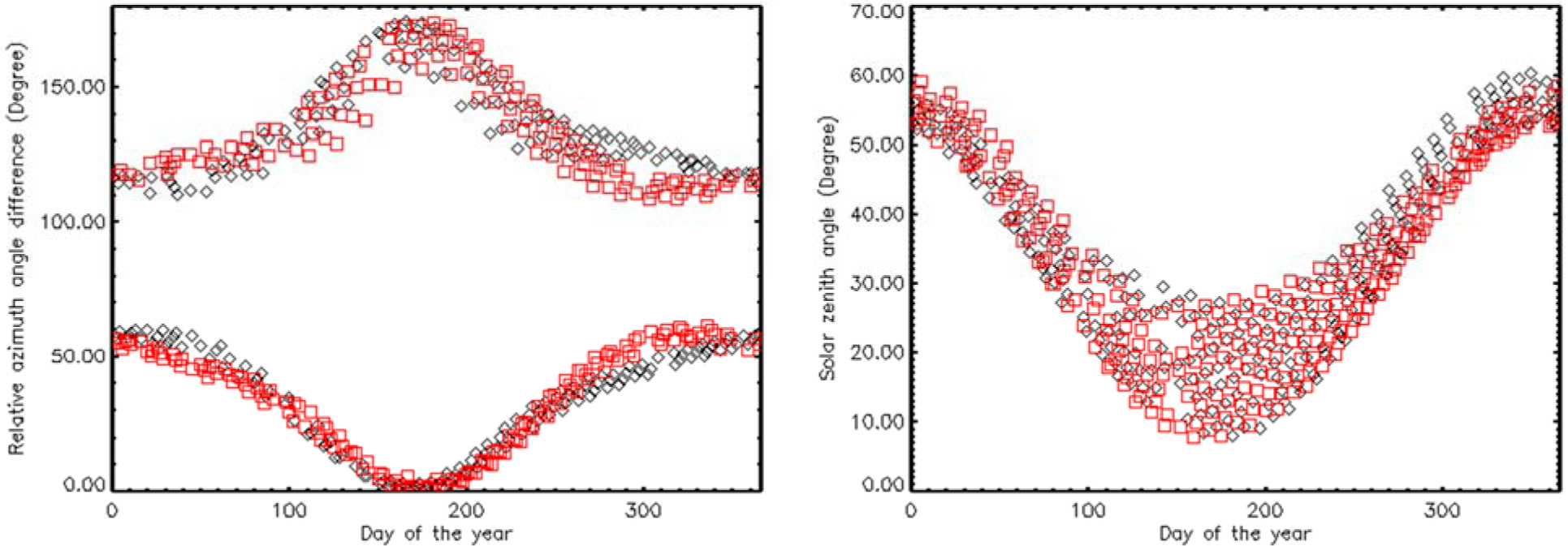
The correlation of the relative azimuth angle with day of the year (left) and solar zenith angle with day of the year (right) for Libya Desert 4 in year 2003. Each symbol presents the average of reflectance measurement of the pixels in one granule. The black diamonds are for Aqua and the red squares are for Terra.
The ratio between Aqua and Terra for a VIS/NIR band can be derived from the least-square regression of the reflectance measurements using BRDF model. The regressions are performed for bands 1 to 9. Figure 3 shows the results of regression of Aqua and Terra measurements with the semi-empirical BRDF model for bands 3 and 8 for Libya desert 4 in year 2003. The goodness of the regression is shown using the measurements from Aqua and Terra RA⊕αT against the modeled values k0 + k1f1A⊕T + k2f2A⊕T , where Terra measurements have been adjusted using the derived ratio. A 3-sigma outlier rejection is used to eliminate out-of-family pixels. The Terra measurements, after adjusted using the optimized ratio, have the almost the same goodness of fit as compared to Aqua. Similar regressions have been performed using the empirical BRDF model presented in section 2.3.2.
Figure 3.
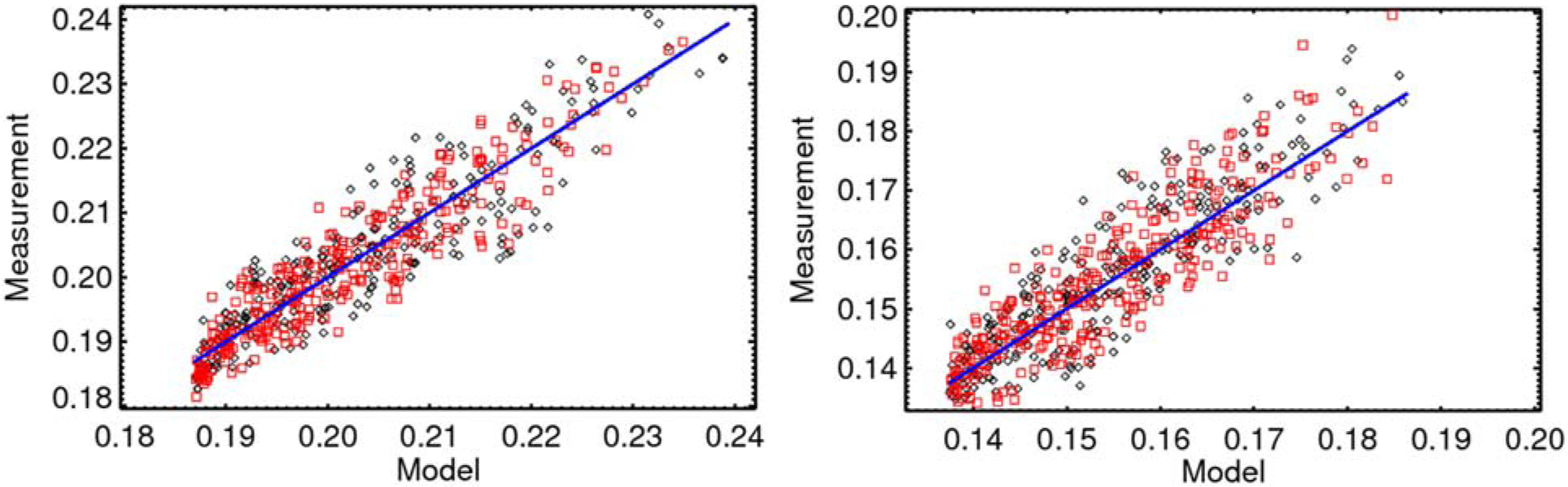
The regressions of Libya desert 4 reflectance measurement of band 3 and 8 in year 2003 using semi-empirical model. The plots are the measurements from both Aqua and Terra RA⊕αT with optimized ratio against the modeled values k0 + k1f1A⊕T + k2f2A⊕T. Each symbol presents the average of reflectance measurement of the pixels in one granule. The black diamonds are Aqua measurements and the red squares are Terra measurements adjusted by the optimized ratio factor. The blue lines represent the model fitting.
4.2. BRDF corrected reflectance
The regression for determining the Aqua/Terra ratio, the BRDF corrected reflectance for Aqua and Terra are also derived ( k0 and k0 / α ). With the analysis results for year 2003 to 2014, the long-term trending of the normalized BRDF corrected reflectance are obtained. The reflectance for both Aqua and Terra are normalized to that of 2003 Aqua and are shown in Figure 4. Bands 1 and 2 show greater than 1% differences between Aqua and Terra. Aqua bands 1 and 2 show downward trends while Terra bands 1 and 2 show upward trends. Bands 8 and 9 of both Aqua and Terra show large variations (larger vertical scales are used) and Terra band 8 is worse than Aqua. For bands 3–7, Terra measurements are higher than those of Aqua
Figure 4.
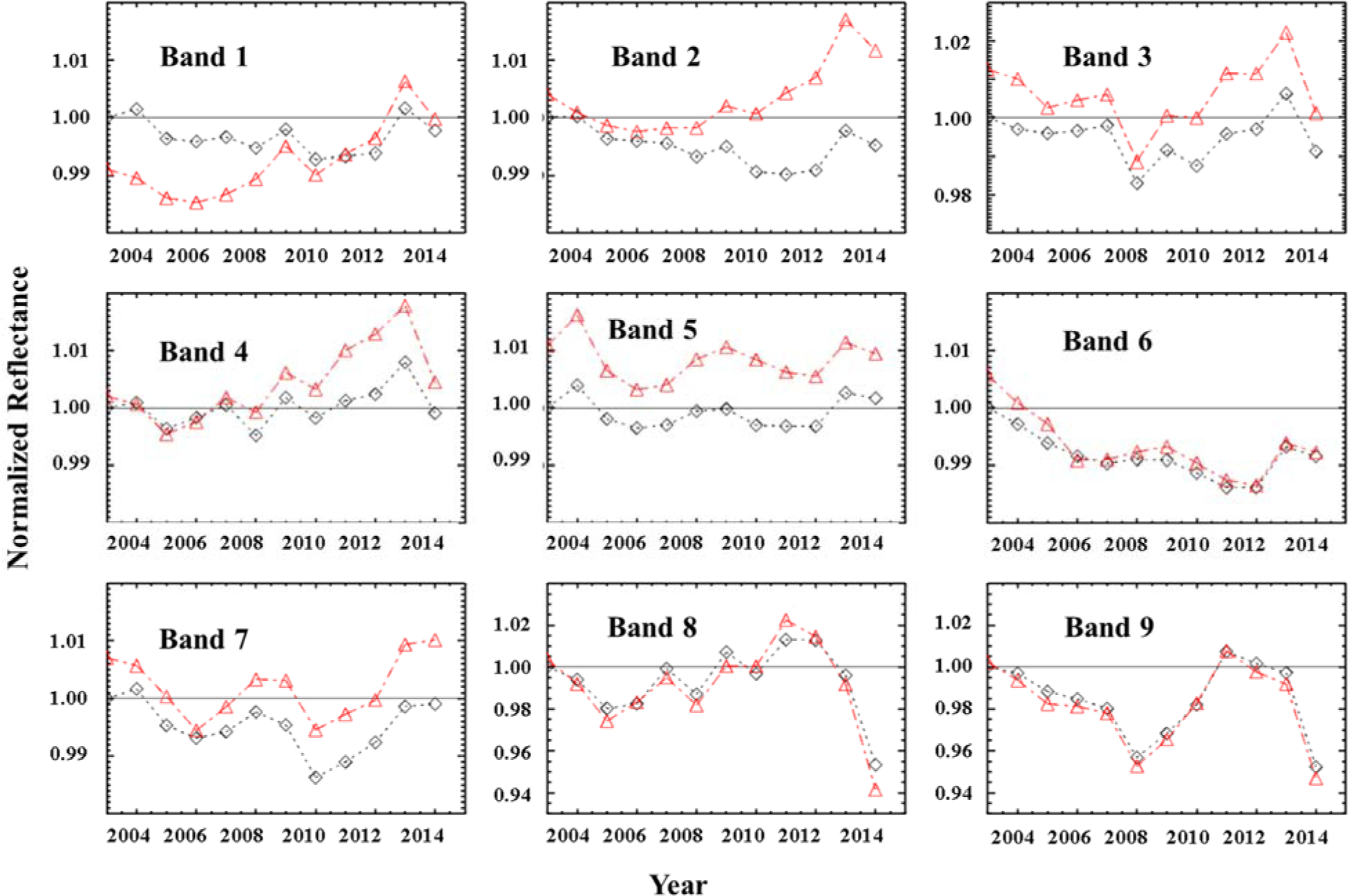
BRDF effect corrected reflectance for Aqua from year 2003 to 2014 derived from the averaged results of three desert sites. The corrected reflectance are normalized to 2003 reflectance. The black diamonds are the corrected reflectance for Aqua and red triangles are for Terra.
4.3. Aqua and Terra comparison
The objective of this comparative analysis is to determine the ratio of BRDF corrected measurement between Aqua and Terra. Figure 5 shows the Aqua-to-Terra ratios for band 1 to 9 for years 2003 and 2014. The ratios from different sites are close and the ratios derived from the two different BRDF models show good agreement within 0.1% for both year 2003 and 2014. The difference between these three sites are consistent using two different BRDF model. The site differences are larger for short wavelength bands such as bands 8, 9, 3, and 4. For year 2014, the large sites differences are also shown for bands 1 and 2. For year 2003, the ratios are in the range of 0.985 to 1.010 for band 1 to 9. Band 3 shows the lowest ratio while band 1 shows the highest ratio. For year 2014, the ratio ranges from approximately 0.983 for bands 2 and 3 to 1.012 for band 8. Some changes are observed from year 2003 to 2014 and bands 1, 2, 8, and 9 show the significant changes.
Figure 5.
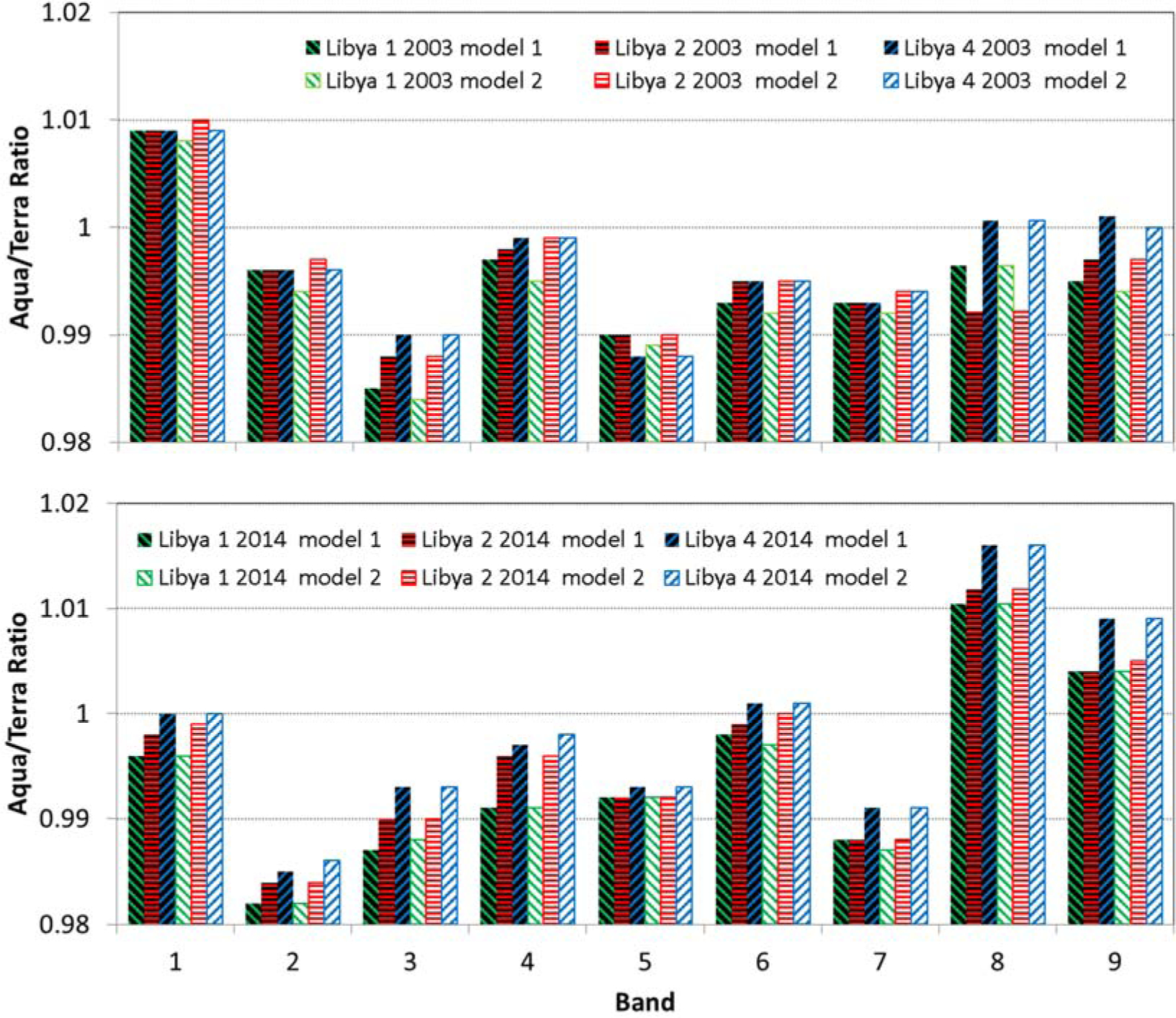
Aqua/Terra ratio for band 1 to 9 for year 2003 (Top) and for 2014 (Bottom). The ratios are from the regression of the reflectance measurement over Libya Desert 1, 2, and 4 using semi-empirical BRDF model (labeled as model 1) and verified using pure empirical BRDF model (model 2).
The stability of the Aqua/Terra ratio and the trends provide useful information regarding the calibration performance of each sensor. The Aqua/Terra ratios from year 2003 to 2014 are processed using two different BRDF models. Figure 6 shows the long-term trending of the ratio derived from the average of the ratio using three desert sites for band 1 to 9. The ratios from two different BRDF model have very good agreement, especially for early mission. The ratio for band 1 shows a 1.5% decrease from year 2004 to 2013. Similarly, band 2 also exhibits a 2% decrease from year 2004 to 2013. Similar pattern is also seen in band 4. Band 6 shows best agreement between this two sensors. Band 8 ratio shows more than 2% variation. For bands 2–7, the ratios are less than 1 for most years, except a couple years for bands 4 and 6.
Figure 6.
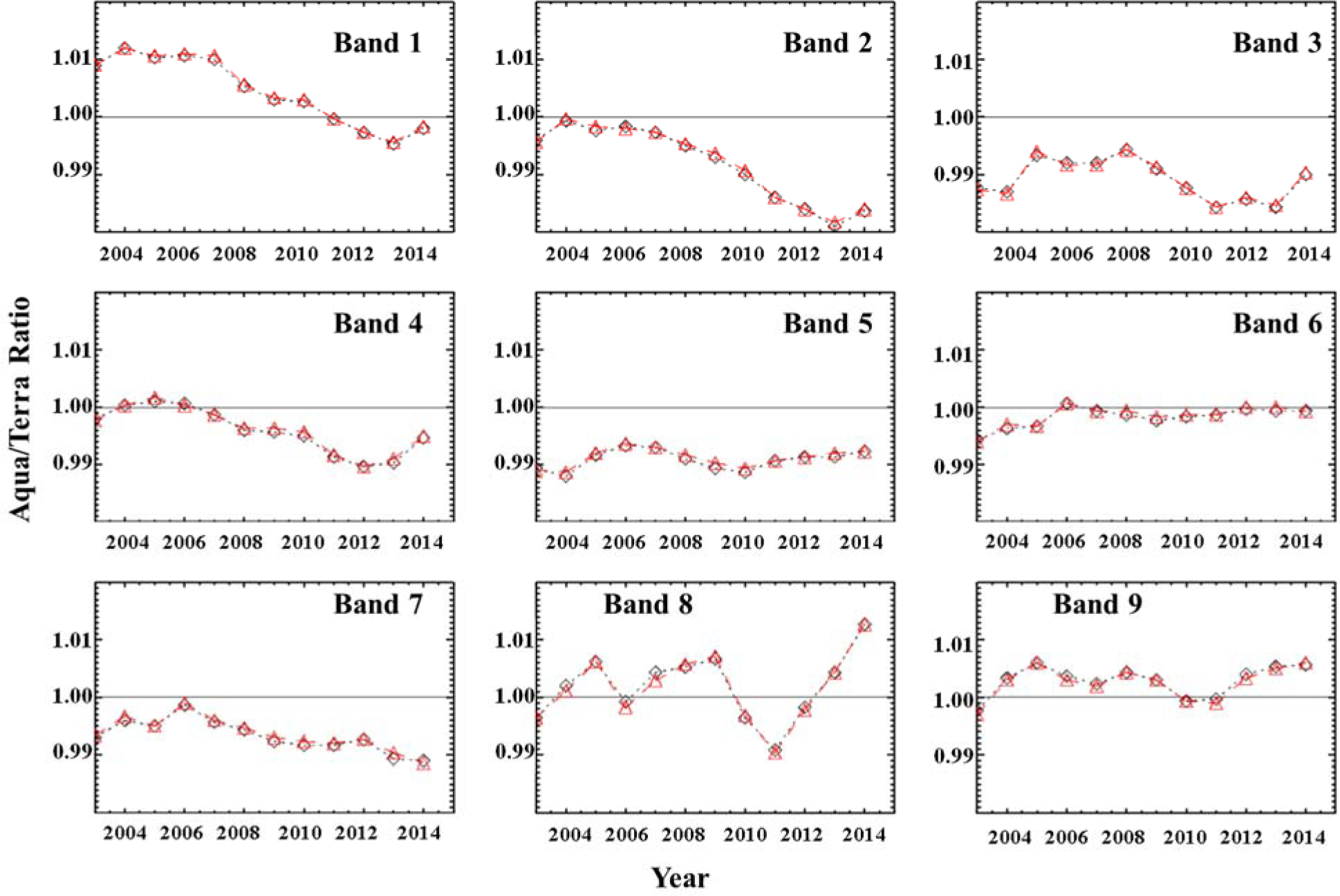
Aqua/Terra ratio from year 2003 to 2014. The ratio is the averaged results of three desert sites. The results using semi-empirical BRDF model are black diamonds and results using empirical model are red triangles.
4.4. Result assessment
The ratio between Aqua and Terra is the key result of this work. It is assume that the bias is proportional to the reflectance measurement. This assumption is reasonable since RSB detector nonlinearity is insignificant and the error in background subtraction is also ignorable. The bias factor is applied to all the measurements with different solar and view angles. The Aqua/Terra ratio derived in this work is the average over all the sensor zenith angle or all the Angle of Incidence (AOI). The uncertainty in RVS characterization can cause AOI dependent bias.
Generally, if a perfect physical model is used to fit measurement, the fitting residue can be used to estimate uncertainty. However, if the model used is not perfect and has uncertainty, the uncertainty from modeling and measurement uncertainty are coupled. In this work, two models (6SV model and BRDF model) are used. The models are certainly not perfect and have uncertainties. The 6SV model is very complicated and the model uncertainty can have dependencies on scene, solar and view angles, and spectral band. It is very challenging to estimate the model uncertainty. The BRDF models are semi-empirical or empirical and it is very challenging to decouple the model uncertainty with measurement uncertainty. The uncertainty estimation is normally for traceable measurement or result, which is very challenging for inter-comparison using correction models. The atmospheric scattering is significant for short wavelength bands due to a large Rayleigh scattering. The parameters used in the 6SV model may differ with those in the real measurements and these differences can cause certain systematic bias on the correction. Since the comparison is focused to assess the reflectance differences between Terra and Aqua MODIS, a systematic bias effect from 6SV can be insignificant. Similarly, the effective bias induced by applying BRDF model on the ratio can also be reduced. The use of different BRDF models can be helpful for the assessment of impact of the BRDF model accuracy. The results from the two models show good agreement for the ratio trending as well as the reflectance comparison, especially for early mission. The RVS and polarization effects may affect the use of the model and can cause the difference in the comparison results. Figure 7 shows the difference between the ratios using these two models from year 2003 to 2014. Their differences are normally within ±0.1% for most bands except band 8. As presented in section 2.3, these two model are very different and their differences can be used for estimation of the model impact on the comparison.
Figure 7.
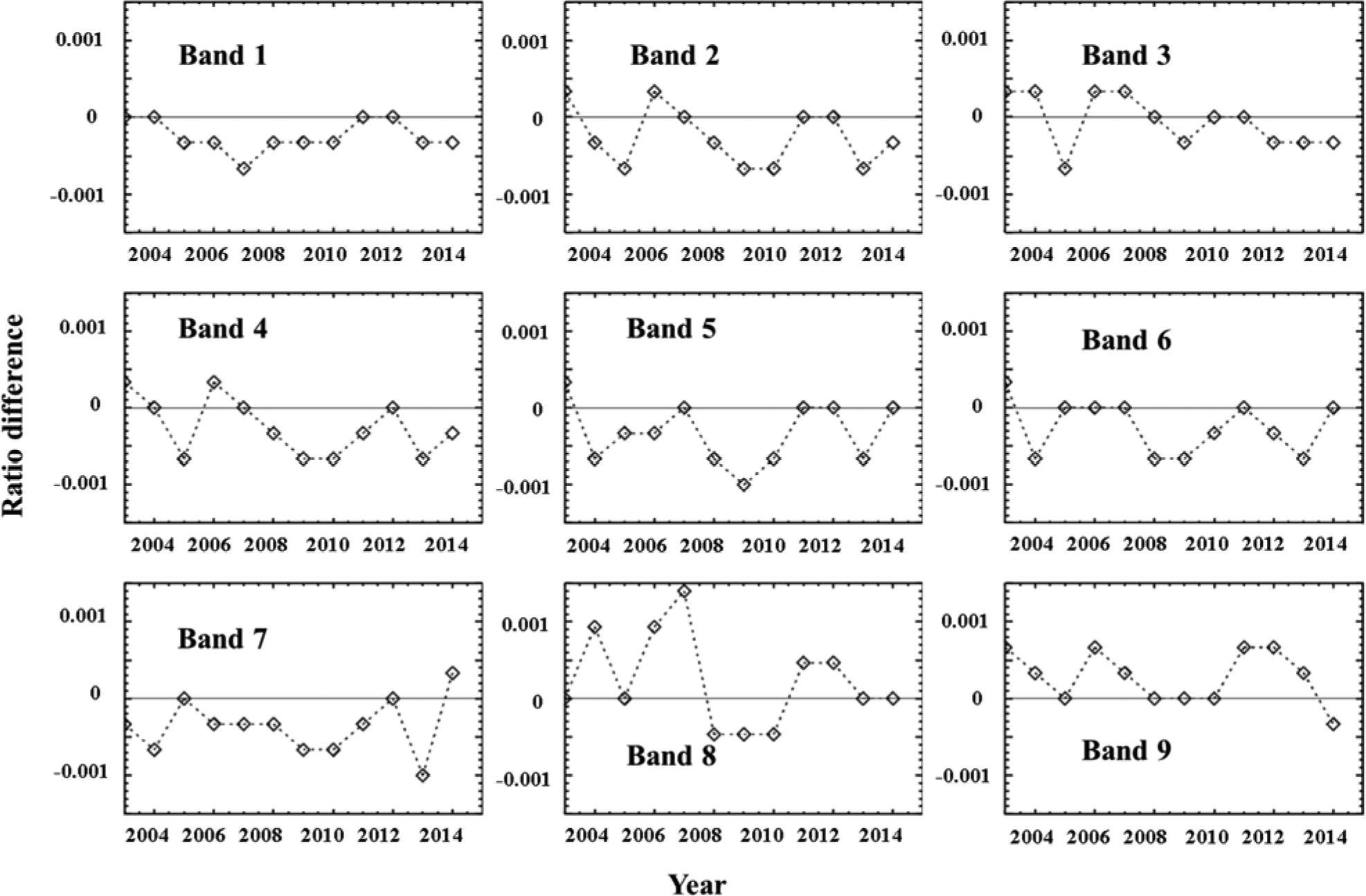
The ratio difference between the results using two BRDF models from year 2003 to 2014.
5. SUMMARY AND DISCUSSION
The inter-comparison of the reflective solar bands for the sensors on two polar orbiting satellites typically requires a SNO. However, for MODIS on Terra and Aqua, due to the lack of SNOs between the two instruments, and the differences in solar angles and view angles make the inter-comparison more challenging. Although the two MODIS instruments have identical spectral characteristics, the differences in the view geometry parameters add further complexity to this inter-comparison. An inter-comparison method is developed for the instrument measurement over a selected Earth site with significant difference in solar and view angles, and is applied to evaluate the calibration differences between the two MODIS instruments. The measurements from both Terra and Aqua MODIS over Libya Desert sites 1, 2, and 4 from year 2003 to 2014 are processed and analyzed. The atmospheric scattering correction is performed using the 6SV modeling. A least-square regression is used to derive the ratio between the measurements from the two instruments with BRDF model applied for the correction of effect of solar angle and view angle. The ratios over the three Libya Desert sites agree with each other very well for most of the bands. The ratio between Aqua and Terra reflectance measurements are derived for bands 1 to 9 and the results from different sites show good agreement. The results using two different BRDF models are also consistent. For year 2003, the ratios are in the range of 0.985 to 1.010 for band 1 to 9. Band 3 shows the lowest ratio while band 1 shows the highest ratio. For year 2014, the ratio ranges from approximately 0.983 for bands 2 and 3 to 1.012 for band 8. The BRDF corrected reflectance for the two instruments are also derived for every year from 2003 to 2014 for stability assessment. Bands 1 and 2 show greater than 1% differences between Aqua and Terra. Aqua bands 1 and 2 show downward trends while Terra bands 1 and 2 show upward trends. Bands 8 and 9 of both Aqua and Terra show large variations. The calibration of both Terra and Aqua MODIS is independently conducted, including their prelaunch tests. Thus, it is expected that there are some existing systematic differences or errors in the key calibration parameters, which are unknown and could affect their measurements.
The focus of this paper is the methodology development of the comparison between sensors on different satellites, with a demonstration using the Libya Desert sites. The calibration is assessed with the overall trending over Libya Desert sites with Aqua as reference for Terra. The comparison is performed for band average results using the reflectance over different AOI. The MODIS RSB are sensitive to the polarization of incident light, especially at short wavelengths and for Terra. The polarization sensitivity, determined by the polarization factor and the phase angles is essential to determine accurate TOA reflectance. While the polarization sensitivity of both instruments was characterized prelaunch, tracking its on-orbit change has been challenging. The science teams investigated the polarization and RVS effects [35–38]. The RVS and polarization effects can affect comparison results and also cause AOI dependency. The RVS uncertainty is also has dependency on C6 on-orbit RVS characterization approaches. Their difference between Terra and Aqua bands 1–4 can have effect on BRDF characterization and comparison. For these 4 bands, due to reduced SD reliability, the on-orbit RVS for Terra is characterized using earth-view based RVS. In contrast the Aqua bands 1–4 still rely on on-board calibrators to characterize the RVS; however recent analyses has shown a deviation in the on-board calibrator trends. Consequently, an EV-based correction has been incorporated in the forward C6 products for these bands. The on-orbit RVS characterized using earth-view measurements is expected to have greater uncertainties at AOI other than lunar or SD measurements. Some further investigations, such as polarization effect, season dependency, and AOI dependency, are planned for our future work to provide detailed analysis for uncertainty analysis and calibration improvement.
ACKNOWLEDGMENT
The authors would like MCST team for discussions and for internal reviews of this paper.
REFERENCES
- [1].Barnes WL and Salomonson VV, “MODIS: A global image spectroradiometer for the Earth Observing System,” Crit. Rev. Opt. Sci. Technol, vol. CR47, pp. 285–307, 1993. [Google Scholar]
- [2].Barnes WL, Salomonson VV, Guenther B, and Xiong X, “Development, characterization, and performance of the EOS MODIS sensors,” in Proc. SPIE, 2003, vol. 5151, pp. 337–345. [Google Scholar]
- [3].Barnes WL, Xiong X, and Salomonson VV, “Status of Terra MODIS and Aqua MODIS,” J. Adv. Space Res, vol. 32, no. 11, pp. 2099–2106, Dec. 2003. [Google Scholar]
- [4].Salomonson VV, Barnes WL, Xiong X, Kempler S, and Masuoka E, “An overview of the Earth Observing System MODIS instrument and associated data systems performance,” in Proc. IEEE IGARSS, pp. 1174–1176, 2002. [Google Scholar]
- [5].Xiong X, Sun J, Barnes W, Salomonson V, Esposito J, Erives H, and Guenther B, “Multiyear On-Orbit Calibration and Performance of Terra MODIS Reflective Solar Bands”, IEEE Trans. Geosci. Remote Sens, vol. 45, issue 4, pp. 879–889, 2007. [Google Scholar]
- [6].Xiong X, Sun J, Xie X, Barnes W, and Salomonson V, “On-Orbit Calibration and Performance of Aqua MODIS Reflective Solar Bands”, IEEE Trans. Geosci. Remote Sens, vol. 48, issue 1, pp. 535–546, 2010. [Google Scholar]
- [7].Xiong X, Sun J, Xie X, Barnes W, and Salomonson V, “On-Orbit Calibration and Performance of Aqua MODIS Reflective Solar Bands”, IEEE Trans. Geosci. Remote Sens, vol. 48, issue 1, pp. 535–546, 2010 [Google Scholar]
- [8].Levy RC, Mattoo1 S, Munchak LA, Remer LA, Sayer1 AM, Patadia1 F, and Hsu NC, “The Collection 6 MODIS aerosol products over land and ocean”, Atmos. Meas. Tech, 6, 2989–3034, 2013 [Google Scholar]
- [9].Sun J, Xiong X, Angal A, Chen H, Wu A, and Geng X, “Time-Dependent Response Versus Scan Angle for MODIS Reflective Solar Bands”, IEEE Transactions on Geoscience and Remote Sensing, vol. 52, issue 6, pp. 3159–3174, 2014. [Google Scholar]
- [10].Toller G, Xiong X, Sun J, Wenny BN, Geng X, Kuyper J, Angal A, Chen H, Madhavan S, and Wu A, “Terra and Aqua Moderate-resolution Imaging Spectroradiometer Collection 6 Level 1B Algorithm”, Journal of Applied Remote Sensing, vol. 7, issue 1, 2013. [Google Scholar]
- [11].Cao C, Weinreb M, and Xu H, “Predicting simultaneous nadir overpasses among polar-orbiting meteorological satellites for intersatellite calibration of radiometers,” Journal of Atmospheric and Oceanic Technology, vol. 21, pp. 537–542, 2004. [Google Scholar]
- [12].Ciren P, Cao C , and Sullivan JT, “Consistency in the long-term environmental measurements with NOAA Advanced Very High Resolution Radiometer,” Proceedings of SPIE – Remote Sensing and Modeling of Ecosystems for Sustainability III, 6298, pp. 629810-1–12, 2006. [Google Scholar]
- [13].Cao C, Xu H, Sullivan J, McMillin L, Ciren P, and Hou Y, “Intersatellite radiance biases for the High Resolution Infrared Radiation Sounders (HIRS) onboard NOAA-15, −16, and −17 from simultaneous nadir observations”, Journal of Atmospheric and Oceanic Technology, 22, No. 4, pp. 381–395, 2005. [Google Scholar]
- [14].Wu A, Xiong X, and Cao C, “Terra and Aqua MODIS Inter-comparison of Three Reflective Solar Bands Using AVHRR Onboard the NOAA-KLM Satellites,” Int. J. Remote Sens, vol. 29, no. 7, pp. 1997–2010, 2008. [Google Scholar]
- [15].Chander G, Hewison T, Fox N, Wu X, Xiong X, and Blackwell WJ, “Overview of Intercalibration of Satellite Instruments”, IEEE Transactions on Geoscience and Remote Sensing, vol. 51, issue 3, pp. 1056–1080, 2013 [Google Scholar]
- [16].Chander G, Angal A, Choi T, and Xiong X, “Radiometric Cross-Calibration of EO-1 ALI With L7 ETM+ and Terra MODIS Sensors Using Near-Simultaneous Desert Observations”, IEEE JSTARS, vol. 6, issue 2, pp. 386–399, 2013. [Google Scholar]
- [17].Xiong X, Cao C, and Chander G, “An Overview of Sensor Calibration Inter-comparison and Applications”, Frontiers of Earth Science in China, vol. 4, issue 2, pp. 237–252, 2010. [Google Scholar]
- [18].Kotchenova Svetlana Y., Vermote Eric F., Matarrese Raffaella, and Klemm Frank J. Jr., “Validation of a vector version of the 6S radiative transfer code for atmospheric correction of satellite data. Part I: Path radiance”, APPLIED OPTICS, Vol. 45, No. 26, pp6762–6774, 2006 [DOI] [PubMed] [Google Scholar]
- [19].Kotchenova Svetlana Y. and Vermote Eric F., “Validation of a vector version of the 6S radiative transfer code for atmospheric correction of satellite data. Part II. Homogeneous Lambertian and anisotropic surfaces” APPLIED OPTICS, Vol. 46, No. 20, pp4455–4464, 2007 [DOI] [PubMed] [Google Scholar]
- [20].Levy Robert C., Remer Loraine A., and Dubovik Oleg, “Global aerosol optical properties and application to Moderate Resolution Imaging Spectroradiometer aerosol retrieval over land”, JOURNAL OF GEOPHYSICAL RESEARCH: Atmospheres, VOL. 112, D13210, 2007 [Google Scholar]
- [21].Mobley CD, Werdell PJ, Franz B, Ahmad Z, and Bailey S, 2016. Atmospheric Correction for Satellite Ocean Color Radiometry: A Tutorial and Documentation of the Algorithms Used by the NASA Ocean Biology Processing Group. Sequoia Scientific, Inc. [Google Scholar]
- [22].Vermote E, Tanré D, Deuzé JL, Herman M, Morcrette JJ, and Kotchenova SY, “Second Simulation of a Satellite Signal in the Solar Spectrum - Vector (6SV)”, http://6s.ltdri.org/pages/manual.html
- [23].Walthall CL, Norman JM, Welles JW, Campbell G, and Blad BL, “Simple equation to approximate the bidirectional reflectance from vegetated canopies and bare soil surfaces”, Applied Optics, 24, pp.383–387, 1985. [DOI] [PubMed] [Google Scholar]
- [24].Nilson T and Kuusk A, “A reflectance model for homogeneous plant canopies and its inversion”, Remote Sensing of Environment, 27, pp.157–167, 1989. [Google Scholar]
- [25].Zhang Z, Kalluri S, JaJa J, Liang S, and Townshend JRG, “High performance algorithms for global BRDF retrieval”, IEEE Transactions on Computational Science and Engineering”, 5, pp.16–29, 1998. [Google Scholar]
- [26].Kalluri SNV, Zhang Z, Jaja J, Liang S and Townshend JRG, “Characterizing land surface anisotropy from AVHRR data at a global scale using high performance computing”, Int. j. remote sensing, vol. 22, no.11, pp.2171–2191, 2001. [Google Scholar]
- [27].Roujean JL, Leroy MJ, and Deschamps PY, “A bidirectional reflectance model of the Earth’s surface for the correction of remote sensing data,” J. Geophys. Res, vol. 97, no. D18, pp. 20 455–20 468, Dec. 1992. [Google Scholar]
- [28].Schaaf CLB, Liu J, Gao F and Strahler AH, “MODIS Albedo and Reflectance Anisotropy Products from Aqua and Terra”, Chapter 24 in Land Remote Sensing and Global Environmental Change: NASA’s Earth Observing System and the Science of ASTER and MODIS, Remote Sensing and Digital Image Processing Series, Vol.11, Ramachandran B, Justice C, Abrams M, Eds, Springer-Cerlag, 873 pp., 2011. [Google Scholar]
- [29].Lucht W, Schaaf CB, and Strahler AH, An Algorithm for the retrieval of albedo from space using semiempirical BRDF models, IEEE Trans. Geosci. Remote Sens, 38, 977–998, 2000. [Google Scholar]
- [30].Wu A, Xiong X, Doelling DR, Morstad D, Angal A, and Bhatt R, “Characterization of Terra and Aqua MODIS VIS, NIR, and SWIR Spectral Bands’ Calibration Stability”, IEEE Transactions on Geoscience and Remote Sensing, vol. 51, issue 7, pp. 4330–4338, 2013 [Google Scholar]
- [31].Mishra N, Helder DL, Angal A, Choi J, and Xiong X, “Absolute Calibration of Optical Satellite Sensors Using Libya 4 Pseudo Invariant Calibration Site”, Remote Sens, vol. 6, issue 2, pp. 1327–1346, 2014. [Google Scholar]
- [32].Angal A, Xiong X, Wu A, Chander G, and Choi T, “Multitemporal Cross-Calibration of the Terra MODIS and Landsat 7 ETM+ Reflective Solar Bands”, IEEE Transactions on Geoscience and Remote Sensing, vol. 51, issue 4, pp. 1870–1882, 2013. [Google Scholar]
- [33].Chang T, Wu X, and Weng F, “Postlaunch Calibration Update of MetOp-B AVHRR Reflective Solar Channels Using MetOp-A”, IEEE Transactions on Geoscience and Remote Sensing 04/2015; 53(5). DOI: 10.1109/TGRS.2014.2356334 [DOI] [Google Scholar]
- [34].Vermote Eric and Kotchenova Svetlana, “MODIS Directional Surface Reflectance Product: Method, Error Estimates and Validation”, Chapter 23 in Land Remote Sensing and Global Environmental Change, Ramachandran B et al. (eds.), Remote Sensing and Digital Image Processing 11, DOI 10.1007/978-1-4419-6749-7_23, © Springer Science+Business Media, LLC; 2011 [DOI] [Google Scholar]
- [35].Meister Gerhard and Franz Bryan A., “Corrections to the MODIS Aqua Calibration Derived From MODIS Aqua Ocean Color Products”, IEEE TRANSACTIONS ON GEOSCIENCE AND REMOTE SENSING, Vol. 52, issue 10, pp6534–6541, 2014 [Google Scholar]
- [36].Kwiatkowska Ewa J.,,Franz Bryan A., Meister Gerhard, McClain Charles R., and Xiong Xiaoxiong, “Cross calibration of ocean-color bands from Moderate Resolution Imaging Spectroradiometer on Terra platform”, APPLIED OPTICS, Vol. 47, No. 36 , 2008 [DOI] [PubMed] [Google Scholar]
- [37].Sayer AM, Hsu NC, Bettenhausen C, Jeong M-J, and Meister G, “Effect of MODIS Terra radiometric calibration improvements on Collection 6 Deep Blue aerosol products: Validation and Terra/Aqua consistency”, Journal of Geophysical Research: Atmospheres, 120, 12,157–12,174, doi: 10.1002/2015JD023878, 2015 [DOI] [Google Scholar]
- [38].Lyapustin A, Wang Y, Xiong X, Meister G, Platnick S, Levy R, Franz B, Korkin S, Hilker T, Tucker J, Hall F, Sellers P, Wu A, and Angal A, “Scientific impact of MODIS C5 calibration degradation and C6+ improvements”, Atmos. Meas. Tech, 7, 4353–4365, 2014 [Google Scholar]


