Interactive computation and visualization of deep brain stimulation effects using Duality

Abstract

Deep brain stimulation (DBS) is an established treatment for movement disorders such as Parkinson’s disease or essential tremor. Currently, the selection of optimal stimulation settings is performed by iteratively adjusting the stimulation parameters and is a time consuming procedure that requires multiple clinic visits of several hours. Recently, computational models to predict and visualize the effect of DBS have been developed with the goal to simplify and accelerate this procedure by providing visual guidance and such models have been made available also on mobile devices. However, currently available visualization software still either lacks mobility, i.e., it is running on desktop computers and not easily available in clinical praxis, or flexibility, as the simulations that are visualized on mobile devices have to be precomputed. The goal of the pipeline presented in this paper is to close this gap: Using Duality, a newly developed software for the interactive visualization of simulation results, we implemented a pipeline that allows to compute DBS simulations in near-real time and instantaneously visualize the result on a tablet computer. Therefore, a client-server setup is used, so that the visualization and user interaction occur on the tablet computer, while the computations are carried out on a remote server. We present two examples for the use of Duality, one for postoperative programming and one for the planning of DBS surgery in a pre- or intraoperative setting. We carry out a performance analysis and present the results of a case study in which the pipeline for postoperative programming was applied.

1. Introduction

The goal of neuromodulation is to achieve therapeutic effects by stimulating specific target regions in the human brain using electric or magnetic fields. Both non-invasive and invasive procedures to reach this goal exist. As an invasive procedure, deep brain stimulation (DBS) has become an established treatment for movement disorders, such as Parkinson’s disease or essential tremor, where Level 1 evidence for the efficacy of DBS exists (Deuschl et al. 2006; Weaver et al. 2009). DBS is furthermore under current investigation as a treatment for a variety of other disorders, such as depression, obsessive-compulsive disorder, Alzheimer’s disease, or traumatic brain injury. Depending on the disease to be treated, a target region in the brain, commonly a subcortical brain structure, such as subthalamic nucleus (STN) or globus pallidus interna (GPi) for Parkinson’s disease (Deuschl et al. 2006; Weaver et al. 2009), is determined and the DBS lead is introduced into this structure in a surgical procedure.

A DBS lead commonly has at least four contacts; each contact can be either circular in shape or, for newer DBS leads, also segmented contacts exist, which allow for a better targeted stimulation. The DBS lead is connected to an implanted pulse generator (IPG) that is subcutaneously placed in the patient’s chest. The IPG generates electric potentials with a specific waveform and frequency, which are then applied to the electrode contacts.

The major task to achieve a successful DBS treatment, is the determination of an optimal stimulation pattern, i.e., the selection of the active electrode contacts as well as stimulation waveform and pattern. In most cases, either one contact is chosen to be active with the stimulator case as reference (unipolar stimulation) or two contacts are active with one as anode and one as cathode (bipolar stimulation). Stimulation voltages are in the range of a few volts, pulse widths between 60 and 210 μs, and frequencies around 130 Hz (Volkmann et al. 2002; Butson and McIntyre 2006). Classically, the optimal stimulation pattern has to be found in a trial-and-error approach, i.e., based on the personal experience of the treating physician, the parameter space is sampled and the chosen settings are adjusted based on the observation of the patient. This usually requires multiple outpatient visits for programming sessions and each of them may last multiple hours (Hunka et al. 2005; Ondo and Bronte-Stewart 2005).

Recently, a variety of studies has been published that aims at simplifying the process of finding optimal stimulation settings. Decision-support applications have been developed that allow the visualization of the stimulated brain area together with segmentations of the target structures within the brain (Butson et al. 2007a; Horn and Kühn 2015; Butson et al. 2013). The goal of these applications is to simplify the manual optimization of the patient programming through the visualization of predicted stimulation effects. A common concept in this context is the volume of tissue activated (VTA), which visualizes the brain area that is affected by the neuromodulation (Frankemolle et al. 2010; Pourfar et al. 2015). In this case, a goal of the programming would for example be to maximize the overlap of the VTA with the target structure while avoiding side effects.

An important point that has to be considered to facilitate the usage of decision-support applications in a clinical workflow, is the accessibility and mobility of the medium on which the information is delivered to allow the user, commonly a movement disorder specialist, an easy use of the device during the patient visit. Furthermore, interactivity is desirable to allow manual interventions of the user. In Butson et al. (2013), a tablet-based mobile computing platform using ImageVis3D Mobile (Schiewe et al. 2015; https://itunes.apple.com/us/app/imagevis3d-mobile-universal/id378071694) that allows the interactive visualization of precomputed DBS simulations to assist in the selection of DBS parameters, was presented and evaluated. This platform enables the 2d- and 3d-visualization of the VTA in combination with structural images of the patient’s brain and surfaces of relevant brain structures. It was demonstrated that this kind of tool has a huge potential impact on the required programming time. However, as all visualizations have to be precomputed, the location of the DBS lead has to be selected in advance, so that this tool is limited to the use in postoperative programming and cannot be used in pre- or intraoperative planning. Further limitations that arise concern the amount of possible stimulation settings that can be visualized, i.e., these have to be restricted to the most common uni- and bipolar settings. Also the use of visualization concepts other than the VTA or the interactive computation of optimized stimulation settings are at least complicated.

In this paper, we present an interactive pipeline for the real-time computation and visualization of DBS simulation results. This allows not only for the visualization of manually determined stimulation settings, but also the interactive placement of the DBS lead can be realized. In the future, this pipeline could also be expanded to allow the computation and visualization of automatically optimized stimulation settings in near-real time. The pipeline is based on a client-server concept, which allows to combine the high mobility of a tablet-based visualization with the computational power of modern high-performance computers. Using high-speed networks, the client-server concept furthermore allows the spatial separation of client and server over long distances, so that it can also be used in remote regions.

In the Methods section, we describe the general layout of the client-server concept, as well as the specific needs for the visualization of DBS simulations. We present two examples, how this pipeline can be used in the context of DBS programming and planning. In the Results section, we present time estimates for the computations performed in these examples and a case study, in which the pipeline has been used to assist in the manual postoperative programming of a DBS patient at a community health center, to demonstrate the possibility of the use at remote locations.

2. Methods

In this section, we describe the mathematical and neural foundations for the computational modeling. Therefore, we first introduce the finite element method (FEM) for the modeling of quasi-static bioelectric fields and describe how it is applied to the problem of DBS. Subsequently, we describe how the results for the simulation of the electric fields can be translated into the decision whether neuron activation occurs in a certain region. After this general introduction, we describe the setup of a DBS simulation pipeline for two exemplary use-cases. First, we describe how a postoperative decision support-system can be implemented, i.e., we replicate the functionality that was previously described by Butson et al. (2013). The difference in our approach is that our pipeline allows to forego the necessity of precomputing the simulation results and thereby allows to show simulation results for a larger number of parameter combinations. In a second step, we expand this pipeline by the possibility to interactively select the location of the DBS lead to also enable a use in pre- and intraoperative planning. All data used in these two examples can be found in the supplementary material.

2.1. Modeling of DBS evoked electric fields using the finite element method (FEM)

Assuming the quasi-static approximation for bioelectromagnetism, the electric fields that are evoked by DBS can be described by a Poisson equation (Hämäläinen et al. 1993)

$$\nabla \hspace{0.17em}\cdot \hspace{0.17em}(\sigma \nabla u)=\nabla ·\mathbf{j},$$ (1)

which has to be solved on the head domain (in the following referred to as Ω). u indicates the electric potential that has to be solved for and a is the electrical conductivity distribution.

To apply the FEM to solve this equation system, as a first step it is necessary to create a geometrical representation of the head. Therefore, a tetrahedral model is generated (cf. Sections 2.4,2.5 and B.4). Afterwards, Equation 1 can be transformed into a linear equation system that has to be solved to obtain the discrete representation u of the electric potential (Braess 2007):

$$Au=b$$ (2)

The FEM equations underlying the simulation of DBS electric fields are described in more detail in B.1.

2.2. Approximating neuron axon activation using the activating function

Commonly, multi-compartment cable models are solved using the NEURON-toolbox to estimate the activation of neuron axons through stimulation with electric fields (McIntyre et al. 2002; Butson et al. 2007b). However, the use of these models in the context of near-real time simulations is not feasible, as the computation for a single neuron may take multiple seconds. As an alternative approach to estimate neuron axon activation, the activating function can be used (McNeal 1976; Rattay 1986; Warman et al. 1992; McIntyre et al. 2004). The activating function is proportional to the second difference of the electric potential u along the nodes of Ranvier of the respective neuron. Adopting the activating function, the problem of estimating neuron axon activation reduces to the computation of the second difference of the electric potential in a certain direction; for the further computation of the VTA a simple isosurface computation has to be performed. Thus, to obtain a VTA, a neuron direction has to be chosen and an activation threshold has to be obtained. In our application, we chose neuron orientations perpendicular to the electrode shaft (cf. also Sections 2.4). The threshold values were determined using the exponential curve fit obtained by Butson and McIntyre (2006), which determines the threshold as a function of the product of cathodic voltage and stimulation pulse width.

2.3. Duality - an iPad app for the interactive visualization of high-performance computing generated simulation results

In the following section, we shortly describe the features and some details of the implementation of Duality, which was developed to enable the mobile interactive visualization of simulations solved in near-real time using high-performance computing. Afterwards, we describe two use-cases of Duality, where the focus was on applications in DBS programming. However, the possible use- cases of Duality are not limited to this.

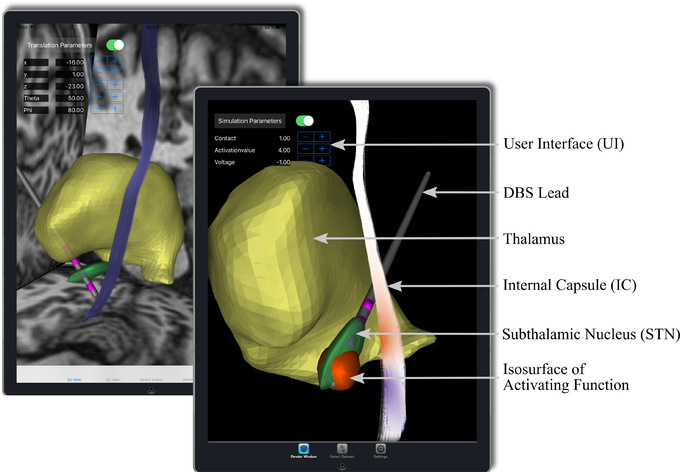
To be able to achieve the goal of visualizing the results of computationally costly simulations in near-real time, Duality was implemented in a client-server concept. The iPad-application performs the visualization and provides a GUI to process the user input. The visualization methods used in the iPad-app are largely based on ImageVis3D Mobile (Butson et al. 2013; Schiewe et al. 2015). Like ImageVis3D Mobile, Duality offers both a 3d and a 2d view. In both views, both volume datasets and texture defined geometries can be shown. In the 3d view, the volume datasets are rendered based on transfer functions, which the user can individually define, while the volumes are simply shown slice-wise in the 2d view. The geometries can be rendered with a user-defined color scheme and transparency in the 3d view, in the 2d view the intersection of the geometry with the currently displayed slice plane is displayed (overlayed onto the slices of possible volumes that are rendered). It is possible for the user to define for each object whether it should be shown in both the 2d and 3d view or in only one of them. An illustration of the visualization in Duality for the use-case of postoperative DBS programming is shown in Figure 1. The rendering is based on OpenGL ES 3.0 and shares parts of its code base with ImageVis3D Mobile. To enable 3d volume rendering, a slice-based volume renderer is implemented, as described by Krüger (2010). No external libraries or engines are employed.

Figure 1.:

Illustration of the Duality iPad-app. Visualization of the activating function through an isosurface, i.e., the VTA, and the projection on a fiber tract (internal capsule) - red corresponds to possible activation and blue to inhibition - and the UI, the DBS lead, and a selection of brain structures

The iPad-app connects to the server application using a TCP connection, the data transfer is based on the JSON-RPC protocol (http://www.jsonrpc.org) and was implemented in a separate library called “mocca” (https://github.com/HPC-Group/Mocca/). Upon a change of the (stimulation) parameters in the GUI by the user, the parameters are sent to the server, the server application runs the computations using the indicated parameters and predefined python-scripts, and sends the geometries to be visualized back to the iPad-app.

As a prerequisite, the graphical scene to be visualized has to be defined. Therefore, a JSON-file (http://www.json.org) scene.json has to be generated for each scene (cf. A.1, A.2). Besides metadata describing the scene, the JSON-file contains the definition of each node of the scene, i.e., each object to be visualized. Amongst other parameters, it is defined whether the object is a geometry or a volume, whether it is static or interactively computed, etc.

The development of Duality is currently in a beta-phase, fully functional versions of both the client- and server-appliation can be freely obtained. Duality-Server can be downloaded on https://github.com/SCIInstitute/Duality_Server and can be compiled and executed under MS Windows, macOS, or several common linux distributions. The client application Duality-iOS can be obtained from https://github.com/SCIInstitute/Duality_iosFrontend and can be compiled using a current version of Xcode. For both the client and the server application, mocca is included as a submodule and automatically downloaded upon checkout of one of the repositories.

2.4. Example 1: Interactive visualization of DBS treatment effect simulations in postoperative programming

As first use-case, we implemented a pipeline for the interactive simulation and visualization of DBS treatment effects for the use in postoperative DBS programming using Duality. This pipeline mainly provides features that could also be achieved using the static visualization of ImageVis3D Mobile (Butson et al. 2013). However, ImageVis3D Mobile has certain limitations with regard to the number of precomputed surfaces that can be stored, making it complicated to enable the simulation of arbitrary stimulation configurations that go beyond simple uni- or bipolar settings. As such limitations can already be problematic with the currently common DBS leads with four circular contacts, the interactive computation gets even more necessary with the increasing number of electrode contacts provided by the emerging directional DBS leads (Pollo et al. 2014; Contarino et al. 2014; Van Dijk et al. 2015; Willsie and Dorval 2015a,b; Buhlmann et al. 2011).

The simulation of DBS treatment effects consists of two steps. First, a FEM simulation is performed to calculate the electric potential distribution u in the patient’s head that is generated by a certain stimulation setting (cf. Section 2.1, B.1). Next, the stimulation of neuron axons in certain regions of the patient’s brain is estimated and visualized (cf. Section 2.2). For the visualization, we chose the common visualization concept of the the volume of tissue activated (VTA) (Frankemolle et al. 2010; Pourfar et al. 2015; Butson et al. 2007b), representing the surface of the brain region for which an activation is predicted. However, Duality is not limited to display an isosurface as the VTA, it would, as well be possible to visualize activated fiber tracts obtained from tractography.

To be able to perform FEM simulations, a geometrical model of the patient’s head has to be generated (cf. B.1, B.4). For our examples, we used an atlas brain (Wakana et al. 2004) for which segmentations and surfaces of relevant brain structures were already available. We chose a realistic trajectory for a DBS lead placed in the STN, as it would be done for, e.g., the treatment of Parkinson’s disease. As mentioned earlier, we did not use a full head model, but restricted ourselves to the modeling of the outer brain surface, which was generated using FSL (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki). Based on the outer brain surface and a surface model of a DBS lead (Medtronic 3387), a tetrahedral finite element head model was generated using the integration of TetGen (http://wias-berlin.de/software/tetgen/; Si 2015) into SCIRun (http://www.sci.utah.edu/cibc-software/scirun.html). As mentioned in Section 2.1, the tetrahedrons that were automatically placed by TetGen inside the surface model of the DBS lead were afterwards clipped (cf. also B.1).

SCIRun was also used for the FEM simulation of the electric potential. The FEM implemented in SCIRun is a first-order CG- (or Lagrange-) FEM, which was shown to achieve high accuracies for bioelectric field problems. Potential inaccuracies as a result of the large conductivity differences between brain, conducting and insulating parts of the DBS lead were circumvented by the modeling through boundary conditions (cf. B.1). To speed-up the FEM computations during the use of the app, the FEM stiffness matrix A (cf. Equation 2) was precomputed.

Next, the neuron axon activation through the simulated electric field has to be computed using the activating function (cf. Section 2.2). To achieve a high flexibility, instead of calculating the second difference with a fixed orientation in each point of interest, we computed the Hessian matrix of second differences on a regular cubic grid. The nodes of this cubic grid were already included into the finite element mesh. The computation of the Hessian matrix allows the easy evaluation of the second difference in arbitrary directions, and the integration of the nodes of the grid on which the Hessian is computed into the finite element mesh guarantees a good approximation of the electric potential through the FEM simulation at these points. A detailed description of the python scripts used to perform the FEM simulation of the electric potential, to compute the Hessian matrix, and to compute the VTA can be found in B.2.

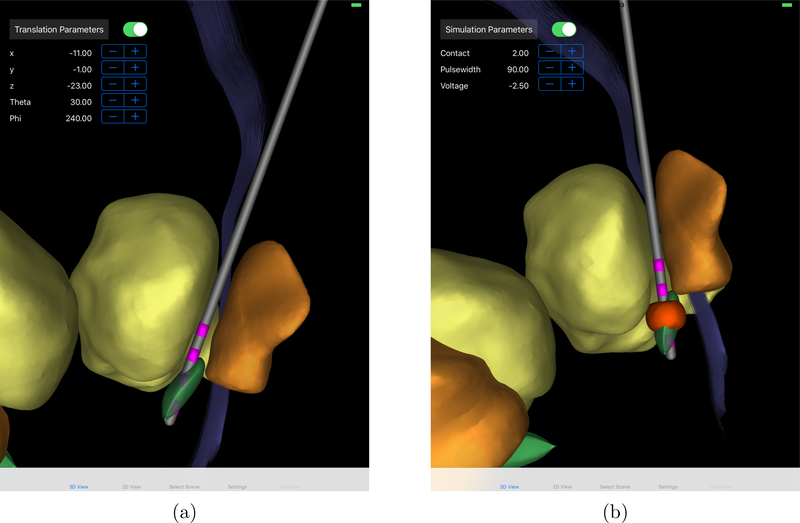
Finally, we needed to set up our example scene including the nuclei surfaces obtained from the brain atlas. We chose to include surfaces of STN, pallidum, and thalamus in the visualized scene, and we additionally included the structural MRI into the 2d view. All surfaces were converted to the g3d format and the structural MRI was converted to the i3m format using the tool uvfconvert, which is delivered with ImageVis3D (https://www.sci.utah.edu/software/imagevis3d.html). A corresponding scene definition scene.json was manually generated (cf. A.1, A.2). Figure 2b shows a screenshot of the 3d view for this scene. All data for this example can be found in the supplementary material in the folder Simulation-Unipolar-postoperative.

Figure 2.:

Screenshot of the Duality iPad-app in 3d view for use in DBS programming; DBS lead positioning for pre- and intraoperative use (a) and visualization of simulation result (b)

2.5. Example 2: Interactive visualization of DBS treatment effect simulations in pre- and intraoperative settings

While the first use-case of DBS treatment effect predictions for postoperative programming (Sections 2.4) could in principal still be covered using precomputed simulations as previously presented for ImageVis3D Mobile (Butson et al. 2013), this is no longer possible in pre- and intraoperative settings. Here, an additionally desired feature is to be able to interactively position the DBS lead within the patients brain previous to the simulation and to be able to directly inspect the obtained stimulation result for different parameters (and possibly also lead models). Thereby, some of the steps necessary to be able to perform the DBS simulations as described in Sections 2.4 can no longer be performed in advance. Particularly, these are the generation of the finite element mesh and the computation of the FE stiffness matrix A (cf. Equation 2).

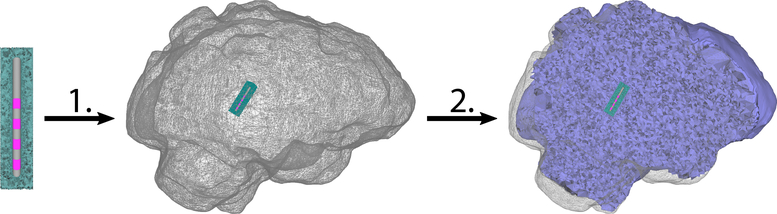
While the computation of the stiffness matrix only takes a few seconds even for a finite element mesh with some 100 thousand nodes, the mesh generation itself is a more time consuming step - especially when additionally aiming to include the nodes of the grid at which the electric potential is evaluated for the computation of the Hessian matrix. Common approaches to speed-up tetrahedral mesh generation rely on domain decomposition, while in the background still algorithms very similar to TetGen, as also used in Sections 2.4, are executed (Lo 2012; Andra et al. 2008). Such approaches perform especially well, if a homogeneous mesh resolution is desired and if the underlying domain can be easily separated into multiple volumes of similar size. However, for the problem at hand, these parallelization approaches are not optimally suited, as the resolution of the mesh is highly anisotropic with a concentration of nodes around the position of the DBS lead. The meshing of this region is also the most time consuming part of the mesh generation. However, as the geometry of the DBS lead remains unchanged in this scenario, since only an affine linear transformation is applied to it, we therefore decided to precompute the mesh in a certain region around the DBS lead, already including the additional grid nodes desired for the computation of the Hessian matrix (cf. Sections 2.4, B.2). In the interactive generation of the patient individual finite element mesh, the boundary of this region is afterwards included as a domain surface, together with the outer surface of the domain Ω that needs to be meshed, i.e., the outer brain surface in our case (cf. Sections 2.4). The generation of additional nodes on boundary surfaces has to be suppressed during the meshing process. In this meshing process, no representation of the DBS lead is included. The volume inside this additionally defined domain is then still discretized during the meshing process. However, as the electrode geometry is not included here and a low mesh resolution and quality can be chosen for this region, the additional time effort is minimal. After this mesh is generated, the mesh elements inside the boundary of this region are clipped (cf. B.1) and the precomputed mesh of the DBS lead and its surrounding volume is merged with the newly generated mesh. Thereby, a high quality mesh containing some 100 thousand mesh nodes with a very high mesh density around the DBS lead can be generated within a few seconds. Figure 3 illustrates the mesh generation.

Figure 3.:

Illustration of high quality mesh generation with precomputed mesh for the DBS lead region: The high-resolution mesh of the region surrounding the DBS lead (left) is transformed into the brain volume using an affine transformation (middle). Afterwards, the remaining brain volume is meshed and the two volume meshes are merged (2.). The resulting mesh is shown in the right subfigure.

To fulfill the needs of this use-case using Duality, two separate scenes have to be defined; one scene to define the position of the DBS lead, and one scene to evaluate the predicted DBS effects. The generation of these two scenes is in detail described in B.3. After fixing the position of the DBS lead in the first scene, the user switches to the second scene and a FEM mesh is generated as previously described (cf. Figure 3). The user can now inspect the space of possible stimulation parameters, where for each change of the stimulation parameters a new FEM equation system has to be solved and a visualization is generated. If the user is not satisfied with the results for the given lead position, he can return to the previous scene and readjust the lead position. This procedure can be iterated until the user is satisfied with the achieved result. Figure 2 shows screenshots of the two scenes developed for this use-case, where the scene for visualizing the simulation result is identical to Sections 2.4. All data for this example can be found in the supplementary material in the folders Position-Electrode-preoperative and Simulation-Unipolar-preoperative.

3. Results

3.1. Performance evaluation

To evaluate the performance of our pipeline, we measured the time effort for the most time consuming substeps of the computations needed for the examples presented in Sections 2.4 and 2.5. These substeps are the setup of a new finite element mesh (cf. Section 2.5), solving the linear equation system (Equation 2), and computing the VTA. Here, the computation time indicates the overall time from the execution of the python call to the termination of the substep, i.e., including startup time of SCIRun from within python and possible times to load and save data within the python-script.

All computations were carried out on a PC running openSUSE Leap 42.1 with a 16-core Intel Xeon E5–1660 v3 CPU @ 3.00 GHz, 94 GB of DDR4-RAM, and a 476 GB SSD. Each computation was repeated five times and the average time required is reported here.

• Set up new FEM mesh: 7.78 s

• Solve Equation 2: 3.12 s

• Generate VTA: 0.49 s

We see that the scene showing the DBS visualization in our second example is already available after only slightly more than ten seconds. Computing the visualization for a new set of parameters in both examples takes less than five seconds. The visualization of a previously considered set of parameters, i.e., executing the server call, parsing the input, and sending a (surface or volume) file to the mobile device, takes less than one second using a common WiFi connection. Obviously, the response time can increase for slow data connections or large data files. Possibilities to further speed-up these computations are evaluated in the Discussion. The visualization is carried out with about 25 frames per second (FPS) on an iPad Air 2, if only the surface meshes, consisting of 26,736 vertices and 29,132 triangles overall; if, as done in Fig. 2, a fiber structure such as the IC is additionally visualized, represented with 7,667 vertices and 7,500 edge elements in our model, about 24 FPS are reached. The FPS rates were measured with the Core Animation profiler from the Xcode Instruments.

The meshes created in this process have about 355k nodes and 2 million elements, which, in combination with the high resolution of the mesh around the lead contacts and the inclusion of the points at which the potential is evaluated to compute the Hessian matrices, can be assumed to be a sufficient mesh resolution to achieve accurate simulation results.

3.2. Case study

As a proof of concept, we applied the interactive visualization of DBS stimulation as presented in Sections 2.4 for a patient diagnosed with Parkinson’s disease. The patient was implanted bilaterally in the STN in late 2016. In early 2017, the patient was programmed by a movement disorder specialist with a classical programming protocol, i.e., the programming was performed in an iterative fashion, until a fitting stimulation pattern could be found. After a change of personnel in the Neurology department, the patient visited the clinic for a second programming session in the spring of 2017 as the outcome of the DBS treatment was so far not satisfying. Thereby, the new movement disorder specialist was essentially blinded with regard to the outcomes of the previous programming session. Visual assistance using Duality based on the example shown in Sections 2.4 was provided in this follow-up programming session.

For this patient, we generated a highly-accurate finite element head model for the simulation of DBS, based on the available standard clinical imaging (preoperative T1-MRI, postoperative CT). The model generation is described in more detail in B.4. To create the visualization scene, the T1-MRI was transformed to the g3d format. Geometric surfaces of relevant brain structures were obtained through the registration of the atlas brain, which was also used in the two previously presented examples, to the T1-MRI and applying the obtained transformation to the segmented surfaces obtained delivered with the atlas brain.

To minimize the travel time for the patient, the programming session was performed at the South Jordan Health Center, which is part of the University of Utah Health Care System and connected to the University of Utah Campus via the Utah Telehealth Network (UTN). Finally, at the South Jordan Health Center the iPad with the Duality-app installed was connected to the UConnect WiFi. Informed consent of the patient about the assisted programming with visualizations of DBS simulations was obtained previous to the patient visit.

Duality was used by the movement disorder specialist previous to the programming session to visualize the current programming settings and the predicted stimulation resulting from it, as well as to screen possible alternative stimulation settings. During the patient visit, Duality was used by the movement disorder specialist to visually validate whether considered stimulation settings could be suited to stimulate the desired target region. It has to be mentioned that Duality was used to provide visual assistance in the determination of possibly more optimal stimulation patterns in advance to and during the programming session, but no direct application of predicted stimulation patterns and voltages without the review of the movement disorder specialist was performed.

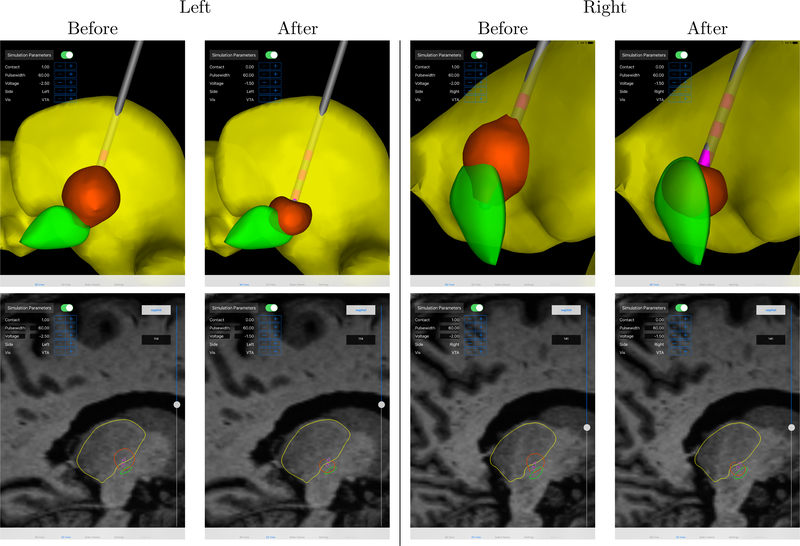
As a result of the programming session that was assisted by the DBS simulations visualized using Duality, the stimulation settings were significantly changed for both sides (Table 1, Figure 4). On both sides, the active contact was changed from contact 1 (second contact from the tip of the electrode) to contact 0 (first contact from the tip of the electrode). Table 1 shows the DBS settings before and after the programming session, Figure 4 shows screenshots of DBS simulation for the stimulation settings previous to and after the programming session. In the 3d views it is visible that both for left and right side stimulation contact 0 is the contact closest to the target and should therefore be preferably considered for the stimulation. Especially the 2d views (Figure 4, bottom row) show that the overlap of the VTA with the STN is clearly increased after the programming session. At the same time, the stimulation voltage and the overlap of the VTA with neighboring areas (especially the thalamus) is reduced. The direct patient feedback after the programming session was positive, whereas a long term evaluation is still outstanding.

Table 1.:

DBS settings before and after visualization assisted programming session

	Before		After
Side	left	right	left	right
Contact	1	1	0	0
Voltage [V]	−2.6	−2.0	−1.5	−1.5
Pulsewidth [ms]	60	60	60	60

Figure 4.:

Comparison of predicted DBS effect before and after the Duality-assisted programming session. The VTA is shown in orange, the STN in green, and the Thalamus in yellow. The DBS lead contacts are shown in pink and the shafts in gray. Left STN DBS is shown on the left, right STN DBS on the right; top row shows 3d and bottom row shows 2d views.

4. Discussion

In this study, we have presented two examples how the newly developed Duality application can be used to easily implement interactive pipelines for the near-real time simulation of DBS treatment effects. All necessary data and tools to reproduce these examples are free for download or can be found in the supplementary material. The performance of the pipeline was evaluated and it was shown that near-real time results can already be obtained with the means used here.

In the examples shown here (Sections 2.4, 2.5), only one type of DBS lead was used (Medtronic 3387). However, this was mainly done for the sake of simplicity, but is not a consequence of any restrictions of Duality. Especially for the pre- and intraoperative programming (Section 2.5), the possibility to choose between different electrode types and determine which of these is best suited for the given patient is of high interest. Given surface models for other electrode types, implementing this additional flexibility is straight-forward.

As a proof of concept, the pipeline for postoperative programming, as described in Sections 2.4, was used in the programming of a DBS patient with Parkinson’s disease. It is shown that the programming settings obtained with assistance through the visualizations differ significantly from the previously obtained stimulation settings, for which a classical, unguided programming approach was used. A visual inspection suggests that the programming settings obtained with the assistance of the simulation results lead to a stimulation that is clearly more likely to reach the stimulation target, the STN. However, as the evaluation of the stimulation settings relies purely on a visual inspection and direct, unstructured patient feedback, this case study should not be confused with a (clinical) validation of VTA guided DBS programming. Instead, it is only meant as a proof of concept, showing that the concept of Duality using a client-server approach for the interactive visualization of DBS simulations can be applied at remote locations.

The goal of a near-real time visualization of DBS simulations was already achieved using the pipeline described in the two examples in this paper. However, a further speed-up of the computations is desirable. Here, especially accelerating the solving of the FEM equation system (Equation 2) would be beneficial, as these computations have to be performed many times for each scene and not only once for the scene setup as, e.g., the mesh generation. The solver employed by SCIRun is a CG-solver with Jacobi-preconditioning. Even without parallelization, a first speedup of the solver could be obtained using more efficient preconditioning, such as incomplete cholesky (IC(0)) or algebraic multigrid (AMG) preconditioning (Lew et al. 2009). Due to the use of python, solvers with more efficient preconditioners can be easily included with moderate effort by embedding freely available toolboxes. Since the CG-algorithm requires several sparse matrix-vector multiplications, a further speedup can be achieved by applying parallelization techniques (Wolters et al. 2002). Here, also the use of GPU-computing is possible (Fu et al. 2014).

In the case of the interactive placement of the DBS lead, further time-consuming steps, which have to be performed once for each relocation of the lead, are the computation of the FEM stiffness matrix A (cf. Equation 2) and the generation of the FEM mesh. The computation of A consists of a numerical integration for each matrix entry and the computations of the matrix entries are completely independent from each other. Thereby, this scenario is optimally suited for parallelization and also GPU computations (Cecka et al. 2011; Markall et al. 2013). In contrast, as previously mentioned, a further speed-up of the mesh generation through parallelization is less easy to achieve. A combination of the existing methods based on domain decomposition (Lo 2012; Andrä et al. 2008) and the here presented precomputation of the FEM mesh around the DBS lead would be desirable. An easier possibility to speed-up the generation of the FEM mesh is to accelerate the merging of the precomputed mesh around the DBS lead with the on-the-fly generated mesh of the brain volume. This task is currently carried out non-parallelized in the SCIRun-module JoinFields and consumes a relatively large amount of the overall time to set up the FEM mesh. A parallelization of this step is relatively straight-forward to implement and could bring a significant performance improvement - especially, if the resolution of the precomputed mesh of the region around the DBS lead is increased.

The possibilities to visualize scientific and medical data on mobile devices have been discussed for more than two decades (Encarnacao et al. 1995; Paelke et al. 2003; Tesch et al. 2003; Zhou et al. 2006; Roudaut 2009; Schiewe et al. 2015). Duality expands upon previous work in the field of mobile scientific and medical visualization by joining high flexibility and interactivity, easy usage, and open source availability. Duality expands the features of ImageVis3D Mobile (Schiewe et al. 2015) by providing the possibility to not only interactively display precomputed datasets, but by generating these in near-real time using a client-server layout. Similar to ImageVis3D Mobile, KiwiViewer is an open source tool for scientific and medical visualization that runs on Android and iOS (https://www.kitware.com/kiwiviewer). Whereas KiwiViewer allows to easily visualize different kinds of data, it lacks the possibility to interactively generate and display data, as implemented in Duality through the client-server layout. The VES framework (http://www.vtk.org/Wiki/VES) was developed based on Kiwi and the visualization toolkit (VTK) to “enable the building of high performance visualization applications on mobile devices” and might enable developers to also implement interactivity comparable to Duality. Based on this framework, Ryabinin and Chuprina (2014) developed a “multiplatform adaptive rendering tools to visualize scientific experiments”, called SciVi, that implements such a client-server system. It allows to create clients both for mobile (iOS, Android) and desktop devices (Windows, GNU/Linux, MacOS). Scientific computations can be performed interactively using different tools/solvers through an interface based on XML. SciVi was positively validated for multiple scenarios (Ryabinin and Chuprina 2014). However, it is, to the best of our knowledge, not freely available at this time.

To reach a broader target audience, it is desirable to make the Duality app available for a larger selection of devices. Currently, the use of Duality is limited to iOS devices, i.e., iPhones and iPads. However, the Duality app is split into an iOS-frontend (Duality_iosFrontend, https://github.com/SCIInstitute/Duality_iosFrontend) implemented in Objective-C++ and a core (Duality_Client, https://github.com/SCIInstitute/Duality_Client) implemented in C++. This design opens the possibility to implement Duality clients for a variety of other devices and operating systems. As no external libraries are used in the implementation of the rendering, the only requirement is OpenGL ES support. The mocca-library can be adapted to other platforms as well. A second goal to reach a broader target audience is to simplify the scene generation. As all scenes contain or are based on individual patient (imaging) data, the generation of the displayed scenes currently involves manual editing of scripts and requires the use of multiple (command line based) tools. For example, the surface and image files have to be converted to the g3d and i3m format, respectively, using the tool uvfconvert and the json-files have to be generated manually. To reach a large target audience of both experimentalists and clinicians it is desirable to unify as many of these steps in a single tool with a graphical user interface in the future. Already now, most of these steps can be simplified by using, e.g., python scripts.

In future studies, we plan to use the pipeline for postoperative programming presented here for the programming of a larger cohort of patients at remote locations. In this study, the results of and the time effort for the DBS programming with and without the support of the iPad-app will be evaluated more systematically. A further goal that will be investigated is the reduction of the caregiver burden that is achieved by performing the DBS programming at a remote location close to the patient’s home.

With the emerging use of segmented leads that have more than the classical four contacts, the automatic determination of stimulation patterns is assumed to gain importance. The size of the parameter space grows exponentially with the number of contacts, which - in combination to the more complicated structure of the electric fields that are generated by segmented lead contacts - makes a completely manual programming nearly impossible. Multiple algorithms that aim to automatically determine optimal stimulation patterns considering target and avoidance regions have been presented recently Anderson et al. (2017); Xiao et al. (2016); Peña et al. (2017). For the approach presented by Anderson et al. (2017), the optimization can be performed within a few seconds.

We plan to implement the algorithm for the automatic computation of optimal DBS stimulation settings presented by (Anderson et al. 2017) in the Duality-framework. Therefore, it is necessary to implement the possibility to be able to send additional data, i.e., the stimulation settings computed by the algorithm, back to the iPad and to display them. A version of Duality that includes this functionality is currently in development.

Finally, we note that as the execution of server-side commands is python-based and the scene definition occurs through JSON-files, the presented pipeline is highly flexible and is not limited to the use-cases presented here, but can be used for the mobile visualization of many kinds of computations/simulations that can be performed in near-real time.

Appendix A. Used file formats and structures

A.1. Description scene.json

In the file scene.json that is used for the scene definition, besides metadata for the respective scene (“name”, “description”), each object that is part of the scene to be visualized is defined. For each object, amongst others, the type of the object (“volume” or “geometry”), whether it is static (“download”) or interactively computed (“python”), the geometry file or the python script to be downloaded or executed (“filename”), respectively, and, in case of an interactively computed object, the parameters to be shown in the GUI (“variables”) are defined. All geometry files have to be in the g3d-format, all volumes in the i3m-format, as they are used by ImageVis3D (http://www.sci.utah.edu/software/imagevis3d.html). A commandline-converter (uvfconvert) from different image formats to g3d and i3m is available with ImageVis3D. The structure of the scene is represented by the folder structure in which the files are placed. All static objects have to be in the “download” sub-folder and all python-scripts in the “python”-subfolder of the scene directory, while the file scene.json is in the parent folder. A minimal example for such a python-script is shown in A.4.

A.2. Minimal example for scene.json

{
 “ met adata “ :
  {
   “name” : “ scene name”
   “ description”: “scene description “
  },
  [
   {
    “ name “: “ static volume object shown in 2d”
    “ type “ : “ volume”
    “ view3d”: “ false”
    “ view2d “ : “ true”
    “ dataset “ :
    {
     “ source”:
     {
      “type”: “ download”,
      “ filename” : “ myvolumefile. i3m”
     }
    }
   },
   {
    “name” : “ static geometric object shown in 3d and transformed”
    “ type “ : “ volume”
    “ view3d “ : “ true”
    “ view2d “ : “ false”
    “ dataset “ :
    {
     “ source” :
     {
      “type”: “ download”,
      “ filename” : “ mygeometryfile. g3d”
     },
     “ transforms “ :
     [
      [ 1, 0, 0, 0,
       0, 1, 0, 0,
       0, 0, 1, 0,
       0, 0, 0, 1 ]
     ]
    }
   },
   {
     “name”: “ dynamic object shown in 2d and 3d”
     “ type “ : “ volume”
     “ view3d “ : “ true”
     “view2d “: “ true”
     “ dataset “ :
     {
      “source”:
      {
       “type “: “python”,
       “ filename” : “ mypythonfile. py”,
       “ variables “ :
       [
        {
         “type “: “ float “,
         “name” : “my float parameter”,
         “ lowerBound” : — 1.0,
         “upperBound”: 1.0,
         “ stepSize “ : 0.1,
         “ defaul tValue “ : 0.0
        },
        {
         “type “ : “enum”,
         “name” : “my enum parameter”,
         “ values “ : [ “a”, “b”, “c” ],
         “ defaultValue” : “b”
        }
       ]
      }
     }
    }
   ]
}

A.3. Description of python-script

For interactive visualizations, the python-scripts that are indicated in scene.json to be executed have to be predefined. The parameters are passed from the server application to the python-script as commandline arguments and can, e.g., be processed using the argparse package. There are three arguments that are handed to the python-script, “--output”, “--scenepath”, and “--variables”. “-output” defines the file and path to which the new object to be visualized is written so that it can be recognized by the server and “--scenepath” indicates the path of the main scene-folder. “--variables” is followed by all parameters associated to this respective object/python-script.

A.4. Minimal example for python-script

def main ( ) :
         import argparse
         import subprocess
         import shutil
         print “ Parsing ˽ input ˽ parameters . . . \ n”
         parser = argparse. ArgumentParser ()
         parser. add_argument ( ‘--variables’, nargs=‘ * ‘)
         parser. add_argument ( ‘--outp ut’, nargs = 1)
         parser. add_argument ( ‘--scenepath ‘, nargs = 1)
         args = parser.parse_args()
         variables = dict ()
         for i in xrange (0, len (args. variables),2):
         variables [ args. variables [ i ] ] = args. variables [ i + 1]
         outputfile = args.output [0]
         scenepath = args. scenepath [0]
         # computations using the variables here !
         print “ Running ˽ computation . . . \ n”
         #args = (“ my/ binary /path “,”— i “, myinputfile,”— o”, myoutputfile )
         #popen = subprocess. Popen(args, stdout=subprocess. PIPE)
         #p open. wait ()
         print “ Copying ˽ outputfile . . . \ n”
         shutil. copyfile (myoutputfile, outputfile)
         print “Done. \ n”
       main ( )

Appendix B.

B.1. Formulation of FEM problem to simulate the electric fields evoked by DBS

Including the terms for boundary conditions, the quasi-static equation for bioelectric fields reads:

$$\nabla \hspace{0.17em}\cdot \hspace{0.17em}(\sigma \nabla u)\hspace{0.17em}=\nabla ·\mathbf{j}\text{for}\mathbf{x}\in \mathrm{\Omega }$$ (B1)

$$\begin{gathered} {\partial }_{\mathbf{n}}u=0\text{for}\mathbf{x}\in {\Gamma }_N, \\ u=u_0\text{for}\mathbf{x}\in {\Gamma }_D. \end{gathered}$$ (B2)

Ω is the domain on which the simulation occurs, i.e., a model of the human head, possibly simplified depending on the degree of modeling accuracy, e.g., as an “electrode in a box”. σ is the (iso- or anisotropic) conductivity distribution in the human head and u the electric potential. j is the distribution of current sources inside the brain and ∂Ω_D and ∂Ω_N are the subsets of the domain boundary with Dirichlet or Neumann boundary condition.

For voltage controlled unipolar stimulation, as simulated in the examples shown here, there are no current sources in the brain, i.e., j = 0, Γ_D consists of the boundaries of the electrode and (parts of) the outer boundary of Ω, ∂Ω. In our examples, where we restrict Ω to a brain mask, we choose the complete outer boundary of Ω to be part of Γ_D. ∂Ω is set to a potential of zero, i.e., u₀(x) = 0 for x ∈ ∂Ω.

As the conductivities of brain tissue, the insulating, and the conducting parts of the DBS lead vary within multiple magnitudes, which can lead to numerical inaccuracies, we chose to remove the volume of the DBS lead from our mesh and instead model the insulating and highly-conducting parts of the lead using boundary conditions. Therefore, a homogeneous Neumann boundary condition is assumed at all boundaries between tissue and the insulating parts of the DBS lead to account for the very low conductivity of these parts. Thereby, any current flow through the insulating parts of the lead is avoided. Accordingly, the boundaries of the insulating parts of the DBS lead are in Γ_Ν. As previously, Dirichlet boundary conditions are assumed at the boundaries between tissue and active contacts, so that these boundaries remain in Γ_D. Finally, for each passive contacts of the lead all boundary nodes to the tissue are linked. Thereby, they collapse to one degree of freedom in the resulting equation system and all nodes of one contact are assigned with the same value for the electric potential to account for the very high conductivity of the contacts.

B.2. FEM-based computation of an activating function based VTA using SCIRun

The FEM simulation of the electric potential is performed using the python-interface of SCIRun. Within the same step, also the Hessian matrix of the electric potential is computed. Upon a negative check whether a simulation for the indicated stimulation settings has already been performed and stored, SCIRun is called with the python-script forwardsimulation.py as input from within the main python-script (simulation.py). This python-script loads a SCIRun-network (forwardsim-ulation.srn5), sets the variables for the SCIRun-modules if necessary, triggers an execution of the SCIRun-network, and quits SCIRun after the execution. In this example, we restricted ourselves to the case of unipolar stimulation settings. However, the implementation of bipolar or arbitrary stimulation settings following this example is straight-forward.

Afterwards, SCIRun is again called with another python-script as input (vta.py), which computes an isosurface based on the second difference in a certain predefined direction. To compute the second differences, the previously computed Hessian matrices are used. If no further information is given, the second difference is calculated in a direction that is perpendicular to the electrode shaft and lies in the plane that is orthogonal to the orientation of the electrode shaft as it is commonly done to calculate a VTA Butson and McIntyre (2006). After the computation, the isosurface is written to an obj-file and SCIRun is quit. From within the main python-script, the commandline-converter delivered with ImageVis3D is called to convert this obj-file to a g3d-file. This g3d-file is then copied to a location that is defined in the commandline arguments delivered to the python script by the server application, so that it is recognized by the server application and transmitted to the iPad.

B.3. FEM-based computation of an activating function based VTA for an interactively placed DBS lead using SCIRun

Two scenes have to be defined to fulfill the needs of the example described in Section 2.5. The sole use of the first scene (“Position-Electrode-preoperative”) is to position the DBS lead in the patient’s brain with the desired position and orientation. Therefore, the coordinates of the tip of the lead, and its rotation around the x- and z-axis can be selected in the GUI. On the server-side, the corresponding geometric transform is computed and a model of the DBS lead that was transformed accordingly is sent back to the iPad for the visualization (cf. Figure 2a). For each change of the parameters, the resulting transformation is stored. Once the desired electrode position is found, the user switches to a second scene for the visualization of DBS stimulation results at the chosen lead position (“Simulate-Unipolar-preoperative”). Upon the initialization of this scene, the python-script simulate.py is executed. As a first step, it checks whether the transformation stored by the positioning scene has changed since the last execution. If this is the case, it copies this transformation and triggers the generation of a new high-quality finite element mesh for the new DBS lead orientation and position as described in Section 2.5 and illustrated in Figure 3. The mesh generation is, again, performed by calling SCIRun with a specific pyton-script (createmesh.py). After the generation of the finite element mesh, now following the pipeline developed in Sections 2.4, a FEM computation for the initial stimulation parameters is performed and a VTA is generated based on the activating function.

B.4. Generation of highly realistic FEM head model

We used FSL (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki) to register the available imaging modalities (preoperative T1-MRI, postoperative CT). FSL was furthermore used to obtain segmentations of the pre-operative MRIs into skin, skull, CSF, and brain compartment. Surfaces of these compartments were subsequently generated using iso2mesh (http://iso2mesh.sourceforge.net). The position and orientation of the DBS lead were estimated from the postoperative CT-image, and a surface model of the lead surface was transformed accordingly and joined with the surfaces of the brain tissues. Based on these surfaces, a tetrahedral finite element head model was generated using the integration of TetGen (http://wias-berlin.de/software/tetgen/; Si (2015)) into SCIRun (http://www.sci.utah.edu/cibc-software/scirun.html). The tetrahedra that were modeled inside the surface model of the DBS lead by TetGen were afterwards removed (cf. Section 2.1, B.1).