Simultaneous Estimation and Variable Selection for Interval-Censored Data with Broken Adaptive Ridge Regression

Abstract

The simultaneous estimation and variable selection for Cox model has been discussed by several authors (Fan and Li, 2002; Huang and Ma, 2010; Tibshirani, 1997) when one observes right-censored failure time data. However, there does not seem to exist an established procedure for interval-censored data, a more general and complex type of failure time data, except two parametric procedures given in Scolas et al. (2016) and Wu and Cook (2015). To address this, we propose a broken adaptive ridge (BAR) regression procedure that combines the strengths of the quadratic regularization and the adaptive weighted bridge shrinkage. In particular, the method allows for the number of covariates to be diverging with the sample size. Under some weak regularity conditions, unlike most of the existing variable selection methods, we establish both the oracle property and the grouping effect of the proposed BAR procedure. An extensive simulation study is conducted and indicates that the proposed approach works well in practical situations and deals with the collinearity problem better than the other oracle-like methods. An application is also provided.

1. Introduction

The statistical analysis of interval-censored failure time data has been extensively discussed and especially, many procedures have been proposed in the literature for their regression analysis (Finkelstein, 1986; Jewell and van der Laan, 2004; Sun, 2006). However, there exists little literature on simultaneous estimation and variable selection for interval-censored data although some literature has been developed for right-censored failure time data (Fan and Li, 2002; Huang and Ma, 2010; Tibshirani, 1997). By interval-censored data, we mean that the failure time of interest is known or observed only to belong to an interval instead of being observed exactly. It is easy to see that they include right-censored data as a special case and can naturally occur in a longitudinal or periodic follow-up study such as clinical trials among other situations. In the following, we will discuss regression analysis of interval-censored data with the focus on simultaneous estimation and covariate selection.

Covariate or variable selection is a commonly asked question in statistical analysis and many methods for it have been developed, especially under the context of linear regression, such as forward selection, backward selection and best subset selection. Among them, the penalized estimation procedure, which optimizes an objective function with a penalty function, has recently become increasingly popular. Among the penalty functions, it is well-known that the L₀ penalty function is usually a desired choice as it directly penalizes the cardinality of a model and seeks the most parsimonious model explaining the data. However, it is non-convex and the solving of an exact L₀-penalized nonconvex optimization problem involves exhaustive combinatorial best subset search, which is NP-hard and computationally infeasible for high dimensional data. Corresponding this, Tibshirani (1996) considered the L₁ penalty function, which gives the closest convex relaxation, and developed the least absolute shrinkage and selection operator (LASSO) procedure. In particular, the L₁-based optimization problem can be solved exactly with efficient algorithms. However, the LASSO procedure does not have the oracle property or the grouping effect, which is especially desirable when covariates are highly correlated as often the case in high dimensional situations. Also the LASSO procedure tends to select too many small noise features and is biased for large parameters.

Following Tibshirani (1996), many authors have proposed other penalty functions, including the smoothly-clipped absolute deviation (SCAD) penalty by Fan and Li (2001), the elastic net by Zou and Hastie (2005), the adaptive LASSO (ALASSO) penalty by Zou (2006), the group LASSO by Yuan and Lin (2006), the smooth integration of counting and absolute deviation (SICA) penalty by Lv and Fan (2009) and the seamless-L₀ (SELO) penalty by Dicker et al. (2013). All of them either have the oracle property or the grouping effect but none has both. In the following, we present a broken adaptive ridge (BAR) penalized procedure that has both the oracle property and the grouping effect. It approximates the L₀-penalized regression using an iteratively reweighted L₂-penalized algorithm and has the advantages of simultaneous variable selection, parameter estimation and clustering. Also the BAR iterative algorithm is fast and converges to a unique global optimal solution.

As mentioned above, many authors have investigated the variable selection problem for right-censored failure time data and in particular, several penalized procedures have been proposed under the framework of the Cox’s proportional hazards (PH) model. For example, Tibshirani (1997), Fan and Li (2002) and Zhang and Lu (2007) generalized the LASSO, SCAD and ALASSO penalty-based procedures, respectively, to the PH model situation with right-censored data. Furthermore, Shi et al. (2014) discussed the same problem but the generalization of the SICA penalty-based procedure. Note that conceptually it may seem to be straightforward to generalize the procedures above to interval-censored data. However, this is not true partly due to the much more complex structures of interval-censored data. For example, with right-censored data under the PH model, a partial likelihood function, which is free of the underlying baseline hazard function and thus is parametric with respect to covariate effects, is available and has been employed as the objective function in all of the penalized procedures described above. In contrast, no such parametric objective function is available for interval-censored data and one has to deal with both regression parameters and the baseline hazard function together.

For the covariate selection based on interval-censored data, two parametric procedures have been developed in Scolas et al. (2016) and Wu and Cook (2015) and in particular, the latter assumed that the baseline hazard function is a piecewise constant function. One drawback of this is that the piecewise constant function is neither continuous nor differentiable. More importantly, there is no theoretical justification available for both procedures. In the following, instead of the piecewise constant function, we will employ Bernstein polynomials to approximate the underlying cumulative hazard function. Note that although the uses of piecewise constant functions and Bernstein polynomials may look similar, the two approaches are actually quite different. One major difference is that unlike the piecewise constant function, the Bernstein polynomial approximation is a continuous approximation and has some nice properties including differentiability. More comments on this are given below.

The remainder of the paper is organized as follows. In Section 2, we will first describe some notation and assumptions that will be used throughout the paper and then the idea behind the proposed BAR regression procedure as well as some background. Section 3 presents the proposed BAR regression procedure and in particular, an iterative algorithm for the determination of the BAR estimators is developed. In Section 4, we establish the oracle property and grouping effect of the proposed method, and Section 5 gives some results obtained from an extensive simulation study conducted for the assessment of the proposed approach. In particular, we compared the BAR regression procedure and the methods that make use of other commonly used penalty functions, and the results indicate that the proposed method can outperform other methods in general. In Section 6, an application is provided and Section 7 contains some discussion and concluding remarks.

2. Notation, Assumptions and Some Background

2.1. Notation, Assumptions and Sieve Maximum Likelihood

Consider a failure time study consisting of n independent subjects. For subject i, let T_i denote the failure time of interest and suppose that there exists α p-dimensional vector of covariates denoted by Z_i = (Z_i1,…, Z_ip)′, i = 1,…, n. Also suppose that one observes interval-censored data given by $\mathcal{D}={\{(L_i,R_i],{\mathit{Z}}_i\}}_{i=1}^n$, where (L_i, R_i] denotes the observed or censored interval to which T_i belongs. It is apparent that L_i = 0 or R_i = ∞ corresponds to a left- or right-censored observation on the ith subject. In the following, we will assume that the censoring mechanism behind the censoring intervals is independent of the failure time of interest. That is, we have independent or non-informative interval censoring (Sun, 2006)

For covariate effects, in the following, we will assume that the T_i’s follow the PH model or that given Z_i, the cumulative hazard function of T_i is given by

$$\mathrm{\Lambda }(t|{\mathit{Z}}_i)={\mathrm{\Lambda }}_0(t)e^{{\mathit{\beta }}^{\prime }{\mathit{Z}}_i}.$$ (1)

In the above, Λ₀(t) denotes an unknown cumulative baseline hazard function and β a vector of regression parameters. Then the likelihood function has the form

$$L_n(\mathit{\beta },{\mathrm{\Lambda }}_0)=\prod _{i=1}^n\left[\exp \{-{\mathrm{\Lambda }}_0(L_i)e^{{\mathit{\beta }}^{\prime }{\mathit{Z}}_i}\}-\exp \{-{\mathrm{\Lambda }}_0(R_i)e^{{\mathit{\beta }}^{\prime }{\mathit{Z}}_i}\}\right].$$ (2)

Here we assume that Λ₀(0) = 0 and A₀(∞) = ∞. In practice, one special case of interval-censored data that occurs quite often is current status or case I interval-censored data in which each subject is observed only once. For the situation, all observations are e left- or right-censored. One type of studies that naturally produce such data is cross-sectional studies, which are commonly conducted in medical studies and social science among others (Jewell and van der Laan, 2004; Sun, 2006). In this case, the likelihood function above reduces to

$$L_n(\mathit{\beta },{\mathrm{\Lambda }}_0)=\prod _{i=1}^n{\left[1-\exp \{-{\mathrm{\Lambda }}_0(R_i)e^{{\mathit{\beta }}^{\prime }{\mathit{Z}}_i}\}\right]}^{{\delta }_i}{\left[\exp \{-{\mathrm{\Lambda }}_0(L_i)e^{{\mathit{\beta }}^{\prime }{\mathit{Z}}_i}\}\right]}^{1-{\delta }_i},$$

where δ_i = 1 for left-censored observations and 0 otherwise.

To estimate ϑ = (β, Λ₀) in general, a natural approach is clearly to maximize the log-likelihood function l_n(β, Λ₀) = log{L_n(β, Λ₀)}. However, it is obvious that this is not an easy task since l_n(β, Λ₀) involves both finite-dimensional and infinite-dimensional parameters. To deal with this and also to give a parametric objective function to be used below, we propose to employ the sieve approach to approximate Λ₀ by using Bernstein polynomials (Wang and Ghosh, 2012; Zhou et al., 2016). More specifically, define

$$\mathrm{\Theta }=\left\{\mathit{\vartheta }=(\mathit{\beta },{\mathrm{\Lambda }}_0)\in \mathcal{B}\otimes \mathcal{M}\right\},$$

denoting the parameter space of ϑ, where $\mathcal{B}=\{\mathit{\beta }|\mathit{\beta }\in R^p,\Vert \mathit{\beta }\Vert \le M\}$ with M being a positive constant and $\mathcal{M}$ is the collection of all bounded and continuous non-decreasing, non-negative functions over the interval [u,v] with 0 ≤ u < v < < ∞ >. In practice, [u,v] is usually taken as the range of the observed data. Furthermore, define the sieve space

$${\mathrm{\Theta }}_n=\left\{{\mathit{\vartheta }}_n=(\mathit{\beta },{\mathrm{\Lambda }}_{0n})\in \mathcal{B}\otimes {\mathcal{M}}_n\right\},$$

where

$${\mathcal{M}}_n=\left\{{\mathrm{\Lambda }}_{0n}(t)=\sum _{k=0}^m{\varphi }_k^{\ast }{B}_k(t,m,u,v):\sum _{0\le k\le m}\left|{\varphi }_k^{\ast }\right|\le M_n,0\le {\varphi }_0^{\ast }\le {\varphi }_1^{\ast }\le \dots \le {\varphi }_m^{\ast }\right\}$$

with the ${\varphi }_k^{\ast }$’s being some parameters and

$$B_k(t,m,u,v)=\left(\begin{array}{c}m\\ k\end{array}\right){\left(\frac{t-v}{u-v}\right)}^k{\left(1-\frac{t-v}{u-v}\right)}^{m-k},k=0,\dots ,m,$$

which are Bernstein basis polynomials of degree m = o(n^s) for some s ∈ (0,1). More discussion about m will be given below.

By focusing on the sieve space Θ_n, the likelihood function given in (2) can be rewritten as

$$L_n(\mathit{\beta },{\varphi }_k^{\ast }\prime s)=\prod _{i=1}^n\left[\exp \{-{\mathrm{\Lambda }}_{0n}(L_i)e^{{\mathit{\beta }}^{\prime }{\mathit{Z}}_i}\}-\exp \{-{\mathrm{\Lambda }}_{0n}(R_i)e^{{\mathit{\beta }}^{\prime }{\mathit{Z}}_i}\}\right],$$ (3)

and if one is only interested in estimating β, it is natural to focus on the sieve profile log-likelihood function $l_p(\mathit{\beta })=\underset{{\varphi }^{*}}{\max }\log \{L_n(\mathit{\beta },{\varphi }_k^{\ast }\prime s)\}$. Note that due to the non-negativity and monotonicity features of Λ₀, in the maximization above, we need the constraint $0\le {\varphi }_0^{\ast }\le {\varphi }_1^{\ast }\le \dots \le {\varphi }_m^{\ast }$, but it can be easily removed by the reparameterization ${\varphi }_0^{\ast }=e^{{\varphi }_0}$ and ${\varphi }_k^{\ast }={\sum }_{i=0}^k{e}^{{\varphi }_i},1\le i\le m$. In the following, we will discuss the development of a penalized or regularized procedure for simultaneous estimation and covariate selection based on $l_p(\mathit{\beta })=\underset{\varphi }{\max }\log \{L_n(\mathit{\beta },{\varphi }_k^{\text{'}}s)\}$.

2.2. Regularized Sieve Maximum likelihood Estimation

For the simultaneous estimation and covariate selection for model (1), we will consider the approach that minimizes the penalized function.

$$l_{pp}(\mathit{\beta }|\stackrel{⌵}{\mathit{\beta }})=-2l_p(\mathit{\beta })+\sum _{j=1}^{p}P(\left|{\mathit{\beta }}_j\right|;\lambda )=-2l_p(\mathit{\beta })+\lambda \sum _{j=1}^p\frac{{\mathit{\beta }}_j^2}{{{\stackrel{⌵}{\mathit{\beta }}}_j}^2},$$ (4)

where λ denotes a tuning parameter and $\stackrel{⌵}{\mathit{\beta }}=(\stackrel{⌵}{{\mathit{\beta }}_1},\dots ,\stackrel{⌵}{{\mathit{\beta }}_p}{)}^{\prime }$ is a consistent estimator of β with no zero components. The choice of $\stackrel{⌵}{\mathit{\beta }}$ will be discussed below. A main motivation behind the procedure above is that given the consistency of $\stackrel{⌵}{\mathit{\beta }}$, the term ${\mathit{\beta }}_j^2/\stackrel{⌵}{{\mathit{\beta }}_j^2}$, is expected to converge to I(|β_j| ≠ 0) in probability as n goes to infinity and therefore the method can be regarded as an automatic implementation of the best subset selection in some asymptotic sense. In other words, the adaptive penalty term in (4) can be taken as an approximation to the L₀ penalty. A similar idea was discussed in Liu and Li (2016) under the context of generalized linear models with complete data and in Kawaguchi et al.(2017) for the PH model with right-censored data, respectively.

It is apparent that instead of the penalty function used in (4), one can employ other penalty functions such as the L₀-penalty P(|β_j|; λ) = λI(|β_j| = 0), which directly penalizes the cardinality of a model and is the most essential sparsity measure due to its discrete nature. However, as mentioned above, its implementation is NP-hard and computationally infeasible for high dimensional data. Other possible choices may include the LASSO penalty P(|β_j|; λ) = λ |β_j|, the ALASSO penalty P(|β_j|; λ) = λ w_j |β_j| with w_j being a weight, the SCAD penalty $P(\left|{\mathit{\beta }}_j\right|;\lambda )=\lambda {\int }_0^{\left|{\mathit{\beta }}_j\right|}\min \left\{1,{(a\lambda -x)}_{+}/(a\lambda -\lambda )\right\}dx$ with a > 2, the SICA penalty $P\left(\left|{\mathit{\beta }}_j\right|;\lambda \right)=\lambda (\tau +1)\left|{\mathit{\beta }}_j\right|/\left(\left|{\mathit{\beta }}_j\right|+\tau \right)$ with $\tau >0$, the SELO penalty

$$P\left(\left|{\mathit{\beta }}_j\right|;\lambda \right)=\frac{\lambda }{\log (2)}\log \left(\frac{\left|{\mathit{\beta }}_j\right|}{\left|{\mathit{\beta }}_j\right|+\gamma }+1\right)$$

with γ > 0, or the minimax concave (MCP) penalty

$$P\left(\left|{\mathit{\beta }}_j\right|;\lambda \right)=\lambda {\int }_0^{\left|{\mathit{\beta }}_j\right|}\frac{{(a\lambda -x)}_{+}}{a\lambda }dx$$

with a > 1 given in Zhang (2010). However, all of these procedures would be quite complex computationally partly because multiple parameters need to be tuned. More importantly, in addition to the oracle property and the grouping effect given below, one will see from the numerical study below that the proposed method generally outperforms the procedures based on other penalty function.

3. BAR Regression Estimation Procedure

Now we will describe how to minimize $l_{pp}(\mathit{\beta }|\tilde{\mathit{\beta }})$ given in (4) or the implementation of the proposed BAR regression procedure. For this, it is apparent that one could directly minimize (4) by some numerical iterative algorithms. For example, given a good initial value β⁽⁰⁾, one can then update β^(k−1) iteratively by the following reweighed L₂ —penalized Cox regression estimator

$${\widehat{\mathit{\beta }}}^{(k)}=\underset{\mathit{\beta }}{\arg \min }\{-2l_p(\mathit{\beta })+{\lambda }_n\sum _{j=1}^p\frac{{\mathit{\beta }}_j^2}{{({\widehat{\mathit{\beta }}}_j^{(k-1)})}^2}\},k\ge 1,$$ (5)

where λ_n is a non-negative penalization tuning parameter. However, it is easy to see that this would be computationally costly. So instead we will present a data-driven algorithm, which is much easier and computationally more efficient. In the algorithm, we will approximate the log-likelihood function using the Newton-Raphson update through an iterative least squares procedure, which solves the least squares problem subject to the reweighted L₂ penalty at each iteration.

Let $\text{ϕ}=({\varphi }_1,\dots ,{\varphi }_m{)}^{\prime }$ and $l_n(\mathit{\beta },\varphi )=\log \{L_n(\mathit{\beta },{\varphi }_k^{\text{'}}s)\}$. Define

$${\dot{l}}_n(\mathit{\beta }|\varphi )=\frac{\partial l_n(\mathit{\beta },\varphi )}{\partial \mathit{\beta }},{\ddot{l}}_n(\mathit{\beta }|\varphi )=\frac{{\partial }^2{l}_n(\mathit{\beta },\varphi )}{\partial \mathit{\beta }\partial {\mathit{\beta }}^{\prime }},$$

the partial gradient vector and the partial Hessian matrix about β, respectively. Suppose that $(\tilde{\mathit{\beta }},\tilde{\varphi })$ satisfies ${\dot{l}}_n(\tilde{\mathit{\beta }},\tilde{\varphi })=0$. Then for β within a small neighborhood of $\tilde{\mathit{\beta }}$, the second-order Taylor expansion gives

$$l_p(\mathit{\beta })\approx \frac{1}{2}{\left[{\dot{l}}_n(\mathit{\beta }|\tilde{\varphi })\right]}^{\prime }{\left[{\ddot{l}}_n(\mathit{\beta }|\tilde{\varphi })\right]}^{-1}\left[{\dot{l}}_n(\mathit{\beta }|\tilde{\varphi })\right]+c,$$

where c is a constant. Let the matrix X be defined by the Cholesky decomposition of $-{\ddot{l}}_n(\mathit{\beta }|\tilde{\varphi })$ as $-{\ddot{l}}_n(\mathit{\beta }|\tilde{\varphi })={\mathit{X}}^{\prime }X$ and define the pseudo response vector $\mathit{y}={({\mathit{X}}^{\prime })}^{-1}[{\dot{l}}_n(\mathit{\beta }|\tilde{\varphi })-{\ddot{l}}_n(\mathit{\beta }|\tilde{\varphi })\mathit{\beta }]$. Then we have

$${\Vert \mathit{y}-\mathit{X}\mathit{\beta }\Vert }^2=-{\left[{\dot{l}}_n(\mathit{\beta }|\tilde{\varphi })\right]}^{\prime }{\left[{\ddot{l}}_n(\mathit{\beta }|\tilde{\varphi })\right]}^{-1}\left[{\dot{l}}_n(\mathit{\beta }|\tilde{\varphi })\right],$$

where ║·║ denotes the Euclidean norm for a given vector. This implies that minimizing (4) is asymptotically equivalent to minimizing the following penalized least squares function

$${\Vert \mathit{y}-\mathit{X}\mathit{\beta }\Vert }^2+{\lambda }_n\sum _{j=1}^p\frac{{\mathit{\beta }}_j^2}{\stackrel{⌵}{{\mathit{\beta }}_j^2}}.$$

A similar least squares approximation was discussed in Wang and Leng (2007) to get a unified LASSO estimation.

Now we are ready to present the iterative algorithm. Define

$$g(\stackrel{⌵}{\mathit{\beta }})=\underset{\mathit{\beta }}{\arg \min }\{{\Vert \mathit{y}-\mathit{X}\mathit{\beta }\Vert }^2+{\lambda }_n\sum _{j=1}^p\frac{{\mathit{\beta }}_j^2}{\stackrel{⌵}{{\mathit{\beta }}_j^2}}\}.$$ (6)

By some algebraic manipulations, one can show that

$$g(\stackrel{⌵}{\mathit{\beta }})={\{{\mathit{X}}^{\prime }X+2{\lambda }_n\mathit{D}(\stackrel{⌵}{\mathit{\beta }})\}}^{-1}{\mathit{X}}^{\prime }y$$ (7)

and one can obtain the BAR regression estimator given by minimizing (4) by solving (6) or (7), where $\mathit{D}(\stackrel{⌵}{\mathit{\beta }})=\text{diag}\{\stackrel{⌵}{{\mathit{\beta }}_1^{-2}},\dots ,\stackrel{⌵}{{\mathit{\beta }}_p^{-2}}\}$, a p × p matrix. In the following, we will focus on the situation where p can diverge to infinity but p < n, and for this, we will denote p by p_n to emphasize the dependence of p on n. Let Ω_n = Ω_n(β) = X′X and v_n = v_n(β) = X′y. For a fixed λ_n, which will be discussed below, one can solve (6) as follows.

• Step 1. set k = 0 and choose an intial estimator ${\widehat{\mathit{\theta }}}^{(0)}=({\widehat{\mathit{\beta }}}^{(0{)}^{\prime }},{\widehat{\varphi }}^{(0{)}^{\prime }}{)}^{\prime }$ satisfying $\Vert {\widehat{\mathit{\beta }}}^{(0)}-{\mathit{\beta }}_0\Vert =O_p({(p_n/n)}^{1/2})$. As an example, one can take ${\widehat{\varphi }}^{(0)}$ to be a vector of zeros as the proposed algorithm is insensitive to the initial values of ϕ and take ${\widehat{\mathit{\beta }}}^{(0)}$ to be the ridge regression estimator

  $${\widehat{\mathit{\beta }}}^{(0)}=\underset{\mathit{\beta }}{\arg \min }\{-2l_p(\mathit{\beta })+{\xi }_n\sum _{j=1}^{p_n}{\mathit{\beta }}_j^2\},$$ (8)

  where ξ_n is a non-negative tuning parameter to be discussed below.
• Step 2. At the k_th step, compute the partial derivatives ${\dot{l}}_n({\widehat{\mathit{\beta }}}^{(k)}|{\widehat{\varphi }}^{(k)})$ and ${\ddot{l}}_n({\widehat{\mathit{\beta }}}^{(k)}|{\widehat{\varphi }}^{(k)})$, where

  $${\dot{l}}_n(\mathit{\beta }|\varphi )=\sum _{i=1}^n{\mathit{Z}}_i\frac{S(R_i|{\mathit{Z}}_i)\mathrm{\Lambda }(R_i|{\mathit{Z}}_i)-S(L_i|{\mathit{Z}}_i)\mathrm{\Lambda }(L_i|{\mathit{Z}}_i)}{S(L_i|{\mathit{Z}}_i)-S(R_i|{\mathit{Z}}_i)}$$

  and

  $$\begin{gathered} {\ddot{l}}_n(\mathit{\beta }|\varphi )=\sum _{i=1}^n{\mathit{Z}}_i{\mathit{Z}}_i^{\text{'}}[\frac{S(R_i|{\mathit{Z}}_i)\mathrm{\Lambda }(R_i|{\mathit{Z}}_i)\{1-\mathrm{\Lambda }(R_i|{\mathit{Z}}_i)\}-S(L_i|{\mathit{Z}}_i)\mathrm{\Lambda }(L_i|{\mathit{Z}}_i)\{1-\mathrm{\Lambda }(L_i|{\mathit{Z}}_i)\}}{S(L_i|{\mathit{Z}}_i)-S(R_i|{\mathit{Z}}_i)} \\ -\frac{{\{S(R_i|{\mathit{Z}}_i)\mathrm{\Lambda }(R_i|{\mathit{Z}}_i)-S(L_i|{\mathit{Z}}_i)\mathrm{\Lambda }(L_i|{\mathit{Z}}_i)\}}^2}{{\{S(L_i|{\mathit{Z}}_i)-S(R_i|{\mathit{Z}}_i)\}}^2}] \end{gathered}$$ (9)

  with S(t|Z_i) = exp{−Λ(t│Z_i)}, denoting the survival function for subject i given Z_i
• Step 3. Update the estimate of β by

  $${\widehat{\mathit{\beta }}}^{(k+1)}={\{{\text{Ω}}_n+2{\lambda }_n\mathit{D}({\widehat{\mathit{\beta }}}^{(k)})\}}^{-1}{\text{v}}_n,$$

  where ${\text{Ω}}_n=-{\ddot{l}}_n({\widehat{\mathit{\beta }}}^{(k)}|{\widehat{\varphi }}^{(k)})$ and ${\text{v}}_n={\dot{l}}_n({\widehat{\mathit{\beta }}}^{(k)}|{\widehat{\varphi }}^{(k)})-{\ddot{l}}_n({\widehat{\mathit{\beta }}}^{(k)}|{\widehat{\varphi }}^{(k)}){\widehat{\mathit{\beta }}}^{(k)}$.

• Step 4. Given the current estimate ${\widehat{\mathit{\beta }}}^{(k+1)}$, solve $\partial l_n({\widehat{\mathit{\beta }}}^{(k+1)},\varphi )/\partial \varphi =0$ to obtain the updated estimate ${\widehat{\varphi }}^{(k+1)}$.

• Step 5. Go back to Step 2 until the convergence is achieved.

Let ${\widehat{\mathit{\beta }}}^{\ast }={\lim }_{k\to \infty }{\widehat{\mathit{\beta }}}^{(k)}$ denote the estimator of β obtained above, which will be referred to as the BAR estimator. Note that in the iterative process above, one does not really need to carry out the Cholesky decomposition of $-{\ddot{l}}_n(\mathit{\beta }|\varphi )$ as only the calculation of Ω_n and v_n is needed. To implement the algorithm above, one needs to select two tuning parameters ξ_n and λ_n simultaneously and for this, as many other authors, we propose to perform two-dimensional grid search based on the C-fold cross-validation. More specifically, one first divides the observed data into C non-overlapping parts with approximately the same size. For given ξ_n and λ_n, define the cross-validation statistic as

$$CV({\xi }_n,{\lambda }_n)=\sum _{c=1}^C\left[l_n({\widehat{\mathit{\beta }}}^{(-c)},{\widehat{\varphi }}^{(-c)})-l_n^{(-c)}({\widehat{\mathit{\beta }}}^{(-c)},{\widehat{\varphi }}^{(-c)})\right].$$

In the above, $l_n^{(-c)}$ denotes the log likelihood function for the whole data set without the c^th part, and ${\widehat{\mathit{\beta }}}^{(-c)}$ and ${\widehat{\varphi }}^{(-c)}$ are the proposed BAR estimators of β and ϕ based on whole data set without the c^th part. Then one can choose the values of £_n and λ_n that maximize CV(ξ_n, A_n). Instead of the C-fold cross-validation, one may employ other criteria such as the generalized cross-validation and Bayesian information criterion. More comments on this and on the selection of ξ_n and λ_n are given below.

4. The Asymptotic Properties of the BAR Estimator

Now we discuss the asymptotic properties of the proposed BAR estimator ${\widehat{\mathit{\beta }}}^{*}$. For this, let ${\mathit{\beta }}_0=({\mathit{\beta }}_{0,1},\dots ,{\mathit{\beta }}_{0,p_n}{)}^{\prime }$ denote the true value of ft and without loss of generality, assume ${\mathit{\beta }}_0=({\mathit{\beta }}_{01}^{\text{'}},{\mathit{\beta }}_{02}^{\text{'}}{)}^{\prime }$, where β₀₁ consists of all q_n (q_n ≪ p_n) nonzero components and ft₀₂ the remaining zero components. Correspondingly, we will divide the BAR estimator ${\widehat{\mathit{\beta }}}^{*}=({\widehat{\mathit{\beta }}}_1^{{*}^{\prime }},{\widehat{\mathit{\beta }}}_2^{{*}^{\prime }}{)}^{\prime }$ in the same way.

To establish the asymptotic properties, we need the following regularity conditions. (C1). (i) The set $\mathcal{B}$ is a compact subset of ${\mathcal{R}}^{p_n}$ and β₀ is an interior point of $\mathcal{B}$. (ii) The matrix E(ZZ’) is non-singular with Z being bounded. That is, there exists z₀ > 0 such that P(║Z║ ≤ z₀) = 1.

(C2). The union of the supports of L and R is contained in an interval [u,v] with 0 < u < v < ∞, and there exists a positive number ς such that P(R – L ≥ ς) = 1.

(C3). The function Λ₀(·) is continuously differentiable up to order r in [u,v] and satisfies a⁻¹ < Λ₀ (u) < Λ₀(v) < a for some positive constant a.

(C4). There exists a compact neighborhood ${\mathcal{B}}_0$ of the true value β₀ such that

$$\underset{\mathit{\beta }\in {\mathcal{B}}_0}{\sup }\Vert n^{-1}{\mathbf{\Omega }}_n(\mathit{\beta })-I({\mathit{\beta }}_0)\Vert \stackrel{a.s.}{\to }0,$$

where I(β₀) is a positive definite p_n × p_n matrix.

(C5). There exists a constant c > 1 such that c⁻¹ < λ_min(n⁻¹Ω_n) < λ_max(n⁻¹Ω_n) < c for

sufficiently large n, where λ_min(·) and λ_max(·) stand for the smallest and largest eigenvalues of the matrix.

(C6). As $n\to \infty ,p_n{q}_n/\sqrt{n}\to 0$, ${\lambda }_n/\sqrt{n}\to 0$, ${\xi }_n/\sqrt{n}\to 0$, ${\lambda }_n\sqrt{q_n/n}\to 0$ and ${\lambda }_n^2/(p_n\sqrt{n})\to \infty$.

(C7). There exist positive constants a₀ and a₁ such that a₀ ≤ |β_0,j|≤ a₁, 1 ≤ j ≤ q_n.

(C8). The initial estimator ${\widehat{\mathit{\beta }}}^{(0)}$ satisfies $\Vert {\widehat{\mathit{\beta }}}^{(0)}-{\mathit{\beta }}_0\Vert =O_p(\sqrt{p_n/n})$.

Conditions (C1)–(C3) are necessary for the existence and consistence of the sieve maximum likelihood estimator of Λ₀(t) and usually satisfied in practice (Zhang et al., 2010). Conditions (C4) and (C5) assume that n⁻¹Ω_n(β) is positive definite almost surely and its eigenvalues are bounded away from zero and infinity. Condition (C6) gives some sufficient, but not necessary, conditions needed to prove the numerical convergence and asymptotic properties of the BAR estimator. Condition (C7) assumes that the nonzero coefficients are uniformly bounded away from zero and infinity, and condition (C8) is crucial for establishing the oracle property of BAR. First we will establish the oracle property of ${\widehat{\mathit{\beta }}}^{\ast }$.

Theorem 1. (Oracle Property). Assume that the regularity conditions (C1) –(C8) hold. Then with probability tending to 1, the BAR estimator ${\widehat{\mathit{\beta }}}^{\ast }=({\widehat{\mathit{\beta }}}_1^{{*}^{\prime }},{\widehat{\mathit{\beta }}}_2^{{*}^{\prime }}{)}^{\prime }$ has the following properties:

1. ${\widehat{\mathit{\beta }}}_2^{*}=0$.

2. ${\widehat{\mathit{\beta }}}_1^{*}$ exists and is the unique fixed point of the equation ${\mathit{\beta }}_1={({\text{Ω}}_n^{(1)}+{\lambda }_n{\mathit{D}}_1(\mathit{\beta }))}^{-1}{\text{v}}_n^{(1)}$, where ${\mathit{D}}_1({\mathit{\beta }}_1)=\text{diag{}{\mathit{\beta }}_1^{-2}\text{,}\dots \text{,}{\mathit{\beta }}_{q_n}^{-2}\text{}}$, ${\text{Ω}}_n^{(1)}$ is the q_n × q_n leading submatrix of Ω_n, and ${\text{v}}_n^{(1)}$ is the vector consisting of the first q_n components of v_n.

3. $\sqrt{n}({\widehat{\mathit{\beta }}}_1^{*}-{\mathit{\beta }}_{01})$ converges in distribution to a multivariate normal distribution N_qn (0, Σ), where Σ is defined in the Appendix.

As mentioned above, in some situations, covariates have a natural group structure, meaning that the highly correlated covariates may have similar regression coefficients and thus should be selected or deleted simultaneously. One example of this is given by the gene network relationship where some genes are strongly correlated and often referred to as grouped genes (Segal et al., 2003). For the situation, it is clearly desirable that a variable selection approach can have all coefficients within a group clustered or selected together or has the grouping effect. To describe the grouping effect of the proposed BAR regression procedure, note that based on (9), the correlation between Zj and Z_k, the (j, k) components of the original covariates, can be described by that between x_j and x_k, where x_j denotes the jth p_n-dimensional column vector of X = (x₁,…, x_pn), j, k = 1,…, p_n. Thus we have the following grouping effect property.

Theorem 2. Assume that the columns of matrix $\mathit{X}=\left({\mathit{x}}_1,\dots ,{\mathit{x}}_{p_n}\right)$ have been standardized. Then with probability tending to one as n →∞, the BAR estimator ${\widehat{\mathit{\beta }}}^{*}=({\widehat{\mathit{\beta }}}_1^{*},\dots ,{\widehat{\mathit{\beta }}}_{p_n}^{*}{)}^{\prime }$ satisfies the following inequality

$$\left|\frac{1}{{\widehat{\mathit{\beta }}}_i^{*}}-\frac{1}{{\widehat{\mathit{\beta }}}_j^{*}}\right|\le \frac{1}{{\lambda }_n}\Vert \mathit{y}\Vert \sqrt{2(1-{\rho }_{ij})}$$

for nonzero ${\widehat{\mathit{\beta }}}_1^{*}$ and ${\widehat{\mathit{\beta }}}_1^{*}$, where p_ij denotes the sample correlation coefficient between x_i and x_j.

The proof of the asymptotic properties above is sketched in the Appendix.

5. Simulation Studies

Simulation studies were conducted to assess the finite sample performance of the proposed BAR regression procedure and compare it to other methods. In the study, for given p_n, the covariates Z were assumed to follow the multivariate normal distribution with mean zero, variance one, and the correlation between Z_j and Z_k being ρ^|j–k| with p = 0.5, j, k = 1,…, ρ_n. The true failure times T_i’s were generated from model (1) with Λ₀(t) = t or Λ₀(t) = log(t + 1). For the observed data, we considered both current status data and general interval-censored data, and for the generation of the former, we generated the observation times from the uniform distribution over (t₀, 3) and then compared them to the generated true failure times. Here we took t₀ = 0 or 1.5, giving the percentage of right-censored observations being approximately 40% and 20%, respectively. Note that for the situation, the censoring interval was given either from zero to the observation time if the true failure time was smaller than the observation time or from the observation time to infinity otherwise. For the generation of general interval-censored data, to mimic clinical studies, we assumed that there exist M equally spaced examination time points over $(0,\tau )$ and each subject was observed at each of these time points with probability 0.5. Then for subject i, the censoring interval (L_i,R_i] was determined by choosing L_i and R_i as the largest examination time point that is smaller than T_i and the smallest examination time point that is greater than T_i, respectively. The results given below are based on n = 100 or 300 with 500 replications.

Table 1 presents the results on the covariate selection based on current status data with p_n = 10 or 30, and Λ₀(t) = t. Here we set β_j= 0.5 for the first and last two components of the covariates and β_j = 0 for other components. The results given in Tables 2 and 3 were obtained based on the same set-ups but for general interval-censored data with Λ₀(t) = t or Λ₀(t) = log(t + 1), respectively. In all cases, _t was set to be 3, giving approximately 20% to 25% right-censored observations. Define the mean weighted squared error (MSE) to be ${({\widehat{\mathit{\beta }}}^{*}-{\mathit{\beta }}_0)}^{T}E(\mathit{Z}{Z}^{\prime })({\widehat{\mathit{\beta }}}^{*}-{\mathit{\beta }}_0)$. In all tables, we reported the median of MSE (MMSE), the standard deviation of MSE (SD), the averaged number of non-zero estimates of the parameters whose true values are not zero (TP), and the averaged number of non-zero estimates of parameters whose true values are zero (FP). It is easy to see that TP and FP provide the estimates of the true and false positive probabilities, respectively. For the results here, we took m, the degree of Bernstein polynomials, to be 3 and used the ridge regression estimate and 5-fold CV as initial estimates of the proposed algorithm and for the selection of the tuning parameters, respectively.

Table 1.

Results on covariate selection based on current status data data with Λ₀(t) = t

Method	MMSE(SD)	TP	FP	MMSE(SD)	TP	FP
n = 100 and pn = 10
	20% right-censored			40% right-censored
BAR	0.349 (0.744)	3.460	0.704	0.359 (0.536)	3.376	0.754
LASSO	0.296 (0.171)	3.804	1.656	0.282 (0.169)	3.822	1.736
ALASSO	0.345 (0.272)	3.408	1.100	0.350 (0.310)	3.310	1.074
MCP	0.472 (1.865)	3.094	0.704	0.473 (1.165)	3.054	0.746
SCAD	0.483 (0.700)	3.096	0.828	0.481 (0.553)	2.998	0.640
SELO	0.483 (1.692)	3.318	0.932	0.475 (1.371)	3.294	1.040
SICA	0.463 (1.562)	3.206	0.810	0.457 (1.352)	3.188	0.856
Oracle	0.203 (0.676)	4	0	0.189 (0.550)	4	0
n = 300 and pn = 10
	20% right-censored			40% right-censored
BAR	0.062 (0.078)	3.954	0.286	0.062 (0.082)	3.934	0.246
LASSO	0.150 (0.067)	4	1.360	0.127 (0.067)	3.998	1.476
ALASSO	0.120 (0.117)	3.928	0.550	0.108 (0.117)	3.934	0.542
MCP	0.079 (0.117)	3.934	0.406	0.071 (0.116)	3.930	0.406
SCAD	0.078 (0.118)	3.944	0.662	0.075 (0.118)	3.922	0.596
SELO	0.075 (0.111)	3.928	0.404	0.073 (0.112)	3.934	0.440
SICA	0.077 (0.114)	3.952	0.444	0.075 (0.109)	3.958	0.522
Oracle	0.053 (0.085)	4	0	0.046 (0.086)	4	0
n=300 and pn = 30
	20% right-censored			40% right-censored
BAR	0.074 (0.092)	3.876	0.330	0.072 (0.091)	3.882	0.378
LASSO	0.231 (0.081)	3.998	2.856	0.215 (0.081)	3.988	2.782
ALASSO	0.304 (0.210)	3.712	1.004	0.323 (0.210)	3.708	0.812
MCP	0.112 (0.196)	3.864	0.63	0.092 (0.174)	3.874	0.684
SCAD	0.216 (0.107)	3.83	0.984	0.227 (0.099)	3.832	1.016
SELO	0.093 (0.130)	3.864	0.530	0.085 (0.140)	3.864	0.634
SICA	0.104 (0.161)	3.834	0.640	0.086 (0.151)	3.858	0.716
Oracle	0.053 (0.077)	4	0	0.020 (0.047)	4	0

Table 2.

Results on covariate selection based on interval-censored data with Λ0(t) = t

Method	MMSE(SD)	TP	FP	MMSE(SD)	TP	FP
pn = 10	n = 100, M = 10			n = 100, M = 20
BAR	0.133 (0.131)	3.818	0.362	0.107 (0.114)	3.892	0.426
LASSO	0.182 (0.108)	3.966	1.370	0.146 (0.094)	3.976	1.446
LASSO WC	0.148 (0.094)	3.976	1.766	0.120 (0.083)	3.986	1.784
ALASSO	0.207 (0.166)	3.706	0.64	0.170 (0.142)	3.806	0.664
MCP	0.202 (0.194)	3.616	0.588	0.142 (0.148)	3.756	0.638
SCAD	0.319 (0.130)	3.780	0.596	0.258 (0.123)	3.852	0.672
SELO	0.180 (0.176)	3.728	0.588	0.138 (0.138)	3.808	0.548
SICA	0.184 (0.176)	3.660	0.460	0.133 (0.136)	3.772	0.424
Oracle	0.086 (0.108)	4	0	0.073 (0.089)	4	0
pn = 10	n = 300, M =10			n = 300, M = 20
BAR	0.030 (0.026)	4	0.176	0.025 (0.024)	4	0.220
LASSO	0.076 (0.041)	4	1.334	0.058 (0.034)	4	1.464
LASSO WC	0.071 (0.041)	4	1.434	0.055 (0.033)	4	1.476
ALASSO	0.056 (0.060)	3.992	0.404	0.039 (0.049)	3.998	0.468
MCP	0.029 (0.041)	3.994	0.398	0.024 (0.030)	4	0.380
SCAD	0.060 (0.048)	3.998	0.476	0.044 (0.037)	4	0.594
SELO	0.035 (0.040)	3.998	0.600	0.029 (0.032)	4	0.532
SICA	0.033 (0.039)	3.996	0.418	0.028 (0.031)	3.998	0.450
Oracle	0.024 (0.026)	4	0	0.020 (0.021)	4	0
pn = 30	n = 300, M = 10			n = 300, M = 20
BAR	0.034 (0.030)	4	0.286	0.027 (0.025)	4	0.332
LASSO	0.159 (0.062)	4	1.628	0.128 (0.054)	4	1.892
LASSO WC	0.152 (0.060)	4	1.666	0.115 (0.048)	4	1.918
ALASSO	0.138 (0.137)	3.950	0.770	0.142 (0.171)	3.968	0.488
MCP	0.028 (0.054)	3.966	0.578	0.023 (0.035)	3.996	0.658
SCAD	0.183 (0.083)	3.984	0.540	0.142 (0.069)	3.990	0.548
SELO	0.043 (0.047)	4	0.598	0.030 (0.041)	3.988	0.518
SICA	0.039 (0.045)	3.992	0.398	0.026 (0.037)	3.988	0.346
Oracle	0.024 (0.027)	4	0	0.019 (0.022)	4	0

Table 3.

Results on covariate selection based on interval-censored data with Λ0(t) = log(t + 1)

Method	MMSE(SD)	TP	FP	MMSE(SD)	TP	FP
pn = 10	n = 100, M = 10			n = 100, M = 20
BAR	0.172 (0.199)	3.756	0.476	0.133 (0.170)	3.852	0.516
LASSO	0.197 (0.101)	3.938	1.458	0.144 (0.085)	3.966	1.544
LASSO WC	0.164 (0.098)	3.962	1.872	0.145 (0.085)	3.972	1.758
ALASSO	0.206 (0.145)	3.728	1.060	0.153 (0.125)	3.812	1.114
MCP	0.249 (0.283)	3.526	0.626	0.209 (0.230)	3.684	0.690
SCAD	0.351 (0.157)	3.650	0.750	0.272 (0.138)	3.786	0.824
SELO	0.237 (0.270)	3.682	0.756	0.195 (0.226)	3.778	0.756
SICA	0.236 (0.263)	3.622	0.642	0.190 (0.213)	3.76	0.604
Oracle	0.092 (0.157)	4	0	0.083 (0.097)	4	0
pn = 10	n = 300, M =10			n = 300, M = 20
BAR	0.033 (0.036)	4	0.202	0.030 (0.034)	4	0.234
LASSO	0.070 (0.041)	4	1.246	0.048 (0.030)	4	1.422
LASSO WC	0.090 (0.048)	4	1.124	0.071 (0.040)	4	1.192
ALASSO	0.058 (0.062)	3.998	0.392	0.039 (0.043)	3.998	0.380
MCP	0.036 (0.048)	3.996	0.288	0.031 (0.045)	4	0.360
SCAD	0.073 (0.054)	4	0.416	0.060 (0.046)	4	0.434
SELO	0.047 (0.048)	4	0.588	0.040 (0.048)	4	0.582
SICA	0.041 (0.047)	4	0.442	0.036 (0.045)	4	0.446
Oracle	0.029 (0.037)	4	0	0.025 (0.035)	4	0
pn = 30	n = 300, M = 10			n = 300, M = 20
BAR	0.036 (0.037)	3.994	0.196	0.031 (0.031)	3.998	0.226
LASSO	0.128 (0.055)	4	2.324	0.096 (0.046)	4	2.274
LASSO WC	0.133 (0.056)	4	2.706	0.105 (0.051)	4	2.774
ALASSO	0.169 (0.159)	3.920	0.700	0.192 (0.176)	3.904	0.604
MCP	0.038 (0.056)	3.992	0.614	0.032 (0.041)	3.998	0.570
SCAD	0.169 (0.072)	3.986	0.560	0.129 (0.063)	3.998	0.612
SELO	0.033 (0.044)	4	0.490	0.039 (0.045)	4	0.384
SICA	0.048 (0.055)	3.994	0.452	0.040 (0.045)	4	0.434
Oracle	0.027 (0.036)	4	0	0.024 (0.030)	4	0

In addition to the performance of the proposed BAR regression procedure, for comparison, we also obtained the covariate selection results based on minimizing the penalized function (4) with replacing P(|β_j|; λ) by LASSO, ALASSO, MCP, SCAD, SELO or SICA, respectively. Moreover, the method proposed by Wu and Cook (2015), which is referred to as LASSO WC in the tables, was also implemented with the use of the LASSO penalty function for the case of general interval-censored data. In these tables, the oracle method refers to the approach that only includes the covariates whose coefficients are not zero. In other words, for the situation, the truth was assumed to be known and no variable selection was performed. One can see from Tables 1–3 that the BAR approach gave the smallest MMSE and FP in most cases among the methods considered. Also the BAR approach generally yielded the largest TP among all except the procedure based on the LASSO penalty as expected. For all methods, the performance did not seem to depend on the cumulative baseline hazard function and the number of the pre-specified observation times. We also considered other set-ups and obtained similar results.

Tables 4 and 5 give some results on assessing the grouping effects of the methods considered above with Table 4 corresponding to current status data and Table 5 general interval-censored data. Here both types of censored data were generated in the same way as above with ρ _n = 10, n = 300, and the true values of β₁ and β₂ being 0.5, and β₁₀ being 0.8, and the other β_j’s being 0. Also the covariates were grouped into four groups as (Z₁, Z₂₎, (Z₃, Z₄, Z₅), (Z₆, Z₇, Z₈) and (Z₉, Z₁₀), and the covariates in the first two groups were generated from the normal distribution with mean zero and Cov(Z_i, Z_j) = ρ ^|i−j| with ρ = 0.8, 0.9 or 0.95, where i, j ϵ(1,2) or (3, 4, 5). The covariates within the last two groups were generated from the correlated Bernoulli distribution with E(Z_i) = 0.5 and Cov(Z_i, Z_j) = ρ^|i−j|, where i, j ϵ (6, 7, 8) or (9,10), and the covariates in different groups were assumed to be independent. Here in addition to MMSE, TP and FP, we also calculated the statistic

$$G=0.2\times G_1+0.3\times G_2+0.3\times G_3+0.2\times G_4,$$

measuring the grouping effect. In the above, G₁ and G4 denote the percentages of the first and last two components of the estimated regression coefficients being both nonzero, respectively, and G₂ and G₃ denote the percentages of the three components of the estimated regression coefficients corresponding to the covariates in the second and third group all being zero, respectively. The results suggest that the proposed BAR approach generally gave better performance than the other methods on the covariate selection as before and also clearly had higher G values or much better grouping effects than the other methods.

Table 4.

Results on grouping effects based on current status data

Method	MMSE (SD)	TP	FP	G
ρ = 0.8
BAR	0.172 (0.238)	3.684	0.408	0.823
LASSO	0.297 (0.216)	3.966	1.698	0.606
ALASSO	0.311 (0.259)	3.574	0.712	0.732
MCP	0.277 (0.306)	3.300	0.598	0.693
SCAD	0.269 (0.305)	3.506	0.788	0.686
SELO	0.280 (0.311)	3.480	0.802	0.681
SICA	0.273 (0.307)	3.458	0.756	0.685
Oracle	0.106 (0.224)	4	0	1
ρ = 0.9
BAR	0.168 (0.313)	3.446	0.452	0.756
LASSO	0.211 (0.201)	3.900	1.760	0.564
ALASSO	0.261 (0.228)	3.224	0.858	0.628
MCP	0.265 (0.383)	2.912	0.866	0.557
SCAD	0.244 (0.363)	2.956	0.910	0.537
SELO	0.261 (0.371)	3.008	1.020	0.523
SICA	0.276 (0.365)	2.894	0.878	0.536
Oracle	0.099 (0.282)	4	0	1
ρ = 0.95
BAR	0.134 (0.237)	3.014	0.352	0.697
LASSO	0.200 (0.187)	3.750	1.830	0.539
ALASSO	0.191 (0.216)	2.930	1.274	0.473
MCP	0.203 (0.316)	2.614	0.814	0.509
SCAD	0.211 (0.320)	2.602	1.054	0.438
SELO	0.223 (0.289)	2.596	1.020	0.438
SICA	0.225 (0.338)	2.692	1.218	0.423
Oracle	0.097 (0.242)	4	0	1

Table 5.

Results on grouping effects based on interval-censored data

Method	MMSE (SD)	TP	FP	G
ρ = 0.8
BAR	0.061 (0.075)	3.938	0.164	0.940
LASSO	0.162 (0.121)	3.998	1.282	0.695
ALASSO	0.108 (0.126)	3.940	0.598	0.833
MCP	0.081 (0.107)	3.830	0.530	0.811
SCAD	0.068 (0.115)	3.872	0.770	0.773
SELO	0.079 (0.096)	3.894	0.508	0.833
SICA	0.079 (0.102)	3.854	0.460	0.837
Oracle	0.048 (0.063)	4	0	1
ρ = 0.9
BAR	0.063 (0.083)	3.804	0.276	0.882
LASSO	0.093 (0.088)	3.990	2.342	0.526
ALASSO	0.100 (0.118)	3.744	0.634	0.780
MCP	0.104 (0.106)	3.388	0.686	0.680
SCAD	0.090 (0.100)	3.536	0.744	0.703
SELO	0.106 (0.104)	3.298	0.480	0.721
SICA	0.106 (0.099)	3.424	0.636	0.708
Oracle	0.043 (0.069)	4	0	1
ρ = 0.95
BAR	0.067 (0.084)	3.516	0.412	0.784
LASSO	0.083 (0.081)	3.938	2.074	0.533
ALASSO	0.092 (0.098)	3.442	0.878	0.659
MCP	0.108 (0.093)	2.986	1.018	0.535
SCAD	0.107 (0.090)	3.070	1.086	0.534
SELO	0.109 (0.094)	2.988	0.944	0.557
SICA	0.111 (0.092)	2.902	0.802	0.572
Oracle	0.042 (0.069)	4	0	1

6. An Application

In this section, we apply the proposed BAR regression procedure to a set of interval-censored data on childhood mortality in Nigeria collected in the 2003 Nigeria Demographic and Health Survey (Kneib, 2006). In the data, the death time was observed exactly if the death occurs within the first two months of birth and after that, the information on the mortality was collected through interviewing the mothers of the childhood. Thus only interval-censored data were observed on the death time in general. In the study, the covariates on which the information was collected include the age of the child’s mother when giving birth, the mother’s body mass index, whether the baby was delivered in a hospital, the gender of the child, whether the mother received higher education, and whether the family lived in urban. One of the main goals of the study is to determine the covariates or factors that had significant influence on the children’s mortality in Nigeria. For the analysis below, we will focus on 5730 children for whom the information about all of the covariates above is available.

To apply the proposed BAR regression procedure, let AGE and BMI denote the age and body mass index of the mother at birth, and define HOSP = 1 if the baby was delivered in a hospital and 0 otherwise, GENDER = 1 if the baby was male and 0, EDU = 1 if the mother received higher education and 0 otherwise, and URBAN = 1 if the family lived in urban and 0 otherwise. For the analysis, we performed the standardization on the two continuous covariates AGE and BMI and the analysis results given by the proposed BAR regression procedure are presented in Table 6. For the results here, we used m = 3 or 12 for the degree of Bernstein Polynomials and obtained the standard errors of the estimates, given in the parentheses, by using the bootstrap procedure with 100 bootstrap samples randomly drawn with replacement from the observed data. For the selection of the tuning parameters and the initial estimates, as in the simulation study, we used the 5-fold cross-validation and the ridge regression estimate, respectively.

Table 6.

Analysis results of children’s mortality data

Method	AGE	BMI	HOSP	GENDER	EDU	URBAN
m = 3
BAR	-	-	−0.3516(0.1273)	-	−0.2071(0.1235)	−0.3052(0.1104)
LASSO	-	-	−0.3016(0.1054)	0.02 32(0.0595)	−0.1837(0.0916)	−0.2526(0.0941)
ALASSO	-	-	−0.3451(0.1060)	-	−0.1938(0.0940)	−0.2924(0.0959)
MCP	-	-	−0.3556(0.1213)	-	−0.2240(0.1316)	−0.2932(0.0996)
SCAD	-	-	−0.3563(0.1209)	-	−0.2259(0.1324)	−0.3189(0.0997)
SELO	-	-	−0.3549(0.1210)	-	−0.2185(0.1257)	−0.3144(0.1017)
SICA	-	-	−0.3559(0.1232)		−0.2209(0.1308)	−0.3163(0.1018)
Forward (0.05)	-	-	−0.3561(0.1065)	-	−0.2251(0.0986)	−0.3185(0.0970)
Forward (0.01)	-	-	−0.4619(0.0935)	-	-	−0.3464(0.0977)
Best Subset	-	-	−0.3 561(0.1065)	-	−0.2251(0.0986)	−0.3185(0.0970)
m = 12
BAR	-	-	−0.3507(0.1266)	-	−0.2061(0.1209)	−0.3004(0.1067)
LASSO	-	-	−0.2957(0.1033)	0.00 74(0.0562)	−0.1829(0.0948)	−0.2443(0.0946)
ALASSO	-	-	−0.3271(0.1003)	-	−0.1442(0.0852)	−0.2455(0.0939)
MCP	-	-	−0.3582(0.1196)	-	−0.2339(0.1257)	−0.3205(0.0993)
SCAD	-	-	−0.3556(0.1137)	-	−0.2259(0.1120)	−0.3152(0.1005)
SELO	-	-	−0.3552(0.1209)	-	−0.2218(0.1201)	−0.3129(0.1009)
SICA	-	-	−0.3521(0.1246)	-	−0.2118(0.1251)	−0.3028(0.1012)
Forward (0.05)	-	-	−0.3552(0.1055)	-	−0.2243(0.0975)	−0.3140(0.0959)
Forward (0.01)	-	-	−0.4602(0.0926)	-	-	−0.3414(0.0965)
Best Subset	-	-	−0.3552(0.1055)	-	−0.2243(0.0975)	−0.3140(0.0959)

In Table 6, as in the simulation study and for comparison, we also include the analysis results obtained by applying the other penalized procedures discussed there. First one can can see from the table that on the covariate selection, all penalized estimation methods gave consistent results and the results are also consistent with respect to the degree m of Bernstein Polynomials. They suggest that the mother’s age and body mass index and the child’s gender had no relationship with or significant influence on the child’s mortality rate except using the LASSO-based method. Although the latter selected the child’s gender as a non-zero covariate, the estimation suggests that it did not have any significant effect on the child’s mortality or death rate. Based on the estimation results, all methods indicate that the children delivered in a hospital or whose family lived in urban had significantly lower mortality risk. Also it seems that the mother’s education had some mild effect on the mortality and the children who had the mother with a higher education may have lower mortality risk too. For the analysis here, we also tried other m values and obtained similar results. To further see this, Figure 1 presents the obtained estimates of the cumulative baseline hazard function Λ₀(t) with m = 3 and 12 and they seem to be close to each other.

Figure 1.

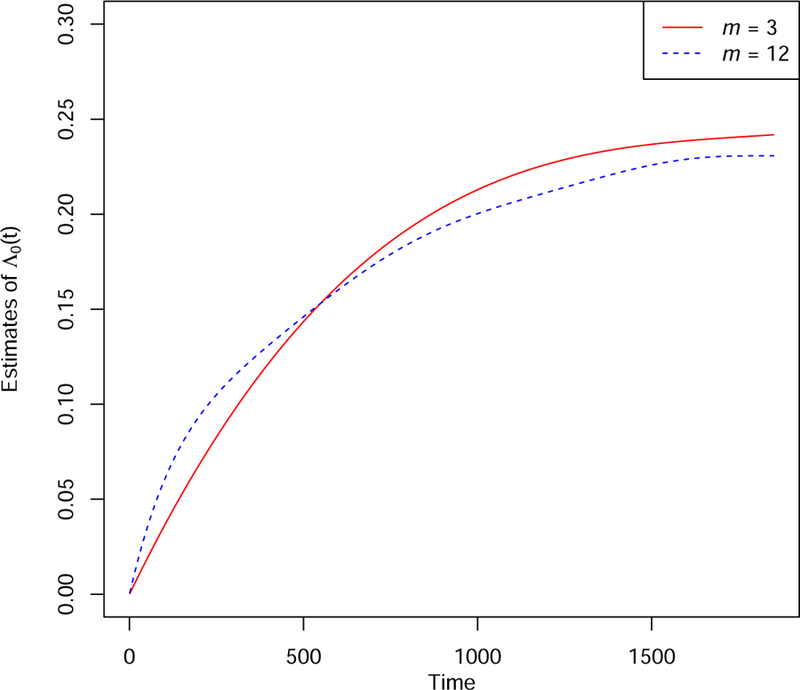
Estimates of the cumulative baseline hazard function Λ₀(t)

By following the suggestion from a reviewer, we also performed the covariate selection by using the two commonly used approaches that do not impose the penalty: the forward variable selection and the best subset selection, and include the obtained results in Table 6. Here for the former, we considered the two inclusion levels of 0.01 and 0.05 and for the latter, the AIC criterion was used. One can see that as expected, the AIC-based best subset selection gave similar results but the results yielded by the forward variable selection depend on the inclusion level. Although the results based on the inclusion level of 0.05 are similar to those given above, the forward variable selection with the inclusion level of 0.01 indicates that the covariate EDU did not seem to have any effect on the mortality of the children. Note that the proposed BAR procedure does not require the subjective selection of an inclusion level.

7. Discussion and Concluding Remarks

This paper discussed simultaneous covariate selection and estimation of covariate effects for the PH model with interval-censored data. As mentioned above, interval-censored data often occur in many fields and include right-censored data as special cases. Although many statistical procedures have been developed in the literature for their analysis (Sun et al., 2015; Zhang et al., 2010), only limited research exists for covariate selection (Scolas et al., 2016; Wu and Cook, 2015) due to the special data structures and the difficulties involved. To address the problem, we presented a BAR regression estimation procedure that can allow one to perform both parameter estimation and variable selection simultaneously. In addition, unlike some of the existing methods, the oracle property of the proposed approach was established along with the clustering effect for the situation when covariates are highly correlated. Furthermore the numerical studies indicated that it usually has better performance than the existing procedures with and without imposing the penalty.

In the proposed approach, we have employed Bernstein polynomials to approximate the underlying unknown function. As mentioned above, the idea discussed above still applies if one prefers to use other approximations such as the piecewise constant function as in Wu and Cook (2015). However, unlike the latter, the Bernstein polynomial approximation is a continuous approximation and has some nice properties including differentiability. In consequence, the resulting log-likelihood function, its gradients and Hessian matrix all have relatively simpler forms, and the resulting method can be easily implemented. In particular, as seen above, it allows the development of a much faster and simpler algorithm for the implementation of the method than the EM algorithm developed in Wu and Cook (2015). Also it allows the establishment of the asymptotic properties of the resulting method including the oracle property. In addition, the proposed method can provide a better and more natural way than that in Wu and Cook (2015) for the estimation of a survival function, which is often of interest in medical studies among others.

It should be noted that although the algorithm given above is quite simpler, the proposed procedure could be slower than the other variable selection procedures discussed in the simulation study due to the need for the selection of two tuning parameters. To improve this, we conducted some simulation studies and they suggested that actually one can fix the tuning parameter ξ_n to be a constant between 1 and 1500 and focus only on the selection of the tuning parameter λ_n by the cross-validation. The resulting simplified BAR procedure gives similar performance to the original BAR procedure on the variable selection but is faster than all of the other procedures discussed in the simulation study.

For the selection of the two tuning parameters in the proposed method, we have used the C-fold cross-validation. It is apparent that the method is still valid if one instead employs other criterion such as the generalized C-fold cross-validation defined as

$$GCV({\xi }_n,{\lambda }_n)=\sum _{c=1}^C\left[\frac{l_n({\widehat{\mathit{\beta }}}^{(-c)},{\widehat{\varphi }}^{(-c)})}{n{(1-k^{(-c)}/n)}^2}-\frac{l_n^{(-c)}({\widehat{\mathit{\beta }}}^{(-c)},{\widehat{\varphi }}^{(-c)})}{n^{(-c)}{(1-k^{(-c)}/n^{(-c)})}^2}\right]$$

using the notation defined for GCV(ξ_n, λ_n) (Bradic et al., 2011). Here n^(−c) denotes the size of the total sample without c^th part and k^(−c) the number of the non-zero β estimates based on the total sample without c^th part. Therefore, the optimal ξ_n and λ_n are the values that minimize GCV(ξ_n, λ_n). Bayesian information criterion is another widely used criterion based on

$$BIC({\xi }_n,{\lambda }_n)=-2l_n(\widehat{\mathit{\beta }},\widehat{\varphi })+q_n\times \log (n)$$

with q_n denoting the number of the non-zero β estimates. Note that this criterion can be more computationally efficient than the two criteria mentioned above as it is unnecessary to partition the data into several parts. We performed some simulation studies for comparing the three criteria, and they suggested that the C-fold cross-validation is generally conservative in the sense that the other two tend to throw away some important covariates.

There exist several directions for future research. One is that in the preceding sections, we have focused on model (1) and it is apparent that sometimes a different model may be preferred or more appropriate. In other words, it would be useful to generalize the proposed method to the situation where the failure time of interest follows some other models such as the additive hazards model or semiparametric transformation model. In the proposed method, it has been assumed that the censoring mechanism that generates the censoring intervals is non-informative or independent of the failure time of interest. It is clear that this may not hold in some situations (Ma et al., 2015; Sun, 2006) and in this case, the proposed method would not be valid or could give biased results. In other words, one needs to modify the proposed BAR procedure or develop some methods that allow for or can take into account the informative censoring.

In the preceding sections, it has been supposed that the dimension of covariates p_n can diverge to infinity but is smaller than the sample size n. It is apparent that there may exist some situations where p_n is larger than n, and one such example is genetic or biomarker studies where there may exist hundreds of thousands genes or biomarkers. For the situation, as mentioned above, some literature has been developed when one observes right-censored data but it is quite difficult to directly generalize these existing procedures to interval-censored data. In other words, more research is clearly needed for the situation. Note that although the idea described above may still apply, the implementation procedure given above would not work due to the irregularity of some involved matrices. That is, one needs to develop some different or new implementation procedures or algorithms as well as working out some other issues.

Appendix: Asymptotic Properties of ${\widehat{\mathit{\beta }}}^{*}$

In this appendix, we will sketch the proofs of the asymptotic properties of the proposed BAR estimator ${\widehat{\mathit{\beta }}}^{*}$ described in Theorems 1 and 2. For this, define

$$\left(\begin{array}{cc}{\mathit{\alpha }}^{*}& (\mathit{\beta })\\ {\mathit{\gamma }}^{*}& (\mathit{\beta })\end{array}\right)\equiv g(\mathit{\beta })={({\text{Ω}}_n+{\lambda }_{n}D(\mathit{\beta }))}^{-1}{\mathbf{\text{v}}}_n,$$ (A.1)

and partition the matrix (n⁻¹Ω_n)⁻¹ into

$${\left(n^{-1}{\mathbf{\Omega }}_n\right)}^{-1}=\left(\begin{array}{cc}A& B\\ B^{\prime }& G\end{array}\right),$$

where A is a q_n x q_n matrix. Note that since Ω_n is nonsingular, it follows by multiplying ${\mathbf{\Omega }}_n^{-1}({\mathbf{\Omega }}_n+{\lambda }_n\mathit{D}(\mathit{\beta }))$ and subtracting β₀ on both sides of (A.1) that we have

$$\left(\begin{array}{c}{\mathit{\alpha }}^{*}-{\mathit{\beta }}_{01}\\ {\mathit{\gamma }}^{*}\end{array}\right)+\frac{{\lambda }_n}{n}\left(\begin{array}{c}A{\mathit{D}}_1({\mathit{\beta }}_1){\mathit{\alpha }}^{*}+B{\mathit{D}}_2({\mathit{\beta }}_2){\mathit{\gamma }}^{*}\\ B^{\prime }{\mathit{D}}_1({\mathit{\beta }}_1){\mathit{\alpha }}^{*}+G{\mathit{D}}_2({\mathit{\beta }}_2){\mathit{\gamma }}^{*}\end{array}\right)=\widehat{\mathit{b}}-{\mathit{\beta }}_0,$$ (A.2)

where a $\widehat{\mathit{b}}={\mathbf{\Omega }}_n^{-1}{\text{v}}_n,{\mathit{D}}_1({\mathit{\beta }}_1)=\text{diag(}{\mathit{\beta }}_1^{-2}\text{,}\dots \text{,}{\mathit{\beta }}_{q_n}^{-2}\text{)}$ and ${\mathit{D}}_2({\mathit{\beta }}_2)=\text{diag}({\mathit{\beta }}_{q_n+1}^{-2}\text{,}\dots \text{,}{\mathit{\beta }}_{p_n}^{-2})$.

To prove Theorem 1, we need the following two lemmas.

Lemma 1. Let { δ_n } be a sequence of positive real numbers satisfying δ_n →∞ and ${\delta }_n^2{p}_n/{\lambda }_n\to 0$. Define $H_n\equiv \{\mathit{\beta }=({\mathit{\beta }}_1^{\text{'}},{\mathit{\beta }}_2^{\text{'}}{)}^{\prime }:{\mathit{\beta }}_1\in {[1/K_0,K_0]}^{q_n},\Vert {\mathit{\beta }}_2\Vert \le {\delta }_n\sqrt{p_n/n}\}$, where K₀ > 1 is a constant such that ${\mathit{\beta }}_{01}\in {[1/K_0,K_0]}^{q_n}$. Then under the regular conditions (C1)-(C8) and with probability tending to 1, we have

1. $\underset{\mathit{\beta }\in H_n}{\sup }\frac{\Vert {\mathit{\gamma }}^{*}(\mathit{\beta })\Vert }{\Vert {\mathit{\beta }}_2\Vert }<\frac{1}{c_0}$ for some constant c₀ > 1;

2. g(·) is a mapping from H_n to itself.

Proof. First from the formula (7), it is easy to see that $\widehat{\mathit{b}}$ is equal to $g(\tilde{\mathit{\beta }})$ with λ_n = 0, which is equivalent to the maximizer of the sieve log-likelihood function. By using arguments similar to those in Zhang et al. (2010), one can obtain that $\Vert \widehat{\mathit{b}}-{\mathit{\beta }}_0\Vert =O(\sqrt{p_n/n})$, and hence it follows from (A.2) that

$$\underset{\mathit{\beta }\in H_n}{\sup }\Vert {\mathit{\gamma }}^{*}+\frac{{\lambda }_n}{n}{B}^{\prime }{\mathit{D}}_1({\mathit{\beta }}_1){\mathit{\alpha }}^{*}+\frac{{\lambda }_n}{n}G{\mathit{D}}_2({\mathit{\beta }}_2){\mathit{\gamma }}^{*}\Vert =O_p(\sqrt{p_n/n}).$$

By condition (C5) and the fact that

$$\Vert B{B}^{\prime }\Vert -\Vert A^2\Vert \le \Vert B{B}^{\prime }+A^2\Vert \le \Vert {(n^{-1}{\mathbf{\Omega }}_n)}^{-2}\Vert <c^2,$$

we can derive $\Vert B\Vert \le \sqrt{2c}$. Furthermore, based on conditions (C5) and (C6) and note that ${\mathit{\beta }}_1\in {[1/K_0,K_0]}^{q_n}$ and $\Vert {\mathit{\alpha }}^{*}\Vert \le \Vert g(\mathit{\beta })\Vert \le \Vert \widehat{\mathit{b}}\Vert =O_p(\sqrt{p_n})$, we have

$$\underset{\mathit{\beta }\in H_n}{\sup }\Vert \frac{{\lambda }_n}{n}{B}^{\prime }{\mathit{D}}_1({\mathit{\beta }}_1){\mathit{\alpha }}^{*}\Vert =o_{p.}(\sqrt{p_n/n}).$$ (A.3)

Since λ_min (G)>c⁻¹, it follows from (A.2) that, with probability tending to 1,

$$c^{-1}\Vert \frac{{\lambda }_n}{n}{\mathit{D}}_2({\mathit{\beta }}_2){\mathit{\gamma }}^{*}\Vert -\Vert {\mathit{\gamma }}^{*}\Vert \le \underset{\mathit{\beta }\in H_n}{\sup }\Vert {\mathit{\gamma }}^{*}+\frac{{\lambda }_n}{n}G{\mathit{D}}_2({\mathit{\beta }}_2){\mathit{\gamma }}^{*}\Vert =O_p(\sqrt{\frac{p_n}{n}})\le {\delta }_n\sqrt{\frac{p_n}{n}}.$$ (A.4)

Let $m_{{\mathit{\gamma }}^{*}/{\mathit{\beta }}_2}=({\gamma }_1^{*}/{\mathit{\beta }}_{q_n+1},{\gamma }_2^{*}/{\mathit{\beta }}_{q_n+2},\dots ,{\gamma }_{p_n-q_n}^{*}/{\mathit{\beta }}_{p_n}{)}^{\prime }$. It then follows from the Cauchy-Schwarz inequality and the assumption $\Vert {\mathit{\beta }}_2\Vert \le {\delta }_n\sqrt{p_n/n}$ that

$$\Vert m_{{\gamma }^{*}/{\mathit{\beta }}_2}\Vert \le \Vert {\mathit{D}}_2({\mathit{\beta }}_2){\mathit{\gamma }}^{*}\Vert {\delta }_n\sqrt{p_n/n},$$

and

$$\Vert {\mathit{\gamma }}^{*}\Vert =\Vert {({\mathit{D}}_2({\mathit{\beta }}_2))}^{-1/2}{m}_{\gamma */{\mathit{\beta }}_2}\Vert \le \Vert m_{{\gamma }^{*}/{\mathit{\beta }}_2}\Vert \cdot \Vert {\mathit{\beta }}_2\Vert \le \Vert m_{{\mathit{\gamma }}^{*}/{\mathit{\beta }}_2}\Vert {\delta }_n\sqrt{p_n/n}$$ (A.5)

for all large n. Thus from (A.4) and (A.5), we have the following inequality

$$\frac{{\lambda }_n}{nC}\frac{\sqrt{n}}{{\delta }_n\sqrt{p_n}}\Vert m_{{\mathit{\gamma }}^{*}/{\mathit{\beta }}_2}\Vert -\Vert m_{\mathit{\gamma }\ast /{\mathit{\beta }}_2}\Vert \frac{{\delta }_n\sqrt{p_n}}{\sqrt{n}}\le \frac{{\delta }_n\sqrt{p_n}}{\sqrt{n}}.$$

Immediately from $p_n{\delta }_n^2/{\lambda }_n\to 0$, we have

$$\Vert m_{{\mathit{\gamma }}^{*}/{\mathit{\beta }}_2}\Vert \le \frac{1}{\frac{{\lambda }_n}{p_n{\delta }_n^{2}c}-1}<\frac{1}{c_0},(c_0>1)$$ (A.6)

with probability tending to one. Hence it follows from (A.5) and (A.6) that

$$\Vert {\mathit{\gamma }}^{*}\Vert <\Vert {\mathit{\beta }}_2\Vert \le {\delta }_n\sqrt{p_n/n}\to 0\text{\hspace{0.17em}\hspace{0.17em}as\hspace{0.17em}\hspace{0.17em}}n\to \infty ,$$ (A.7)

Which implies that conclusion (i) holds.

To prove (ii), we only need to verify that ${\mathit{\alpha }}^{*}\in {[1/K_0,K_0]}^{q_n}$ with probability tending ti 1 since (A.7) has showed that $\Vert {\mathit{\gamma }}^{*}\Vert \le {\delta }_n\sqrt{p_n/n}$ with probability tending to 1 Analogously, given condition (C5), ${\mathit{\beta }}_1\in {[1/K_0,K_0]}^{q_n}$ and $\Vert {\mathit{\alpha }}^{*}\Vert <O_P(\sqrt{p_n})$, we have

$$\underset{\mathit{\beta }\in H_n}{\sup }\Vert \frac{{\lambda }_n}{n}A{\mathit{D}}_1({\mathit{\beta }}_1){\mathit{\alpha }}^{*}\Vert =O_p(\sqrt{p_n/n}).$$

Then from (A.2), we have

$$\underset{\mathit{\beta }\in H_n}{\sup }\Vert {\mathit{\alpha }}^{*}-{\mathit{\beta }}_{01}+\frac{{\lambda }_n}{n}B{\mathit{D}}_2({\mathit{\beta }}_2){\mathit{\gamma }}^{*}\Vert =O_p(\sqrt{p_n/n})\le {\delta }_n\sqrt{p_n/n},$$ (A.8)

and according to (A.4) and (A.7), we have $\Vert \frac{{\lambda }_n}{n}{\mathit{D}}_2({\mathit{\beta }}_2){\gamma }^{*}\Vert \le 2c{\delta }_n\sqrt{p_n/n}$. Hence based on condition (C5), we know that as n → ∞ and with probability tending to one,

$$\underset{\mathit{\beta }\in H_n}{\sup }\Vert \frac{{\lambda }_n}{n}B{\mathit{D}}_2({\mathit{\beta }}_2){\mathit{\gamma }}^{*}\Vert \le \frac{{\lambda }_n}{n}\Vert B\Vert \underset{\mathit{\beta }\in H_n}{\sup }\Vert {\mathit{D}}_2({\mathit{\beta }}_2){\mathit{\gamma }}^{*}\Vert \le \frac{2\sqrt{2}{c}^2{\delta }_n\sqrt{p_n}}{\sqrt{n}}.$$ (A.9)

Therefore from (A.8) and (A.9), we can get

$$\underset{\mathit{\beta }\in H_n}{\sup }\Vert {\mathit{\alpha }}^{*}-{\mathit{\beta }}_{01}\Vert \le \frac{(2\sqrt{2}{c}^2+1){\delta }_n\sqrt{p_n}}{\sqrt{n}}\to 0$$

with probability tending to one, which implies that for any $\in >0,P(\Vert {\mathit{\alpha }}^{*}-{\mathit{\beta }}_{01}\Vert \le \in )\to 1$. Thus it follows from ${\mathit{\beta }}_{01}\in {[1/K_0,K_0]}^{q_n}$ that ${\mathit{\alpha }}^{*}\in {[1/K_0,K_0]}^{q_n}$ holds for large n, which implies that conclusion (ii) holds. This completes the proof.

Lemma 2. Under the regular conditions (C1)–(C8) and with probability tending to 1, the equation $\mathit{\alpha }={({\mathbf{\Omega }}_n^{(1)}+{\lambda }_n{\mathit{D}}_1(\mathit{\alpha }))}^{-1}{\text{v}}_n^{(1)}$ has a unique fixed-point ${\widehat{\mathit{\alpha }}}^{*}$ in the domain ${[1/K_0,K_0]}^{q_n}$.

Proof. Define

$$f(\mathit{\alpha })=(f_1(\mathit{\alpha }),f_2(\mathit{\alpha }),\dots ,f_{q_n}(\mathit{\alpha }){)}^{\prime }\equiv {\left({\mathbf{\Omega }}_n^{(1)}+{\lambda }_n{\mathit{D}}_1(\alpha )\right)}^{-1}{\text{v}}_n^{(1)},$$ (A.10)

where $\mathit{\alpha }=({\alpha }_1,\dots ,{\alpha }_{q_n}{)}^{\prime }$. By multiplying ${\left({\mathbf{\Omega }}_n^{\left(1\right)}\right)}^{-1}\left({\mathbf{\Omega }}_n^{\left(1\right)}+{\lambda }_n{\mathit{D}}_1\left(\mathit{\alpha }\right)\right)$ and then minus β₀₁ on both sides of (A.10), we have

$$f(\mathit{\alpha })-{\mathit{\beta }}_{01}+{\lambda }_n{({\mathbf{\Omega }}_n^{(1)})}^{-1}{\mathit{D}}_1(\alpha )f(\mathit{\alpha })={({\mathbf{\Omega }}_n^{(1)})}^{-1}{\text{v}}_n^{(1)}-{\mathit{\beta }}_{01}={({\mathit{X}}_1^{\text{'}}{\mathit{X}}_1)}^{-1}{\mathit{X}}_1^{\text{'}}\in ,$$

where X₁ is the first q_n columns of X, and ε = y − Xβ. Therefore,

$$\underset{\alpha \in {[1/K_0,K_0]}^{q_n}}{\sup }\Vert f(\mathit{\alpha })-{\mathit{\beta }}_{01}+{\lambda }_n{({\mathbf{\Omega }}_n^{(1)})}^{-1}{\mathit{D}}_1(\alpha )f(\mathit{\alpha })\Vert =O_p(\sqrt{q_n/n}).$$

Similar to (A.3), it can be shown that

$$\underset{\alpha \in {[1/K_0,K_0]}^{q_n}}{\sup }\Vert \frac{{\lambda }_n}{n}{(n^{-1}{\mathbf{\Omega }}_n^{(1)})}^{-1}{\mathit{D}}_1(\alpha )f(\mathit{\alpha })\Vert =O_p(\sqrt{q_n/n}).$$

Thus,

$$\underset{\alpha \in {[1/K_0,K_0]}^{q_n}}{\sup }\Vert f(\mathit{\alpha })-{\mathit{\beta }}_{01}\Vert \le {\delta }_n\sqrt{q_n/n}\to 0,$$

which implies that $f(\mathit{\alpha })\in {[1/K_0,K_0]}^{q_n}$ with probability tending to one. That is, f(α) is a mapping from ${[1/K_0,K_0]}^{q_n}$ to itself.

Also by multiplying ${\mathbf{\Omega }}_n^{(1)}+{\lambda }_n{\mathit{D}}_1(\mathit{\alpha })$ and taking derivative with respect to α on both sides of (A.10), we have

$$(\frac{1}{n}{\mathbf{\Omega }}_n^{(1)}+\frac{{\lambda }_n}{n}{\mathit{D}}_1(\mathit{\alpha }))\dot{f}(\mathit{\alpha })+\frac{{\lambda }_n}{n}\text{diag(}\frac{-2f_1(\alpha )}{{\alpha }_1^3}\text{,}\dots \text{,}\frac{-2f_{q_n}(\alpha )}{{\alpha }_{q_n}^3}\text{)=0,}$$

Where $\dot{f}(\mathit{\alpha })=\partial f(\mathit{\alpha })/\partial {\mathit{\alpha }}^{\prime }$. Then

$$\underset{\alpha \in {[1/K_0,K_0]}^{q_n}}{\sup }\Vert (\frac{1}{n}{\mathbf{\Omega }}_n^{(1)}+\frac{{\lambda }_n}{n}{\mathit{D}}_1(\mathit{\alpha }))\dot{f}(\mathit{\alpha })\Vert =\underset{\alpha \in {[1/K_0,K_0]}^{q_n}}{\sup }\frac{2{\lambda }_n}{n}\Vert \text{diag(}\frac{f_1(\mathit{\alpha })}{{\alpha }_1^3}\text{,}\dots \text{,}\frac{f_q(\mathit{\alpha })}{{\alpha }_{q_n}^3}\text{)}\Vert =o_p(1).$$

According to condition (C6) and the fact that $\mathit{\alpha }\in {[1/K_0,K_0]}^{q_n}$, we can derive

$$\Vert (\frac{1}{n}{\mathbf{\Omega }}_n^{(1)}+\frac{{\lambda }_n}{n}{\mathit{D}}_1(\mathit{\alpha }))\dot{f}(\mathit{\alpha })\Vert \ge \Vert \frac{1}{n}{\mathbf{\Omega }}_n^{(1)}\dot{f}(\mathit{\alpha })\Vert -\Vert \frac{{\lambda }_n}{n}{\mathit{D}}_1(\mathit{\alpha })\dot{f}(\mathit{\alpha })\Vert \ge (\frac{1}{c}-\frac{{\lambda }_n}{n}{K}_0^2)\Vert \dot{f}(\mathit{\alpha })\Vert .$$

Thus we have that ${\sup }_{\mathit{\alpha }\in {[1/K_0,K_0]}^{q_n}}\Vert \dot{f}(\mathit{\alpha })\Vert \to 0$, which implies that f(·) is a contraction mapping from ${[1/K_0,K_0]}^{q_n}$ to itself with probability tending to one. Hence according to the contraction mapping theorem, there exists one unique fixed-point ${\widehat{\mathit{\alpha }}}^{*}\in {[1/K_0,K_0]}^{q_n}$ such that

$${\widehat{\mathit{\alpha }}}^{*}={({\mathbf{\Omega }}_n^{(1)}+{\lambda }_n{\mathit{D}}_1({\widehat{\mathit{\alpha }}}^{*}))}^{-1}{\text{v}}_n^{(1)}.$$ (A.11)

Proof of Theorem 1. First consider conclusion (1). According to the definitions of ${\widehat{\mathit{\beta }}}^{\ast }$ and ${\widehat{\mathit{\beta }}}_2^{(k)}$, it follows from (A.7) that

$${\widehat{\mathit{\beta }}}_2^{*}\equiv \underset{k\to \infty }{\lim }{\widehat{\mathit{\beta }}}_2^{(k)}=0$$ (A.12)

holds with the probability tending to 1.

Next we will show that $P({\widehat{\mathit{\beta }}}_1^{*}={\widehat{\mathit{\alpha }}}^{*})\to 1$. For this consider (A.2) and define ${\mathit{\gamma }}^{*}=0$ if β₂=0. Note that for any fixed n, from (A.2), we have

$$\underset{{\mathit{\beta }}_2\to 0}{\lim }{\mathit{\gamma }}^{*}(\mathit{\beta })=0.$$

Furthermore, by multiplying (Ω_n + λ_nD(β)) on both sides of (A.1), we can get

$$\underset{{\mathit{\beta }}_2\to 0}{\lim }{\mathit{\alpha }}^{*}(\mathit{\beta })={({\mathbf{\Omega }}_n^{(1)}+{\lambda }_n{\mathit{D}}_1({\mathit{\beta }}_1))}^{-1}{\text{v}}_n^{(1)}=f({\mathit{\beta }}_1).$$ (A.13)

By combining (A.12) and (A.13), it follows that

$${\eta }_k\equiv \underset{{\mathit{\beta }}_1\in {[1/K_0,K_0]}^{q_n}}{\sup }\Vert f({\mathit{\beta }}_1)-{\mathit{\alpha }}^{*}({\mathit{\beta }}_1,{\widehat{\mathit{\beta }}}_2^{(k)})\Vert \to 0,\text{\hspace{0.17em}\hspace{0.17em}as\hspace{0.17em}\hspace{0.17em}}k\to \infty .$$ (A.14)

Since f(·) is a contract mapping, (A.11) yields

$$\Vert f({\widehat{\mathit{\beta }}}_1^{(k)})-{\widehat{\mathit{\alpha }}}^{*}\Vert =\Vert f({\widehat{\mathit{\beta }}}_1^{(k)})-f({\widehat{\mathit{\alpha }}}^{\ast })\Vert \le \frac{1}{c}\Vert {\widehat{\mathit{\beta }}}_1^{(k)}-{\widehat{\mathit{\alpha }}}^{\ast }\Vert ,(c>1).$$ (A.15)

Let $h_k=\Vert {\widehat{\mathit{\beta }}}_1^{(k)}-{\widehat{\mathit{\alpha }}}^{\ast }\Vert$. It Then follows from (A.14) and (A.15) that

$$\begin{gathered} h_{k+1}=\Vert {\mathit{\alpha }}^{*}({\widehat{\mathit{\beta }}}^{(k)})-{\widehat{\mathit{\alpha }}}^{*}\Vert \le \Vert {\mathit{\alpha }}^{*}({\widehat{\mathit{\beta }}}^{(k)})-f({\widehat{\mathit{\beta }}}_1^{(k)})\Vert +\Vert f({\widehat{\mathit{\beta }}}_1^{(k)})-{\widehat{\mathit{\alpha }}}^{*}\Vert \\ \le {\eta }_k+\frac{1}{c}{h}_k. \end{gathered}$$

From (A.14), from any ϵ ≥ 0, there exists N > 0 such that when k > N, |η_k| < ϵ. Employing some recursive calculation, we have h_k → 0 as k → ∞. Hence, with probability tending to one, we have

$$\Vert {\widehat{\mathit{\beta }}}_1^{(k)}-{\widehat{\mathit{\alpha }}}^{*}\Vert \to 0\text{\hspace{0.17em}as\hspace{0.17em}}k\to \infty \text{.}$$

Since ${\widehat{\mathit{\beta }}}_1^{*}\equiv {\lim }_{k\to \infty }{\widehat{\mathit{\beta }}}_1^{(k)}$, it follows from the uniqueness of the fixed-point that

$$P({\widehat{\mathit{\beta }}}_1^{*}={\widehat{\mathit{\alpha }}}^{*})\to 1,k\to \infty .$$

Finally, based on (A.11), we have $\sqrt{n}({\widehat{\mathit{\alpha }}}^{*}-{\mathit{\beta }}_{01})={\mathrm{\Pi }}_1+{\mathrm{\Pi }}_2$, where

$${\mathrm{\Pi }}_1\equiv \sqrt{n}\left[{({\mathbf{\Omega }}_n^{(1)}+{\lambda }_n{\mathit{D}}_1({\widehat{\mathit{\alpha }}}^{*}))}^{-1}{\mathbf{\Omega }}_n^{(1)}-I_{q_n}\right]{\mathit{\beta }}_{01},$$

and

$${\mathrm{\Pi }}_2\equiv \sqrt{n}{({\mathbf{\Omega }}_n^{(1)}+{\lambda }_n{\mathit{D}}_1({\widehat{\mathit{\alpha }}}^{*}))}^{-1}({\text{v}}_n^{(1)}-{\mathbf{\Omega }}_n^{(1)}{\mathit{\beta }}_{01}).$$

It follows from the first order resolvent expansion formula that

$${({\mathbf{\Omega }}_n^{(1)}+{\lambda }_n{\mathit{D}}_1({\widehat{\mathit{\alpha }}}^{*}))}^{-1}={({\mathbf{\Omega }}_n^{(1)})}^{-1}-{\lambda }_n{({\mathbf{\Omega }}_n^{(1)})}^{-1}{\mathit{D}}_1({\widehat{\mathit{\alpha }}}^{*}){({\mathbf{\Omega }}_n^{(1)}+{\lambda }_n{\mathit{D}}_1({\widehat{\mathit{\alpha }}}^{*}))}^{-1}.$$ (A.16)

This yields that

$${\mathrm{\Pi }}_1=-\frac{{\lambda }_n}{\sqrt{n}}{(\frac{1}{n}{\mathbf{\Omega }}_n^{(1)})}^{-1}{\mathit{D}}_1({\widehat{\mathit{\alpha }}}^{*}){(\frac{1}{n}{\mathbf{\Omega }}_n^{(1)}+\frac{{\lambda }_n}{n}{\mathit{D}}_1({\widehat{\mathit{\alpha }}}^{*}))}^{-1}\frac{1}{n}{\mathbf{\Omega }}_n^{(1)}{\mathit{\beta }}_{01}.$$

By the assumption (C5) and (C6), we have

$$\Vert {\mathrm{\Pi }}_1\Vert =O_p({\lambda }_n\sqrt{q_n/n})\to 0.$$ (A.17)

Furthermore, it follows from (A.16) and the assumption ${\lambda }_n/\sqrt{n}\to 0$ hat

$$\begin{gathered} {\mathrm{\Pi }}_2=\sqrt{n}\left[{(\frac{1}{n}{\mathbf{\Omega }}_n^{(1)})}^{-1}-o_p(1/\sqrt{n})\right](\frac{1}{n}{\text{v}}_n^{(1)}-\frac{1}{n}{\mathbf{\Omega }}_n^{(1)}{\mathit{\beta }}_{01}) \\ ={(\frac{1}{n}{\mathbf{\Omega }}_n^{\left(1\right)})}^{-1}\frac{1}{\sqrt{n}}\text{(}{\mathbf{\text{v}}}_n^{(1)}-{\mathbf{\Omega }}_n^{(1)}{\mathit{\beta }}_{01})+o_p(1), \end{gathered}$$ (A.18)

where $n^{-1/2}({\text{v}}_n^{(1)}-{\mathbf{\Omega }}_n^{(1)}{\mathit{\beta }}_{01})=n^{-1/2}{\dot{l}}_n^{(1)}({\widehat{\mathit{\beta }}}^{*}|{\widehat{\varphi }}^{*})+o_p(1)$ with ${\dot{l}}_n^{(1)}({\widehat{\mathit{\beta }}}^{*}|{\widehat{\varphi }}^{*})$ denoting the first q_n components of ${\dot{l}}_n^{(1)}({\widehat{\mathit{\beta }}}^{*}|{\widehat{\varphi }}^{*})$ Let $I(\mathit{\beta })=E\{-{\ddot{l}}_n(\mathit{\beta }|{\widehat{\varphi }}^{*})\}$ be the Fisher information matrix, where ${\ddot{l}}_n(\mathit{\beta }|\varphi )$ is the partial Hessian matrix about β. Since $n^{-1/2}{\ddot{l}}_n({\widehat{\mathit{\beta }}}^{*}|{\widehat{\varphi }}^{*})\to N(0,n^{-1}I({\mathit{\beta }}_0))$, we have $\sqrt{n}({\widehat{\mathit{\alpha }}}^{*}-{\mathit{\beta }}_{01})\to N_{q_n}(0,\mathrm{\Sigma })$ with $\mathrm{\Sigma }=n{({\mathbf{\Omega }}_n^{(1)}({\mathit{\beta }}_0))}^{-1}{I}^{(1)}({\mathit{\beta }}_0){({\mathbf{\Omega }}_n^{(1)}({\mathit{\beta }}_0))}^{-1}$, where $I^{(1)}({\mathit{\beta }}_0)$ is the leading q_n × q_n sub-matrix of I(β₀). This completes the proof.

Proof of Theorem 2. Let

$$Q(\mathit{\beta }|{\widehat{\mathit{\beta }}}^{(k)})\equiv {\Vert \mathit{y}-\mathit{X}\mathit{\beta }\Vert }^2+{\lambda }_n\sum _{l=1}^{p_n}\frac{{\mathit{\beta }}_l^2}{{({\widehat{\mathit{\beta }}}_l^{(k)})}^2},$$

and ${\widehat{\epsilon }}^{(k+1)}=\mathit{y}-\mathit{X}{\widehat{\mathit{\beta }}}^{(k+1)}$, where ${\widehat{\mathit{\beta }}}^{(k+1)}=\arg {\min }_{\mathit{\beta }}Q(\mathit{\beta }|{\widehat{\mathit{\beta }}}^{(k)})$. On the one hand, from $Q({\widehat{\mathit{\beta }}}^{(k+1)}|{\widehat{\mathit{\beta }}}^{(k)})\le Q(0|{\widehat{\mathit{\beta }}}^{(k)})$, we have

$${\Vert {\widehat{\epsilon }}^{(k+1)}\Vert }^2+{\lambda }_n\sum _{l=1}^p\frac{{\left({\widehat{\mathit{\beta }}}_l^{(k+1)}\right)}^2}{{({\widehat{\mathit{\beta }}}_l^{(k)})}^2}\le {\Vert \mathit{y}\Vert }^2.$$

Therefore,

$$\Vert {\widehat{\epsilon }}^{(k+1)}\Vert \le \Vert \mathit{y}\Vert .$$

On the other hand, when ${\widehat{\beta }}_l\mathrm{\ne }0$, note that

$$\frac{\partial Q(\mathit{\beta }|{\widehat{\mathit{\beta }}}^{(k)})}{\partial {\mathit{\beta }}_l}{|}_{\mathit{\beta }={\widehat{\mathit{\beta }}}^{(k+1)}}=-2{\mathit{x}}_l^{\text{'}}{\widehat{\epsilon }}^{(k+1)}+2{\lambda }_n\cdot \frac{{\widehat{\mathit{\beta }}}_l^{(k+1)}}{{({\widehat{\mathit{\beta }}}_l^{(k)})}^2}=0,$$

where l ε {1,…, p_n}. It then follows that

$${\widehat{\mathit{\beta }}}_l^{(k+1)}=\frac{{\left({\widehat{\mathit{\beta }}}_l^{(k)}\right)}^2}{{\lambda }_n}\cdot {\mathit{x}}_l^{\text{'}}{\widehat{\epsilon }}^{(k+1)}.$$ (A.19)

Since ${\lim }_{k\to \infty }{\widehat{\mathit{\beta }}}_l^{(k+1)}={\lim }_{k\to \infty }{\widehat{\mathit{\beta }}}_l^{(k)}={\widehat{\mathit{\beta }}}_l^{*}$ and by taking the limitation on both sides of (A.19),l we have that

$$\frac{1}{{\widehat{\mathit{\beta }}}_i^{*}}=\frac{1}{{\lambda }_n}{\mathit{x}}_i^{\text{'}}{\widehat{\epsilon }}^{*}\text{\hspace{1em}and\hspace{1em}}\frac{1}{{\widehat{\mathit{\beta }}}_j^{*}}=\frac{1}{{\lambda }_n}{\mathit{x}}_j^{\text{'}}{\widehat{\epsilon }}^{*}$$

hold with probability tending to 1 for any i, j ϵ {1,…, p_n} and ${\widehat{\mathit{\beta }}}_i^{*}{\widehat{\mathit{\beta }}}_j^{*}\ne 0$, where ${\widehat{\epsilon }}^{*}=\mathit{y}-\mathit{X}{\widehat{\mathit{\beta }}}^{*}$. Therefore

$$\left|\frac{1}{{\widehat{\mathit{\beta }}}_i^{*}}-\frac{1}{{\widehat{\mathit{\beta }}}_j^{*}}\right|\le \frac{1}{{\lambda }_n}\Vert {\widehat{\epsilon }}^{*}\Vert \cdot \Vert {\mathit{x}}_i-{\mathit{x}}_j\Vert \le \frac{1}{{\lambda }_n}\Vert \mathit{y}\Vert \sqrt{2(1-{\rho }_{ij})}.$$

This complete the proof.