Abstract
Background
Cardiac surgery–associated acute kidney injury (CSA-AKI) is a major complication that results in increased morbidity and mortality after cardiac surgery. Most established prediction models are limited to the analysis of nonlinear relationships and fail to fully consider intraoperative variables, which represent the acute response to surgery. Therefore, this study utilized an artificial intelligence–based machine learning approach thorough perioperative data-driven learning to predict CSA-AKI.
Methods
A total of 671 patients undergoing cardiac surgery from August 2016 to August 2018 were enrolled. AKI following cardiac surgery was defined according to criteria from Kidney Disease: Improving Global Outcomes (KDIGO). The variables used for analysis included demographic characteristics, clinical condition, preoperative biochemistry data, preoperative medication, and intraoperative variables such as time-series hemodynamic changes. The machine learning methods used included logistic regression, support vector machine (SVM), random forest (RF), extreme gradient boosting (XGboost), and ensemble (RF + XGboost). The performance of these models was evaluated using the area under the receiver operating characteristic curve (AUC). We also utilized SHapley Additive exPlanation (SHAP) values to explain the prediction model.
Results
Development of CSA-AKI was noted in 163 patients (24.3%) during the first postoperative week. Regarding the efficacy of the single model that most accurately predicted the outcome, RF exhibited the greatest AUC (0.839, 95% confidence interval [CI] 0.772–0.898), whereas the AUC (0.843, 95% CI 0.778–0.899) of ensemble model (RF + XGboost) was even greater than that of the RF model alone. The top 3 most influential features in the RF importance matrix plot were intraoperative urine output, units of packed red blood cells (pRBCs) transfused during surgery, and preoperative hemoglobin level. The SHAP summary plot was used to illustrate the positive or negative effects of the top 20 features attributed to the RF. We also used the SHAP dependence plot to explain how a single feature affects the output of the RF prediction model.
Conclusions
In this study, machine learning methods were successfully established to predict CSA-AKI, which determines risks following cardiac surgery, enabling the optimization of postoperative treatment strategies to minimize the postoperative complications following cardiac surgeries.
Keywords: Cardiac surgery, Acute kidney injury, Machine learning, Prediction
Introduction
Cardiac surgery–associated acute kidney injury (CSA-AKI) is a complication following cardiac surgery and is associated with increased morbidity and mortality as well as prolonged hospital stay and higher medical costs [1, 2]. One meta-analysis of global incidence and outcomes of CSA-AKI during the period 2004–2014 indicated that the incidence was approximately 22% for all stages of AKI. The pooled short- and long-term mortality rates were 10.7% and 30%, respectively, and increased with the severity of AKI [1]. Even a slight increase in serum creatinine after cardiac surgery is related to a significant increase in 30-day mortality [3].
The pathophysiology of CSA-AKI is multifactorial and remains incompletely understood. Hypoperfusion, ischemia-reperfusion injury, neurohormonal activation, inflammation, nephrotoxin exposure, and cardiopulmonary bypass (CPB)–related nonpulsatile perfusion are known to be contributing factors [4, 5]. All of the aforementioned events may occur perioperatively [6]. To appropriately manage CSA-AKI, a precise prediction model for identifying high-risk patients is required to optimize the postoperative treatment strategy. Several previously published prediction models have shown reasonable ability to discriminate patients with the risk of severe AKI or AKI requiring dialysis [7–14]. However, the definitions of AKI in these models have been inconsistent, and only a handful of models have used intraoperative variables, which may critically affect the prediction of AKI. No unified definition of AKI has been reported in the literature until the development of Risk, Injury, Failure, Loss, End-Stage Kidney Disease (RIFLE) and Acute Kidney Injury Network (AKIN) criteria [15]. The Kidney Disease: Improving Global Outcomes (KDIGO) criteria for AKI staging is modified by AKIN and demonstrates more sensitive AKI detection [16]. The first model for the prediction of all AKI stages, including less severe stage 1 cases, was developed using consensus KDIGO criteria in a prospective study [17]. All risk models were developed using the logistic regression method, which requires the statistical assumption of a linear relationship between the variables and outcome. Moreover, logistic regression requires independent variables and selects small subsets of input variables based on their statistical significance for multiple regression models. But some variables that have causal effects on the output variable may not be statistically significant [18]. We might reduce the available information and miss unexpected relationships that could be utilized to improve predictive power if we excluded the variables only due to statistical assumptions.
To analyze numerous variables with nonlinearity and complex relationships that may be associated with CSA-AKI development, an alternative and effective approach is required for the development of precise prediction models. Machine learning has been applied in areas of medicine such as outcome prediction, diagnosis, medical image interpretation, and treatment [19, 20]. Machine learning techniques require no assumptions regarding input variables and their relationships with the output. The advantage of completely data-driven learning without reliance on rules-based programming is that machine learning constitutes a reasonable approach. Therefore, this study applied machine learning methods to develop a model for the accurate prediction of CSA-AKI. Preoperative variables and intraoperative time-series physiological data were used to optimize the prediction model.
Methods
Study population
We retrospectively reviewed the medical records of 671 patients who underwent coronary artery bypass (CABG), valve replacement surgery, and a combination of both treatments at Far Eastern Memorial Hospital (FEMH), New Taipei City, from August 2016 to August 2018. Institutional Review Board approval from FEMH (106159-E) was obtained prior to the commencement of this study, and informed consent was waived because the research involved no more than minimal risk to patients. The waiver does not adversely affect the rights and welfare of the participants.
Data collection and preprocessing of data
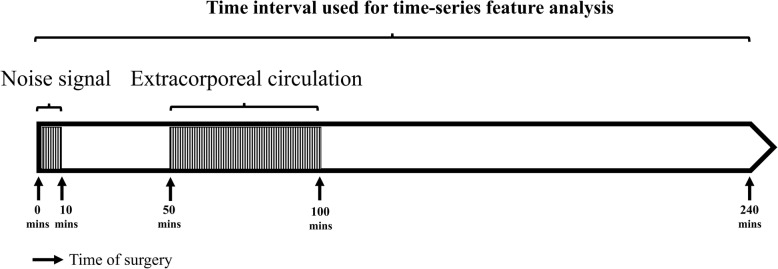
We collected data on demographic characteristics, clinical condition, preoperative biochemistry data, preoperative medication, and intraoperative time-series hemodynamic features (systolic blood pressure [SBP], diastolic blood pressure [DBP], mean arterial blood pressure [MAP], and heart rate [HR]) from electronic medical records and records on intraoperative variables at FEMH. All data except for the time-series features were collected through manual review of the medical records. Time-series data were obtained from electronic records saved at the database. Patients with an estimated glomerular filtration rate (eGFR) < 60 mL/min/1.73 m2 for more than 3 months were defined as having chronic kidney disease (CKD). Furthermore, eGFR was calculated for all patients using the Chronic Kidney Disease Epidemiology Collaboration creatinine (CKD-EPI) equation [21]. For the time-series features (SBP, DBP, HR), the 240-min period after the beginning of the operation was used for analysis. The mean arterial pressure (MAP) was calculated using the equation: MAP = DBP + 0.01exp (4.14–40.74/HR) (SBP-DBP) [22]. We also used the average real variability (ARV) index to represent short-term, reading-to-reading, within-subject variability in blood pressure [23]; this provided a more accurate estimator of variance compared with other measures of dispersion, including standard deviation (SD), coefficient of variation (CV), and weighted SD [24]. Before ARV calculation, we excluded data for 10 min after the operation began because of excessive noise signals and data from 50 to 100 min after the operation because many patients underwent extracorporeal circulation during that time interval (Fig. 1). The other time-series data comprised 180 readings. We calculated the ARVs of SBP, DBP, and HR using the following formula:
where n is the number of BP readings, and Wk is the time interval between BPk and BPk−1. A total of 179 real variabilities existed for the time-series features in each patient. We used principal component analysis (PCA) to reduce the dimensionality from 179 to 10 for the real variability (RV) data calculated using SBP, DBP, and HR. We directly used PCA to reduce the dimensionality of the absolute value of MAP instead of RV. Moreover, we used the maximal RVs of time-series features as predictive variables.
Fig. 1.
Time period obtained during operation for ARV calculation. We obtained data for the 240 min after operation except the initial 10 min (due to noise signals) and the period between 50 and 100 min after operation due to extracorporeal circulation
Among all the variables, the overall rate of missing data was 0.16%. The missing data were inputted as the average values or modes for the variables.
Definition of cardiac surgery–associated acute kidney injury
Development of postoperative AKI was defined according to KDIGO criteria during the first 7 days after operation [16]. Postoperative AKI was defined as either at an increase of at least 50% within 7 days or 0.3 mg/dL elevation within 48 h compared with the reference serum creatinine level. The serum creatinine level measured before surgery was used as the reference value.
Machine learning
The data were randomly divided, with 70% used for training and 30% for validation. To overcome the imbalance of data in the training set, we copied the positive cases 5 times to prevent overfitting. All analyses were developed in Python (version 3.5). We attempted the following supervised machine learning methods to develop the predictive models, which are the most popular and up-to-date machine learning methods used for the problem of classification: logistic regression, simple decision tree, random forest (RF), support vector machine (SVM), eXtreme Gradient Boosting (XGboost), and ensemble (RF + XGboost). The logistic regression model accurately predicts the probability of the binary dependent variable using maximum likelihood estimation to determine the regression coefficient. Tree-based learning algorithms include the simple decision tree, RF, and XGboost. A decision tree method is a tree-like model of decisions that can predict the best choice mathematically. We used an optimized version of the Classification and Regression Trees algorithm to develop the simple decision tree [25]. We used the Gini index as a metric to identify the split point. The Gini index is the probability of randomly classify incorrectly in the dataset. The weakness of the simple decision tree is instability and a risk of overfitting, and thus RF and XGboost are created to improve the prediction. RF is an ensemble classifier that combines multiple decision trees through majority voting [26, 27]. XGboost is an optimized distributed gradient boosting library that provides superior prediction through the conversion of a set of weak learners to strong learners. The algorithm is powerful by some innovations, such as the approximate greedy search, parallel learning, and hyperparameters [28]. We also attempted SVM, an algorithm for identifying a high-dimensional boundary that distinctly classifies data points.
To evaluate the prediction and accuracy of various machine learning models, we calculated and compared areas under the receiver operating characteristic curve (AUC). The correct interpretation of a prediction model for machine learning is a challenge. We used SHapley Additive exPlanation (SHAP) values to provide consistent and locally accurate attribution values for each feature within each prediction model [29]. This is a unified approach for explaining the outcome of any machine learning model. SHAP values evaluate the importance of the output resulting from the inclusion of feature A for all combinations of features other than A.
Results
We reviewed the medical records of 671 patients undergoing cardiac surgery from August 2016 to August 2018. The demographics and perioperative variables are listed in Table 1. We divided the patients randomly and allocated 70% of them to the training set and the remaining 30% to the test set. Among the patients, 250 (37.3%) received CABG, 347 (51.7%) received valve replacement surgery, and 74 (11%) underwent combined CABG and valve surgery. For the time-series features (SBP, DBP, MAP, HR), we calculated the ARVs of the time-series features, and the data are listed in Table 1. For all variables, the differences between the training set and the test set were nonsignificant. The clinical characteristics and perioperative variables for patients who developed CSA-AKI or did not are listed in Additional file 1.
Table 1.
Patient characteristics and perioperative variables
| Variables | All | Training set | Test set | pvalue |
|---|---|---|---|---|
| Patient population,n | 671 | 469 | 202 | |
| Demographic data | ||||
| Age (years) | 63 (53–70) | 62 (53–69) | 63 (53–71) | 0.323 |
| Male, n (%) | 454 (67.7) | 323 (68.9) | 131 (64.9) | 0.307 |
| BMI (kg/m2) | 24.8 (22.5–27.8) | 24.8 (22.5–27.6) | 24.8 (22.7–27.4) | 0.956 |
| Allergy, n (%) | 598 (89.1) | 42 (9.0) | 31 (15.3) | 0.015 |
| ABO, n (%) | ||||
| Type A | 196 (29.2) | 135 (28.8) | 61 (30.2) | 0.715 |
| Type B | 144 (21.5) | 110 (23.5) | 34 (16.8) | 0.055 |
| Type AB | 42 (6.3) | 30 (6.4) | 12 (5.9) | 0.823 |
| Type O | 289 (43.1) | 194 (41.4) | 95 (47.0) | 0.174 |
| Smoking, n (%) | 244 (36.4) | 171 (36.5) | 73 (36.1) | 0.937 |
| Surgery type | ||||
| CABG only, n (%) | 250 (37.3) | 166 (35.4) | 84 (41.6) | 0.128 |
| Valve surgery only, n (%) | 347 (51.7) | 246 (52.5) | 101 (50.0) | 0.560 |
| Combined CABG + valve surgery, n (%) | 74 (11.0) | 57 (12.2) | 17 (8.4) | 0.156 |
| Minimally invasive surgery, n (%) | 336 (50.1) | 237 (50.5) | 99 (49.0) | 0.717 |
| Preoperative condition | ||||
| ER stay > 1 day, n (%) | 59 (8.8) | 42 (9.0) | 17 (8.4) | 0.821 |
| Previous cardiac surgery, n (%) | 96 (14.3) | 59 (12.6) | 37 (18.3) | 0.052 |
| Preoperative ventilator support, n (%) | 45 (6.7) | 33 (7.0) | 12 (5.9) | 0.603 |
| Preoperative IABP, n (%) | 19 (2.8) | 10 (2.1) | 9 (4.5) | 0.096 |
| Cardiogenic shock, n (%) | 24 (3.6) | 14 (3.0) | 10 (5.0) | 0.209 |
| Arrhythmia, n (%) | 138 (20.6) | 93 (19.8) | 45 (22.3) | 0.472 |
| Medical history | ||||
| Family history of CAD, n (%) | 80 (11.9) | 59 (12.6) | 21 (10.4) | 0.423 |
| Diabetes mellitus, n (%) | 215 (32) | 152 (32.4) | 63 (31.2) | 0.756 |
| Dyslipidemia, n (%) | 258 (38.5) | 177 (37.7) | 81 (40.1) | 0.564 |
| HTN, n (%) | 453 (67.5) | 313 (66.7) | 140 (69.3) | 0.515 |
| TIA, n (%) | 23 (3.4) | 13 (2.8) | 10 (5.0) | 0.155 |
| Cerebrovascular accident, n (%) | 39 (5.8) | 27 (5.8) | 12 (5.9) | 0.926 |
| Infective endocarditis, n (%) | 34 (5.1) | 21 (4.5) | 13 (6.4) | 0.289 |
| COPD, n (%) | 73 (10.9) | 49 (10.4) | 24 (11.9) | 0.584 |
| PAOD, n (%) | 17 (2.5) | 13 (2.8) | 4 (2.0) | 0.549 |
| Chronic kidney disease, n (%) | 207 (30.8) | 136 (29.0) | 71 (35.1) | 0.114 |
| Congestive heart failure, n (%) | 131 (19.5) | 93 (19.8) | 38 (18.8) | 0.760 |
| Myocardial infarction, n (%) | 104 (15.5) | 70 (14.9) | 34 (16.8) | 0.531 |
| Baseline laboratory findings | ||||
| Serum creatinine (mg/dL) | 0.91 (0.71–1.16) | 0.90 (0.70–1.14) | 0.95 (0.73–1.28) | 0.128 |
| eGFR (CKD-EPI: mL/min/1.73 m2) | 78.0 (53.2–99.7) | 80.6 (55.6–100.9) | 73.0 (47.4–98.4) | 0.057 |
| Hgb (g/dL) | 13.2 (11.4–14.6) | 13.3 (11.5–14.6) | 13.1 (11.4–14.3) | 0.403 |
| Preoperative LVEF (%) | 62.0 (47.0–69.0) | 62.0 (49.0–70.0) | 61.0 (44.0–68.3) | 0.323 |
| LVEDD (mm) | 51.6 (46.0–56.0) | 51.6 (46.0–56.0) | 51.6 (45.0–56.0) | 0.864 |
| Number of diseased coronary vessels, n (%) | ||||
| One vessel disease | 68 (10.1) | 48 (10.2) | 20 (9.9) | 0.896 |
| Two vessel disease | 59 (8.8) | 40 (8.5) | 19 (9.4) | 0.713 |
| Three vessel disease | 255 (38.0) | 175 (37.3) | 80 (39.6) | 0.575 |
| CCS Angina Score, n (%) | ||||
| Score 0 | 125 (18.6) | 88 (18.8) | 37 (18.3) | 0.892 |
| Score 1 | 134 (20.0) | 97 (20.7) | 37 (18.3) | 0.482 |
| Score 2 | 356 (53.1) | 243 (51.8) | 113 (55.9) | 0.326 |
| Score 3 | 50 (7.5) | 37 (7.9) | 13 (6.4) | 0.511 |
| Score 4 | 6 (0.9) | 4 (0.9) | 2 (1.0) | 0.862 |
| NYHA functional class, n (%) | ||||
| Class I | 113 (16.8) | 84 (17.9) | 29 (14.4) | 0.259 |
| Class II | 365 (54.4) | 251 (53.5) | 114 (56.5) | 0.486 |
| Class III | 161 (24.0) | 109 (23.2) | 52 (25.7) | 0.486 |
| Class IV | 32 (4.8) | 25 (5.3) | 7 (3.5) | 0.298 |
| ASA Physical Status Classification, n (%) | ||||
| Class I | 10 (1.5) | 7 (1.5) | 3 (1.5) | 0.994 |
| Class II | 119 (17.7) | 84 (17.9) | 35 (17.3) | 0.856 |
| Class III | 485 (72.3) | 337 (71.9) | 148 (73.3) | 0.708 |
| Class IV | 51 (7.6) | 38 (8.1) | 13 (6.4) | 0.455 |
| Preoperative medications | ||||
| Beta blockers, n (%) | 297 (44.3) | 212 (45.2) | 85 (42.1) | 0.455 |
| ACEi, n (%) | 68 (10.1) | 51 (10.9) | 17 (8.4) | 0.333 |
| ARB, n (%) | 138 (20.6) | 93 (19.8) | 45 (22.3) | 0.472 |
| Intravenous nitroglycerin, n (%) | 20 (3.0) | 14 (3.0) | 6 (3.0) | 0.992 |
| Anticoagulants, n (%) | 162 (24.1) | 105 (22.4) | 57 (28.2) | 0.106 |
| Steroids, n (%) | 26 (3.9) | 19 (4.1) | 7 (3.5) | 0.718 |
| Aspirin, n (%) | 181 (27.0) | 127 (27.1) | 54 (26.7) | 0.926 |
| Lipid-lowering agents, n (%) | 268 (39.9) | 185 (39.4) | 83 (41.1) | 0.690 |
| Dobutamin, n (%) | 7 (1.0) | 4 (0.9) | 3 (1.5) | 0.460 |
| OHA, n (%) | 162 (24.1) | 115 (24.5) | 47 (23.3) | 0.728 |
| Insulin, n (%) | 39 (5.8) | 22 (4.7) | 17 (8.4) | 0.059 |
| Intraoperative variables | ||||
| Operation time (mins) | 225.0 (190.0–270.0) | 225.0 (195.0–270.0) | 220.0 (180.0–261.3) | 0.101 |
| Elective, n (%) | 625 (93.1) | 439 (93.6) | 186 (92.1) | 0.577 |
| Robotic technology assisted, n (%) | 7 (1.0) | 4 (0.9) | 3 (1.5) | 0.460 |
| Cross clamp time (mins) | 44.0 (0.0–70.0) | 46.0 (0.0–70.5) | 40.5 (0.0–67.3) | 0.179 |
| Perfusion time (mins) | 95.0 (0.0–132.0) | 97.0 (0.0–136.0) | 93.0 (0.0–124.3.0) | 0.096 |
| Lowest core temperature (°C) | 33.0 (32.0–37.0) | 32.0 (32.0–37.0) | 34.0 (32.0–37.0) | 0.704 |
| Cardioversion, n (%) | 192 (28.6) | 131 (27.9) | 61 (30.2) | 0.551 |
| Intraoperative IV fluid infusion (mL/kg/h) | 11.2 (8.4–15.2) | 11.0 (8.4–15.2) | 11.8 (9.0–15.2) | 0.302 |
| Intraoperative urine output (mL/kg/h) | 2.2 (1.2–3.8) | 2.2 (1.3–3.7) | 2.2 (1.2–4.0) | 0.765 |
| Intraoperative estimated blood loss (mL/kg/h) | 2.5 (1.7–3.6) | 2.5 (1.7–3.5) | 2.6 (1.7–3.7) | 0.547 |
| Cardiopulmonary bypass utilization, n (%) | 471 (70.2) | 336 (71.6) | 135 (66.8) | 0.211 |
| pRBC transfusion during surgery (units) | 3.0 (0.0–6.0) | 3.0 (0.0–6.0) | 4.0 (0.0–6.25) | 0.302 |
| FFP transfusion during surgery (units) | 0.0 (0.0–3.0) | 0.0 (0.0–3.0) | 0.0 (0.0–3.0) | 0.979 |
| PLT transfusion during surgery (units) | 0.0 (0.0–0.0) | 0.0 (0.0–0.0) | 0.0 (0.0–6.0) | 0.151 |
| Time-series features (ARV) | ||||
| ARV of HR (beats/min) | 3.7 (2.7–5.2) | 3.7 (2.7–5.2) | 3.5 (2.5–5.3) | 0.979 |
| ARV of SBP (mmHg) | 7.3 (5.9–8.7) | 7.3 (5.9–8.7) | 7.3 (5.8–8.9) | 0.736 |
| ARV of DBP (mmHg) | 4.7 (3.7–6.1) | 4.8 (3.7–6.1) | 4.6 (3.6–5.9) | 0.819 |
| ARV of MAP (mmHg) | 5.5 (4.3–6.7) | 5.5 (4.3–6.7) | 5.3 (4.3–6.6) | 0.889 |
| AKI according to KDIGO criteria | 163 (24.3) | 114 (24.3) | 49 (24.3) | 0.989 |
| Stage I, n (%) | 119 (17.7) | 87 (18.6) | 32 (15.8) | 0.399 |
| Stage II, n (%) | 20 (3.0) | 14 (3.0) | 6 (3.0) | 0.992 |
| Stage III, n (%) | 24 (3.6) | 13 (2.8) | 11 (5.4) | 0.087 |
Data are presented as median (interquartile range) or number (%). Abbreviations: BMI body mass index, CABG coronary artery bypass grafting, ER emergency room, CAD coronary artery disease, HTN hypertension, TIA transient ischemic stroke, COPD chronic obstructive pulmonary disease, PAOD peripheral artery occlusive disease, eGFR estimated glomerular filtration rate, CKD-EPI Chronic Kidney Disease Epidemiology Collaboration, LVEF left ventricular ejection fraction, LVEDD left ventricular end-diastolic diameter, CCS Canadian Cardiovascular Society, NYHA New York Heart Association, ASA American Society of Anesthesiologists, ACEi angiotensin-converting-enzyme inhibitor, ARB angiotensin II receptor blocker, OHA oral hypoglycemic agents, IV intravenous, pRBC packed red blood cell, FFP fresh frozen plasma, PLT platelet, ARV average real variability, HR heart rate, SBP systolic blood pressure, DBP diastolic blood pressure, MAP mean arterial pressure, AKI acute kidney injury, KDIGO kidney disease improving global outcome
We utilized the following machine learning methods with all the variables as input variables, including logistic regression, simple decision tree, RF, SVM, XGboost, and RF + XGboost to predict postoperative AKI, and the AUCs are presented in Fig. 2. Regarding the efficacy of the single model for outcome prediction, RF exhibited the largest AUC (0.839, 95% confidence interval [CI] 0.772–0.898). The AUC (0.843, 95% CI 0.778–0.899) for the ensemble model was larger than that for the RF model alone. The simple decision tree exhibited the smallest AUC (0.78, 95% CI 0.71–0.85).
Fig. 2.
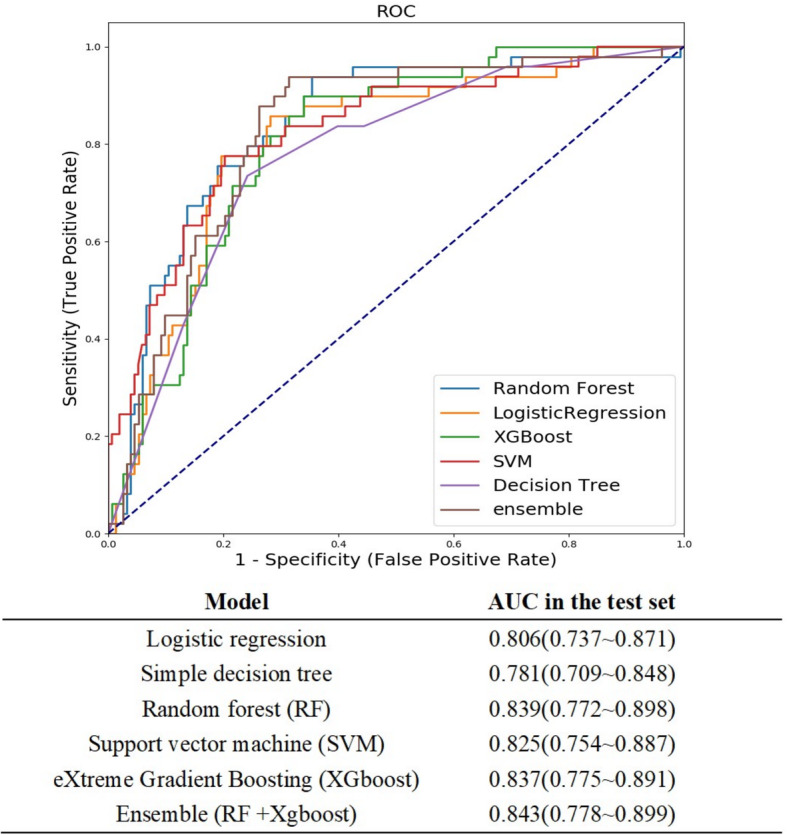
Comparison of AUCs among machine learning models. RF yielded the greatest AUC for single-model prediction. The AUC for RF + XGboost was even greater than for the RF model alone
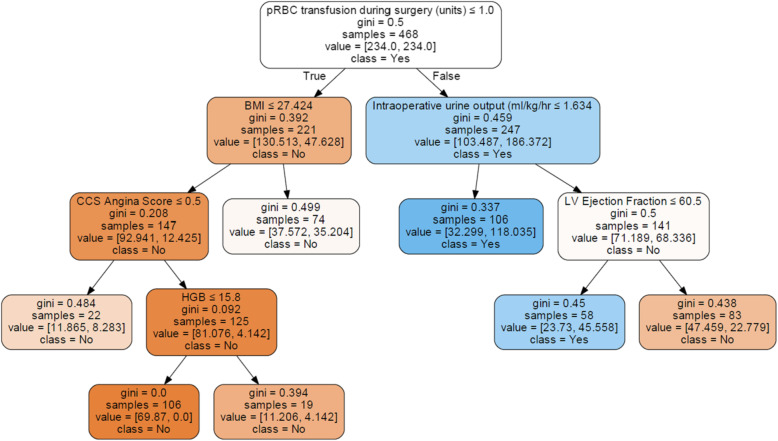
Figure 3 presents a simple decision tree model for classifying patients into with or without AKI. The Gini index in the terminal leaf exceeded 0.45 in 3 of 7 leaf nodes, which implied that the classification was inaccurate.
Fig. 3.
Simple decision tree model illustrating the classification of patients with (class = yes) and without (class = no) acute kidney injury. Each box has the following components: selected variables for classification, Gini index, number of samples classified to the box according to the previous variable, the average number of patients for each classification with 5-cross validation, and the majority of classes at the split node. Blue and orange represent the yes class and the no class, respectively, and the color densities increase when the Gini indexes decrease. Abbreviations: pRBC, packed red blood cell; BMI, body mass index; CCS, Canadian Cardiovascular Society; LV, left ventricular; HGB, hemoglobin
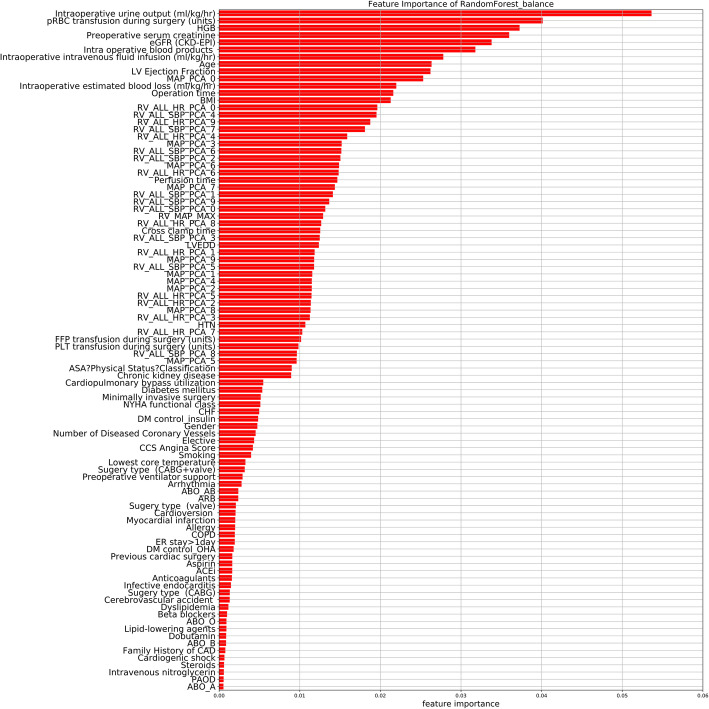
The importance matrix plot for the RF method is shown in Fig. 4 and reveals that the top 5 most important variables contributing to the model were intraoperative urine output, pRBC transfusion during surgery, preoperative hemoglobin (HGB), preoperative serum creatinine, and preoperative eGFR. Of the top 20 most important features, 14 were intraoperative variables and 8 were time-series variables.
Fig. 4.
Importance matrix plot of the RF model. This importance matrix plot depicts the importance of each covariate in the development of the final predictive model. Abbreviations: HGB, hemoglobin; eGFR, estimated glomerular filtration rate; CKD-EPI, Chronic Kidney Disease Epidemiology Collaboration; LV, left ventricular; MAP, mean arterial pressure; PCA, principal component analysis; BMI, body mass index; RV, real variability; HR, heart rate; SBP, systolic blood pressure; LVEDD, left ventricular end-diastolic diameter; HTN, hypertension; FFP, fresh frozen plasma; PLT, platelet; ASA, American Society of Anesthesiologists; CHF, congestive heart failure; DM, diabetes mellitus; CCS, Canadian Cardiovascular Society; CABG, coronary artery bypass grafting; ARB, angiotensin II receptor blocker, COPD, chronic obstructive pulmonary disease; OHA, oral hypoglycemic agent; ER, emergency room; ACEi, angiotensin-converting-enzyme inhibitor; CAD, coronary artery disease; PAOD, peripheral artery occlusive disease
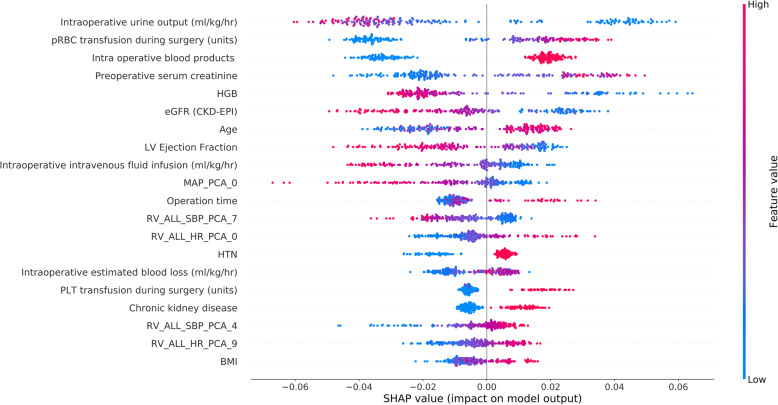
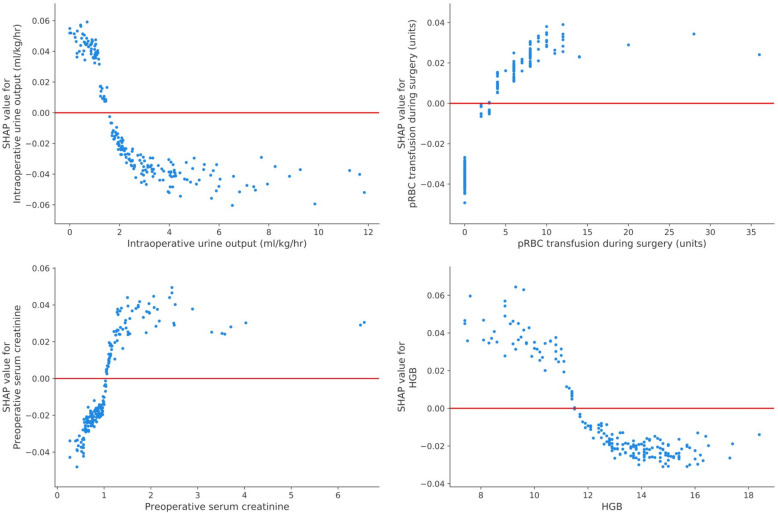
To identify the features that influenced the prediction model the most, we depicted the SHAP summary plot of RF (Fig. 5) and the top 20 features of the prediction model. This plot depicts how high and low features’ values were in relation to SHAP values in the training dataset. According to the prediction model, the higher the SHAP value of a feature, the more likely AKI becomes. The SHAP dependence plot (Fig. 6) can also be used to understand how a single feature affects the output of the RF prediction model. The y-axis values indicated the SHAP values of features, and the values of features for the x-axis were in the SHAP dependence plot. We could visualize how the feature’s attributed importance changed as its values varied in the plot. SHAP values for specific features exceeding zero represent an increased risk of AKI development.
Fig. 5.
SHAP summary plot of the top 20 features of the RF model. The higher the SHAP value of a feature, the higher the probability of postoperative acute kidney injury development. A dot is created for each feature attribution value for the model of each patient, and thus one patient is allocated one dot on the line for each feature. Dots are colored according to the values of features for the respective patient and accumulate vertically to depict density. Red represents higher feature values, and blue represents lower feature values. Abbreviations: pRBC, packed red blood cell; HGB, hemoglobin; eGFR, estimated glomerular filtration rate; CKD-EPI, Chronic Kidney Disease Epidemiology Collaboration; LV, left ventricular; MAP, mean arterial pressure; PCA, principal component analysis; SBP, systolic blood pressure; HR, heart rate; RV, real variability; HTN, hypertension; PLT, platelet; BMI, body mass index
Fig. 6.
SHAP dependence plot of the RF model. The SHAP dependence plot shows how a single feature affects the output of the RF prediction model. SHAP values for specific features exceed zero, representing an increased risk of acute kidney injury development. Abbreviations: pRBC, packed red blood cell; HGB, hemoglobin; eGFR, estimated glomerular filtration rate; CKD-EPI, Chronic Kidney Disease Epidemiology Collaboration
Discussion
In this retrospective cohort study, we developed and validated machine learning algorithms using 94 preoperative and intraoperative features to predict CSA-AKI. The RF model exhibited the best performance for single-model prediction, whereas the RF + XGboost model exhibited the greatest AUC among the models we tested. The RF and XGboost models are bootstrapping method applications, which can improve the predictive power when available datasets are small. Over half of the top 20 features on the importance matrix plot and the SHAP summary plot of RF were intraoperative features, which implies that the major effects of intraoperative condition on early kidney function decline following cardiac surgery. This study demonstrated the value of intraoperative data, which reflected acute physiological responses during surgery relevant to CSA-AKI prediction; the previously used prediction models emphasized preoperative conditions.
Established risk scores for AKI prediction following cardiac surgery were reviewed by Huen et al. and classified into AKI requiring dialysis and severe AKI according to a broad definition. Four clinical risk scores for AKI prediction requiring dialysis, including the Continuous Improvement in Cardiac Surgery Study score [8], the Cleveland Clinic Score [9], the Mehta score [10], and the Simplified Renal Index score [11], were developed using only preoperative variables. Another 3 clinical scores—the Multicenter Study of Perioperative Ischemia Score [12], the Acute Kidney Injury After Cardiac Surgery Score [13], and the Northern New England Cardiovascular Disease Study Group Score [14]—were developed to predict severe AKI. Two of these enrolled some intraoperative variables for the generation of postoperative AKI risk scores. Most of the studies were analyzed with the multivariable logistic regression method, with the performance regarding AUC ranging from 0.76 to 0.84. None used the currently accepted definitions for AKI. One prospective study of more than 30,000 patients in the UK used KDIGO criteria for CSA-AKI prediction [17]. This model demonstrated improved discrimination compared with the Cleveland Clinic Score and similar discrimination to the Mehta score.
The first study in the literature to use a machine learning approach for CSA-AKI at all stages of prediction reported that the optimal AUC was achieved with XGboost (0.78, 95% CI 0.75–0.80) [30]. The study demonstrated that the performances of machine learning models were significantly superior to those of traditional logistic regression models for the prediction of AKI following cardiac surgery. In addition, the study revealed that the AUCs of the previously used risk score models were often only 0.55 in their datasets, potentially due to the small numbers of predictors used and the lack of intraoperative variables. Our SHAP summary plot for RF exhibited some similar predictors known to be associated with CSA-AKI according to traditional risk score models. However, our plot revealed additional novel predictors, some of which were consistent with the importance matrix plot of gradient boosting in the previous machine learning study. Moreover, 5 of the top 20 features that contributed to the model obtained through the use of a SHAP summary plot were time-series variables, which were not analyzed by the aforementioned study but may have improved the AUC in our research. One single-center cohort study proposed a machine learning algorithm to reclassify approximately 40% of patients undergoing any surgery, who were considered to be at low risk of AKI by a preoperative model but were reclassified as high risk after the inclusion of intraoperative features [31]. This also proved that intraoperative features play a major role in AKI risk stratification. In their study, intraoperative time-series features were processed into the minimum, maximum, mean, short-term, and long-term variability [32], which may lead to the loss of useful information compared with our method of PCA for time-series features to preserve as much of the variability in the original data as possible.
The reasons we used ARV and RV to represent time-series features variability are as follows: There are three indexes that were commonly used to evaluate 24-h blood pressure (BP) variability (BPV) in the literature. The first one is the standard deviation (SD) of 24-h ambulatory BP monitoring recordings, which accounts only for the dispersion of values around the mean, not considering the ordering of BP readings [33]. Because the SD is correlated with mean BP, it can be inadequate in a multivariate prognostic model if more than two different measurements were used. The second one is the coefficient of variation (CV), which is the solution to overcome the above problem of SD [34]. Another major weakness of the 24-h SD is that its value is significantly affected by the nocturnal BP decrease. The third index is “weighted” 24-h SD (wSD), which is the average of diurnal and nocturnal SDs by weighting for their respective durations. It can minimize the effect of nocturnal dipping without losing the information on BPV [35]. However, no standardized methods exist for the accurate estimation of BPV. According to the published systemic review and meta-analysis, ARV is a more accurate estimator of 24-h BPV [24]. Despite using ARV in our study, we also used PCA of RV to reserve the most information of the time-series features variability.
The advantage of our study is the use of SHAP values to uncover the black box of machine learning. Although several risk factors have been identified by previously used risk score models, such as preoperative HGB, preoperative renal function, age, operation time, left ventricular ejection fraction, body mass index, and hypertension [7–14], the recognition of intraoperative urine output, IV fluid infusion, blood product transfusion, and dynamic changes of hemodynamic features are important risk factors that have been neglected by traditional risk score models. Notably, some well-known risk factors were not ranked among the top 20 features in our study, such as diabetes mellitus, CPB time, and surgery type. The pathophysiology of CSA-AKI may explain why intraoperative features are so crucial to AKI prediction. Although the definite mechanism is not completely elucidated, renal hypoperfusion is known to result from low-flow, low-pressure, nonpulsatile perfusion with hemodilution; moreover, rapid temperature reduction because of CPB usage, bleeding complications, and inflammatory response play vital roles in CSA-AKI development [4]. Hemodynamic change, blood product transfusion, IV fluid supplement, and intraoperative urine output all reflect the acute response for renal hypoperfusion and the management required. The risk of AKI following cardiac surgery was determined by the preoperative health condition–related susceptibility to acute stress and large dynamic physiological responses intraoperatively, reflecting the ongoing response to surgery. Therefore, software may be developed that can identify high-risk patients who are prone to AKI for the optimization of treatment strategies after cardiac surgery. Moreover, extremely few values are missing from the dataset because most of the data were recorded by hand. Therefore, missing values would not have negatively affected the results.
This study was subject to some limitations. First, our analysis used only single-center data and included relatively few patients. The performance of the machine learning algorithm might differ for larger datasets with differently distributed patient characteristics and different institutions. As such, external validation is required to prevent overfitting. Second, the algorithm learned from the input features, and some hidden relationships may have been lost because of unknown or neglected features that were not enrolled by physicians. Third, most of the input features were achieved manually. We are working on developing a real-time automated electronic health record algorithm that can aggregate perioperative information of patients from various data sources. With these techniques, a machine learning–based predictive model may have the potential for use in clinical practice. Fourth, we used PCA to reduce the dimensionality of time-series features instead of analyzing the original data because of the small numbers of participants in this cohort study, which may have led to the loss of chronological and implied information. Deep learning methods might be used for numerous time-series features if more patients are enrolled. Fifth, we did not use the previous risk scores for performance comparison because of the unavailability of all the variables required in the previously used risk score models. Lastly, predictive ability was impaired by the relatively small numbers of positive events resulting from data imbalance. Future prospective studies are required to evaluate the application of machine learning–based predictive models to clinical practice for the reduction of AKI risks.
Conclusions
In conclusion, we successfully applied the machine learning method to predict AKI after cardiac surgery, which can be used to determine risks after surgery. We demonstrated that the intraoperative time-series and other features are crucial for AKI prediction. Further software development is ongoing for the real-time adjustment of AKI risks following cardiac surgery, which in turn will optimize treatment to improve prognosis.
Supplementary information
Additional file 1. Characteristics and perioperative variables of patients developed acute kidney injury or not after cardiac surgery.
Acknowledgements
We appreciated the funders presented in the funding. The funders have no role in study design; data collection, analysis, and interpretation; or writing of the manuscript.
Authors’ contributions
Study design: PT, YC, CW, KC, YP, SH, KC, CY, and OKL. Data collection: PT, YC, CW, and KC. Data analysis: PT, YC, CW, CY, and OKL. Data interpretation: PT, YC, CW, KC, YP, SH, KC, CY, and OKL. Drafting manuscript: PT. Revising manuscript content: CY and OKL. Approving the final version of the manuscript: PT, YC, CW, KC, YP, SH, KC, CY, and OKL.
Funding
This work was supported financially for research purposes by the NYMU-FEMH Joint Research Programs (107DN02, 108DN03, 109DN04); the Ministry of Science and Technology, Taiwan (MOST 103-2314-B-010-053-MY3, MOST 105-2628-B-075-008-MY3, MOST 106-2321-B-010-008, MOST 106-2911-I-010-502, MOST 106-3114-B-010-002, MOST108-2923-B-010-002-MY3, MOST 108-2633-B-009-001, and MOST109-2321-B-010-005); the Taipei Veterans General Hospital, Taiwan (V106D25-003-MY3 and VGHUST107-G5-3-3); and “Yin Yen-Liang Foundation Development and Construction Plan” of the School of Medicine, National Yang-Ming University, Taipei, Taiwan (107F-M01-0504). Partial financial support for the research was also provided by the Center for Intelligent Drug Systems and Smart Bio-devices (IDS2B) from The Featured Areas Research Center Program within the framework of the Higher Education Sprout Project by the Ministry of Education in Taiwan.
Availability of data and materials
Non-applicable
Ethics approval and consent to participate
This study was approved by an Institutional Review Board approval from East Memorial Hospital (106159-E) prior to the commencement of this study, and informed consent was waived because of the study design.
Consent for publication
Non-applicable
Competing interests
The authors declare that they have no competing interests.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Chih-Yu Yang, Email: cyyang3@vghtpe.gov.tw.
Oscar Kuang-Sheng Lee, Email: oscarlee9203@gmail.com.
Supplementary information
Supplementary information accompanies this paper at 10.1186/s13054-020-03179-9.
References
- 1.Hu J, Chen R, Liu S, Yu X, Zou J, Ding X. Global incidence and outcomes of adult patients with acute kidney injury after cardiac surgery: a systematic review and meta-analysis. J Cardiothorac Vasc Anesth. 2016;30(1):82–89. doi: 10.1053/j.jvca.2015.06.017. [DOI] [PubMed] [Google Scholar]
- 2.Vandenberghe W, Gevaert S, Kellum JA, Bagshaw SM, Peperstraete H, Herck I, Decruyenaere J, Hoste EA. Acute kidney injury in cardiorenal syndrome type 1 patients: a systematic review and meta-analysis. Cardiorenal Med. 2016;6(2):116–128. doi: 10.1159/000442300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lassnigg A, Schmidlin D, Mouhieddine M, Bachmann LM, Druml W, Bauer P, Hiesmayr M. Minimal changes of serum creatinine predict prognosis in patients after cardiothoracic surgery: a prospective cohort study. J Am Soc Nephrol. 2004;15(6):1597–1605. doi: 10.1097/01.ASN.0000130340.93930.DD. [DOI] [PubMed] [Google Scholar]
- 4.Wang Y, Bellomo R. Cardiac surgery-associated acute kidney injury: risk factors, pathophysiology and treatment. Nat Rev Nephrol. 2017;13(11):697–711. doi: 10.1038/nrneph.2017.119. [DOI] [PubMed] [Google Scholar]
- 5.Mao H, Katz N, Ariyanon W, Blanca-Martos L, Adybelli Z, Giuliani A, Danesi TH, Kim JC, Nayak A, Neri M, et al. Cardiac surgery-associated acute kidney injury. Cardiorenal Med. 2013;3(3):178–199. doi: 10.1159/000353134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ortega-Loubon C, Fernandez-Molina M, Carrascal-Hinojal Y, Fulquet-Carreras E. Cardiac surgery-associated acute kidney injury. Ann Card Anaesth. 2016;19(4):687–698. doi: 10.4103/0971-9784.191578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Huen SC, Parikh CR. Predicting acute kidney injury after cardiac surgery: a systematic review. Ann Thorac Surg. 2012;93(1):337–347. doi: 10.1016/j.athoracsur.2011.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chertow GM, Lazarus JM, Christiansen CL, Cook EF, Hammermeister KE, Grover F, Daley J. Preoperative renal risk stratification. Circulation. 1997;95(4):878–884. doi: 10.1161/01.CIR.95.4.878. [DOI] [PubMed] [Google Scholar]
- 9.Thakar CV, Arrigain S, Worley S, Yared JP, Paganini EP. A clinical score to predict acute renal failure after cardiac surgery. J Am Soc Nephrol. 2005;16(1):162–168. doi: 10.1681/ASN.2004040331. [DOI] [PubMed] [Google Scholar]
- 10.Mehta RH, Grab JD, O'Brien SM, Bridges CR, Gammie JS, Haan CK, Ferguson TB, Peterson ED. Bedside tool for predicting the risk of postoperative dialysis in patients undergoing cardiac surgery. Circulation. 2006;114(21):2208–2216. doi: 10.1161/CIRCULATIONAHA.106.635573. [DOI] [PubMed] [Google Scholar]
- 11.Wijeysundera DN, Karkouti K, Dupuis JY, Rao V, Chan CT, Granton JT, Beattie WS. Derivation and validation of a simplified predictive index for renal replacement therapy after cardiac surgery. JAMA. 2007;297(16):1801–1809. doi: 10.1001/jama.297.16.1801. [DOI] [PubMed] [Google Scholar]
- 12.Aronson S, Fontes ML, Miao Y, Mangano DT. Risk index for perioperative renal dysfunction/failure: critical dependence on pulse pressure hypertension. Circulation. 2007;115(6):733–742. doi: 10.1161/CIRCULATIONAHA.106.623538. [DOI] [PubMed] [Google Scholar]
- 13.Palomba H, de Castro I, Neto AL, Lage S, Yu L. Acute kidney injury prediction following elective cardiac surgery: AKICS score. Kidney Int. 2007;72(5):624–631. doi: 10.1038/sj.ki.5002419. [DOI] [PubMed] [Google Scholar]
- 14.Brown JR, Cochran RP, Leavitt BJ, Dacey LJ, Ross CS, MacKenzie TA, Kunzelman KS, Kramer RS, Hernandez F, Jr, Helm RE, et al. Multivariable prediction of renal insufficiency developing after cardiac surgery. Circulation. 2007;116(11 Suppl):I139–I143. doi: 10.1161/CIRCULATIONAHA.106.677070. [DOI] [PubMed] [Google Scholar]
- 15.Lopes JA, Jorge S. The RIFLE and AKIN classifications for acute kidney injury: a critical and comprehensive review. Clin Kidney J. 2013;6(1):8–14. doi: 10.1093/ckj/sfs160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Thomas ME, Blaine C, Dawnay A, Devonald MA, Ftouh S, Laing C, Latchem S, Lewington A, Milford DV, Ostermann M. The definition of acute kidney injury and its use in practice. Kidney Int. 2015;87(1):62–73. doi: 10.1038/ki.2014.328. [DOI] [PubMed] [Google Scholar]
- 17.Birnie K, Verheyden V, Pagano D, Bhabra M, Tilling K, Sterne JA, Murphy GJ. Predictive models for kidney disease: improving global outcomes (KDIGO) defined acute kidney injury in UK cardiac surgery. Critical care (London) 2014;18(6):606. doi: 10.1186/s13054-014-0606-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Smith G. Step away from stepwise. J Big Data. 2018;5(1):32. doi: 10.1186/s40537-018-0143-6. [DOI] [Google Scholar]
- 19.Jiang F, Jiang Y, Zhi H, Dong Y, Li H, Ma S, Wang Y, Dong Q, Shen H, Wang Y. Artificial intelligence in healthcare: past, present and future. Stroke Vasc Neurol. 2017;2(4):230–243. doi: 10.1136/svn-2017-000101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rajkomar A, Dean J, Kohane I. Machine learning in medicine. N Engl J Med. 2019;380(14):1347–1358. doi: 10.1056/NEJMra1814259. [DOI] [PubMed] [Google Scholar]
- 21.Levey AS, Stevens LA, Schmid CH, Zhang YL, Castro AF, 3rd, Feldman HI, Kusek JW, Eggers P, Van Lente F, Greene T, et al. A new equation to estimate glomerular filtration rate. Ann Intern Med. 2009;150(9):604–612. doi: 10.7326/0003-4819-150-9-200905050-00006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Moran D, Epstein Y, Keren G, Laor A, Sherez J, Shapiro Y. Calculation of mean arterial pressure during exercise as a function of heart rate. Appl Hum Sci. 1995;14(6):293–295. doi: 10.2114/ahs.14.293. [DOI] [PubMed] [Google Scholar]
- 23.Mena L, Pintos S, Queipo NV, Aizpurua JA, Maestre G, Sulbaran T. A reliable index for the prognostic significance of blood pressure variability. J Hypertens. 2005;23(3):505–511. doi: 10.1097/01.hjh.0000160205.81652.5a. [DOI] [PubMed] [Google Scholar]
- 24.Mena LJ, Felix VG, Melgarejo JD, Maestre GE. 24-hour blood pressure variability assessed by average real variability: a systematic review and meta-analysis. J Am Heart Assoc. 2017;6(10):e006895. [DOI] [PMC free article] [PubMed]
- 25.Breiman L, Friedman J, Olshen R, Stone C. Classification and regression trees. Boca Raton: CRC press; 1984. [Google Scholar]
- 26.Kulkarni VY, Sinha PK, Petare MC. Weighted hybrid decision tree model for random forest classifier. J Inst Eng (India): Series B. 2016;97(2):209–217. [Google Scholar]
- 27.Breiman L. Random forests. Mach Learn. 2001;45(1):5–32. doi: 10.1023/A:1010933404324. [DOI] [Google Scholar]
- 28.Chen T, Guestrin C. XGBoost: A scalable tree boosting system. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco: Association for Computing Machinery; 2016. p. 785–794. 10.1145/2939672.2939785.
- 29.Lundberg SM, Erion GG, Lee S-I. Consistent individualized feature attribution for tree ensembles. 2018. [Google Scholar]
- 30.Lee HC, Yoon HK, Nam K, Cho YJ, Kim TK, Kim WH, Bahk JH. Derivation and validation of machine learning approaches to predict acute kidney injury after cardiac surgery. J Clin Med. 2018;7(10):322. [DOI] [PMC free article] [PubMed]
- 31.Adhikari L, Ozrazgat-Baslanti T, Ruppert M, Madushani R, Paliwal S, Hashemighouchani H, Zheng F, Tao M, Lopes JM, Li X, et al. Improved predictive models for acute kidney injury with IDEA: intraoperative data embedded analytics. PLoS One. 2019;14(4):e0214904. doi: 10.1371/journal.pone.0214904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Saria S, Rajani AK, Gould J, Koller D, Penn AA. Integration of early physiological responses predicts later illness severity in preterm infants. Sci Transl Med. 2010;2(48):48ra65. doi: 10.1126/scitranslmed.3001304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Dolan E, O'Brien E. Blood pressure variability: clarity for clinical practice. Hypertension. 2010;56(2):179–181. doi: 10.1161/HYPERTENSIONAHA.110.154708. [DOI] [PubMed] [Google Scholar]
- 34.Parati G, Ochoa JE, Lombardi C, Bilo G. Assessment and management of blood-pressure variability. Nat Rev Cardiol. 2013;10(3):143. doi: 10.1038/nrcardio.2013.1. [DOI] [PubMed] [Google Scholar]
- 35.Bilo G, Giglio A, Styczkiewicz K, Caldara G, Maronati A, Kawecka-Jaszcz K, Mancia G, Parati G. A new method for assessing 24-h blood pressure variability after excluding the contribution of nocturnal blood pressure fall. J Hypertens. 2007;25(10):2058–2066. doi: 10.1097/HJH.0b013e32829c6a60. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional file 1. Characteristics and perioperative variables of patients developed acute kidney injury or not after cardiac surgery.
Data Availability Statement
Non-applicable