Spatial proximity moderates genotype uncertainty in genetic tagging studies

Significance

We present a statistical framework for the estimation of animal demographic parameters, such as abundance, density, and growth rate, from noninvasive genetic samples (e.g., hair, scat). By integrating a genetic classification model with a spatial population model, we show that accounting for spatial proximity of samples reduces genotype uncertainty and improves parameter estimation. Our method provides a fundamentally different approach to genetic capture–recapture by sharing information between the normally disjunct steps of assigning individual identities to genetic samples and modeling spatial population processes. Our approach may also be used in other ecological classification problems such bioacoustics, remote camera images, and environmental DNA, where current approaches make assignments disconnected from the ecological and spatial context of the population under study.

Abstract

Accelerating declines of an increasing number of animal populations worldwide necessitate methods to reliably and efficiently estimate demographic parameters such as population density and trajectory. Standard methods for estimating demographic parameters from noninvasive genetic samples are inefficient because lower-quality samples cannot be used, and they assume individuals are identified without error. We introduce the genotype spatial partial identity model (gSPIM), which integrates a genetic classification model with a spatial population model to combine both spatial and genetic information, thus reducing genotype uncertainty and increasing the precision of demographic parameter estimates. We apply this model to data from a study of fishers (Pekania pennanti) in which 37% of hair samples were originally discarded because of uncertainty in individual identity. The gSPIM density estimate using all collected samples was 25% more precise than the original density estimate, and the model identified and corrected three errors in the original individual identity assignments. A simulation study demonstrated that our model increased the accuracy and precision of density estimates 63 and 42%, respectively, using three replicated assignments (e.g., PCRs for microsatellites) per genetic sample. Further, the simulations showed that the gSPIM model parameters are identifiable with only one replicated assignment per sample and that accuracy and precision are relatively insensitive to the number of replicated assignments for high-quality samples. Current genotyping protocols devote the majority of resources to replicating and confirming high-quality samples, but when using the gSPIM, genotyping protocols could be more efficient by devoting more resources to low-quality samples.

Species extinction risk is tied to the loss of individual populations, with recent studies demonstrating range contractions of 94 to 99% in some of the world’s large carnivores (1). Accelerating declines of an increasing number of animal populations worldwide necessitate methods to reliably and efficiently estimate demographic parameters such as population size and vital rates such as survival probability, recruitment rate, and the population trajectory through time. Unfortunately, many species of conservation concern are managed without having the necessary information on population status or trends, which is largely a consequence of the cost and difficulty of studying species in decline and the difficulty of applying statistical models to sparse data, which can produce imprecise and biased estimates of demographic parameters.

Noninvasive genetic monitoring has become an invaluable tool for estimating population parameters and quantifying population status because genetic samples are efficient to collect for a large number of species (2). The DNA contained in noninvasive samples, such as tissue, hair, or scat, can be extracted and amplified (e.g., via PCR) (3) and then used to identify microsatellite markers (4) or, more recently, single-nucleotide polymorphisms (SNPs) (5), which serve as the basis for estimating population genetics or population dynamics parameters. The role of genetic markers in genetic capture–recapture studies is to provide individual identities for the collected samples, which are then used to construct the capture histories (i.e., records of when and where each individual was detected) required by capture–recapture models. Individual identities are inferred from the combination of allele values observed across enough genetic loci that it is improbable that multiple individuals in the collected samples share the same multilocus genotype by chance.

Two key challenges in the application of noninvasive genetic sampling are that genetic markers from noninvasive samples are observed with error, potentially creating “false individuals,” and the markers may provide insufficient power to discriminate between individuals, potentially causing multiple individuals to be mistakenly classified as a single individual (the “shadow effect”) (6). These errors become increasingly more likely when not all loci amplify successfully, which is common when using noninvasive samples that typically contain a low quantity and quality of DNA (4, 7). Errors in the observed multilocus genotypes are especially problematic when used in capture–recapture models that strictly assume that all samples are identified to individuals correctly (8). Error rates as low as 1 to 5% can introduce strong bias into population parameter estimates using typical capture–recapture models, with the main concern being false individuals, which inflate population abundance estimates (6, 9, 10).

The extreme sensitivity of capture–recapture models to even small error rates in individual identity (6, 10) has largely determined the structure of genotyping protocols used for genetic capture–recapture to date. Genetic markers were established as a reliable tool for capture–recapture analyses by the development of standardized laboratory protocols that minimized genotyping errors (3, 4, 11) and statistical tools that aid in determining the required number of markers and identifying the reliable samples (e.g., refs. 12 and 13). These tools were originally developed for microsatellite markers, which is our focus here; however, much of our discussion also applies to SNPs or other genetic markers. Genotyping protocols vary across studies, but common features used to reduce errors are 1) the use of enough highly variable loci to minimize shadow events, 2) some form of replicate genotyping to identify and limit genotyping errors, and 3) the removal of samples judged to be unreliable. After this process of data curation and filtering, the individual identities are treated as if they are error-free, so no remaining uncertainty in the individual identities can be propagated to the demographic parameters of interest. We briefly describe this “typical approach” to assigning individual identities to samples—see Lampa et al. (7) and Sethi et al. (14) for comprehensive reviews.

First, shadow events are minimized by using a marker set with sufficient discriminatory power. The main statistic used to measure the discriminatory power of a marker set is $P_{ID}$, which quantifies the probability that two randomly selected individuals in the population will have the same genotype by chance, given the number of loci and estimated allele frequencies (15). In practice, the more conservative $P_{IDsib}$, the probability two randomly selected siblings in the population will have the same genotype by chance (12), is typically used. For simplicity, we refer to both of these statistics as $P_{ID}$. Generally, a low $P_{ID}$ threshold is used to determine how many markers to use, and this threshold varies widely across studies—Lampa et al. (7) documented studies with $P_{ID}$ thresholds spanning seven orders of magnitude (8.2 × ${\mathrm{10}}^{-4}$ to 2.${\mathrm{7}}^{-11}$). One factor partially accounting for this variability is that to limit the absolute number of shadow events, the $P_{ID}$ threshold must scale with the number of individuals captured (11), a product of the population size and capture probability. Unfortunately, the population size, capture probability, and number of individuals captured are quantities to be estimated and are by definition unknown, or imprecisely known, in advance. Given this and other sources of uncertainty, $P_{ID}$ thresholds are typically chosen to be overly conservative, which can lead to the culling of large numbers of samples that do not amplify at all loci or otherwise cannot be scored at all loci due to potential genotyping errors. We refer to these samples as partial genotypes.

Genotyping errors are then minimized using some form of replication of the genotyping process from which consensus genotypes are constructed. Generally, the most rigorous (and expensive) method for generating consensus genotypes from low-quality DNA samples is the “multitubes” approach (4, 13) where the DNA product from each sample is split across multiple subsamples and then amplified and scored independently. The consensus genotype is then determined by comparing the scores across replications and scoring a locus only if the same single-locus genotype is seen a minimum number of times across replicates (4). These scoring rules vary somewhat subjectively across studies and by zygosity (homozygotes vs. heterozygotes) (7). Less comprehensive and more efficient protocols for generating consensus genotypes are also in use, where only samples suspected of containing errors are replicated (11, 16). After consensus genotypes are generated, samples are matched to individuals using one of a number of algorithms (e.g., refs. 9 and 17), while discarding samples whose consensus genotypes are missing too many locus scores due to failed amplification or insufficient genotype confirmation.

This typical approach to producing individual identities from replicated genotype scores (the “individual identity observation process”) can be conceptualized as a random thinning process (depicted in Box A, Fig. 1) where the complete capture history is thinned to produce a capture history of known identity samples (possibly with errors) and a set of unidentified samples, which are discarded. The thinning rate is a function of the overall quantity and quality of DNA in the samples, but also the level of conservativeness used for accepting samples as reliable. For the same set of samples, a more conservative genotyping protocol will increase the thinning rate, leading to fewer errors in the constructed capture history, but at the cost of discarding more samples. This trade-off cannot be avoided if no errors in individual identity are allowed. One further thing to note is that information from the ecological and capture processes in the capture–recapture dataset (including the spatial locations associated with samples) is not used to formally assign individual identities. Usually, the genotype frequencies (part of the ecological process) are estimated from independent datasets, and abundance and capture probability are only included informally and imprecisely when setting the $P_{ID}$ threshold.

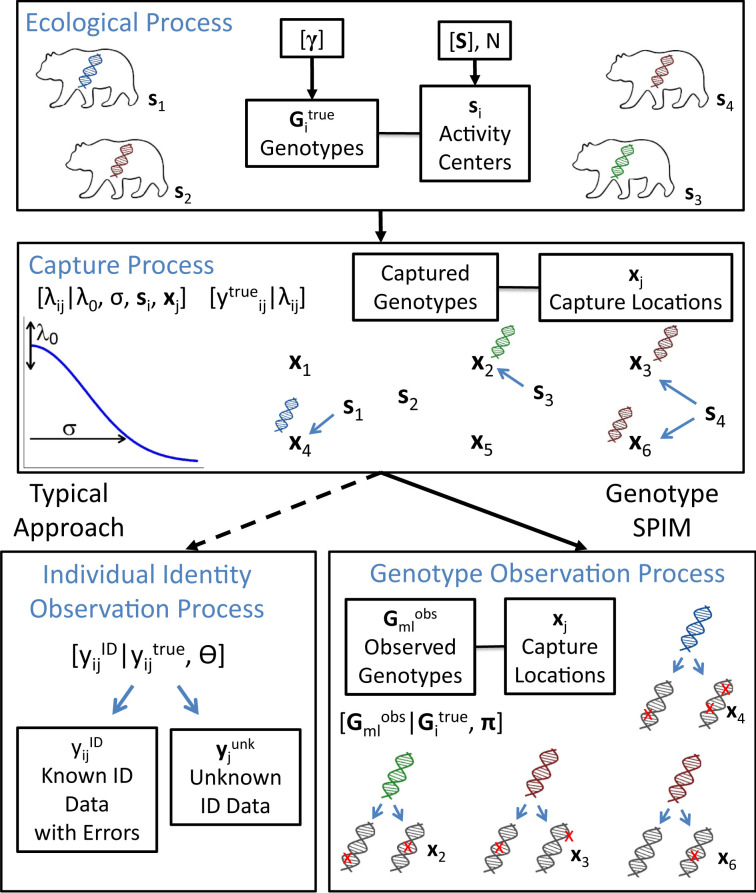
Fig. 1.

A graphical depiction of the gSPIM contrasted with the typical approach to genetic capture–recapture.

Box A.

The gSPIM is a three-level hierarchical model, with submodels for the ecological, capture, and genotype observation processes. The ecological process determines the abundance (N), density, and spatial locations ($\mathit{S}$) of the individuals in the study area and associates a genotype (${\mathit{G}}_i^{true}$) with each individual, which are governed by the locus-level genotype frequencies, $\mathit{\gamma }$. These genotypes may not be unique (shadow effect)—we depict unique genotypes with unique colors, with two individuals sharing a “red” genotype. The capture process then determines where and how many times each individual will be captured, $y_{ij}^{true}$, governed by a detection function between the location of individual $i$, ${\mathit{s}}_i$, and trap location, ${\mathit{x}}_j$. The detection function parameters are ${\lambda }_0$, the baseline detection rate, and $\sigma$ the spatial scale parameter, which are used in conjunction with the distances between activity centers and traps to determine ${\lambda }_{ij}$, the detection rate for individual $i$ at location $j$. When captured, individuals leave a record of their genotype, not their unique individual identity, due to the possibility of the shadow effect. The genotype observation process then determines which genotype we observe, ${\mathit{G}}_{ml}^{obs}$, for sample $m$ on replicate $l$, conditional on the true genotype of the individual that was captured and the genotype observation probabilities in $\pi$. We gray out the observed genotypes, because the true genotypes are no longer observed perfectly, and indicate possible genotyping errors with red exes. The data for the gSPIM are the spatially referenced observed genotypes, which are used to probabilistically reconstruct ${\mathit{Y}}^{true}$ and ${\mathit{G}}^{true}$, while incorporating the uncertainty in individual identity into the population and genetic parameter estimates. To contrast the gSPIM with the typical approach, we can conceptualize the individual identity observation process as a random thinning process where the true capture history, ${\mathit{Y}}^{true}$ is split into a capture history of known identity samples, ${\mathit{Y}}^{ID}$, and a vector of trap-level or a matrix of trap by occasion-level counts, ${\mathit{Y}}^{unk}$, which is discarded. A possible thinning process for an individual by trap capture history is $y_{ij}^{ID}\sim \text{Binomial}\left(y_{ij}^{true},\theta \right)$, where the $\theta$ parameter determines the probability that a sample can be identified to an individual. $\theta$ is then a function of the overall quantity and quality of DNA in the samples, but also the level of conservativeness used for accepting samples as reliable. For the same set of samples, a more conservative genotyping protocol will raise $\theta$, leading to fewer individual identity errors in ${\mathit{Y}}^{ID}$ at the cost of discarding more samples. This trade-off cannot be avoided if no errors are allowed in individual identity and we cannot guarantee that ${\mathit{Y}}^{ID}$ has no errors.

These limitations can be resolved with an appropriately structured capture–recapture model that allows for errors and uncertainty in individual identity (10, 18–21) and allows parameters of both the capture–recapture model and the genetic classification model to be jointly estimated from the data in hand. One approach to achieve these goals is to use a Bayesian hierarchical model (22) that explicitly includes the ecological, capture, and genotype observation processes. By adopting a Bayesian estimation framework for analysis of this model, the posterior distribution of the true capture history can be obtained, and this posterior distribution incorporates the information in the data from the ecological and capture processes. Further, all pairwise match probabilities (pairwise probabilities that any two focal samples belong to the same individual) can be derived from the posterior distribution of the true capture history (21). This probabilistic identity assignment contrasts with the typical genetic laboratory approach where pairwise match probabilities are regarded to either be 0 (no match) or 1 (match). In the context of genotyping error, this integrated approach effectively “averages over” all possible capture histories consistent with the observed data—any one sampled capture history may contain “shadow events” and false individuals, but these errors are averaged (more formally, integrated over) to propagate the uncertainty in individual identity to the posterior distributions of ecological parameters that we care about, such as abundance. If nonspatial ecological and capture models (e.g., classical capture–recapture) (8) are integrated with a genetic classification model (19), the information in the data about abundance and capture probability is directly exploited when sampling the capture histories, instead of included informally and imprecisely using the $P_{ID}$ threshold.

More recently, uncertain identity capture–recapture models have been extended to utilize the information about individual identity contained in the spatial location where samples are collected (e.g., unmarked spatial capture–recapture [SCR], spatial mark–resight [SMR], and spatial partial identity models [SPIMs]) (21, 23, 24). Using a joint model for the spatial distribution of individuals across the landscape and a spatially explicit model of sampling that exploits the movement of individuals about their home ranges, the individual identities of samples can be more precisely resolved compared to those in nonspatial models. The increase in precision in individual identity is then propagated to the precision of the demographic parameters. The key mechanism leading to increased precision is that uncertainty in individual identity scales with home range overlap—a function of local population density and home range size—rather than total abundance (21). Further, when using a spatially explicit model to address genotyping uncertainty, the observed genotypes of neighboring samples become more informative about the true genotype of a focal sample than those farther away because samples collected closer together in space are more likely to belong to the same individual. However, to date, no comprehensive uncertain identity model exists that includes all of the features relevant to the genotyping process and that capitalizes on spatial information in this manner.

Here, we present the genotype spatial partial identity model (gSPIM)—a unified probabilistic framework that removes subjective processing and interpretation of genetic data, a feature of the typically used approach. Our approach combines a model of genetic and individual classification with a model for spatially explicit individual detections to make inference about animal population parameters. This model, with clearly articulated probability assumptions about each component of the system, allows for uncertainty to be propagated among the ecological, capture, and genotyping processes; uses all available sources of information; and removes the need for data culling. The net result is increased efficiency in noninvasive genetic capture–recapture studies—by making use of all available data, the statistical accuracy and precision of population parameter estimates are improved. This integrated modeling approach that propagates uncertainty in classification into inferences about state variables of interest (e.g., species abundance or distribution) is widely relevant to other spatially explicit classification problems including classifying individuals or species from remote activated cameras or classifying species in eDNA applications (Discussion and SI Appendix). We apply the gSPIM to a previously analyzed dataset of fishers (Pekania pennanti) in New York (25), making use of the 37% of samples that were originally discarded due to uncertain individual identity (Fig. 2). We then investigate the performance of the model via simulation. For both the fisher and simulated datasets, we compare the parameter estimates from our model to those from analogous SCR models (26, 27) that use a single capture history, containing only the samples with high-certainty individual assignments and assumed to be error-free.

Fig. 2.

A fisher at a baited hair snare.

Results

Fisher Application.

The gSPIM analysis produced abundance and density estimates that were 25% more precise than the SCR estimate as judged by the coefficient of variation (Table 1). The increased precision was largely driven by an increase in individual detectability and more precise detection spatial scale parameter estimates when including the 157 samples originally discarded. The overall detection parameter ($a_0$) point estimate increased 44% from 3.28 to 4.73 and the number of individuals detected was estimated at 272, a 44% increase over the 189 detected individuals in the original, curated dataset. The gSPIM abundance point estimate was 15% higher than the SCR estimates; however, given the level of uncertainty in both estimates, there is no indication that these two estimators would differ on average in their point estimates.

Table 1.

SCR process and observation model parameter estimates from the SCR and SPIM analyses of the fisher dataset

	SCR				SPIM
	Estimate	CV	LB	UB	Estimate	CV	LB	UB
$a_0$	3.28	20.8	2.19	4.83	4.73	15.4	3.39	6.22
$\sigma$	1.43	19.2	0.96	2.04	1.32	13.4	1.02	1.71
${\sigma }^{sd}$	0.84	20.0	0.58	1.20	0.65	16.4	0.50	0.90
N	2,321	22.4	1,572	3,529	2,672	16.8	1,974	3,690
$n^{cap}$	187	—	—	—	273	1.6	263	280
D	4.27	22.4	2.89	6.49	4.92	16.8	3.63	6.79

a₀ is the overall detection parameter, σ is the population-level detection function spatial-scale parameter in kilometers, ${\sigma }^{sd}$ is the SD of the individual-level variance in the spatial-scale parameter, N is the population abundance, $n^{cap}$ is the number of individuals captured, and D is the population density (individuals per 100 km²). Posterior modes are presented as point estimates, posterior standard deviations/posterior modes are presented as the coefficient of variation, and 95% HPD interval upper bounds (UB) and lower bounds (LB) are presented as interval estimates.

The certain identity assignments made by the gSPIM (posterior match probability of 1) corresponded to those made in the original study except for five cases described in Dataset S1. Two of these five cases were examples where the gSPIM assignment implied that the genetic laboratory assignment (using the typical approach) was too confident (assigned a match when the gSPIM estimated match probability was <1, but >0.75), indicating agreement in the assignment but not in the level of certainty. In two other cases, the gSPIM assignments implied the genetic laboratory assigned different individual identities to samples that were actually from the same individual with probabilities 1 and 0.92, respectively (false individuals). In the final case, the gSPIM assignment implied the genetic laboratory incorrectly assigned two samples to the same individual with probability 1 (shadow event). Spatially explicit depictions of the posterior identity matches can be visualized for every sample using code provided (28), with a subset of these matches (including these just referenced) illustrated in Dataset S1.

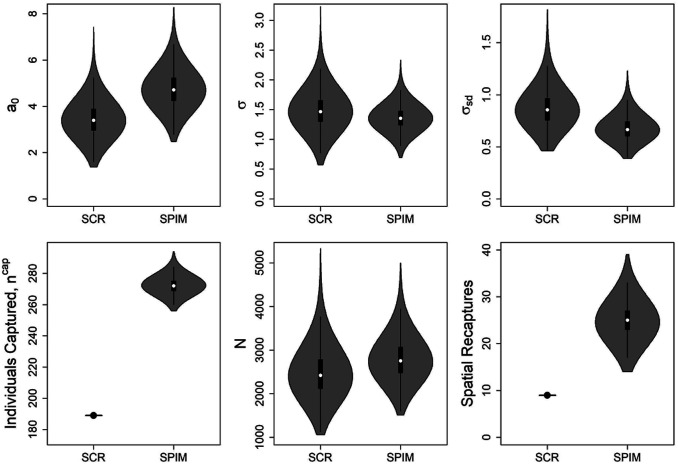
Point estimates of the detection function spatial-scale point estimates were roughly similar between the gSPIM and the SCR model (Table 1 and Fig. 3), but they were more precisely estimated by the gSPIM. This gain in precision is likely due to the greater number of spatial recaptures (individuals captured in more than one location), especially high-probability spatial recaptures, contained in the partial genotype samples. The use of 105 partial genotype samples effectively doubled the number of certain (probability = 1) spatial recaptures as seen through the posterior for the total number of spatial recaptures (Fig. 3), which takes a minimum value of 14, compared to the 9 available in the original dataset and SCR analysis. The posterior mode for spatial recaptures (Fig. 3) was 24, with a 95% highest posterior density (HPD) interval of [18, 31], indicating a high probability that there were more than two times as many spatial recaptures than included in the original dataset. Among the 157 samples originally discarded, the gSPIM matched 6 to another sample with probability greater than 0.99, 17 with probability greater than 0.9, and 30 with probability greater than 0.75. For these same discarded samples, the gSPIM assigned 11 samples to unique individuals (individuals with one capture event) with a probability greater than 0.99, 31 with a probability greater than 0.9, and 49 with a probability greater than 0.75.

Fig. 3.

SCR process and observation model posterior distributions from the SCR and SPIM analyses of the fisher dataset. $a_0$ is the overall detection parameter, $\sigma$ is the population-level detection function spatial-scale parameter in kilometers, ${\sigma }^{sd}$ is the SD of the individual-level variance in the spatial-scale parameter, $n^{cap}$ is the number of individuals captured, and $N$ is the population abundance. The number of captured individuals and spatial recaptures in the SCR analysis are known statistics.

The genotype observation probabilities differed between sample types (high vs. low quality; Table 2). Because allelic dropout can only occur for heterozygous genotypes and false allele rates were estimated to be very low (0.001 to 0.015, depending on zygosity and sample quality), homozygous single-locus genotypes were estimated to be almost always scored correctly for both sample types ($>$0.994). The major difference in reliability between sample types was the probability of an allelic dropout observation, which was roughly 2.7 times more likely for low-quality samples (0.496 vs. 0.185). Despite the general unreliability of the poor-quality samples, the overall improvement in the precision of the abundance estimate stemming from their use demonstrates that they do contain substantial information about the population parameters of interest. The single-locus genotype frequency estimates corrected for genotyping error can be found in Dataset S1.

Table 2.

Single-locus genotype observation probability parameter estimates for high- and low-quality samples in the Fisher dataset

	High quality			Low quality
Class type	Estimate	LB	UB	Estimate	LB	UB
Het-Correct	0.806	0.795	0.818	0.489	0.460	0.518
Het-AD	0.185	0.174	0.197	0.496	0.466	0.525
Het-FA	0.009	0.006	0.011	0.015	0.009	0.022
Hom-Correct	0.994	0.991	0.997	0.999	0.998	1.000
Hom-FA	0.006	0.003	0.009	0.001	0.000	0.002

“Het” indicates a heterozygous single-locus genotype and “Hom” indicates a homozygous single-locus genotype. “Correct,” “AD,” and “FA” indicate a correct, an allelic dropout, and a false allele observation, respectively. Posterior means are presented as point estimates and 95% HPD interval upper and lower bounds are presented as interval estimates.

Simulation Study.

The gSPIM abundance estimates were approximately unbiased ($\approx -$1%) with near nominal coverage (Table 3) except when using only one genotype assignment (e.g., one PCR). In this case, bias was $-$3.6% when including the low-quality samples and $-$2.1% when using only the high-quality samples. The 95% coverage for abundance was less than nominal only in the scenario including the low-quality samples with only one genotype assignment, where it was 0.91. The gSPIM including the low-quality samples (48% of total samples) with three replicated assignments was 42% more precise, as judged by the 95% CI width averaged across simulated datasets, and 63% more accurate, as judged by the mean-squared error, than the SCR estimator that did not use the low-quality samples. With only two replicated assignments, the gSPIM was 41% more precise and 59% more accurate than the SCR estimator. With just one assignment, the gSPIM was 35% more precise and 39% more accurate than the SCR estimator. By including the low-quality samples, 27.4 additional individuals were captured, on average, representing an increase of 31% over the number captured in the high-quality samples alone. The uncertainty in the number of individuals captured, $n^{cap}$, came almost entirely from the low-quality samples except when using only one genotype assignment. The mean 95% CI width for $n^{cap}$ when not using low-quality samples was effectively zero when using two and three replicated assignments (scenarios SPIM2B and SPIM3B) and the posterior modes of $n^{cap}$ matched the true value exactly 98 and 99% of the time, respectively (two vs. three replicated assignments). Thus, the individual identities of all high-quality samples were assigned correctly with probability 1 nearly 100% of the time, except when there was only one genotype assignment (all assignments completely correct for almost all simulated datasets). With one assignment, the individual identities of nearly all high-quality samples were assigned correctly with probability 1 (nearly all assignments completely correct for each simulated dataset).

Table 3.

gSPIM simulation results for the detection model and abundance

Scenario	${\lambda }_0$	$\sigma$	N	$n^{cap}$	N Cov	n Cov	N Wid	n Wid	N MSE
True	0.570	1.320	166.0	115.8	—	—	—	—	—
SPIM3A	0.562	1.321	165.2	115.6	0.933	0.983	36.9	2.3	105.0
SPIM2A	0.566	1.321	164.0	115.0	0.958	0.950	37.6	4.8	119.1
SPIM1A	0.574	1.329	159.8	112.8	0.908	0.908	41.5	10.8	171.2
True	0.297	1.320	166.0	88.4	—	—	—	—	—
SPIM3B	0.296	1.311	163.8	88.3	0.950	0.992	64.0	0.01	279.7
SPIM2B	0.296	1.310	163.9	88.3	0.958	0.975	64.3	0.07	277.6
SPIM1B	0.297	1.313	162.5	88.2	0.967	0.950	64.0	1.62	281.1
SCR	0.295	1.311	163.9	—	0.983	—	64.1	—	282.7

Scenarios indicate the model used (SPIM or SCR), the number of replicated assignments (1 to 3), and whether the low-quality samples were included (A) or not (B). The low-quality samples were not included in the SCR analysis by default. ${\lambda }_0$ is the baseline detection rate, σ is the detection function spatial-scale parameter, N is abundance, and $n^{cap}$ is the number of individuals captured (fewer when excluding the low-quality samples). The values listed here are the mean point estimates across 120 simulated datasets. “Cov” indicates the coverage of the 95% credible intervals, “Wid” indicates the mean width of the 95% credible intervals, and “MSE” indicates the mean-squared error of the point estimates.

The genotype observation probability estimates (correct assignment, allelic dropout, false allele) for heterozygous and homozygous true genotypes were approximately unbiased when using more than one genotype assignment, except when low-quality samples were included, where they were approximately unbiased when using three replicated assignments (Table 4). In scenarios with bias, the allelic dropout probability ($p_{AD}^{het}$) and false allele probability ($p_{FA}^{het}$ and $p_{FA}^{hom}$) estimates were positively biased, with a corresponding negative bias in the correct observation probability estimates ($p_C^{het}$ and $p_C^{hom}$). There was more bias in the genotyping error probabilities for the low-quality samples; however, there was less overall bias in the genotyping error probabilities for the high-quality samples when including the low-quality samples and using only one genotype assignment (scenarios SPIM1A vs. SPIM1B), likely due to the overall greater precision in the detection and abundance parameters when including these samples. The estimates of ${\mathit{p}}^{het}$ and ${\mathit{p}}^{hom}$ for high-quality samples with one genotype assignment were 1 to 6% more precise (depending on the parameter), as judged by the posterior SD when including the low-quality samples compared to when they were excluded. There were also some precision gains in the estimates of ${\mathit{p}}^{het}$ and ${\mathit{p}}^{hom}$ by including the low-quality samples with two replicated assignments, but they were less pronounced (1 to 2% precision gain). Precision gains in the estimates of ${\mathit{p}}^{het}$ and ${\mathit{p}}^{hom}$ including the low-quality samples with three genotype assignment were negligible ($<$1%).

Table 4.

gSPIM simulation results for the genotype observation model

	$p_C^{het1}$	$p_{AD}^{het1}$	$p_{FA}^{het1}$	$p_C^{het2}$	$p_{AD}^{het2}$	$p_{FA}^{het2}$	$p_C^{hom1}$	$p_{FA}^{hom1}$	$p_C^{hom2}$	$p_{FA}^{hom2}$
True	0.806	0.185	0.009	0.489	0.496	0.015	0.994	0.006	0.999	0.001
SPIM3A	0.806	0.185	0.009	0.486	0.498	0.016	0.993	0.007	0.997	0.003
SPIM2A	0.805	0.185	0.009	0.484	0.500	0.016	0.993	0.007	0.996	0.004
SPIM1A	0.797	0.194	0.010	0.479	0.503	0.018	0.993	0.007	0.989	0.011
SPIM3B	0.806	0.185	0.009	—	—	—	0.994	0.006	—	—
SPIM2B	0.805	0.186	0.009	—	—	—	0.994	0.006	—	—
SPIM1B	0.792	0.198	0.010	—	—	—	0.993	0.007	—	—

Scenarios indicate the model used (SPIM), the number of replicated assignments (1 to 3), and whether the low-quality samples were included (A) or not (B). C, AD, and FA indicate correct, allelic dropout, and false allele probabilities, respectively. Het indicates heterozygous genotypes and hom indicates homozygous genotypes. The high-quality sample parameters are indicated with a “1” and low-quality parameters are indicated with a “2.”

Discussion

We developed the gSPIM, a unified probabilistic framework for the processes of determining the true genotypes of samples, matching samples to individuals, and estimating population parameters using spatial capture–recapture. The gSPIM recognizes that uncertainty in the genetic classification and population estimation processes is sequentially connected and propagates this uncertainty from one process to another, using a hierarchical model. The gSPIM allows for a fundamental shift in the use of genetic data in capture–recapture, eliminating the need for decision rules that determine the (minimized) expected level of error in the individual identity assignments and that do not propagate identity error probabilities to the population parameter estimates. Perhaps most importantly, the gSPIM eliminates the need for data culling, which can be extreme in many noninvasive datasets where DNA quality is typically poor, and leverages the additional information to increase the precision and accuracy of population parameter estimates. This is especially important in conservation applications of many species that are of concern largely because of their extremely low population sizes.

Unlike all existing approaches to address genotype uncertainty in capture–recapture surveys, the gSPIM recognizes that ecological systems are spatially explicit and uses the spatial location where genetic samples were collected to reduce genotype uncertainty. Two key features of our model that allow it to exploit the spatial information of genetic samples are a spatially explicit model for the number and distribution of individuals and genotypes across the study area and a spatially constrained model for individual detection (Box A). This genotype-augmented ecological and capture model provides the scaffolding that allows for the shadow effect to be efficiently resolved (disallowed in the most similar nonspatial model of ref. 19) and which formally links the ecological concepts of population density and home range size to the uncertainty in assigning samples to individuals (21). The gSPIM recognizes that samples collected closer together in space are more likely to come from the same individual, so each sample carries information about the true genotype of its neighboring samples and the genotyping errors that likely did or did not occur in these neighboring samples. This contrasts with previous approaches for matching samples to individuals in the presence of genotyping errors that assume the samples are independent of one another (e.g., refs. 17, 29, and 30). Using the spatial locations where samples were collected reduces the uncertainty in each captured individual’s estimated genotype, improves the estimation of genotype frequencies and genotyping error rates, and improves the probabilistic assignment of samples to individuals. The net result is improved estimates of population parameters. Posterior distributions of identity assignments can be visualized for every sample, providing an understanding of how the ecological, capture, and genotype observation models combine to produce the probabilistic assignments (examples in Dataset S1).

The population parameters of interest in this paper are abundance and density and we demonstrated (via simulation) that the gSPIM estimates of these parameters are significantly more accurate and precise than when using a more typical approach that discards samples with remaining uncertainty in individual identity. Further, these estimates were 25% more precise for the empirical example with fisher. We expect these improvements in precision and accuracy to propagate to other population parameters of interest that can be estimated using SCR models when modified to include the genotype observation process. For example, estimation of survival, recruitment, and movement/dispersal (e.g., ref. 31); resource selection (32); and landscape-connectivity parameters (33) are likely to be improved with the additional data from partial genotypes. Further, the uncertainty in individual identity should also be reduced by sharing information about individual locations and genotypes across time or by leveraging these more complex models of individual space use. Finally, it is also possible that a model for genetic recombination could be used to further improve estimation, but also make better inferences about parentage (34) and other genetic parameters. In fact, the parentage model of Hadfield et al. (34) includes distance between parents and offspring to inform parentage and accommodates genotyping error using the model of Wang (35), but requires extensive prior information on individual home range locations. We expect this prior knowledge could be replaced with capture–recapture data as our model exploits.

It is the spatial structure of the gSPIM that allows for the substantial contributions from the low-quality samples. Whether in the additional identity assignments of the fisher application, improved inference in the simulation study, or the identifiability of the model parameters with only one genotype assignment (Simulation Study and SI Appendix), our model allowed low-quality samples to become valuable. Unlike the most similar nonspatial model of Wright et al. (19), the gSPIM is identifiable with no genotype information at all, at least when the level of home range overlap between individuals is not high (higher home range overlap contributes to higher uncertainty in individual identity) (21) because it reduces to the unmarked SCR model (23) that uses spatial information alone to resolve individual identities. Further, Augustine et al. (21) showed that introducing just a few genetic loci known with certainty can lead to the model parameters being identifiable when they are not identifiable using only the spatial information, and not much genetic information is required to achieve certain individual identities across a wide range of home range overlap. In this respect, the gSPIM is a lower-information version of the model of Augustine et al. (21) because it recognizes the practical reality that genotypes are observed with error, particularly the heterozygous single-locus genotypes subject to allelic dropout. Therefore, the importance of spatial information in these previous models carries over to the gSPIM, and the spatial locations will be more influential as the information content of the observed genotypes decreases, due to either fewer observed loci across replicates or increased genotyping error rates.

The gSPIM should be relatively robust to misspecification of the genotyping error model (see ref. 21, for comments specific to the genotype distribution model). In many populations, particularly lower-density populations, there may only be a few possible individuals with home ranges near any particular focal sample and even fewer with similar genotypes. Genotyping error rates may vary as a function of error type (allelic dropout vs. false allele), zygosity (heterozygote vs. homozygote), sample quality, locus, replicate number, or individual. Of these factors, we expect the largest differences to be between error types and sample quality, both of which we accommodated in the gSPIM. Error rates could be generalized to vary by locus and replicate number, although we do not see a plausible reason why they would vary by individual. Paetkau (11) identified that faulty laboratory procedures can lead to a lack of independence between samples and that sample quality can lead to a lack of independence across markers for the same sample. The former source of dependence could be accommodated with replicate covariates and the latter with sample type covariates, which we used. Instead of dividing samples into “low” and “high” quality categories, one could use sample covariates that correlate with the amount and/or quality of the DNA in each sample, if they are available. In the absence of these covariates, the cruder sample type categories based on the amplification rates across replicated assignments that we used should improve inference.

Perhaps the most critical assumption of the gSPIM is the proper specification of the detection model, which will be important for species with especially large individual variation in space use and movement, whether due to variable home range sizes for residents, long-distance movements by dispersing individuals, or extraterritorial forays. These features can be accommodated by introducing covariate effects on the spatial-scale parameter, if the explanatory covariates are available, or by including a general random effect for individual heterogeneity if the explanatory covariates are not available. The fisher application contained three known cases of individuals with particularly long-distance movements (confirmed with high-quality samples), two males and one female, which we believe were likely dispersal events or extraterritorial forays. We were able to accommodate this rather extreme individual heterogeneity in space use in the fisher application using a modified version of the model of Efford and Mowat (36), which specifies a deterministic, negative relationship between individual movement scale (${\sigma }_{0_i}$) and baseline encounter rate (${\lambda }_{0_i}$) with a single random effect on movement scale, for which we provided a prior (on the SD of $\sigma$), informed by the ecology of the species. The adequacy of this space use model for the low-quality samples could not be directly assessed, but we expect that the level of variation in space use documented by the high-quality samples (two-thirds of all samples) was similar to that present when including the low-quality samples. Given the importance of individual heterogeneity in detection function parameters to the performance of SPIMs (21, 37), we recommend further research and model development.

As is the case for any statistical model, further exploration of the gSPIM via simulation studies and application to different datasets can help identify which assumptions are most vital and which components may need more realism. One particular advantage of the gSPIM in this respect is that thousands of genetic capture–recapture datasets exist to which the gSPIM could be applied and the probabilistic individual identity assignments it makes can be compared with those made using typical methods. In our fisher application, after allowing for individual heterogeneity in space use, the gSPIM made the exact same individual identity assignments for the high-quality samples as the genetic laboratory except for two cases where the gSPIM suggested the genetic laboratory was too confident in an assignment, two cases where the gSPIM convincingly suggested the genetic laboratory created false individuals, and one case where the gSPIM convincingly suggested the genetic laboratory created a shadow event. These discrepancies can be inspected in Dataset S1. The accuracy with which the gSPIM probabilistically assigned the low-quality samples could not directly be assessed (although see arguments above regarding space use), but this may be assessed in the future in two ways. First, the gSPIM could be applied to datasets with many high-quality samples and high-certainty assignments after thinning the observed genotype scores to produce low-quality samples so that the individual identities of these low-quality samples are known with near certainty. Second, we believe goodness-of-fit statistics could be developed for many aspects of the gSPIM, allowing for model fit to be quantified by posterior predictive checks (38).

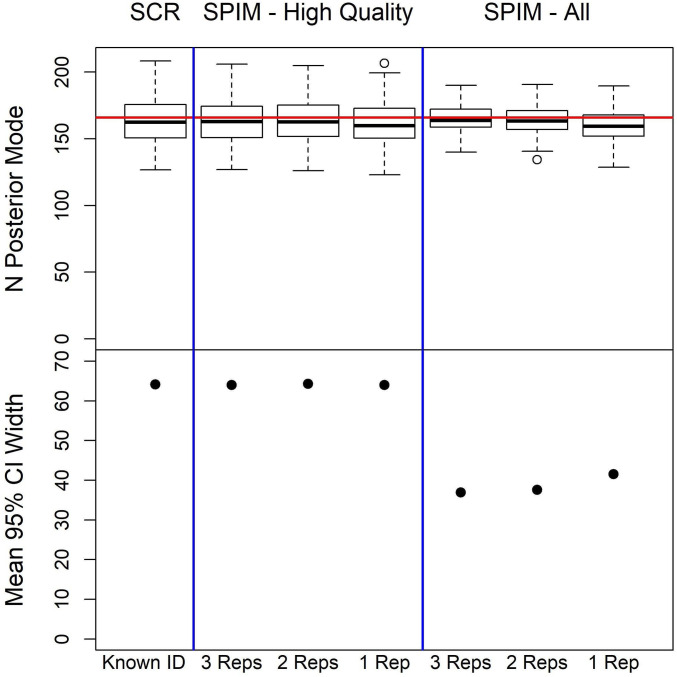
While the gSPIM can improve inference for datasets produced using the current genotyping protocols, which seek to maximize certainty in individual identity for just a subset of samples, these genotyping protocols may not be optimal when using our model that exploits uncertain-identity samples. The simulation study demonstrates that the amount of information obtained about individual identity from each replicate assignment declines exponentially, while the costs increase linearly, so less replication in general may provide a better compromise between project cost and the precision of population parameter estimates. Further, it is possible that more replication of the low-quality samples that are typically discarded as unreliable leads to larger improvements in population parameter estimates than replication of the high-quality samples which have been the focus to date. In the simulation study, adding replicate assignments over the first assignment improved the abundance estimate precision and accuracy very minimally when using only the high-quality samples (Fig. 4 and Table 3). Including the low-quality samples improved both the precision and accuracy of the abundance estimate and adding a second replicated assignment in this scenario reduced bias, substantially improved the accuracy, and modestly improved precision. Thus, it is possible that current applications of the multitubes approach may be allocating too much effort to replicating high-quality samples, and protocols that preclude the replication of poorly performing samples may be misallocating resources when the gSPIM can be used. Because the gSPIM provides a single probabilistic framework for genetic capture–recapture, different genotyping protocols can be evaluated via simulation using clearly defined assumptions about the ecological, capture, and genotyping processes. The minimum level of replication required in practice will depend on the specifics of the dataset, but see SI Appendix for an application demonstrating that density can be estimated with only one replicated assignment per sample using a real dataset.

Fig. 4.

Plots of simulation study results for the estimation of abundance. Top row displays boxplots of the posterior modes for abundance (simulated value is 166), showing estimator accuracy, and Bottom row displays the mean 95% CI width, a measure of estimator precision. The estimators from Left to Right are the SCR estimator using only certain identity samples; followed by the gSPIM estimators using only the high-quality samples with three, two, and one replicated assignments; followed by the gSPIM estimators using both high- and low-quality samples with three, two, and one replicated assignments.

Classification methods are being increasingly applied to ecological monitoring and assessment problems such as bioacoustics (39, 40), remote cameras (41, 42), and environmental DNA (43). In the context of individual identification using remote cameras (44), classification methods assign individual identities using the photographs alone, with no linkage to the ecological or capture processes, and typically require training data of known-identity individuals. The gSPIM model we developed here suggests a very broad class of models which integrate or couple ecological models of abundance or species distribution with explicit models of classification. As we demonstrated in this paper, individual classification should be improved by linking the process of identifying individuals to the ecological and capture processes, especially in situations of lower signal-to-noise ratios (i.e., relatively poor classifiers), and this linkage would facilitate the propagation of uncertainty to the population parameters of interest. To date, the use of machine learning to produce individual identities from photographs has been mostly applied to problems with a high signal-to-noise ratio, for example, spot patterns on animal flanks (e.g., refs. 41 and 44), and the uncertainty in assigning the individual identities has not been propagated to the population parameters of interest (but see ref. 45). Our approach is an example of unsupervised learning (uses no labeled training data), while most machine-learning applications to camera trap photographs implement supervised learning; however, our approach requires easily quantifiable features, which are not typically available for photographs. It is possible these two approaches could be combined to exploit the power of deep learning for extracting information about individual identity in photographs (e.g., ref. 42) while connecting this information to the ecological and capture processes. To illustrate how our approach could be applied to camera trap photos directly, we provide a small simulation study and an application of a simplified version of the gSPIM to a camera trap dataset in SI Appendix. We argue that the model did not perform well in this application due to a very low signal-to-noise ratio; however, this example shows how an application could work in a situation where more information about individual identity can be reliably extracted from photographs. Finally, we note that linking the species identification process to the ecological and capture processes when using machine learning to produce species records for occupancy studies should also improve inference.

Noninvasive genetics has revolutionized the study of animal populations by capture–recapture, allowing for the study of many species that could not have been studied effectively using conventional methods based on physical capture or species that cannot be individually identified from camera traps. However, noninvasive studies often result in sparse datasets that can lead to imprecise population parameter estimates which are of limited use in conservation decisions because they lead to an inability to discriminate between a population in need of conservation action and one that is not. Biased estimates of population parameters can be even more problematic, potentially falsely indicating that an imperiled population does not warrant conservation action, risking extinction, or that a healthy population does warrant conservation action, leading to an ineffective allocation of resources. Therefore, unbiased and precise estimation of population parameters is vital for making reliable, evidence-based, conservation decisions. Our gSPIM links genetic classification with the ecological and capture process and accordingly results in increased accuracy and precision of density estimates with less bias and no data loss, which can lead to more informed conservation decision making.

Materials and Methods

Model Description.

Here, we present an ecologically integrated genetic classification model (gSPIM), which is the main focus of our paper, but see SI Appendix for a model formulation presented in a more general classification context and for an application to individual identification from camera trap images using human classifiers of images. The gSPIM is a three-level hierarchical model (22) (Box A, Fig. 1), with the first two levels being models for the ecological and capture processes. We use a joint ecological process model, the first component of which describes the number and distribution of individuals across a two-dimensional state space, $\mathcal{S}$, by use of a spatial point process in which realized point locations ${\mathit{S}}_{N\times 2}$ represent each individual’s mean location (activity center) during the survey. We assume activity centers are distributed uniformly—${\mathit{s}}_i\sim \text{Uniform}\left(\mathcal{S}\right)$, $i=1,\dots ,N$, although other models could be used. The second process model component describes the population of multilocus genotypes, ${\mathit{G}}^{true}$, which we define to be an individual’s true values at $n^{cat}$ genetic loci. Each locus $l$ has $n_l^{levels}$ possible single-locus genotypes, $l=1,\dots ,n^{cat}$, which are enumerated $1,\dots ,n_l^{levels}$ for each $l$. Associated with each locus $l$ are single-locus genotype frequencies ${\mathit{\gamma }}_l$, the probabilities with which each single-locus genotype occurs in the population. We assume genotypes are independent across individuals and loci: $g_{il}^{true}\sim \text{Categorical}\left({\mathit{\gamma }}_l\right)$. Together, these models for the activity centers and genotypes provide a spatially explicit description for the distribution of genotypes across space. Note that this genotype distribution model allows multiple individuals in the population to have the same multilocus genotype (shadow effect).

The capture process then describes how animals are encountered, conditional on their activity centers. This model has two parameters, ${\lambda }_0$, the expected number of detections per occasion of an individual whose activity center is located exactly at a trap location, and $\sigma$, the parameter that governs how quickly the detection rate declines with distance from an individual activity center (depicted in Box A, Fig. 1). The spatial-scale parameter relates directly to the home range size of the species being studied (27) and thus has an ecological interpretation. We assume individuals are detected at specific point locations in the state space (i.e., “traps”), ${\mathit{x}}_j;j=\mathrm{1,2},\dots ,J$. The true (but latent) number of captures for individual $i$ at trap $j$ across $K$ occasions is $y_{ij}^{true}$. We assume the individual by trap by occasion detection process is Poisson, where the baseline detection rate of individual $i$ at trap $j$ is $\lambda \left({\mathit{s}}_i,{\mathit{x}}_j\right)={\lambda }_0\exp \left(-\frac{{\Vert {\mathit{s}}_i-{\mathit{x}}_j\Vert }^2}{2{\sigma }^2}\right)$, and $y_{ij}^{true}\sim \text{Pois}\left(K\lambda \left({\mathit{s}}_i,{\mathit{x}}_j\right)\right)$. It is important to note that this detection model requires that at least some individuals are captured in multiple locations (i.e., spatial recaptures), putting some minimal requirements on the spatial sampling relative to home range size (27). Then, because we do not observe individual identities directly, the observed capture data are recorded at the sample level. The capture data for sample $m$ are ${\mathit{y}}_{m.}^{obs}$, where $y_{mj}=1$ if sample $m$ was detected at trap $j$ and 0 otherwise.

Finally, the genotype observation process describes how the genetic loci are observed conditional on the true multilocus genotypes of each sample. We suppose that the locus-level genotypes will not always be observed correctly using an explicit genotype observation process (Box A, Fig. 1). We allow for three observation events: correct observation, allelic dropout (heterozygote observed as homozygote), and false allele (any other error). We use a simple model for these genotype observation events that assumes that each possible allelic dropout event is equally likely (previously assumed by refs. 19 and 30), each possible false allele event is equally likely (previously assumed by ref. 30), and the allelic dropout and false allele probabilities do not vary across sample (relaxed below), locus, individual, or replicate number. We define ${\mathit{p}}^{hom}$ and ${\mathit{p}}^{het}$ to be vectors of the observation probabilities for homozygous and heterozygous locus-level genotypes, respectively. Then, ${\mathit{p}}^{hom}=\left(p_C^{hom},p_{FA}^{hom}\right)$ for homozygous correct and false allele observation and ${\mathit{p}}^{het}=\left(p_C^{het},p_{AD}^{het},p_{FA}^{het}\right)$ for heterozygous correct, allelic dropout, and false allele observation. These observation probabilities then make up the elements of ${\mathit{\pi }}_l$, the observation probability matrix for locus $l$, conditional on the true locus-level genotypes. Details of how these matrices are constructed along with more technical details of the model can be found in SI Appendix.

Fisher Application.

We applied the gSPIM to a hair snare dataset from fishers surveyed in New York, collected in 2014. The full details of this study can be found in Linden et al. (25). There were 608 traps, operated for three 1-wk occasions, yielding 420 hair samples. Each sample was amplified one to seven times across nine microsatellite loci. In the original study, 263 samples were assigned individual identities using the methods of Creel et al. (9) with a $P_{ID-sib}$ criterion of 0.005, although some additional matches were made using the methods of MacBeth et al. (17). The 263 samples were assigned to 189 distinct individuals. There were 157 samples (37%) discarded because they produced partial genotypes not informative enough to be confidently assigned individual identities (105 samples) or they did not amplify at all (52 samples). Among the individually identified samples in the original study, there were 74 recaptures from 50 individuals and 9 spatial recaptures across 8 individuals. The low rate of spatial recaptures was largely due to a survey that was primarily designed for an occupancy analysis aiming for independent trap sites.

We applied the gSPIM to all 420 collected samples and compared it to the estimates from the regular SCR analysis using the 263 samples originally assigned certain individual identities using typical methods. For both the gSPIM and SCR analyses, we used the individual heterogeneity model for the detection function parameters described in SI Appendix, because the distribution of spatial recapture numbers and distances suggested strong individual heterogeneity in space use. We allowed genotyping error rates to vary by two sample quality categories as described in SI Appendix. We defined “high-quality” samples to be those that amplified at an average of eight or more of nine loci across the first three replication attempts and “low-quality” samples as those amplifying at an average of fewer than eight loci across the same three replication attempts. This criterion is somewhat arbitrary, but it is more realistic than assuming all samples have the same genotyping error probabilities and is consistent with the fact that samples with less DNA product have both higher genotyping error rates and lower locus-level amplification rates (4, 46). To compare the precision of selected parameter estimates between the gSPIM and SCR analyses, we used the coefficient of variation (CV)—the posterior SD divided by the posterior mode. See SI Appendix for the Markov chain Monte Carlo (MCMC) specifications for this analysis.

Simulation Study.

We conducted a small simulation study motivated by the fisher analysis with a large proportion of originally discarded samples to demonstrate the performance of the gSPIM in general (e.g., bias and coverage) and to compare 1) the regular SCR estimate using only high-quality samples to the gSPIM estimates using all samples, 2) the gSPIM estimates with one to three replicated assignments per sample, and 3) the gSPIM estimates using or discarding the low-quality samples. The simulation study was designed to replicate the design that produced the fisher dataset with a few caveats. Specifically, we did not consider the individual heterogeneity model for the detection function parameters to reduce computation time; we used a smaller trapping array with traps spaced optimally for SCR to better reflect the typical resources available for survey effort, and we considered a higher population density so that the scenario is more challenging for uncertain-identity methods (more home range overlap) (21). See SI Appendix for the full simulation study specifications.

Data Availability.

All data and code necessary to reproduce this analysis are available on the Dryad Digital Repository at https://doi.org/10.5061/dryad.4qrfj6q6b.