Epidemics as an adaptive driving force determining lifespan setpoints

Significance

Aging is an evolutionary paradox. Traditionally, it is assumed as a maladaptive and nonprogrammed process of physical deterioration. Hypotheses of programmed aging are currently regarded as unfeasible since the evolutionary benefits of senescence are unclear. Here, we develop a model indicating that limiting lifespan is beneficial to control epidemics, providing a possible explanation for species lifespan setpoint selection and the absence of biologically immortal mutants. Our study suggests a unifying hypothesis in which lifespan is selected to prevent and limit outbreaks of chronic infectious diseases.

Abstract

Species-specific limits to lifespan (lifespan setpoint) determine the life expectancy of any given organism. Whether limiting lifespan provides an evolutionary benefit or is the result of an inevitable decline in fitness remains controversial. The identification of mutations extending lifespan suggests that aging is under genetic control, but the evolutionary driving forces limiting lifespan have not been defined. By examining the impact of lifespan on pathogen spread in a population, we propose that epidemics drive lifespan setpoints’ evolution. Shorter lifespan limits infection spread and accelerates pathogen clearance when compared to populations with longer-lived individuals. Limiting longevity is particularly beneficial in the context of zoonotic transmissions, where pathogens must undergo adaptation to a new host. Strikingly, in populations exposed to pathogens, shorter-living variants outcompete individuals with longer lifespans. We submit that infection outbreaks can contribute to control the evolution of species’ lifespan setpoints.

Epidemics, the spread of a pathogen through a population, can be abrupt or can continue over long periods at low levels. The properties of the pathogen determine the modes of disease spread, including its capacity of transmission and mortality rate, the length of its infectious period, and the density and structure of the host population. Mathematically, the epidemic process can be described by R₀, the basic reproduction number. R₀ represents how many susceptible individuals, on average, are infected by a single infected individual. If R₀ is more than 1, then pathogens are spreading through the population (1). R₀ depends on pathogen transmissibility (β), host population density (N), and the average length of the infectious period (1/γ): R₀ = Nβ/γ. The length of infection can be described as 1/γ = 1/(δ + ρ + μ), where δ is disease-induced mortality rate, ρ is the recovery rate, and μ is the natural mortality of the host. In the case of chronic infectious diseases, where infection is neither cleared nor fatal (δ ∼ 0, ρ ∼ 0), the duration of infection and, therefore, the R₀ mainly depend on the intrinsic, species-specific mortality (1/γ ∼ 1/μ). Thus, increasing natural mortality by shortening lifespan could reduce R₀ and protect from epidemics.

These epidemiologic considerations provide a framework suggesting that epidemics could drive the selection of lifespan setpoints as a function of the natural history of a given population. The evolutionary determinants for lifespan limits in nature are the subject of intense debate. Modern hypotheses of how lifespan setpoints are determined can be divided into two general groups: nonprogrammed and programmed hypotheses. Nonprogrammed hypotheses propose that aging is not selected for through evolution, but instead is an unavoidable adverse side effect of useful biological functions or damage accumulated during life (2–5). However, many closely related species, with similar cellular, molecular, and metabolic characteristics, exhibit very different lifespan setpoints, suggesting that lifespan can be modulated by environmental conditions in which a given species evolved.

Accordingly, programmed theories argue that aging is genetically programmed, and that limiting lifespan can be evolutionarily advantageous. In this view, aging is an adaptive biological function that increases the fitness of the organism and can, thus, be modulated by the evolutionary history of the individual (6–10). However, because a long fertile lifespan is expected to be positively selected through evolution, a central question is what are the selective forces setting a limit on lifespan advantageous.

One proposed factor for the selection of short lifespan setpoints is the pressure posed by infection (10). Indeed, genes involved in immunity are among the most rapidly evolving in the genome of most organisms, highlighting the tremendous evolutionary pressure posed by pathogens (11).

In this study, we determined whether limiting the lifespan of individuals within a population provides a selective advantage by protecting them from infectious diseases. Using well-established epidemiological models, we examined the properties of the pathogen and the population structure, leading to the establishment of epidemics. Our analyses identified the advantage of limiting lifespan to prevent the spread of pathogens in a population and provide a general rationale for the selection of lifespan setpoints determined by organism interaction with pathogens. This hypothesis is particularly relevant in the context of pathogens that cause chronic infections, such as HIV, leprosy, or syphilis. Limiting individual lifespans is especially beneficial to reduce the likelihood of zoonotic outbreaks. This framework affords a rationale for a number of lifespan-related observations, including the absence of immortal mutants, the existence of genes with aging-related pleiotropic effects (12, 13), the correlation between longevity and flight (14), and the evolutionary determinants of longevity outliers, such as naked mole rats (15). Our hypothesis offers a potential explanation to the long-standing paradox of why organisms age with species-specific lifespan setpoints.

Results

Epidemiological Models Reveal That Shorter Lifespan Setpoints Benefit Population Fitness.

No species is entirely isolated. Indeed, every individual organism is in constant interaction with other species, including microorganisms. These interactions often have significant effects on individual fitness and are critical drivers of evolution (16).

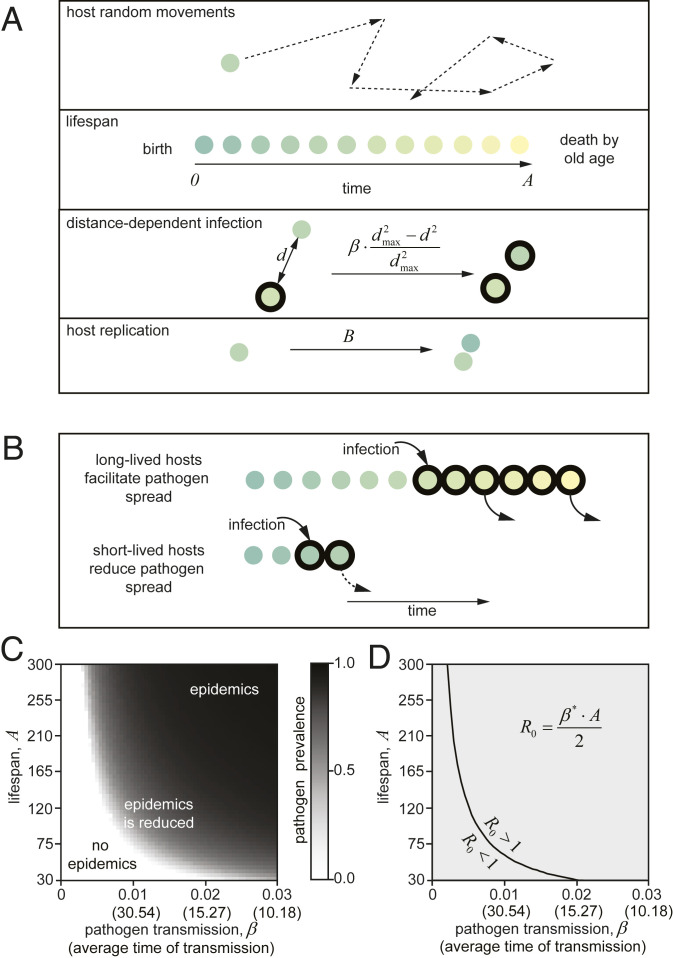
We hypothesized that the limitation on lifespan setpoints represents one of the earliest, nonspecific, defense mechanisms limiting the spread of pathogens. To examine the potential link between lifespan setpoints, population dynamics, and protection from infection, we adapted previously developed models (1) to focus on lifespan setpoints as an epidemiological parameter. In the initial simulations, we considered a starting population of 5,000 individuals with a range of defined lifespans in a flexible model where arbitrary time units can reflect days, months, or years, depending on the given organism. We then exposed the population to pathogens (Fig. 1 and SI Appendix, Fig. S1 and Movie S1) and assumed that there are no other reasons for death except reaching the maximum lifespan. We do not consider a gradual age-dependent fitness decline, as in nature, early signs of age-related deterioration result in an individual’s death. The initial simulations considered no recovery from diseases, no vertical pathogen transmission, and no pathogen effects on the individual’s fitness (Fig. 1A). The field is a square with a side of 10⁴ length units, and the animals are moving randomly at a constant speed of 10² length units per unit of time. Under these conditions, the population is uniformly mixed, as in previous epidemiological models (1, 10, 17). We then examined the effect on the host population of pathogens with different transmission rates, assuming that pathogens are continuously present in the system: When the last infected host dies, pathogens are reintroduced from another host species or the environment. In this manner, our model considers the progression of existing infections and the establishment of new epidemics. Infection efficiency depends directly on the proximity of an infected individual to an uninfected. Transmission efficiency (β) is the probability that a pathogen from one infected individual is transmitted to other individuals in a healthy population of maximum density (e.g., the distance between them is minimal [d = 0]). With an increase of the distance between individuals (d), the transmission efficiency was calculated as $\beta \cdot \left(\left(d_{\max }^2-d^2\right)/d_{\max }^2\right)$, where d_max was a constant set to 200 length units (Methods and Fig. 1A and Movie S1). We also assumed that transmission is not affected by age, and pathogens are transmitted through the entire host life with equal probability.

Fig. 1.

Model I. Length of lifespan controls the establishment and progression of epidemics. (A) Basic rules of the stochastic model I. Individuals are randomly moving across the experimental niche. Death is determined by the age of an individual and the species-specific lifespan setpoint $\left(A\right)$. Infection depends on the distance between individuals $\left(d\right)$ and on pathogen transmission efficiency $\left(\beta \right)$. Reproduction depends on basal fecundity $\left(B\right)$. In this model, neither fecundity nor longevity was affected by infection. Population limit was set arbitrarily to 5,000 individuals (see Methods for details). (B) Restriction of the lifespan results in inefficient spread of chronic low-transmissible pathogen. (C) Systemic analysis of pathogen prevalence dependence on $A$ and $\beta$. Short lifespan inhibits low-transmissible pathogens (“no pathogen replication”) and reduces pathogens with moderate transmission. Here and below, the average time of transmission (in parentheses) was estimated experimentally as an average time required for a single infected host to infect a single susceptible host in uninfected population. It is expressed in the same units as lifespan (A). See Movie S1. (D) A simplistic analytic model of dependence of $R_0$ on $A$ and $\beta$. $\beta \ast$ stands for $\beta$ corrected for the empirically estimated parameter for distance-dependent infection (Methods). For sample simulations, see Movie S1.

We first analyzed whether lifespan setpoints impact pathogen prevalence in the population, using a wide range of lifespan setpoints. We observed a direct correlation between lifespan and pathogen prevalence in the population. In agreement with previous results (10), when the pathogen transmission efficiency was relatively low (β = 0.001 to 0.02), the ability of the pathogen to establish epidemics correlates with the lifespan (Fig. 1 B and C, “no epidemics”). Thus, the model is consistent with the hypothesis that individuals with longer lifespans render the population more susceptible to epidemics. Populations with shorter-lived individuals also experience a fitness benefit even when facing pathogens with higher transmission efficiency (β = 0.02 to 0.03; Fig. 1C, “epidemics is reduced”), as reported (9, 10). Since older animals have a higher probability of possessing a chronic pathogen than younger individuals, the shorter lifespan setpoint will reduce the overall burden of pathogens in the population within a wide range of transmission efficiency. However, this beneficial effect is less significant when compared to epidemics prevention.

In these initial simulations, we considered sharp mortality of the individuals at a given lifespan setpoint. However, we obtained similar results with Gompertzian curves of mortality with a high age-dependent component (SI Appendix, Fig. S1 B and C) or with a high age-independent component (SI Appendix, Fig. S1 D and E). Thus, the observed effects in epidemics progression are independent of the type-of-mortality model (Movie S1).

An analytic solution to the model also supports the idea that populations with shorter lifespans will be protected from epidemics (Fig. 1D). As noted above, R₀ is the number of individuals infected by pathogens shed from a single infected host. Because our model assumes a constant density of individuals (N) and we posited that pathogens establish a chronic infection without causing an increase in mortality, R₀ can be expressed as transmission efficiency (β) multiplied by the duration of the infection. Considering that all individuals have the same probability of getting infected at the beginning of the epidemics, R₀ averages half of the host lifespan $\left(A/2\right)$. For simplicity, the population density-related component was considered to be constant and was omitted from the calculations. Given that during epidemics, for a pathogen to spread through the population, R₀ should exceed 1, the interdependence of $\left(\beta \cdot A\right)/2>1$ or $\beta >2/A$ demonstrates that epidemic progression is a function of lifespan (Fig. 1D). If the lifespan is shorter than the time required for spreading through the population, pathogens are unable to establish an epidemic. Thus, populations of shorter-lived individuals are expected to be more resistant to epidemics of persistent low transmissible pathogens. Notably, such persistent infections are often detected in animal populations. The best-documented examples in humans are leprosy, herpes, tuberculosis, AIDS, hepatitis B and C, and infections by helminths species.

Benefits from Limiting Lifespan during Zoonotic Transmission.

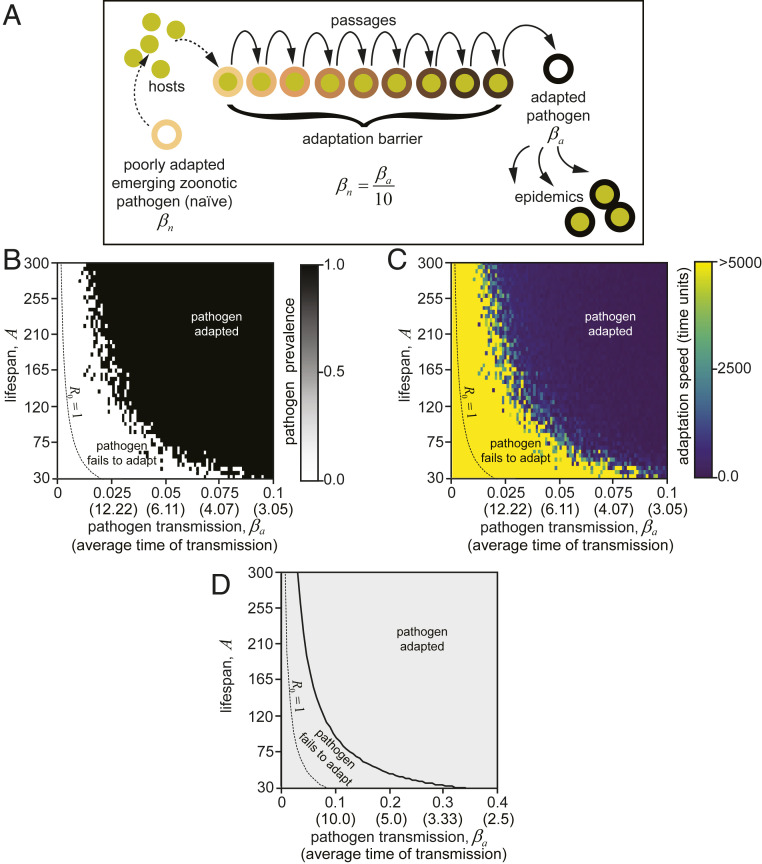
A common source of new pathogens is the transmission of pathogens between different host species, also called zoonotic transmission in the case of transmission from animals to humans. In this scenario, due to species differences, pathogens often undergo several cycles of replication in the new hosts before adapting and gaining optimal transmissibility, which can then lead to epidemics (Fig. 2A).

Fig. 2.

Model II. Zoonotic transmission, pathogen adaptation, and lifespan setpoints. (A) Schematic representation of pathogen adaptation in the context of zoonotic transmission. The model assumes that naive low-transmissible (β_n) pathogens required 10 passages to reach its adapted state and increase transmission (β_a). (B and C) Stochastic model showing a dependence of pathogen adaptation on A and β. If adaptation of the pathogen is required, the parametric space, where the shorter lifespan prevents increases in epidemics (Movie S2). The dotted line limits the domain of the adapted pathogen feasibility as in Fig. 1 C and D. (B) Pathogen shows high prevalence in all cases if it can adapt within the time of simulation (5,000 time units). (C) Time required for pathogen adaptation. (D) A simplistic deterministic model supports the conclusions of the stochastic model, showing an extended domain, where the short lifespan prevents the adaptation. The numeric differences between stochastic and deterministic models come from the differences in simulation of the infection and the stochastic nature of the adaptation process (see Methods for details).

To examine how lifespan setpoints impact the ability of zoonotic infections to establish epidemics in a new host population, we modified our simulation (Fig. 1) to incorporate an obligated step of pathogen adaptation to the new host. Thus, the initial efficiency of nonadapted pathogens transmission (Fig. 2A, β_n, “n” denotes “naive”) is 10-fold lower before adaptation occurs (β_a = 10 × β_n) (“a” stands for “adapted”). We assumed that adaptation requires the pathogen to undergo 10 rounds of replication in the new host to reach its final higher transmission efficiency β_a. This period of adaptation extends the time required for the establishment of epidemics and increases the beneficial effect of limiting lifespan. Indeed, the efficiency of adaptation of a pathogen to a new host depends on lifespan “A.” Under these “zoonotic infection” conditions, we observed that a larger set of pathogens, with a wider range of efficiency of transmission (β), were prevented from establishing epidemics in populations with shorter lifespan individuals (Fig. 2 B and C, “no pathogen adaptation”; Movie S2). These results were confirmed using an analytic solution to the model, similar to that used in Fig. 1D. By incorporating a period necessary for pathogen adaptation in our model, we observed an increase in the area where shorter lifespan can protect against epidemics outbreaks. We conclude that lifespan setpoints are a significant factor determining the ability of a zoonotic pathogen to establish epidemics (Fig. 2D and Methods).

Shorter Lifespan Setpoints Facilitate Pathogen Clearance during Host Population Bottleneck.

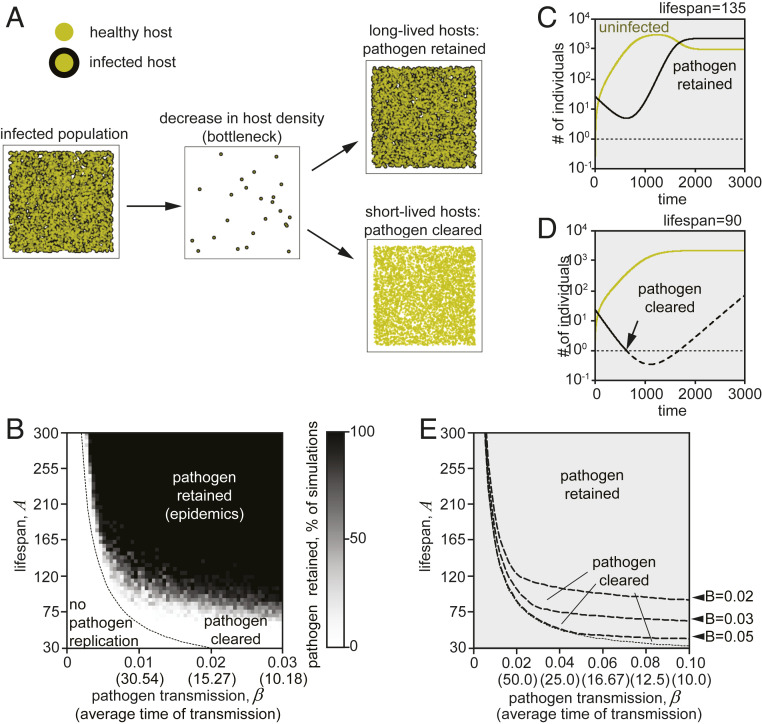
Populations often migrate to colonize new environments or encounter conditions that substantially reduce population density. Thus, we next studied the relationship between lifespan setpoint and pathogen load in the case of host populations migrating to a new environment, involving population size reduction or “bottlenecking” (18). We considered that a small group (25) of individuals from an infected population migrated to colonize the new environment (Fig. 3A and Movie S3). Under these conditions, since the initial population density is low, pathogens will not spread efficiently soon after migration until a critical density is reached. In this case, density depends directly on population size (N). Strikingly, our stochastic simulation shows that, in populations with shorter lifespans, the infected founders will die before the population density reached a level that allows efficient pathogen transmission (Fig. 3B). Accordingly, short-lived (SL) individual populations will clear the pathogens more efficiently than longer-lived populations.

Fig. 3.

Model III. Short lifespan facilitates pathogens clearance during critical declines in the host’s density or population bottlenecks. (A) Pathogen clearance after host migration to a new environment. Infected individuals of short lifespan died before the population reached a density sufficient for epidemics expansion. As a consequence, pathogens suffer severe bottlenecking and, therefore, are cleared from the population in the new niche. (B) Stochastic simulation reveals a region where the pathogen is cleared during the bottleneck. Bottleneck size was 25, maximum population number was 5,000, B = 0.05, and the number of replicates per data point was 10. The dotted line limits the domain of the pathogen feasibility as in SI Appendix, Fig. S1 C and D. See also Movie S3 for sample simulations. (C and D) Two examples of a deterministic simulation (Methods). B = 0.02, β = 0.04, bottleneck size was 25, and maximum population number 5,000. (C) A = 135, pathogen passes the bottleneck. (D) A = 90, pathogen does not pass the bottleneck (the number of infected animals goes below 1). (E) Deterministic model prediction of the clearance efficiency at different on A, B, and β. Clearance efficiency decreases with increase in B. Numeric differences between stochastic and deterministic models are due to differences in simulations of infection. See Methods for details.

The analytic solution confirmed these results (Fig. 3 C–E); the number of infected individuals reached less than one in populations composed of SL individuals (Fig. 3D, “pathogen clearance”). In contrast, in the case of long-lived (LL) individuals, pathogens survived the bottleneck (Fig. 3C, “pathogen maintenance”).

Given that density is an important parameter affecting epidemics progression, we next studied the role of host fecundity in pathogen clearance during host migration. Fecundity (B) is the number of individuals in the progeny produced per unit of time. By examining different B values, we find that clearance efficiency depends on the basal fecundity rate. Populations with highly fecund individuals will reach high densities faster, and thus the probability of pathogen spread will increase accordingly (Fig. 3E and Movie S3). In summary, these results indicate that short lifespan setpoints promote pathogen clearance by preventing the spread of infection when the host population undergoes significant density reductions, whereas the fecundity can modulate this effect.

Cost–Benefit Trade-Off of Extending Lifespan in “Well-Mixed” Populations.

The evolution of genetic traits that limit lifespan, common to most organisms, is counterintuitive. Individuals that live longer are likely to reproduce for longer times and be more effective in passing on their genes. On the other hand, the results described above establish that lengthening the lifespan facilitates epidemics. Thus, the advantage of extending lifespan to an individual appears to conflict with the detrimental effects on the population.

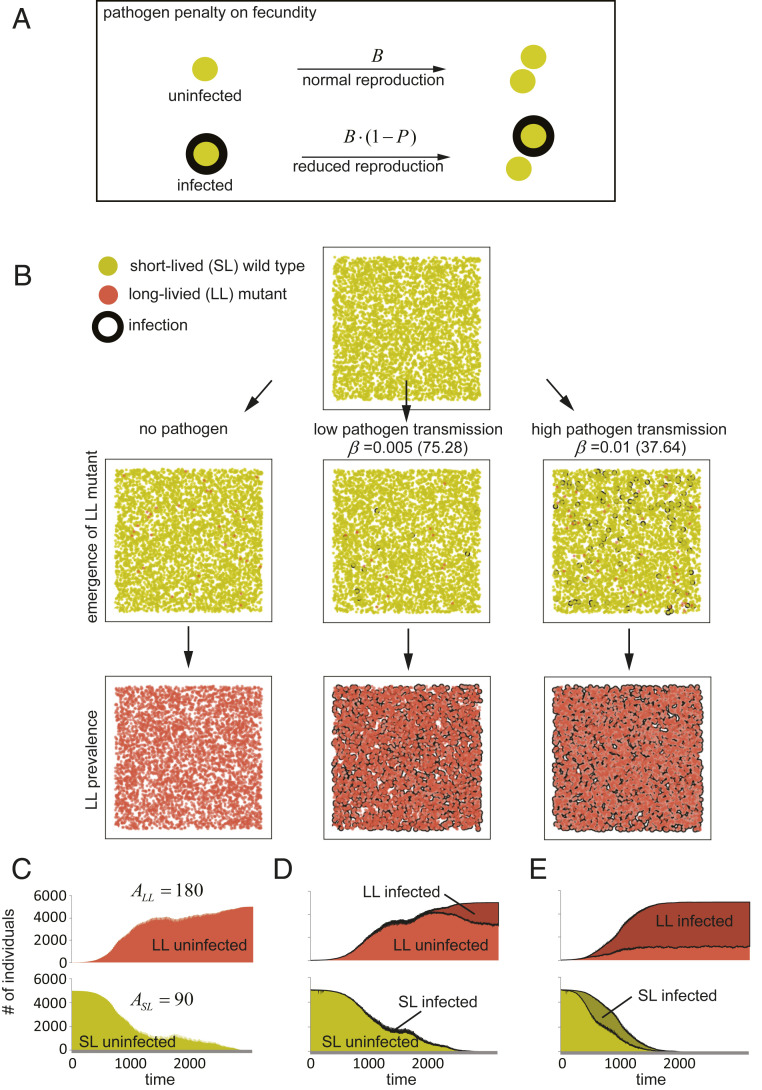
To directly determine whether short lifespan setpoints can be selected by infection, we next analyzed the population dynamics when a long-lived individual (Fig. 4B, light red) emerges in a population of SL individuals (Fig. 4B, yellow). We simulated the emergence of LL variants with a lifespan twice longer than that of the SL strain (A_SL = 90; A_SL = 180). For simplicity here and below, we assumed the asexual reproduction of both types of individuals and no age-dependent changes in fecundity.

Fig. 4.

Invasion of the long-lived mutant in uniformly mixed populations. (A) To account for disease-associated fitness cost we introduced a pathogen penalty P = 0.9 into model I (Fig. 1A). Thus, reproduction in infected animals is reduced 10-fold. (B–E) In uniformly mixed populations of short-lived individuals (A_SL = 90), long-lived mutants (A_LL = 180) were winning in competitions if pathogens were absent (C) or have had low (β = 0.005; D) or high transmission rates (β = 0.01; E). See Methods and Movie S4 for sample simulations.

To determine whether epidemics can be a selection force determining lifespan setpoints, we introduced a detrimental effect on the host fitness due to infection into the model. Our model assumes that infection reduces fitness and, therefore, the fecundity (but not the lifespan) of the infected individual. Accordingly, the fecundity of an infected individual was calculated as B×(1 – P), where P is the fitness effect on fecundity due to infection (Fig. 4A). The assumption that infection has a negative effect on the reproductive capacity of the infected individuals has been well documented and generally accepted (16, 19–21). Initially, we incorporated in our simulation a substantial detrimental effect on fecundity (P = 0.9).

Under conditions where all individuals in a population intermix evenly (i.e., long- and short-lifespan individuals have equal probabilities of interacting with each other), the longer-lived variants efficiently outcompete shorter-lived individuals (Fig. 4 B–E and Movie S4). Under these conditions, the presence of pathogens does not modify the outcome of the experiment (Fig. 4 C–E). Thus, in evenly mixed populations, the shorter-lived individuals are displaced by the emerging longer-lived variants even if this trait is detrimental to the fitness of a population when facing pathogens.

Selection of Lifespan Setpoints by Infection in Viscous Populations.

In nature, groups of organisms belonging to the same species and living in the same area do not exist as homogeneous populations, but rather as viscous populations in which the movement of organisms from their place of birth is relatively slow. This viscosity has one important effect: Local interactions tend to be among relatives.

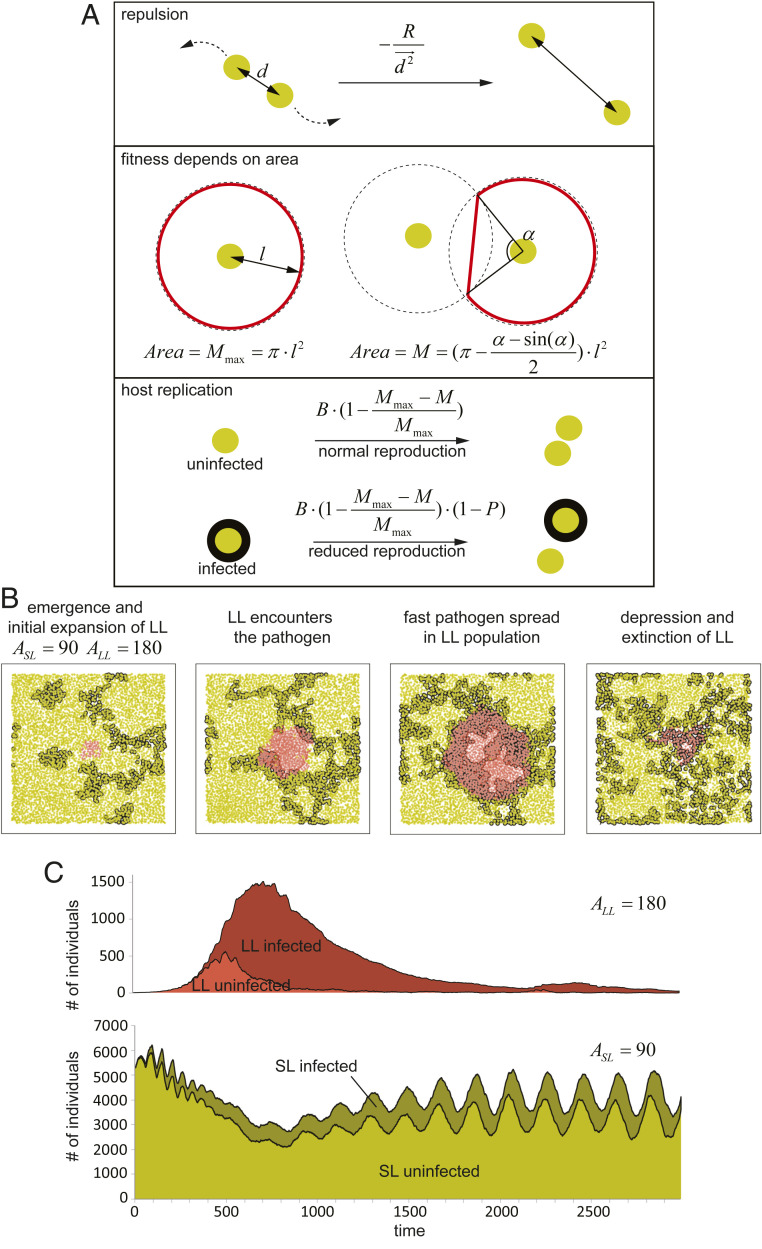
Given that this is a more realistic condition for many species (22), we modified our model to incorporate population viscosity into our simulations (Fig. 5). We considered that population dynamics within the niche are affected by the availability of the resources (e.g., food, water, shelters). The amount of resources that each individual can utilize is determined by the territory it controls. If the territories of two individuals overlap, it results in resource sharing and the reproductive fitness penalty to both individuals. Thus, individuals attempt to stay away from each other to prevent competition and to maximize their territories (Fig. 5A). To this end, in each round of simulation the resulting speed of individuals is calculated through a vector sum of quadrates of distances between neighbors. Maximum speed of movement is limited to 10 units to avoid individuals from crossing each other. These conditions result in the formation of irregular lattice-like distribution of organisms behaving similarly to a group of point electric charges of the same polarity floating on the surface of the dielectric liquid, with a constant “breathing” due to individual’s death and replication (Movie S5). Replication of individuals in a given sector is controlled by the local density context since resource availability depends on the individual’s territory. Thus, individuals are replicating faster in the sparse regions due to resource abundance and slower in the dense areas. The assumptions in our model are consistent with the territorial behavior described for many animal populations (23). While the model reveals a typical directional dispersal from densely inhabited regions to more sparsely populated areas, it does not exhibit migration over the long distances, but rather slow gradual changes of the individual territories driven by population pressures and resource abundance.

Fig. 5.

Model IV. Infection in viscous populations favors selection of short-lived hosts. (A) Modifications made to the model I to simulate viscosity. The maximum speed of individuals was limited, and the repulsion between individuals was introduced. Individual areas were calculated and used to find the dependence of fitness on local density (see Movie S5 for illustration of viscosity simulation and Movie S6 for epidemics progression in viscous populations). See Methods for details. (B) The principal stages of the selection scenario. After the initial expansion of the long-lived strain, the pathogen is encountered. Epidemics spread rapidly within long-lived individuals, resulting in its depression and extinction. (C) An example of simulation. β = 0.03, A_SL = 90, A_LL = 180, P = 0.9, B = 0.05, and R = 3 × 10⁵. See Movie S7.

Under viscous population conditions, lifespan affects epidemics in a similar manner as that observed in uniformly mixed populations (Fig. 1); namely, shorter lifespan reduces pathogen spread and the probability of epidemics establishment (Movie S6). We then examined whether LL mutants outcompete the SL strain in the absence of the infection as observed in homogenous populations (Fig. 4C and Movie S4). The simulation assumes similar conditions as described above (Fig. 4), specifically a small group of LL individuals (A_SL = 180) emerges in the center of a field populated by SL individuals (A_SL = 90). As observed in evenly mixed populations, in the absence of pathogens, LL variants displace SL individuals in viscous populations (Movie S6).

We next examined the effect of infection on lifespan selection. We considered a pathogen, with an intermediate transmission efficiency (β = 0.03), causing a significant reduction in the reproductive fitness of infected individuals (P = 0.9). The pathogen was introduced into the system by 10 random SL infected hosts, whose emergence concurred with the appearance of the LL strain. Strikingly, under these conditions, individuals with shorter lifespan efficiently outcompete the LL variants (Fig. 5 B and C and Movie S7). The process follows four successive steps: 1) LL individuals emerge and propagate in the population. Due to extended lifespan, the growth of their population is strongly accelerated. Pathogens establish minor but stable epidemics in SL population; 2) LL individuals get infected with pathogens circulating in the SL population; 3) as the LL population expands, the pathogens establish stronger epidemics in the area populated by LL individuals due to the effects described in Fig. 1. This more severe epidemic imposes a penalty for fitness, which mitigates the replication benefits of longer lifespan; 4) as a consequence, the SL individuals are dispersing in a population pressure-dependent manner into relatively sparse areas, previously occupied by LL individuals (Fig. 5B). Over time, the entire LL subpopulation is extinguished. Thus, chronic pathogens with a penalty on reproduction restrict the emergence of longer lifespan in viscous populations.

The Interplay among Infection, Population Viscosity, and Fertility during Lifespan Setpoints Evolution.

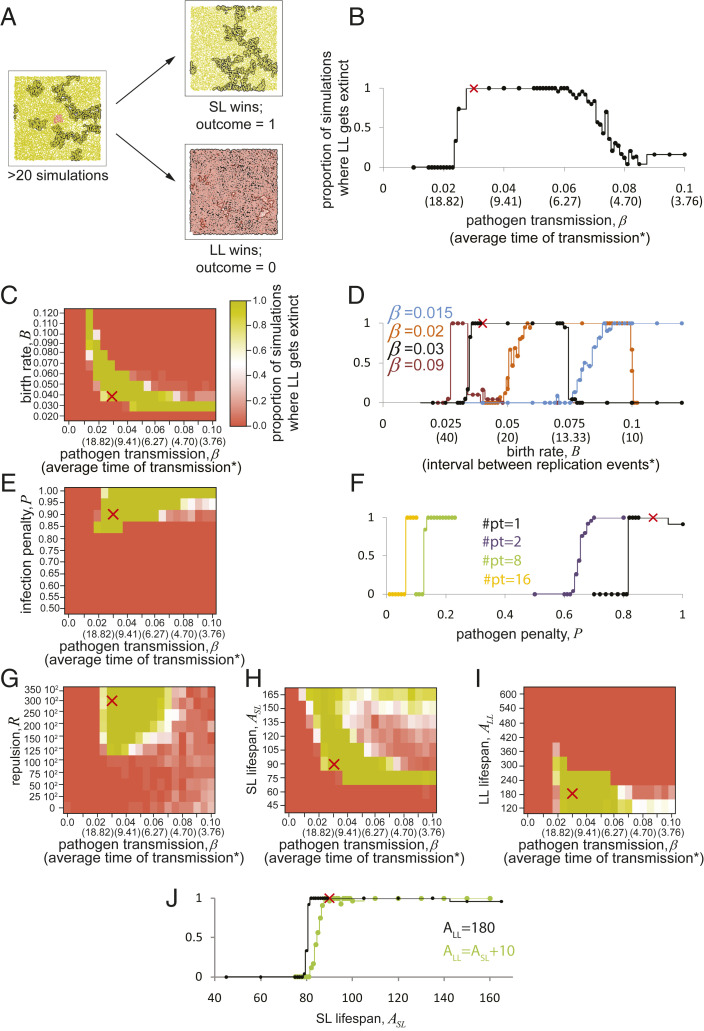
Next, we performed a sensitivity analysis to understand the range of parameters and conditions that enable the selection of lifespan setpoints. Our analyses indicate that five parameters are critical for lifespan setpoint selection: 1) pathogen transmission $\left(\beta \right)$, 2) pathogen penalty $\left(P\right)$, 3) host’s birth rate $\left(B\right)$, 4) the repulsion between individuals as a measure of population viscosity $\left(R\right)$, and 5) the ratio between lifespan of the SL (A_SL) and LL (A_LL) individuals (Fig. 6). These analyses define the conditions in which, based on our model, SL individuals have a fitness advantage over LL variants, and explain for the selection of shorter lifespan setpoint.

Fig. 6.

Sensitivity analysis of the lifespan selection in infected viscous populations. (A) We varied the parameters in simulation model IV (Fig. 5) to find the crucial determinants of the lifespan evolution. The outcome of simulation was considered to be 1 if short-lived individuals were taking over the whole population and 0 if long-lived were prevailing. Each data point was an average of at least 20 simulations. The black lines (B, D, and F) are the simulations performed as in Fig. 5 with only one parameter varied. The combinations of parameters exactly corresponding to the simulation in Fig. 5 are shown with the red crosses. The colored lines correspond to the simulation series with additional parameters changed: different values of β (in D) and coinfection with multiple pathogens (in F). The descriptions of the modifications are shown with the same color as the line itself. In the heatmaps (C, E, G, and I), parameters are analyzed at different values of β, and the outcome is expressed by color (see the scale in C). (B) The effect of pathogen transmission. Long-lived individuals were prevailing at low (<0.025) and high (>0.07) values of β. (C and D) Birth rate (B) affected lifespan evolution. At low values of B, long-lived individuals can take over in population, but in the region of higher values of B, short-lived individuals can win in presence of pathogens with particular values of β. Interval between replication events is calculated for a sparse population of individuals, without taking into account their overlapping territories. (E and F) The sterilizing effect of the pathogen (P) defines the selection of the lifespan. In case of a single pathogen, the penalty of P < 0.85 is insufficient to promote extinction of long-lived variant (E). However, if several independent pathogens with similar β and P are present in the population (F), much lower sterilization effects per pathogen are sufficient to favor the evolution of limited lifespan. #pt are the numbers of pathogens coinfecting the population. (G) Repulsion between individuals (R) is here a parameter of population viscosity. It is a key parameter determining lifespan setpoint evolution. Low viscosity is associated with the evolution of longer lifespan. (H and I) Larger difference in the lifespan between SL and LL is associated with the increased success of the long-lived variant invasion. The lifespan of SL (A_SL) and LL (A_LL) are analyzed in H and I correspondingly. (J) The presence of equilibrium lifespan in our model. A_LL was set to 180 t.u. as in H (black line) or to A_SL + 10 t.u. (green line). Both approaches display similar shapes of curves pointing to an equilibrium lifespan setpoint in the region of 90 t.u. The variants of such lifespan are able to invade the populations of individuals with shorter lifespan (e.g., A = 80), and at the same time are capable of resisting invasions of more long-lived variants (e.g., A = 100). See also SI Appendix, Fig. S2 for more detailed sensitivity analysis.

Our analysis shows that shorter-lived individuals have a fitness advantage within a range of transmissibility $\beta$from 0.02 to ∼0.07 (Fig. 6B). If the pathogen transmission is too low $\left(\beta <0.02\right)$, the spread of epidemics in LL population is insufficient to produce a high penalty on fitness. If pathogen transmission is higher, $\beta >0.08$, infection spreads rapidly in LL and SL hosts, equally decreasing the fitness of both. Under these conditions, infection was not specific, and we observed no fitness advantage for SL individuals. Thus, low pathogen transmission observed in persistent infections provides the most effective selective force for short lifespan setpoint selection. We observed that there is a substantial range of β that may be able to drive evolution of shorter lifespan, and this interval is expected for chronic diseases and many zoonotic pathogens at the start of the outbreak.

The host’s fecundity $\left(B\right)$ also had a significant effect on the outcome of the lifespan selection (Fig. 6 C and D). At high values of $B>0.075$, the density of the host population increases, and this enables the pathogen to spread equally in SL and LL hosts. We do not consider this effect critical: In nature, maximum densities of populations are rarely defined by the birth rate. Additionally, this effect could be mitigated at different parameters of β (Fig. 6 C and D and SI Appendix, Fig. S2 G and H). On the contrary, at low values $\left(B<0.025\right)$, the LL strain wins the competition independently of β.

A key role in our models is played by population pressures that depend on both fecundity and mortality. To provide a simplistic analytic explanation for the longevity–fecundity trade-off, we consider population growth as $dN/dt=N\cdot \left(B\cdot \left(1-n\cdot P\right)\hspace{0.17em}-\left(1/A\right)\right)$, where n stands for a proportion of infected individuals. Next, we simplify the population dynamics by assuming that SL and LL do not intermix. A condition that favors SL over LL would be as follows: $dN\mathrm{SL}/dt>dN\mathrm{LL}/dt$ that, if we assume$\hspace{0.17em}{N}_{\mathrm{SL}}\approx N_{\mathrm{LL}}$, comes to the following:$-\left(1/A_{\mathrm{SL}}\right)+B\cdot \left(1-n_{\mathrm{SL}}\cdot P\right)>-\left(1/A_{\mathrm{LL}}\right)+B\cdot \left(1-n_{\mathrm{SL}}\cdot P\right)$, that by trivial transformations gives $\left(\left(1/A_{\mathrm{SL}}\right)-\left(1/A_{\mathrm{LL}}\right)\right)\cdot 1/\left(BP\cdot \left(n_{\mathrm{LL}}-n_{\mathrm{SL}}\right)\right)<1$, where $n_{\mathrm{LL}}>n_{\mathrm{SL}}$. B staying in the denominator indicates that higher fecundity would positively affect selection pressure toward shorter lifespans. Intuitively, the bigger is the value of B, the faster is the accumulation of the difference in numbers between infected and uninfected populations, and stronger is selection against infected variants therefore. We consider this effect a potential explanation of the fecundity–longevity trade-off (4).

A strong penalty on reproduction imposed by infection $\left(P=0.9\right)$, which corresponds to a 10-fold decrease in reproduction, is a key component of the selection scenario. While infection by some pathogens (i.e., leprosy, severe herpes, gonorrhea, tuberculosis, or AIDS) may result in such a significant effect, other chronic infections may not produce such fitness penalties. We noticed that a decrease of $P$ below 0.8 resulted in insufficient penalty to prevent the emergence of LL variants (Fig. 6 E and F and SI Appendix, Fig. S2 N and O). However, natural populations are often infected simultaneously by multiple pathogens, and infection with one pathogen may facilitate infection with a second one (e.g., HIV and tuberculosis). Under conditions of multiple chronic infections, we observed that, even with much lower $P$per pathogen, the LL strain can no longer compete with SL individuals (Fig. 6F). Since the LL strain tended to accumulate multiple pathogens, the frequency of coinfection was higher in this variant, driving it to extinction due to the cumulative pathogen penalty (Movie S8). Indeed, SL individuals may be less likely to be infected with multiple pathogens simultaneously. Therefore, selection toward shorter lifespan might be mediated by a combination of several pathogens with relatively mild individual effects on reproductive fitness. Such pathogens might circulate in the population of SL hosts without a significant effect on fitness, and become a substantial selection factor only via multiple coinfection in the emergent LL variant.

The degree of repulsion between the individuals $\left(R\right)$ is an important parameter controlling population viscosity. As expected, we found that with a decrease of $R$, the long-lived variants prevail over SL individuals (Fig. 6G and SI Appendix, Fig. S2 I–M), as in the case of well-mixed, homogenous populations (Fig. 4). Thus, our model predict that highly mobile animal species should have relatively long lifespans.

Finally, we used our model to study the range of short- and long-lifespan setpoints that prevents the selection of LL organisms. To this end, we carried out simulation in which we fixed the lifespan of the LL emerging variant and varied the lifespan of the SL individuals. We found that to prevent the LL variants (A_LL = 180) from outcompeting SL individuals, the A_SL must be more than 90 (Fig. 6H and SI Appendix, Fig. S2 C and D).

A similar value of equilibrium lifespan was found if the difference between A_SL and A_LL has been fixed to 10 t.u. Populations with A_SL = 80 were susceptible to the invasion of mutants with A_LL = 90. However, populations with A_SL = 90 were capable of resisting the propagation of variants with A_LL = 100. Thus, we concluded that the equilibrium lifespan for the given epidemiological environment is found around 90 t.u. (Fig. 6J).

Similar results were obtained if the shorter-lived individual lifespan was kept fixed (A_SL = 90) and a range of LL variant lifespans was examined. Under these conditions, we observed that A_LL > 300 leads the LL strain to take over the population (Fig. 6I and SI Appendix, Fig. S2 E and F). These effects result from a general increase in time and reproductive opportunity of the long-lived strain that is sufficient to overcome the pathogen-associated penalty. Appearance of such extreme LL mutants seems to be unexpected from the mechanistic point of view, and their invasiveness could be obviously reduced by infections that result in 100% sterility, as well as by the extrinsic age-independent mortality.

Thus, we found a wide range of lifespan parameters favoring selection of shorter lifespan setpoints in the presence of a single chronic pathogen. Interestingly, a further increase in selective pressure toward shorter lifespan was observed if the individuals were assumed to infect their progeny during or immediately after the birth, a condition typical of many chronic diseases (SI Appendix, Fig. S2).

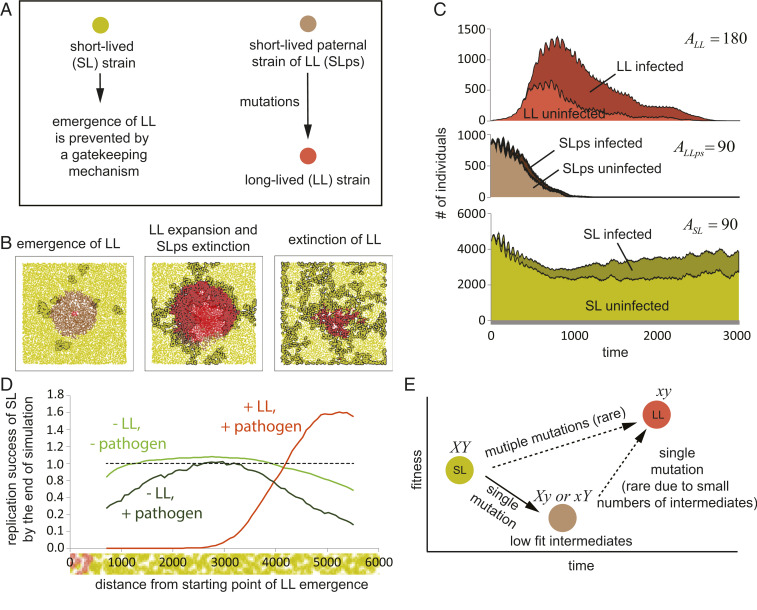
Adverse Effect of the Long-Lived Variants on the Short-Lived Paternal Strain.

The model for selection proposed above is unusual in a way that the same allele responsible for lifespan elongation can be advantageous in a short-term perspective (before LL encounters the pathogen) and detrimental a time later (upon the pathogen comes into the play). We thus tested whether the mechanism of selection proposed here is only acting on the LL variants, or if it also affects the SL paternal individuals. To this end, we examined the effect of the emerging LL variants on SL individuals that are in close contact. Given that our model assumes viscosity in the population, relative individuals are more frequently found close to each other than nonrelatives. Thus, the animals in the proximity to the site of LL mutant emergence were considered to be a “paternal strain” of the LL mutant (Fig. 7A). Strikingly, a simulation performed under conditions defined in Fig. 5 showed that the paternal strain is displaced during the initial expansion of LL strain and by the fitness consequences of epidemic outbreaks (Fig. 7 B and C and Movie S9). To quantify the effect of parental strain extinction relative to initial position of its founder, we marked all SL individuals relative to their distance from the site of the LL mutant emergence. After simulation, we calculated the number of “marked” individuals to estimate the reproductive success of distinct lineages relative to their initial position. Strikingly, the model predicts that the introduction of the LL mutant (red line) resulted in an entire extinction of the SL individuals located in proximity to the position where the LL variant emerged (Fig. 7D). Thus, not only the longevity by itself has a fitness cost, but even the ability to produce an LL mutant might be detrimental due to infection-related penalties.

Fig. 7.

Mechanism of selection favoring fixation of pleiotropic genes. (A) Two variants of SL with identical A_SL = 90 are presented. Normal SL (dark yellow) is not capable of producing LL mutants (A_LL = 180). With the short-lived individuals, the brown-color variant can generate long-lived A_LL variant (short-lived paternal strain [SLps]). (B) We considered a region of SLps individuals surrounded by SL individuals. The LL mutant was introduced in the middle of this region. During initial invasion of LL variant, the SLps strain is efficiently displaced (see Movie S9 for a sample simulation). (C) Graphs represent the population dynamics of different variants in B (n = 50). (D) Replication success of SL individuals in simulations with LL invasion depends strongly on the distance from the initial LL locus. Individuals were labeled with respect to this distance, and these labels were consequently inherited by their progeny. By the end of simulation, the numbers of individuals were plotted against the initial positions of their ancestors. In uninfected populations in the absence of LL (light green line), underrepresented individuals are lost due to genetic drift, and this effect is slightly enhanced in the presence of the pathogen (dark green line). Introduction of LL (red line) in presence of pathogen results in a dramatic extinction of SL lineages in the proximity of the locus of introduction. Thus, not only the long lifespan per se but even the ability to produce long-lived mutant might be detrimental in viscous populations in the presence of pathogens. (E) A hypothetical mechanism for prevention of LL mutant emergence. Mutations in two genes X and Y are required to extend lifespan. Single mutants might express extended longevity but are compromised in fitness and do not accumulate in population, ensuring genetic stability of the aging program. Thus, genes X and Y behave as pleiotropic genes.

Discussion

Why organisms age is a long-standing paradox (24–27). A long life should be selected through evolution since the longer an individual lives, the more progeny it should produce. Since aging, defined as an age-dependent increase in mortality, is almost universal (28, 29), lifespan is clearly under negative selection. On the other hand, the evolution of a long lifespan is possible, as exemplified by very long-lived species that are closely related to short-lived species (30, 31). For example, mice typically live ∼3 y, and naked mole rats live over 30 y (32). Different bat species range in lifespan from 2 to over 40 y (14, 33). Lifespan setpoints can vary within the same species [e.g., between different castes of eusocial insects (34, 35) or developmental types, such as dauer larvae in Caenorhabditis elegans (36)]. Thus, aging is not biologically inevitable, and it is possible to successfully (and sometimes rapidly) evolve increased longevity (13, 37). The existence of species with very long lifespans also argues that essential biological functions do not necessarily carry unavoidable adverse side effects resulting in aging, as proposed (2–5). Why then longer lifespan does not evolve is not explained by the current nonprogrammed evolutionary theories of aging.

Here, we present a hypothesis that limiting lifespan reduces the likelihood of epidemics. Our study thus suggests that infection can be a driving force for the selection of genetically determined lifespan setpoints. Using this theoretical framework, we define specific factors and conditions linked to the evolution of lifespan setpoints. For example, the natural history of infection could explain why closely related species, with very similar molecular, biochemical, and cellular characteristics, display very different lifespan setpoints (14, 29). Infection is an important driving force in evolution (38). Indeed, rapidly evolving genes are under selection by the antagonistic interactions between pathogens and their host (11, 39). Previous studies proposed that the progression of epidemics can be reduced in populations of hosts with shorter lifespan (10). However, that model predicts that short lifespan is beneficial only if organisms suffer from constant epidemics of a sterilizing disease, which is not generally observed. Also, the pressure for short lifespan selection would be relaxed by the evolution of resistance to pathogens. Furthermore, this previous model proposes that entire groups (clusters) of individuals would randomly extinguish, a controversial assumption that implies group selection (40, 41).

In contrast, our model proposes that the evolution of lifespan setpoints is determined by zoonotic outbreaks of chronic infections that reduce fecundity in the infected individuals or by cumulative effects of multiple milder chronic pathogens circulating in the population. These two scenarios are more realistic and are less prone to the evolution of the host’s resistance. Indeed, in the case of the zoonotic transmission of a single pathogen the period of interaction between hosts and pathogens is relatively short. If lifespan is determined by infection with multiple benign pathogens (Fig. 6B and Movie S8), any single pathogen itself does not impose a strong selective pressure, and thus, evolution of resistance is relatively slow in population of short-lived individuals.

Our study reveals that in well-mixed populations, without viscosity, a long lifespan can successfully evolve even in the face of epidemics (Fig. 4). However, individuals within a population often do not interact with each other promiscuously (22, 42). Instead, the populations display some degree of viscosity, which we model as repulsion between individuals (Fig. 5A and Movie S5), resulting from optimization of the resource supply or due to the territorial animal behavior prevalent in nature (23). This viscosity increases the likelihood that infections spread more frequently on relatives than nonrelative individuals. Thus, infection in a given region modulates population density distributions, resulting in asymmetric dispersal of animals from neighboring densely populated areas, which leads to the displacement of the long-living emerging variants (Fig. 6 B and C).

We thus propose a general model for the forces driving lifespan setpoints and argue that limiting lifespan may represent one of the earliest mechanisms preventing the spread of new pathogens. According to our model, chronic low-transmissible pathogens that are not cleared by the immune system play a central role in the lifespan selection. A considerable selective pressure toward shorter lifespans may also arise from pathogens present in the environment but not yet adapted to a given host and by coinfections with several benign pathogens. Extension of the lifespan setpoint is beneficial only in the absence of pathogens, which is not a realistic scenario for most species in an evolutionary context (16). Thus, the lifespan of a species may be a result of a trade-off between the pressure produced by pathogens and the pressure toward life extension and fecundity.

Relation to Group Selection and Evolution of Altruism.

The models shown here do not imply stable cooperative interactions between individuals nor the multilevel selection nor formal definitions of subgroups of individuals, neither any other attribute of a group selection theory (40, 41). We instead consider our model to be a kin-selection hypothesis. In viscous populations, the evolution of altruism can be driven by the frequent interactions between relatives, but competition between them diminishes the altruism advantage. Given that these forces oppose each other, the evolution of altruism is unlikely (43, 44). These restrictions do not apply to the model proposed here. In a viscous population, disease will spread preferably into the relatives, resulting in a cumulative penalty for the individual’s inclusive fitness [e.g., reproduction efficiency of genes involved in reproduction of close relatives (22)]. This penalty is expected to grow exponentially with the spread of the disease and can extend the fitness value of the residual lifespan of the individual, who may have spread the disease or initiated the epidemics by adapting the pathogen. This fitness effect might provide selection pressure strong enough for evolution of altruistic traits.

Model Assumptions and Constraints.

Our model depends on two types of assumptions:

• 1)Abundance and properties of the pathogens. All animal species should be exposed to the risks of zoonotic transmission of chronic pathogens and should harbor many chronic pathogens, and these pathogens should have adverse effects on an individual’s reproductive fitness. Importantly, our model does not require constantly ongoing severe epidemics and can be satisfied with sporadic outbreaks of chronic pathogens or with multiple mild infections constantly persisting in population. Infection reduces fecundity, and thus, infection should result in reduced population density (16, 19–21). These conditions are expected in most living species.
• 2)Population characteristics. First, the limited speed of individuals dispersal should favor infectious contacts between relative versus nonrelative individuals. Animal populations should display some degree of viscosity driven by resource availability and by the individual’s territorial behavior (23). In turn, this should favor an enhanced dispersal of the individuals from densely populated areas to the less populated (45, 46). Such dispersal might occur as a slow, gradual change in individual territories as modeled here (Fig. 5 and Movie S7). The assumptions that viscosity is a common characteristic in a population, that increases the probability that pathogens are transmitted among members of the same kin, and that the host’s dispersal depends on density are consistent with our current knowledge in population dynamics (46).

If the prevention of epidemics can indeed drive the evolution of lifespan setpoint, it may explain the fixation of senescence, which is detrimental for an individual. Indeed, an increase in mortality with age (type I survivorship curve) was observed in many wild populations, especially in the large mammals, including hunter-gatherer humans (29, 47, 48). However, the selection pressure and fitness cost exerted by pathogens may vary. Thus, animals are expected to display a long lifespan when zoonotic transmission and epidemics are rare or if the individuals form part of a low viscosity population (see below). Under these conditions, lifespan would exceed the expected average in natural conditions and no age-dependent increase in mortality (type II survivorship curve) (48). In this case, aging is expected to become evolutionarily near-neutral, matching the proposals of the selection shadow theory (3). Nevertheless, the extreme changes of the lifespan setpoint are prevented by the action of the pleiotropic genes, as discussed below.

Absence of Biologically Immortal “Aging Escape Mutants” and Existence of Pleiotropic Genes.

A key feature of our analysis is that selection disfavors not only the long lifespan itself but also the parental strain capable of producing LL mutants (Fig. 7). We find that during the invasion of the long-living strain, SL individuals near to the locus where the long-living mutants emerge are also at risk for extinction (Fig. 7). We thus propose that infection exerts a pleiotropic negative selection at the population level that explains the near absence of immortal variants. Accordingly, short-living animals able to produce such LL mutants are exposed to the catastrophic risks of being either displaced by these strains or decimated after epidemic outbreaks. Thus, we propose that organisms have evolved “multilayer” or “network”-based mechanisms that prevent LL variants from emerging. In principle, this could be achieved by linking aging effectors and some vital function, as proposed by the antagonistic pleiotropy theory (5). A significant extension of lifespan might require several mutations to be combined, such as epistatic gene interactions, whereas, when occurring individually, these mutations would reduce the individual’s fitness (Fig. 7E). Our study proposes that pleiotropic genes form “gatekeeping” mechanisms that were fixed not by chance, but because they are evolutionarily beneficial. Thus, our model explains the extreme genetic stability of senescence in the context of the adaptive aging hypothesis.

Rationalizing Lifespan-Related Observations.

Our hypothesis can explain several aging-relative observations. For instance, we identified a negative correlation between longevity and fecundity (Figs. 3E and 6 C and D), a well-documented association (49). Population density is a crucial parameter of epidemiological models, and the animal’s body size is in good negative correlation with the density (50). These correlations provide a possible explanation of the well-renowned connection between body size and lifespan (51, 52).

Extremely long-living queens of eusocial animals (e.g., bees, ants, termites, rodents from the Fukomys genus) are paradoxical when compared to other members of the colony (35, 53). According to our hypothesis, the queens make up a minimal proportion of the population and are well protected from zoonotic pathogen transmission; thus, their longevity probably contributes little to the epidemiological risks. Outstanding longevity of all castes in naked mole rats is another observation challenging traditional views on aging (32). We suggest eusociality to be the fundamental ecological reason for naked mole rats’ longer lifespan. A eusocial species can involve a better way of dealing with pathogens: hypersensitivity. If the very first infected individual dies by a “suicide” before the pathogen transmission, the outbreak will be interrupted. With this adaptation, the colony population might be kept pathogen-free, thus making aging redundant. Little is known about naked mole rat immunity, although one report describes its hypersensitivity to virus infection when compared to mice (54). Further experiments are required to test whether it is a general phenomenon for the worker caste of naked mole rats and whether the queens are more resistant to infections, according to the prediction of our hypothesis (55).

Another important conclusion is the linkage between lifespan setpoints and the mobility of the individuals. If population viscosity is disrupted by high animal mobility, the long-living variants will disperse to the whole area of distribution, and the kin-specificity of infection will be minimized (Fig. 6G). Interestingly, this prediction is consistent with the atypically long-living characteristics observed in highly mobile flying birds and bats (14, 29, 48, 56, 57).

Thus, the hypothesis proposed here can explain many aging-associated observations, including those poorly explained by other aging theories (e.g., naked mole-rat longevity or correlation with flight). Importantly, it defines factors and conditions in which short lifespan setpoints are beneficial, providing a general framework to explain how beneficial lifespan setpoints are selected under conditions that vary in different species and ecological situation,

Predictions.

Pathogen abundance.

Our hypothesis predicts an evolutionary connection between lifespan setpoints and exposure to zoonotic pathogens. Thus, animals living in relatively abiotic environments [e.g., arctic animals (30, 31) or troglobites (58)] are expected to have longer lifespan setpoints. On the other hand, animals exposed to a rich diversity of pathogens from related species should display shorter lifespans.

Immunity.

The ability to alleviate the fitness penalty of chronic infections due to tolerance or resistance might relax the selection pressure toward shortening the lifespan. Since our model implies chronic diseases to be the main lifespan setpoint selective force, animals with low ability to clear parasites should tend to have shorter lifespans [e.g., persistent viral infections in insects (59, 60)].

Allocation of aging benefits to the kin.

A fundamental assumption of our model is that the penalty of adapting zoonotic pathogen is, to some extent, specific to each individual’s kin. Our model considers the viscous population in which relative individuals are interacting more intensively (Fig. 5 and Movie S5). We thus propose that higher animal mobility should increase interactions between individuals, decreasing selection for shorter-living individuals. Therefore, lesser mobility is predicted to correlate negatively with longevity. Besides, other factors that increase the probability of infecting the individual’s kin should negatively affect the lifespan. For example, viviparous animals, which are expected to have a higher occurrence of pathogen’s vertical transmission (SI Appendix, Fig. S2), are predicted to have relatively shorter lifespan setpoints than ovipositors or species with external fertilization. Also, social structure enhancing the contacts between relative individuals is predicted to have a negative evolutionary effect on lifespan.

Mechanisms of aging.

Our work identifies host–pathogen interactions as a major selective pressure driving evolution of lifespan setpoints. However, our theory does not provide insights into the mechanisms leading to aging. The lifespan setpoints likely exploit similar mechanisms across different species, such as modulation of DNA and protein damage responses, stress responses, and senescence pathways (2, 61–63). Nevertheless, some mechanistic predictions can be drawn from our model. For example, it predicts that unlike other environmental stressors, chronic infections should not result in lifespan extension. Intriguingly, chronic induction of some immune pathways has a detrimental effect on lifespan (64, 65). Future experiments are required to study this in detail.

Research on aging, searching for lifespan determinants may lead to an effective increase in human lifespans. Our ability to describe and model aging as an evolutionary process linked to infection might provide a paradigm to identify lifespan determination programs, which can be prevented or even reversed. On the other hand, our theory also notes potential epidemiological risks associated with an extended lifespan that should be taken into consideration to develop strategies that mitigate such risks.

Methods

All scripts were coded in Python 2.7 (Python Software Foundation). Generation of uniformly distributed random numbers in all cases was performed with the random Python library, which uses a standard Mersenne Twister algorithm. Differential equations were analyzed with the odeint function of the scipy library. Data were plotted with matplotlib and seaborn Python packages and with Excel (Microsoft). See SI Appendix for details.

Data Availability.

Scripts are available for download at 4TU.Centre for Research Data, https://data.4tu.nl/repository/uuid:91978ed6-1f6f-49fd-adde-f8bd2c072be6 (66). All of the data generated are included in the manuscript.