River basin salinization as a form of aridity

Significance

Combining observations and model results, we show that soil salinization does affect the long-term soil–water balance of saline river basins, eventually acting as an aridity enhancer. The strength of this control depends on the capability of vegetation to cope with salt stress through specific functional traits—i.e., salt tolerance—and is key to the understanding of vegetation–water relations in arid and transitional watersheds. Our approach can also be applied to infer crucial data about the salinization level and vegetation salt tolerance of river basins. Such information is essential to develop reverse-engineering measures to mitigate catchment-scale aridity and salinization, based on salt-tolerance plant traits.

Abstract

Soil-salinization affects, to a different extent, more than one-third of terrestrial river basins (estimate based on the Food and Agriculture Organization Harmonized World Soil Database, 2012). Among these, many are endorheic and ephemeral systems already encompassing different degrees of aridity, land degradation, and vulnerability to climate change. The primary effect of salinization is to limit plant water uptake and evapotranspiration, thereby reducing available soil moisture and impairing soil fertility. In this, salinization resembles aridity and—similarly to aridity—may impose significant controls on hydrological partitioning and the strength of land–vegetation–atmosphere interactions at the catchment scale. However, the long-term impacts of salinization on the terrestrial water balance are still largely unquantified. Here, we introduce a modified Budyko’s framework explicitly accounting for catchment-scale salinization and species-specific plant salt tolerance. The proposed framework is used to interpret the water-budget data of 237 Australian catchments—29% of which are already severely salt-affected—from the Australian Water Availability Project (AWAP). Our results provide theoretical and experimental evidence that salinization does influence the hydrological partitioning of salt-affected watersheds, imposing significant constraints on water availability and enhancing aridity. The same approach can be applied to estimate salinization level and vegetation salt tolerance at the basin scale, which would be difficult to assess through classical observational techniques. We also demonstrate that plant salt tolerance has a preeminent role in regulating the feedback of vegetation on the soil water budget of salt-affected basins.

River salinization has grown at an unprecedented pace over the last decades, gradually assuming the dimension of a global environmental issue (1–3). In this context, many authors have explored the effects of river salinization from the water quality (4–6), ecological (1, 7–9), and public health (10) perspectives. In contrast, much less emphasis has been placed on the hydrological aspects of the problem (11–14), such as the impacts of salinity on the soil water budget of river basins as hydrological units. However, fast-spreading soil salinization and the increasing salinity of rivers are intimately connected processes, which can hardly be tackled independently (15).

From a hydrological viewpoint, the main consequence of the increasing concentration of soluble salts in the soil is the drastic lowering of the soil water potential, ${\psi }_s$, as a result of osmotic effects (16). As ${\psi }_s$ becomes more and more negative and salt starts to accumulate within plant tissues beyond toxic levels (ref. 17; ionic stress), evapotranspiration is progressively impaired (18–20), affecting water and energy fluxes at the interface between land and atmosphere (13, 21). The strength of this feedback depends on plant salt tolerance and largely resembles the effects of aridity on hydrological partitioning (22). However, while aridity and salinization both limit evapotranspiration, the physical mechanisms behind this control are substantially different. During a drought, soil dries down to the point where evaporable soil water is fully depleted, and sensible heat fluxes become predominant (23). In the process, available soil water is entirely evaporated into the atmosphere, and the atmospheric water content locally increases. Salinity, in contrast, limits evapotranspiration by making energetically disadvantageous to extract water from the soil, lowering the soil moisture available to plants for uptake (13, 24) and suppressing bare-soil evaporative fluxes (25, 26). As a result, latent heat fluxes are reduced. Water from saline soils marginally contributes to atmospheric water vapor and remains stored in the soil, from where it can only return to the hydrological cycle through percolation (24).

Unsurprisingly, salt-tolerant species (halophytes) have developed hydraulic traits, which allow them to contrast salt stress and sustain transpiration also under saline conditions (21, 27, 28). Their capability to cope with salt exposure is based on complex osmoregulation strategies (28) and allows halophytes to exert appreciable feedbacks on leaching frequency and salinization (13). Salt resilience could, hence, hold a central role in regulating the hydrological partitioning of salt-affected basins, in the same way that the functional traits of drought-resilient species (xerophytes) have been shown to modulate land–atmosphere interactions in water-limited environments (29–31). Here, we show that as river-basin salinization continues to grow at a fast pace, the interplay of salinity and plant salt tolerance could trigger a series of major, and yet unexplored, feedbacks on hydrological partitioning and plant–water relations at the catchment scale. Such feedbacks could, in turn, enhance aridity and the strength of vegetation–climate interactions in already soil-moisture-limited transitional climates (32, 33).

Results and Discussion

The Global Dimension of River-Basin Salinization.

Although river-basin salinization has long been recognized as a major environmental issue worldwide (6, 37), a global assessment of its extent and severity is still missing. Using soil-salinity data from the Food and Agriculture Organization of the United Nations (FAO) Harmonized World Soil Database (HWSD; ref. 34), we undertake here a basic appraisal of river-basin salinization at the global scale (Fig. 1A).

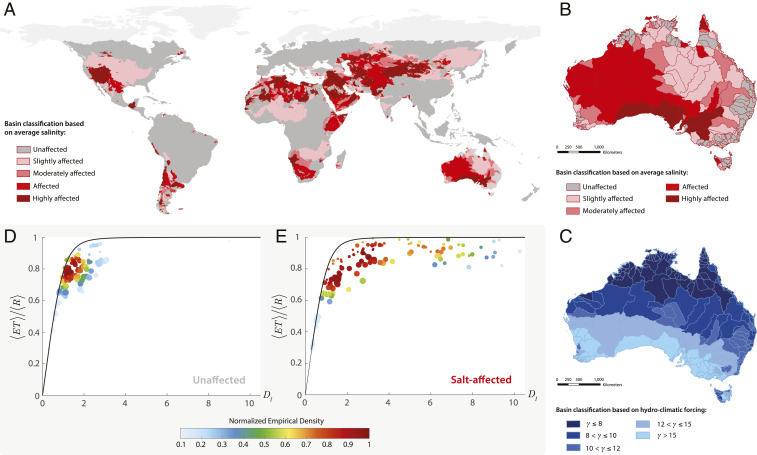
Fig. 1.

Observed departure of salt-affected basins from the classic Budyko’s framework. (A) Classification of world drainage basins by average level of salinization (${\hat{\mu }}_{C,i}$) based on salinity data from the HWSD (34). (B and C) Australian sub-basins categorized by salinization level (B) and hydro-climatic forcing $\gamma$ (C; Results and Discussion, Observed Partitioning in Saline River Basins and ref. 35). (D and E) Observed terrestrial water balance of unaffected (D) and salt-affected (E) sub-basins of Australia. Catchment-scale evaporative fraction, $⟨ET⟩/⟨R⟩$, and dryness index, $D_I$, are inferred from AWAP data (Materials and Methods; dots) and contrasted with the theoretical Budyko’s curves obtained via the stochastic water-balance method introduced by Porporato et al., 2004 (P04; ref. 36). The P04’s theoretical curves do not account for salinity effects on hydrological partitioning.

Mean salinity, ${\mu }_C$, is estimated as the weighted mean of the saturated soil-paste electric conductivity (${\mathrm{E}\mathrm{C}}_e$; measured in dS/m) in the topsoil and subsoil at each HWSD pixel of size $30^{″}\times {\mathrm{30}}^{″}$. The mean level of salinization of each basin $i$, ${\hat{\mu }}_{C,i}$, is then inferred as the catchment-wide average of ${\mu }_C$. Depending on the value of ${\hat{\mu }}_{C,i}$, basins are grouped into five salinization categories (Materials and Methods) ranging between unaffected (gray shading) and highly affected (dark red; Fig. 1 A and B). This simple classification enables us to show that moderately to highly affected basins (affected from now on) account for 29% of drainage basins globally, while slightly affected basins sum up to 7.5%, for a total of 36.5% of catchments affected by some diffuse or more localized form of soil salinization. These include macro river basins like the Mississippi, the Colorado, and the Murray–Darling, whose increasing salinization has already been extensively documented in the literature (6, 38–40). The region encompassing the highest number of affected basins is the Middle East (51%), followed by Africa (43%) and Australia (29%). In these regions, the effects of soil salinization on catchment-scale hydrological partitioning are expected to be the most apparent.

Observed Partitioning in Saline River Basins.

Australia represents an ideal benchmark to assess the long-term effects of salinization on hydrological partitioning at the catchment scale. It is characterized by widespread dry-land salinity (ref. 41 and Fig. 1B), a broad range of hydro-climatic conditions spanning from tropical rain forest to hot desert climates (Fig. 1C), and the abundance of native salt-tolerant species.

Based on gridded data of daily precipitation ($R$), potential evapotranspiration ($E{T}_p$), and actual evapotranspiration ($ET$) from the Australian Water Availability Project (AWAP; ref. 42), we show that salinity exerts a detectable control on the terrestrial water budget of salt-affected basins. Such control is identified by contrasting long-term observations of hydrological partitioning at 1) unaffected and 2) salt-affected basins and evidencing the different probabilistic structure which characterizes these two groups. AWAP is a gridded dataset providing high-resolution (5 km), historical estimates of the terrestrial water balance across Australia, based on the combination of weather-station observations from the Australian Data Archive for Meteorology (ADAM; ref. 42), remotely sensed products, and a water-balance model (WaterDyn, Version 26M; ref. 43 and Materials and Methods).

Here, the AWAP data for the period 1950 to 2017 are used to estimate the evaporative index, $⟨ET⟩/⟨R⟩$, i.e., the fraction of total precipitation lost by evapotranspiration, and the dryness index, $D_I=E{T}_p/⟨R⟩$, of each of the 237 Australian sub-basins. The notation $⟨\cdot ⟩$ designates a long-term mean (i.e., across the 68 y of the dataset), spatially averaged over each sub-basin. The water budget of the unaffected (Fig. 1D) and affected (Fig. 1E) sub-basins is then represented in the form of a density scatter plot in the Budyko’s space, where the color of the dots represents the normalized empirical density of the data points in the $\left\{D_I,⟨ET⟩/⟨R⟩\right\}$ plane, and the dot size is proportional to the climatological precipitation input to the basin, $⟨R⟩$. The observed partitioning is compared with the theoretical Budyko’s curves (bold black line; ref. 44) obtained by forcing the classic stochastic water-balance model proposed by Porporato et al. (P04 hereafter; ref. 36) with the average hydro-climatic and soil conditions of the two basin groups (unaffected and affected).

Hydro-climatic forcing is quantified through the dimensionless parameter $\gamma =n{Z}_r{s}_1/\alpha$, which is inversely proportional to the mean depth of rainfall for event $\alpha$ and directly related to the maximum soil water storage through the effective field capacity, $s_1$, the vertically averaged rooting depth, $Z_r$, and soil porosity, $n$ (35). To distinguish such a forcing from the effects of salinity, we selected unaffected and affected sub-basins characterized, on average, by the same hydro-climatic conditions and soil properties ($\gamma \simeq 10.5$, $\lambda =0.1\hspace{0.17em}{\mathrm{d}}^{-1}$, $E{T}_p=3.5$ mm/d, $n=0.4$, $s_1=0.85$, and $Z_r=35$ cm). The P04 accounts for hydro-climatic variability through random daily precipitation inputs and has been previously used to extend and interpret hydrological partitioning in the Budyko’s framework (36, 45). However, it does not include the effects of salinity; i.e., should salinization have any impact on the long-term soil water balance, the P04 would not be able to capture it. Despite its simplicity, this process-based stochastic description of the terrestrial water budget well reproduces the relation between aridity and hydrological partitioning in unaffected basins (Fig. 1D).

In contrast, the observed partitioning of salt-affected basins shows a clear deviation from the theoretical curve (Fig. 1E). Here, salinization seems to pose an additional energy limitation on evapotranspiration. Also, this control appears to be the strongest in transitional and wet sub-basins, where the impairment of $ET$ due to osmotic effects can potentially retain larger volumes of water into the soil compared with already arid and hyper-arid climates. This energy limitation leads to an enhancement of aridity, which cannot be explained by the P04, and could be interpreted as follows: Under saline conditions, evapotranspiration gets impaired as a result of the decreasing effective soil moisture availability. The fraction of soil water lost to $ET$ is a function of the strength of the soil osmotic potential and plant salt tolerance, so that the observed evaporative index corresponds to an aridity index, $D_I$, higher than the one which could be inferred from the climatological values of $R$ and $E{T}_p$ alone.

If this is the case, the long-term soil water budget of saline basins should depend on the catchment salinization level and exhibit a probability structure markedly different from the one of basins where salinity controls are negligible. At the same time, the observed deviation of saline basins from the classic Budyko’s framework could be simply a result of the statistical variability of the sample. To rule out this last hypothesis, we tested the water budget data of unaffected and salt-affected basins using a two-dimensional (2D) two-sample Kolmogorov–Smirnov (KS) statistic (ref. 46 and Materials and Methods). The bivariate nonparametric test is applied to the joint distribution of the variables defining the Budyko’s space (i.e., the evaporative index, $⟨ET⟩/⟨R⟩$, and the dryness index, $D_I$) and allows us to reject the null hypothesis that water-budget samples from affected and unaffected basins are drawn from the same parent distribution. This conclusion supports the hypothesis that the departure of salt-affected basins from the Budyko’s curve shown in Fig. 1E is the result of a different underlying probabilistic structure.

Many factors could play a role in shaping the long-term water budget of saline basins. These include different forms of soil degradation and endorheic regimes (47, 48). In what follows, however, we show that the observed divergence of salt-affected basins from the classic Budyko’s framework can be primarily explained by accounting for the explicit dependence of $ET$ on salinity and plant salt tolerance. Note that such dependence does not violate the basic Budyko’s assumption of “negligible changes in sub-surface water storage” since soil salinization evolves over temporal scales significantly longer than those characterizing the changes in the average soil water balance.

The agreement between the observations and the salinity-dependent model we introduce in the following section corroborates the hypothesis that soil salinization does exert a significant control on hydrological partitioning at the catchment scale.

A Theoretical Interpretation of Salinity Effects.

We introduce here an alternative formulation of the long-term terrestrial water balance, incorporating the dependence of $ET$ on soil moisture $s$, the vertically averaged mass of soluble salts in the soil $m$, and vegetation salt tolerance. The parameter $m$ represents a proxy for the level of soil salinization and, together with $s$ and the soil properties, regulates the concentration of soluble salts in the soil, $C=m/\left(n{Z}_{r}s\right)$. Salt tolerance is described through the species-specific dependence of $ET$ on salt concentration $C$ and modeled by a step-wise linear relation, where transpiration remains unaffected by salinity up to a species-dependent concentration threshold, $C_T$, and declines with slope $\beta$ (also determined by species-specific traits; refs. 13 and 18) above $C_T$.

As a consequence of this dependence, vegetation is unable to take up water from salt-affected soils when soil moisture drops below a specific value $𝜗=\beta m/\left[n{Z}_r\left(1+\beta C_T\right)\right]$, elsewhere defined as the virtual wilting point (13), and corresponding to the relative soil water content at which plant transpiration is completely impaired due to salt stress. Noting that soil properties and salinization level remain approximately constant over the typical timescales of soil-moisture dynamics (11, 13, 49, 50), the normalized terrestrial water balance conditional to the level of salinization of the basin ($m$) and vegetation salt tolerance ($\left\{\beta ,C_T\right\}$) can be written as (Materials and Methods):

$$1=\frac{⟨ET|m⟩}{⟨R⟩}\hspace{0.17em}+\hspace{0.17em}\frac{⟨LQ⟩}{⟨R⟩}=D_I^{*}⟨x|m⟩+\hspace{0.17em}\frac{⟨LQ⟩}{⟨R⟩},$$ [1]

where $⟨x|m⟩$ = $\left(⟨s|m⟩-𝜗\right)/\left(s_1-𝜗\right)$ represents the mean effective relative soil moisture (36) for given salt mass in the soil, $⟨LQ⟩$ is the average rate of runoff and deep percolation, and $D_I^{*}$ is an alternative form of the Budyko’s dryness index, $D_I$, accounting for the additional energy required to extract water from the soil at highly negative ${\psi }_s$ and for the modulation of this effect due to plant salt tolerance.

The $D_I^{*}$ can be linked to the classic Budyko’s dryness index through the relation:

$$D_I^{*}=D_I\left(\mathrm{\Theta }-C_s\beta \right)s_1,$$ [2]

where $\mathrm{\Theta }=1+\beta C_T$ is a parameter incorporating the effects of plant salt tolerance, and $C_s=m/\left(n{Z}_r\right)$ is the concentration of soluble salts (predominantly NaCl) in the saturated soil paste. The latter is proportional to the ${\mathrm{E}\mathrm{C}}_e$, which represents the most commonly adopted measure of soil salinity. Eq. 2—through the fit of the generalized Budyko’s curve given by Eq. 1—allows an indirect estimate of catchment-scale salinization ($C_s$) and plant salt-tolerance properties ($\beta$ and $C_T$) that would be otherwise difficult to infer. In unaffected basins (i.e., for $m=0$), $D_I^{*}=D_I$, and the long-term soil water balance in Eq. 1 simply reduces to the water balance in the absence of salinity effects (36).

Salinity as a Form of Aridity.

The salinity-dependent soil water budget (S-D SWB) in Eq. 1 can be used to explore the effects of salinity and vegetation salt tolerance in the Budyko’s framework.

In Fig. 2A, the S-D SWB (solid lines) is contrasted with the long-term soil water balance in absence of salinity controls (P04; ref. 36; dashed lines) for climatic conditions ranging between hyper-arid ($\gamma$ = 1,000) and humid ($\gamma =1$; Fig. 2A) and with the original semiempirical formulation of Budyko (refs. 36 and 44; black dots). The salinity-dependent Budyko’s curves are obtained for an intermediate level of salinization (${\mathrm{E}\mathrm{C}}_e\simeq 5$ dS/m), corresponding to the salt-concentration threshold $C_T$ of the moderately salt-tolerant species considered dominant over the basins, and typical soil parameter values ($n=0.4$ and $Z_r=35$ cm; ref. 36). Similar to the observations in Fig. 1E, salinity imposes here a substantial limitation on the long-term average of $ET$, thus increasing the demand limit of the S-D SWB when compared with the balance in the absence of salinity effects.

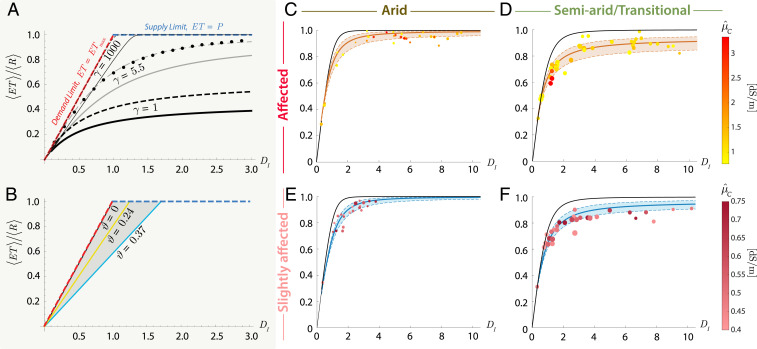
Fig. 2.

Salinity-dependent hydrological partitioning. (A) Average soil water balance as a function of the level of salinization of the basin and vegetation salt tolerance (S-D SWB; continuous lines) from Eq. 1, as contrasted to the balance in absence of salinity controls (P04; ref. 36; dashed lines), for wet ($\gamma =1$; bold black line), temperate ($\gamma =5.5$; thin gray line), and hyper-arid ($\gamma$ = 1,000; thin black line) hydro-climatic conditions. Black dots represent the classic semiempirical Budyko’s curve $⟨ET⟩/⟨R⟩={\left\{D_I\left[1-\exp \left(-D_I\right)\right]\tanh \left(1/D_I\right)\right\}}^{1/2}$, which matches the P04’s curve for $\gamma =5.5$, $n=0.4$, and $Z_r=35$ cm (36). The S-D SWB is obtained for an ${\mathrm{E}\mathrm{C}}_e$ of about 5 dS/m (equivalent to a saturated soil past concentration, $C_s$, of 3.84 g/L for $m=538$ g/${\mathrm{m}}^2$, $Z_r=350$ mm, and $n=0.4$). This level of soil salinization also corresponds to the onset of salt stress for the moderately salt-tolerant species considered dominant over the basin ($\beta =0.084$ L/g, $C_T=C_s=3.84$ g/L). (B) Demand limit for different values of virtual wilting point $𝜗=0,\hspace{0.17em}0.24,\hspace{0.17em}0.37$, corresponding to increasing salinity values and different plant salt-tolerance levels (i.e., $C_s=0$, $C_s=3.84\hspace{0.17em}\mathrm{g}/\mathrm{L}$ and moderately salt-tolerant dominant species, and $C_s=3.84\hspace{0.17em}\mathrm{g}/\mathrm{L}$ and salt-sensitive dominant species, respectively; soil parameters as above). (C–F) Observed versus theoretical terrestrial water balance of affected (C and D) and slightly affected (E and F) river basins across arid (C and E) and semiarid (D and F) conditions. Bold black continuous lines represent the Budyko’s curves in the absence of salinity effects (P04; ref. 36) corresponding to the average hydro-climatic conditions of the four subgroups (arid-affected, semiarid-affected, arid-slightly affected, and semiarid-slightly affected). Solid orange (for affected) and blue (for slightly affected) lines represent the best estimate of the salinity-dependent Budyko’s curve obtained by fitting Eq. 1 to an ensemble of 1,000 subsamples randomly drawn from each basin subgroup (Materials and Methods). Dashed lines account for hydro-climatic variability across each basin subgroup and correspond to the 10th and 90th percentiles of $\gamma$, respectively. Dot size is proportional to $⟨R⟩$.

This limitation is the strongest in humid basins, although it is in semiarid and transitional climates—on the verge of irreversible aridification—that it is expected to have the strongest impacts. Salt stress acts here as a form of water stress, reducing the amount of water that vegetation and evaporative processes can extract from the soil and exchange with the atmosphere. However, while aridity overbalances the hydrological partitioning toward its supply and demand limits by sustaining elevated $ET$ fluxes and negligible $LQ$ (Fig. 2A), salinity modifies the demand limit itself. The strength of this control on the energy limit is a function of the virtual wilting point $𝜗$ (Fig. 2B). It increases with both salinity—in response to the progressive lowering of ${\psi }_s$—and plant salt sensitivity, being the highest for glycophytes, whose transpiration is already impaired at an ${\mathrm{E}\mathrm{C}}_e$ of a few dS/m, and the lowest for halophytes, which can sustain transpiration in severely salt-affected soils.

The S-D SWB can also be used to interpret the observed hydrological partitioning of salt-affected basins in the Budyko’s space (Fig. 2 C–F). Here, the basins are subdivided into salt-affected and slightly affected and then further classified into arid and semiarid/transitional, based on their average hydro-climatic conditions ($\gamma$). The parameter $\gamma$ is inferred from AWAP data, while soil characteristics are obtained from the literature (Materials and Methods and refs. 54–56). The S-D SWB (solid orange line for affected basins, Fig. 2 C and D; and solid blue line for the slightly affected ones, Fig. 2 E and F) is fitted to observations and compared to the predicted water balance without salinity feedback (P04; solid black curves). The S-D SWB’s salinity and salt-tolerance parameters are estimated by applying a nonlinear least-squares fitting to 1,000 subsamples of basins, randomly extracted from each salinization class (bootstrapping). The expected values of the different parameters are then obtained as an average of the 1,000 subsample estimates (Materials and Methods).

The P04 appears to underestimate runoff and percolation systematically in saline Australian sub-basins. In contrast, the S-D SWB is able to capture the observed features of the terrestrial water balance in both slightly affected and affected basins, corroborating the hypothesis that the departure of observations from the P04 can be the result of the salinity controls on $ET$. The most significant deviation of the observed hydrological partitioning (dots) from the P04’s curve is found in semiarid/transitional basins, where the evaporative index $⟨ET⟩/⟨R⟩$ cannot attain the supply limit, even in the case of elevated $D_I$. Here, soil salinity significantly reduces $ET$, eventually enhancing runoff and deep percolation. We quantify the impact of salinity on the hydrological partitioning of semiarid/transitional basins by comparing the S-D SWB fitting of affected and slightly affected catchments (Fig. 2 D and F, respectively). For a fixed dryness index, $D_I$ = 2, corresponding to an ideal transition between arid and semiarid climatic conditions (57), we find that the evaporative fraction of transitional slightly affected basins is about 11$\%$ higher than the one of the transitional affected.

The effects of salinity are substantially less marked in arid and hyper-arid basins, where the long-term water balance already approaches its water and energy limits, due to the exiguous water supply and elevated atmospheric evaporative demand. Here, $⟨ET⟩/⟨R⟩$ is slightly higher (1$\%$) in affected catchments than in slightly affected arid catchments. This counterintuitive difference can be explained as a result of the higher salt tolerance of vegetation adapted to the elevated aridity and salinity of arid-saline basins. These species are, in fact, able to maintain transpiration at salinities that can totally impair the functioning of the moderately tolerant plants characterizing slightly affected basins. To validate this hypothesis, we generated two synthetic Budyko’s curves for affected arid basins and slightly affected arid basins, using observed aridity and salinity and prescribing moderately tolerant vegetation across the two classes. As expected, in this case, the evaporative fraction at $D_I=$ 2 for slightly affected basins is 3$\%$ larger than that of the affected basins.

It is important to note that the average values of plant salt tolerance and soil salinity used to fit the S-D SWB to observations span a realistic range, representative of salt-affected basins and moderately salt-tolerant species of Australia (52). In particular, the expected values of the model parameters are indicative of moderately tolerant species for slightly affected basins (i.e., $\beta$ = 0.45 L/g, $C_T$ = 4.8 g/L, and $m$ = 500 g/${\mathrm{m}}^2$) and highly tolerant species for affected ones (i.e., $\beta$ = 0.29 L/g, $C_T$ = 7.28 g/L, and $m$ = 750 g/${\mathrm{m}}^2$). If, in general, high tolerance is coupled with elevated salinity, this cannot be considered a rule in managed basins. Here, deep-rooted and salt-tolerant native species have been replaced with shallow-rooted crops and pastures during the transition to intensive agriculture at the beginning of the 20th century. However, these results suggest that, when interpreted through the S-D SWB, the observed hydrological partitioning of saline river basin can provide useful insights on catchment-scale salinization, plant salt tolerance, and the controls exerted by vegetation on soil salinity (13), which would be otherwise challenging to infer from direct observations and remote-sensing techniques (58).

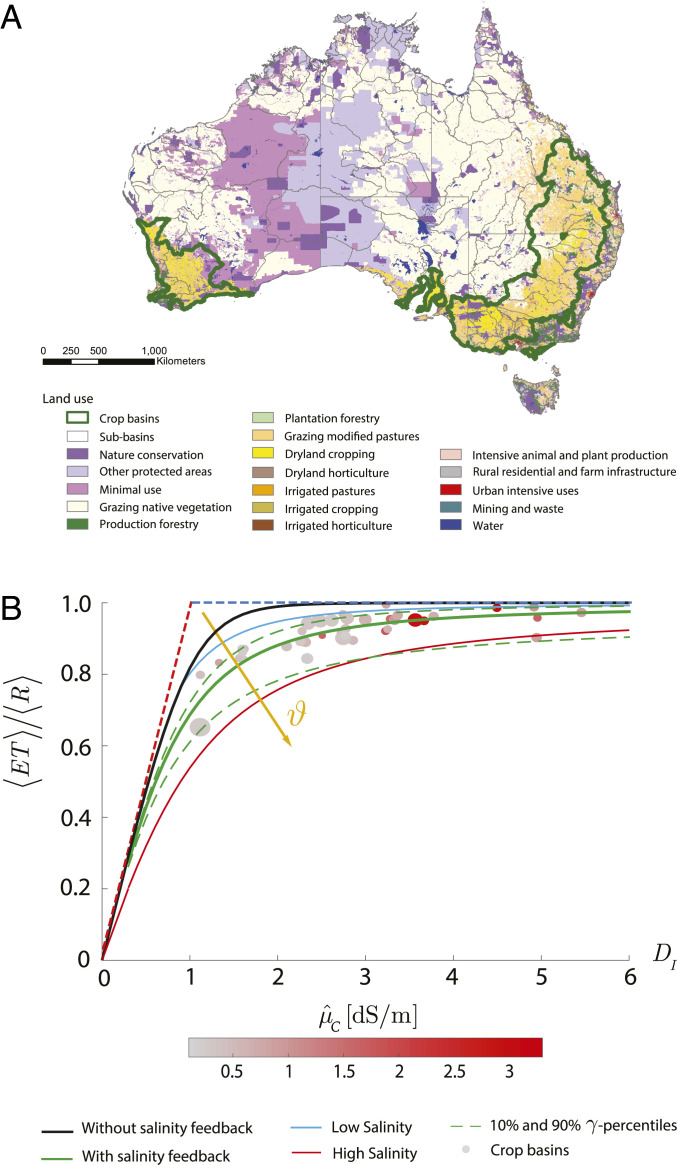
As a further example, Fig. 3 shows the observed long-term soil water balance of 35 basins in the Southeast and Southwest Australia, predominately dedicated to rain-fed agriculture and grazing (Fig. 3A). It is interesting to note that, if fitted with the S-D SWB, the observed soil water budget of agricultural basins yields average values of $\beta$ and $C_T$ ($\beta$ = 0.37 L/g and $C_T$ = 5.9 g/L), which well reproduce the experimentally observed traits of moderately tolerant crops and grazing species dominating the study area—like canola, guar, rye, sorghum, and wheat (refs. 52 and 53 and Fig. 3B).

Fig. 3.

Inferring basin-scale salinization from observed hydrological partitioning. (A) Australian sub-basins subject to intensive agriculture and grazing (bold green contour) and land-use map from the Australian Bureau of Agricultural and Resource Economics and Sciences (ABARES; refs. 51 and 52). (B) Observed long-term water balance of crop-dominated Australian sub-basins (dots) versus the corresponding salinity-dependent soil water balance (Eq. 1; continuous green curve) and the classic hydrological partitioning in absence of salinity feedback (solid black line). Dashed lines and dot size are as in Fig. 2 C–F. The effect of different levels of salinization is highlighted by letting salinity vary between low ($m$ = 400 g/${\mathrm{m}}^2$; blue line) and high ($m$ = 800 g/${\mathrm{m}}^2$; red line) and keeping constant all of the other variables. The estimated parameters ($\beta$ = 0.37 L/g, $C_T$ = 5.9 g/L, and $m$ = 650 g/${\mathrm{m}}^2$) well reproduce the average level of salinization and plant salt tolerance of the moderately tolerant crops (e.g., canola, guar, rye, sorghum, and wheat; ref. 52) characterizing the study region (52, 53).

These crops are known to exhibit high values of the salinity threshold, $C_T$, but also an extremely rapid yield decay above $C_T$ (ref. 18; i.e., elevated values of the parameter $\beta$). Similar physiological traits—combined with the systematic clearing of salt-tolerant native species—could have contributed to the increasing salinization of Southern Australian basins and the modification of their hydrological regime (53, 59). Elevated values of $C_T$ can, in fact, favor salinization by reducing the frequency of salt removal through leaching (13). Once soil-salinization approaches $C_T$, transpiration and plant growth are rapidly impaired, due to the high value of $\beta$, potentially triggering a cascade of secondary feedbacks on the soil water budget and water-table dynamics.

These results highlight the central role of vegetation salt tolerance in controlling the long-term hydrological partitioning of salt-affected basins. At the same time, the case study of Southeast and Southwest Australia agricultural basins demonstrates how the fitting of the S-D SWB to hydrological observations can provide crucial insights on salinization and vegetation salt tolerance at the basin scale—otherwise difficult to infer through classic observational techniques. This “inverse problem” approach could thus represent the first step toward the development of reverse-engineering techniques for the control and mitigation of aridity and salinization at the catchment scale.

Conclusions

This study investigates the hydrological aspects of river-basin salinization and the role of plant salt tolerance in modulating the long-term soil water balance at the catchment scale. Combining observations from the AWAP (42) and a physically-based salinity-dependent soil water budget model (the S-D SWB), we show that salinity exerts a definite and detectable control on hydrological partitioning.

Our minimalist approach accounts for the effects of salinity on evapotranspiration and the species-specific character of these effects. In salt-affected basins, soil salinization is shown to act as an aridity enhancer, limiting $ET$ and increasing the demand limit of the S-D SWB when compared with the balance in the absence of salinity effects (P04), used here as a baseline.

The strength of this enhancement largely depends on the capability of vegetation to cope with salinity. Halophytes can maintain relatively high transpiration in saline conditions, while in glycophytes, transpiration is already impaired at low soil salinity. As salinization becomes widespread, failure to consider these effects could result in incorrect estimates of hydrological, surface-energy partitioning, and land–vegetation–atmosphere interactions at the catchment scale.

Through the lens of the S-D SWB, we were able to explore the role of moderately salt-tolerant crops in shaping the water balance of rain-fed cropland in Southeastern and Southwestern Australia. We have discussed how the relatively high salt-stress threshold ($C_T$) of these crops (canola, guar, rye, sorghum, and wheat) combined with a fast decay of transpiration and growth above $C_T$ may initiate a cascade of secondary feedbacks on the soil water budget and water-table dynamics of Southern Australian croplands.

This case study shows that, by fitting the S-D SWB to hydrological observations, it is possible to obtain crucial information on salinization and plant salt tolerance at the scale of the basin. The use of the S-D SWB in the solution of similar inverse problems may be pivotal to the future management of salt-affected basins and the understanding of vegetation–water relations in drylands. Also, it is interesting to note that soil salinization, acting as an aridity enhancer, could play a crucial role in many aspects of vegetation dynamics at the catchment scale and above, including the occurrence of fires.

Finally, we have seen that salinity limits $ET$ by making it energetically disadvantageous to extract water from the soil. At the same time, water vapor is a powerful greenhouse gas. In light of its effect on $ET$, salinity may affect climate in a radically different way from other forms of aridity—which substantially tend to enhance the concentration of water vapor in the atmosphere. This long-term feedback of salinization on climate may require a better investigation in the future.

Materials and Methods

Global Appraisal of River-Basin Salinization.

Soil-salinity data expressed as electric conductivity (dS/m) of the saturated soil paste (${\mathrm{E}\mathrm{C}}_e$) were obtained from the HWSD (34), a global dataset including soil characteristics for both the topsoil (0 to 30 cm) and the subsoil (30 to 100 cm). Each pixel (30″ $\times$ 30″) of the HWSD is divided into up to nine soil units (sublayers), identifying the share (percent) of each soil component, such as clay, silt, or sand. Salinity in the topsoil and subsoil was inferred as a weighted average of the different soil units and used to determine the mean soil salinity at each pixel, ${\mu }_C$, as a weighted average of salinity in the topsoil and the subsoil (34, 60). Catchment-scale salinity, ${\hat{\mu }}_{C,i}$, was then obtained as the spatially averaged value of ${\mu }_C$ over each basin $i$. Our classification of saline basins is based on the definition of salt-affected soil of the Soil Science Society of America (ref. 61; i.e., a soil is regarded as saline if ${\mathrm{E}\mathrm{C}}_e\ge 2$ dS/m at 25 °C) and the percentage of basin area that can be defined as salt-affected relying on the same definition. For example, a basin is classified as unaffected if less then 20% of its area can be classified as saline—namely, if the average areal salinity is at $\le 0.4$ dS/m. Based on these criteria, basins were classified in: unaffected (${\hat{\mu }}_{C,i}<0.4$ dS/m, i.e., less then 20% of the basin area is saline), slightly affected (0.4 dS/m $\le {\hat{\mu }}_{C,i}<$ 0.75 dS/m, i.e., the saline fraction of the basin area is between 20% and 37.5%), moderately affected (0.75 dS/m $\le {\hat{\mu }}_{C,i}<$ 1 dS/m; between 37.5% and 50% of the basin area is saline); affected (1 dS/m $\le {\hat{\mu }}_{C,i}<$ 1.5 dS/m; between 50% and 75% of the basin area is saline), and highly affected (${\hat{\mu }}_{C,i}\ge$ 1.5 dS/m; more than 75% of the basin area is saline), as shown in Fig. 1 A and B.

Long-Term Catchment-Scale Water Budget from AWAP Data.

The AWAP (42) gridded dataset is obtained by incorporating high-temporal-resolution (30 min) in situ data from the automated weather stations of the ADAM into a simple water-balance model (WaterDyn; ref. 43). We used run 26j, supported by the last version of WaterDyn (26M). This version of the AWAP dataset relies on bias-corrected solar-radiation data. Daily AWAP data are projected onto an equirectangular 5-km grid across Australia and are available from 1900 to present. Here, long-term averages are calculated over the period 1950 to 2017, corresponding to the time span with the maximum station/data coverage over the region. In AWAP, precipitation, solar radiation, and temperature data from ADAM are used to force WaterDyn to obtain water fluxes. Evapotranspiration ($ET$) is obtained as the sum of soil evaporation ($E$) and plant transpiration ($T_r$). $E$ is obtained by using the Priestley–Taylor method (62), while $T_r$ is calculated as the minimum of an energy-limited $T_r$ (from Priestley–Taylor) and a water-limited $T_r$ proportional to soil moisture. As a result, the AWAP dataset does not explicitly incorporate the effects of salinity on $T_r$ and the hydrological partitioning. The closure of the water balance was validated against multidecadal records of daily outflow from approximately 200 nominally unimpaired gauged catchments (43). Soil properties (saturated volumetric water content, soil depth, and saturated hydraulic conductivity) were parametrized through pedometric functions (63, 64) based on data from the Digital Atlas of Australian Soils (65) and do not account for landscape processes such as salinization and erosion (63, 64).

Statistical Analysis and Hypothesis Testing.

A 2D two-sample generalization of the KS test (Fasano and Franceschini’s test; ref. 46) was adopted here to verify whether the observed long-term water budgets of unaffected and affected Australian catchments (Fig. 1 D and E) belong to the same parent probability distribution. With this goal, we considered the water budget in the Budyko’s space and applied the test to evaluate the distributions of evaporative index, $⟨ET⟩$/$⟨R⟩$, and the dryness index, $D_I$. Our objective was to test whether the sample joint distributions of $⟨ET⟩$/$⟨R⟩$ and $D_I$ for affected and unaffected basins are drawn from the same underlying distribution. The 2D-KS compares two 2D probability distributions and estimates the bidimensional KS statistic, $Z_n$ (a function of the supremum of the absolute distance between the two samples’ cumulative density functions). The statistic $Z_n$ was then compared to the critical value $Z_{n,SL}$ depending on the sample size and the confidence level (here set to be $95\%$). The null hypothesis (i.e., the samples belong to the same distribution) is verified if $Z_n\le Z_{n,SL}$. The 2D-KS test allowed us to reject the null hypothesis at the $95\%$ confidence level, suggesting that the observed soil water balance of salt-affected and unaffected basins was drawn from different parent distributions.

A Stochastic Formulation of the Soil Water Balance of Saline River Basins.

Following the approach proposed in ref. 13, the soil water balance was initially formulated at the daily time scale, for a surface soil layer of thickness $Z_r$, soil porosity $n$, and salinization level $m$ (vertically averaged mass of soluble salts in the soil), as:

$$n{Z}_r\frac{ds}{dt}=\begin{array}{c}\hfill R-\hspace{0.17em}ET\left(s,C\right)\hspace{0.17em}-\hspace{0.17em}LQ\left(s\right).\hfill \end{array}$$ [3]

The dynamics of soil moisture, $s$, was determined by the stochastic precipitation input $R$, the evapotranspiration rate, $ET$ (here a function of both $s$ and the concentration of soluble salts in the soil, $C=m/\left(n{Z}_{r}s\right)$; ref. 13), and the rate of runoff and deep percolation, $LQ$ (modeled based on a “field-capacity threshold” as in refs. 11, 13, and 36). Precipitation was modeled as a compound Poisson process with storm-occurrence frequency $\lambda$ and exponentially distributed rainfall depths of mean $\alpha$ (11, 35, 36, 66–68). The latter is inversely proportional to the dimensionless hydrological-forcing parameter $\gamma$ (Fig. 1) through $\alpha =n{Z}_r{s}_1/\gamma$, where $s_1$ is the effective field capacity. Soil moisture, $s$, was allowed to vary between the virtual wilting point $𝜗$ (greater than or equal to the actual wilting point, $s_w=0$) and field capacity, $s_1$ (11, 13, 36). To account for the species-specific traits of salt tolerance, the dependence of $ET$ from $C$ is modeled as a step-wise linear relation, where transpiration remains unaffected by salinity up to a species-dependent concentration threshold ($C_T$) and then declines with slope $\beta$ (13, 18). Also, considering that $m$ varies over temporal scales many orders of magnitude longer than the ones characterizing the evolution of $s$, the two dynamics can be considered decoupled, and $m$ assumed approximately constant over typical hydrological scales (11, 13, 49, 50). Based on these hypotheses, we solved the stochastic daily soil-moisture balance in Eq. 3 at steady-state for fixed value of $m$, to obtain the probability density function $p\left(s|m\right)$, and the long-term mean $⟨s|m⟩$ of the soil water content conditional to a given degree of soil salinization (13, 67). The mean effective relative soil moisture was then inferred through the property of linearity of expectation as $⟨x|m⟩$ = $\left(⟨s|m⟩-𝜗\right)/\left(s_1-𝜗\right)$ and used to obtain the salinity-dependent, long-term soil water balance of Eq. 1.

Model Parameter Estimation.

Hydro-climatic parameters such as the average rainfall depth per event $\alpha$ and the precipitation frequency $\lambda$ were directly inferred from AWAP data. The level of salinization of the basin ($m$) and plant salt-tolerance parameters ($\beta$ and $C_T$) in Fig. 2 C–F were estimated based on a classic bootstrapping procedure (69) in which 1,000 subsamples, each one containing two-thirds of the catchments from each salinization class (affected or slightly affected), are randomly resampled. For each subsample $j$, a set of parameters (${\left\{m,C_T,\beta \right\}}_j$) was inferred by fitting of long-term soil water balance in Eq. 1 to observations through a Levenberg–Marquardt algorithm (nonlinear least-squares fitting). To reduce the size of the parametric space, the different parameters were constrained to fall into physically realistic ranges. In particular, 0 $\le C_T\le$ 20 g/L, 0 $\le \beta \le$ 1 L/g, and 0 $\le m\le$ 2,000 g/${\mathrm{m}}^2$. The bootstrapping procedure was repeated across all of the subsamples, ultimately obtaining the expected values of the different parameters as an average of the subsample estimates ($\widehat{\mu }=\frac{1}{N}{\sum }_{j=1}^N{\mu }_j$ with N = 1,000 and $\mu$ indicating a generic parameter). We found that more than $95\%$ of the 1,000 estimates of $m$, $C_T$, and $\beta$ fall within the interval $\left[\widehat{\mu }-5\%\widehat{\mu },\widehat{\mu }+5\%\widehat{\mu }\right]$, demonstrating the robustness of the salinity-dependent theoretical model introduced here in reproducing the long-term soil water balance of salt-affected river basins (70). The average values of soil properties ($n=0.4$, $s_1=0.85$, and $Z_r=35$ cm) were selected as representing the best fit of the classic Budyko’s curve (36) and in agreement with root surveys in water-limited ecosystems (55, 56). This represents a conservative choice for Australian soils, given that a deeper root depth would increase the fraction of precipitation lost to $ET$, further enhancing the discrepancy between observed and predicted water balance in absence of salinity effects.

Data Availability.

The salinity data used in the global assessment of river-basin salinization were obtained from the FAO HWSD (Version 1.2) (34, 71) and are publicly available from the FAO repository at http://www.fao.org/soils-portal/soil-survey/soil-maps-and-databases/harmonized-world-soil-database-v12/en/. Watershed boundaries were provided by the HydroSHEDS project and are available at https://www.hydrosheds.org. Land-use data from ABARES can be obtained at https://www.agriculture.gov.au/abares. The AWAP dataset is available on request from the Commonwealth Scientific and Industrial Research Organisation (https://www.csiro.au/).